The Degradation Prediction of Proton Exchange Membrane Fuel Cell Performance Based on a Transformer Model
Abstract
1. Introduction
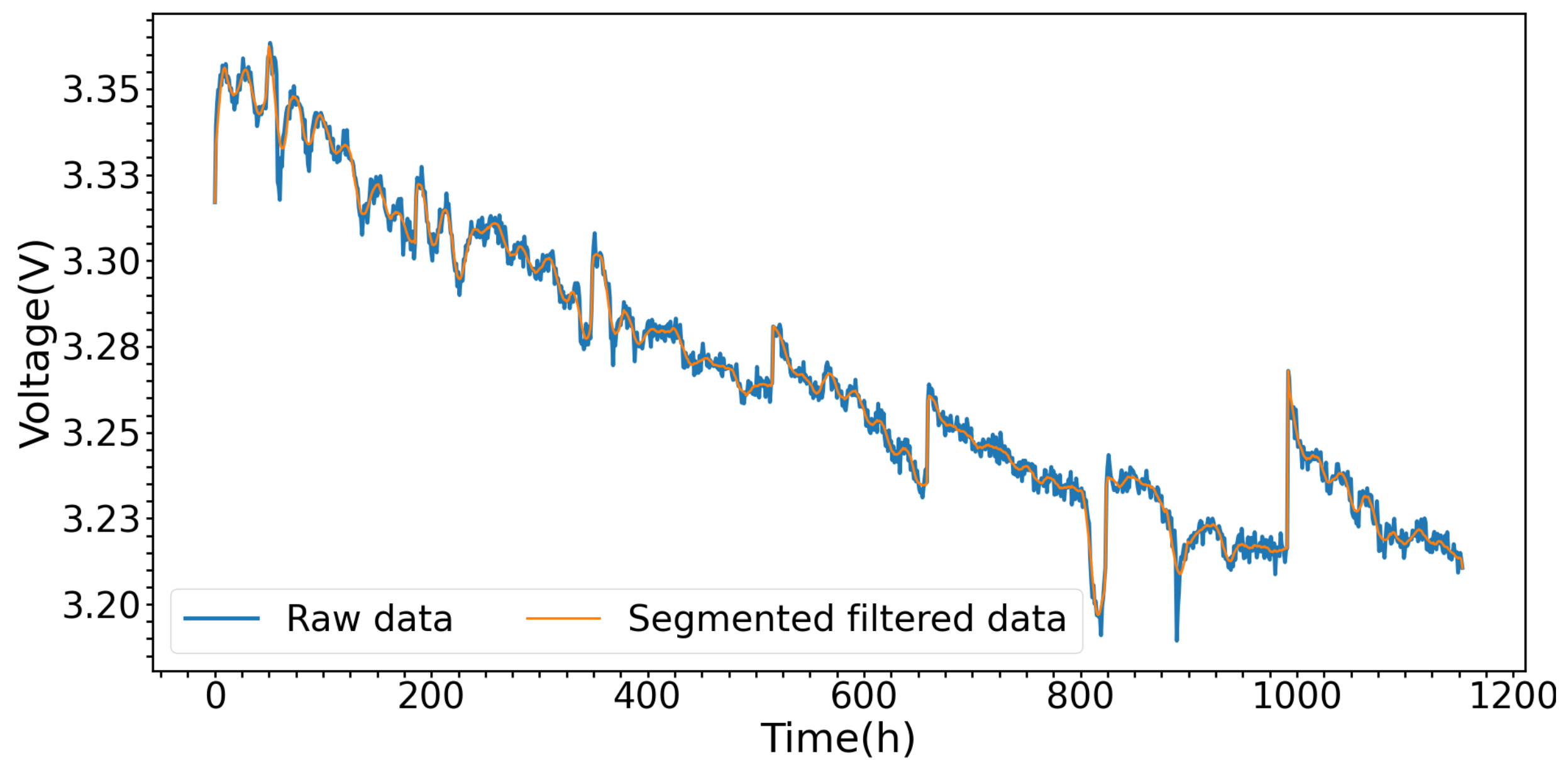
- Taking the moment at which the recovery of the reversible voltage loss takes place as the boundary point, the fuel cell aging data are segmented and filtered to retain important information while filtering out noise effectively.
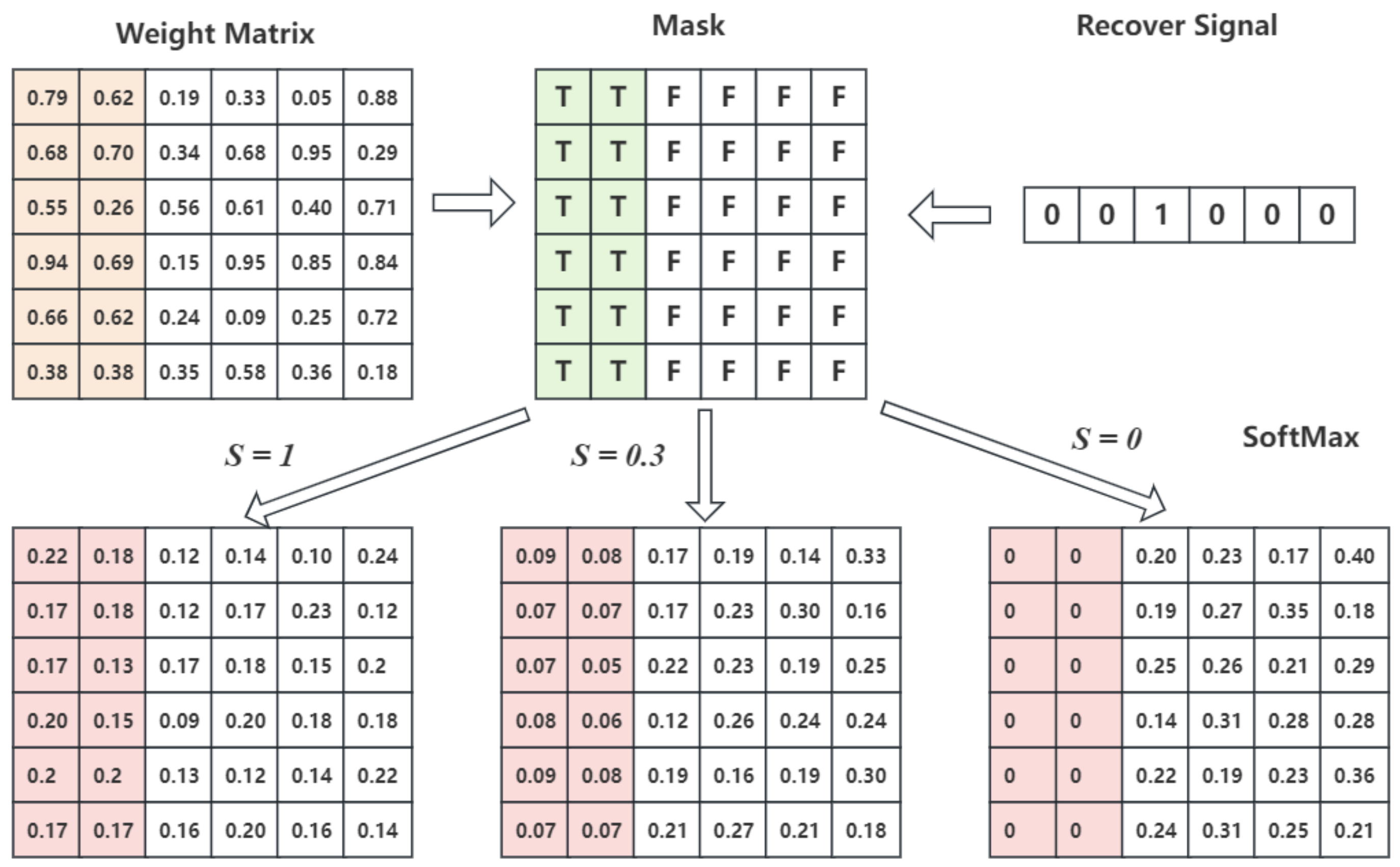
- When the recovery of reversible voltage loss occurs, it is used as input for the model, and the information before the recovery of reversible voltage loss is masked, thereby improving the model performance.
- The Transformer model is used to predict the performance degradation of fuel cells, and the influencing effects of the masking degree on the model performance are studied.
2. Method
2.1. Fuel Cell Aging Experiment
2.2. Data Preprocessing
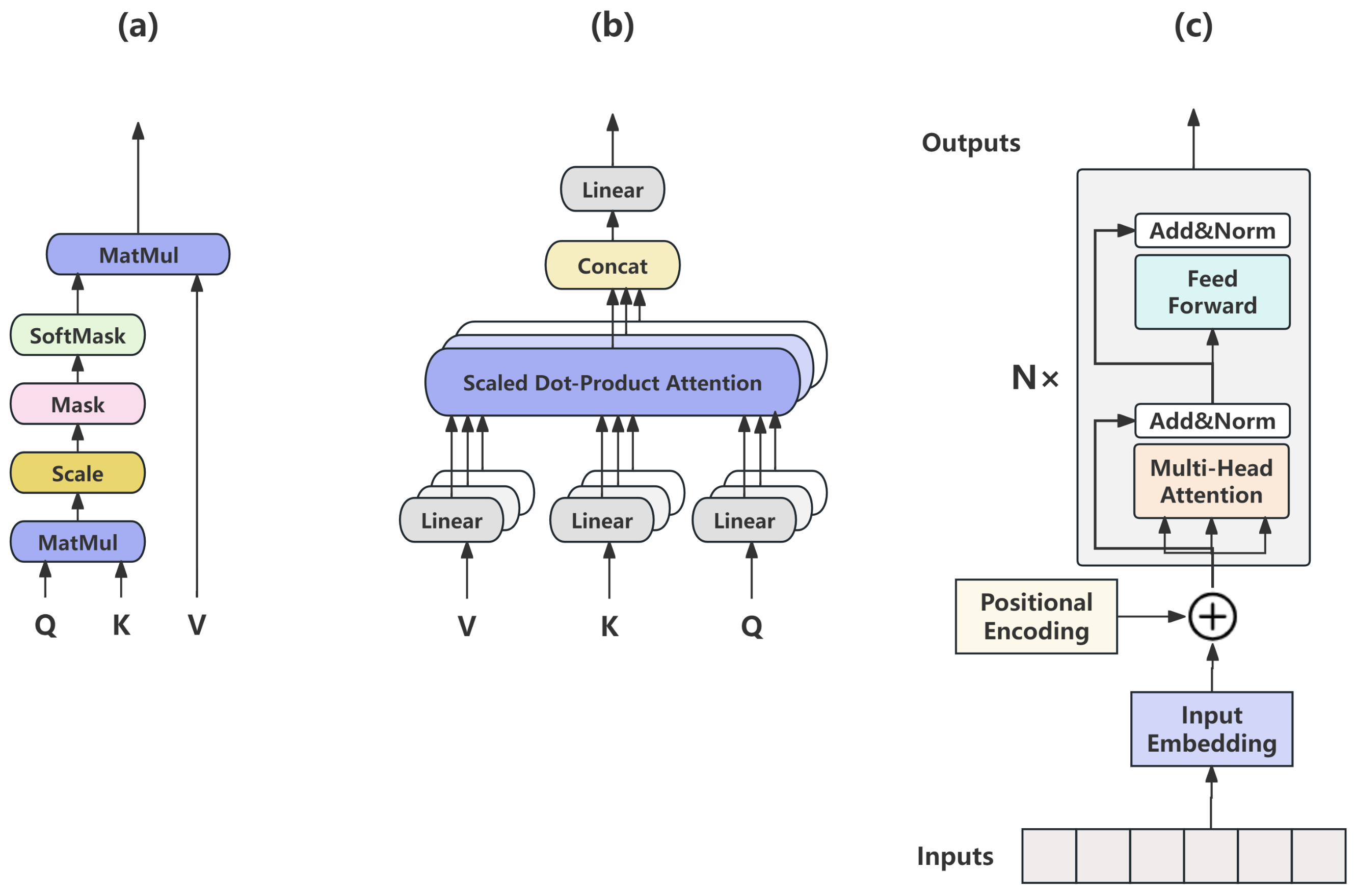
2.3. Transformer
2.4. Model
2.5. Evaluation Indicators for Prediction Results
3. Results and Discussion
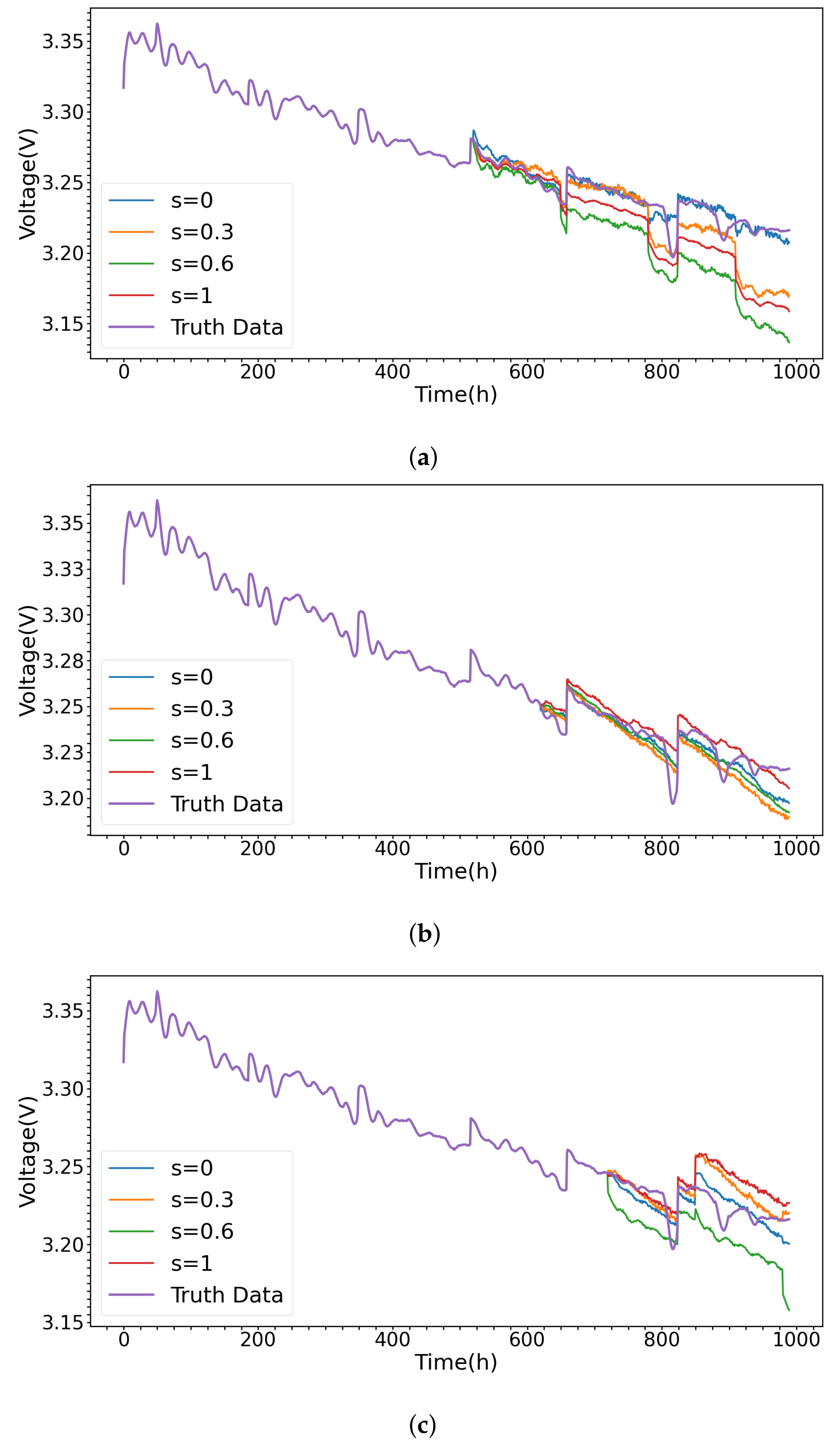
3.1. The Influence of Masking Degree s on Model Prediction Results
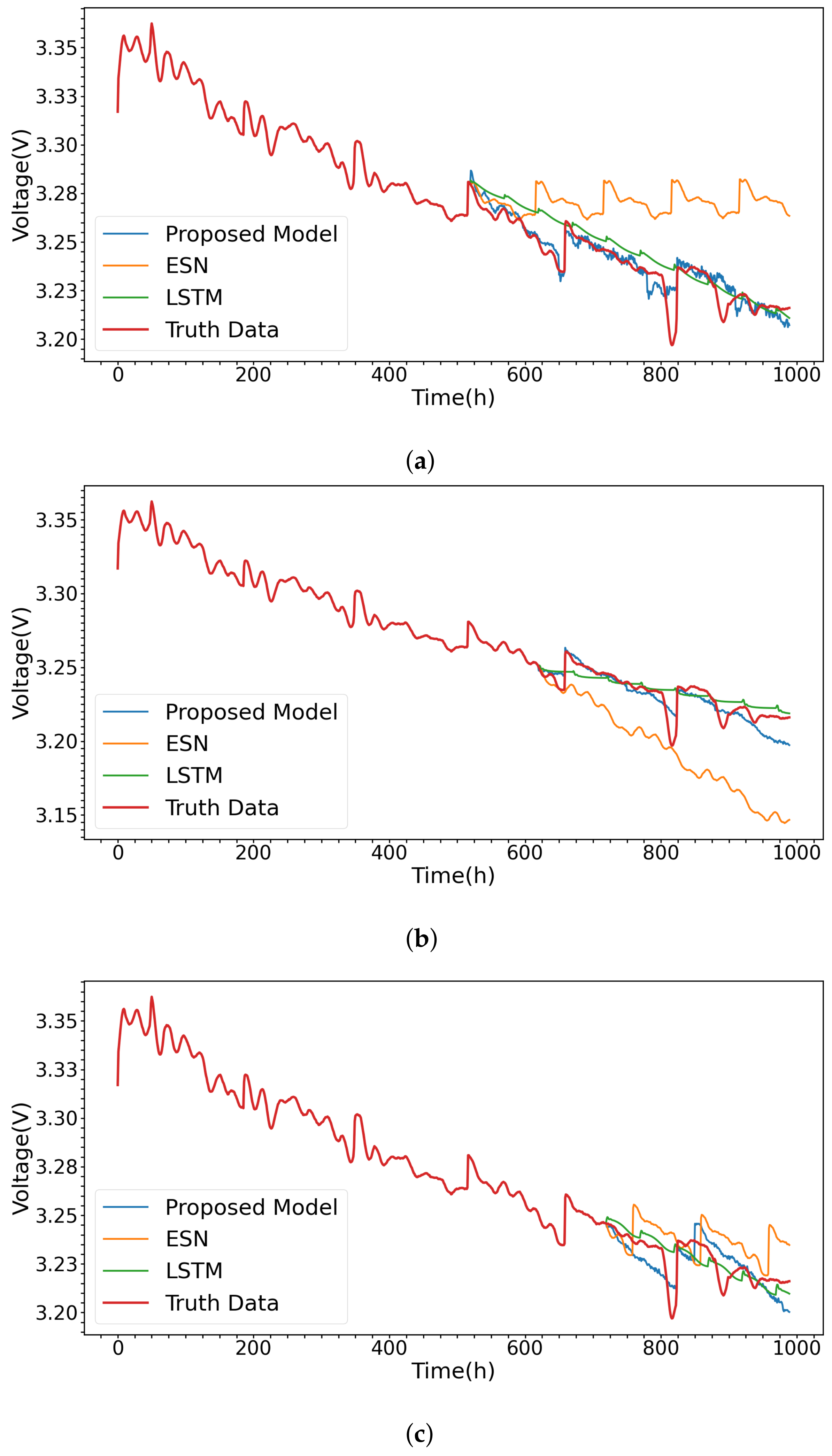
3.2. Comparison of Predictive Performance for Different Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, S.; Yang, M.; Sun, C.; Xu, S. Liquid water characteristics in the compressed gradient porosity gas diffusion layer of proton exchange membrane fuel cells using the lattice boltzmann method. Energies 2023, 16, 6010. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, Z.; Chen, W. Life prediction based on ds elm for pemfc. Energies 2019, 12, 3752. [Google Scholar] [CrossRef]
- Barzegari, M.M.; Rahgoshay, S.M.; Mohammadpour, L.; Toghraie, D. Performance prediction and analysis of a dead-end pemfc stack using data-driven dynamic model. Energy 2019, 188, 116049. [Google Scholar] [CrossRef]
- Tang, X.; Yang, M.; Shi, L.; Hou, Z.; Xu, S.; Sun, C. Adaptive state-of-health temperature sensitivity characteristics for durability improvement of pem fuel cells. Chem. Eng. J. 2024, 491, 151951. [Google Scholar] [CrossRef]
- Ma, R.; Xie, R.; Xu, L.; Huangfu, Y.; Li, Y. A hybrid prognostic method for pemfc with aging parameter prediction. IEEE Trans. Transp. Electrif. 2021, 7, 2318–2331. [Google Scholar] [CrossRef]
- Li, H.; Liu, L.; Zhang, L.; Xie, L.; Chen, Q. A fusion intelligent degradation interval prediction method based on hybrid health indicator for proton exchange membrane fuel cells. IEEE Trans. Transp. Electrif. 2024, in press. [CrossRef]
- Zhang, H.; Sun, C. Cost-effective iron-based aqueous redox flow batteries for large-scale energy storage application: A review. J. Power Sources 2021, 493, 229445. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Y.; Xu, S. Temperature sensitivity characteristics of pem fuel cell and output performance improvement based on optimal active temperature control. Int. J. Heat Mass Transf. 2023, 206, 123966. [Google Scholar] [CrossRef]
- Rao, M.; Wang, L.; Chen, C.; Xiong, K.; Li, M.; Chen, Z.; Dong, J.; Xu, J.; Li, X. Data-driven state prediction and analysis of sofc system based on deep learning method. Energies 2022, 15, 3099. [Google Scholar] [CrossRef]
- Kanani, H.; Shams, M.; Hasheminasab, M.; Bozorgnezhad, A. Model development and optimization of operating conditions to maximize pemfc performance by response surface methodology. Energy Convers. Manag. 2015, 93, 9–22. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, H.; Zhu, C. A short-term and long-term prognostic method for pem fuel cells based on gaussian process regression. Energies 2022, 15, 4844. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Y.; Xu, S. Experimental study of pem fuel cell temperature characteristic and corresponding automated optimal temperature calibration model. Energy 2023, 283, 128456. [Google Scholar] [CrossRef]
- Mayur, M.; Gerard, M.; Schott, P.; Bessler, W.G. Lifetime prediction of a polymer electrolyte membrane fuel cell under automotive load cycling using a physically-based catalyst degradation model. Energies 2018, 11, 2054. [Google Scholar] [CrossRef]
- Xiao, L.; Bian, M.; Sun, Y.; Yuan, J.; Wen, X. Transport properties evaluation of pore-scale gdls for pemfc using orthogonal design method. Appl. Energy 2024, 357, 122445. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, K.; Li, J.; Wei, Z. A performance degradation prediction model for pemfc based on bi-directional long short-term memory and multi-head self-attention mechanism. Int. J. Hydrogen Energy 2024, 60, 133–146. [Google Scholar] [CrossRef]
- Zhao, J.; Li, S.; Tu, Z. Development of practical empirically and statistically-based equations for predicting the temperature characteristics of pemfc applied in the cchp system. Int. J. Hydrogen Energy 2024, 52, 894–904. [Google Scholar] [CrossRef]
- Hua, Z.; Zheng, Z.; Pahon, E.; Péra, M.-C.; Gao, F. A review on lifetime prediction of proton exchange membrane fuel cells system. J. Power Sources 2022, 529, 231256. [Google Scholar] [CrossRef]
- Chandesris, M.; Vincent, R.; Guetaz, L.; Roch, J.-S.; Thoby, D.; Quinaud, M. Membrane degradation in pem fuel cells: From experimental results to semi-empirical degradation laws. Int. J. Hydrogen Energy 2017, 42, 8139–8149. [Google Scholar] [CrossRef]
- Ou, M.; Zhang, R.; Shao, Z.; Li, B.; Yang, D.; Ming, P.; Zhang, C. A novel approach based on semi-empirical model for degradation prediction of fuel cells. J. Power Sources 2021, 488, 229435. [Google Scholar] [CrossRef]
- Bressel, M.; Hilairet, M.; Hissel, D.; Bouamama, B.O. Extended kalman filter for prognostic of proton exchange membrane fuel cell. Appl. Energy 2016, 164, 220–227. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Outbib, R.; Dou, M.; Zhao, D. A novel long short-term memory networks-based data-driven prognostic strategy for proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2022, 47, 10395–10408. [Google Scholar] [CrossRef]
- Zuo, J.; Lv, H.; Zhou, D.; Xue, Q.; Jin, L.; Zhou, W.; Yang, D.; Zhang, C. Deep learning based prognostic framework towards proton exchange membrane fuel cell for automotive application. Appl. Energy 2021, 281, 115937. [Google Scholar] [CrossRef]
- Benaggoune, K.; Yue, M.; Jemei, S.; Zerhouni, N. A data-driven method for multi-step-ahead prediction and long-term prognostics of proton exchange membrane fuel cell. Appl. Energy 2022, 313, 118835. [Google Scholar] [CrossRef]
- Mezzi, R.; Yousfi-Steiner, N.; Péra, M.C.; Hissel, D.; Larger, L. An echo state network for fuel cell lifetime prediction under a dynamic micro-cogeneration load profile. Appl. Energy 2021, 283, 116297. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, Z.; Outbib, R. Adaptive prognostic of fuel cells by implementing ensemble echo state networks in time-varying model space. IEEE Trans. Ind. Electron. 2019, 67, 379–389. [Google Scholar] [CrossRef]
- Zhou, D.; Gao, F.; Breaz, E.; Ravey, A.; Miraoui, A. Degradation prediction of pem fuel cell using a moving window based hybrid prognostic approach. Energy 2017, 138, 1175–1186. [Google Scholar] [CrossRef]
- Cheng, Y.; Zerhouni, N.; Lu, C. A hybrid remaining useful life prognostic method for proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2018, 43, 12314–12327. [Google Scholar] [CrossRef]
- Gouriveau, R.; Hilairet, M.; Hissel, D.; Jemei, S.; Jouin, M.; Lechartier, E.; Morando, S.; Pahon, E.; Pera, M.C.; Zerhouni, N. IEEE phm 2014 data challenge: Outline, experiments, scoring of results, winners. In Proceedings of the IEEE Conference on Prognostics and Health Management, Cheney, WA, USA, 22–25 June 2014; pp. 1–6. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I.; Kaiser, Ł. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Tang, X.; Shi, L.; Zhang, Y.; Li, B.; Xu, S.; Song, Z. Degradation adaptive energy management strategy for FCHEV based on the Rule-DDPG method: Tailored to the current SOH of the powertrain. IEEE Trans. Transp. Electrif. 2024, in press. [CrossRef]



| Start Point Time | 520 h | 620 h | 720 h | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE | |
| 0 | 0.006 | 0.004 | 0.001 | 0.007 | 0.005 | 0.001 | 0.008 | 0.007 | 0.002 |
| 0.3 | 0.020 | 0.014 | 0.004 | 0.011 | 0.008 | 0.003 | 0.013 | 0.009 | 0.003 |
| 0.6 | 0.037 | 0.030 | 0.009 | 0.009 | 0.007 | 0.002 | 0.023 | 0.021 | 0.007 |
| 1 | 0.026 | 0.020 | 0.006 | 0.008 | 0.006 | 0.002 | 0.017 | 0.013 | 0.004 |
| Start Point Time | 520 h | 620 h | 720 h | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE |
| Proposed | 0.006 | 0.004 | 0.001 | 0.007 | 0.005 | 0.001 | 0.008 | 0.007 | 0.002 |
| ESN | 0.036 | 0.032 | 0.010 | 0.042 | 0.037 | 0.011 | 0.017 | 0.014 | 0.004 |
| LSTM | 0.011 | 0.008 | 0.003 | 0.009 | 0.006 | 0.002 | 0.009 | 0.006 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Mei, J.; Tang, X.; Jiang, J.; Sun, C.; Song, K. The Degradation Prediction of Proton Exchange Membrane Fuel Cell Performance Based on a Transformer Model. Energies 2024, 17, 3050. https://doi.org/10.3390/en17123050
Meng X, Mei J, Tang X, Jiang J, Sun C, Song K. The Degradation Prediction of Proton Exchange Membrane Fuel Cell Performance Based on a Transformer Model. Energies. 2024; 17(12):3050. https://doi.org/10.3390/en17123050
Chicago/Turabian StyleMeng, Xuan, Jian Mei, Xingwang Tang, Jinhai Jiang, Chuanyu Sun, and Kai Song. 2024. "The Degradation Prediction of Proton Exchange Membrane Fuel Cell Performance Based on a Transformer Model" Energies 17, no. 12: 3050. https://doi.org/10.3390/en17123050
APA StyleMeng, X., Mei, J., Tang, X., Jiang, J., Sun, C., & Song, K. (2024). The Degradation Prediction of Proton Exchange Membrane Fuel Cell Performance Based on a Transformer Model. Energies, 17(12), 3050. https://doi.org/10.3390/en17123050









