Innovative Multigeneration System with Heat Exchangers for Harnessing Thermal Energy from Cement Kiln Exhaust Gases
Abstract
1. Introduction
2. Materials and Methods
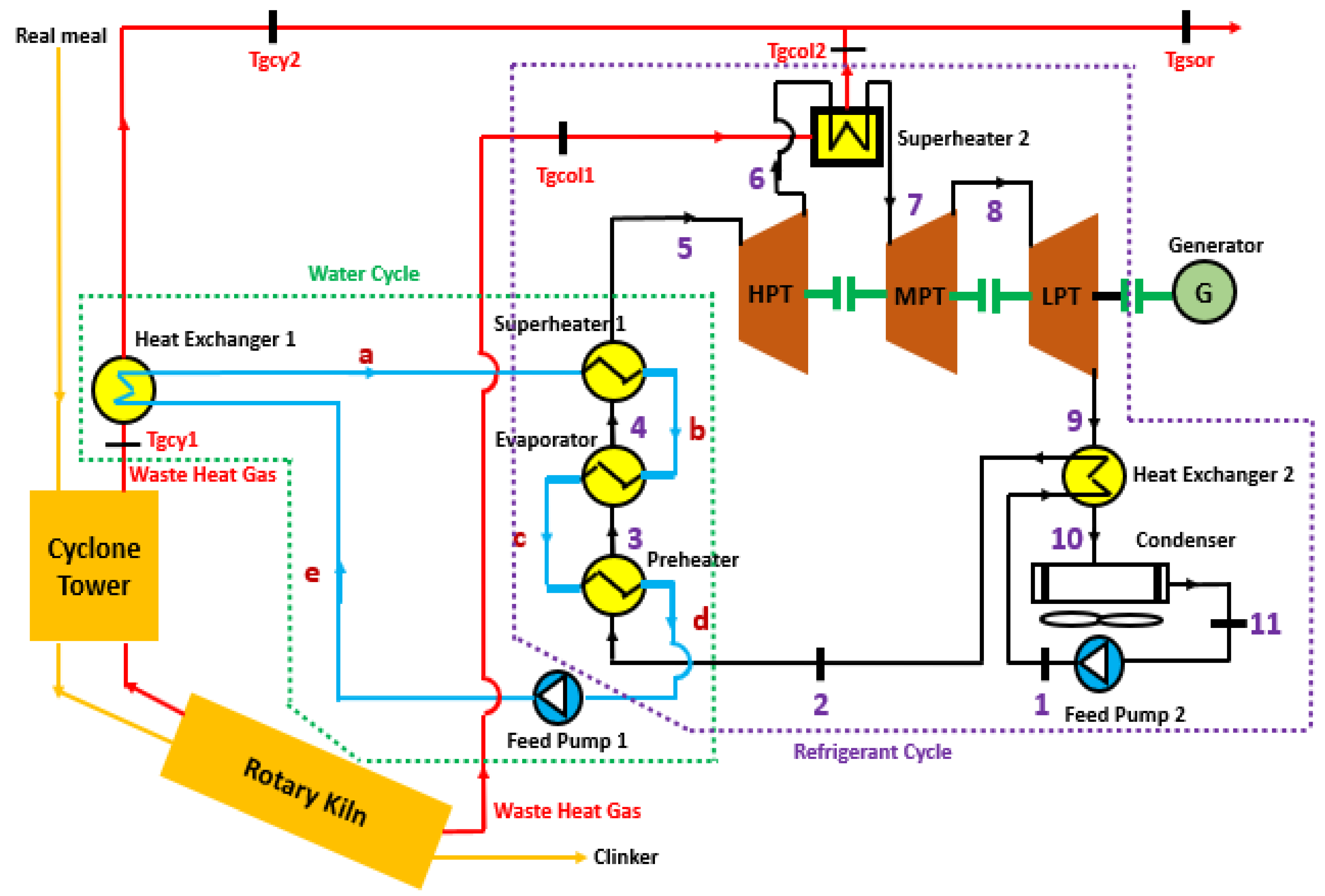
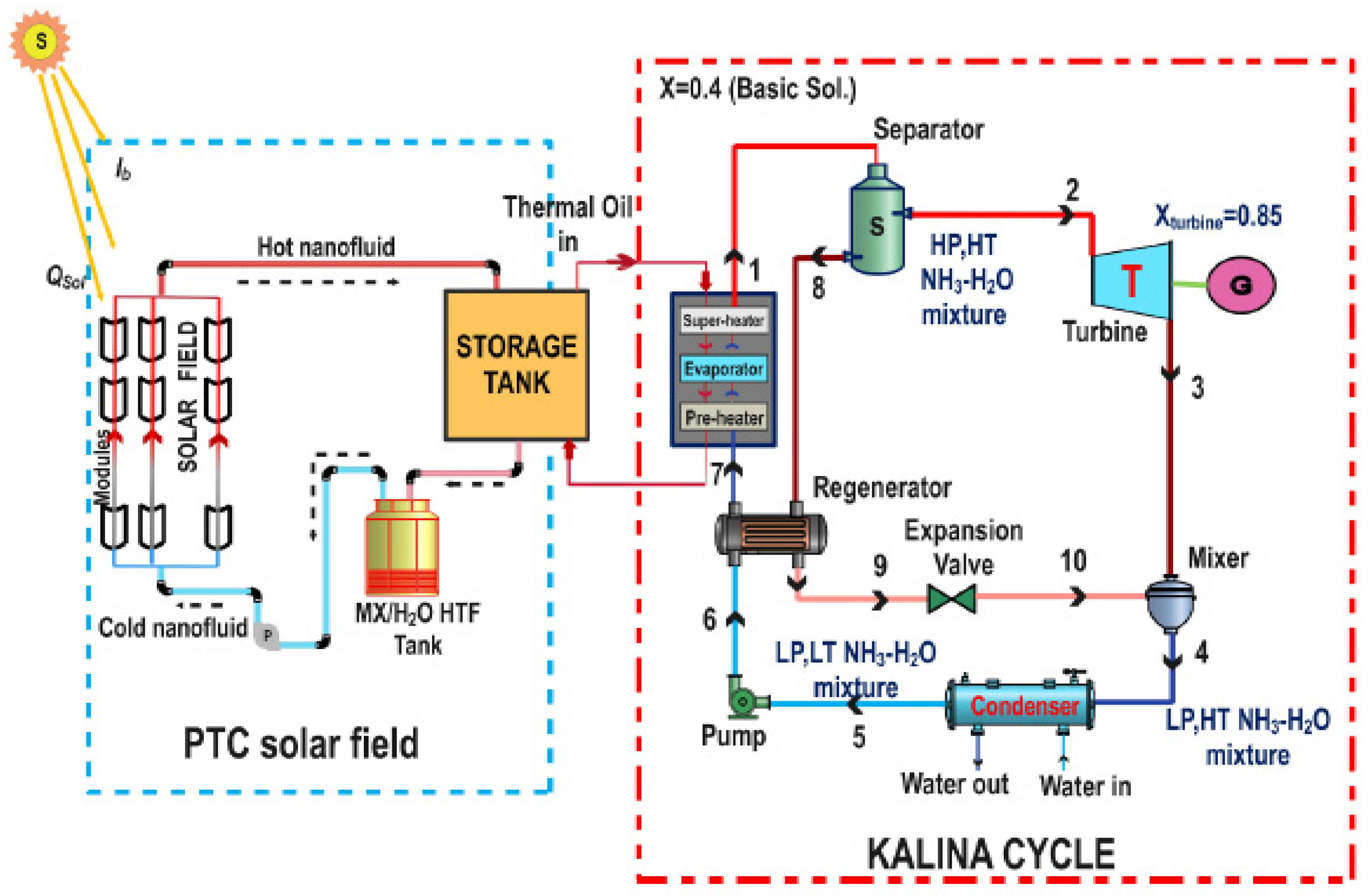
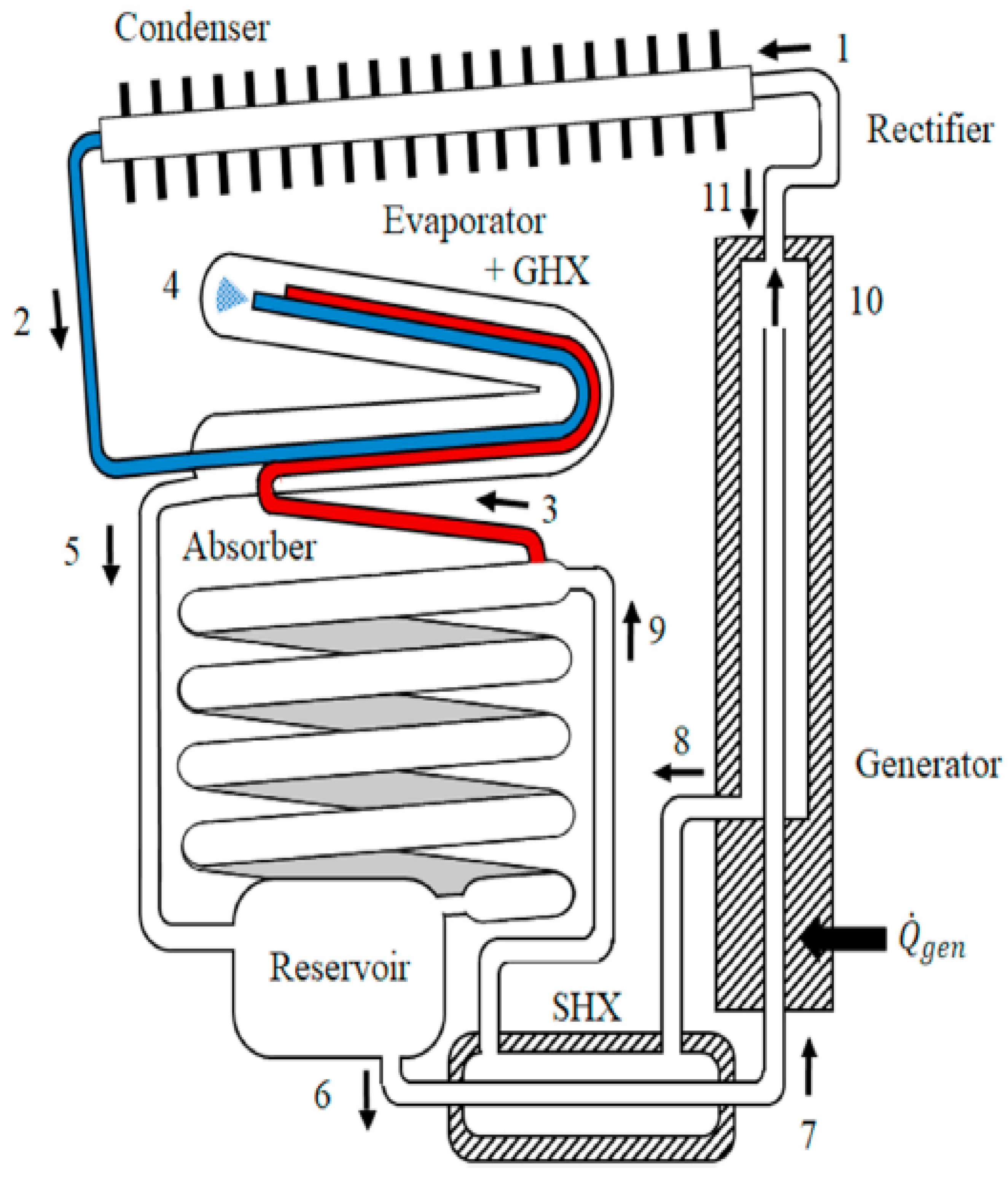
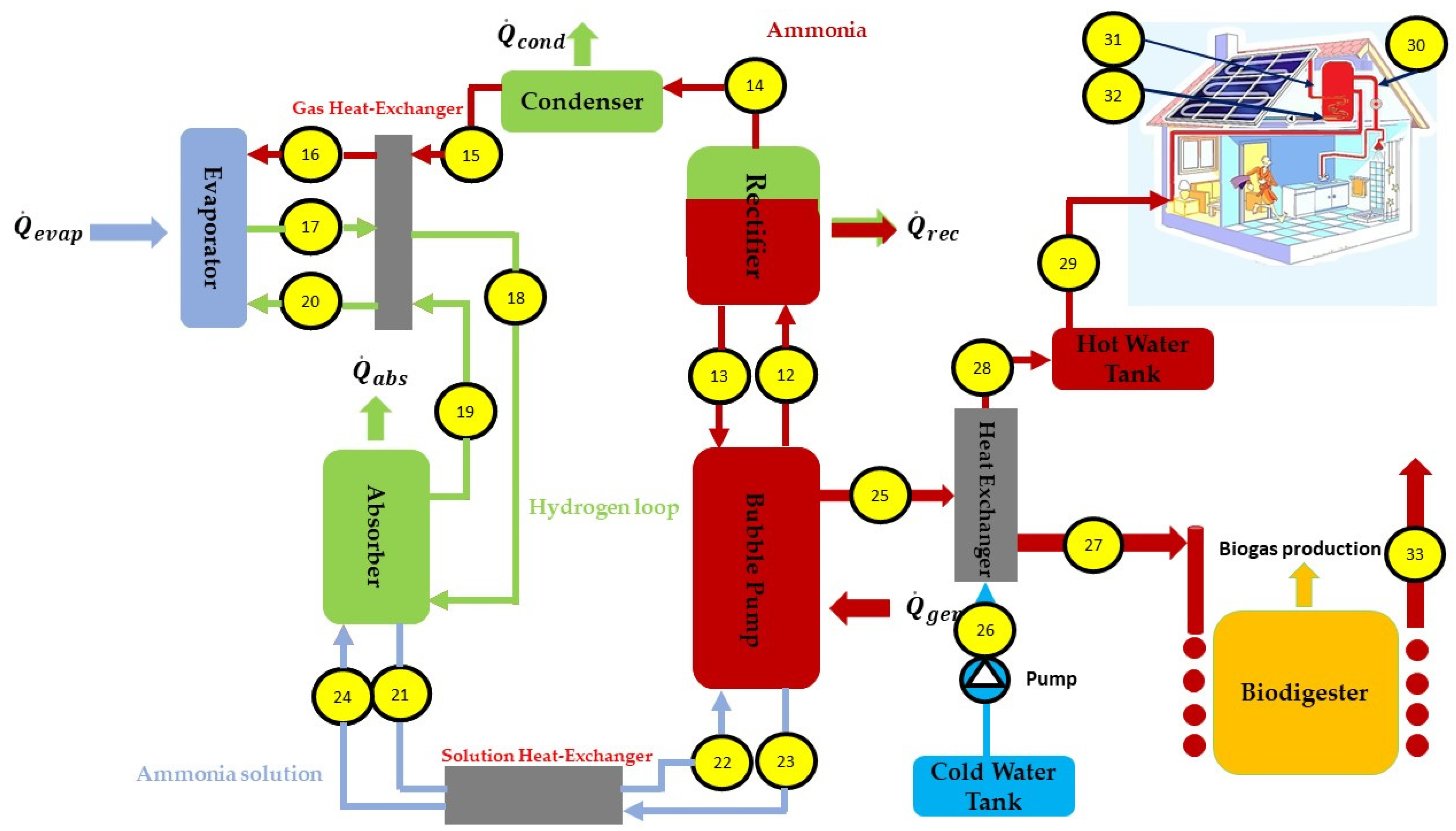
2.1. System Description
- Pump 1 is responsible for drawing the water–ammonia mixture under atmospheric conditions and transferring it to a preheater.
- Once preheated, the mixture proceeds to an evaporator, undergoing evaporation. The resulting steam is then directed to the first superheater for additional heating.
- The superheated mixture enters the high-pressure turbine, where thermal energy is converted into kinetic energy at the turbine shaft.
- After expansion in the high-pressure turbine, the steam passes through the second superheater before entering the medium-pressure turbine. This process converts thermal energy into kinetic energy, driving an electric generator.
- Following expansion in the medium-pressure turbine, the steam moves on to the low-pressure turbine, further expanding and contributing to additional electrical energy generation through coupling with the generator.
- Maintaining a constant concentration, the steam passes through a heat exchanger or recuperator, preheating the mixture from the pump.
- Exiting the recuperator, the mixture then enters the condenser. The pump then draws in the condensed mixture to repeat the cycle.
2.2. Absorption Working Fluids Selection
2.3. Benefits, Safety Risks, and Remedies of Using Ammonia
3. Modeling of the Multigeneration System
3.1. Main Assumptions
- For the Kalina Cycle, additional details are available in a previous publication [40]:
- The system is in a state of equilibrium, with no consideration given to kinetic or potential energies.
- ○
- Pump 1 operates under ambient room temperature conditions.
- ○
- Ammonia and water mixing takes place at room temperature.
- Heat losses from both the power cycle components and the surrounding environment are disregarded.
- A pinch point of 10 K is assumed for the superheaters, while a fixed efficiency of 60% is assigned to the remaining exchangers.
- Both Pump 1 and Pump 2 draw fluids at a temperature of 30 °C.
- At the inlet, the concentration is 88% for NH3 (ammonia) and 12% for water.
- For the DAR Cycle:
- -
- Temperature variations directly influence changes in the NH3 concentration.
- -
- The temperature at points 24 and 15 is equal (T24 = T15).
3.2. Mass, Energy, and Exergy Analysis
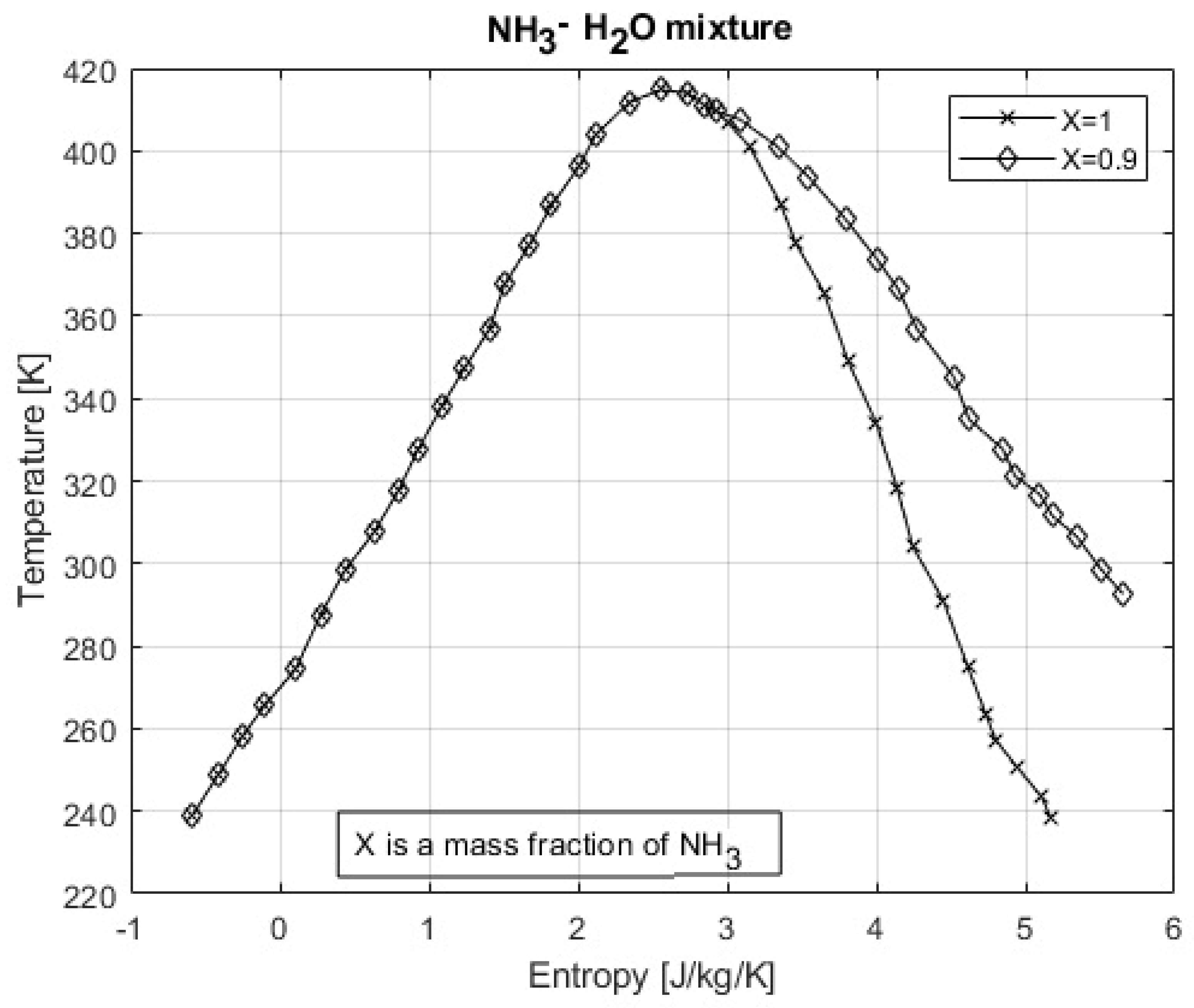
3.3. Thermodynamic Modeling of Refrigerant Mixing
4. Model Validation
4.1. Kalina Cycle System Results Validation
4.2. Comparison of DAR Cycle System Results with Similar Literature Applications
5. Results and Discussion
5.1. Data of Study
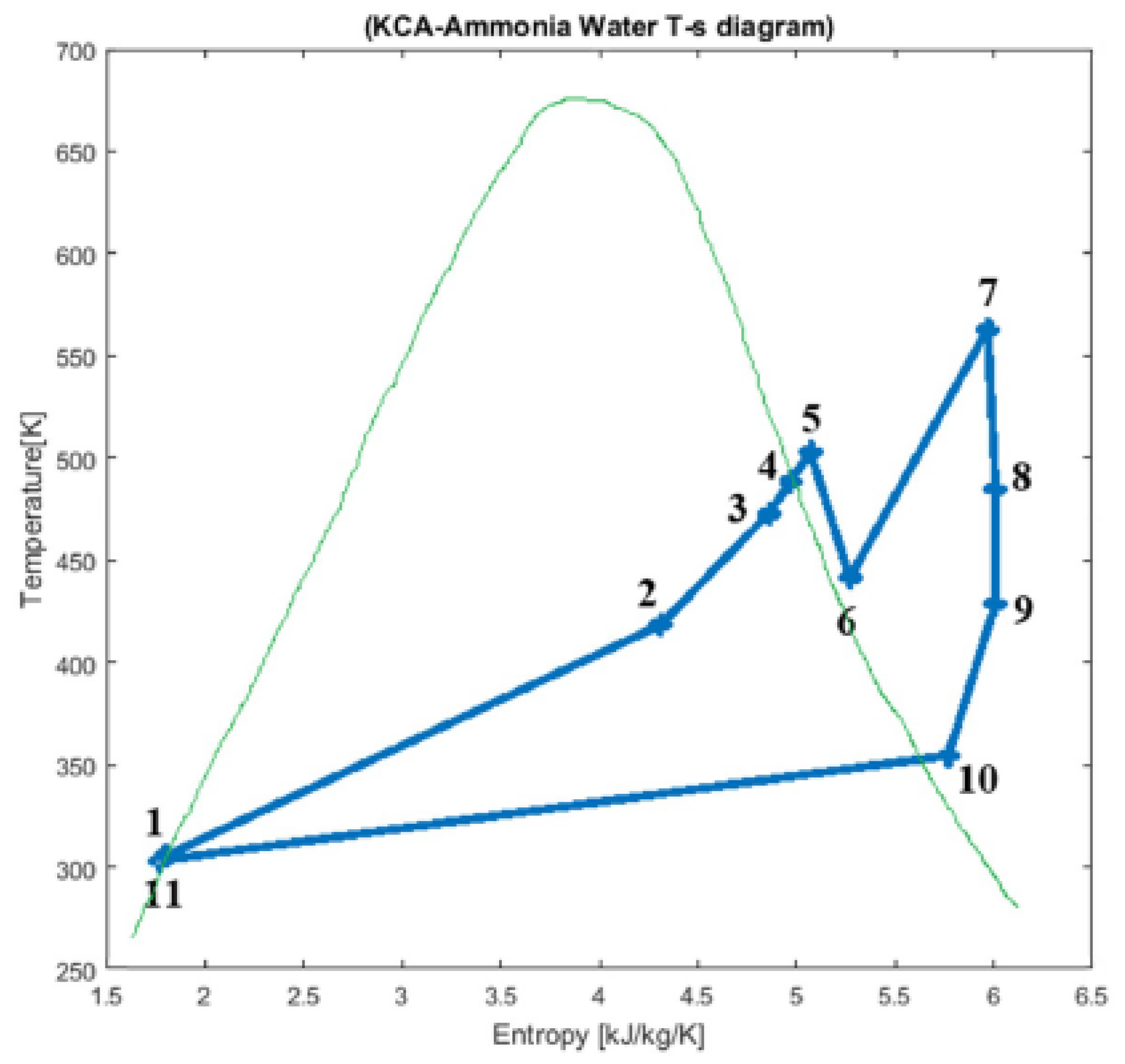
5.2. Kalina Cycle System
5.2.1. Thermodynamic Performance
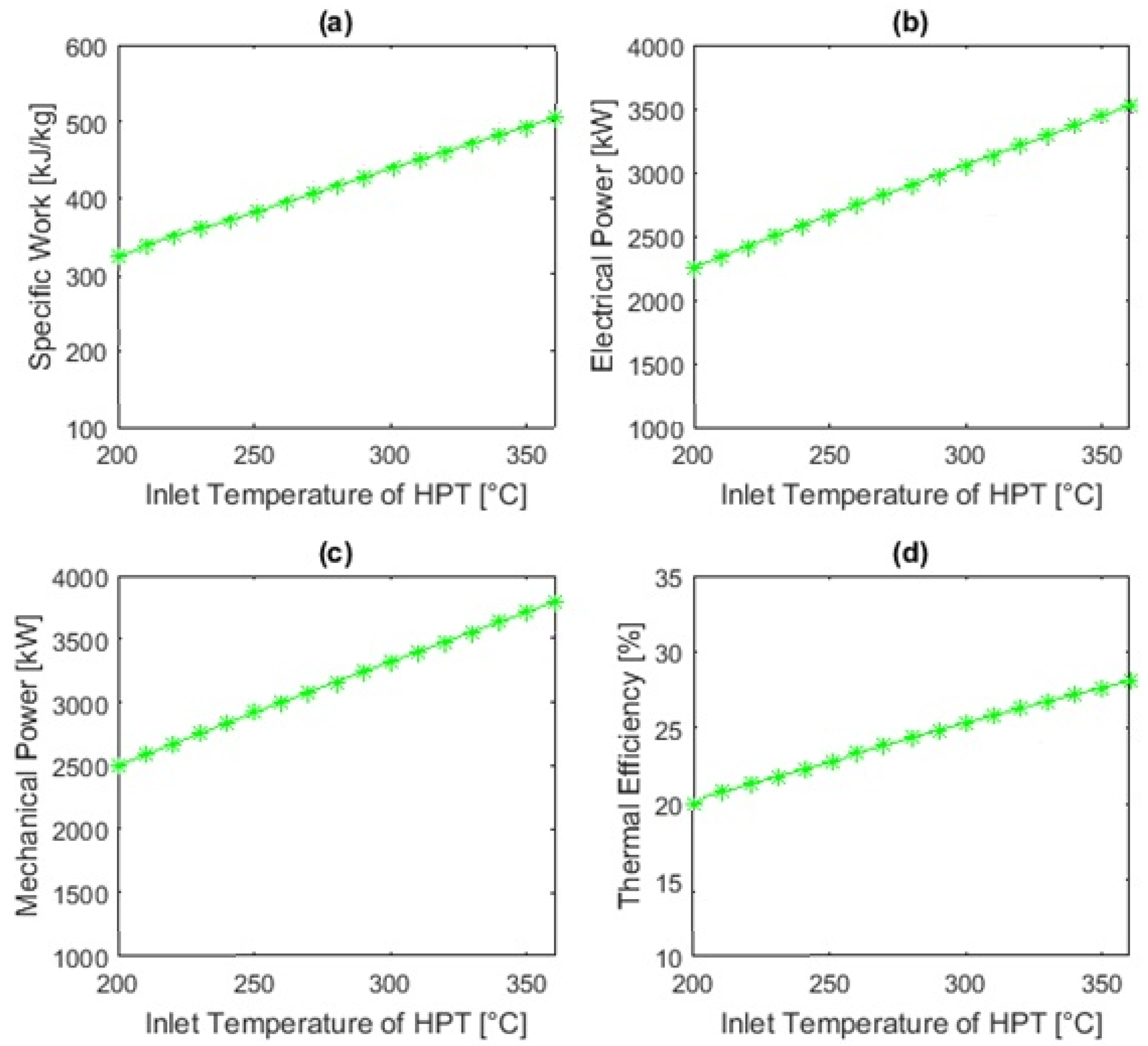
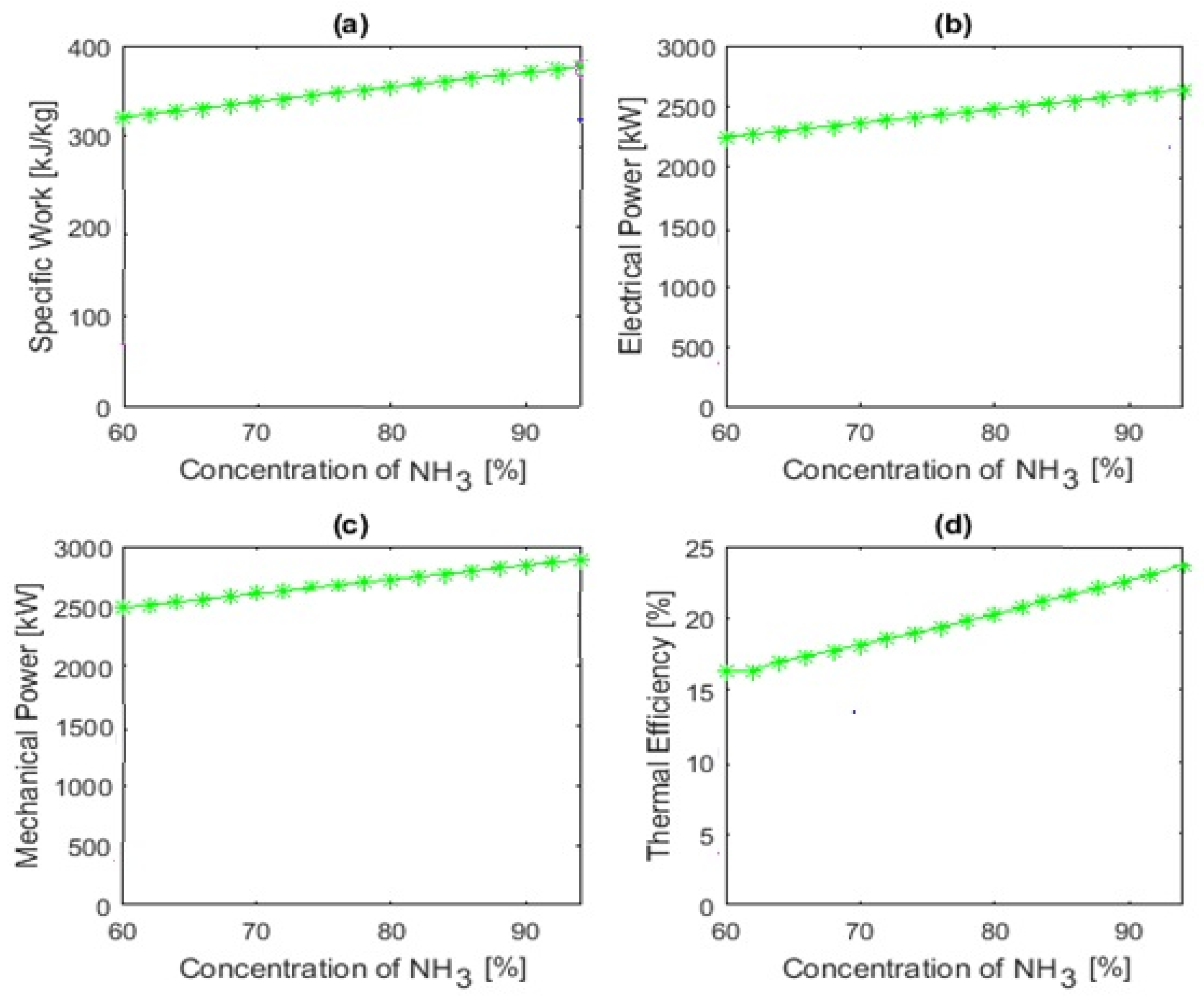
5.2.2. Sensitivity of the Kalina Cycle
5.3. DAR Cycle System
5.3.1. Thermodynamic Performance
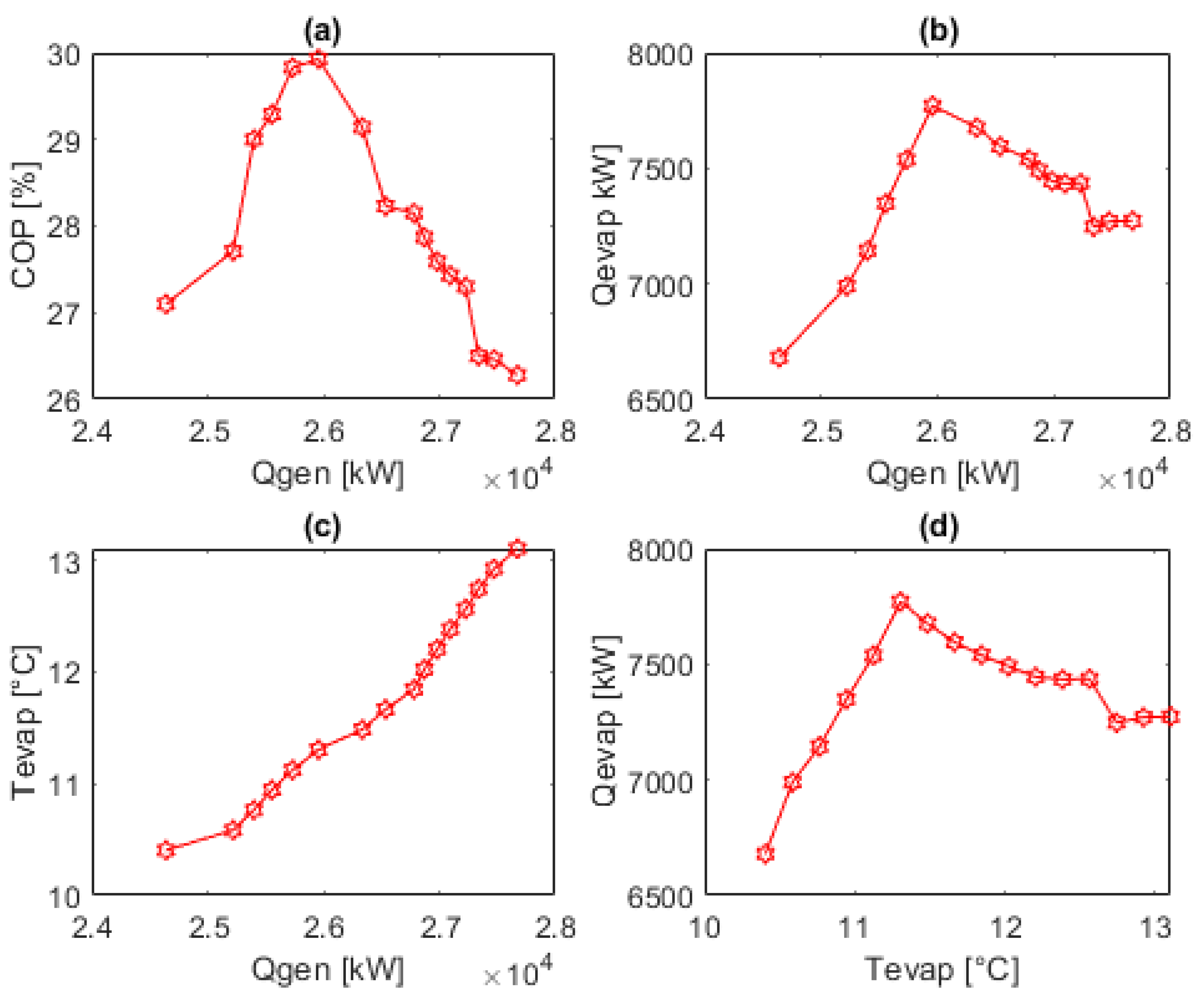
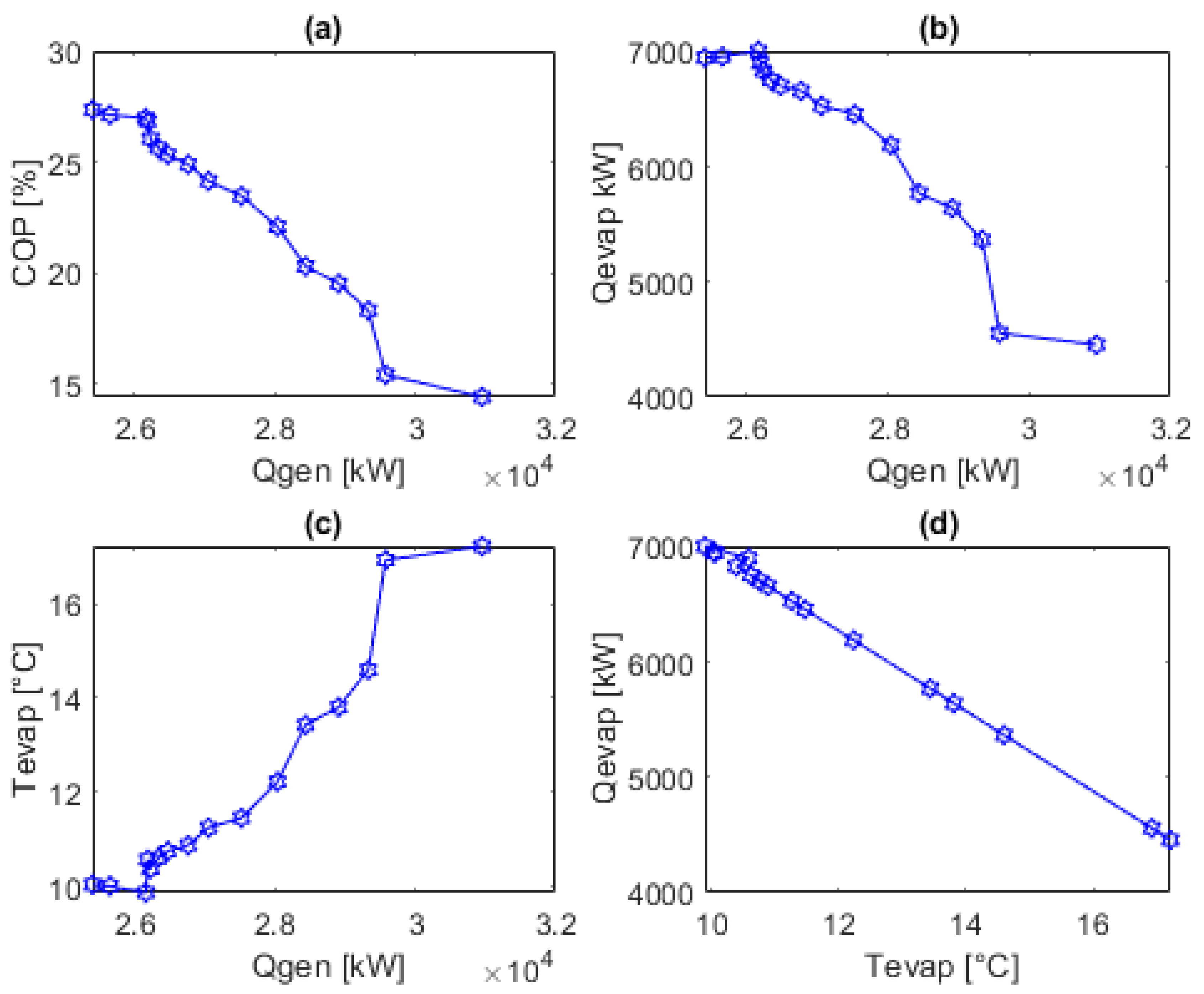
5.3.2. Sensitivity of the DAR System
5.4. Domestic Hot Water System
5.5. Biogas Production System
6. Conclusions and Perspectives
- The three turbines and two superheaters in the Kalina cycle are intended to make the system efficient.
- The energy in the hot gases was recovered in two places: the hot gases exiting the preheating tower and those exiting the clinker cooler.
- The Kalina cycle system aims to produce electricity, thanks to the recovery of the energy in the gases leaving the rotary kiln. The Kalina cycle gives an electrical power of 2565.03 kWe. The efficiencies of the two laws of thermodynamics are 22.15% and 45.12%, respectively, thermal efficiency and exergy efficiency. The model gives satisfactory results in the different sensitivity cases studied.
- The DAR cycle aims to produce cold using the energy of the gases leaving the Kalina cycle circuit.
- The gas energy rejected by the DAR cycle is used to heat domestic hot water and waste in a biodigester.
- In the case of the DAR cycle, a coefficient of performance of 0.268, an evaporation temperature of 10.57 °C, and a refrigeration capacity of 6766.023 kW were found. The study of the model’s sensitivity to generator temperature and pressure variations also gave good results. In the case of a water heating network, the hot water temperature found in the present work falls within the range of setpoint values, i.e., 40 to 50 °C (for the case of residential houses).
- In the biogas production circuit, the waste sensible heat per unit of time (thermal power), after heat exchange with the hot gases, amounts to 206.75 MW for a flow rate of 500 kg/s.
- The results of the different sub-models of this article were the subject of a comparison and validation study with data from the literature. This study, therefore, validated all the sub-models. Although the proposed multigeneration system gives promising results, it is important to analyze its critical parameters while reducing the assumptions and recalculating the optimal system parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations and Symbols
| Symbol | Signification | Unit |
| Heat Transfer Surface area | m2 | |
| Primary exergy | kJ | |
| Specific exergy | kJ/kg | |
| Dimensional factor | - | |
| Specific enthalpy | kJ/kg | |
| Global coefficient of heat transfers | kW/m2/K | |
| Mass flow rate | kg/s | |
| Thermal power | kW | |
| Exhausted gas heat transfer rate | kW | |
| Specific entropy | kJ/kg/K | |
| Temperature | K | |
| Exit gas temperature | K | |
| Variation in temperature | K | |
| Work per time unit | kJ/s | |
| NH3 concentration in the mixture | % |
| Efficiency | % | |
| Efficiency | % |
| Absorber | |
| Ambient | |
| Biogas production | |
| Condenser | |
| Evaporator | |
| Gas from cooler | |
| Exit gas from cooler before heat exchanger 2 | |
| Exit gas from cooler after heat exchanger 2 | |
| Exit gas from cyclone | |
| Exit gas from cyclone before heat exchanger 1 | |
| Exit gas from cyclone after heat exchanger 1 | |
| Generator | |
| Gas heat exchanger | |
| Heat exchanger 1 | |
| Heat exchanger 2 | |
| Heat exchanger of hot water | |
| Potential amount of heat recovery from this process | |
| Recovery of heat 1 | |
| Recovery of heat 2 | |
| Hot water | |
| Hot water tank | |
| Hot water tank 2 | |
| Inlet | |
| Isentropic, high-pressure turbine | |
| Isentropic, low-pressure turbine | |
| Isentropic, pump | |
| LMTD | Due to the Logarithmic Mean Temperature Difference |
| Outlet | |
| Pump | |
| Preheater | |
| Feed pump 1 | |
| Feed pump 2 | |
| Heat recovered amount in the regenerator | |
| Rectifier | |
| Rejected (gas rejected from the DAR cycle) | |
| Rejected (gas rejected from the domestic hot water) | |
| Solution heat exchanger | |
| Superheater 1 | |
| Superheater 2 | |
| Turbine | |
| Solid waste | |
| Solid waste before heat exchanger with hat gas | |
| Solid waste after heat exchanger with hat gas | |
| Environmental condition. |
| Concerned exergy destroyed | |
| Refers to heat transfer | |
| Refers to power |
| DAR | Diffusion–absorption refrigerant |
| GHX | Gas heat exchanger |
| HPT | High-pressure turbine |
| IEA | International Energy Agency |
| KCA | Kalina cycle (A) |
| LNG | Liquefied natural gas |
| LPT | Low-pressure turbine |
| MPT | Medium-pressure turbine |
| ORC | Organic Rankine cycle |
| RDF | Refuse-derived fuel |
| SHX | Solution heat exchanger |
References
- Mollahosseini, A.; Abdelrasoul, A.; Sheibany, S.; Amini, M.; Salestan, S.K. Renewable Energy-Driven Desalination Opportunities—A Case Study. J. Environ. Manag. 2019, 239, 187–197. [Google Scholar] [CrossRef] [PubMed]
- Ghasemiasl, R.; Khalili Abhari, M.; Javadi, M.A.; Ghomashi, H. 4E Investigating of a Combined Power Plant and Converting It to a Multigeneration System to Reduce Environmental Pollutant Production and Sustainable Development. Energy Convers. Manag. 2021, 245, 114468. [Google Scholar] [CrossRef]
- Júnior, E.P.B.; Arrieta, M.D.P.; Arrieta, F.R.P.; Silva, C.H.F. Assessment of a Kalina Cycle for Waste Heat Recovery in the Cement Industry. Appl. Therm. Eng. 2019, 147, 421–437. [Google Scholar] [CrossRef]
- Varma, G.V.P.; Srinivas, T. Parametric Analysis of Steam Flashing in a Power Plant Using Waste Heat of Cement Factory. Energy Procedia 2016, 90, 99–106. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, J.; Yang, P.; Wang, Y.; Chen, G.; Zhao, P.; Dai, Y. Comparison of Control Strategies and Dynamic Behaviour Analysis of a Kalina Cycle Driven by a Low-Grade Heat Source. Energy 2022, 242, 122958. [Google Scholar] [CrossRef]
- Hossain, M.M.; Hossain, M.S.; Ahmed, N.A.; Ehsan, M.M. Numerical Investigation of a Modified Kalina Cycle System for High-Temperature Application and Genetic Algorithm Based Optimization of the Multi-Phase Expander’s Inlet Condition. Energy AI 2021, 6, 100117. [Google Scholar] [CrossRef]
- Kumar Singh, S.; Kumar Tiwari, A.; Paliwal, H.K. Techno-Economic Assessment of Retrofitted Parabolic Trough Collector for Kalina Power Cycle. Appl. Therm. Eng. 2024, 236, 121550. [Google Scholar] [CrossRef]
- da Costa Horta, G.R.; Barbosa, E.P.; Moreira, L.F.; Arrieta, F.R.P.; de Oliveira, R.N. Comparison of Kalina Cycles for Heat Recovery Application in Cement Industry. Appl. Therm. Eng. 2021, 195, 117167. [Google Scholar] [CrossRef]
- Ma, H.; Xie, Y.; Duan, K.; Song, X.; Ding, R.; Hou, C. Dynamic Control Method of Flue Gas Heat Transfer System in the Waste Heat Recovery Process. Energy 2022, 259, 125010. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, H.; Li, S.; Li, W.; Pan, P.; Liu, T.; Wu, L.; Xu, G. Thermodynamic and Economic Analysis of a Novel Design Combining Waste Tire Pyrolysis with Silicon Production Waste Heat Recovery and Organic Rankine Cycle. Energy 2023, 283, 128500. [Google Scholar] [CrossRef]
- Cao, Y.; Zhan, J.; Jia, B.; Chen, R.; Si, F. Optimum Design of Bivariate Operation Strategy for a Supercritical/Transcritical CO2 Hybrid Waste Heat Recovery System Driven by Gas Turbine Exhaust. Energy 2023, 284, 129325. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, S.; Sun, B.; Liu, J.; Yan, J. Design on a Novel Waste Heat Recovery System Integrated with the Bypass Flue and Outside Primary Air Preheater for Bitumite-Fired Power Plants. Energy 2024, 291, 130341. [Google Scholar] [CrossRef]
- Fu, B.-R.; Hsieh, J.-C.; Cheng, S.-M.; Royandi, M.A. Thermoeconomic Analysis of a Novel Cogeneration System for Cascade Recovery of Waste Heat from Exhaust Flue Gases. Appl. Therm. Eng. 2024, 247, 123034. [Google Scholar] [CrossRef]
- Feng, J.; Cheng, X.; Wang, H.; Zhao, L.; Dong, H. Effect of Flue Gas Outlet Temperature in Evaporator on Thermal Economic Performance of Organic Rankine Cycle System for Sinter Waste Heat Recovery. J. Iron Steel Res. Int. 2023, 30, 2378–2390. [Google Scholar] [CrossRef]
- Wang, Q.; Macián-Juan, R.; Li, D. Analysis and Assessment of a Novel Organic Flash Rankine Cycle (OFRC) System for Low-temperature Heat Recovery. Energy Sci. Eng. 2022, 10, 3023–3043. [Google Scholar] [CrossRef]
- Benvenuto, G.; Trucco, A.; Campora, U. Optimization of Waste Heat Recovery from the Exhaust Gas of Marine Diesel Engines. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2016, 230, 83–94. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, W.; Luo, X.; Chen, J.; Yang, Z.; Chen, Y. Multi-Objective Optimization of Supercritical CO2 Brayton Cycles for Coal-Fired Power Generation with Two Waste Heat Recovery Schemes. Energy Convers. Manag. 2024, 300, 117962. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, J.; Ge, M.; Gu, H.; Wang, S. Numerical and Experimental Study of a Non-Frosting Thermoelectric Generation Device for Low Temperature Waste Heat Recovery. Appl. Energy 2023, 352, 121952. [Google Scholar] [CrossRef]
- Adjibade, M.I.S.; Thiam, A.; Awanto, C.; Azilinon, D. Experimental Analysis of Diffusion Absorption Refrigerator Driven by Electrical Heater and Engine Exhaust Gas. Case Stud. Therm. Eng. 2017, 10, 255–261. [Google Scholar] [CrossRef]
- Karamangil, M.I.; Coskun, S.; Kaynakli, O.; Yamankaradeniz, N. A Simulation Study of Performance Evaluation of Single-Stage Absorption Refrigeration System Using Conventional Working Fluids and Alternatives. Renew. Sustain. Energy Rev. 2010, 14, 1969–1978. [Google Scholar] [CrossRef]
- Starace, G.; De Pascalis, L. An Enhanced Model for the Design of Diffusion Absorption Refrigerators. Int. J. Refrig. 2013, 36, 1495–1503. [Google Scholar] [CrossRef]
- Zohar, A.; Jelinek, M.; Levy, A.; Borde, I. Numerical Investigation of a Diffusion Absorption Refrigeration Cycle. Int. J. Refrig. 2005, 28, 515–525. [Google Scholar] [CrossRef]
- Chua, H.T.; Toh, H.K.; Ng, K.C. Thermodynamic Modeling of an Ammonia–Water Absorption Chiller. Int. J. Refrig. 2002, 25, 896–906. [Google Scholar] [CrossRef]
- Mansouri, R.; Boukholda, I.; Bourouis, M.; Bellagi, A. Modelling and Testing the Performance of a Commercial Ammonia/Water Absorption Chiller Using Aspen-Plus Platform. Energy 2015, 93, 2374–2383. [Google Scholar] [CrossRef]
- Mansouri, R.; Bourouis, M.; Bellagi, A. Steady State Investigations of a Commercial Diffusion-Absorption Refrigerator: Experimental Study and Numerical Simulations. Appl. Therm. Eng. 2018, 129, 725–734. [Google Scholar] [CrossRef]
- Lee, G.; Choi, H.W.; Kang, Y.T. Cycle Performance Analysis and Experimental Validation of a Novel Diffusion Absorption Refrigeration System Using R600a/n-Octane. Energy 2021, 217, 119328. [Google Scholar] [CrossRef]
- Dhindsa, G.S. Review on Performance Enhancement of Solar Absorption Refrigeration System Using Various Designs and Phase Change Materials. Mater. Today Proc. 2021, 37, 3332–3337. [Google Scholar] [CrossRef]
- Alcântara, S.C.S.; Lima, A.A.S.; Ochoa, A.A.V.; de Leite, N.P.G.; da Costa, J.Â.P.; dos Santos, C.A.C.; Cavalcanti, E.J.C.; Michima, P.S.A. Implementation of the Characteristic Equation Method in Quasi-Dynamic Simulation of Absorption Chillers: Modeling, Validation and First Results. Energy Convers. Manag. X 2022, 13, 100165. [Google Scholar] [CrossRef]
- Fouda, A.; Khaliq, A.; Elattar, H.F.; Al-Zahrani, A.; Almohammadi, B.A.; Refaey, H.A. Evaluation of a Concentrated Solar Power-Driven System Designed for Combined Production of Cooling and Hydrogen. Case Stud. Therm. Eng. 2024, 59, 104567. [Google Scholar] [CrossRef]
- Almohammadi, B.A.; Al-Zahrani, A.; Refaey, H.A.; Attia, E.-A.; Fouda, A. Energy Analysis of a Novel Solar Tri-Generation System Using Different ORC Working Fluids. Case Stud. Therm. Eng. 2023, 45, 102918. [Google Scholar] [CrossRef]
- Mazouz, S.; Mansouri, R.; Bellagi, A. Experimental and Thermodynamic Investigation of an Ammonia/Water Diffusion Absorption Machine. Int. J. Refrig. 2014, 45, 83–91. [Google Scholar] [CrossRef]
- Cefarin, M. Design of NH3-H2O Absorption Chiller for Low Grade Waste Heat Recovery. Università degli Studi di Udine. Available online: https://core.ac.uk/download/pdf/158819668.pdf (accessed on 16 December 2023).
- Vijayaraghavan, S. Thermodynamic Studies on Alternate Binary Working Fluid Combinations and Configurations for a Combined Power and Cooling Cycle. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2003. [Google Scholar]
- Aziz, M.; Juangsa, F.B.; Irhamna, A.R.; Irsyad, A.R.; Hariana, H.; Darmawan, A. Ammonia Utilization Technology for Thermal Power Generation: A Review. J. Energy Inst. 2023, 111, 101365. [Google Scholar] [CrossRef]
- Shanmugam, S.K.G.; Mital, M. An Ultra-Low Ammonia Charge System for Industrial Refrigeration. Int. J. Refrig. 2019, 107, 344–354. [Google Scholar] [CrossRef]
- Yamamoto, E.Y.; Leal Da Silva, R.; Higa, M. Performance Improvements on Energy and Exergy Basis for an Ammonia-Water Absorption Refrigeration System in a Coffee Industry. Sustain. Energy Technol. Assess. 2022, 52, 102284. [Google Scholar] [CrossRef]
- Mehr, A.S.; Zare, V.; Mahmoudi, S.M.S. Standard GAX versus Hybrid GAX Absorption Refrigeration Cycle: From the View Point of Thermoeconomics. Energy Convers. Manag. 2013, 76, 68–82. [Google Scholar] [CrossRef]
- Han, W.; Chen, Q.; Sun, L.; Ma, S.; Zhao, T.; Zheng, D.; Jin, H. Experimental Studies on a Combined Refrigeration/Power Generation System Activated by Low-Grade Heat. Energy 2014, 74, 59–66. [Google Scholar] [CrossRef]
- SCFP L’ammoniac. Available online: https://scfp.ca/lammoniac#:~:text=L'ammoniac%20est%20corrosif%20pour,ammoniac%20lib%C3%A9r%C3%A9%20dans%20l'atmosph%C3%A8re (accessed on 16 December 2023).
- Mungyeko Bisulandu, B.-J.R.; Ilinca, A.; Tsimba Mboko, M.; Mbozi Mbozi, L. Thermodynamic Performance of a Cogeneration Plant Driven by Waste Heat from Cement Kilns Exhaust Gases. Energies 2023, 16, 2460. [Google Scholar] [CrossRef]
- Rattner, A.S.; Garimella, S. Low-Source-Temperature Diffusion Absorption Refrigeration. Part I: Modeling and Cycle Analysis. Int. J. Refrig. 2016, 65, 287–311. [Google Scholar] [CrossRef]
- Rattner, A.S.; Garimella, S. Low-Source-Temperature Diffusion Absorption Refrigeration. Part II: Experiments and Model Assessment. Int. J. Refrig. 2016, 65, 312–329. [Google Scholar] [CrossRef]
- Yousuf, N.; Biteau, E.; Anderson, T.; Gschwendtner, M.; Nates, R. Modelling the Performance of a Diffusion Absorption Refrigeration System. In Proceedings of the 2014-Asia-Pacific Solar Research Conference, Sydney, Asutralia, 8–10 December 2014. [Google Scholar]
- Long, Z.; Luo, Y.; Li, H.; Bu, X.; Ma, W. Performance Analysis of a Diffusion Absorption Refrigeration Cycle Working with TFE–TEGDME Mixture. Energy Build. 2013, 58, 86–92. [Google Scholar] [CrossRef]
- Hu, Z.; Deng, Z.; Gao, W.; Chen, Y. Experimental Study of the Absorption Refrigeration Using Ocean Thermal Energy and Its Under-Lying Prospects. Renew. Energy 2023, 213, 47–62. [Google Scholar] [CrossRef]
- Mansouri, R.; Bourouis, M.; Bellagi, A. Experimental Investigations and Modelling of a Small Capacity Diffusion-Absorption Refrigerator in Dynamic Mode. Appl. Therm. Eng. 2017, 113, 653–662. [Google Scholar] [CrossRef]
- Mungyeko Bisulandu, B.-J.R.; Marias, F. Numerical Modeling of Thermochemical Conversion of Biomass and Tires as Fuels for Cement Clinker Production. Recycling 2023, 8, 41. [Google Scholar] [CrossRef]





| Components | Mass Balance Equations | Energy Balance Equations | Exergy Balance Equations |
|---|---|---|---|
| KALINA CYCLE | |||
| Preheater | AND | ||
| Evaporator | AND | ||
| Superheater 1 | AND | ||
| Superheater 2 | AND | ||
| HPT | |||
| LPT | |||
| MPT | |||
| Heat Exchanger 2 | AND | ||
| Condenser | |||
| Feed Pump 1 | |||
| Feed Pump 2 | |||
| Heat Exchanger 1 | AND | ||
| DAR SYSTEM | |||
| Bubble Pump | |||
| Rectifier | |||
| Condenser | |||
| GHX Exchanger | |||
| Evaporator | |||
| Absorber | |||
| SHX Exchanger | AND | ||
| DOMESTIC HEATING NETWORK | |||
| Heat Exchanger | AND | ||
| Hot Water Tank | |||
| Hot Water Tank 2 | AND | ||
| BIODIGESTER | |||
| Biogas Production | |||
| Components | Performance Parameters |
|---|---|
| KALINA CYCLE | |
| Net work | |
| Energy efficiency | |
| Exergy efficiency | |
| DAR SYSTEM | |
| COP | |
| Temperature of evaporator | 1 |
| Net cooling capacity | |
| DOMESTIC HEATING NETWORK | |
| Thermal power | |
| Energy efficiency | |
| BIODIGESTER | |
| Thermal power | |
| Energy efficiency | |
| Parameters | Júnior et al. [3] | Present Model | Error % |
|---|---|---|---|
| Temperature [°C] | 390 | 300 | 23.08 |
| Exergetical Efficiency [%] | 47.8 | 40.35 | 15.59 |
| Thermal Efficiency [%] | 23.3 | 22.15 | 4.94 |
| Net Electrical Power [kWe] | 2429.056 | 2565.03 | 5.60 |
| Parameters | Rattner and Garimella [41,42] | Present Model | Gap |
|---|---|---|---|
| Type of refrigeration machine | DAR | DAR | - |
| Ambient temperature | 24 °C | 30 °C | +6 °C |
| Exchange temperature at the generator | 130 °C | 109 °C | −21 °C |
| Pressure | 11.5 bars | 20 bars | +8.5 bars |
| Working fluids | NH3-NaSCN-He | NH3-H2O-H2 | - |
| COP found | 26% | 26.82% | +0.82% |
| Operating Parameters | Values |
|---|---|
| Gas temperature at generator inlet (Tgas.gen) | 109.5 °C |
| The mass flow rate of working fluid (H2O+NH3) | 22.32 kg/s |
| The mass flow rate of H2 | 14.83 kg/s |
| Ambient temperature | 30 °C |
| Rectifier pinch-point temperature difference | 10 °C |
| The efficiency of the absorber | 80% [44] |
| The efficiency of evaporator | 80% 1 |
| The efficiency of heat exchangers | 70% [45] |
| The concentration of NH3 in the mixture at the pump discharge | 30% [43] |
| Evaporator pinch-point temperature difference | 10 °C [46] |
| SHX efficiency | 70% [45] |
| The mass flow rate of waste (biomass) | 500 kg/s |
| Average waste temperature | 20 °C |
| Lower calorific Value | 17.2 MJ/kg |
| Thermodynamic Parameters | Values |
|---|---|
| Specific Work [kJ/kg] | 367.66 |
| Net Mechanical Power [kW] | 2817.83 |
| Net Electrical Power [kWe] | 2565.03 |
| Thermal Efficiency [%] | 22.15 |
| Exergy Efficiency [%] | 45.12 |
| Thermal Power to the DAR Cycle [kW] | 7368.20 |
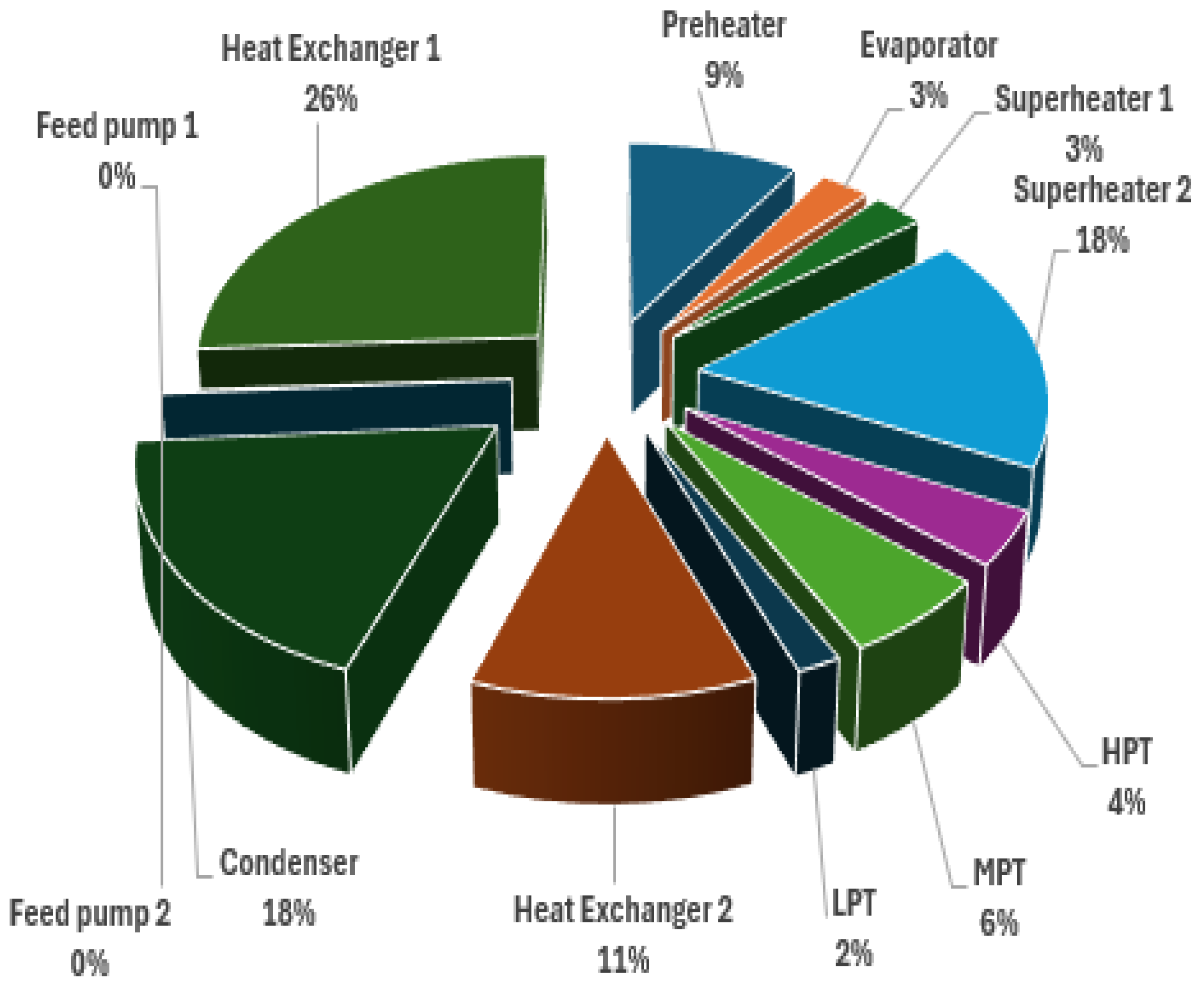
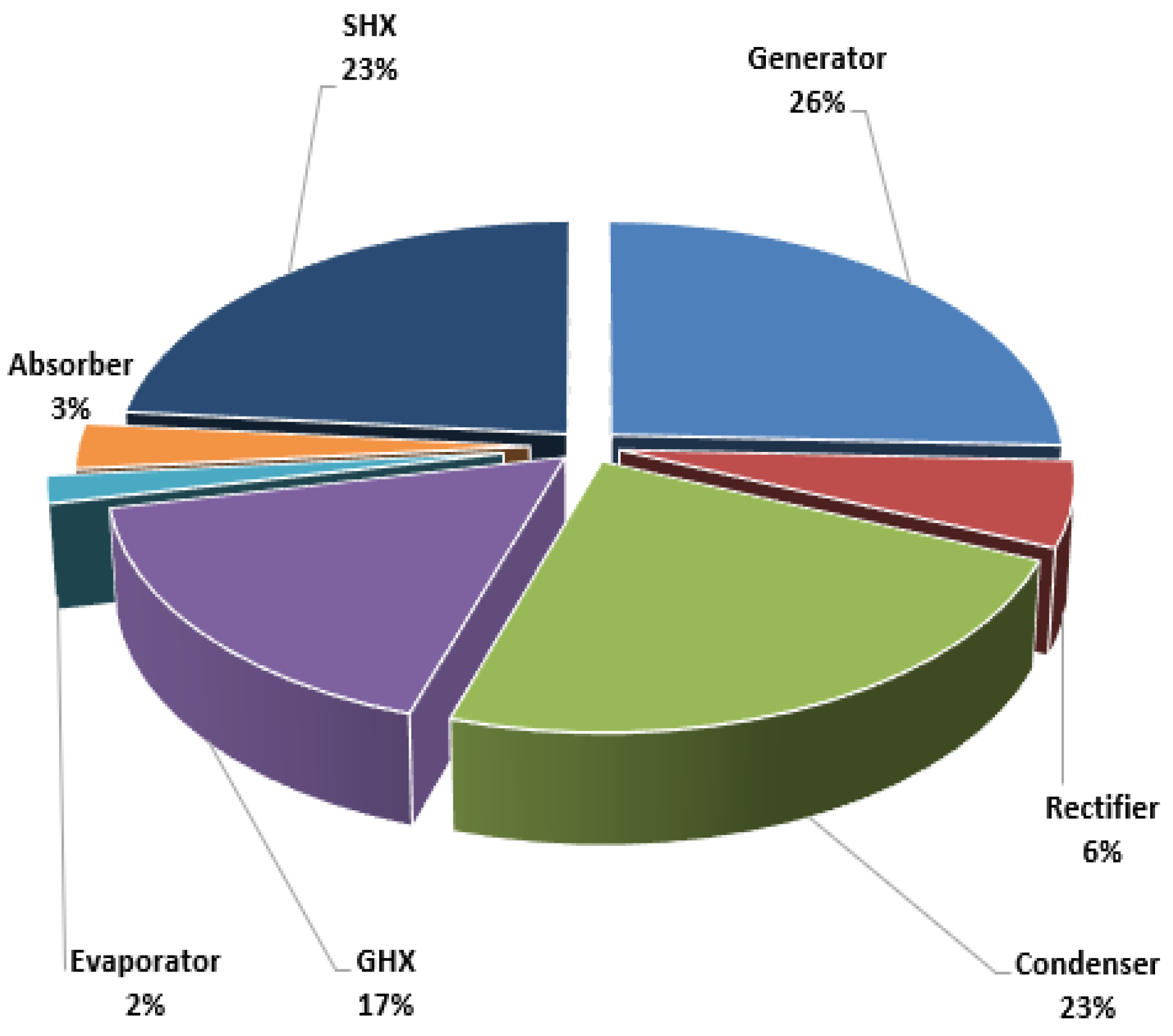
| Components | Exergy Destruction [kW] | Exergy Efficiency [%] |
|---|---|---|
| Preheater | 2637.58 | 84.59 |
| Evaporator | 758.72 | 50.91 |
| Superheater 1 | 790.32 | 65.68 |
| Superheater 2 | 5086.29 | 64.55 |
| HPT | 1159.70 | 53.70 |
| MPT | 1745.38 | 35.69 |
| LPT | 509.47 | 20 |
| Heat Exchanger 2 | 3261.88 | 79.85 |
| Condenser | 5332.39 | 21.72 |
| Feed Pump 2 | 29.34 | 29.88 |
| Feed Pump 1 | 8.83 | 88.69 |
| Heat Exchanger 1 | 7456.85 | 89.86 |
| Operating Parameters | Values |
|---|---|
| Heat transfer from Evaporator [kW] | 6766.023 |
| Heat transfer from Condenser [kW] | 8464.306 |
| Heat transfer from Absorber [kW] | 26,322.392 |
| Heat transfer from Generator [kW] | 25,226.022 |
| Heat transfer from Rectifier [kW] | 5743.233 |
| Coefficient of Performance [-] | 0.268 |
| Evaporator Temperature [°C] | 10.57 |
| State Point | Mass Flux [kg/s] | Temperature [°C] | Pressure [bar] | Enthalpy [kJ/kg] | xNH3 [%] | xH2O [%] | xH2 [%] |
|---|---|---|---|---|---|---|---|
| 12 | 22.32 | 93.6 | 20 | 1303 | 0.9652248 | 0.0347752 | 0 |
| 13 | 15.21 | 83.6 | 20 | 860 | 0.0347752 | 0.97317555 | 0 |
| 14 | 6.94 | 83.6 | 20 | 1480 | 0.97317555 | 0.02682445 | 0 |
| 15 | 6.94 | 40.72 | 20 | 259.78 | 0.97317555 | 0.02682445 | 0 |
| 16 | 6.94 | 5.72 | 20 | 1480 | 0.97317555 | 0.02682445 | 0 |
| 17 | 14.47 | −9.28 | 20 | 2594 | 0.045405 | 0 | 0.954595 |
| 18 | 14.47 | 25.72 | 20 | 2594 | 0.045405 | 0 | 0.954595 |
| 19 | 7.36 | 26.63 | 20 | 2778 | 2.314 × 10−5 | 3.4066 × 10−8 | 0.99997683 |
| 20 | 7.36 | 1.49 | 20 | 2788 | 2.314 × 10−5 | 3.4066 × 10−8 | 0.99997683 |
| 21 | 22.32 | 13.46 | 20 | 173 | 0.58182 | 0.41818 | 0 |
| 22 | 22.32 | 77.06 | 20 | 173 | 0.58182 | 0.41818 | 0 |
| 23 | 15.21 | 104.32 | 20 | 860 | 0.0347752 | 0.97317555 | 0 |
| 24 | 15.21 | 40.72 | 20 | 860 | 0.0347752 | 0.97317555 | 0 |
| Components | Exergy Destroyed [kW] | Exergy Efficiency [%] |
|---|---|---|
| Bubble Pump | 18,618.06 | 3.28 |
| Rectifier | 4152.44 | 3.45 |
| Condenser | 16,987.36 | 28.94 |
| GHX Exchanger | 12,174.98 | 54.99 |
| Evaporator | 1314.92 | 28.43 |
| Absorber | 2177.83 | 15.50 |
| SHX Exchanger | 17,017.18 | 15.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mungyeko Bisulandu, B.-J.R.; Mansouri, R.; Tsimba Mboko, M.; Mbozi Mbozi, L.; Ilinca, A. Innovative Multigeneration System with Heat Exchangers for Harnessing Thermal Energy from Cement Kiln Exhaust Gases. Energies 2024, 17, 3041. https://doi.org/10.3390/en17123041
Mungyeko Bisulandu B-JR, Mansouri R, Tsimba Mboko M, Mbozi Mbozi L, Ilinca A. Innovative Multigeneration System with Heat Exchangers for Harnessing Thermal Energy from Cement Kiln Exhaust Gases. Energies. 2024; 17(12):3041. https://doi.org/10.3390/en17123041
Chicago/Turabian StyleMungyeko Bisulandu, Baby-Jean Robert, Rami Mansouri, Marcel Tsimba Mboko, Lucien Mbozi Mbozi, and Adrian Ilinca. 2024. "Innovative Multigeneration System with Heat Exchangers for Harnessing Thermal Energy from Cement Kiln Exhaust Gases" Energies 17, no. 12: 3041. https://doi.org/10.3390/en17123041
APA StyleMungyeko Bisulandu, B.-J. R., Mansouri, R., Tsimba Mboko, M., Mbozi Mbozi, L., & Ilinca, A. (2024). Innovative Multigeneration System with Heat Exchangers for Harnessing Thermal Energy from Cement Kiln Exhaust Gases. Energies, 17(12), 3041. https://doi.org/10.3390/en17123041






