1. Introduction
Renewable energy generation is an important direction for the development of the current power system [
1]. Among renewable energy sources, distributed photovoltaics (DPVs) have the advantages of flexible installation and a short construction period, which has attracted much attention. However, the output of DPVs is random due to a variety of factors such as installation location and weather [
2,
3,
4]. With the increasing penetration rate of DPVs, problems such as power backward transmission and voltage overruns have occurred in some areas, bringing challenges to the safe operation of the distribution network [
5].
The current means of regulating the voltage of the distribution network mainly rely on traditional voltage-regulating devices such as static synchronous compensators and shunt capacitors. In fact, with the increasing penetration of DPVs in the distribution network, a DPV inverter is an efficient voltage-regulating resource that does not require any additional investment [
6]. However, DPVs are large in number, small in capacity, and widely distributed [
7]. The participation of each PV in the regulation of the power system individually would bring problems such as solving difficulty, long calculation times, and many decision variables [
8]. Comparatively speaking, it is more feasible to participate in the flexible regulation of the power system using cluster response.
For the study of PV aggregations, the key lies in the extraction of clustering features and the selection of clustering methods. Currently, on the extraction of clustering features, reference [
9] proposes a DPV system aggregation model based on interconnection point voltages and inverter types; this model can obtain a similar power output. Reference [
10] proposes a weighted dynamic aggregation model for grid-following inverters and their controllers in applications such as photovoltaic farms or any renewable distributed generation integrated microgrids. Reference [
11] presents an aggregation method involving wind power and photovoltaic correlation to accurately reflect the characteristics of original wind–photovoltaic output power, and maintain the correlation between wind–photovoltaic output power. Reference [
12] proposes a methodology based on Voronoi decomposition to spatially aggregate small-scale solar generation.
In the selection of clustering methods, reference [
13] proposes a real-time distributed clustering algorithm for the aggregation of distributed energy storage systems into heterogeneous virtual power plants. Reference [
14] proposes a new time aggregation method. Each representative period constructed by the proposed method can include more than one representative day. Reference [
15] improves the piecewise aggregation approximation algorithm to achieve effective dimension reduction of oscillation data. Reference [
16] proposes a wind and photovoltaic power time-series data aggregation method based on an ensemble clustering and Markov chain. The wind and photovoltaic power time-series data were divided into scenarios, and ensemble clustering was used to cluster the divided scenarios.
In the current study, the selection of typical clustering characteristics is not sufficient, focusing on the power curve of the PV and failing to fully consider external factors such as the location of the PV and voltage tier. Due to the coupling between the power injected into the distribution network and the node voltage, some PVs under certain nodes may have a more obvious voltage regulation effect. However, considering the PV aggregations formed by the characteristics of the power curve to participate in distribution network voltage regulation may ignore these PVs, resulting in unreasonable clustering.
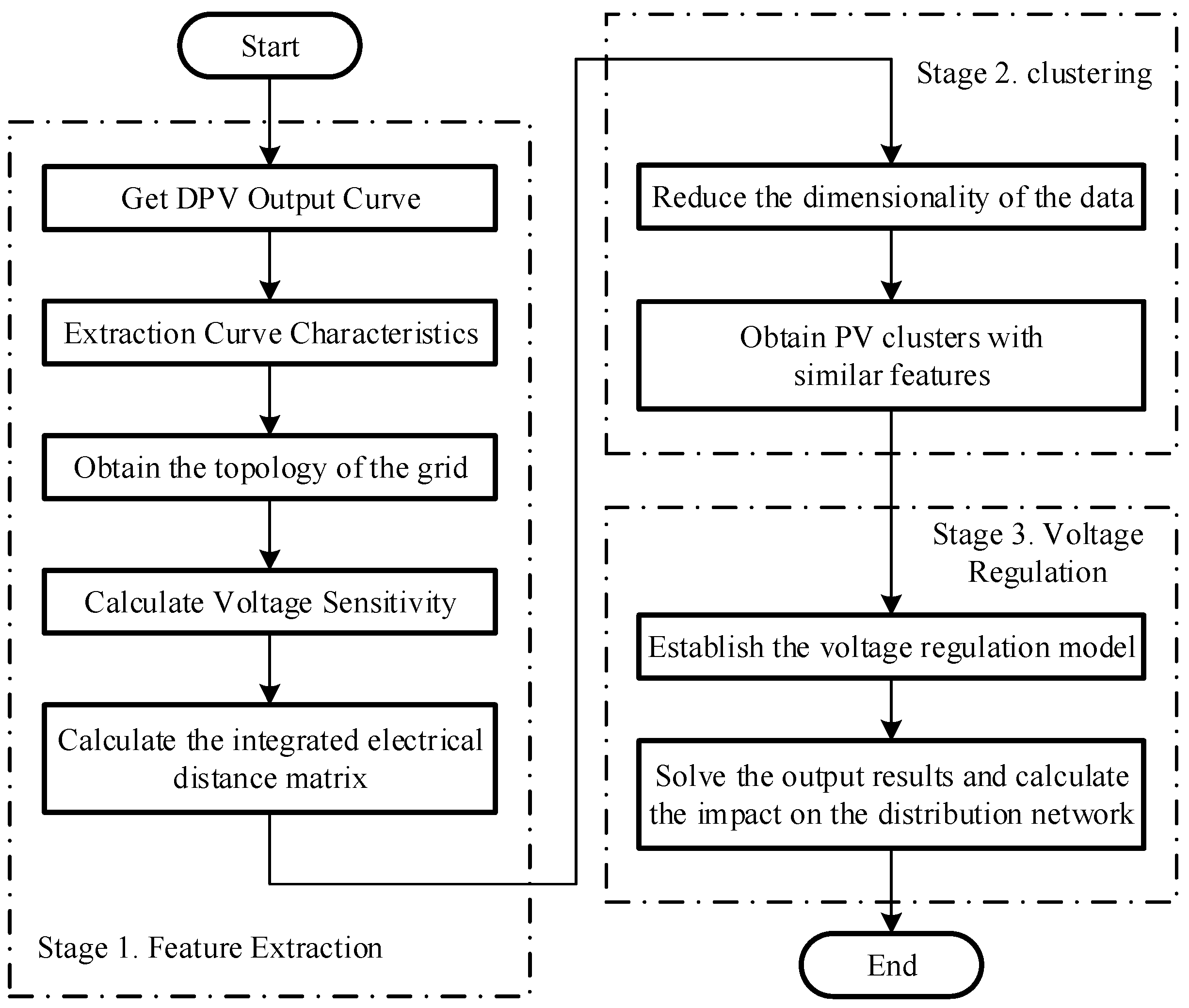
To address the above issue, this paper proposes a DPV cluster aggregation strategy considering the distribution network topology. Firstly, the PV power curve characteristics and the voltage sensitivity of the nodes are extracted, and the high-dimensional data features calculated are processed by using a dimensionality reduction technique; the PV is clustered by the K-means clustering algorithm; finally, a DPV aggregation voltage regulation model in the distribution network is established by taking the security of the distribution network as a constraint. Finally, the simulation is built in MATLAB to verify the reasonableness of the strategy for dividing aggregations and participating in voltage regulation.
The contributions of the paper include:
- (1)
This paper proposes a DPV cluster aggregation method that fully considers the distribution network topology and the voltage sensitivity of DPVs, which can establish DPV aggregations with the best voltage regulation effect in the distribution network.
- (2)
Based on the proposed aggregation method, a DPV-aggregation-based voltage regulation model for the distribution network is constructed, which achieves accurate and efficient voltage regulation by using the DPV aggregations.
The paper is organized as follows:
Section 2 introduces voltage sensitivity, data dimensionality reduction, and the proposed DPV aggregation method;
Section 3 establishes the DPV aggregation voltage regulation model;
Section 4 provides a simulation that compares the proposed aggregation strategy with the traditional aggregation method.
Section 5 concludes the paper.
2. DPV Aggregation Considering Distribution Network Topology
Considering the limitations of the existing DPV aggregation methods discussed above, this paper proposes a DPV aggregation method that considers distribution network topology and the nodal voltage sensitivity feature of DPVs.
2.1. Studied System
This paper focuses on low-voltage radial distribution networks below 10 kV with DPVs. On the one hand, when DPVs inject power into the grid, it may pose the problem of overvoltage in key nodes in the distribution network or even in the upstream grid. On the other hand, DPVs’ inverters have voltage-regulating capability, so proper regulation of DPVs can effectively relieve the overvoltage problem in the distribution network.
To realize the mitigation of overvoltage caused by high injected power, the key problem is how to screen out proper DPVs. So, this paper will form DPV aggregation with voltage-sensitive DPVs based on extracted DPV power curves and distribution network topology features, data dimensionality reduction, clustering, and other methods. Finally, the formed DPV aggregations are used to realize efficient voltage regulation in the distribution network.
2.2. DPV Feature Extraction Considering Distribution Network Topology
2.2.1. Extraction of Power Curve Features of DPVs
The PV power curve is a curve that describes the output power of PV modules under different light conditions. Peak, average, and threshold time percentages are commonly used indicators to characterize different PV power curves [
17,
18,
19].
Assuming that the PV in a certain area samples a total of T points per day, the sequence is obtained, where denotes the active power of the ith PV station at the Tth point. The above three reference indicators are defined as follows:
- (3)
Threshold time percentage:
where
represents the number of hours in a day when the output of the
ith PV reaches the threshold value, and
is set as the threshold value.
The selection of features based on curve characteristics only considers the annual output characteristics of the PV itself, but in the actual power system, the installation location of the PV as well as the topology of the grid will also affect the output of the PV. Therefore, the aggregation of PVs should not only consider the time series of their power curves but also pay attention to the indicators that can reflect the topology of the grid.
2.2.2. Nodal Voltage Sensitivity of DPVs
When DPVs are connected to the grid, the PV output power changes, and the voltage of each node changes, i.e., the power change in a node causes a change in the bus voltage, which is the sensitivity relationship between the PV output power and the voltage and can be referred to as the voltage sensitivity [
20].
The voltage sensitivity of each node in the system can be obtained from the inverse of the Jacobi matrix in the following calculation:
The matrix inverse of Equation (4) is then performed:
where
and
denote the phase angle and voltage of the node, respectively;
and
denote the active and reactive power injected into the node;
,
,
, and
denote the variations, respectively;
denotes the Jacobi matrix; the sensitivity factors,
and
, denote the node voltage variations resulting from the changes in active and reactive power on the node, respectively.
When the active and reactive power transmission on a single node or some nodes in the distribution network changes, the amount of voltage change at each node in the system can then be expressed as
where
and
denote the effect of active and reactive power changes at node
j on node
i, respectively;
N is the number of nodes of the distribution network.
Define node
i as the disturbed node and node
j as the interfering node, then the voltage variation at the disturbed node is
From Equation (7), it can be seen that the higher the voltage sensitivity, the greater the power change in the interfering node causing the voltage change in the disturbed node.
According to the voltage sensitivity, the electrical distance matrix
,
, reflecting the degree of coupling between nodes, can be defined, and its calculation formula is
where
,
represent the electrical distances between nodes
i and
j, and the smaller their electrical distance is, the closer the voltage connection between the two points is.
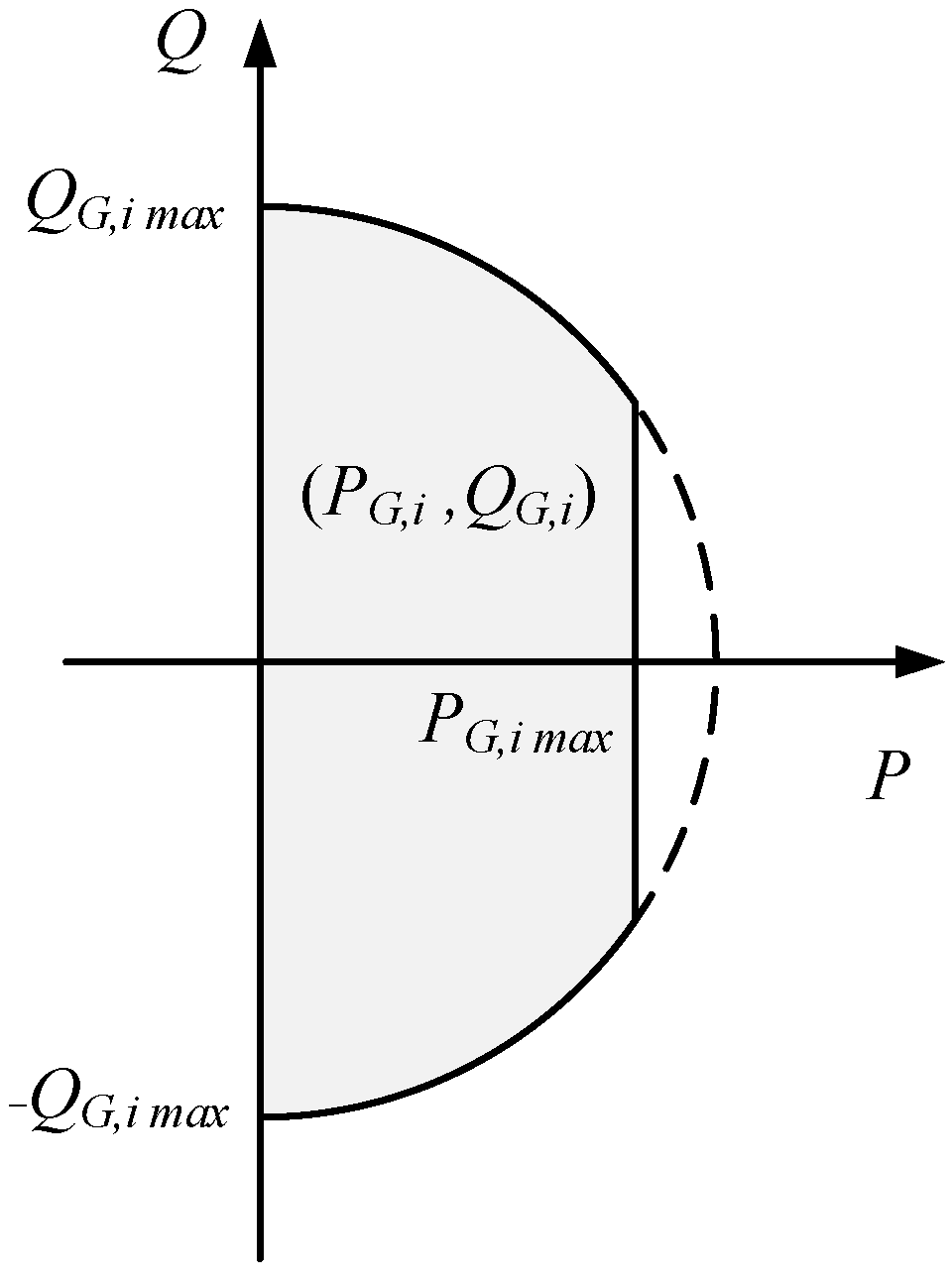
In the distribution network, since the influence of both reactive and active power variations on the voltage of the node in the distribution network is not negligible, the integrated electrical distance can be defined as
where
is the weight value, representing the degree of contribution of active power to the integrated electrical distance
. Although the effect of active power on voltage is not negligible in the distribution network, in the ideal case, it is still desired to control the voltage through reactive power, so
is generally set to 0.2–0.3.
2.2.3. Data Dimensionality Reduction for Clustering Features
Each column of the integrated electrical distance matrix reflects the impact of a specific interfering node on all the disturbed nodes, if the influence of each disturbed node is taken as the coordinate axis, the interference of a single interfering node j can be described as a high-dimensional point D, the coordinates of which are . Clustering the high-dimensional points increases the arithmetic burden, so data dimensionality reduction should be used to alleviate the arithmetic pressure.
Principal component analysis (PCA) is a data dimensionality reduction technique that transforms the original multiple variables into several comprehensive indicators [
21]. The idea is to utilize the interrelationships between the original variables to obtain uncorrelated principal components through linear combinations. This replaces the original larger number of variables. In this way, the information reflected by the original variables is retained as much as possible, simplifying the process of the problem.
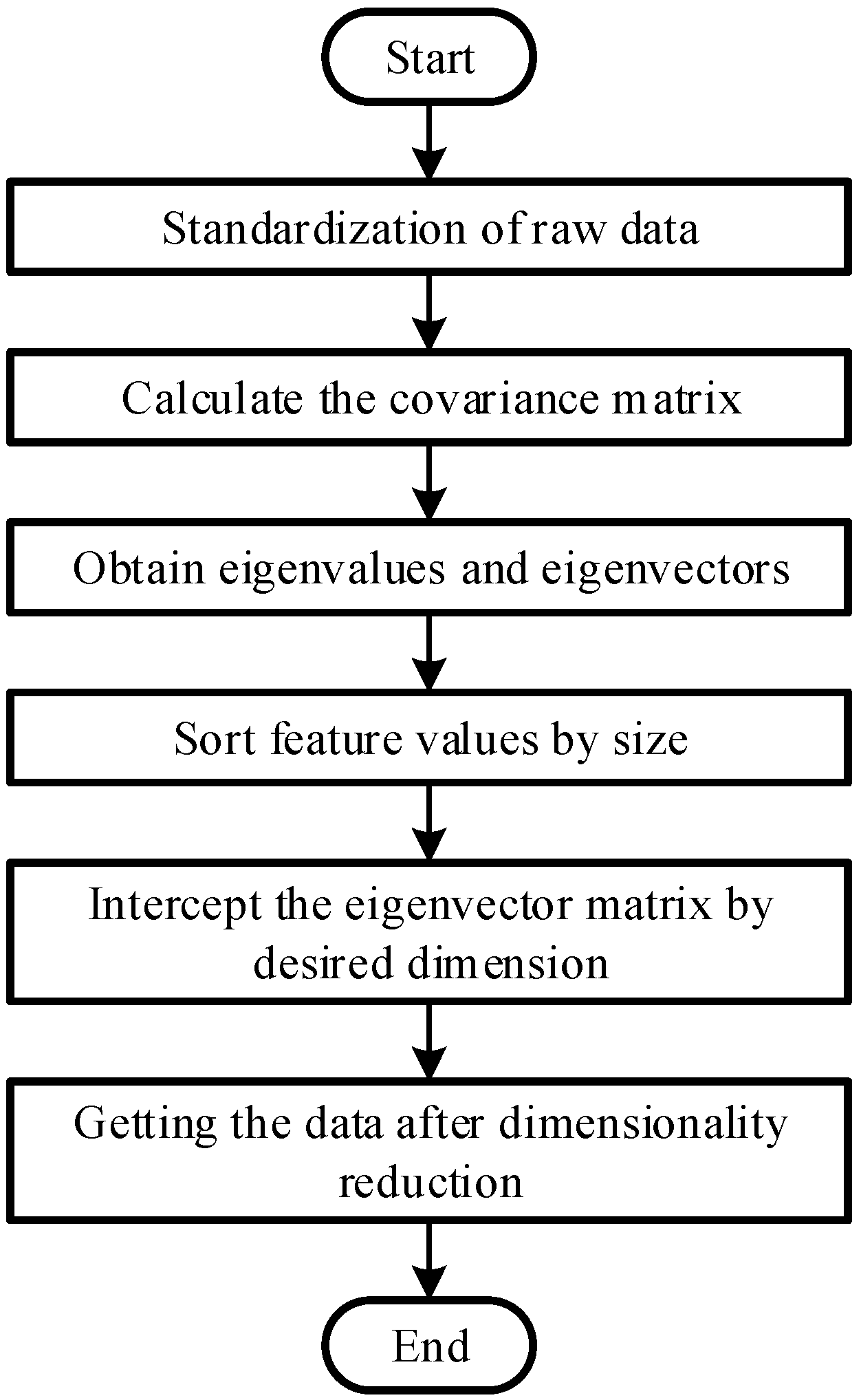
The process of the principal component analysis method is as follows, and
Figure 1 illustrates this process.
- (1)
Arrangement of raw data
In the comprehensive electrical distance matrix
proposed above, the column of nodes containing PVs is extracted, and assuming that there are
nodes equipped with PV, the new sample matrix
is an
matrix.
where
denotes the impact of the
mth PV on the voltage of the
ith node, i.e.,
.
- (2)
Subtract the mean value from each data point:
- (3)
Find the covariance matrix C:
Before calculating the covariance matrix, the covariance of the two datasets is
where
and
are the
th and
th rows, respectively;
are the means of
and
which are determined in step 2.
Therefore, the covariance matrix has the following calculation procedure:
When the covariance is 0, it means that row is linearly uncorrelated with row . Therefore, to realize the reduction of an N-dimensional vector to K dimensions, it is necessary to choose K unit orthogonal bases, so that after transforming the original data to this set of bases, the covariance of each variable is 0.
- (4)
Find the eigenvalues and corresponding eigenvectors of the covariance matrix
where
is the eigenvector of
, and
is the eigenvalue of
.
Use elementary transformations to reduce all elements except the diagonal to 0. Since
is a real symmetric array, the eigenvectors corresponding to different eigenvalues are orthogonal, so one has
where
consists of eigenvectors.
- (5)
The eigenvectors are arranged in rows according to the value of the corresponding eigenvalues from top to bottom, and the first k rows form a K × M matrix P.
where
is the sorted eigenvector matrix;
is the first
k rows of
; and
is the reduced dimension transformation matrix.
- (6)
Matrix Y is the data after reduction to k dimensions:
2.3. Formation of DPV Aggregation
The features of DPVs (peak, mean, threshold time percentage, and voltage sensitivity) were obtained above through calculation and data dimensionality reduction. To reduce the complexity of analyzing and processing DPV output data, this paper proposes to cluster DPVs according to similar clustering characteristics through the K-means clustering algorithm.
Figure 2 illustrates this algorithm.
Before the K-means algorithm clustering, it is necessary to set the number of clusters
k. Setting the value of
k empirically or randomly will lead to unstable clustering results, and the elbow method is usually utilized to determine the
k value.
where
is the
ith cluster after completion of clustering,
is the sample point in
; and
is the mean distances of all sample data points in
, i.e., the clustering center.
The process of the basic K-means algorithm is as follows: first, initialize the dataset and determine the number of clusters k; randomly select the initial clustering center, using the Euclidean distance as a measure to allocate other sample points; after the formation of clusters, calculate the mean to obtain a new clustering center. The above process iterates until the clustering center is no longer updated to complete the clustering process.
4. Simulations and Analysis
4.1. Case Settings
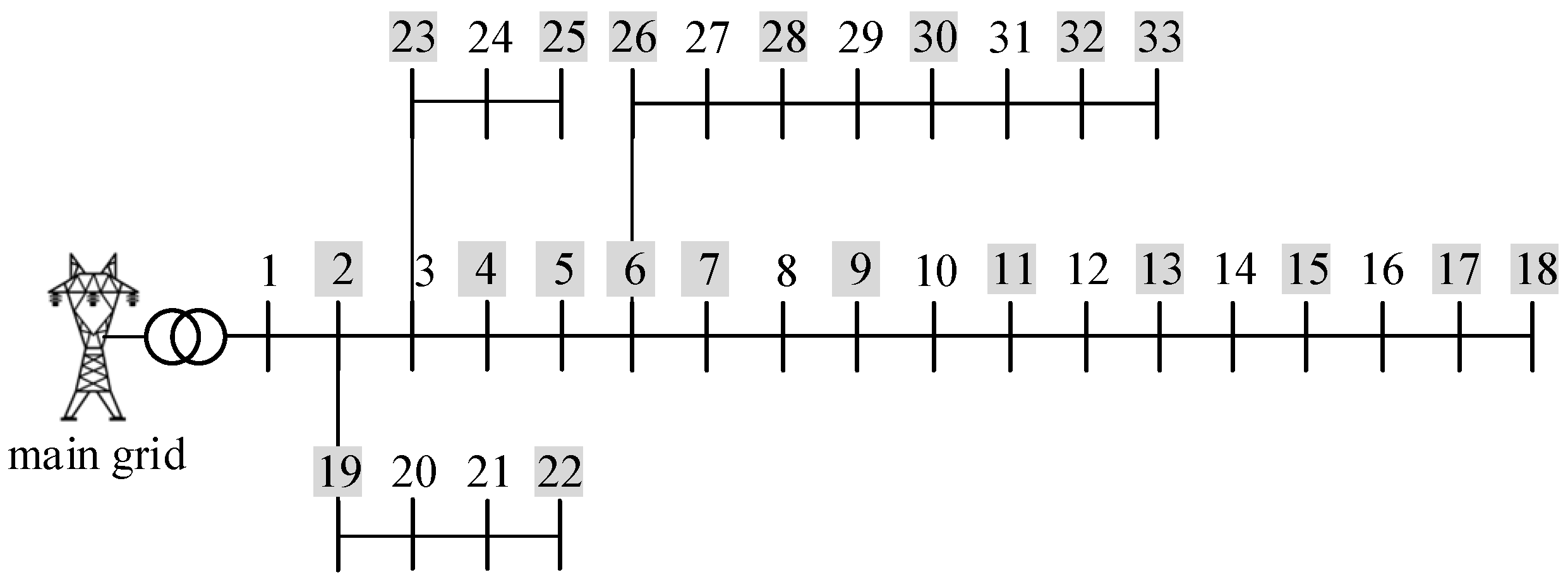
In this paper, the IEEE 33-node system is used for simulation. The system has 33 nodes with 32 branches. As shown in
Figure 5, the gray nodes in the figure are the nodes equipped with PVs and there are 20 DPVs. Each DPV has a capacity of 10 kVA. A power reference value of 10 MVA and a voltage reference value of 12.66 kV are taken, all of which are analyzed in the following based on the per unit case. The solar data are collected from Belgium’s power network operator Elia Group. The paper applies data from different regions to different DPVs. Samples are collected every 15 min.
The simulation environment is as follows: 12th Gen Intel(R) Core(TM) i7-12700 2.10 GHz processor, 64 GB RAM, 64-bit OS computer. The models and algorithms are implemented in MatlabR2023a. The following three scenarios are set up:
Scheme 1: Distribution network regulation without aggregation for DPV;
Scheme 2: Distribution network regulation using the traditional DPV clustering method based on power curves;
Scheme 3: Distribution network regulation using the DPV clustering method proposed in this paper.
4.2. Analysis of Aggregation Results
This section shows the aggregation results, which are verified by calculating the average voltage sensitivity of the aggregations, and the DPV aggregations under the scheme of this paper have better voltage regulation per PV on average.
4.2.1. Aggregation Based on Power Curve Features
Three indicators, peak, average, and threshold time percentage are used for feature extraction of single-day PV power curves. Due to the large difference in the values of each indicator, it is necessary to normalize each feature quantity.
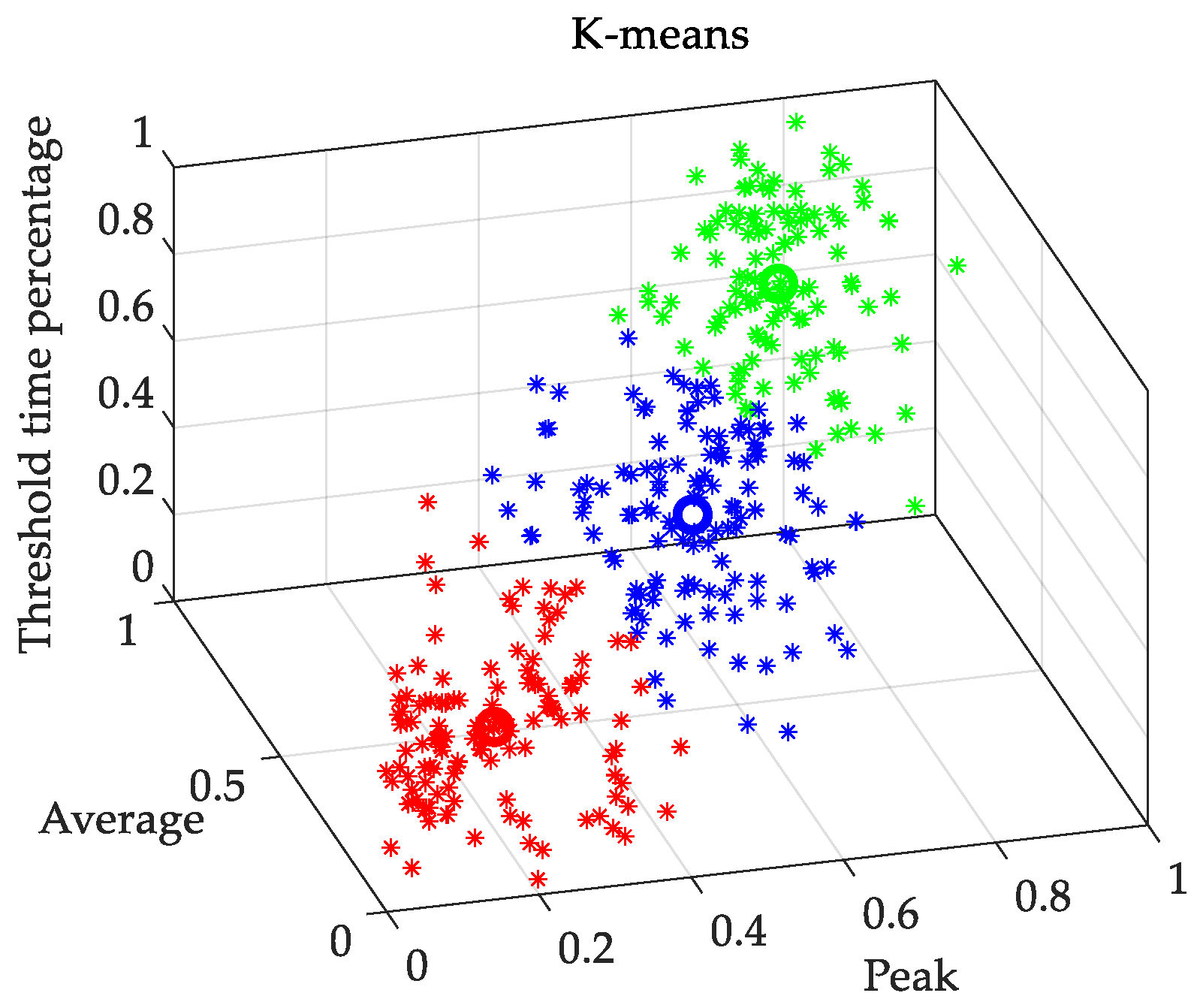
Figure 6 shows the clustering results of power curve features of a PV in one year (366 days), and it can be found that the 366 days of data are divided into three categories, which are represented by red, blue, and green colors.
The clustering operation of the power curves is performed for all 20 PVs. Since the three clustering centers of each PV are 3-dimensional points, data compression is required to compress the clustering centers with peak, average, and threshold time percentages as axes to one dimension to obtain the curve features of the 20 PVs.
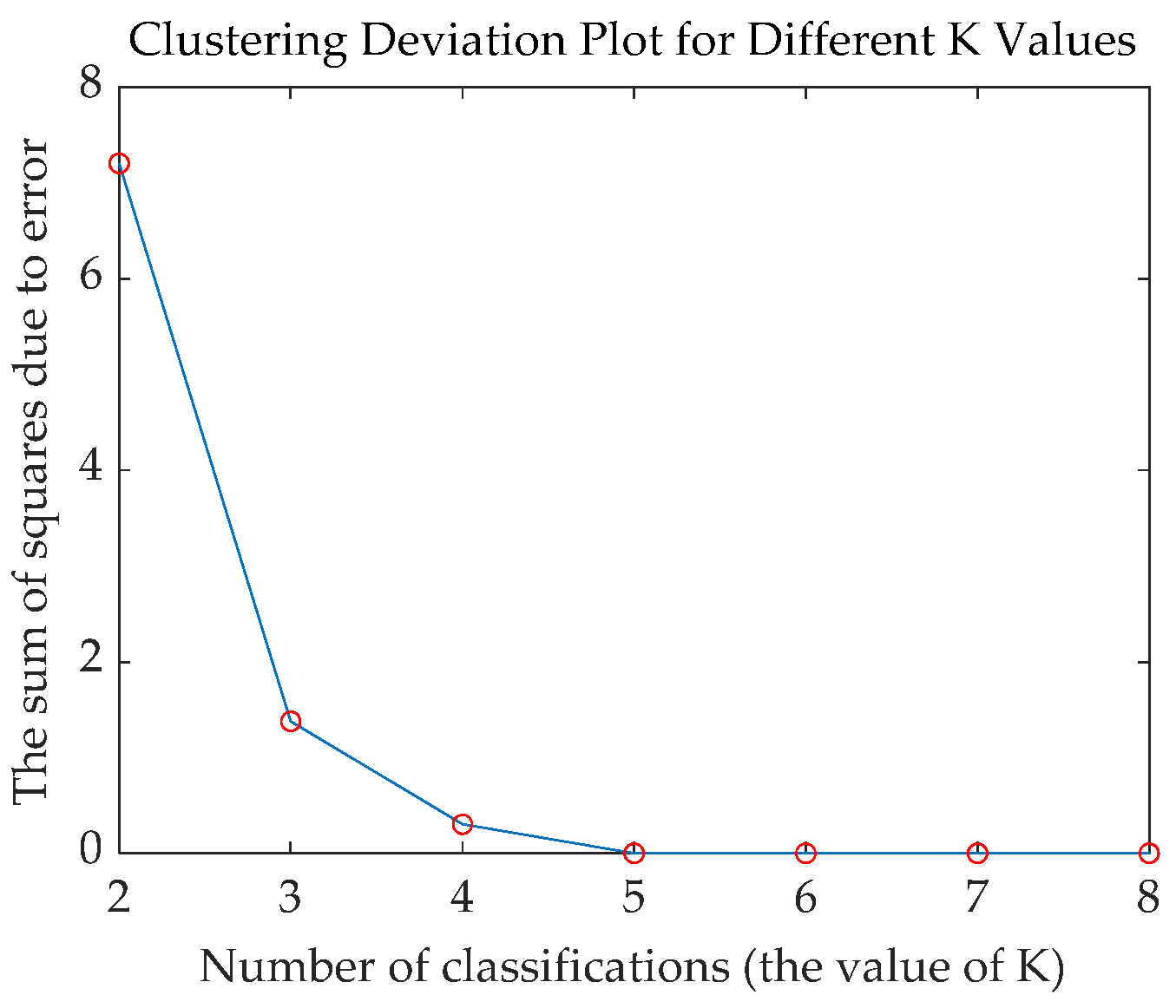
Figure 7 shows the SSE descent curve under the traditional curve feature clustering. It can be seen that when
k = 3, the slope of the descent curve changes the most, indicating that the optimal clustering is achieved when the number of aggregations is selected as three.
Shown in
Table 1 are the clustering results based on the traditional power curve characteristics when the optimal number of aggregations
k = 3. The PVs within each cluster are regarded as an aggregation, forming a total of three aggregations.
4.2.2. Aggregation Considering Distribution Network Topology
After extracting the features of single-day PV power curves above, the Jacobi matrix and the integrated electrical distance matrix are additionally calculated. The data compression is performed to obtain the sensitivity features of 20 PVs. Finally, the features are clustered by using the K-means algorithm.
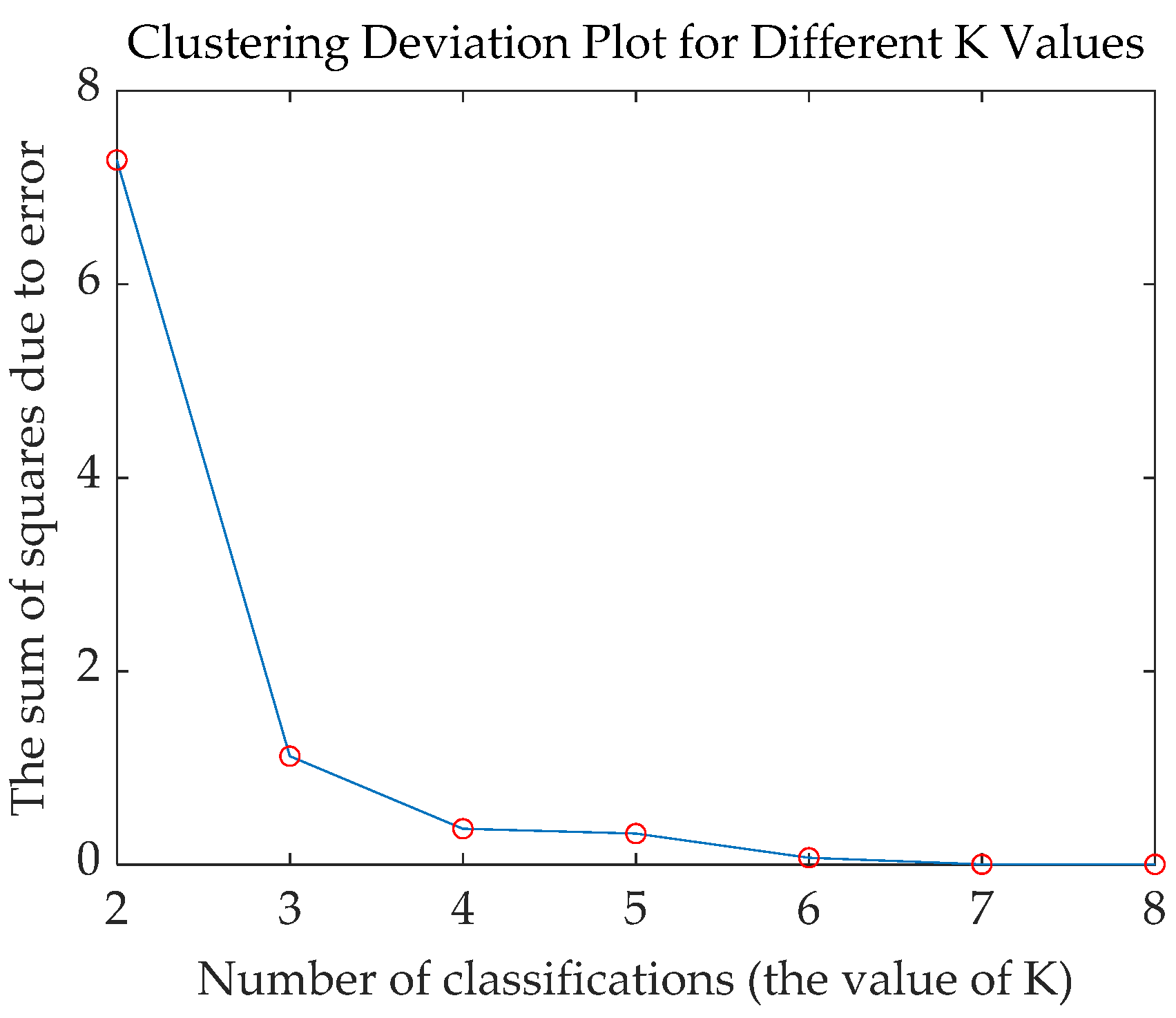
Figure 8 shows the SSE descent curve under the consideration of distribution network topology clustering, and it can be seen that the slope of the descent curve changes the most when
k = 3, indicating that the optimal clustering effect is achieved when the number of aggregations is selected as three.
Shown in
Table 2 are the clustering results for considering the distribution network topology in this paper when the optimal number of aggregations
k = 3. Also, three aggregates are formed.
4.2.3. Comparison of Aggregation Results
The average voltage sensitivity
of DPV aggregations under various schemes is calculated to reflect the degree of the regulation ability of the aggregation on the whole network voltage:
where
is a set denoting all the nodes where PVs are installed.
,
denote the active voltage sensitivity to node
j and to node
i, respectively, and
denotes the weights.
denotes the number of PVs contained in the aggregation. The larger the value of
is, the better each PV in the aggregation regulates the voltage through outputting the power.
The average voltage sensitivity for the three scenarios is shown in
Table 3. Compared with no clustering, the traditional scheme forms three types of aggregations: A1, A2, and A3. The regulating effect is A3 > A1 > A2, so A3 can be used to participate in voltage regulation with the best regulating effect. However, such clustering ignores the location of the PVs, and the regulating effect of some PVs is more obvious but not fully utilized. The scheme proposed in this paper considers the distribution network topology for clustering and also forms three types of aggregations B1, B2, and B3; the regulating effect is B3 > B1 > B2, and B3 > A3, indicating that the scheme in this paper finds the aggregation B3 which has the best regulating effect. It has the highest average voltage sensitivity.
4.3. Participation of PV Aggregations in Voltage Regulation of Distribution Network
The DPV aggregation voltage regulation model in the distribution network is solved using MATLAB and GUROBI. The scheme without aggregation involves all PVs in voltage regulation. The traditional scheme lets the aggregation A3 participate in voltage regulation, and the scheme in this paper lets the aggregation B3 participate in voltage regulation. The DPV single-day output is shown in
Table 4.
Table 4 shows the voltages of all nodes before and after voltage regulation for the three scenarios, as well as the single-day PV output. The effect of voltage regulation of DPVs is reflected by calculating the change in voltage of all nodes on a single day and the change in power of aggregation on a single day, and this voltage-to-power ratio is denoted as
:
where
is the scaling factor. In order to reflect the greater impact of the reactive power output of the DPV on the distribution network,
is taken as 0.2. A larger value of
indicates that the aggregation has a higher value of regulating the voltage of the whole network after injecting units of active and reactive power for regulation.
The final regulation results are shown in
Table 5; the lowest voltage-to-power ratio of the non-aggregation scheme indicates that on average each PV has the worst regulation effect if no aggregation is performed; the aggregation based on the characteristics of the power curves does not consider the grid topology, and the selected aggregations have a medium regulation effect; the selected aggregations of the scheme in this paper have the highest voltage-to-power ratios, which indicates that compared with the aggregation strategy based on the clustering of the power curves, this paper’s aggregation strategy, which comprehensively takes into account the grid topology, is more effective at filtering the PVs that have high regulation ability and has a more responsive regulation effect.
4.4. Discussion
The proposed aggregation strategy and the voltage regulation model built can be applied to low-voltage distribution networks. In practice, if the PV output curve and the topological information of the distribution network are known, the most sensitive DPVs in terms of voltage regulation capability, i.e., a large voltage variation with a minimum power variation, can be obtained by the proposed aggregation strategy.
The application of the proposed method does not require additional investment as DPVs are used for voltage regulation. The proposed method can be deployed in the platform in the control center of the distribution network. Moreover, this paper focuses on DPV aggregation and screening the DPVs with optimal voltage regulation. So, the influence of DPVs on other types of voltage regulation devices is not fully considered in the paper, which will be left for future research.