Sequential Data-Based Fault Location for Single-Line-to-Ground Fault in a T-Connection Power Line
Abstract
1. Introduction
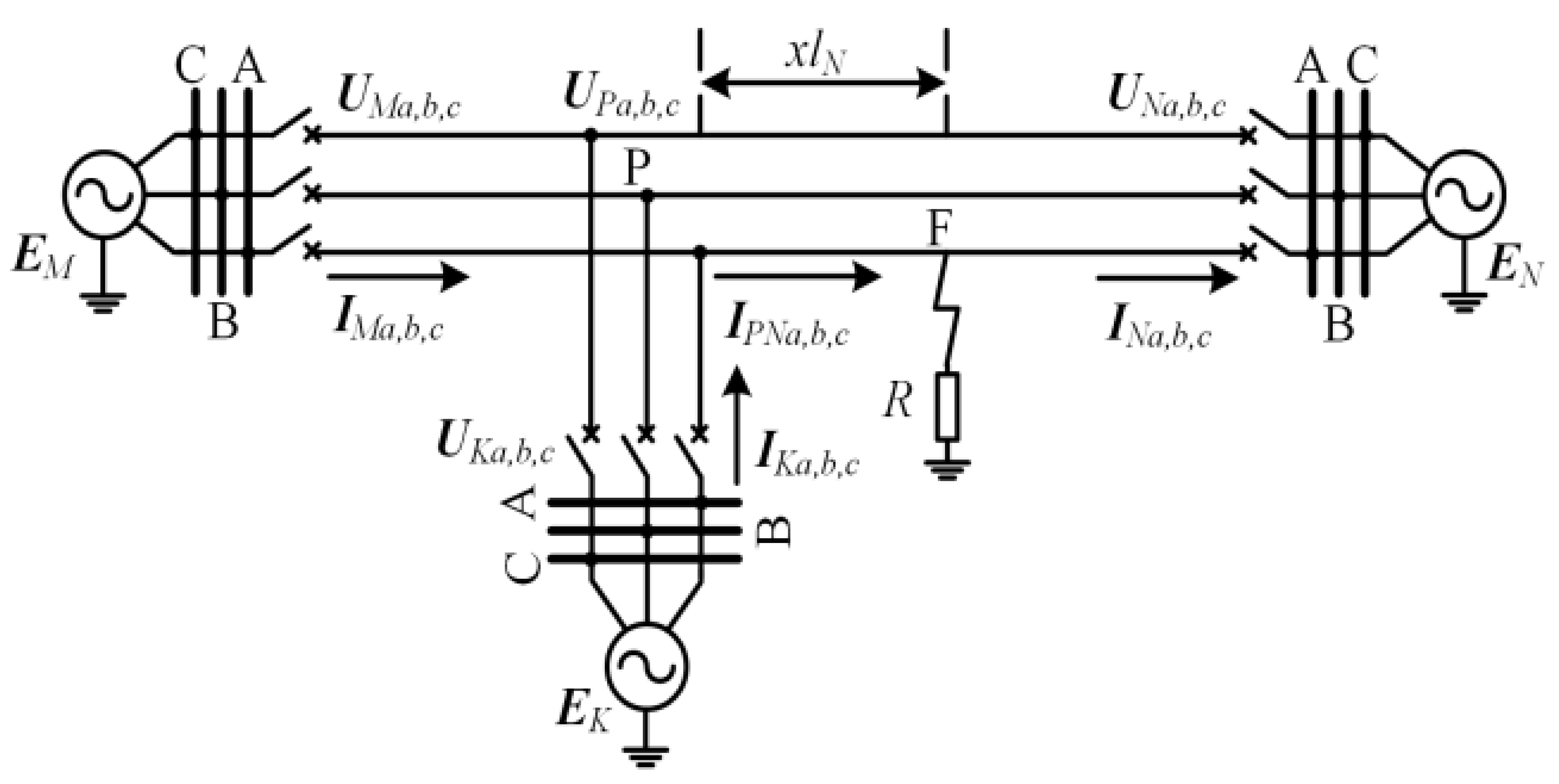
2. Sequential Characteristic Analysis of Single-Line-to-Ground Fault in a T-Connection Power Line
2.1. The Stage after Fault Occurrence
2.2. The Stage after One Opposite Terminal (Suppose N Terminal) Circuit Breaker Tripping
2.3. The Stage after the Second Opposite Terminal (K Terminal) Circuit Breaker Tripping
3. Applying Sequential Data for Fault Location
3.1. The Simplification of Fault Location Equations
3.2. The Algorithm of Equation Solving
4. Case Simulations
4.1. The Impacts of Fault Distance
4.2. The Impacts of Fault Resistance
4.3. The Impacts of the Hypothetical Error of Equivalent Impedance of a Branch
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, G.; Zha, K.; Zhang, J.; Wang, Z.; Zhang, F.; Cao, J. Grounding fault in series-connection-based offshore wind farms: Fault clearance. IEEE Trans. Power Electron. 2020, 35, 9357–9367. [Google Scholar] [CrossRef]
- Ajinkya, J.S.; Amod, C. Umarikar. Small-signal stability analysis of PV-based synchronverter including PV operating modes and DC-Link voltage controller. IEEE Trans. Ind. Electron. 2022, 69, 8028–8039. [Google Scholar]
- Naidu, O.D.; Pradhan, A.K. Precise Traveling Wave-Based Transmission Line Fault Location Method Using Single-Ended Data. IEEE Trans. Ind. Inform. 2021, 17, 5197–5207. [Google Scholar] [CrossRef]
- Lopes, G.N.; Menezes, T.S.; Gomes, D.P.S.; Vieira, J.C.M. High Impedance Fault Location Methods: Review and Harmonic Selection-Based Analysis. IEEE Open Access J. Power Energy 2023, 10, 438–449. [Google Scholar] [CrossRef]
- Terzija, V.; Preston, G.; Stanojević, V.; Elkalashy, N.I.; Popov, M. Synchronized measurements-based algorithm for short power line fault analysis. IEEE Trans. Smart Grid 2015, 6, 2639–2648. [Google Scholar] [CrossRef]
- Davoudi, M.; Sadeh, J.; Kamyab, E. Parameter-free fault location for power lines based on optimization. IET Gener. Transm. Distrib. 2015, 9, 1061–1068. [Google Scholar] [CrossRef]
- Yuan, B.; Wang, B.; Lu, Y.; Lu, L.; Liu, H.; Chen, C.; Wu, L. Error analysis of single-end fault location for single-line-to-ground fault in power line with wind farm connection. Power Syst. Prot. Control 2016, 44, 63–69. [Google Scholar]
- Jiang, J.; Chuang, C.; Wang, Y.; Hung, C.; Wang, J.; Lee, C.; Hsiao, Y. A hybrid framework for fault detection, classification, and location-part I: Concept, structure, and methodology. IEEE Trans. Power Deliv. 2011, 26, 1988–1998. [Google Scholar] [CrossRef]
- Wang, B.; Dong, X.; Lan, L.; Xu, F. Novel location algorithm for single-line-to-ground faults in power line with distributed parameters. IET Gener. Transm. Distrib. 2013, 7, 560–566. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, H.; Song, Y. A new fault location algorithm for extra-high-voltage mixed lines based on phase characteristics of the hyperbolic tangent function. IEEE Trans. Power Deliv. 2016, 31, 1203–1212. [Google Scholar] [CrossRef]
- Ji, L.; Booth, C.; Dyśko, A.; Kawano, F.; Beaumont, P. Improved fault location through analysis of system parameters during autoreclose operations on power lines. IEEE Trans. Power Deliv. 2014, 29, 2430–2438. [Google Scholar] [CrossRef]
- Geng, J.; Wang, B.; Dong, X. A novel one-Terminal single-line-to-ground fault location algorithm in power line using post-single-phase-trip data. Trans. China Electrotech. Soc. 2015, 30, 184–193. [Google Scholar]
- Anderson, P.M. Power System Protection; Wiley-IEEE Press: Hoboken, NJ, USA, 1998. [Google Scholar]
- Hartley, H.O. The modified Gauss-Newton method for the fitting of non-linear regression functions by least squares. Technometrics 1961, 3, 269–280. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt Algorithm: Implementation and Theory, Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]

| Sequence | Line (ohm/km) | M Side System (ohm) | N Side System (ohm) | K Side System (ohm) |
|---|---|---|---|---|
| Positive Seq. | 0.02 + j 0.28 | 28.3 ∠ 90° | 32 ∠ 78.4° | 43.2 ∠ 88.6° |
| Zero Seq. | 0.172 + j 0.84 | 26.3 ∠ 90° | 28.14 ∠ 86.7° | 29.09 ∠ 90° |
| Fault Distance (km) | Calculated Distance (km) | Absolute Error (km) | Relative Error (%) | Calculated R (ohm) |
|---|---|---|---|---|
| 5 | 4.97 | −0.03 | −0.06 | 100.03 |
| 10 | 10.02 | 0.02 | 0.04 | 99.99 |
| 15 | 14.96 | −0.04 | −0.08 | 99.99 |
| 20 | 20.15 | 0.15 | 0.30 | 99.99 |
| 25 | 24.79 | −0.21 | −0.42 | 100.06 |
| 30 | 30.32 | 0.32 | 0.64 | 99.92 |
| 35 | 34.60 | −0.40 | −0.80 | 100.13 |
| 40 | 39.80 | −0.20 | −0.40 | 100.07 |
| 45 | 45.32 | 0.32 | 0.64 | 99.90 |
| Grounding Resistance (ohm) | Fault Distance (km) | Calculated Distance (km) | Absolute Error (km) | Relative Error (%) |
|---|---|---|---|---|
| 5 | 10 | 10.27 | 0.27 | 0.54 |
| 25 | 24.93 | −0.07 | −0.14 | |
| 40 | 39.90 | −0.10 | −0.20 | |
| 50 | 10 | 10.01 | 0.01 | 0.02 |
| 25 | 24.92 | −0.08 | −0.16 | |
| 40 | 40.24 | 0.24 | 0.48 | |
| 100 | 10 | 10.02 | 0.02 | 0.04 |
| 25 | 24.79 | −0.21 | −0.42 | |
| 40 | 39.80 | −0.20 | −0.40 | |
| 200 | 10 | 9.93 | −0.07 | −0.14 |
| 25 | 24.68 | −0.32 | −0.64 | |
| 40 | 40.59 | 0.59 | 1.18 | |
| 300 | 10 | 10.12 | 0.12 | 0.24 |
| 25 | 24.73 | −0.27 | −0.54 | |
| 40 | 40.89 | 0.89 | 1.78 |
| Assumed Zero Sequence Impedance at K Terminal | Fault Distance (km) | |||||
|---|---|---|---|---|---|---|
| 5 | 15 | 25 | 30 | 35 | 45 | |
| 29.09 ∠ 90° | 4.99 | 15.03 | 24.92 | 30.11 | 34.86 | 44.66 |
| 39.82 ∠ 90° | 5.27 | 15.49 | 25.58 | 30.88 | 35.71 | 45.69 |
| 20.36 ∠ 90° | 4.71 | 14.5 | 24.11 | 29.18 | 33.8 | 43.37 |
| 29.09 ∠ 80° | 5.10 | 15.21 | 25.16 | 30.40 | 35.18 | 45.05 |
| 29.09 ∠ 70° | 5.22 | 15.39 | 25.42 | 30.68 | 35.49 | 45.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Yu, H.; Wang, B.; Liu, Y.; Lu, Y.; Liu, W. Sequential Data-Based Fault Location for Single-Line-to-Ground Fault in a T-Connection Power Line. Energies 2024, 17, 2975. https://doi.org/10.3390/en17122975
Li L, Yu H, Wang B, Liu Y, Lu Y, Liu W. Sequential Data-Based Fault Location for Single-Line-to-Ground Fault in a T-Connection Power Line. Energies. 2024; 17(12):2975. https://doi.org/10.3390/en17122975
Chicago/Turabian StyleLi, Lisheng, Haidong Yu, Bin Wang, Yang Liu, Yuanyuan Lu, and Wenbin Liu. 2024. "Sequential Data-Based Fault Location for Single-Line-to-Ground Fault in a T-Connection Power Line" Energies 17, no. 12: 2975. https://doi.org/10.3390/en17122975
APA StyleLi, L., Yu, H., Wang, B., Liu, Y., Lu, Y., & Liu, W. (2024). Sequential Data-Based Fault Location for Single-Line-to-Ground Fault in a T-Connection Power Line. Energies, 17(12), 2975. https://doi.org/10.3390/en17122975








