1. Introduction
The transition towards sustainable energy systems is a critical challenge for developing sustainable cities and societies [
1]. The European Union (EU) has set the ambitious target of achieving net zero Greenhouse Gas (GHG) emissions by 2050, thus requiring significant efforts in sectors such as electricity, transportation, and industry [
2,
3]. Machine Learning and optimization have emerged as essential tools for managing the growing number of renewable resources, Electric Vehicles (EVs), and other technologies are being integrated into the grid [
4].
Energy Communities (ECs) are a promising concept that can help accelerate the transition towards sustainable energy systems while promoting local technological and societal development [
5,
6]. Citizen Energy Communities, in particular, are community-based organizations that enable citizens to invest in and benefit from renewable energy resources such as solar energy and that share power among the involved parties through several emergent mechanisms such as consumer/prosumer markets [
7]. Another EC guise, Local Energy Communities (LECs), have been linked to the Sustainable Development Goals (SDG) as an enabler for sustainable and social development [
8], while works such as [
9] delve in greater detail into the potential impacts considering individual goals of SDG.
Resource optimization has been widely studied in the context of Energy Communities, with many works focusing on scheduling, planning, energy resources management, and energy trading [
10,
11,
12,
13]. Common approaches include Linear Programming (LP), Mixed Integer Linear Programming (MILP), and other methods such as metaheuristics [
6]. However, the use of optimization in ECs is not without its challenges. In particular, the mutating nature of the interactions with the grid—be it by the aforementioned growing number of technologies to interact with it or market strategies—introduces uncertainty and constitutes an additional layer of complexity. High-quality modeling is then required, as poor EC definitions can lead to suboptimal results, such as constraints not reflecting real-world situations correctly. Furthermore, the computational requirements of optimization algorithms can be significant, thus making it infeasible to apply them in some contexts such as real-time scenarios [
14].
Metaheuristics appear as a competitive alternative that can alleviate some of the modeling costs and provide a way to obtain possible solutions, even if they are not optimal [
14]. However, with rapid expansion in the field and the introduction of new algorithms, there is a lack of literature on the benchmarking and methodologies for doing so [
15]. While some works have already benchmarked existing algorithms in different contexts, e.g., [
16,
17], there is currently no literature that benchmarks metaheuristics in the context of Energy Communities.
To bridge the identified lack of metaheuristic benchmark works in ECs, we propose a benchmark on an Energy Community scenario available online. The data and source code are available at
https://github.com/ECGomes/pyecom/tree/main (accessed on 11 June 2024) through the PyECOM GitHub repository. This work then provides a benchmark of six algorithms—the Mountain Gazelle Optimizer (MGO) [
18], the Dandelion Optimizer (DO) [
19], the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) [
20], Differential Evolution (DE) [
21], the Genetic Algorithm (GA) [
22], and Particle Swarm Optimization (PSO) [
23]. The algorithms are applied in the context of energy management and scheduling in an Energy Community and are compared based on their objective function, execution times, and the effect of each solution on EC management. The used EC provides a testing ground that has both renewable and non-renewable energy sources in an attempt to exemplify how Renewable Energy Sources (RESs) can be integrated into the workings of the community. Our contributions can be described as follows:
The development of an Energy Community benchmark procedure to evaluate and compare the performance of various metaheuristics.
Providing a comparative analysis of the different methods based on key metrics such as objective function values, computational efficiency (iterations per second), and solution component quality.
The remainder of this paper is organized as follows. In
Section 2, we present a literature review of the relevant work on optimization in Energy Communities. In
Section 3, we present the formulation of the objective functions used throughout this work. In
Section 4, we describe the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) algorithm, as well as the other methods used for the benchmark. In
Section 5, we present the results of our experiments and compare the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) with the remaining methods, thus providing a brief analysis of each. In
Section 6, we provide our insights on the performance of the algorithms from a more technical perspective, thus elucidating possible reasons for their behavior. Finally, in
Section 7, we discuss the implications of our results and provide some concluding remarks.
2. Background and Related Work
The energy transition is a trending area of research, thus intending to move away from pollutant energy sources to others that are less pollutant and renewable. However, the literature indicates that a complete energy transition has never taken place, and this may cause its own set of problems [
24,
25,
26]. Regarding issues that arise from the rise of Renewable Energy Sources (RESs), ref. [
25] highlights the social components, thus drawing attention to the potential lack of access to energy, energy costs inflation, and the loss of revenue brought on by declining industries such as coal, as well as the implications on environments where it is a source of income. In [
26], the authors discuss the meaning of “transition” and argue how it is more akin to “addition”, thus expanding the energy pool instead of replacing certain aspects of energy production. In particular, the authors discuss how the consumption of previous sources has continued to grow despite the introduction of new technologies.
Energy Communities are a concept that has been gaining traction in recent years, thus having gained the backing of the EU [
5], and they are expected to contribute to the EU’s emission goals while paving the way for more sustainable environments [
27]. Having as base principles the facilitation of the access of energy to a wider population—thus providing incentives to renewable technology integration, citizen participation, and energy equity—ECs have the potential to play an active part in the energy sector while aiming to provide social benefits and opportunities to the parties involved [
28]. However, management in this context requires careful planning and has been widely studied in recent years, with many works exploring the potential benefits through the use of optimization techniques. This section provides a review of the literature on the relevant research on optimization in ECs, thus highlighting key findings and contributions.
In the electricity sector, optimization is crucial for addressing various challenges. Key research areas encompass forecasting [
29], scheduling [
30], storage control [
31], energy trading [
32], and load disaggregation [
33]. Additional research focuses on maximizing self-consumption [
34] and minimizing costs [
35]. Specifically, ECs are influenced by all these issues.
Scheduling in ECs becomes a quintessential aspect of their functioning. It is vital, as it helps to manage the use of renewable energy resources to maximize efficiency and minimize costs. ECs often have different sources of generation, storage solutions, and consumption profiles, and scheduling can be used to optimize the interactions between components. Battery Energy Storage Systems (BESSs) are often studied, because they provide the opportunity to store energy when generation is abundant and to supply it later when necessary, thus reducing waste and costs. In [
36], the authors studied a Renewable Energy Community (REC) that possesses photovoltaic generation and analyzed the impact of a Battery Energy Storage Systems (BESS), thus providing an economic assessment of the impact of the optimization strategy adopted.
Energy trading has also gained attention, thus facilitated by technological developments where consumers have become an active part of energy generation by becoming prosumers [
7]. Peer-to-Peer (P2P) has emerged as a way for prosumers to exchange energy between them, thus lowering the requirements imposed upon the main grid [
37]. This shift has led to the need for new market solutions that consider not only the main grid but also the new roles of prosumers [
7,
38]. User preferences have been studied, with works such as [
39] analyzing the benefits beyond the technological and economic perspectives. Furthermore, works such as [
35] explore the integration of EVs through a Vehicle-to-Grid (V2G) approach and how their interactions with ECs can be modeled, thereby also highlighting their potential advantages in markets.
Overall, optimization techniques play a critical role in the management of ECs, thus providing a means to optimize the use of Renewable Energy Sources (RESs), storage systems, and other technologies. LP is a common optimization technique used in EC research, which is a mathematical method that is used to find the optimal solution to a problem composed of linear constraints and objective functions. MILP is a similar method to LP, with the addition of binary variables. In [
6], the authors mention MILP as the most-used approach for ECs research. It has been used to find the optimal generation, storage, and charging schedule that minimize the cost of energy while supplying the required power demand, e.g., [
35,
40].
While LP and MILP are capable of finding an optimal solution, these methods are reliant on the quality of the constraints imposed and the definition of the objective function. This can be troublesome, as some constraints may not necessarily reflect the real-world behavior of systems, such as battery interactions and their degradation. Approximation methods such as the mentioned metaheuristics can prove helpful in these cases. However, metaheuristics require significant computational resources, and there is a tradeoff between solution quality and time expended [
14].
In [
14], the authors presented a comprehensive review of the use of metaheuristics in the context of smart grids and some of the main tasks involved, such as Optimal Power Flow (OPF). Differential Evolution (DE), the Genetic Algorithm (GA), and Particle Swarm Optimization (PSO) were among the most commonly applied methods and the most common benchmarks for other proposed algorithms. Furthermore, the success of metaheuristics and the appeal of being adaptable to various problems, unlike regular heuristics that are problem-dependent, resulted in the search for natural behaviors that can be emulated mathematically. This is the case for recent methods such as the Dandelion Optimizer (DO) and the Mountain Gazelle Optimizer (MGO), which have already proven to be capable in the energy domain, with works such as [
41,
42].
However, as mentioned in [
15], the field of metaheuristics lacks benchmarks and methodologies, as well as reproducible use cases to standardize the testing of new methods. This is also the case in the field of Energy Communities where, to the best of the author’s knowledge, there are currently no published benchmarks on metaheuristic optimization.
3. Energy Community Formulation
The work presented is based on a scenario described in [
43], thus describing an Energy Community comprising renewable (n = 5) and non-renewable generators (n = 2), BESSs (n = 3), EVs (n = 5), and import and export capabilities. The presented scenario has a horizon of 24 timesteps, thus intending to minimize operational and economic costs.
Table 1 presents an overview of the Energy Community used throughout this work, with the values representing the sum of the grouped components.
Each of the resource groups obeys the constraints described in [
43], which are common to all algorithms. The objective function utilized can be described as the sum of all the production and consumption costs, with an added penalty to reflect imbalance situations. The penalty is formulated in a way such that all algorithms can achieve solutions that respect the imposed constraints and maintain grid stability, thereby being heavily penalized otherwise. Equation (1) presents the objective function used throughout this work, except for BESSs and EVs, where Equation (2) is utilized.
In particular, Equation (2) follows the proposed formulation found in [
44], thus implemented to consider storage degradation costs. The values
and
were chosen upon experimenting with the cost curves and can be found in PyECOM’s repository. The penalty was added as a fixed value, at each timestep, whenever the excess or deficit energy could not be handled by the community’s imports and exports.
As such, the resulting objective function, including penalties, can be found in Equation (3):
4. Materials and Methods
This section describes the algorithms, tools, encoding, solution handling strategies, and the methodology that was used to evaluate the performance and consistency of various optimization methods.
4.1. Algorithms
As previously mentioned, the algorithms benchmarked in this paper are the Mountain Gazelle Optimizer (MGO), the Dandelion Optimizer (DO), the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF), Differential Evolution (DE), the Genetic Algorithm (GA), and Particle Swarm Optimization (PSO). The last three algorithms were chosen for being commonly used in the literature [
6,
14,
16], while the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) appears as an improvement to Differential Evolution (DE). The Mountain Gazelle Optimizer (MGO) and the Dandelion Optimizer (DO) reflect the emergence of newer algorithms inspired by nature. Overall, the selected algorithms represent two large families of metaheuristics, namely population-based methods (HyDE-DF, DE, and GA) and swarm-based methods (PSO).
4.1.1. Differential Evolution
The Differential Evolution (DE) algorithm [
21,
45] is a simple optimization method that generates new solution candidates by selecting three existing vectors from the population at a time. The difference between the second and third vectors is then added to the first. This makes it so that Differential Evolution (DE) is easily applied to various scenarios. The operator is described in Equation (4).
A population size of 20 was used, thus being the default value in the optimization framework utilized throughout this work. For the crossover rate, a value of
was selected following the recommendations for the type of problem tackled, which is found in [
46].
Jitter, a technique where the weighting factor
F is randomly chosen for each difference vector, was available for use, as it helps the convergence of the algorithm [
46]. However, it was disabled due to errors during execution.
4.1.2. Hybrid Adaptive Differential Evolution with a Decay Function (HyDE-DF)
Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) is a modified version of Hybrid Adaptive differential Evolution (HyDE), which is a successor to Differential Evolution (DE). Population generation is inspired by the original differential evolution algorithm [
21], in which each population element is updated by a factor of the difference between two other elements. The operator, as described by the authors, is presented in Equation (5):
where
is the current vector,
represents the best solution found thus far, and
and
represent two individuals from the population. Vectors
,
, and
are different among themselves. The hybrid adaptive component of the algorithm is responsible for keeping track of scale factors for each population element throughout iterations. These are represented in Equation (5) by
,
, and
, where
, which is inspired by [
47]. The term
promotes convergence in the direction of current best candidate solutions [
20], thus having its weight reduced over time by a decay factor
, which is similar to Simulated Annealing (SA) [
48].
The Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) implementation for this work follows the implementation provided by the original authors in [
49]. As with the original implementation, elitismis promoted, with the best solution of each iteration being injected into the next iteration. However, said implementation only allows for the definition of a single value range shared across all variables. This constitutes a challenge in problems where, for example, different variables operate in different ranges. Motivated by this issue, this paper’s implementation of Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) allows for the specification of individual variable value ranges, thus furthering the algorithm’s capabilities. The chosen parameters for the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) were a population size of 20 coupled with a crossover rate
. The crossover value was preserved from the Differential Evolution (DE) algorithm, while a reduced population size was set, as empirical experiments with larger values did not alter the results obtained.
4.1.3. Genetic Algorithm
The Genetic Algorithm (GA) is a classical optimization algorithm that attempts to emulate biological evolution [
22]. A population of potential solutions is initialized and evaluated using a fitness function. The candidates in the population are then selected according to a set of criteria, such as their fitness score or their position in the population. The selected options undergo crossover, where information from two solutions is combined to create a new solution, and mutation, where new, random variations are introduced into the population. The resulting population is then evaluated again, and the process repeats until an optimal solution is found. The settings for this algorithm, such as the population size, the probabilities of crossover and mutation, and the selection method, were left at their default values.
4.1.4. Particle Swarm Optimization
Particle Swarm Optimization (PSO) [
48] attempts to leverage the behavior of swarms found in nature. A population is initialized and spread across the solution space, with each swarm particle moving along the space using a dynamic velocity component. This component incorporates information on how well the individual particle performs, as well as the swarm’s best found solution. Both individual and swarm components can have different weights, thus constituting a tradeoff between personal or global importance, with higher personal values promoting exploration, whereas higher global importance promotes exploitation. Pymoo possesses an adaptive option, thus updating these weights with each generation.
As an evolutionary algorithm, Particle Swarm Optimization (PSO) can explore the global search space. However, a possible issue can be encountered whenever a local minimum is found, as the swarm may converge toward it. This is more frequent when the population size is too small for the problem at hand, as there is an insufficient exploration across the solution space. Mentioned by [
50] as an
“Exploration and exploitation strategy based on behavior in swarms", the swarm may be drawn to exploiting the local optima found.
4.1.5. Mountain Gazelle Optimizer
The Mountain Gazelle Optimizer (MGO) [
18] is a method inspired by the behavior of mountain gazelles, and it is split into stages that attempt to emulate the cycle of the rise and fall of a gazelle population. The Mountain Gazelle Optimizer (MGO) counts with four update mechanisms per existing solution, at the end of which a new solution is added to the population. Whenever the entire population is updated, the amount of solutions is sorted in ascending order and trimmed to the maximum population value set by the user. This results in the best gazelles surviving for the next iteration.
The update stages are based on the bachelor male herds, maternity herds, solitary territorial males, and migration. These operators were designed to create new gazelles such that issues such as getting stuck on local optima happen less often.
It should be noted that while the algorithm can promote exploration and produce quality results, the number of operators and new solutions injected into the population results in added computational time, as the evaluated solutions become per iteration. This algorithm was implemented in Python by the authors of this work, thereby following the MATLAB source code (version 1.0.1) of the authors of the method.
4.1.6. Dandelion Optimizer
The Dandelion Optimizer (DO) [
19] tries to replicate the spread of dandelion seeds through the wind in nature. It is comprised of a rising stage, a descending stage, and a landing stage. The rising and descending stages focus on the exploration aspect of the landscape, thus serving to disseminate the various solutions across the terrain, while the landing stage focuses on exploiting. The landing stage attempts to converge to a location that is best suited for survival, thereby eventually reaching the global optima.
The dandelion seeds are updated at the end of each landing stage, thus resulting in a new population of solutions to carry over. As is the case with the Mountain Gazelle Optimizer (MGO), this algorithm was implemented in Python by the authors of this work, thereby following the MATLAB source code (version 1.0.4) of the authors of the method.
4.2. Tools
The entire work was implemented in Python using the PyECOM package [
51], which is available on GitHub. The Mountain Gazelle Optimizer (MGO), Dandelion Optimizer (DO), and Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) optimization algorithms are provided by PyECOM, while the three other algorithms described in the previous subsection are implemented by the package Pymoo (version 0.6.0.1). These algorithms were selected, as they are prevalent among related works using metaheuristics [
14].
Code efficiency was taken into account during the development of this work, as the metaheuristics implemented, as well as the repair procedures, prioritized matrix-based calculations whenever possible instead of resorting to loops.
Pymoo [
52] is a Python package that focuses on optimization, thus providing a simple and common interface to several existing and well-known optimization algorithms such as those previously mentioned, as well as implementations of methods such as NSGA-II [
53]. To complement the algorithms, it also provides constraint handling and several customization options for developing new algorithms. A stop criterion was set on all Pymoo algorithms to ensure fast execution and reduce excess computation. The stop criterion used is Pymoo’s default single objective termination, thus considering the number of generations and evaluations, as well as objective tolerance.
All the results in this paper were obtained on a laptop with an Apple M3 chip (12 core) and 18 GB RAM. The implementations relied solely on the CPU.
4.3. Encoding and Solution Handling
The encoded solutions throughout this work are in the form of a vector with length N, which is calculated by . This is achieved by flattening and concatenating the variable matrices. Decoding is possible, as the placement of any given variable within the vector is known beforehand.
Due to the nature of metaheuristics, a repair procedure for each candidate solution is required to ensure that produced solutions are viable. For this purpose, each solution is decoded and repaired before being evaluated in terms of fitness. The repair procedure is the same across all methods, whether implemented by PyECOM or Pymoo.
The initial population is dependent on the method used, with Genetic Algorithm (GA), Differential Evolution (DE), and Particle Swarm Optimization (PSO) using Pymoo’s initial population conditions, while Dandelion Optimizer (DO), Mountain Gazelle Optimizer (MGO), and Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) generate an initial population within lower and maximum bounds for each dimension. It should be noted that while this work does not provide an initial solution to have a fair comparison between algorithms, providing an initial solution to the methods can lead to an overall improvement in performance.
4.4. Hyperparameter Settings
To assess the performance and consistency of each method, 10 experiments were run for each algorithm, with the maximum number of iterations set to 20,000. An epsilon stopping criteria of
was set, with a tolerance of 1000 iterations. The experiments were performed with random seeds to evaluate the variability of the results.
Table 2 displays the hyperparameters used for each algorithm.
4.5. Evaluation Procedure
Each algorithm was analyzed considering the solutions produced and execution speeds, thus making it possible to judge both the quality of the solution and the computational performance. The metric for evaluating solutions is the objective function value, thus giving an overall idea of the costs of the solution, as well as providing an objective value to compare solutions at a glance. Finally, each solution can be decomposed into the several components that make up the Community, such as generation and storage usage, which enables the evaluation of the effects of the optimization in the EC.
5. Results
In this section, the various optimization algorithms are compared, with an analysis of objective function values, iterations per second, total number of iterations, and provided solutions.
Table 3 reports the values of the objective function of all runs conducted throughout this work, with
Table 4 providing insights on the execution speeds, which are reported in iterations per second.
Table 5 informs the number of iterations utilized by each method before established stopping criteria take effect.
Figure 1 showcases the difference in the computational performance outcomes between the compared methods. The Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) was vastly superior to the other benchmarked methods, thus boasting over double the average speed compared to the second-fastest method (Differential Evolution (DE)). This difference was further exacerbated when compared to the remaining methods, thus widening the gap to a factor of 10 times the speed of the Mountain Gazelle Optimizer (MGO).
Among the tested methods, the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) achieved the best results, with consistently lower objective function values. This was followed by the Differential Evolution (DE) algorithm, with an average difference of 3% comparred to the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF), but with a significantly lower variance, which was the lowest among all methods. At a high level, the Dandelion Optimizer (DO) performed capably, with its average objective function value ranking third. The Genetic Algorithm (GA) did not achieve good results compared to the three methods that found more suitable solutions, both in terms of objective function and speed. The Mountain Gazelle Optimizer (MGO) and Particle Swarm Optimization (PSO) were found to have high variance, thus indicating inconsistencies when producing results, and they were overall the worst-performing methods.
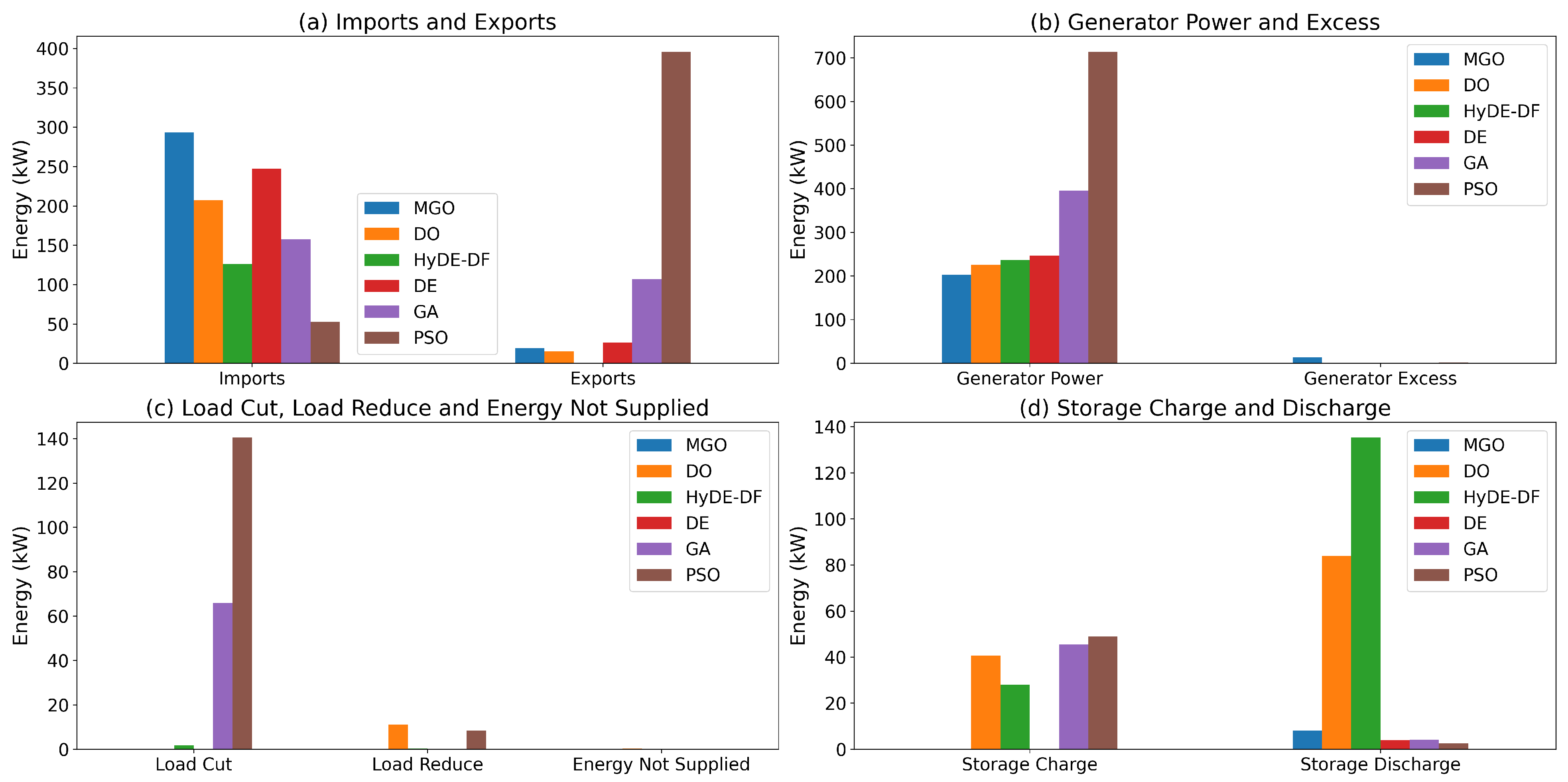
Figure 2 presents the individual components of the generated best solutions of each algorithm to facilitate comparisons between methods.
5.1. MGO
The Mountain Gazelle Optimizer (MGO) presented a high standard deviation on the objective function values (
) and the lowest amount of iterations per second (
), thus indicating that the method is not particularly well suited for the proposed task. Regarding the achieved solutions, its best solution attained a value of
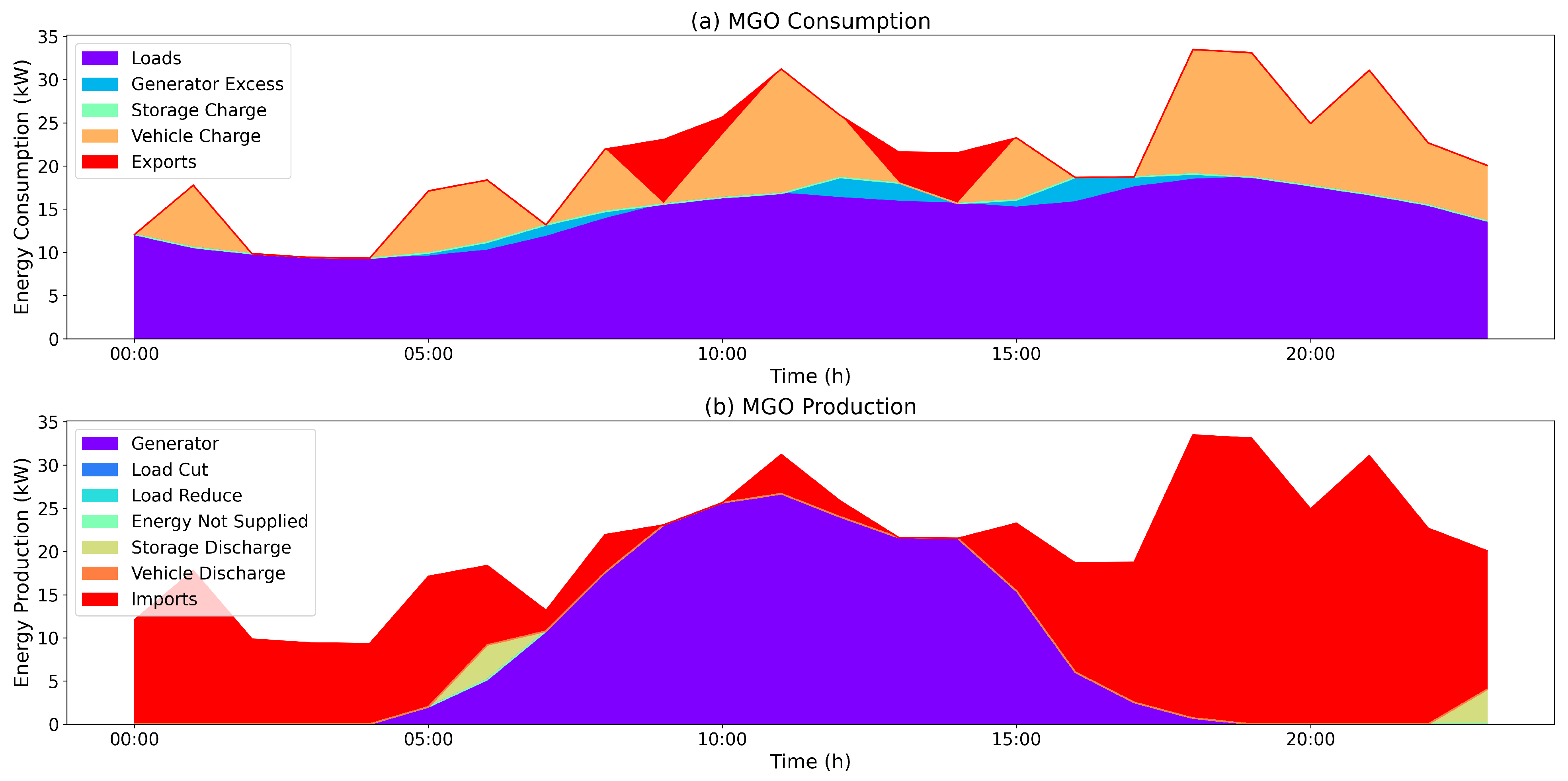
throughout the maximum allowed iterations. More concretely, the Mountain Gazelle Optimizer (MGO) made use of a large volume of imports, thus managing to guarantee the necessities of the community albeit at the cost of some generated energy being wasted, as per
Figure 2. This method did not employ the storage systems present in the scenario at all.
Figure 3 presents a more detailed view of the utilization of resources chosen by the best solution.
5.2. DO
The Dandelion Optimizer (DO) algorithm obtained an average objective function value of
and
iterations per second. The analyzed run presents an overall balanced approach that made the most of renewable generators whenever possible, thereby only resorting to a non-renewable generator at night, as seen in
Figure 4. The additional consumption profile of the solution was met using the storage technologies and imports from the main grid. However, the small use of energy not supplied and load-reducing techniques hampered the solution, thus making it unsuitable for practical applications.
5.3. HyDE-DF
The Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) was the best-performing algorithm, with its best run achieving an objective function value of
over the maximum allowed iterations.
Figure 5 presents the distribution of the resources used through the considered window, which is categorized into generation and consumption domains presented by the solution.
The chosen solution for the HyDE-DF algorithm presented a stable renewable generation, thereby only complemented by a non-renewable source in two instances. Taking into account the deterministic behavior of the electric vehicles, the solution achieved presented a greater focus on discharging BESS components to achieve system balance. Although a supplementary non-renewable generator was part of the community formulation, it was not utilized; instead, the algorithm preferred to import the remaining energy from the grid. Overall, the solution presented by the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) is a feasible one that does not need to resort to load-cutting or load-reducing techniques to preserve the well-being of the system.
Regarding the performance, the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) boasts the highest iterations per second values and was significantly faster than the rest of the algorithms compared in this work. Coupled with the achieved objective function values, the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) is well posed to solve EC-related tasks in the future.
5.4. Differential Evolution
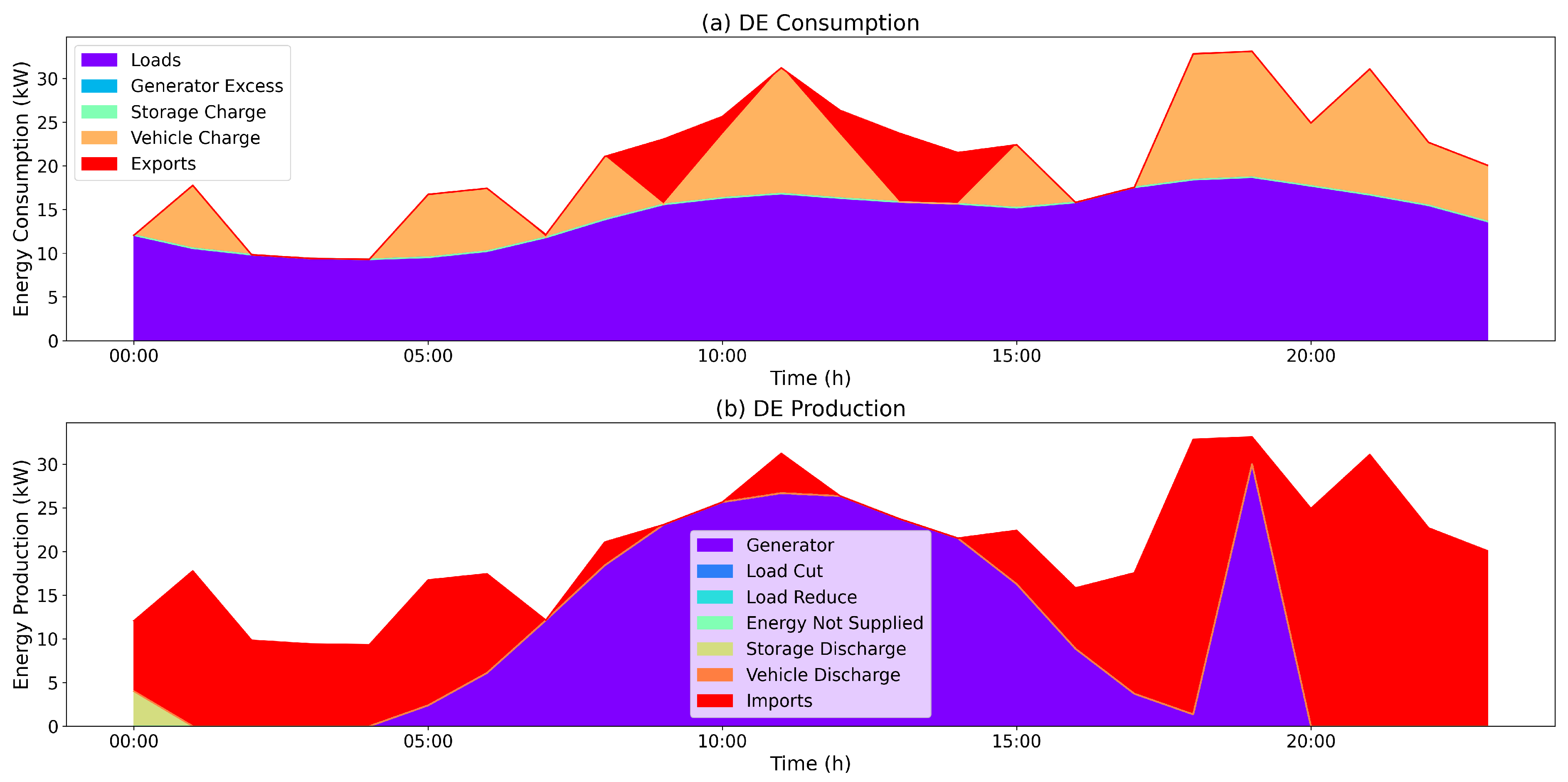
Differential Evolution (DE) ranked second in terms of its objective function value (
) while being comparable to the Dandelion Optimizer (DO) in terms of iterations per second. Comparatively to the most similar algorithm, the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF), the solution given made less use of load cut, but it significantly used less of the storage systems, thus barely charging any and having almost no discharge amount. Furthermore, it exhibited a significant amount of imports that could potentially be avoided with the aforementioned storage usage.
Figure 6 depicts the solution’s temporal evolution of its respective components, which is grouped according to consumption and generation. Overall, the Differential Evolution algorithm proved to be an adequate candidate to tackle the proposed problem, thereby comparable to newer methods in computational performance. The termination criteria set was able to stop the algorithm within a reasonable amount of time and retain good solutions.
5.5. Genetic Algorithm
The Genetic Algorithm (GA) obtained an objective function value of
on average. Although the provided solution made extensive use of generators, engaging in both renewable and non-renewable generators, it did not manage to achieve a state of an absence of load cut. Storage systems were scarcely used to provide power to the community, thus leaving room for improvement on that end. In addition, the export value reported is significantly higher compared to the previous approaches. These factors make it so that the solution is not satisfactory, as energy generated was not used internally (i.e., to charge storage) but instead sold to the grid. The breakdown of the resulting solution can be found in
Figure 7.
5.6. Particle Swarm Optimization
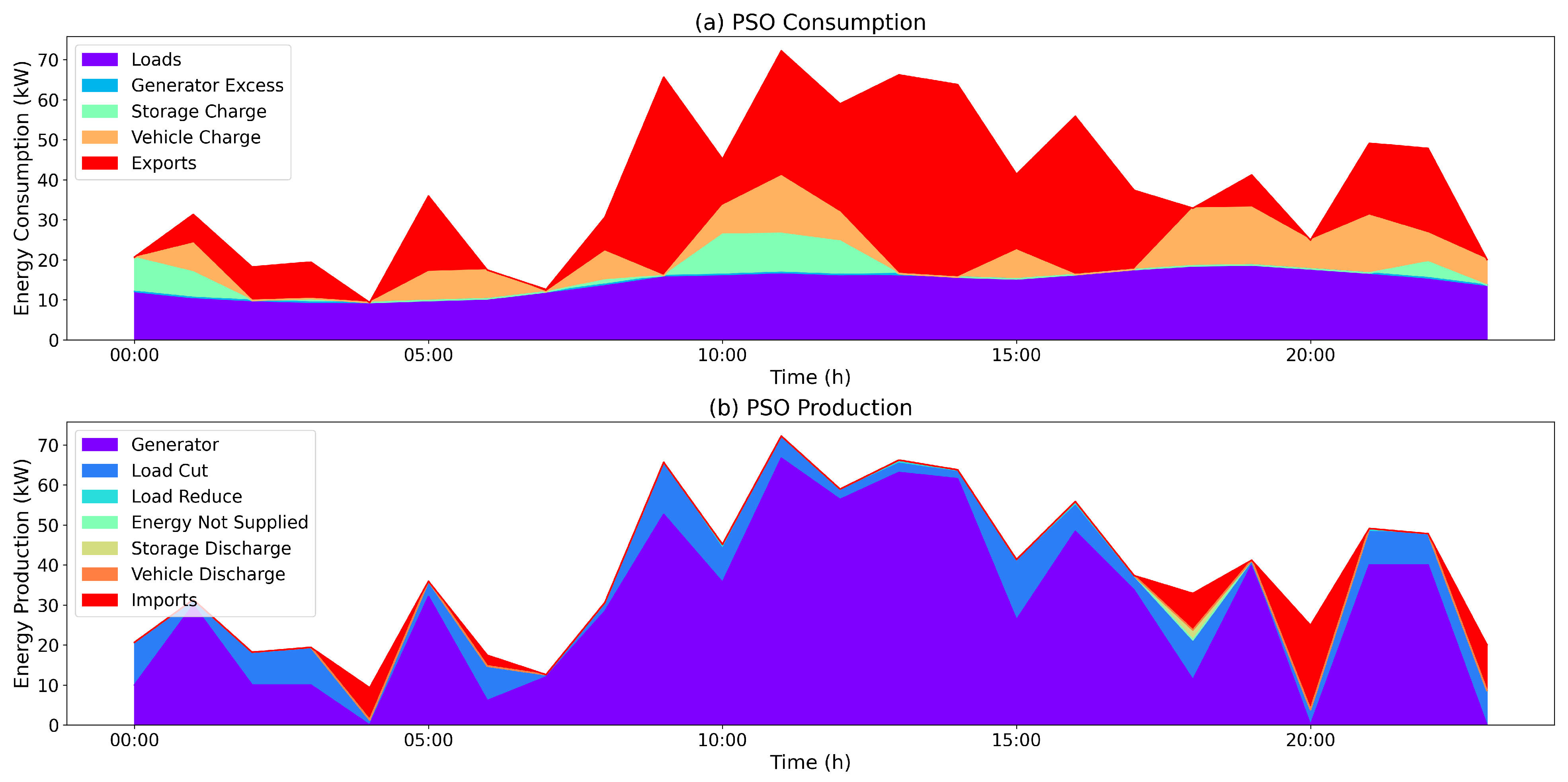
Particle Swarm Optimization (PSO) achieved the worst average objective function values among all the benchmarked algorithms, with an average of
. This is reflected in the solution presented in
Figure 8, where non-renewable generators were engaged throughout the day and mostly used to export energy. This reflects a poor decision process, as the solution still requires imports to achieve grid balance. Coupled with the generation issues, the observed run made use of load cutting, thus resulting in an overall poor solution. All in all, Particle Swarm Optimization (PSO) was not capable of providing a stable alternative for the presented problem while also being one of the slowest methods.
6. Discussion
Taking into account all the benchmark results presented thus far, we argue that the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) algorithm is the most suited for the task proposed. The Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) not only presented good solutions overall but also possesses the highest speed among all methods. This makes it well suited for time-critical tasks such as energy balance management. Contrary to the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF), the Mountain Gazelle Optimizer (MGO) had the lowest iterations per second value, which we attribute to the number of operators executed, as well as the population growing mechanism. Coupled with the sorting of the expanded population and the additional evaluation steps, the Mountain Gazelle Optimizer (MGO) proved to be quite inefficient. Finally, we observed that the Mountain Gazelle Optimizer (MGO) algorithm quickly stagnated, thus demonstrating a quick descent in objective function values over the first 1000 iterations but then decreasing just enough to not trigger an early stopping.
The Dandelion Optimizer (DO) successfully achieved a feasible solution at a glance, but it was not a practical one. Still, it can be considered a working solution that, with some minor tweaks, can achieve a good balance between the utilization of all available resources. The objective function value plot is unusual, thus sharply descending over the first 1000 iterations, much like the Mountain Gazelle Optimizer (MGO), but suffering from visible perturbations on its descent over the remaining iterations. This noise was reduced by the tail end of the iterations. We attribute this behavior to the levy flight embedded into the landing stage of the method.
Differential Evolution (DE) was surprising, especially when compared with the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF)—a more modern approach to Differential Evolution (DE). It managed to score objective function values that were very similar to the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) within a significantly shorter amount of iterations, thus regularly stopping at under the 5000 iteration mark. We believe the reasons for this great performance are due to the small nature of the problem, thereby requiring further testing with a larger population dimension to assess viability.
The Genetic Algorithm (GA) performed within expectations, thus achieving middling results. However, we acknowledge that it is a method that scales better with larger population values and could attain significantly better results. Due to the benchmark iterations per second component, the population size needed to be fixed to the mentioned value of 20, as the number of evaluations within a single iteration scales with the size of the population and would lead to a more disadvantageous setting for the Genetic Algorithm (GA) otherwise. With a larger population size, the Genetic Algorithm (GA) could be useful for solving problems similar to the one tackled with this benchmark.
Particle Swarm Optimization (PSO) did not manage to provide a feasible practical solution to this problem. While it made use of all the 20,000 iterations, the objective function value evolution presented stagnant periods, thus indicating that the algorithm was easily stuck in local optima. In short, we do not believe the Particle Swarm Optimization (PSO) algorithm is well suited for EC related tasks.
7. Conclusions
This work compared the performance of six different optimization methods—the Mountain Gazelle Optimizer (MGO), the Dandelion Optimizer (DO), the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF), the Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Differential Evolution (DE)—for use in Energy Communities. The findings presented indicate that the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) method is the most effective optimization method for this task, as it achieved the best results in terms of both solution quality and iterations per second. The Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) method is particularly useful for time-sensitive applications, as it had a significantly faster runtime compared to the other methods considered. These results suggest that the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) method may be more widely adopted in energy community optimization scenarios in the future.
However, this study has some limitations that should be taken into account. The effects of storage degradation required an analysis over a longer time frame, and the presented results may not generalize to scenarios with a larger number of resources. To address these limitations, future research should explore the scalability of these methods by increasing the number of resources considered and by studying the effects of storage degradation over a longer time frame, as the population size and dimension can skew the results in favor of certain methods. Additionally, other optimization methods, such as Reinforcement Learning, could be considered to further improve the operation of Energy Communities.
Overall, our findings suggest that the Hybrid Adaptive Differential Evolution with Decay Function (HyDE-DF) is a promising tool for optimizing operations in energy communities and that further research should be conducted to understand its potential benefits and limitations fully.