Example of Using Particle Swarm Optimization Algorithm with Nelder–Mead Method for Flow Improvement in Axial Last Stage of Gas–Steam Turbine
Abstract
:1. Introduction
2. Methodology
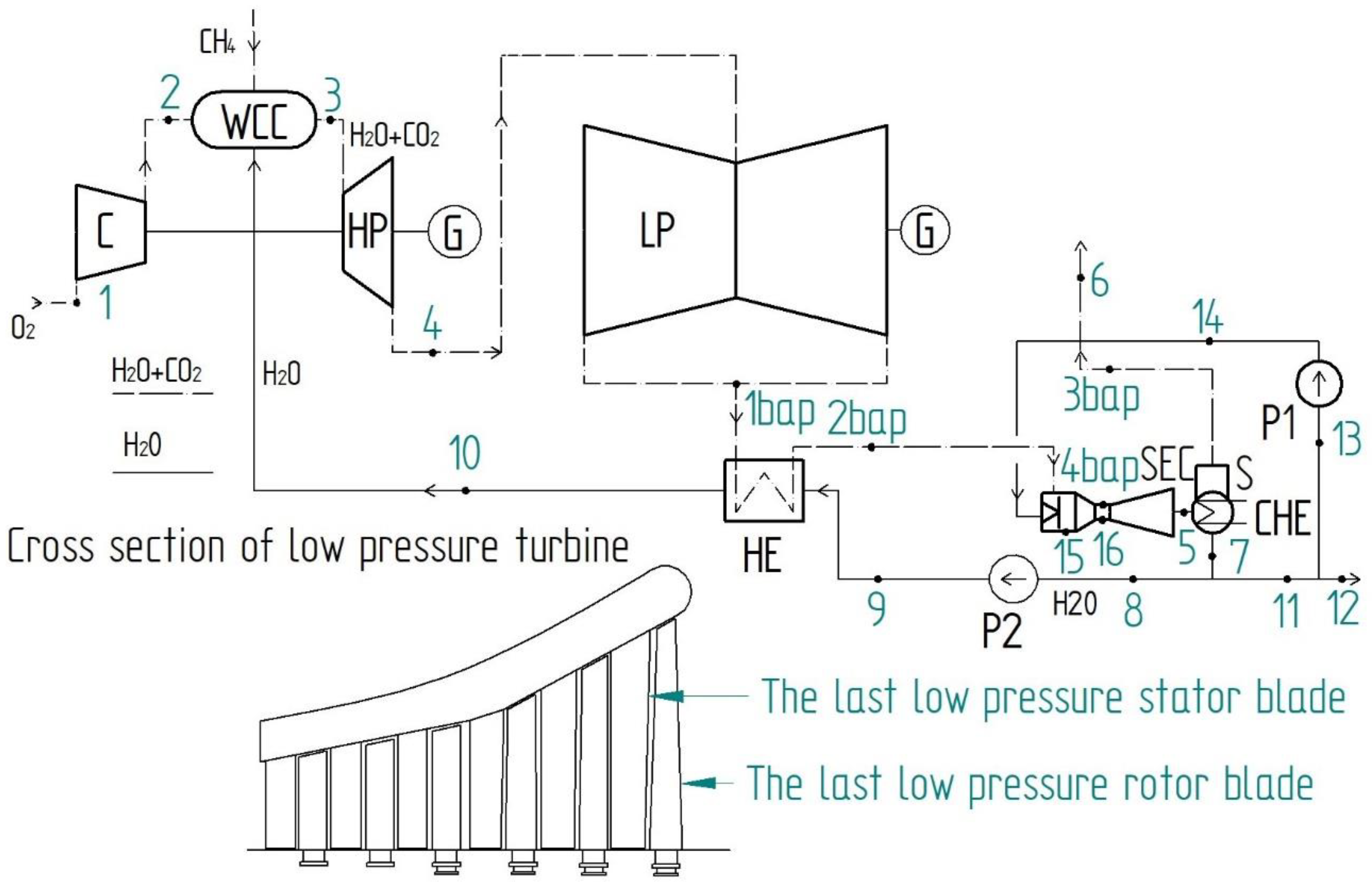
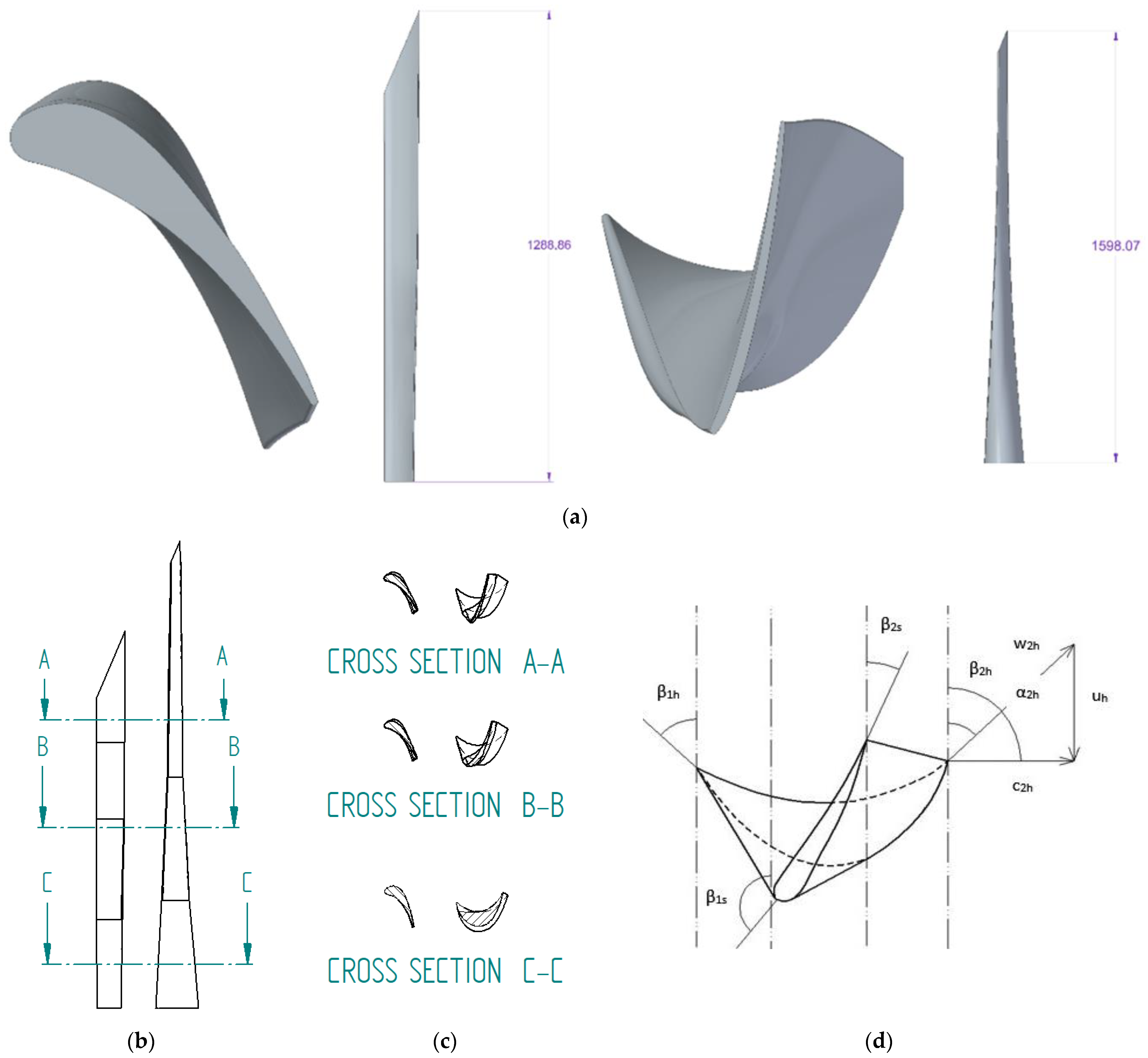
2.1. Twisted Stage Geometry Description
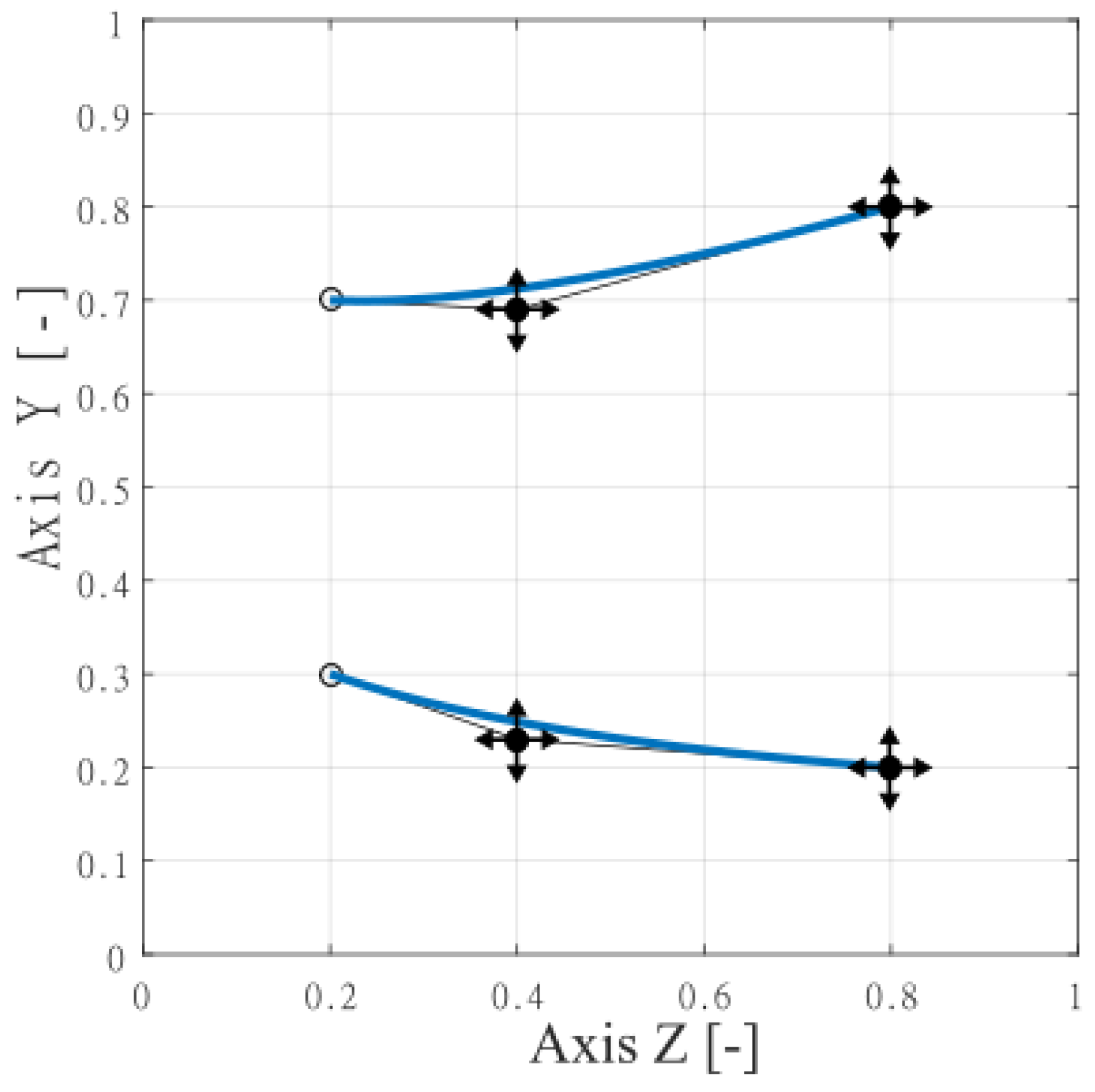
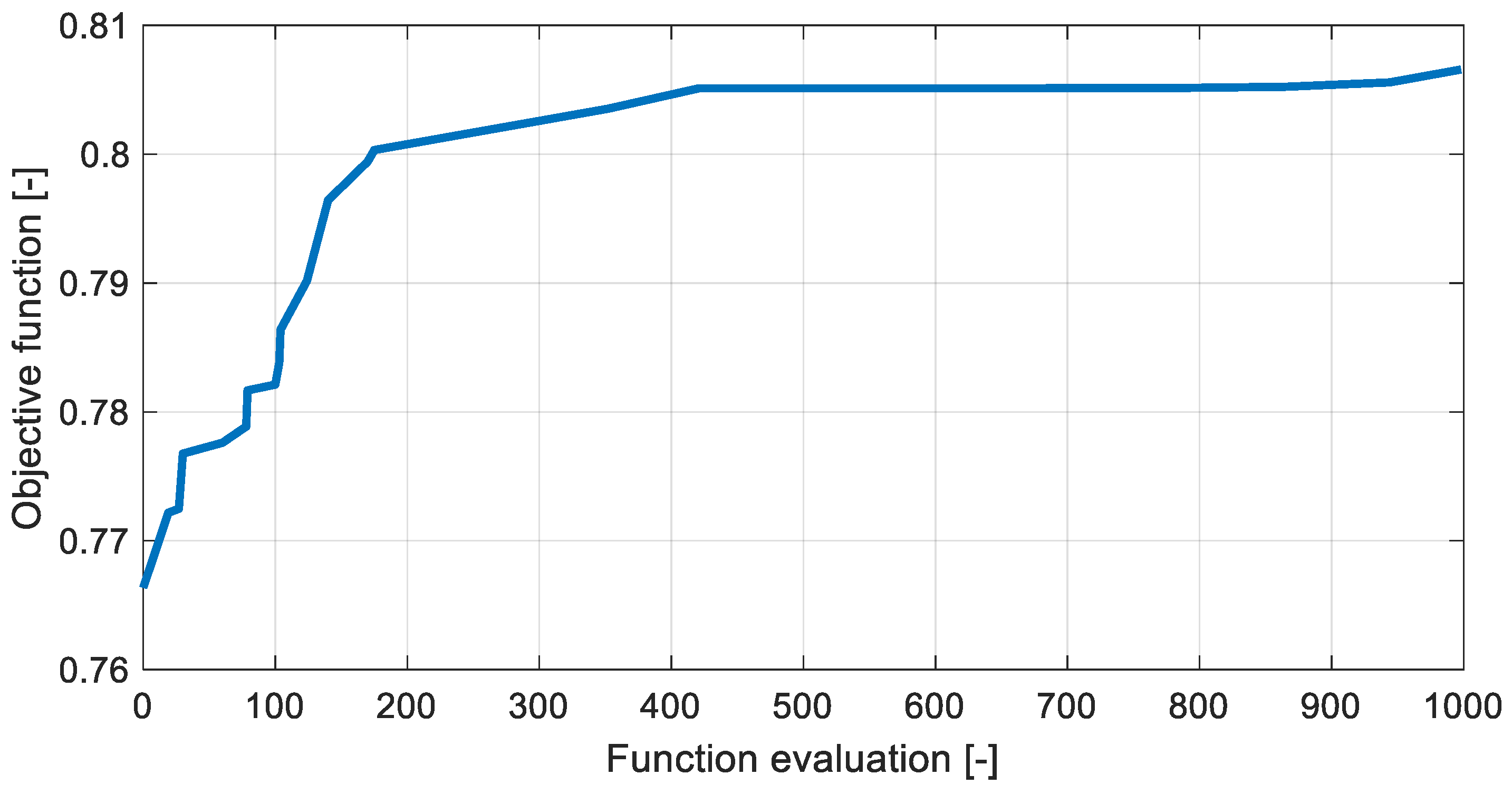
2.2. Optimization Framework
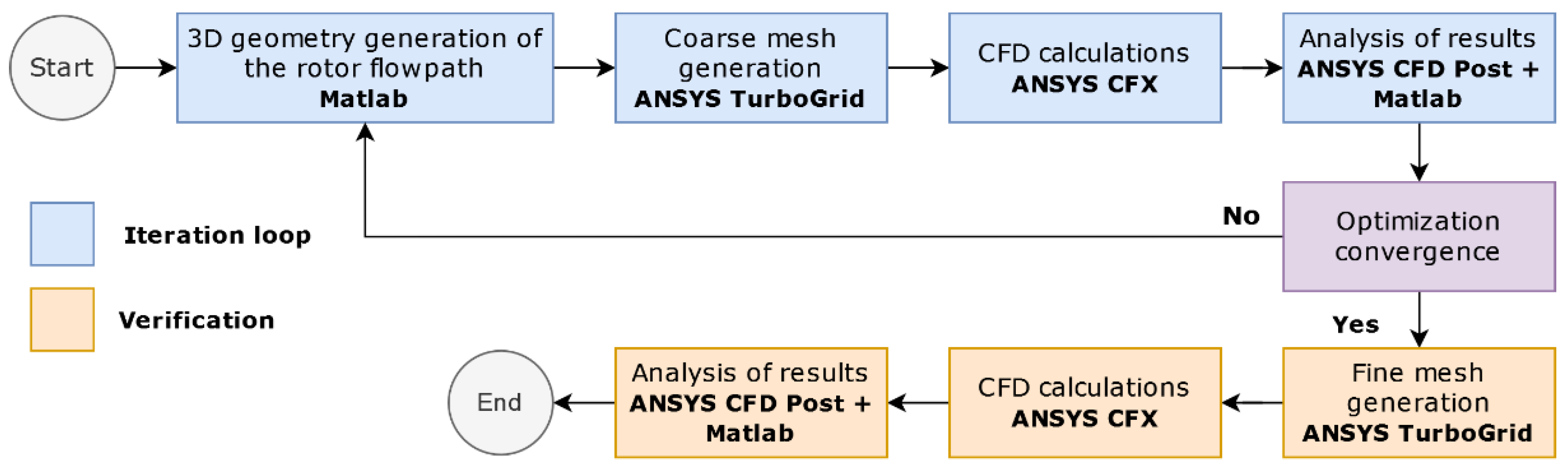
2.3. Computational Methodology
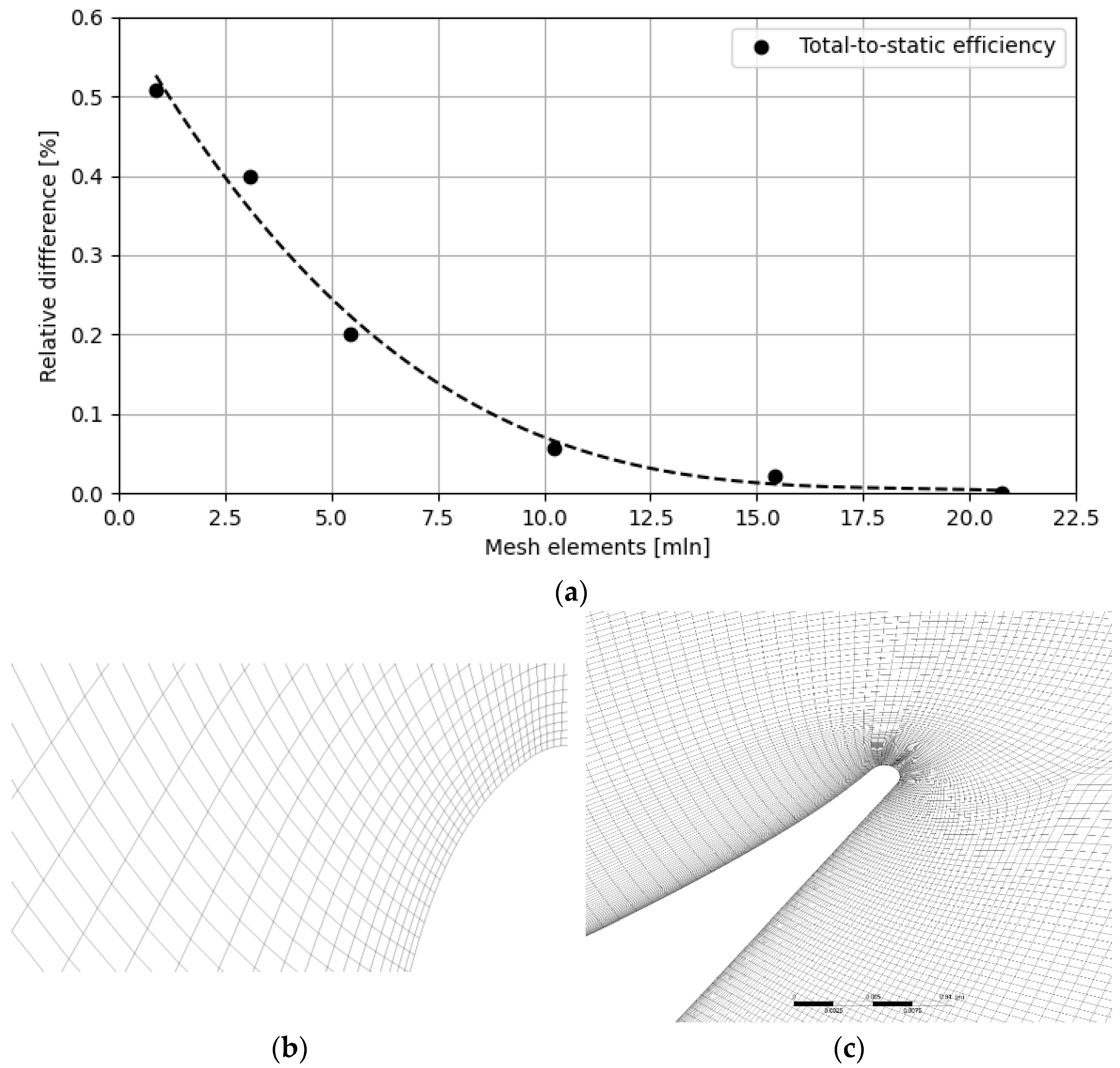
2.4. Method Validation
3. Results and Discussion
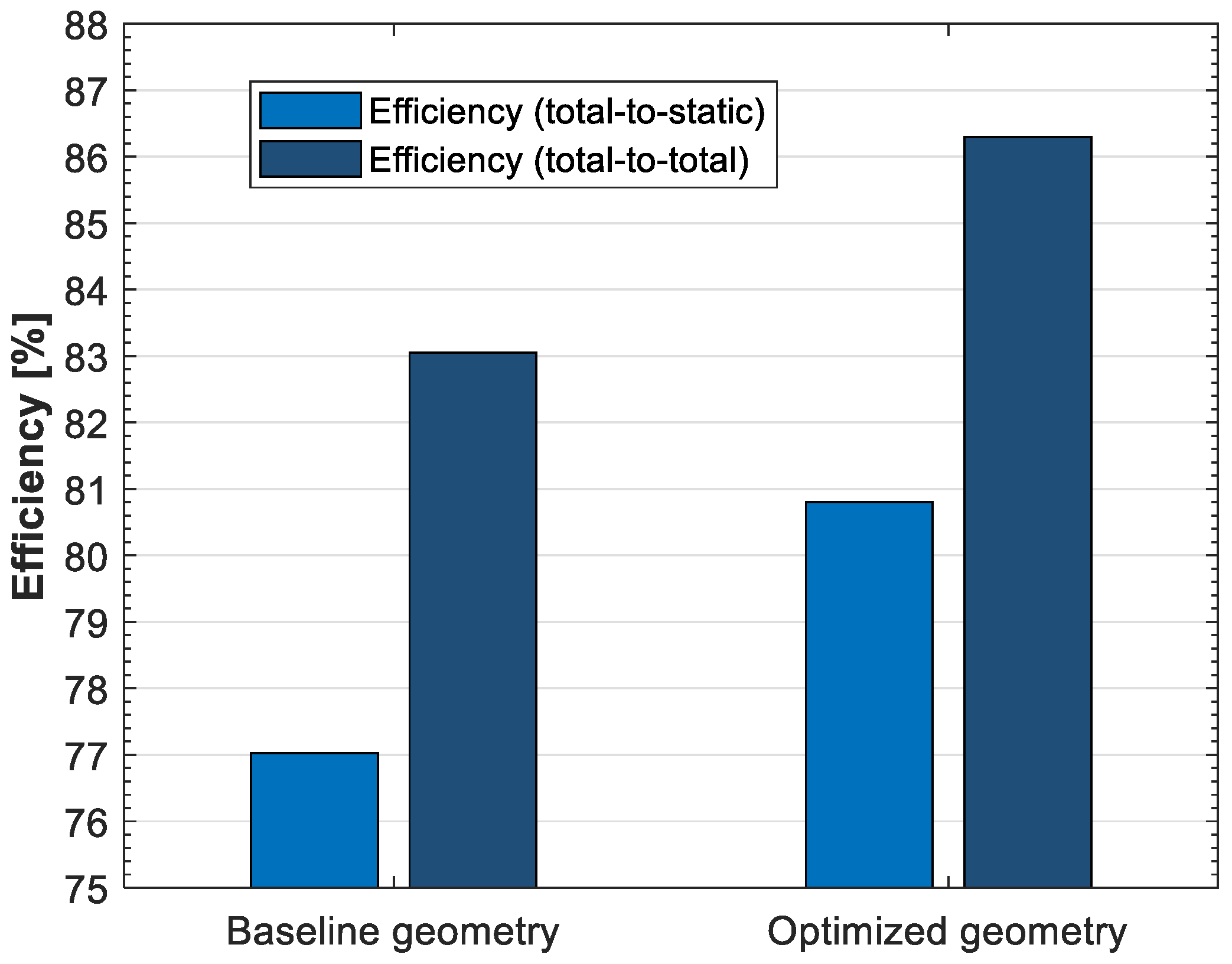
3.1. Comparison of Total-to-Static and Total-to-Total Efficiency
3.2. Comparison of Geometry
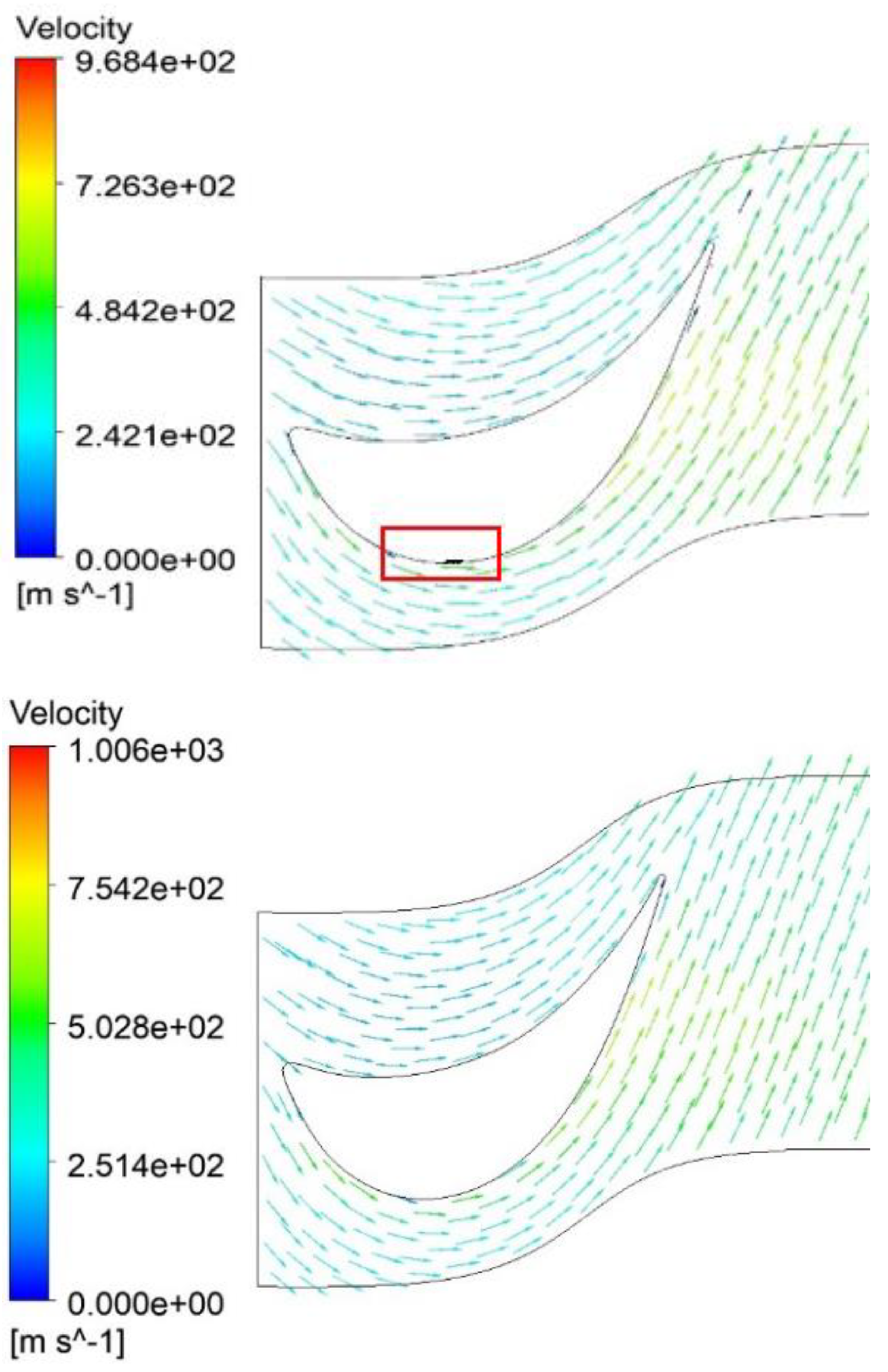
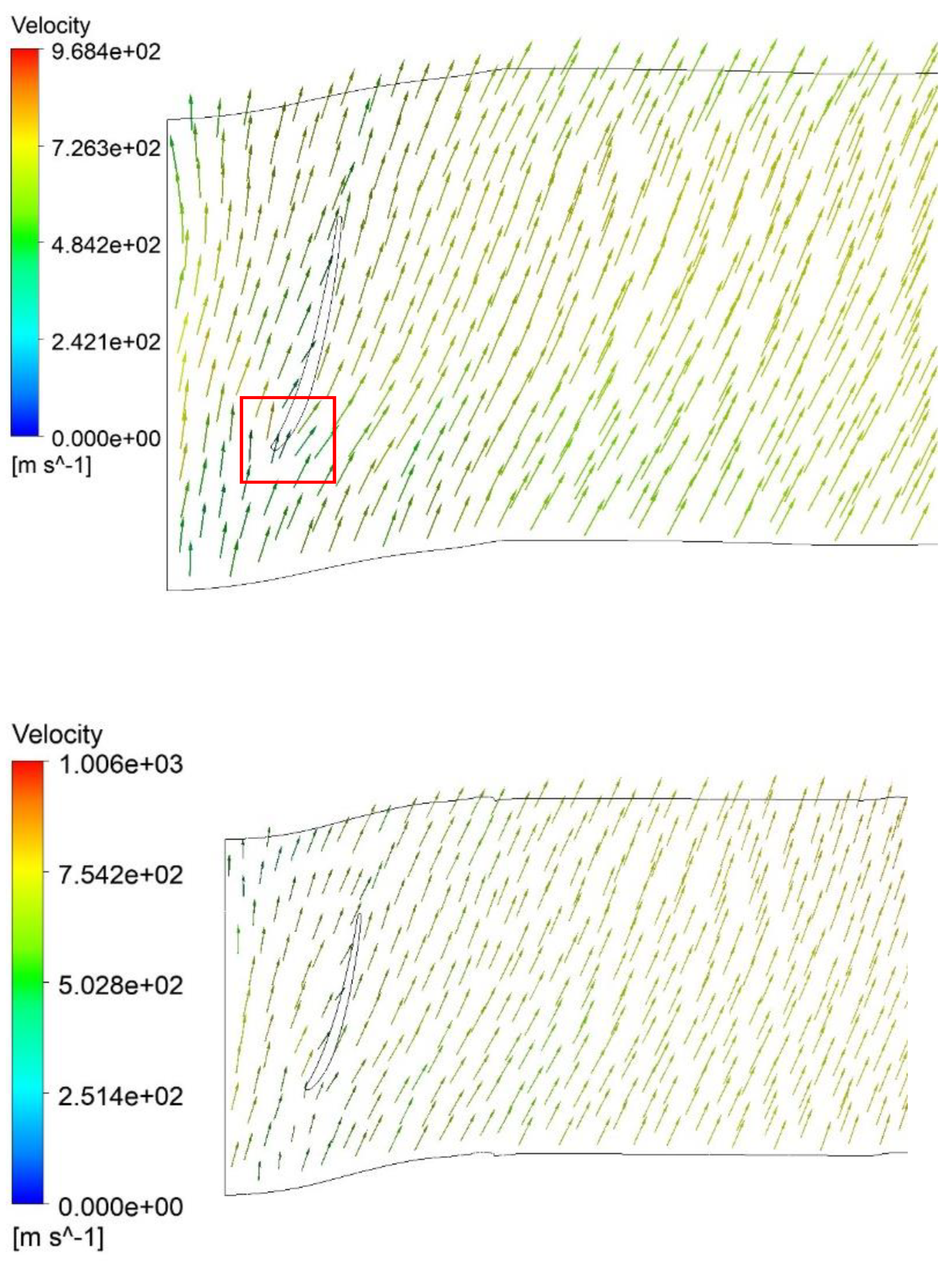
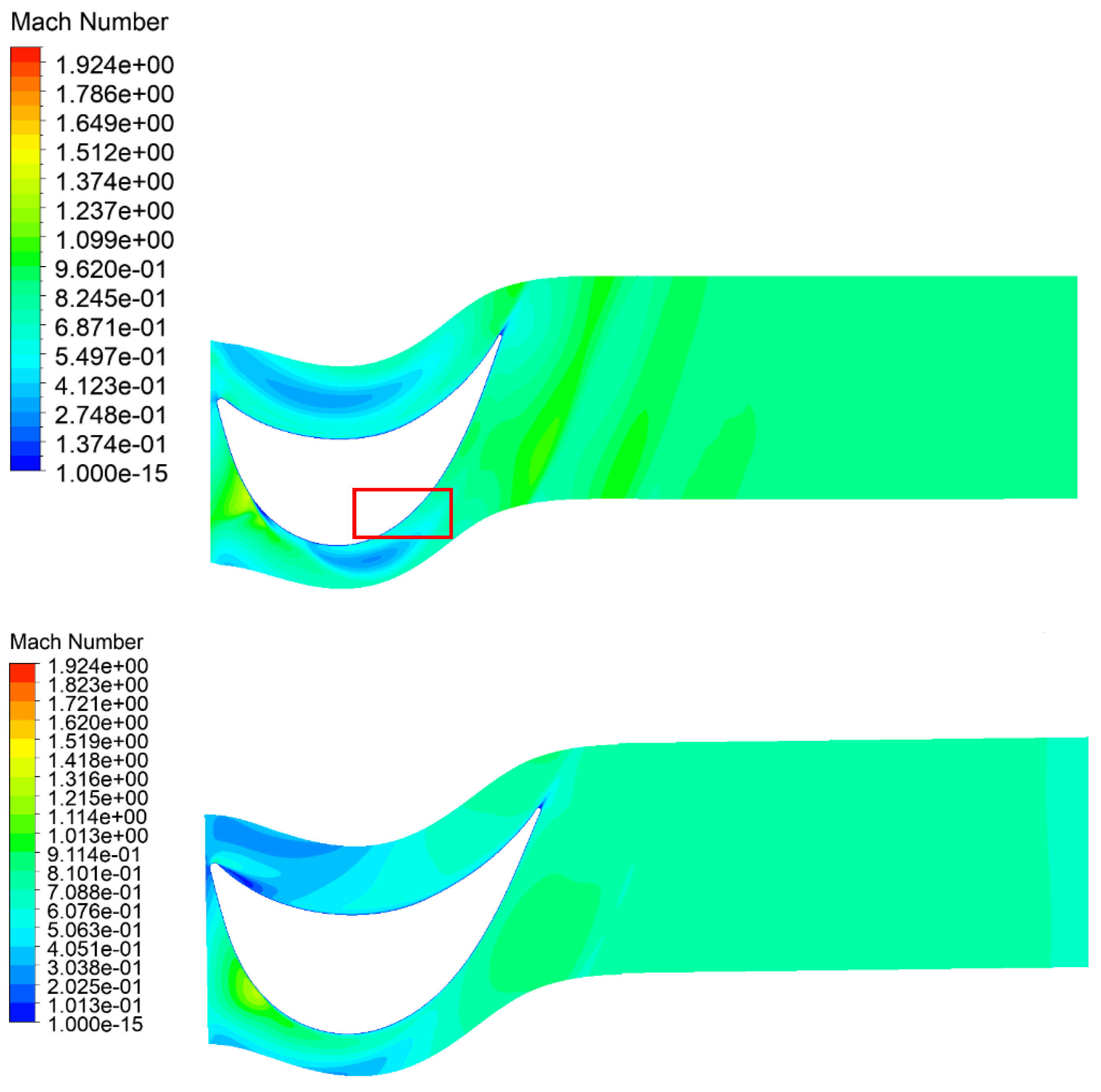
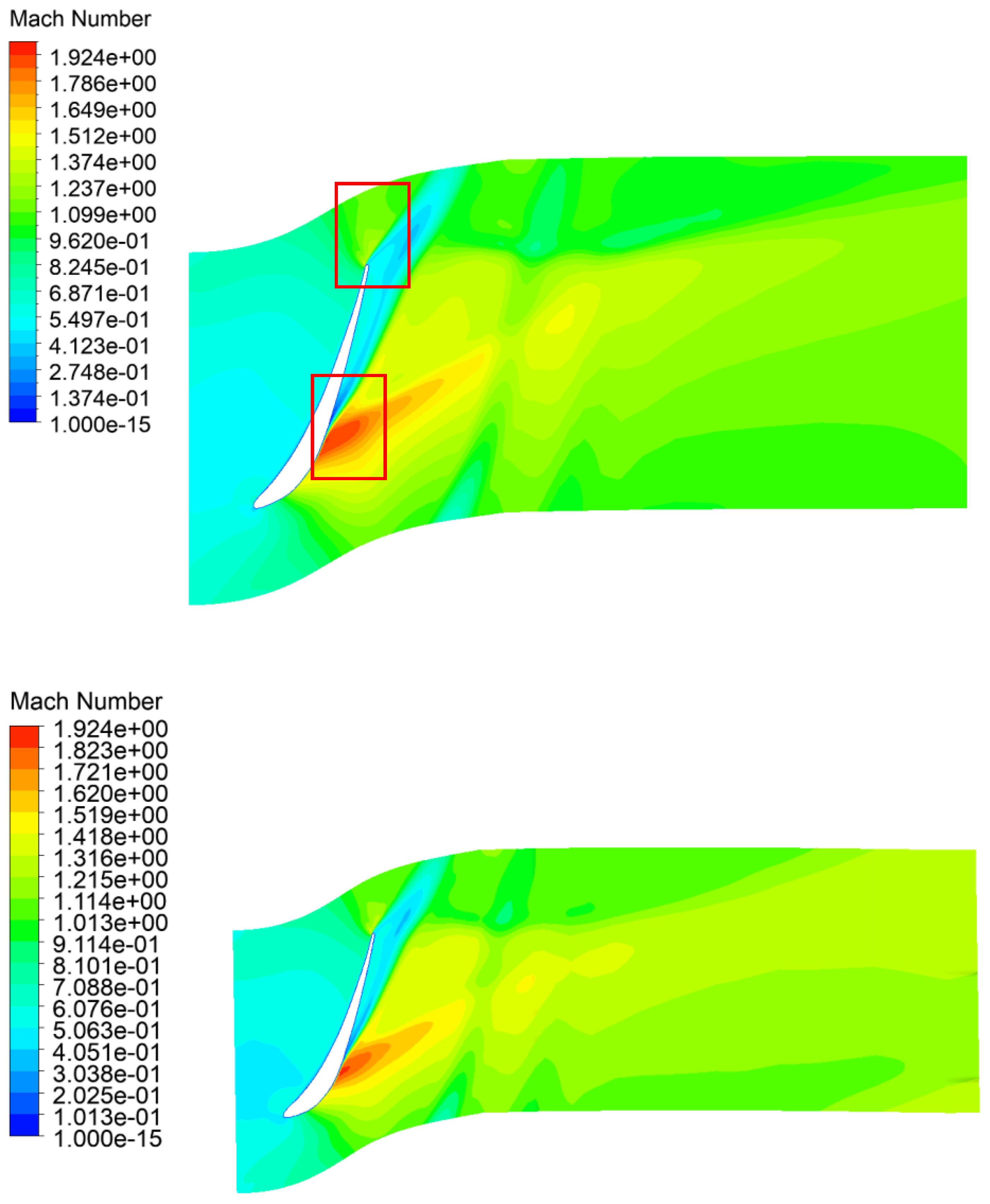
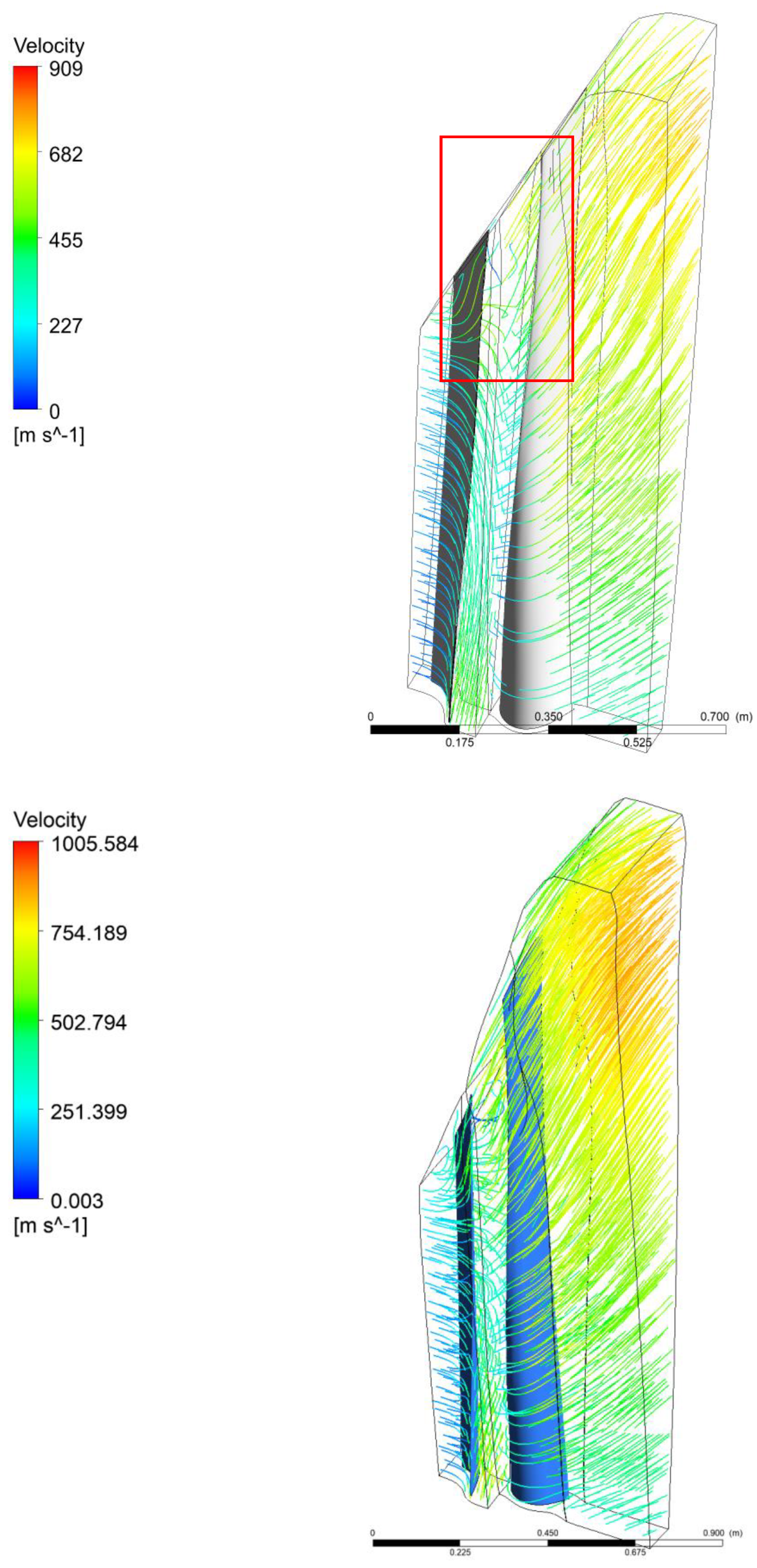
3.3. Comparison of Velocity
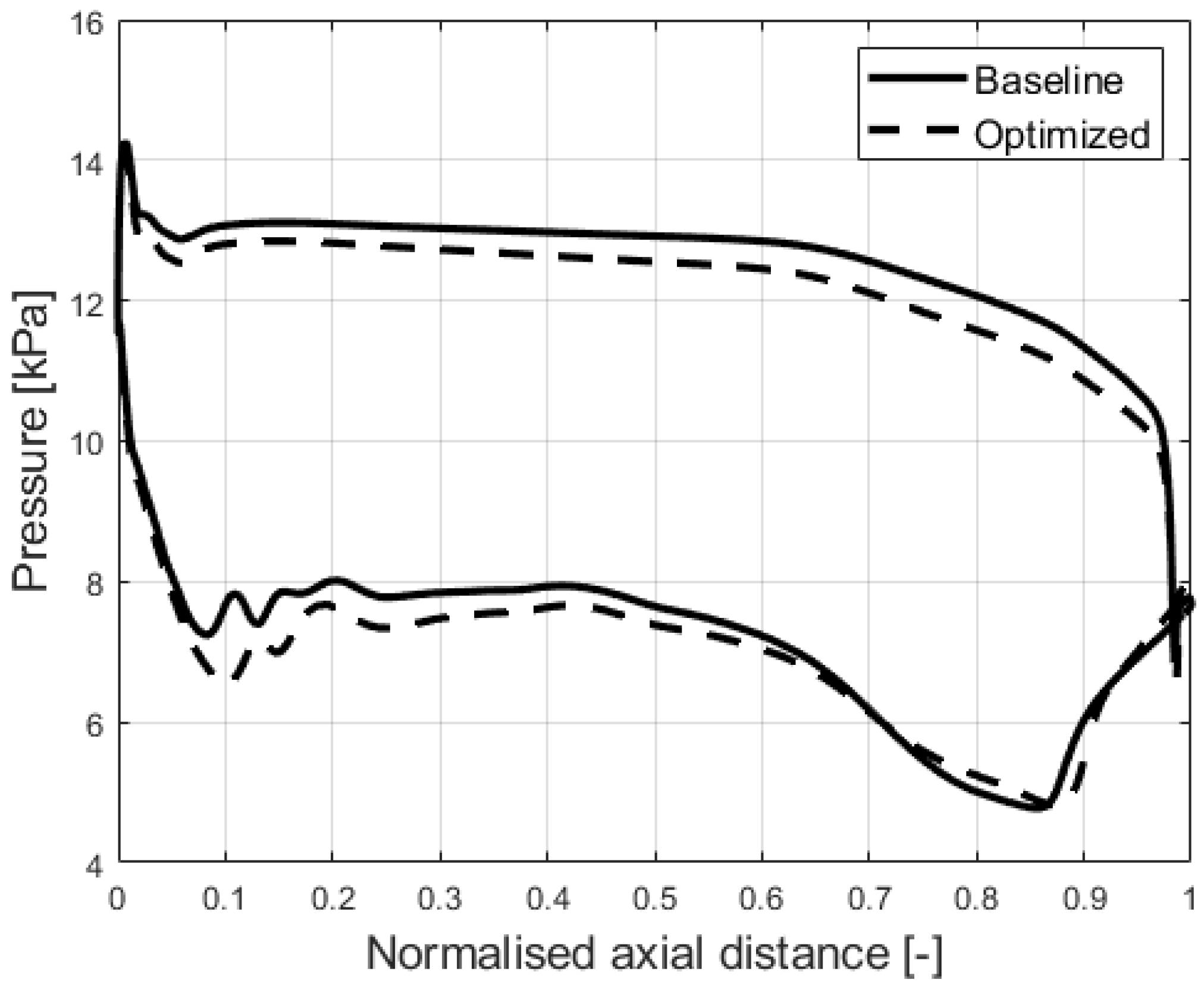
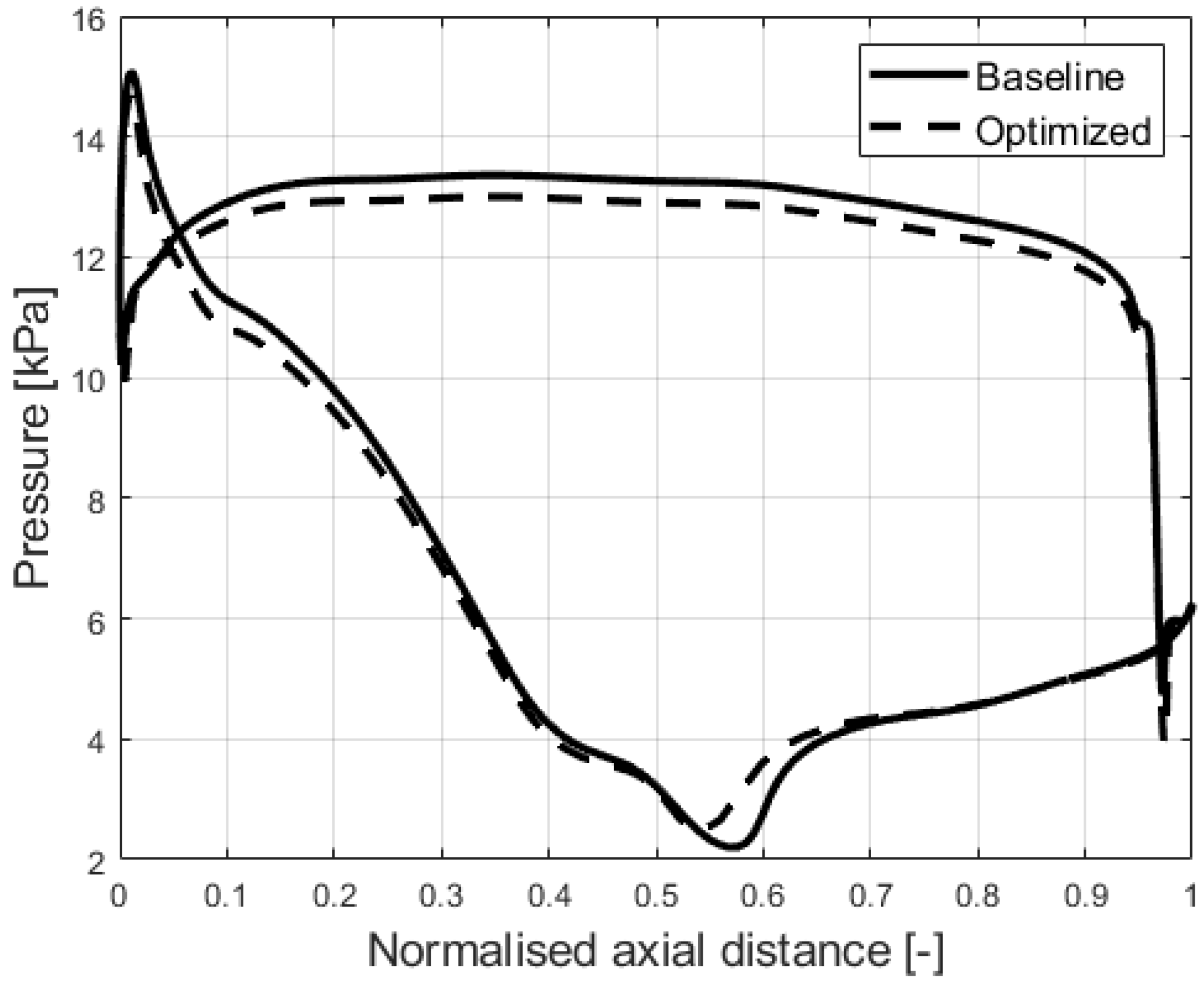
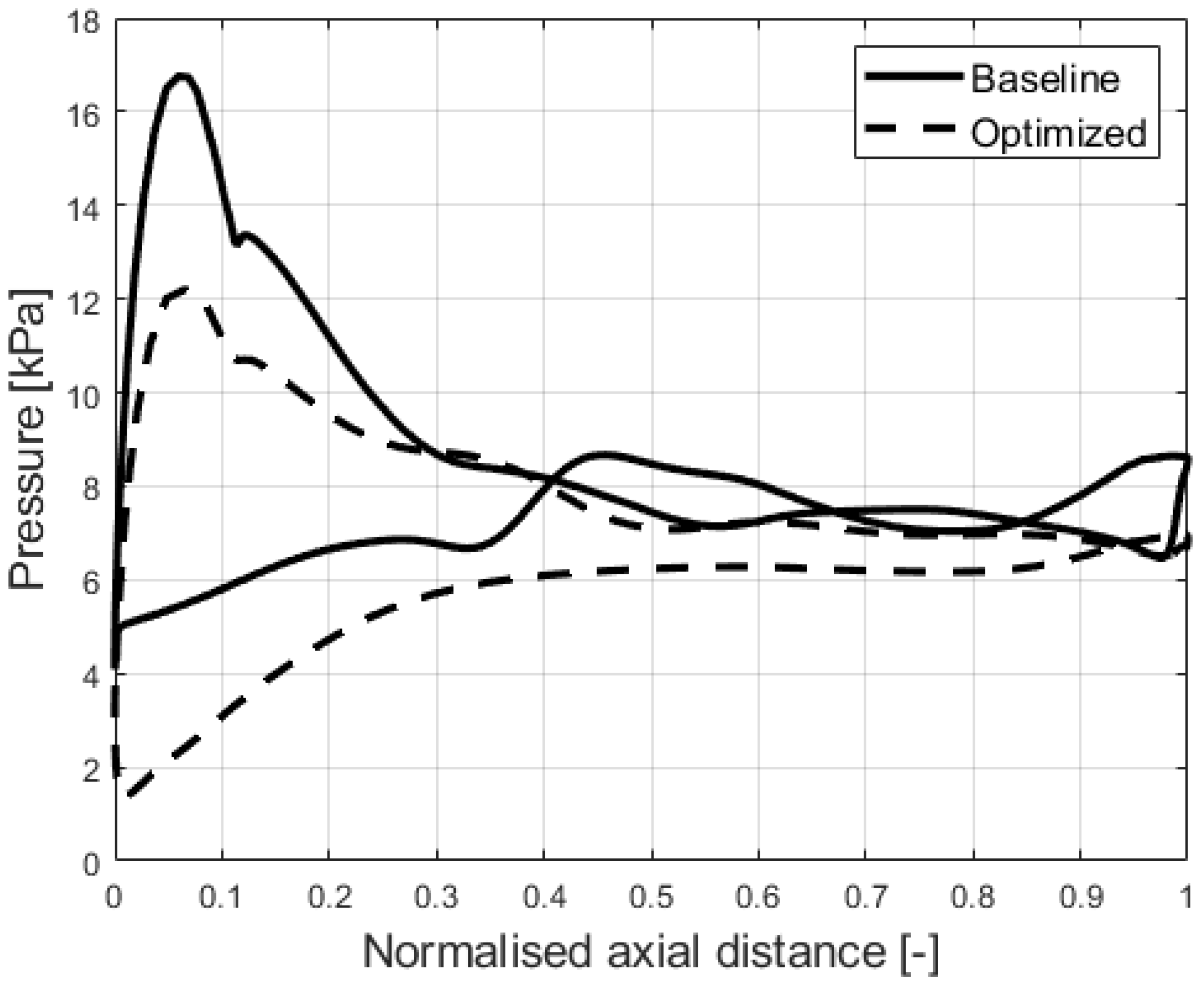
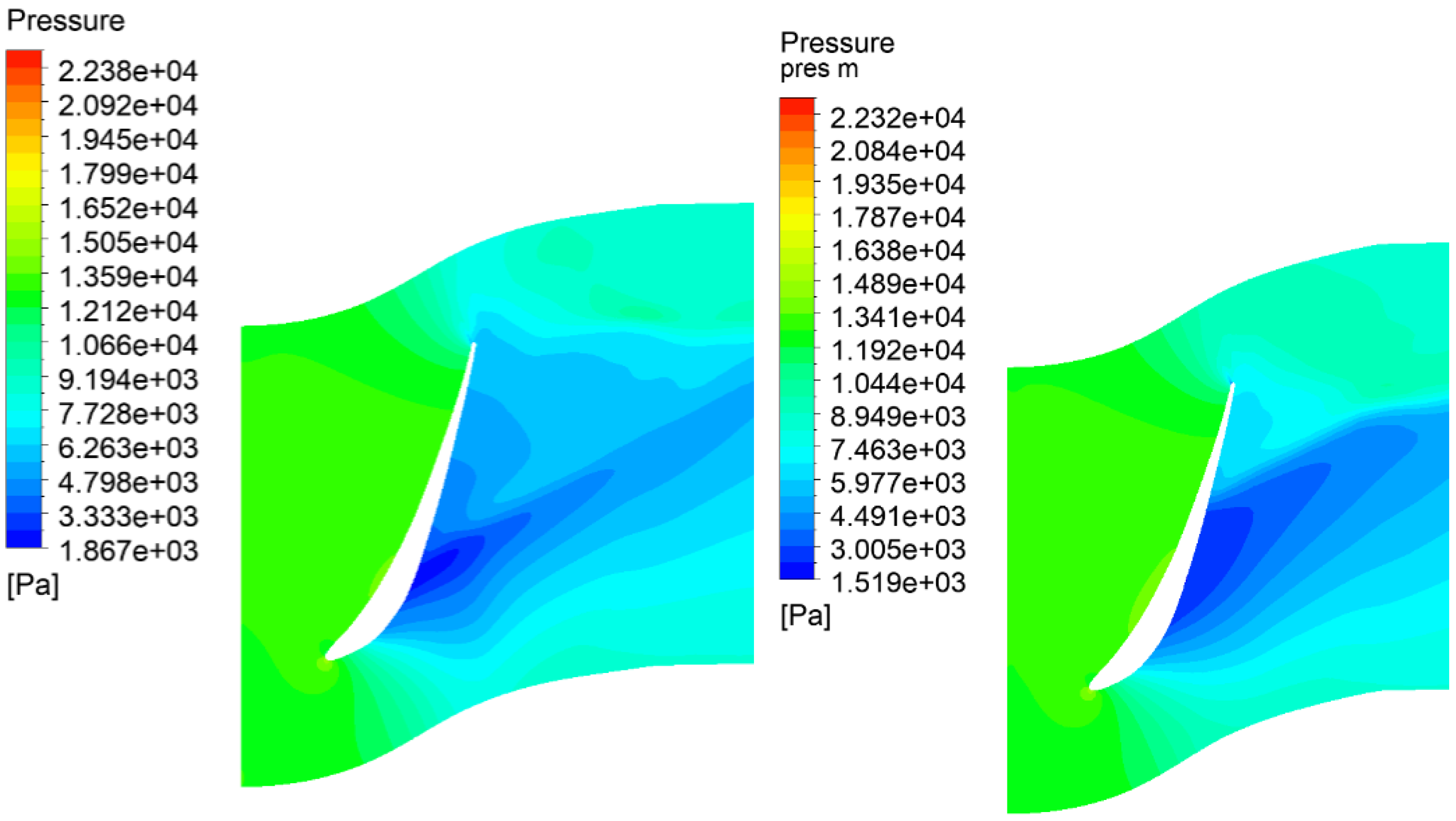
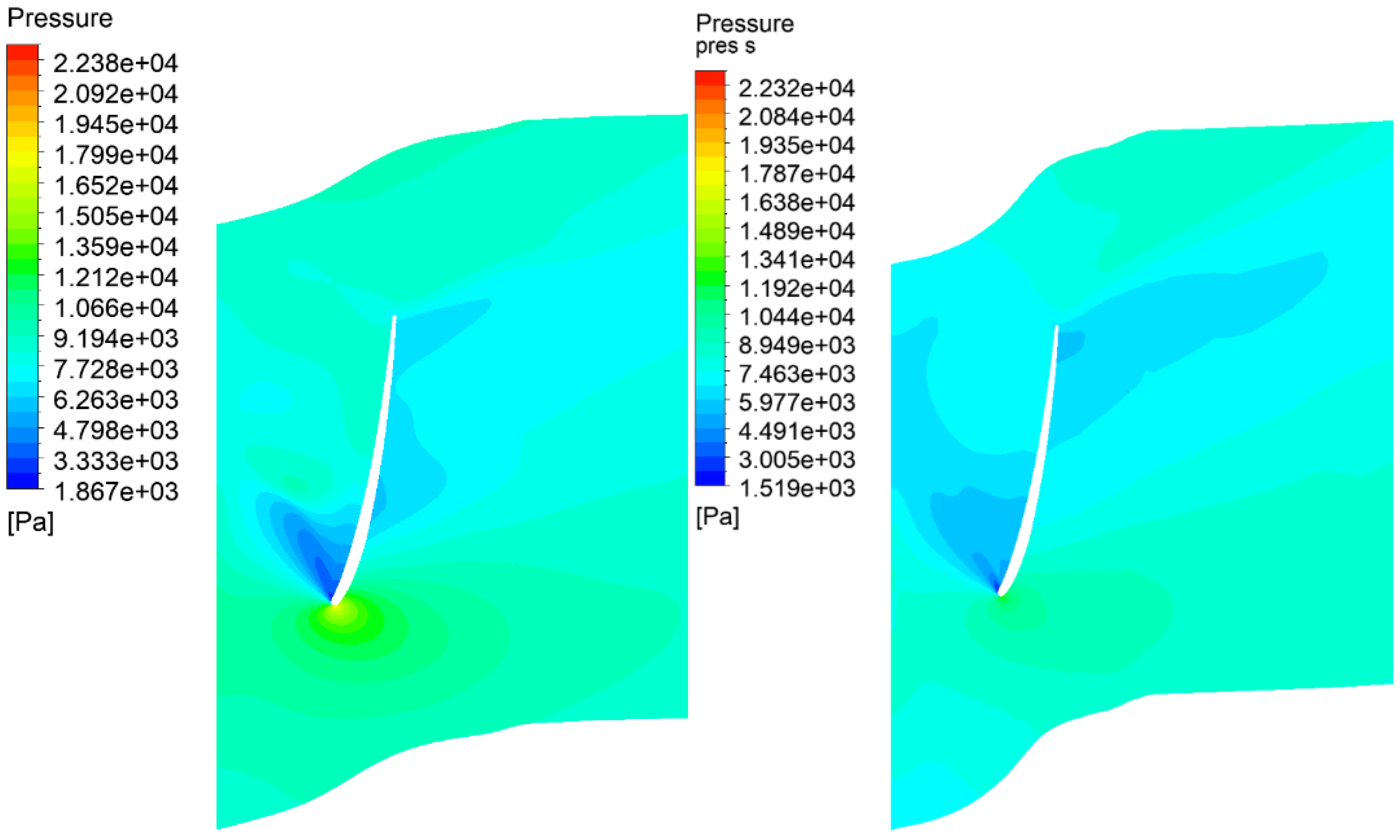
3.4. Comparison of Pressure
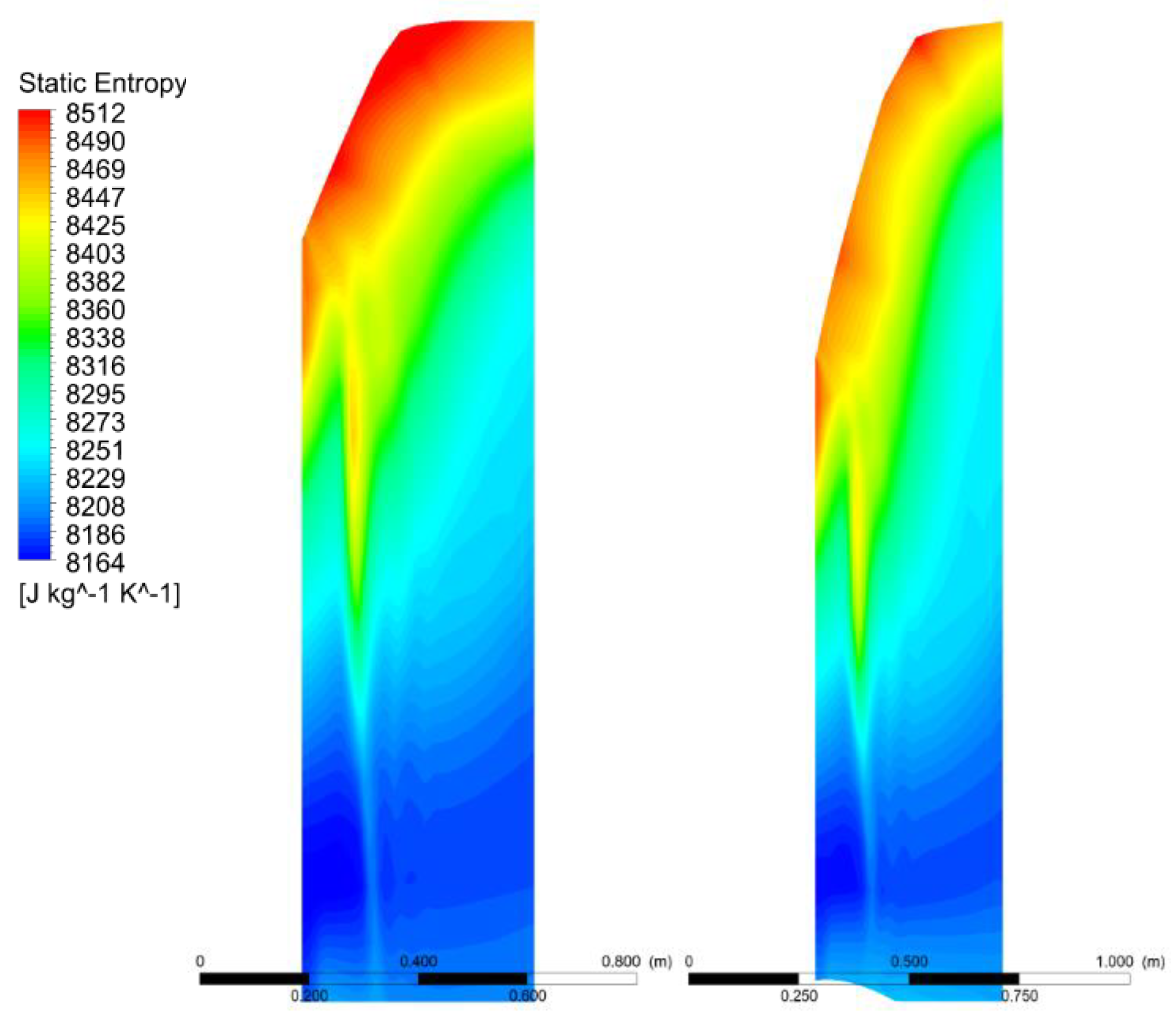
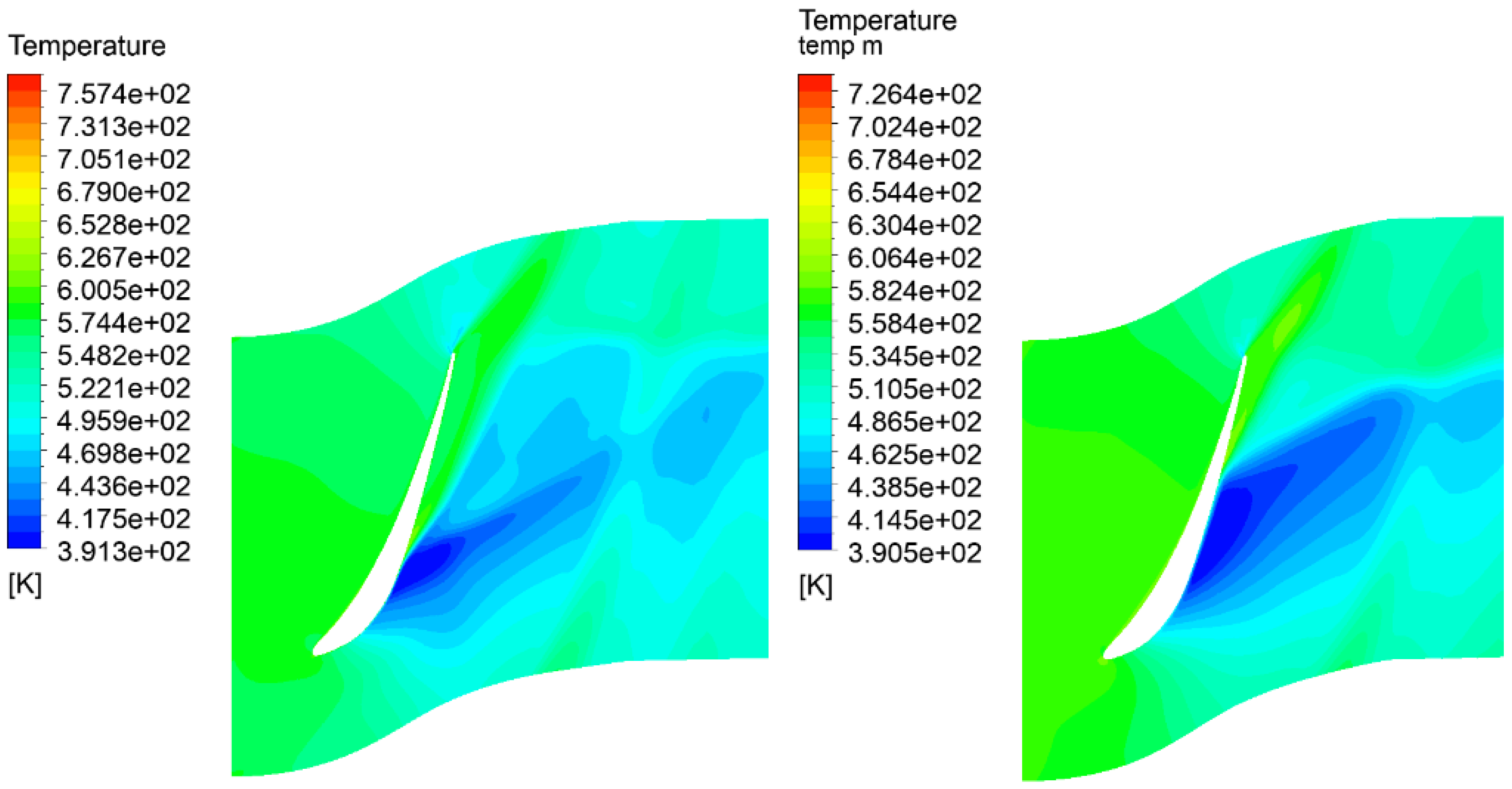
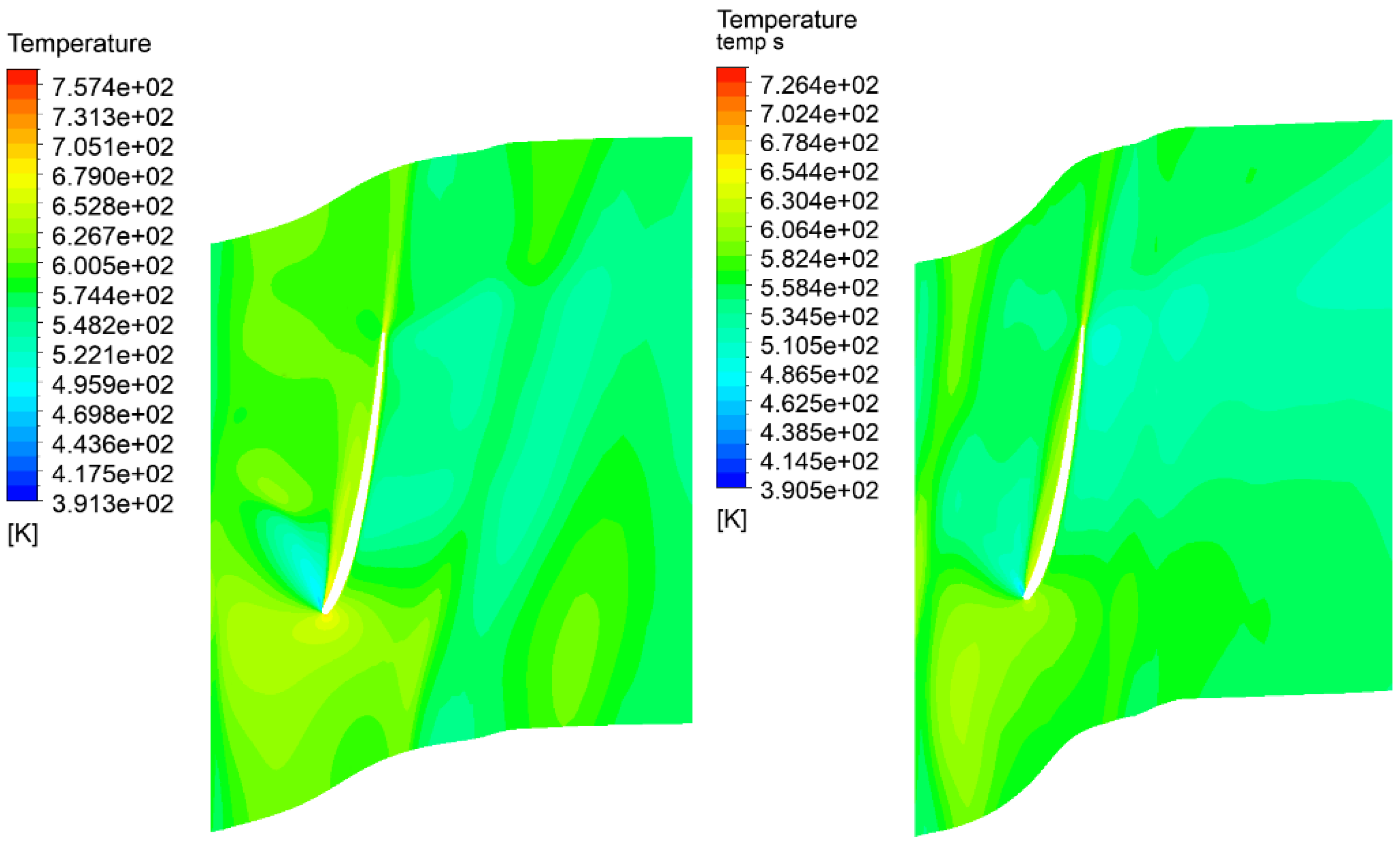
3.5. Comparison of Temperature
4. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Głuch, J. Selected Problems of Determining an Efficient Operation Standard in Contemporary Heat-and-Flow Diagnostics. Pol. Marit. Res. 2009, 16, 22–26. [Google Scholar] [CrossRef]
- Kowalczyk, T.; Badur, J.; Bryk, M. Energy and exergy analysis of hydrogen production combined with electric energy generation in a nuclear cogeneration cycle. Energy Convers. Manag. 2019, 198, 111805. [Google Scholar] [CrossRef]
- Madejski, P.; Żymełka, P. Calculation methods of steam boiler operation factors under varying operating conditions with the use of computational thermodynamic modeling. Energy 2020, 197, 117221. [Google Scholar] [CrossRef]
- Dudda, W.; Banaszkiewicz, M.; Ziółkowski, P.J. Validation of a Burzyński plasticity model with hardening—A case of St12T. AIP Conf. Proc. 2019, 2077, 020016. [Google Scholar] [CrossRef]
- Badur, J.; Bryk, M. Accelerated start-up of the steam turbine by means of controlled cooling steam injection. Energy 2019, 173, 1242–1255. [Google Scholar] [CrossRef]
- Szewczuk-Krypa, N.; Grzymkowska, A.; Głuch, J. Comparative analysis of thermodynamic cycles of selected nuclear ship power plants with high-temperature helium-cooled nuclear reactor. Pol. Marit. Res. 2018, 25, 218–224. [Google Scholar] [CrossRef]
- Delgado-Torres, A.M.; García-Rodríguez, L. Analysis and optimization of the low-temperature solar organic Rankine cycle (ORC). Energy Convers. Manag. 2010, 51, 2846–2856. [Google Scholar] [CrossRef]
- Ziółkowski, P.; Głuch, S.; Ziółkowski, P.J.; Badur, J. Compact High Efficiency and Zero-Emission Gas-Fired Power Plant with Oxy-Combustion and Carbon Capture. Energies 2022, 15, 2590. [Google Scholar] [CrossRef]
- Głuch, S.J.; Ziółkowski, P.; Witanowski, Ł.; Badur, J. Design and Computational Fluid Dynamics Analysis of the Last Stage of Innovative Gas-Steam Turbine. Arch. Thermodyn. 2021, 42, 255–278. [Google Scholar] [CrossRef]
- Ziółkowski, P.; Witanowski; Klonowicz, P.; Głuch, S. Optimization of the Last Stage of Gas-Steam Turbine Using a Hybrid Method. In Proceedings of the 14th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, ETC 2021, Virtual, 12–16 April 2021; pp. 1–15. [Google Scholar]
- Martelli, E.; Alobaid, F.; Elsido, C. Design Optimization and Dynamic Simulation of Steam Cycle Power Plants: A Review. Front. Energy Res. 2021, 9, 676969. [Google Scholar] [CrossRef]
- Anderson, R.; Hustad, C.; Skutley, P.; Hollis, R. Oxy-Fuel Turbo Machinery Development for Energy Intensive Industrial Applications. Energy Procedia 2014, 63, 511–523. [Google Scholar] [CrossRef]
- Ziółkowski, P.; Głuch, S.; Kowalczyk, T.; Badur, J. Revalorisation of the Szewalski’s concept of the law of varying the last-stage blade retraction in a gas-steam turbine. E3S Web Conf. 2021, 323, 00034. [Google Scholar] [CrossRef]
- Dolatabadi, A.M.; Pour, M.S.; Ajarostaghi, S.S.M.; Poncet, S.; Hulme-Smith, C. Last stage stator blade profile improvement for a steam turbine under a non-equilibrium condensation condition: A CFD and cost-saving approach. Alex. Eng. J. 2023, 73, 27–46. [Google Scholar] [CrossRef]
- Turek, V.; Kilkovský, B.; Daxner, J.; Babička Fialová, D.; Jegla, Z. Industrial Waste Heat Utilization in the European Union—An Engineering-Centric Review. Energies 2024, 17, 2084. [Google Scholar] [CrossRef]
- Szewczuk-Krypa, N.; Drosińska-Komor, M.; Głuch, J.; Breńkacz, L. Comparison Analysis of Selected Nuclear Power Plants Supplied with Helium from High-Temperature Gas-Cooled Reactor. Pol. Marit. Res. 2018, 25, 204–210. [Google Scholar] [CrossRef]
- Mikielewicz, D.; Mikielewicz, J. Analytical Method for Calculation of Heat Source Temperature Drop for the Organic Rankine Cycle Application. Appl. Therm. Eng. 2014, 63, 541–550. [Google Scholar] [CrossRef]
- Micheli, D.; Pinamonti, P.; Reini, M.; Taccani, R. Performance Analysis and Working Fluid Optimization of a Cogenerative Organic Rankine Cycle Plant. ASME J. Energy Resour. Technol. 2013, 135, 021601. [Google Scholar] [CrossRef]
- Kupecki, J.; Motylinski, K.; Jagielski, S.; Wierzbicki, M.; Brouwer, J.; Naumovich, Y.; Skrzypkiewicz, M. Energy analysis of a 10 kW-class power-to-gas system based on a solid oxide electrolyzer (SOE). Energy Convers. Manag. 2019, 199, 111934. [Google Scholar] [CrossRef]
- Travieso Pedroso, D.; Blanco Machin, E.; Pérez, N.P.; Braga, L.B.; Silveira, J.L. Technical assessment of the Biomass Integrated Gasification/Gas Turbine Combined Cycle (BIG/GTCC) incorporation in the sugarcane industry. Renew Energy 2017, 114, 464–479. [Google Scholar] [CrossRef]
- Kotowicz, J.; Job, M.; Brzęczek, M. Thermodynamic Analysis and Optimization of an Oxy-Combustion Combined Cycle Power Plant Based on a Membrane Reactor Equipped with a High-Temperature Ion Transport Membrane ITM. Energy 2020, 205, 117912. [Google Scholar] [CrossRef]
- Ertesvåg, I.S.; Kvamsdal, H.M.; Bolland, O. Exergy Analysis of a Gas Turbine Combined-Cycle Power Plant With Precombustion CO2 Capture. Energy 2005, 30, 5–39. [Google Scholar] [CrossRef]
- Sadrian, V.; Lakzian, E.; Kim, H.D. Optimization of operating conditions in the stage of steam turbine by black-box method. Int. Commun. Heat Mass Transf. 2024, 155, 107499. [Google Scholar] [CrossRef]
- Nadirgil, O. Carbon price prediction using multiple hybrid machine learning models optimized by genetic algorithm. J. Environ. Manag. 2023, 342, 118061. [Google Scholar] [CrossRef]
- Sui, Y.; Chen, J.; Chu, P.; Lan, J.; Ren, S.; Wu, H.; Xu, Y.; Xie, J.; Ding, J. Aerodynamic optimization of the last stage turbine blade for an industrial gas turbine. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1081, 012026. [Google Scholar] [CrossRef]
- Zheng, J.; Zhong, J.; Chen, M.; He, K. A reinforced hybrid genetic algorithm for the traveling salesman problem. Comput. Oper. Res. 2023, 157, 106249. [Google Scholar] [CrossRef]
- Lampart, P.; Hirt, Ł. Complex multidisciplinary optimization of turbine blading systems. Arch. Mech. 2012, 64, 153–175. [Google Scholar]
- Meng, M. A hybrid particle swarm optimization algorithm for satisficing data envelopment analysis under fuzzy chance constraints. Expert Syst. Appl. 2014, 41, 2074–2082. [Google Scholar] [CrossRef]
- Sundkvist, S.G.; Dahlquist, A.; Janczewski, J.; Sjödin, M.; Bysveen, M.; Ditaranto, M.; Langørgen, Ø.; Seljeskog, M.; Siljan, M. Concept for a combustion system in oxyfuel gas turbine combined cycles. J. Eng. Gas Turbine Power 2014, 136, 101513. [Google Scholar] [CrossRef]
- Rogalev, A.; Rogalev, N.; Kindra, V.; Komarov, I.; Zlyvko, O. Research and Development of the Oxy-Fuel Combustion Power Cycles with CO2 Recirculation. Energies 2021, 14, 2927. [Google Scholar] [CrossRef]
- Mathieu, P.; Nihart, R. Sensitivity analysis of the MATIANT cycle. Energy Convers. Manag. 1999, 40, 1687–1700. [Google Scholar] [CrossRef]
- Rogalev, A.; Rogalev, N.; Kindra, V.; Zlyvko, O.; Vegera, A. A Study of Low-Potential Heat Utilization Methods for Oxy-Fuel Combustion Power Cycles. Energies 2021, 14, 3364. [Google Scholar] [CrossRef]
- Hollis, R.; Skutley, P.; Ortíz, C.; Varkey, V.; Lepage, D.; Brown, B.; Davies, D.; Harris, M. Oxy-Fuel Turbomachinery Development for Energy Intensive Industrial Applications. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 431–439. [Google Scholar]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Khan, I.A.; Alkhammash, H.I.; Sajjad, I.A.; Hussain, B. An improved particle swarm optimization with chaotic inertia weight and acceleration coefficients for optimal extraction of PV models parameters. Energies 2021, 14, 2980. [Google Scholar] [CrossRef]
- Ehteram, M.; Binti Othman, F.; Mundher Yaseen, Z.; Abdulmohsin Afan, H.; Falah Allawi, M.; Abdul Malek, M.B.; Najah Ahmed, A.; Shahid, S.; Singh, V.P.; El-Shafie, A. Improving the Muskingum flood routing method using a hybrid of particle swarm optimization and bat algorithm. Water 2018, 10, 807. [Google Scholar] [CrossRef]
- Yang, J.; Peng, T.; Xu, G.; Hu, W.; Zhong, H.; Liu, X. A Study and Optimization of the Unsteady Flow Characteristics in the Last Stage Impeller of a Small-Scale Multi-Stage Hydraulic Turbine. Energies 2023, 17, 107. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar] [CrossRef]
- Lampart, P.; Yershov, S.; Rusanov, A. Increasing Flow Efficiency of High-Pressure and Low-Pressure Steam Turbine Stages from Numerical Optimization of 3D Blading. Eng. Optim. 2005, 37, 145–166. [Google Scholar] [CrossRef]
- Lampart, P. Numerical Optimization of Stator Blade Sweep and Lean in an LP Turbine Stage. In Proceedings of the 2002 International Joint Power Generation Conference, Scottsdale, AZ, USA, 24–26 June 2002; pp. 579–592. [Google Scholar]
- Perycz, S. Steam and Gas Turbines, 1st ed.; Wydawnictwo Politechniki Gdańskiej: Gdańsk, Poland, 1988. [Google Scholar]
- Szewalski, R. A Novel Design of Turbine Blading of Extreme Length. Trans. Inst. Fluid-Flow Mach. 1976, 70–72, 83–86. [Google Scholar]
- Szewalski, R. Rational Blade Height Calculation in Action Turbines. Czas. Tech. 1930, 1, 83–86. [Google Scholar]
- Szewalski, R. Present Problems of Power Engineering Development. Increase of Unit Power and Efficiency of Turbines and Power Palnts; Ossolineum: Wrocław, Poland, 1978. [Google Scholar]
- Lampart, P.; Gardzilewicz, A.; Kwidzyński, R. On the Control of Flow Losses in LP Turbine Stages—Computation of Advanced Designs Based on a Solver of 3D Navier-Stokes Equations. In Proceedings of the Seminar Topical Problems of Fluid Mechanics, Prague, Czech Republic, 16 February 2000; pp. 53–56. [Google Scholar]
- Witanowski, Ł.; Klonowicz, P.; Lampart, P.; Suchocki, T.; Jędrzejewski, Ł.; Zaniewski, D.; Klimaszewski, P. Optimization of an Axial Turbine for a Small Scale ORC Waste Heat Recovery System. Energy 2020, 205, 118059. [Google Scholar] [CrossRef]
- ANSYS® Academic Research Mechanical and CFD, Release 19.0 2019; ANSYS Inc.: Canonsburg, PA, USA, 2019.
- Yang, X.-S. Recent Advances in Swarm Intelligence and Evolutionary Computation; Springer: Cham, Switzerland, 2015; ISBN 978-3-319-13825-1. [Google Scholar]
- Ting, T.O.; Yang, X.-S.; Cheng, S.; Huang, K. Hybrid Metaheuristic Algorithms: Past, Present, and Future; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2015; Volume 585, pp. 71–83. ISBN 9783319138268. [Google Scholar]
- Tesch, K.; Kaczorowska-Ditrich, K. The Discrete-Continuous, Global Optimisation of an Axial Flow Blood Pump. Flow Turbul. Combust. 2020, 104, 777–793. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Zahara, E.; Kao, Y.T. Hybrid Nelder-Mead Simplex Search and Particle Swarm Optimization for Constrained Engineering Design Problems. Expert Syst. Appl. 2009, 36, 3880–3886. [Google Scholar] [CrossRef]
- Fan, S.K.S.; Zahara, E. A Hybrid Simplex Search and Particle Swarm Optimization for Unconstrained Optimization. Eur. J. Oper. Res. 2007, 181, 527–548. [Google Scholar] [CrossRef]
- Ayouche, S.; Ellaia, R.; Aboulaich, R. A Hybrid Particle Swarm Optimization-Nelder- Mead Algorithm (PSO-NM) for Nelson-Siegel- Svensson Calibration. Int. J. Econ. Manag. Eng. 2016, 10, 1365–1369. [Google Scholar] [CrossRef]
- Barzinpour, F.; Noorossana, R.; Niaki, S.T.A.; Ershadi, M.J. A Hybrid Nelder–Mead Simplex and PSO Approach on Economic and Economic-Statistical Designs of MEWMA Control Charts. Int. J. Adv. Manuf. Technol. 2013, 65, 1339–1348. [Google Scholar] [CrossRef]
- Tsai, H.H.; Fuh, C.C.; Ho, J.R.; Lin, C.K. Design of Optimal Controllers for Unknown Dynamic Systems through the Nelder–Mead Simplex Method. Mathematics 2021, 9, 2013. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, A.; Yang, L.; Hu, C.; Bai, Y. Investigation on optimization design of offshore wind turbine blades based on particle swarm optimization. Energies. 2019, 12, 1972. [Google Scholar] [CrossRef]
- Sulaiman, A.T.; Bello-Salau, H.; Onumanyi, A.J.; Mu’azu, M.B.; Adedokun, E.A.; Salawudeen, A.T.; Adekale, A.D. A Particle Swarm and Smell Agent-Based Hybrid Algorithm for Enhanced Optimization. Algorithms 2024, 17, 53. [Google Scholar] [CrossRef]
- Rong, L.; Böhle, M.; Yandong, G. Improving the hydraulic performance of a high-speed submersible axial flow pump based on CFD technology. Int. J. Fluid Eng. 2024, 1, 013902. [Google Scholar] [CrossRef]
- Zanetti, G.; Siviero, M.; Cavazzini, G.; Santolin, A. Application of the 3D inverse design method in reversible pump turbines and Francis turbines. Water 2023, 15, 2271. [Google Scholar] [CrossRef]
- Witanowski, Ł.; Klonowicz, P.; Lampart, P.; Klimaszewski, P.; Suchocki, T.; Jędrzejewski, Ł.; Zaniewski, D.; Ziółkowski, P. Impact of Rotor Geometry Optimization on the Off-Design ORC Turbine Performance. Energy 2023, 265, 126312. [Google Scholar] [CrossRef]
- Witanowski, Ł.; Klonowicz, P.; Lampart, P.; Ziółkowski, P. Multi-Objective Optimization of the ORC Axial Turbine for a Waste Heat Recovery System Working in Two Modes: Cogeneration and Condensation. Energy 2023, 264, 126187. [Google Scholar] [CrossRef]
- Zhao, J.; Pei, J.; Yuan, J.; Wang, W. Structural optimization of multistage centrifugal pump via computational fluid dynamics and machine learning method. J. Comput. Des. Eng. 2023, 10, 1204–1218. [Google Scholar] [CrossRef]
- Zych, P.; Żywica, G. Optimisation of stress distribution in a highly loaded radial-axial gas microturbine using FEM. Open Eng. 2020, 10, 318–335. [Google Scholar] [CrossRef]
- Zych, P.; Żywica, G. Fatigue analysis of the microturbine rotor disc made of 7075 aluminium alloy using a new hybrid calculation method. Materials 2022, 15, 834. [Google Scholar] [CrossRef]
- Fan, S.; Wang, Y.; Yao, K.; Shi, J.; Han, J.; Wan, J. Distribution characteristics of high wetness loss area in the last two stages of steam turbine under varying conditions. Energies 2022, 15, 2527. [Google Scholar] [CrossRef]
- Dykas, S.; Majkut, M.; Smołka, K.; Strozik, M. Study of the wet steam flow in the blade tip rotor linear blade cascade. Int. J. Heat Mass Transf. 2018, 120, 9–17. [Google Scholar] [CrossRef]
- Han, Z.; Zeng, W.; Han, X.; Xiang, P. Investigating the dehumidification characteristics of turbine stator cascades with parallel channels. Energies 2018, 11, 2306. [Google Scholar] [CrossRef]
- Głuch, J. Fault detection in measuring systems of power plants. Pol. Marit. Res. 2008, 18, 45–51. [Google Scholar] [CrossRef]
- Gluch, J.; Krzyzanowski, J. New Attempt for Diagnostics of the Geometry Deterioration of the Power System Based on Thermal Measurement. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 531–539. [Google Scholar]






| t inlet last stage = 336.794 | °C | ||
| m inlet last stage = 91.15 | kg/s | ||
| p outlet last stage = 0.07955 | bar | ||
| 3000. | rpm | ||
| XCO2 | XH2O | XN2 | Sum |
| 0.0894 | 0.9084 | 0.0022 | 1 |
| YCO2 | YH2O | YN2 | Sum |
| 0.1933 | 0.8037 | 0.003 | 1 |
| Unit | 1 = Hub | 2 | 3 = Mid span | 4 | 5 = Shroud | |
|---|---|---|---|---|---|---|
| m | 0.8632 | 1.1218 | 1.4667 | 1.8116 | 2.0703 | |
| m | 0.8727 | 1.1883 | 1.6091 | 2.03 | 2.3455 | |
| - | 0.1906 | 0.5221 | 0.7152 | 0.8084 | 0.8503 | |
| m/s | 274.17 | 373.32 | 505.52 | 637.72 | 736.87 | |
| ° | 14.661 | 19.008 | 24.95 | 30.089 | 33.623 | |
| m/s | 529.8 | 413.9 | 328.02 | 277.18 | 251.01 | |
| m/s | 495.38 | 393.2 | 311.6 | 263.32 | 238.46 | |
| ° | 20.988 | 19.127 | 16.476 | 13.861 | 12.262 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziółkowski, P.; Witanowski, Ł.; Głuch, S.; Klonowicz, P.; Feidt, M.; Koulali, A. Example of Using Particle Swarm Optimization Algorithm with Nelder–Mead Method for Flow Improvement in Axial Last Stage of Gas–Steam Turbine. Energies 2024, 17, 2816. https://doi.org/10.3390/en17122816
Ziółkowski P, Witanowski Ł, Głuch S, Klonowicz P, Feidt M, Koulali A. Example of Using Particle Swarm Optimization Algorithm with Nelder–Mead Method for Flow Improvement in Axial Last Stage of Gas–Steam Turbine. Energies. 2024; 17(12):2816. https://doi.org/10.3390/en17122816
Chicago/Turabian StyleZiółkowski, Paweł, Łukasz Witanowski, Stanisław Głuch, Piotr Klonowicz, Michel Feidt, and Aimad Koulali. 2024. "Example of Using Particle Swarm Optimization Algorithm with Nelder–Mead Method for Flow Improvement in Axial Last Stage of Gas–Steam Turbine" Energies 17, no. 12: 2816. https://doi.org/10.3390/en17122816
APA StyleZiółkowski, P., Witanowski, Ł., Głuch, S., Klonowicz, P., Feidt, M., & Koulali, A. (2024). Example of Using Particle Swarm Optimization Algorithm with Nelder–Mead Method for Flow Improvement in Axial Last Stage of Gas–Steam Turbine. Energies, 17(12), 2816. https://doi.org/10.3390/en17122816








