Abstract
In order to address the energy imbalance issue of a series-connected lithium-iron battery pack, this paper proposes an active equalization method based on a reduced-order solving strategy for the Hanoi Tower problem. The proposed scheme utilizes a combined structure of a switching-network circuit and a bidirectional Cuk converter and leverages an ultracapacitor cell as the energy-transfer carrier. Simulation and comparison demonstrate that the exchange of unbalanced energy within the battery pack can be achieved. The proposed approach can effectively achieve various balancing modes such as cell-to-cell, cell-to-string, string-to-cell, and string-to-string with a relatively fast balancing speed.
1. Introduction
Energy storage technology plays a crucial role in various applications, such as electric vehicles and smart grids [1]. Currently, the rated voltage of lithium-iron battery cells is limited to the range of 2.4–4.2 V [2]. In order to meet the voltage level requirements, it is often necessary to connect battery cells in series [3,4,5]. As a result, the imbalanced voltage phenomenon of cells is commonly observed [6]. As depicted in Figure 1, on one hand, there are certain differences in performance indicators such as the initial capacity, equivalent internal impedance, and self-discharge rate among individual cells due to the influence of production processes. On the other hand, the initial state differences of individual cells will be accumulated along with numerous charging and discharging cycles. The voltage imbalance in individual cells will affect the chargeable capacity and dischargeable capacity of the battery pack, leading to a reduction in the overall available capacity and a shortened lifespan of the pack [7]. Therefore, it is of necessity to study efficient balancing methods for battery cells [8].
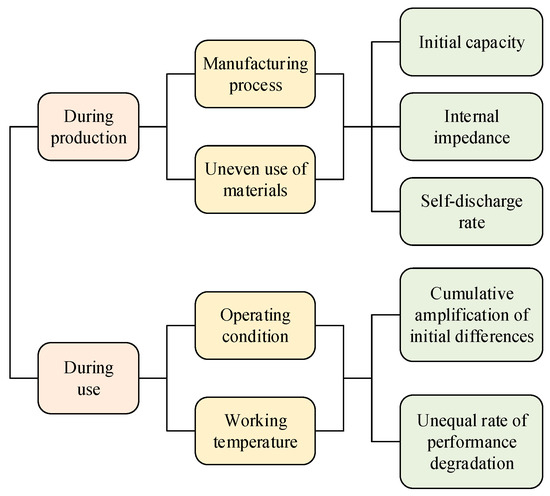
Figure 1.
The reasons for the voltage imbalance.
Technically, the balancing methods for battery packs can be divided into passive and active approaches. The first one, also known as the energy dissipation balancing approach, commonly uses a set of resistors to absorb excessive energy from battery cells, which have the advantages of simple topology, low cost, and being easy to implement in applications [9]. However, these passive schemes usually have lower energy utilization efficiency. Additionally, the heat generated during the balancing process may lead to thermal runaway; thus, an extra thermal management system is required for such a design. The active balancing schemes transfer the imbalanced energy between cells based on different ways of “peak shaving and valley filling”, which generally have a higher energy utilization efficiency [10]. Therefore, research on active balancing strategies has been widely developed in recent years [11].
According to the different energy transfer strategies and circuit structures used, active balancing systems can be classified into four main types: those using capacitors, inductors, transformers, and power electronic converters [12,13,14,15,16,17,18,19,20,21,22,23,24]. The first ones use capacitors as carriers to transfer the imbalanced energy among battery cells. By using these schemes, the voltage of the capacitor will not experience sudden changes during the energy transfer process [12,13,14]. Reference [14] proposed a mesh balancing topology with an energy-transfer capacitor that realizes the voltage balance between cells. However, as the voltage difference between individual cells gradually decreases, the balancing current of this scheme decreases gradually, leading to a slow balancing speed and a limited balancing accuracy. The second ones use inductors as carriers to transfer the imbalanced energy among battery cells [15,16,17]. Reference [15] proposed a balancing circuit with an energy-transfer inductor and put forward its control strategies for both constant voltage and constant current charging and discharging conditions. In comparison to the active balancing method using capacitors, the inductor-based balancing method offers faster balancing speed but relatively lower balancing efficiency. The third ones use the mutual inductance of transformers to transfer the imbalanced energy among battery cells [18,19,20]. Reference [19] proposed the active balancing method by using a multi-winding transformer, which has the advantages of short balancing paths and fast balancing speed. However, as the number of battery cells increases, the winding of transformer coils becomes more complex, while the cost and volume of the balancing circuit also increase. The last ones use power electronic converters to balance battery cells [21,22,23]. Reference [21] proposed an active balancing scheme by using a bidirectional L2C3 resonant converter, which realizes the voltage balance between cells and different strings of the battery pack. However, a portion of the battery cells in this scheme have to participate in the balancing process since the entire battery pack is connected to one end of the bidirectional converter, thus resulting in additional charge and discharge operations that are detrimental to the battery’s lifespan. Reference [22] proposed a four-switch bidirectional converter-based active balancing scheme and used the density-based spatial clustering of applications with noise (DBSCAN) clustering algorithm, which enables rapid balancing of battery packs. However, the control strategy of this scheme is relatively complex. Moreover, in cases where there is a significant difference in the state of charge among adjacent cells or when a fine balance is required, the clustering-based balancing algorithm may struggle, thereby adding extra computational burden to the controller.
In this work, an active balancing method is developed based on a reduced-order solving strategy of the Hanoi Tower problem and uses an ultracapacitor cell (UC) as the energy-transfer carrier with the help of a bidirectional Cuk converter and a switching-network circuit. To present the achievements in detail, the rest of this paper is organized as follows: Section 2 provides a detailed demonstration of the mapping relationship between the game process of Hanoi Tower and the balancing process of battery cells. Section 3 presents the balancing topology and the working principles of the proposed balancing scheme. Section 4 validates the proposed scheme through simulation and comparison. Section 5 concludes the work.
2. Active Equalizing Scheme Based on Solving the Hanoi Tower Problem
2.1. Preliminaries
The Hanoi tower problem originated from an ancient Indian legend and serves as a mathematical conundrum. It is commonly presented in the form of a game and stands as one of the classic examples of computer science education.
Assuming n represents the disc number of Hanoi Tower, the rules and objectives of an n-disk Hanoi Tower problem can be summarized as follows:
(1) There are three adjacent pillars labeled as Pillar A (the starting pillar), Pillar B (the auxiliary pillar), and Pillar C (the target pillar).
(2) Pillar A initially holds n discs in ascending order of size from top to bottom, forming a tower.
(3) Only one disc can be moved at a time, and a larger disc cannot be placed on top of a smaller one.
(4) The objective of the game is to move the entire tower of discs from the starting pillar A to the target pillar C. Upon completion of the carrying process, the order of the discs’ positions should match their original positions on the starting pillar.
Accordingly, for the n-layer Hanoi Tower Problem, the solving processes are as shown in Figure 2.
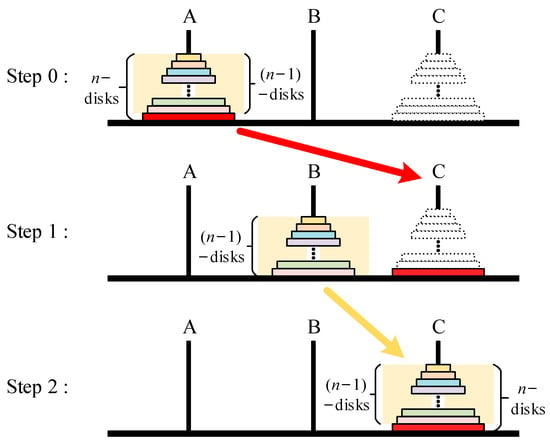
Figure 2.
Solving principle for the n-layer Hanoi Tower problem.
Map the above two-step solving process to the battery cell balancing scenario. The active balancing process involves transferring the energy between cells, essentially constituting an energy “carrying” process. Therefore, the battery balancing process has a potential correlation with the solving process of the Hanoi Tower problem, as illustrated in Figure 3.
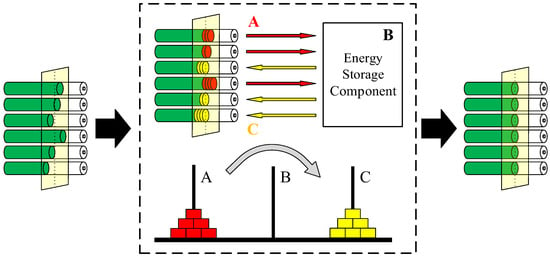
Figure 3.
The correspondence between the balancing process of battery cells and the solving process of the Hanoi tower problem.
In specific, the balancing process of battery cells must satisfy the following constraints:
- (1)
- When energy is transferred from one battery to energy storage components (such as capacitors, inductors, transformers, etc.) as an intermediate carrier of energy transfer, the equalization operation starts from the battery with the highest state of charge (SOC).
- (2)
- When energy is transferred from the intermediate carrier of energy transfer to battery cells, the energy is preferentially transferred to the battery cells with the lowest SOC.
With the above constraints, the active equalization process of battery cells performs the following mapping relationship with the plate handling process in the Hanoi Tower game:
- (1)
- Unbalanced energy will be distributed among three groups: Group A consists of battery cells with energy levels higher than the equilibrium target; Group B comprises intermediate energy storage components; and Group C includes battery cells with energy levels lower than the equilibrium target.
- (2)
- In the initial state, there are SOC differences between each individual cell in the battery pack. The control unit allows for the sorting operation of these differences.
- (3)
- The balancing process gives priority to balancing the battery cell with the largest state deviation in the battery pack.
- (4)
- During the balancing process, the unbalanced energy of battery cells in Group A is temporarily transferred to Group B and directed to the target Group C, ultimately causing all cells to be in a balanced state.
2.2. Balancing Strategy Based on the Solving Strategy of the Hanoi Tower Problem
Suppose the minimum moves required to solve the n-layered Hanoi tower problem are: , where , , and . When , the n-layered Hanoi tower problem can be divided into the movement of a large disk and the resolution of two (n − 1)-layered smaller Hanoi tower problems. Accordingly, the following recursive formula can be obtained:
The general formula for can be derived as follows:
From Equation (2), it can be observed that as the number of layers n increases, the minimum number of moves required to solve the problem also increases. Therefore, this paper proposes a reduced-order solving strategy.
Technically, the voltage of a lithium-iron battery cell is relatively flat when its SOC is within the range of 20% to 80%. Significant variations of the cell voltage can be observed in the SOC range of 0% to 20% and 80% to 100%. However, within the relatively flat SOC range of 20% to 80%, there is still a certain degree of slope variation in the voltage trend. In practice, one can obtain the variation of cell voltage with very high precision. Accordingly, we take the battery voltage as the equalization indicator and consider an n-cell series battery pack as an example. Initially, the voltages of individual cells and the terminal voltage of the intermediate energy storage components are collected. The average cell voltage can be obtained:
Next, set as the equalization target, and calculate the voltage deviation of each battery cell from the equalization target :
Thus, a set of deviations can be obtained:
When the absolute error of the battery cell i exceeds the predefined threshold , it indicates that the cell i deviates from the equalization state, and needs to be balanced. Conversely, when is less than , it signifies that the cell i is already in an equalization state.
Define the maximum and minimum deviation and as follows:
If the balancing operation is carried out completely according to the above mapping relationship, balancing operations are required for a battery pack with n series cells. However, within a battery pack with n series cells, the voltage of each cell may not necessarily have n different SOC states in practice.
Accordingly, a reduced-order solving strategy is developed in this work to reduce the time of operations. Specifically, map the above solving process to the battery cell balancing scenario. The equalization process can be divided into the following two steps:
(1) Taking the battery cell with the highest voltage as the object, a searching operation is conducted to evaluate the voltage status of its neighboring cells. If the deviation is greater than , the cell will be included in the discharge-requiring battery string . The searching operation ends until all the neighboring cells requiring discharge are included in . Assuming that the battery string contains a total of p adjacent battery cells, the set is defined as:
which meets the following conditions:
The selected battery string will be connected to the switching-network circuit matrix and a bidirectional power electronic converter, with an ultracapacitor cell serving as the temporary storage unit for excess energy from the battery string .
(2) Taking the battery cell with the lowest voltage as the object, a searching operation is also carried out to select a charge-requiring battery string . The searching operation ends until all the neighboring cells requiring charge are included in . Assuming that the battery string contains a total of q adjacent battery cells, the set is:
which meets the following conditions:
The selected battery string will also be connected to the switching-network circuit matrix and a bidirectional power electronic converter. The ultracapacitor cell will serve as the temporary source unit to release stored energy to the battery string .
Repeat the above two stages until all the imbalanced energy in the battery string is transferred to the battery string , and ensure that the voltage of each cell is within the allowable error range of the equalization target. The schematic diagram of the two-stage equalization strategy is depicted in Figure 4.
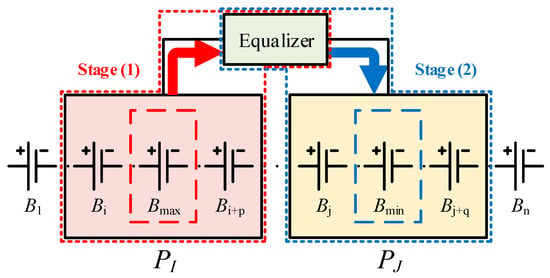
Figure 4.
Two-stage balancing process.
Assuming there are m cells to be selected as objects in the battery pack with n series cells, according to the above configuration, battery cells are classified into groups. Consequently, the balancing problem of n cells will transform into a problem of balancing (n − m + 1) cells. Similar to the process of playing the game of Hanoi Tower, the largest disk at the bottom gradually becomes smaller. When this disk shrinks to the size of the disk above it, these two disks are considered one larger disk and move simultaneously. Similarly, the problem of n-level river towers is transformed into the problem of (n − 1) level towers.
When the voltage of a cell within one of the sets and enters the allowable error range of the equalization target, the cell will be automatically removed from sets and . Consequently, the frequency of charging and discharging cycles for a single cell can be reduced. The approach effectively decreases redundant balancing operations. The intermediary energy carrier, the ultracapacitor cell, “sends” its remaining energy back to the entire battery pack in the final stage. The flow chart of the proposed balancing strategy is as shown in Figure 5.
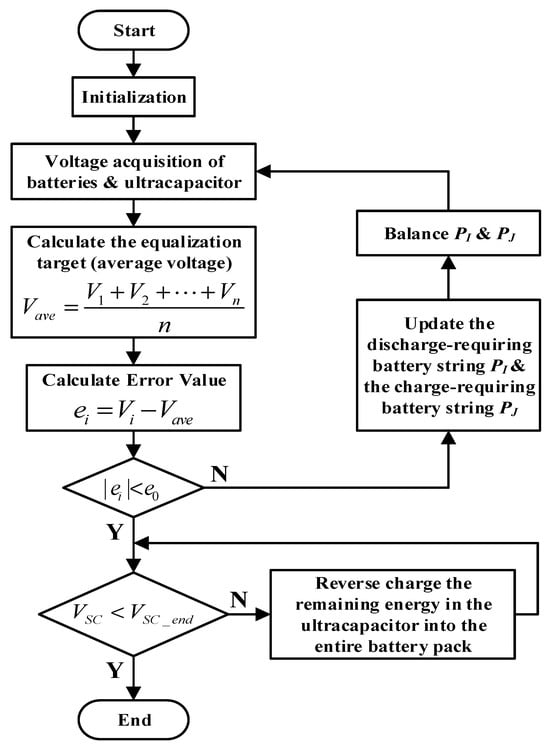
Figure 5.
Flowchart of the proposed reduced-order balancing strategy.
3. Balancing Topology and Its Working Principle
3.1. Balancing Topology Design
To achieve the active balancing strategy in Section 2, this paper develops the following circuit system, which contains a bidirectional Cuk converter, switching network, and an ultracapacitor cell, as shown in Figure 6.
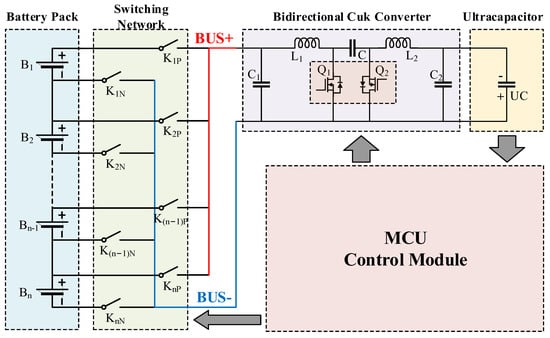
Figure 6.
Bidirectional Cuk converter-based balancing system.
In Figure 6, the positive terminal of each battery cell is connected to one end of the switch , and the negative terminal is connected to one end of the switch , where i represents the number of the corresponding cell for the switch. All the other ends of the positive terminal switches are interconnected to form the positive bus, while the other ends of the negative terminal switches are interconnected to form the negative bus. The positive and negative buses are connected to the positive and negative pins of the bidirectional Cuk converter, respectively. The switching network in the above figure consists of 2n bidirectional switching units, which can be achieved by the following four circuit forms [24], as shown in Figure 7.
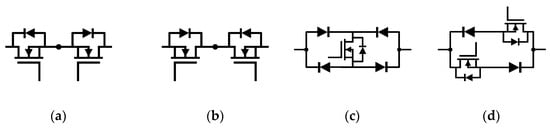
Figure 7.
Four possible topologies of bidirectional switches in the switching network. (a) scheme A; (b) scheme B; (c) scheme C; (d) scheme D.
Note that an ultracapacitor cell is used as an intermediary carrier for energy transfer, which corresponds to the central Pillar B in the Hanoi Tower game.
When the switches and of the bidirectional Cuk converter are in complementary conduction states, with their duty cycles satisfying:
In Equation (12), represents the duty cycle of switch , and represents the duty cycle of switch .
When the battery pack discharges to the ultracapacitor cell, the input and output of the converter satisfy:
The duty cycle of switch can be obtained:
When the ultracapacitor cell discharges into the battery pack, the calculation of the duty cycle of switch is the same as above.
3.2. Working Principle
In this work, the proposed active equalizer can be operated in four modes: cell-to-cell (C2C), cell-to-string (C2S), string-to-cell (S2C), and string-to-string (S2S). Taking S2S and C2C modes as examples, their operational principles are as follows:
In S2S mode, the imbalanced energy will be transferred from the discharge-requiring series string to charge-requiring series string , the equivalent circuit of this mode is as shown in Figure 8.
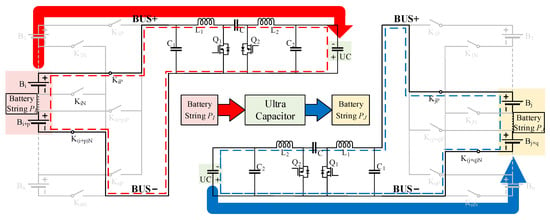
Figure 8.
Equivalent circuit of S2S mode.
The equalization process in S2S mode comprises the following two stages:
(1) Turn on the switches and connected to the series string , the string is the source of the bidirectional Cuk converter, and the ultracapacitor cell will be charged. In this process, the converter operates in forward buck mode. Combining the sub-process (1) of Section 2.2, the duty cycle of the switch is determined by the following:
In the above equation, the term represents a predetermined coefficient for the forward output voltage, which is closely related to the forward charging voltage of the ultracapacitor cell. stands for a predetermined coefficient for the forward input discharge. denotes the number of battery cells in the collection of discharge-requiring string . The duty cycle of the main switch will automatically adjust with the variation of . When the voltage of the ultracapacitor cell reaches the predetermined upper voltage threshold , the inconsistency of the battery pack rapidly diminishes, thus ending this stage.
(2) Turn off switches and , turn on switches and connected to the series string , the string is as the load of the bidirectional Cuk converter, and the ultracapacitor cell serves as the source. In this process, the converter operates in reverse boost mode. Combining the sub-process (2) of Section 2.2, the duty cycle of the switch is determined by the following:
In the above equation, the term represents the charging coefficient of the predetermined reverse output terminal, stands for the number of battery cells in the collection of charge-requiring string , and denotes the real-time voltage of the ultracapacitor cell. The duty cycle of the main switch is adjusted instantaneously with the variation of . The reverse output voltage of the bidirectional Cuk circuit is represented by the term . When remains constant, the reverse output voltage is held constant. When the voltage of the ultracapacitor cell reaches the predetermined lower voltage threshold , this stage ends.
Repeat the above two stages until all the imbalanced energy in the series string is transferred to the series string , and the energy/voltage/SOC difference among all cells falls within the predetermined error range. The S2S mode equalization process ends.
In C2C mode, the imbalanced energy will be transferred from individual cell to another cell , where i and j represent the indices of the cells corresponding to the switches. The equivalent circuit of this mode is as shown in Figure 9.
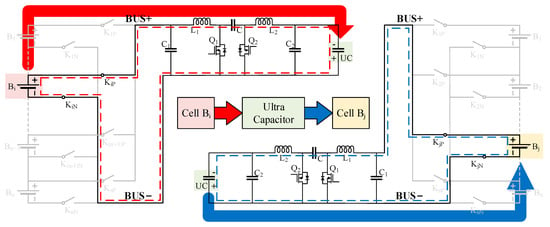
Figure 9.
Equivalent circuit of C2C mode.
The equalization process in C2C mode also comprises the above two stages, which are fundamentally similar those in S2S mode, with the main differences lying in the selection of conducting switches in the switching network circuit and the duty cycles of power switches in the bidirectional Cuk converter. The key parameters that need to be determined in S2S mode and C2C mode are the configuration of duty cycles of the bidirectional Cuk converter, as shown in Equations (15) and (16). In specific, the parameters , , and are predetermined constants in the design, represents the real-time voltage value of the ultracapacitor collected by the controller. Therefore, the primary parameters to be determined for duty cycles are the number of and . When the equalizer is operating in S2S mode, denotes the number of battery cells in the collection of discharge-requiring string PI, and stands for the number of battery cells in the collection of charge-requiring string PJ. In C2C mode, . Additionally, when the remaining energy of the ultracapacitor is charged back to the battery pack, the duty cycle of Q2 is determined by Equation (16), and .
4. Validation and Discussion
Taking a battery pack with 4 cells as an example, a circuit-level simulation was constructed, as depicted in Figure 10. The parameters of the simulation model are as follows: the two inductors are both 10μH, the capacitor is 50 μF, the working frequency of power switches is 100 kHz, the ON-state resistance of the MOSFET is 50 mΩ, and the forward voltage drop of the MOSFET body diode is 0.8 V. The rated voltage of the lithium battery cell is 3.7 V with a rated capacity of 1.5 Ah, and the value of the ultracapacitor cell is 10 F/6 V.
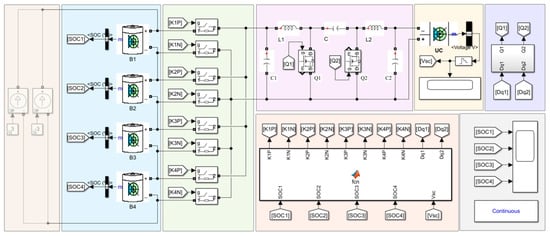
Figure 10.
Circuit-level simulation of the proposed balancing system.
4.1. Test Scenario 1: Equalization under Rest State
In this test scenario, the battery pack is initially in a rest state, and the initial SOC of 4 cells is 83%, 82%, 80%, and 79%, respectively.
4.1.1. Equalization without the Proposed Reduced-Order Strategy
In the absence of the proposed reduced-order strategy, only one battery cell is selected to be connected to the equalization circuit at a time during the balancing process. The variation curves of SOC values for each cell are as shown in Figure 11.
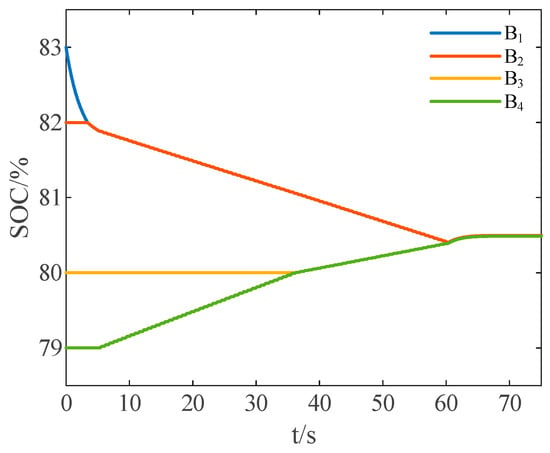
Figure 11.
SOC variation curves under rest state without the reduce-order strategy.
After around 60.5 s, the SOC deviation among battery cells reaches the pre-defined balancing error range. Within the time period of 60.5 to 70.5 s, the remaining energy of the ultracapacitor cell is used to charge the entire battery pack. After around 70.5 s, the balancing process of the battery pack is completed.
4.1.2. Equalization with the Proposed Reduced-Order Strategy
In this test scenario, the proposed reduced-order strategy is introduced to the balancing process. The variation curves of SOC values for each cell are as shown in Figure 12.
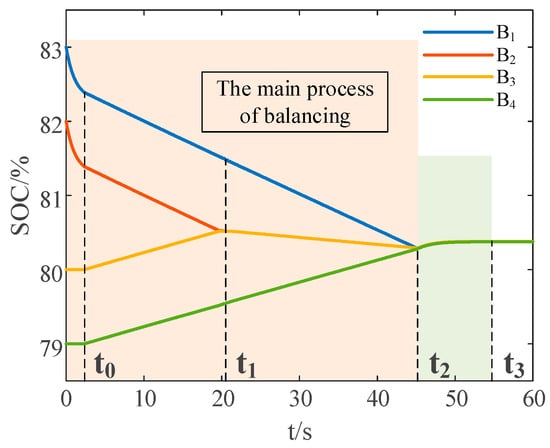
Figure 12.
SOC variation curves under rest state with the reduce-order strategy.
One can find that, after introducing the proposed reduce-order strategy, the system experiences the following states in different time periods:
(1) In the time range of 0–t0, switches and are turned on, the battery cells and are as the discharge-requiring string , that is, . The battery cells and are as the charge-requiring string , that is, . The battery string commences charging the ultracapacitor cell. The upper voltage threshold for charging the ultracapacitor cell is set to . The inconsistency among the battery group rapidly decreases.
(2) At time t0, the terminal voltage of the ultracapacitor cell reaches the preset threshold voltage , and the battery string stops discharging.
(3) In the time range of t0–t1, , . Energy cycling between battery strings , , and the ultracapacitor cell. The equalizer operates in S2S mode throughout this time period. At 10 s, the bidirectional Cuk converter operates in forward buck mode, and the battery string charges the ultracapacitor cell. The typical steady-state waveforms of the bidirectional Cuk converter after 10 s of the equalization process are as shown in Figure 13, in which represents the drive signal for switch , while and denote the currents of inductors L1 and L2, respectively.
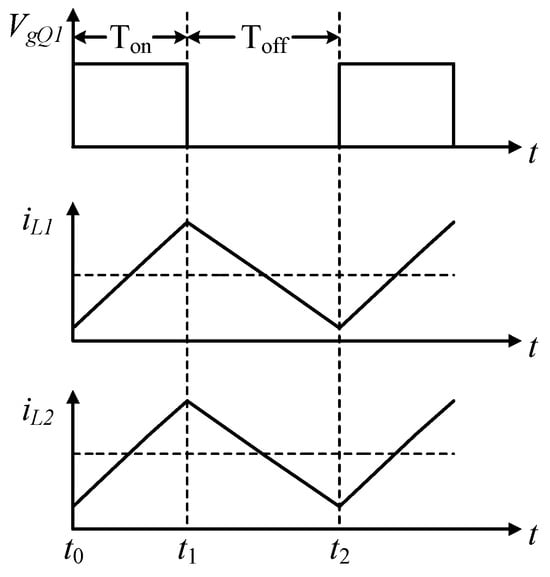
Figure 13.
Typical steady-state waveforms of the bidirectional Cuk converter in stage (3).
(4) At time t1, the discharge-requiring battery string and the charge-requiring battery string are updated, that is, and .
(5) In the time range of t1–t2, the energy from the string continues to transfer to the string . The equalizer operates in S2C mode throughout this time period.
(6) At time t2, when the SOC difference of each battery cell reaches the preset error range, the ultracapacitor cell begins to transfer its remaining energy to the entire battery pack.
(7) In the time range of t2–t3, the bidirectional Cuk converter operates in reverse boost mode, switches and are turned on, and the ultracapacitor cell acts as the source to charge the entire battery pack. The steady-state waveforms after 46 s of the equalization process are depicted in Figure 14, where represents the drive signal for switch , and and denote the currents of inductors L1 and L2, respectively.
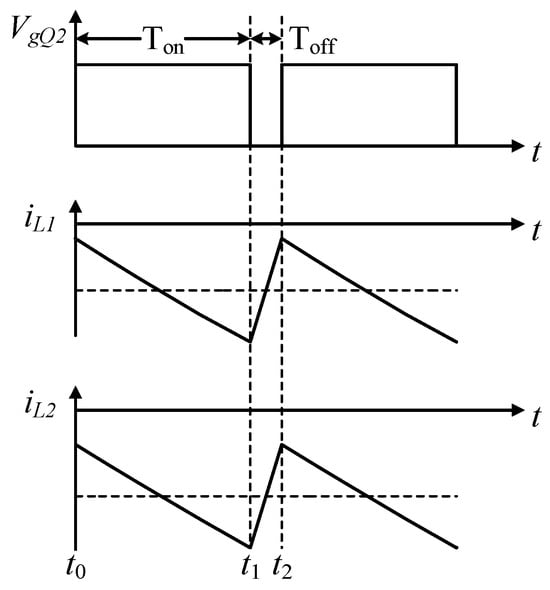
Figure 14.
Typical steady-state waveforms of the bidirectional Cuk converter in stage (7).
(8) At time t3, the terminal voltage of the ultracapacitor cell reaches the preset lower discharge voltage threshold . The balancing process ends.
Throughout the balancing process, from the initial state to the end, the variation curve of the terminal voltage of the ultracapacitor cell is as shown in Figure 15.
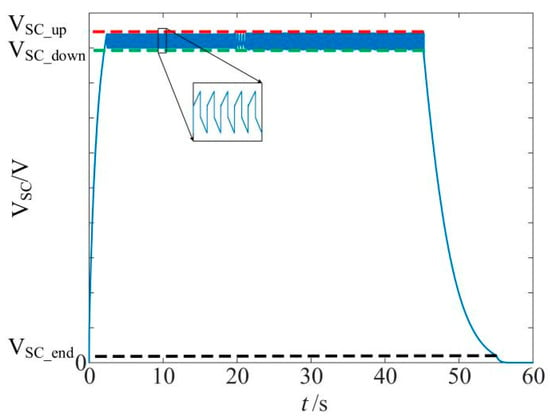
Figure 15.
Voltage variation curve of the ultracapacitor cell.
After around 45 s, the SOC deviation among battery cells reaches the pre-defined balancing error range. Within the time period of 45 to 55 s, the remaining energy of the ultracapacitor cell is used to charge the entire battery pack. After around 55 s, the balancing process of the battery pack is completed.
In comparison, with the inclusion of the proposed reduced-order strategy, the time required to reach the preset balancing error range is reduced by 25.6%, and the overall balancing time is decreased by approximately 22%.
4.2. Test Scenario 2: Equalization under Charge State
In this test scenario, the battery pack is initially in charge, the charge current is a constant value of 3A, and the initial SOC of 4 cells is 83%, 82%, 80%, and 79%, respectively.
Without the inclusion of the proposed reduced-order strategy, the variation curves of SOC values for each cell are as shown in Figure 16.
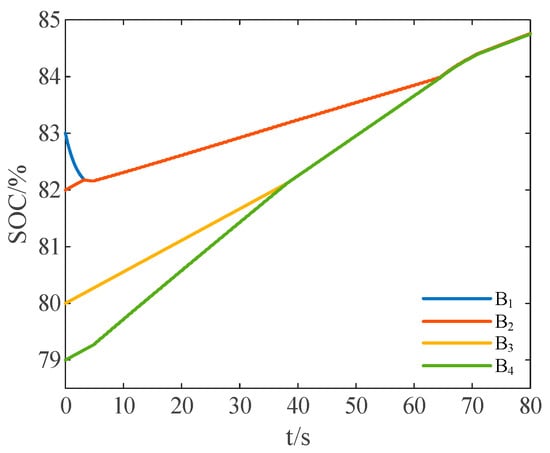
Figure 16.
SOC variation curves under charge state without the reduce-order strategy.
After around 64.5 s, the SOC deviation among battery cells reaches the preset balancing error range. Within the time period of 64.5 to 78 s, the remaining energy of the ultracapacitor cell is utilized to charge the entire battery pack. After around 78 s, the balancing process of the battery pack is completed.
Under the same initial conditions, the proposed reduced-order strategy is introduced to the balancing process. The variation curves of SOC values for each cell are as shown in Figure 17.
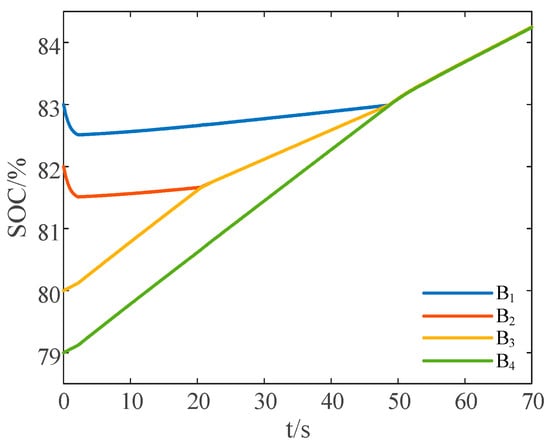
Figure 17.
SOC variation curves under charge state with the reduce-order strategy.
After around 49 s, the SOC deviation among battery cells reaches the predetermined balancing error range. Within the time period of 49 to 63 s, the remaining energy of the ultracapacitor cell is utilized to charge the entire battery pack. After around 63 s, the balancing process of the battery pack is completed.
In comparison, with the inclusion of the proposed reduced-order strategy, the time required to reach the preset balancing error range is reduced by 24%, and the overall balancing time is reduced by approximately 19.2%.
4.3. Test Scenario 3: Equalization under Discharge State
In this test scenario, the battery pack is in discharge state initially, the discharge current is a constant value of 3A, and the initial SOC of 4 cells is 83%, 82%, 80%, and 79%, respectively.
Without the inclusion of the proposed reduced-order strategy, the variation curves of SOC values for each cell are as shown in Figure 18.
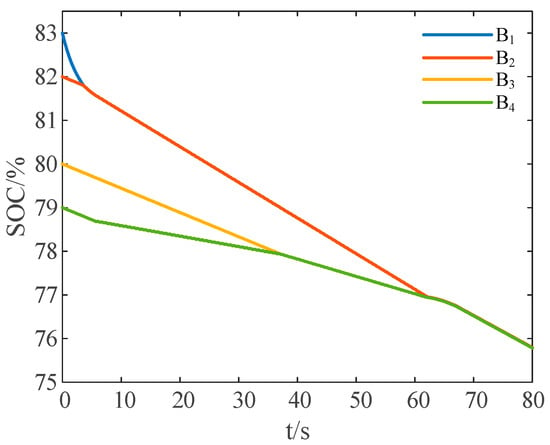
Figure 18.
SOC variation curves under discharge state without the reduce-order strategy.
After around 62.5 s, the SOC deviation among battery cells reaches the predefined balancing error range. Within the time period of 62.5 to 72 s, the remaining energy of the ultracapacitor cell is utilized to charge the entire battery pack. After around 72 s, the balancing process of the battery pack is completed.
Under the same initial conditions, the proposed reduced-order strategy is introduced to the balancing process. The variation curves of SOC values for each cell are as shown in Figure 19.
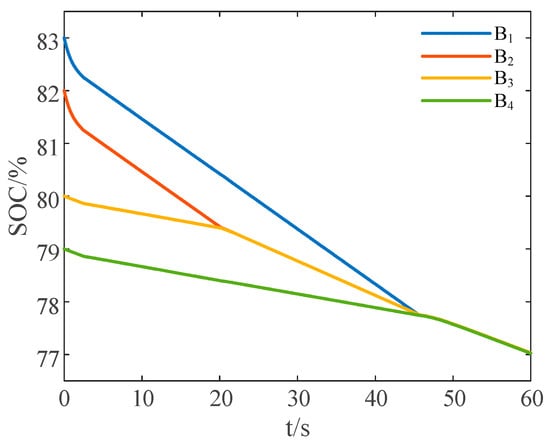
Figure 19.
SOC variation curves under discharge state with the reduce-order strategy.
After around 46 s, the SOC deviation among battery cells reaches the predetermined balancing error range. Within the time period of 46 to 55 s, the remaining energy of the ultracapacitor cell is utilized to charge the entire battery pack. After around 55 s, the balancing process of the battery pack is completed.
In comparison, with the inclusion of the proposed reduced-order strategy, the time required to reach the preset balancing error range is reduced by 26.4%, and the overall balancing time is reduced by approximately 23.6%.
4.4. Comparison
A comparative analysis is conducted in this part, where the performance of the proposed scheme is compared with that of existing active schemes based on the “time multiplexing” principle. Several key performance indicators are listed in Table 1.

Table 1.
Comparison of the proposed method with different equalization methods.
From the table, it is evident that the proposed active balancing method utilizes a relatively small number of energy-storage components. The topology structure offers four achievable balancing modes, which provides greater flexibility in system balancing energy flow types and thereby allows for a wider range of choices in balancing strategy algorithm design. Moreover, the system presents low control complexity; it imposes minimal computing power requirements on the controller. Consequently, the proposed scheme exhibits relatively faster balancing speeds.
4.5. Further Discussion
4.5.1. Feasibility in Scenarios with More Pronounced SOC Differences
To further validate the feasibility of the proposed method, scenarios with more pronounced SOC differences are considered. The initial SOC of 4 cells is 73%, 72%, 60%, and 59%, respectively. The variation curves of SOC values for each cell are as shown in Figure 20.
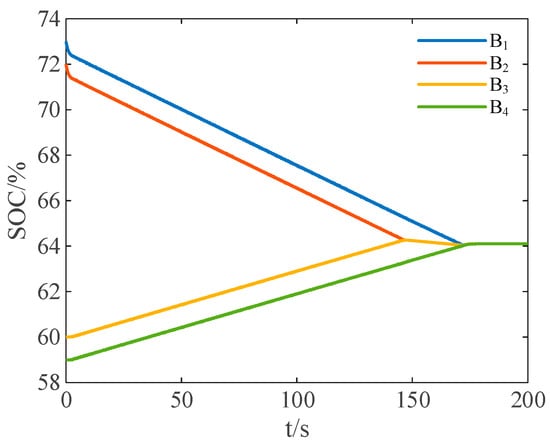
Figure 20.
SOC variation curves under rest state with the reduce-order strategy—Further experiment 1.
From Figure 20:
Within the time period of 0 to 147 s, battery cells B1 and B2 constitute the discharge-requiring battery string PI, battery cells B3 and B4 form the charge-requiring battery string PJ, and PI charges PJ through the ultracapacitor.
Within the time period of 147 to 172.1 s, battery cells B1, B2, and B3 form the discharge-requiring battery string PI, battery cell B4 forms the charge-requiring battery string PJ, and PI charges PJ until the SOC difference among the four cells reaches the preset error range.
Within the time period of 172.1 to 182.4 s, the remaining energy from the ultracapacitor charges the entire battery pack, and then the balancing process ends.
When the initial SOC of 4 cells is 73%, 72%, 70%, and 60%, the variation curves of SOC values for each cell are as shown in Figure 21.
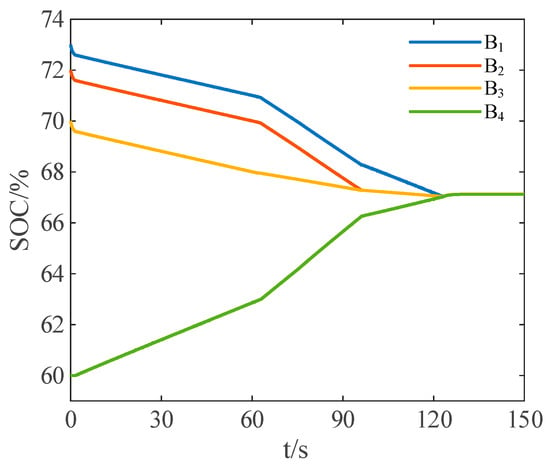
Figure 21.
SOC variation curves under rest state with the reduce-order strategy—Further experiment 2.
From Figure 21:
Within the time period of 0 to 123.1 s, battery cells B1, B2, and B3 constitute the discharge-requiring battery string PI, battery cell B4 forms the charge-requiring battery string PJ, and PI charges PJ through the ultracapacitor.
Within the time period of 123.1 to 132.8 s, the remaining energy from the ultracapacitor charges the entire battery pack, and then the balancing process ends.
When the initial SOC of 4 cells is 70%, 65%, 64%, and 56%, the variation curves of the SOC values for each cell are as shown in Figure 22.
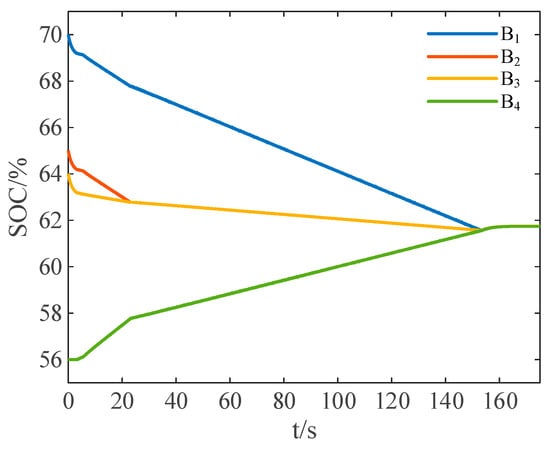
Figure 22.
SOC variation curves under rest state with the reduce-order strategy—Further experiment 3.
From Figure 22:
Within the time period of 0 to 153.3 s, battery cells B1, B2, and B3 constitute the discharge-requiring battery string PI, battery cell B4 forms the charge-requiring battery string PJ, and PI charges PJ through the ultracapacitor.
Within the time period of 153.3 to 172.8 s, the remaining energy from the ultracapacitor charges the entire battery pack, and then the balancing process ends.
The above results demonstrate that the proposed equalization scheme remains capable in scenarios with more pronounced SOC differences.
4.5.2. Discussion on the Influence of Ultracapacitor Capacity
The selection of circuit component parameters will influence the equalization performance. In order to analyze the impact of the rated voltage and the rated capacity of the ultracapacitor on the speed (time) of equalization, comparisons are conducted as follows:
Firstly, the rated voltage of the ultracapacitor is kept constant at 6V, the rated capacitance is set to 20F and 50F, respectively. The results for the three balancing states are depicted as Figure 23:
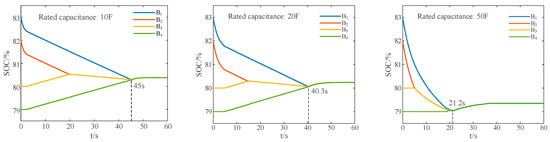
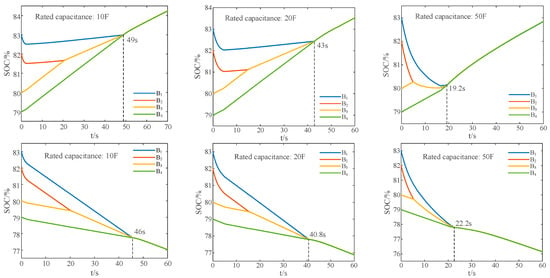
Figure 23.
SOC variation curves under rest, charge, and discharge states when only changing the rated capacitance of the ultracapacitor.
Furthermore, the rated capacitance of the ultracapacitor is kept constant at 10F, and the rated voltage is set to 20V and 50V, respectively. The results for three balancing states are depicted as Figure 24:
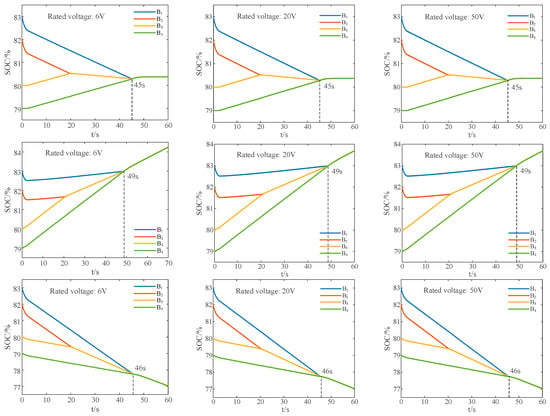
Figure 24.
SOC variation curves under rest, charge, and discharge states when only changing the rated voltage of the ultracapacitor.
The results indicate that under the same conditions, the capacitance of the ultracapacitor directly affects the balancing speed of the proposed balancing system. A larger capacitance results in a faster equalization speed because an ultracapacitor with a relatively large capacitance allows for more charge transfer in the balancing process. However, the rated voltage of the ultracapacitor has little impact on the speed (time) of equalization.
5. Conclusions
This paper develops an active equalization method based on a reduced-order solving strategy for the Hanoi Tower problem. With the help of the balancing circuit composed of a bidirectional Cuk converter, a switching matrix, and an ultracapacitor cell, the system allows for four balancing modes with a relatively high balancing speed. Simulation results demonstrate the feasibility of the proposed balancing system and its excellent balancing performance. The comparative results indicate that the proposed method exhibits greater flexibility in balancing pathways, lower control complexity, and relatively faster balancing speed.
Author Contributions
Software, writing—original draft preparation, validation, Z.X.; conceptualization, formal analysis, writing—review and editing, X.C. (Xi Chen); writing—review and editing, X.C. (Xingjiang Chi); data curation, B.Z.; supervision, L.Z.; project administration, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
The work was partly supported by the Natural Science Project of Yichang, China (A20-3-014) and the University Science Research and Application Project of Yichang, China (A21-3-015).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Xingjiang Chi was employed by the company State Grid Beijing Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zou, C.F.; Zhang, L.; Hu, X.S.; Wang, Z.P.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.S.; Liu, J.F.; Lin, X.K.; Liu, B. A review of equalization strategies for series battery packs: Variables, objectives, and algorithms. Renew. Sustain. Energy Rev. 2019, 116, 109464. [Google Scholar] [CrossRef]
- Cano, Z.P.; Banham, D.; Ye, S.Y.; Hintennach, A.; Lu, J.; Fowler, M.; Chen, Z.W. Batteries and fuel cells for emerging electric vehicle markets. Nat. Energy 2018, 3, 279–289. [Google Scholar] [CrossRef]
- Wang, J.X.; Chen, L.D.; Tan, Z.F.; Du, E.; Liu, N.; Ma, J.; Sun, M.Y.; Li, C.B.; Song, J.; Lu, X.; et al. Inherent spatiotemporal uncertainty of renewable power in China. Nat. Commun. 2023, 14, 5379. [Google Scholar] [CrossRef]
- Andwari, A.M.; Pesiridis, A.; Rajoo, S.; Martinez-Botas, R.; Esfahanian, V. A review of battery electric vehicle technology and readiness levels. Renew. Sustain. Energy Rev. 2017, 78, 414–430. [Google Scholar] [CrossRef]
- Uno, M.; Yashiro, K.; Hasegawa, K. Modularized Equalization Architecture With Voltage Multiplier-Based Cell Equalizer and Switchless Switched Capacitor Converter-Based Module Equalizer for Series-Connected Electric Double-Layer Capacitors. IEEE Trans. Power Electron. 2019, 34, 6356–6368. [Google Scholar] [CrossRef]
- Peng, F.X.; Wang, H.Y.; Yu, L. Analysis and Design Considerations of Efficiency Enhanced Hierarchical Battery Equalizer Based on Bipolar CCM Buck-Boost Units. IEEE Trans. Ind. Electron. 2019, 55, 4053–4063. [Google Scholar] [CrossRef]
- Cai, M.Y.; Zhang, E.; Lin, J.; Wang, K.L.; Jiang, K.; Zhou, M. Review on Balancing Topology of Lithium-ion Battery Pack. Proc. CSEE 2021, 41, 5294–5311. [Google Scholar]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, M.I.; Guerrero-Martinez, M.A. A novel active battery equalization control with on-line unhealthy cell detection and cell change decision. J. Power Sources 2015, 299, 356–370. [Google Scholar] [CrossRef]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, M.I.; Guerrero-Martinez, M.A. Battery equalization active methods. J. Power Sources 2014, 246, 934–949. [Google Scholar] [CrossRef]
- Ghaeminezhad, N.; Ouyang, Q.; Hu, X.S.; Xu, G.T.; Wang, Z.S. Active cell equalization topologies analysis for battery packs: A systematic review. IEEE Trans. Power Electron. 2021, 36, 9119–9135. [Google Scholar] [CrossRef]
- Kim, M.Y.; Kim, C.H.; Kim, J.H.; Moon, G.W. A chain structure of switched capacitor for improved cell balancing speed of lithium-ion batteries. IEEE Trans. Ind. Electron. 2014, 61, 3989–3999. [Google Scholar] [CrossRef]
- Shang, Y.L.; Zhang, C.H.; Cui, N.X.; Mi, C.C. A delta-structured switched-capacitor equalizer for series-connected battery strings. IEEE Trans. Power Electron. 2019, 34, 452–461. [Google Scholar]
- Shang, Y.L.; Zhang, Q.; Cui, N.X.; Duan, B.; Zhang, C.H. An optimized mesh-structured switched-capacitor equalizer for lithium-ion battery strings. IEEE Trans. Transp. Electrif. 2019, 5, 252–261. [Google Scholar] [CrossRef]
- Zheng, X.X.; Liu, X.T.; He, Y.; Zeng, G.J. Active vehicle battery equalization scheme in the condition of constant-voltage/current charging and discharging. IEEE Trans. Veh. Technol. 2017, 66, 3714–3723. [Google Scholar]
- Phung, T.H.; Collet, A.; Crebier, J.C. An optimized topology for next-to-next balancing of series-connected lithium-ion cells. IEEE Trans. Power Electron. 2014, 29, 4603–4613. [Google Scholar] [CrossRef]
- Ding, X.F.; Zhang, D.H.; Cheng, J.W.; Wang, B.B.; Chai, Y.M.; Zhao, Z.H.; Xiong, R.; Luk, P.C.K. A novel active equalization topology for series-connected Lithium-ion battery packs. IEEE Trans. Ind. Appl. 2020, 56, 6892–6903. [Google Scholar] [CrossRef]
- Li, S.Q.; Mi, C.C.; Zhang, M.Y. A high-efficiency active battery-balancing circuit using multiwinding transformer. IEEE Trans. Ind. Appl. 2013, 49, 198–207. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.F.; Cui, Y.Y.; Zou, J.M.; Yang, S.Y. A multiwinding transformer cell-to-cell active equalization method for lithium-ion batteries with reduced number of driving circuits. IEEE Trans. Power Electron. 2016, 31, 4916–4929. [Google Scholar]
- Shang, Y.L.; Cui, N.X.; Zhang, C.H. An Optimized Any-Cell-to-Any-Cell Equalizer Based on Coupled Half-bridge Converters for Series-Connected Battery Strings. IEEE Trans. Power Electron. 2019, 34, 8831–8841. [Google Scholar] [CrossRef]
- Wei, Z.Q.; Wang, H.Y.; Lu, Y.Q.; Shu, D.D.; Ning, G.D.; Fu, M.F. Bidirectional Constant Current String-to-Cell Battery Equalizer Based on L2C3 Resonant Topology. IEEE Trans. Power Electron. 2023, 38, 666–677. [Google Scholar] [CrossRef]
- Wang, L.J.; Ke, J.Y.; Zhan, M.; Tian, A.N.; Wu, T.Z.; Zhang, X.X.; Jiang, J.C. Efficient and Fast Active Equalization Method for Retired Battery Pack Using Wide Voltage Range Bidirectional Converter and DBSCAN Clustering Algorithm. IEEE Trans. Power Electron. 2022, 37, 13824–13833. [Google Scholar]
- Qi, J.; Lu, D.D.C. A preventive approach for solving battery imbalance issue by using a bidirectional multiple-input Cuk converter working in DCVM. IEEE Trans. Ind. Electron. 2017, 64, 7780–7789. [Google Scholar] [CrossRef]
- Qi, X.B.; Wang, Y.; Fang, M.Z.; Wang, H.; Wang, Y.B.; Chen, Z. A Family of Integrated Cascade Multiport Converters for Centralized Equalization Systems: Derivation, Analysis, and Verification. IEEE Trans. Power Electron. 2023, 38, 7398–7415. [Google Scholar] [CrossRef]
- Daowd, M.; Antoine, M.; Omar, N.; van den Bossche, P.; van Mierlo, J. Single Switched Capacitor Battery Balancing System Enhancements. Energies 2013, 6, 2149–2174. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).