Abstract
The simulation of engine combustion processes, such as autoignition, an important process in the co-optimization of fuel-engine design, can be computationally expensive due to the large number of thermo-chemical scalars needed to describe the full chemical system. Yet, the inherent correlations between the different chemical species during oxidation can significantly reduce the complexity of representing this system. One strategy is to select a subset of representative species that accurately captures the combustion process at a fraction of the computational cost of the full system. In this study, we compare the performance of four different techniques to select these species. They include the two-step principal component analysis (PCA) approach, directed relation graphs (DRGs), the global pathway selection (GPS) approach, and the manifold-informed species selection method. A parametric study of the representative species selection is carried out on data from the simulation of homogeneous and perfectly stirred reactors by investigating seven cumulative variances and 47 different cut-off percentages for the two-step PCA, and 65 and 51 thresholds for the DRGs and GPS, respectively. Results show that these selection methods capture key important species that can accurately describe the chemical system and track each stage of oxidation. The two-step PCA is sensitive to the cumulative variance, and DRGs and GPS are sensitive to the choice of target variables. By selecting key representative species and reducing the number of thermo-chemical scalars, these three methods can be used to develop computationally efficient hybrid chemistry schemes.
1. Introduction
The combustion of practical fuels involves the reaction and transport of many chemical species. The multiscale nature of combustion chemistry and the large number of species that must be solved impose significant constraints on the ability to implement high-fidelity simulations of practical combustion devices.
Different approaches have been adopted in the combustion literature to overcome these constraints. Among these approaches, chemistry reduction and acceleration strategies have played a central role in reducing the number of reactions and species and managing the stiffness of the reaction chemistry. Both classes of approaches attempt to reduce the complexity of the chemical mechanisms by identifying a subset of species of the full chemical system, labeled here as representative species [1].
In chemistry reduction, these species are featured in global or skeletal mechanisms, while the contribution of non-representative species and their associated reactions are eliminated through chemistry reduction. The selection of representative species is also a key component in the development of reduced-order or hybrid chemistry (HyChem) models [2,3,4,5,6,7,8]. In more recent years, we have implemented the HyChem approach and the choice of representative species with machine learning tools to accelerate the chemistry integration of complex fuel oxidation [9,10,11,12]. More recently, Kumar and Echekki [13] proposed a novel chemistry acceleration scheme for use in reacting flow simulations that relies on the transport of representative species, which represent a very small subset of the chemical mechanism. The approach relies on the use of deep operator networks (DeepONets) [14] to map the evolution of the representative species between time increments. The goal of the selection is to retain species that will be adequate markers for the progress of fuel oxidation. Representative species also have played an important role in constructing low-dimensional manifolds for the chemical system [15] as data-driven alternative approaches to traditional turbulent combustion models. Further reduction in this manifold can be achieved through the implementation of principal component analysis (PCA) [16]. Therefore, beyond chemistry reduction, the use of representative species can be extended to different strategies for chemistry acceleration.
Different approaches may serve to select representative species from a full set of thermo-chemical scalars. They include direct relations graphs (DRGs) [17,18,19], global pathway selection (GPS) [20], the two-step PCA selection process [11] and the more recent manifold-informed reduction method [21]. The first two methods, DRG, and its variants, and GPS, were designed with the primary purpose of chemistry reduction. Regardless, these methods use a range of parameters for their optimum implementation. More strict thresholds for these parameters may be designed to construct skeletal mechanisms for complex fuels. In contrast, less strict thresholds can be used to construct representative species from which other species in a mechanism can be recovered through training data.
In this study, different methods of selecting representative species are compared. The comparison is carried out for n-heptane low-temperature oxidation for DRG, GPS, and the two-step PCA. For the manifold-informed method, the comparison between two-step PCA and this method is implemented on simpler fuels, hydrogen, syngas and ethylene, primarily because of the inherent computational cost of the manifold-informed approach when implemented for complex fuels. One principal goal of the comparisons is to identify whether the various methods yield similar selections of representative species, or whether specific details of their formulations can yield different ones.
2. Methodology
In this section, we briefly discuss the 4 methods considered in this study.
2.1. Two-Step Principal Component Analysis (PCA)
The two-step PCA by Alqahtani and Echekki [11] is used to reduce the total number of species in a detailed mechanism to a lower representative set of the data variance associated with the reaction rates of species in a mechanism. PCA is carried out in two steps: the first step is carried out on the full set of species’ reaction rates in the detailed mechanism, excluding the fuel, to select the leading set of species; a second PCA is carried on the species retained from the first PCA.
The species’ reaction rates are centered by subtracting their mean:
where i is the ith species index. PCA is carried on the covariance matrix of the centered reaction rates and vector of the PCs is obtained as:
The obtained PCs are then ordered using as a criterion the magnitude of the eigenvalues from highest to lowest to identify the importance of the associated thermo-chemical scalars. Since the first few PCs represent most of the data variance, we retain the leading PCs that contain a determined cumulative contribution to the total variance, which is set in the present study at 99%. We express these PCs as follows:
The matrix contains the leading PCs eigenvectors of . To identify the most important species, we implement a cut-off criterion as follows:
where are coefficients of the matrix . A cut-off percentage is used to determine the number b of thermo-chemical scalars with the most contributions to the PCs. Steps 1–4 are repeated on the reaction rates of the retained species from the first PCA to obtain the final set of selected species.
2.2. Manifold-Informed Selection
Recently, Zdybal et al. [21,22] proposed a manifold-informed method for selecting a subset of state variables. This PCA-based method identifies a subset of the state variable that minimizes non-uniqueness and small feature size on low-dimensional manifolds. To obtain the subset state, a backward variable elimination algorithm is used to remove variables that decrease a specified cost function. The cost function used by Zdybal et al. [21] is based on the normalized variance derivative metric [23] and is defined as:
where is the largest feature size in the ith manifold , and is the penalty function defined as
where tilde denotes a log10-transformed quantity. The total cost from specified target dependent variables is the cumulative sum .
2.3. Directed Relation Graphs (DRG)
DRG was developed by Lu and Law [17,18,19] as a chemistry reduction method that represents kinetic models as graphs. The graph model consists of nodes and directed edges. In the graph model, chemical species are represented by nodes, and their inter-dependence is represented by directed edges. An illustration of a graph of a six-species kinetic model is shown in Figure 1 [17], where line thickness shows the level of dependency between species. Let us consider species B as a target species, which can be the fuel or a major combustion product. The thick directed edge from B to D shows that these two species directly react with each other and are both needed in the model to accurately calculate their production or consumption. B also depends on A and C; however, their dependence is not as strong as the one between B and D. Removing A or C from the kinetic model would not lead to significant errors in the production/consumption of B. Similarly, the dependence between C and both B and D is negligible. E and F are not connected to and do not react with species B, but they strongly depend on one another [24].
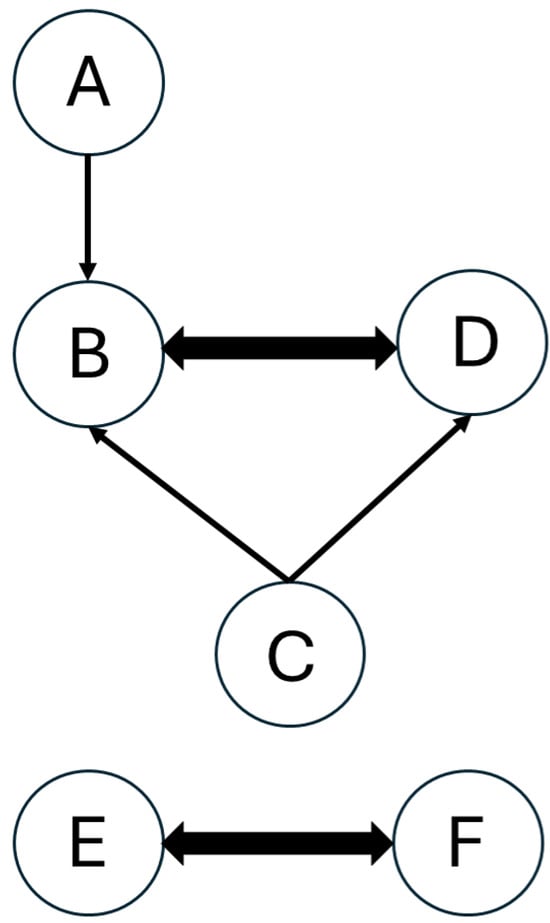
Figure 1.
Example of a graph representing a model with six species.
In DRG, the direct interaction coefficient is used to measure the dependence between species and to quantify one species’s contribution to other species’ production or consumption. For our six species graph with target B, the direct interaction coefficient for species B and D is given by:
and
where is an index of species D’s presence in the ith reaction, is the total number of reactions in the kinetic model, is the net stoichiometric coefficient of species B in reaction i, and is the reaction rate of the ith reaction. To retain important species reacting with the target species, a threshold is applied to the graph such that edges where are removed because the dependence is considered weak and negligible. A deep first search is applied starting from the target species to identify and retain species with strong dependence () to the target species and eliminate the ones with a negligible dependence. Reactions involving species with strong dependence are kept in the model, while reactions involving eliminated species are removed.
2.4. Global Pathway Selection (GPS)
GPS, first developed by Gao et al. [20], is an algorithm for chemistry reduction that identifies global pathways and removes species and reactions that are not important to these pathways. This is performed by constructing element flux graphs and selecting hub species. The construction of element flux graphs is carried individually on carbon (C), hydrogen (H), and oxygen (O), which are the main elements involved in the combustion of hydrocarbon fuels. For each of these graphs, nodes represent species present in the kinetic mechanism, and directed edges represent element fluxes from one node to another. For GPS, a direct edge is also a measure of the rate of atoms of elements C, H, and O transferred from one species to another from every elementary reaction found in the detailed mechanism. For an element e, the flux or direct edge from ith to j species is calculated as:
where , the element flux from the ith to jth species contributed by the rth elementary reaction, is:
and is the net reaction rate of the rth reaction. , the number of e atoms transferred from species i to j in the rth elementary reaction, is given by:
where is the number of eth element atoms transferred from or to species i in reaction r. is the stoichiometric coefficient, negative if a reactant and positive if a product, of species i in reaction r. is the number of e atoms in species i. is the number of e atoms involved in reaction r and can be calculated as or .
By defining this directed edge from the ith to jth node for each element, the total element flux between a target species A and other species from all reactions in the detained mechanism is defined as:
Using Equation (11) and a user-defined threshold value , a set of “hub species” is kept if for each element. For each hub species, global pathways are identified. These are chemistry pathways where elemental transfer from initial reactants to final products passes through the hub species. A hub species can have many pathways. The top K fastest pathways can be identified using the graph algorithm by Yen [25] by searching the K shortest pathways from the inverse element graph. Additionally, the top reactions of species found in the global pathways are also selected if . , defined in Equation (12), is a measure of the total contribution of the reactions, and is a user-defined threshold value [20,26]. In this work, only the fastest pathways are selected with K = 1 and :
3. Results and Discussion
The four methods, which were discussed earlier, are applied to combustion data of perfectly stirred reactors (PSRs) and constant pressure homogeneous reactors to retain representative species, and the results of the number of species retained are shown below. The comparisons between the different methods are implemented for n-heptane. The KAUST lumped mechanism is used as a detailed chemistry mechanism [27], which consists of 538 species and 2824 reactions. For the homogeneous reactor simulations, we consider 5 different equivalence ratios of 0.5, 0.8, 1, 1.2 and 1.5, and initial temperatures varying from 700 K to 850 K at 10-degree increments. For the PSR simulations, 4 residences times of , , and s are considered.
The data are generated by solving Equations (13) and (14), describing the PSR and homogeneous reactor, respectively, using Cantera 2.6.0 [28]:
where the subscript denotes inlet conditions, T is the temperature, h is the enthalpy, is the density, and is the constant pressure specific heat. , , and are the sth species’ mass fraction, enthalpy (sensible and chemical), reaction rate, and molecular weight, respectively.
The selected species are obtained by applying each method above on the data generated by solving Equations (13) and (14), and the final representative species are species common between the selected ones and those that are also part of the list of species found in the smaller C0–C4 foundational chemistry mechanism USC Mech-II [29]. After retaining the representative species, we estimate the reduction percentage from the detailed mechanism as , where is the number of representative species, and is the number of species in the detailed mechanism. A parametric study is conducted for each method by varying (1) the PCA variance and cut-off percentage for the two-step PCA, (2) the threshold for DRG, and (3) the threshold value for GPS with constant . For the different methods, we adopt a set of threshold parameters;
- Two-step PCA: 7 PCA cumulative variances of 85, 90, 95, 99, 99.9, 99.99, and 99.999% are used to retain the first PCs. In total, 47 different cut-off percentages varying from 80 to 99.999% are set as the cut-off criterion to select the number b of thermo-chemical scalars with the most contributions to the PCs.
- DRG: 65 thresholds varying from 0.1 to 0.74 by an increment of 0.01 are used as the cut-off threshold for the removal of directed edges.
- GPS: 51 of values of 0.001 and 0.01 to 0.5 by increment of 0.01 are prescribed as the threshold to select hub species.
It is important to note that both DRG and GPS, along with the manifold-informed selection, require the specification of target species. Here, we investigate four different sets of target species. These species are chosen from either reactants, products, or key intermediates for low-temperature and high-temperature oxidation. These sets are summarized as follows:
- Target species set 1: nC7H16, H2O, CO2, CO, CH2O, H2O2, HO2,
- Target species set 2: nC7H16, H2O, CO2,
- Target species set 3: nC7H16, H2O, CO2, CO,
- Target species set 4: nC7H16.
3.1. Two-Step PCA
Figure 2 shows the number of selected representative species as a function of the cut-off criterion for the two-step PCA. The PCA is performed on the PSR and homogeneous data from time s up to equilibrium. The number of selected representative species increases as the PCA cumulative variance and cut-off percentage increase. This trend is expected because a larger number of PCs is needed to retain a higher cumulative variance of the original data. Subsequently, a greater number of b of scalars will be retained to obtain a higher contribution to the PCs. However, for cumulative variances of 85 and 90%, the same number of representative species is obtained as shown by the orange line in Figure 2. This occurs because the same number of PCs is retained to obtain a cumulative variance between 85 and 90%.
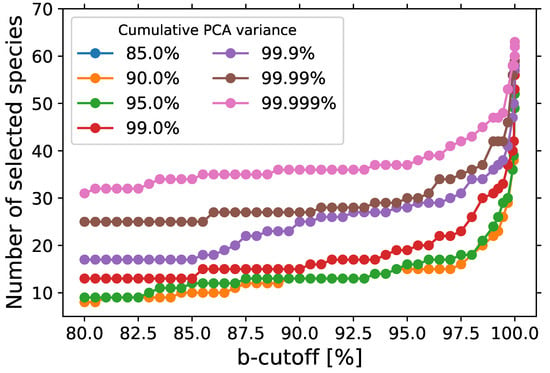
Figure 2.
Number of species retained as a function of the cut-off percentage. USC Mech II is used as a foundational chemistry mechanism.
Similarly, the number of retained species with a cumulative variance of 95% is very close to 85 and 90%. The number of representative species is also sensitive with regards to PCA variance when they are less than 99.999% and the cut-off percentage is less than 99.9%, but not as sensitive when the variance is greater than 99.999% or the cut-off percentage is greater than 99.9%.
The minimum number of retained species is 8 when the cumulative variance is 85% and cut-off percentage is 80, and the maximum number of retained species is 63 when the cumulative variance and cut-off percentage are both 99.999%. With 8 retained species, a reduction of 99% from the original 538 species is achieved, and we have a reduction of 88% when retaining 63 species. The 8 retained species, which are the common species across all cumulative variances and cut-off percentages analyzed, are n-C7H16, O2, H2O, CO2, CO, CH3, C2H4 and C2H5. The minimum retained species include the fuel, oxidizer, and major products of combustion, H2O and CO2, which are great markers of the two stages of ignition for fuel oxidation as shown in Figure 3. CH3, C2H4, and C2H5 are great trackers of the second stage of ignition and important markers of the chemistry description in the PSR as shown in the Figure 4.
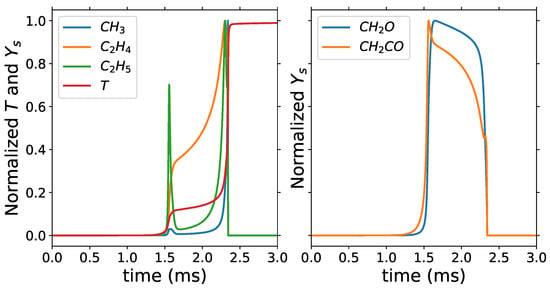
Figure 3.
Homogeneous reactor: normalized temperature and mass fractions with = 740 K and equivalence ratio of 1.
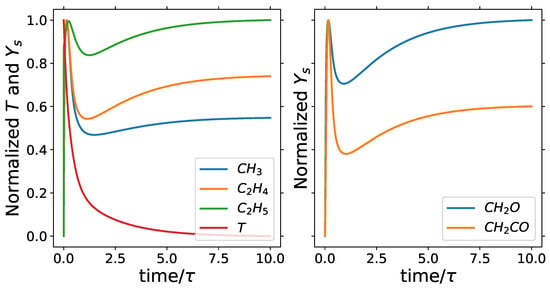
Figure 4.
PSR: normalized temperature and mass fractions with = 700 K, s, and equivalence ratio of 1.
As the cut-off percentage increases, additional species are retained, such as H and O radicals, OH, and H2. More low-temperature chemistry species that track the first stage of ignition, such as CH2O and CH2CO, are retained as the cut-off percentage increases. As the cumulative variance increases, these species are retained at a lower cut-off percentage. For example, CH2O and CH2CO are both retained when cumulative variance and cut-off percentage are both, respectively, 90 and 98% with 18 total retained species, 99 and 96.5% with 25 total retained species, and 99.9 and 85.5% with 18 total retained species.
3.2. Manifold-Informed Selection
The manifold-informed approach was applied to our homogeneous reactor and PSR data using PCAfold 2.2.0 [22]; however, no species selection was obtained because of the intensive iterative process and computational cost of the backward variable elimination algorithm, and the size of our data, which have 1.2 million observations and 538 variables. Similarly, when applied to the data provided with the PCAfold 2.2.0 software, which have 50,000 observations and 11 variables, the algorithm still took two days to complete the selection. For reference, the homogeneous reactor and PSR data were generated in less than 12 h, and the two-step PCA for one parameter was completed in under one minute. Data generation and all selection methods were carried out on the Intel Xeon Gold 6234 3.30 GHz CPU. Due to this computational limitation associated with the manifold-informed selection, we applied the two-step PCA using the seven cumulative variances and 47 cut-off percentages listed above to the hydrogen, syngas, and ethylene combustion data provided by Zdybal et al. [21] and compared selected species from the two-step PCA to the manifold-informed selection method. The two-step PCA completed the parametric study of all seven variances and cut-off percentages in less than 3, 2, and 4 s for the hydrogen, syngas, and ethylene data, respectively, on the same CPU used for PCAfold 2.2.0 software. For a very negligible computational cost, our method yielded similar selected species to those reported in Table 2 in [21]. For example, for a cumulative variance of 99.99% and 82.5% cut-off, common species between the two methods are H2, O, OH, and O2 for hydrogen combustion, O, OH, CO and CO2 for syngas combustion, and H2, O2, OH, H2O, CH3, CO2, C2H2 and C2H4. For these parameters, both methods achieved a 58 and 50% reduction from the total number of hydrogen and syngas combustion scalars, respectively. The two-step PCA achieved a reduction of 61% for ethylene combustion, and the manifold-informed reduction achieved 64%. H is a common species among the hydrogen, syngas, and ethylene data that was selected by the manifold-informed selection but not the two-step PCA. This can be attributed to the small magnitude of this species and the lower contribution of its corresponding PC to the overall cumulative variance. Thus, with the two-step PCA, species with small magnitudes close to zero are not retained.
3.3. DRG
The total number of selected representative species resulting from the parametric study of the cut-off threshold can be seen in Figure 5. The number of representative species decreases with increasing the threshold. This trend makes sense since increasing the threshold would result in the elimination of the directed edges with a small direct interaction coefficient. The selected representative species become very sensitive to the specified target species as the threshold increases, especially between values of 0.3 and 0.5, e.g., at , the number of selected species decreases from 31 for target species set 1, which has 7 target species, to 24 for target species set 4, which has 1 species, the fuel. Increasing the number of target species will increase the number of selected representative species. Target species set 3, which has the same species as target species set 2, in addition to CO, leads to the same number of selected representative species as target species set 2. Changing the additional species CO in the target set 3 to a different species, such as CH2O, could change the observed trend and result in a different set of selected species depending on the ones involved in the reaction with CH2O. Target species sets 1, 2, and 3 have the same number of selected species from of 0.1 to 0.26, and beyond 0.26, the selected species from target set 1 changes slightly from those of target sets 2 and 3.
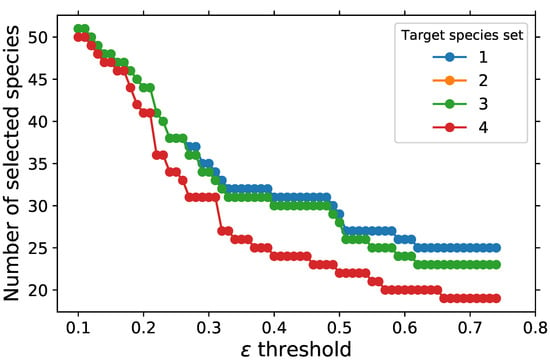
Figure 5.
Number of representative species selected as a function of threshold with USC Mech II.
At the threshold , target species sets 1 to 3 lead to the same number of representative species of 51, while target species set 4 has 50, where CH3COCH3 is the species not selected for the target set 4. The minimum number of retained species is 19 with target species set 4 and . This is a 96% reduction from the 538 species in the detailed mechanism. Target species sets 1, 2, and 3 with of 0.1 give the maximum number 51 of retained species, which is a reduction of 91% from the total number of species. The minimum retained species include species such as H radical, OH, and HCO, which are great markers of the second stage of ignition, and HO2, CH2O, CH2CO, CH3CO, CH2CHO, CH3CHO, and C2H3CHO, which are great markers of the first stage of ignition as shown in Figure 6. CH3, C2H4 and C2H5 are also part of the minimum retained species as in the case of the two-step PCA; however, CO and CO2 are not retained in the minimum list for DRG. While these are important species, they are not retained because reactions involving the fuel do not have a strong dependency, i.e., of 0.66, with CO and CO2. As decreases to 0.65 and 0.54, CO2 and CO are added to the list of retained species for target species set 4.
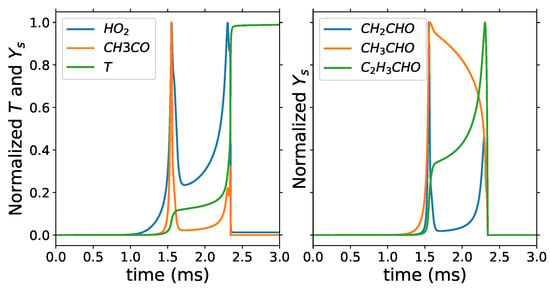
Figure 6.
Homogeneous reactor: normalized temperature and mass fractions with = 740 K and equivalence ratio of 1.
3.4. GPS
The number of selected representative species obtained by varying the threshold can be seen in Figure 7 for the GPS method. Similarly to the DRG method, the number of representative species decreases with increasing threshold and increases as the number of target species increases. The selected representative species are very sensitive to the specified target species of the fuel as compared to DRG results shown in the red dotted line in Figure 5. Target species sets 2 and 3 have the same number of representative species for threshold between 0.14 and 0.46, and outside this range, the number of selected species is very close for target species sets 1, 2 and 3. At a small threshold of 0.001, target species sets 1 to 3 have the same number of representative species.
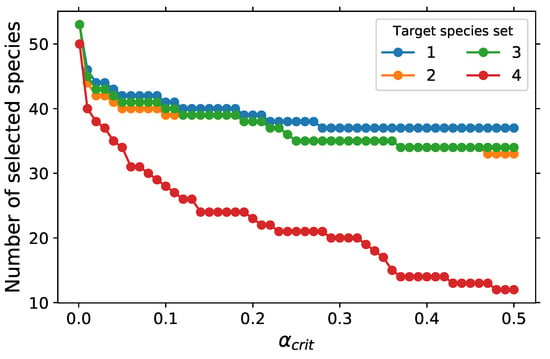
Figure 7.
Number of species retained as a function of with USC Mech II.
Similar to DRG, the minimum number of selected species is 12 with target species set 4 and of 0.48, and the maximum is 53 with 0.001 and target species sets 1, 2 and 3. With 12 and 53 retained species, reductions of 98 and 90% from the detailed mechanism, respectively, are achieved. At , the target set 4 has 50 retained species, which are also included in the retained species for the first three target sets. N2, O, and CH4 are the three additional species retained in the first three target sets. The minimum retained species include H radical, OH, CH3, C2H2, C2H3, C2H4, CO, and main products of combustion. We can see in Figure 8 that C2H4 is a great marker for the first stage of ignition, while the other C2 species track the first stage of ignition. More low-temperature chemistry-specific species are retained as decreases. For target sets 1 to 3, however, low-temperature specific species such as CH2O, CH3O, and CH3CHO are retained at of 0.48.
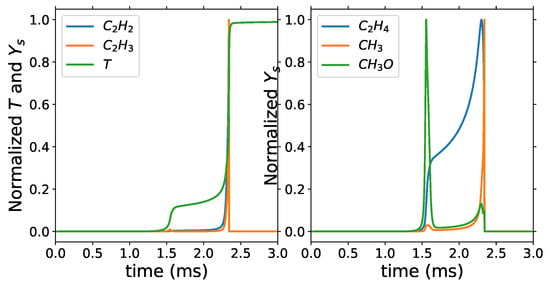
Figure 8.
Homogeneous reactor: normalized temperature and mass fractions with = 740 K and equivalence ratio of 1.
3.5. Common Species between Two-Step PCA, DRG and GPS
Table 1 lists the maximum representative species obtained from the three selection methods. For the cut-off conditions selected, we can see that there are common species between the three selection methods. N2 is selected by DRG and GPS but not two-step PCA. N2 remains constant and has a reaction rate of zero; therefore, its PC contribution would be minimal and neglected during the two-step PCA. However, O2 is an oxidizer and has a strong dependence on the fuel because it is involved in fuel consumption. Except for N2, all remaining species selected by DRG and GPS are also selected by the two-step PCA. DRG yields the smallest number of retained species out of all three methods. The two-step PCA is computationally cheap out of the three methods, and GPS is the most expensive due to the construction element flux graph.

Table 1.
List of representative species.
3.6. Representative Species Coupling with Foundational Chemistry
An application of the representative selection is demonstrated by evaluating a hybrid chemistry model that uses artificial neural networks (ANNs) to model the reaction rates of representative species, and the remaining species that are not selected as representative species are modeled using the foundational chemistry USC Mech II [29]. This validation is performed for the homogeneous chemistry of n-heptane at an initial temperature of 700 K and pressure of 20 atm. From the parametric study conducted on all training data, 20 representative species are selected via two-step PCA for a variance of 85% and 98.5% cut-off, DRG with of 0.57 and target species set 4, and GPS with of 0.29 and target species set 4. These parameters are selected because of the number of representative species they lead to, and because the selected species contain the major species observed during n-heptane oxidation. Other parameters and their corresponding representative species can be chosen depending on the accuracy and computational saving that we would like the model to achieve.
ANNs are used to model the reaction rates of the representative species, with a similar implementation to that of our recent work [12]. For this validation, the ANN tabulation is carried only for the reaction rates of DRG-selected representative species. The temperature and mass fractions of the fuel, O2, H2O2, and CH2, are used as inputs to the ANNs. These species, which are also part of the representative species, are chosen as inputs because they adequately track all stages of ignition, and they are highly correlated with other representative species. Five single-output ANNs, with two hidden layers with 20 neurons per layer, are used to model the reaction rate of each input, while one multiple-output ANN, with three hidden layers with 20 neurons per layer, is used to model the reaction rates of the remaining representative species. Training a separate ANN for each input has shown to improve prediction accuracy [12]. A hyperbolic tangent function is used as the transfer function, and errors between the true and predicted reaction rates are minimized via the mean squared error (MSE) function. The Levenberg–Marquardt backpropagation algorithm is used to optimize the ANN inputs, and each ANN is trained for 5000 epochs. The remaining species’ ANN is optimized using PyTorch 1.13.1’s Adam optimizer with training carried over 100,000 epochs. Like in [12], the learning rate and weight decay are respectively set to 0.005 and during the first 20,000 epochs, after which they are decreased to and , respectively. The training/test/validation ratio is , respectively. The ANNs achieved an average accuracy of .
Using USC Mech II, we reconstruct species that are not included in the list of representative ones by solving Equation (14). Figure 9 shows the results of the species reconstructed using foundational chemistry (symbols) and original species from the detailed mechanism (solid lines). CO, CH4, and C2H2 are not part of the DRG-selected representative species, but they are reconstructed well using the foundational chemistry. Similarly, HO2 and CH2O, which are included in the representative species, along with the temperature, match well with the detailed chemistry. Between 4 and 4.6 ms in Figure 9, we can observe that the CO, CH4, and C2H2 results from the hybrid chemistry model do not exactly match the detailed mechanism results, although the hybrid model correctly captures the trend and maximum mass fractions. The accuracy of these predictions would be improved if these species were in the list of representative species and modeled by the ANNs. This demonstrates the importance of analyzing a wide range of parameters in the species selection process to achieve better prediction accuracy of important species.
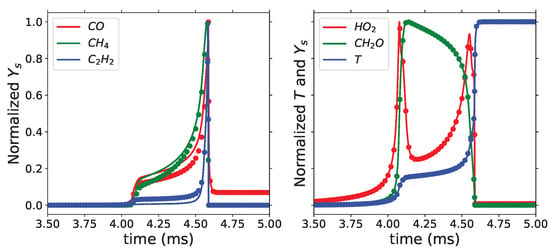
Figure 9.
Normalized temperature and mass fractions with = 700 K and equivalence ratio of 1 from detailed mechanism (solid lines) and hybrid chemistry model (symbols).
4. Conclusions
This work compares four methods to select representative species. First, the two-step PCA approach is a PCA-based method selected based on two key parameters, the cumulative variance and the cut-off percentage, which is a measure of the contribution of each species to a PC. The second approach is the manifold-informed reduction, a PCA-based method using the number of PCs as one parameter and selecting species that minimize the non-uniqueness and feature size of the low-dimensional manifold. DRG is the third approach, which selects species based on a threshold parameter that measures the dependence strength of species during their production or consumption. GPS is the final method, where species are selected based on a parameter measuring their contribution to the overall combustion.
The selection of representative species via two-step PCA, DRG and GPS is carried out on low temperature, constant pressure homogeneous chemistry and PSR of n-heptane using a detailed mechanism with 538 species. Two-step PCA achieved 88 and 99% reductions from detailed mechanism species, while DRG achieved 91 and 96% reductions, and GPS, 90 and 98%.
The minimum reduction, where most species are retained, is achieved using the highest variance and cut-off percentage for the two-step PCA, and the smallest and for DRG and GPS, respectively. Inversely, we can achieve the maximum reduction, a more aggressive reduction where a small number of representative species are selected. In both cases, these three approaches can select key species that track all stages of fuel oxidation.
The manifold-informed reduction is a computationally intensive approach that does not yield results with the homogeneous chemistry and PSR data due to the data size and the expensive iterative optimization of the quality of the low-dimensional manifold. However, a comparison between this reduction method and the two-step PCA yields using hydrogen, syngas, and ethylene data [21] similar selected species, with the two-step PCA carrying a parametric study under 1 min.
DRG and GPS are sensitive to the set of target species, while the two-step PCA is sensitive to the cumulative variance. Additionally, both DRG and GPS require a chemical mechanism to achieve reduction based on reaction paths between species. The two-step PCA does not depend on an existing chemical mechanism. Selected species from the two-step PCA can then be used to develop global reactions, for example, using chemical reaction neural networks [30,31]. Since the latter approach leads to similar species to DRG and GPS, the two-step PCA can successfully be used for data with missing chemical mechanisms or for new fuels with non-existing chemical mechanisms. It can also be used for a faster species’ selection given its low computational cost. On the other hand, if a detailed chemical mechanism is available, along with the knowledge of species to target in the selection process, DRG can be used.
Finally, these selection approaches can be used for the development of hybrid chemistry models. Although this study is carried out using n-heptane, the species selection methods in this work can be applied to other hydrocarbons or fuels and yield a smaller set of representative species that correctly describe the full combustion process. Using the selected representative species, a surrogate model or regression of the representative species’ reaction rates, such as with artificial or deep neural networks, can be coupled with foundational chemistry [11]. The selected representative species can be adjusted to achieve the desired accuracy of the reduced-order or hybrid chemistry model, and the total number of selected species still achieves a very high reduction rate and has the potential to accelerate chemistry simulation significantly.
Author Contributions
Conceptualization, K.M.G. and T.E.; methodology, K.M.G. and T.E.; software, K.M.G.; validation, K.M.G.; formal analysis, K.M.G. and T.E.; writing—original draft preparation, K.M.G. and T.E.; writing—review and editing, K.M.G. and T.E.; supervision, T.E.; project administration, T.E.; funding acquisition, T.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Abdullah University of Science and Technology (KAUST) through the Competitive Research Grants (CRG) Program, CRG-2020-CRG9-4351.
Data Availability Statement
The data presented in this study are available upon reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest, and that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Pope, S. Small scales, many species and the manifold challenges of turbulent combustion. Proc. Combust. Inst. 2013, 34, 1–31. [Google Scholar] [CrossRef]
- Wang, H.; Xu, R.; Wang, K.; Bowman, C.T.; Hanson, R.K.; Davidson, D.F.; Brezinsky, K.; Egolfopoulos, F.N. A physics-based approach to modeling real-fuel combustion chemistry-I. Evidence from experiments, and thermodynamic, chemical kinetic and statistical considerations. Combust. Flame 2018, 193, 502–519. [Google Scholar] [CrossRef]
- Xu, R.; Wang, K.; Banerjee, S.; Shao, J.; Parise, T.; Zhu, Y.; Wang, S.; Movaghar, A.; Lee, D.J.; Zhao, R.; et al. A physics-based approach to modeling real-fuel combustion chemistry-II. Reaction kinetic models of jet and rocket fuels. Combust. Flame 2018, 193, 520–537. [Google Scholar] [CrossRef]
- Tao, Y.; Xu, R.; Wang, K.; Shao, J.; Johnson, S.E.; Movaghar, A.; Han, X.; Park, J.W.; Lu, T.; Brezinsky, K.; et al. A Physics-based approach to modeling real-fuel combustion chemistry-III. Reaction kinetic model of JP10. Combust. Flame 2018, 198, 466–476. [Google Scholar] [CrossRef]
- Wang, K.; Xu, R.; Parise, T.; Shao, J.; Movaghar, A.; Lee, D.J.; Park, J.W.; Gao, Y.; Lu, T.; Egolfopoulos, F.N.; et al. A physics based approach to modeling real-fuel combustion chemistry-IV. HyChem modeling of combustion kinetics of a bio-derived jet fuel and its blends with a conventional Jet A. Combust. Flame 2018, 198, 477–489. [Google Scholar] [CrossRef]
- Saggese, C.; Wan, K.; Xu, R.; Tao, Y.; Bowman, C.T.; Park, J.W.; Lu, T.; Wang, H. A physics-based approach to modeling real-fuel combustion chemistry-V. NOx formation from a typical Jet A. Combust. Flame 2020, 212, 270–278. [Google Scholar] [CrossRef]
- Xu, R.; Saggese, C.; Lawson, R.; Movaghar, A.; Parise, T.; Shao, J.; Choudhary, R.; Park, J.W.; Lu, T.; Hanson, R.K.; et al. A physics-based approach to modeling real-fuel combustion chemistry-VI. Predictive kinetic models of gasoline fuels. Combust. Flame 2020, 220, 475–487. [Google Scholar] [CrossRef]
- Xu, R.; Wang, H. A physics-based approach to modeling real-fuel combustion chemistry-VII. Relationship between speciation measurement and reaction model accuracy. Combust. Flame 2021, 224, 126–135. [Google Scholar] [CrossRef]
- Ranade, R.; Alqahtani, S.; Farooq, A.; Echekki, T. An ANN based hybrid chemistry framework for complex fuels. Fuel 2019, 241, 625–636. [Google Scholar] [CrossRef]
- Ranade, R.; Alqahtani, S.; Farooq, A.; Echekki, T. An extended hybrid chemistry framework for complex hydrocarbon fuels. Fuel 2019, 251, 276–284. [Google Scholar] [CrossRef]
- Alqahtani, S.; Echekki, T. A data-based hybrid model for complex fuel chemistry acceleration at high temperatures. Combust. Flame 2021, 223, 142–152. [Google Scholar] [CrossRef]
- Alqahtani, S.; Gitushi, K.M.; Echekki, T. A Data-Based Hybrid Chemistry Acceleration Framework for the Low-Temperature Oxidation of Complex Fuels. Energies 2024, 17, 734. [Google Scholar] [CrossRef]
- Kumar, A.; Echekki, T. Combustion chemistry acceleration with DeepONets. Fuel 2024, 365, 131212. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.; Pang, G.; Zhang, Z.; Karniadakis, G.E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Int. 2021, 3, 218–229. [Google Scholar] [CrossRef]
- Ranade, R.; Echekki, T. A framework for data-based turbulent combustion closure: A priori validation. Combust. Flame 2019, 206, 490–505. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Lu, T.; Law, C.K. A directed relation graph method for mechanism reduction. Proc. Combust. Inst. 2005, 30, 1333–1341. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. Linear time reduction of large kinetic mechanisms with directed relation graph: N-Heptane and iso-octane. Combust. Flame 2006, 144, 24–36. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. On the applicability of directed relation graphs to the reduction of reaction mechanisms. Combust. Flame 2006, 146, 472–483. [Google Scholar] [CrossRef]
- Gao, X.; Yang, S.; Sun, W. A global pathway selection algorithm for the reduction of detailed chemical kinetic mechanisms. Combust. Flame 2016, 167, 238–247. [Google Scholar] [CrossRef]
- Zdybał, K.; Sutherland, J.C.; Parente, A. Manifold-informed state vector subset for reduced-order modeling. Proc. Combust. Inst. 2023, 39, 5145–5154. [Google Scholar] [CrossRef]
- Zdybał, K.; Armstrong, E.; Parente, A.; Sutherland, J.C. PCAfold: Python software to generate, analyze and improve PCA-derived low-dimensional manifolds. SoftwareX 2020, 12, 100630. [Google Scholar] [CrossRef]
- Armstrong, E.; Sutherland, J.C. A technique for characterising feature size and quality of manifolds. Combust. Theo. Model. 2021, 25, 646–668. [Google Scholar] [CrossRef]
- Niemeyer, K.E. Theory: Directed Relation Graph (DRG) Method. Available online: https://niemeyer-research-group.github.io/pyMARS/theory.html (accessed on 14 May 2024).
- Yen, J.Y. Finding the k shortest loopless paths in a network. Manag. Sci. 1971, 17, 712–716. [Google Scholar] [CrossRef]
- Mishra, R.; Nelson, A.; Jarrahbashi, D. Adaptive global pathway selection using artificial neural networks: A-priori study. Combust. Flame 2022, 244, 112279. [Google Scholar] [CrossRef]
- Xie, C.; Lailliau, M.; Issayev, G.; Xu, Q.; Chen, W.; Dagaut, P.; Farooq, A.; Sarathy, S.M.; Wei, L.; Wang, Z. Revisiting low temperature oxidation chemistry of n-heptane. Combust. Flame 2022, 242, 112177. [Google Scholar] [CrossRef]
- Goodwin, D.G.; Moffat, H.K.; Schoegl, I.; Speth, R.L.; Weber, B.W. Cantera: An Object-oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.6.0. 2022. Available online: https://www.cantera.org (accessed on 2 February 2023).
- Wang, H.; You, X.; Joshi, A.V.; Davis, S.G.; Laskin, A.; Egolfopoulos, F.; Law, C.K. USC Mech Version II. High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds. Available online: https://ignis.usc.edu:80/Mechanisms/USC-Mech%20II/USC_Mech%20II.htm (accessed on 15 May 2021).
- Ji, W.; Deng, S. Autonomous Discovery of Unknown Reaction Pathways from Data by Chemical Reaction Neural Network. J. Phys. Chem. 2021, 125, 1082–1092. [Google Scholar] [CrossRef]
- Ji, W.; Richter, F.; Gollner, M.J.; Deng, S. Autonomous kinetic modeling of biomass pyrolysis using chemical reaction neural networks. Combust. Flame 2022, 240, 111992. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).