Analysis of Ferroresonance Mitigation Effectiveness in Auxiliary Power Systems of High-Voltage Substations
Abstract
1. Introduction
2. Experimental Studies of Damping Devices and Their Effectiveness
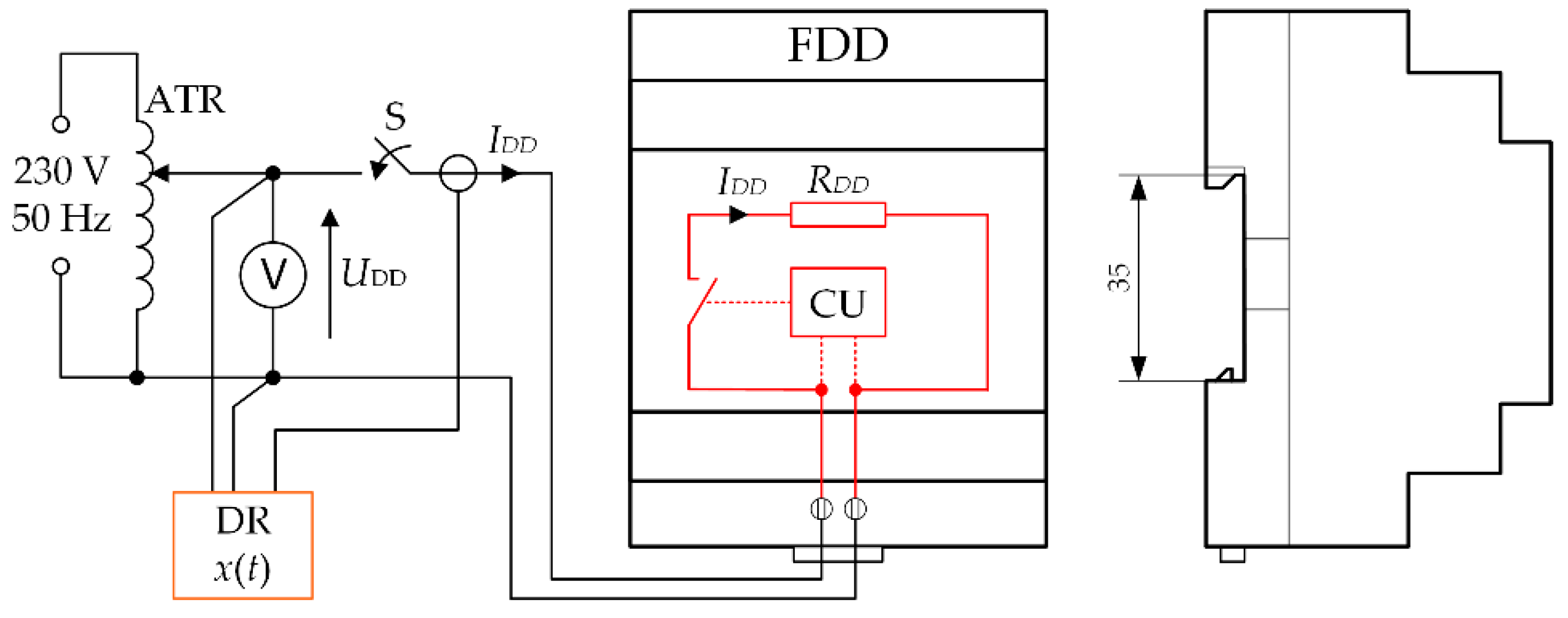
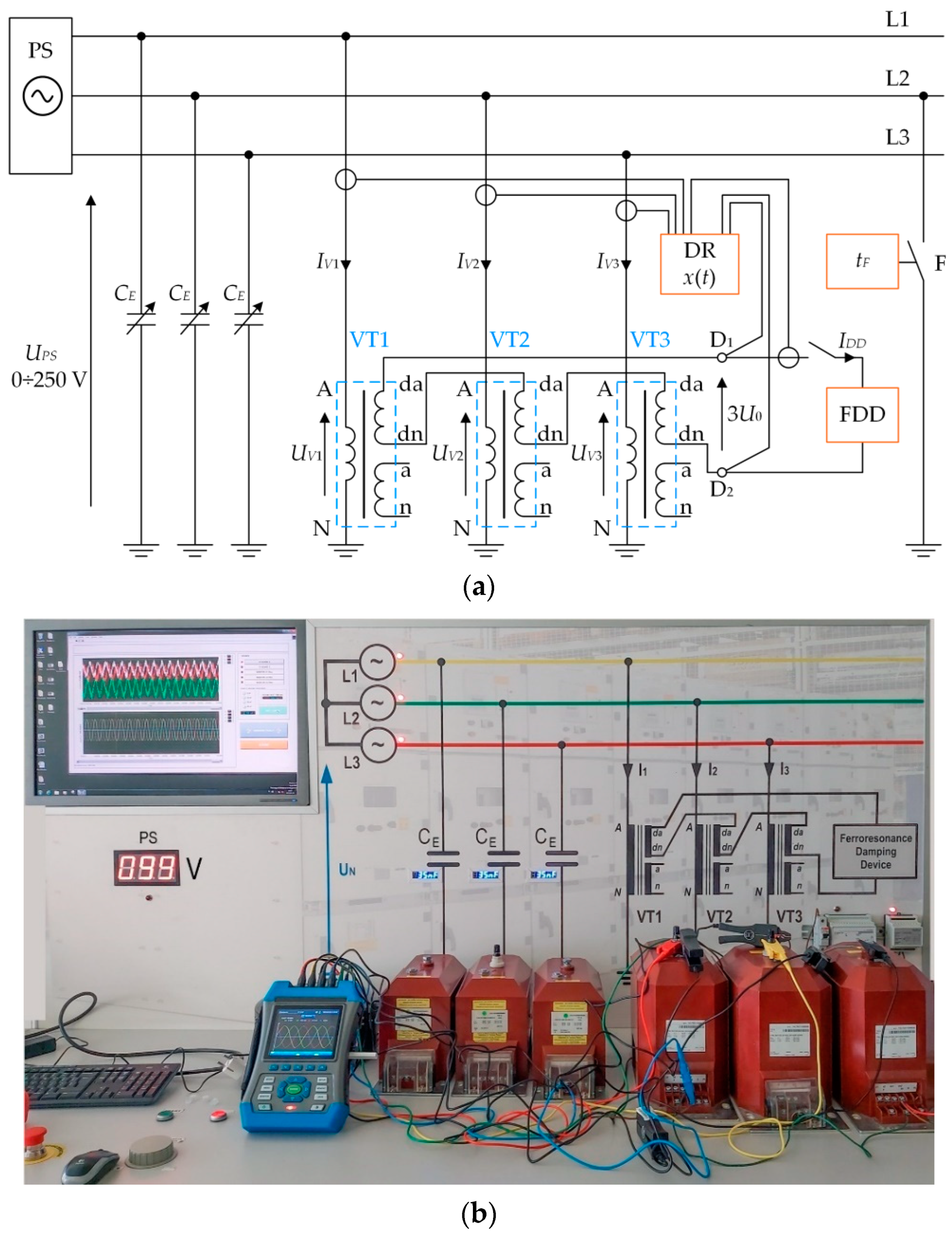
2.1. Testing of Damping Devices
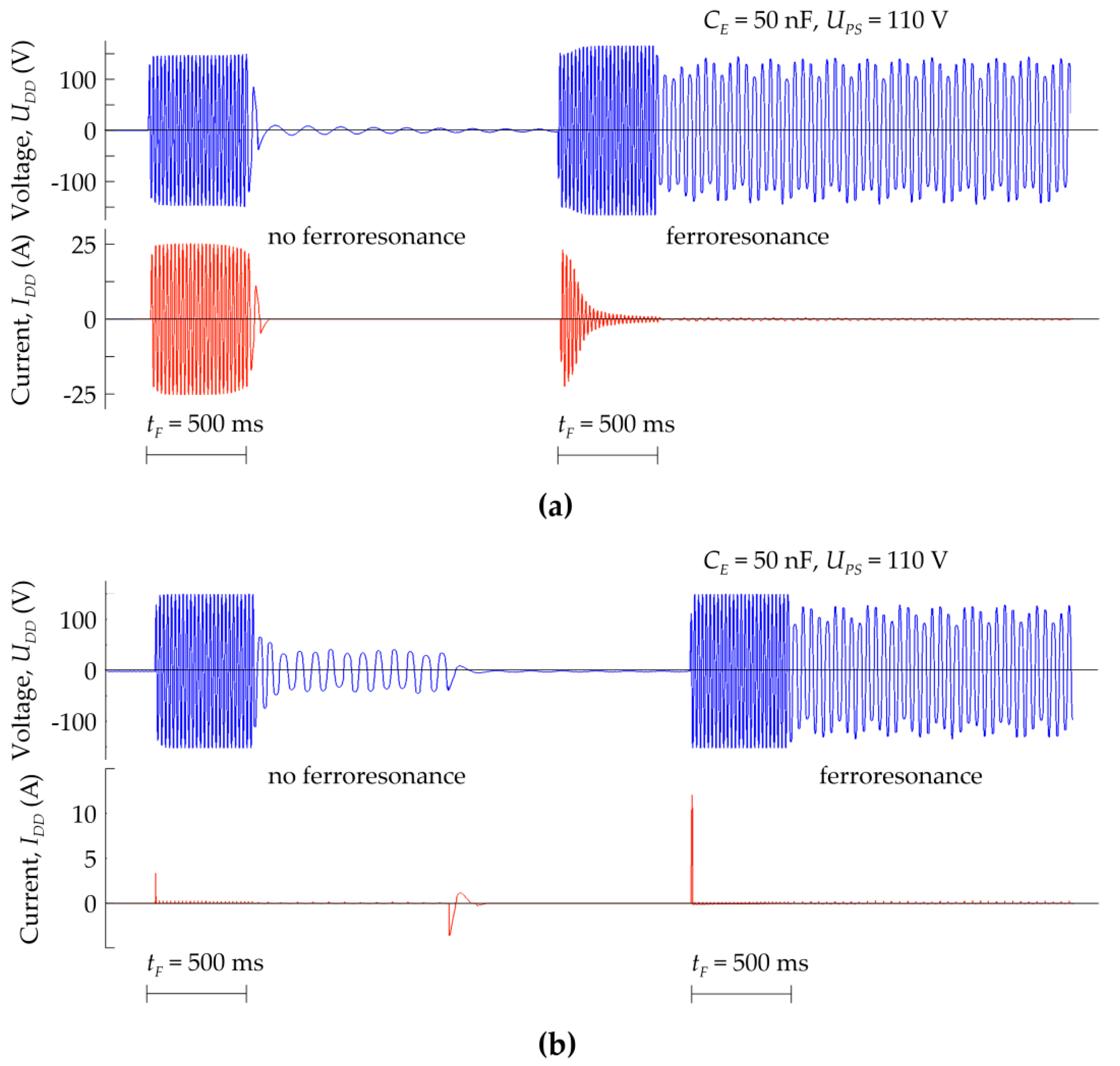
2.2. Investigations in a Laboratory System of the Effectiveness of Ferroresonance Damping Devices
- Regulated three-phase source of voltage (autotransformer PS), 0–250 V;
- Regulated capacities CE (0–150 nF), representing the earth capacity of the network;
- Factory-made low-voltage models of medium-voltage transformers (VTs) with a primary winding 173 V/, secondary windings 110 V/ and additional windings 100 V/3;
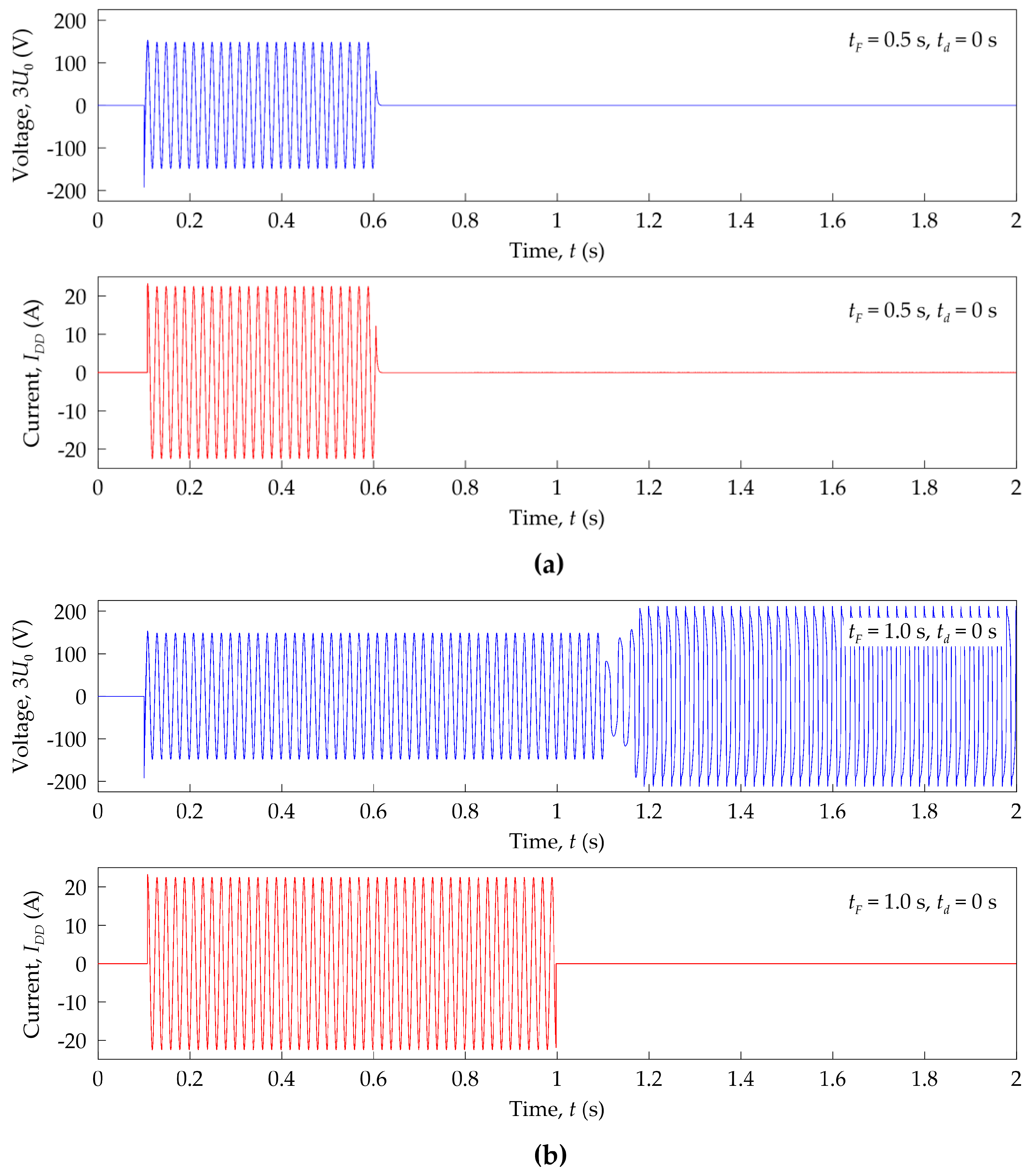
- Computer-controlled switch F simulating an earth fault which is switched off after time tF;
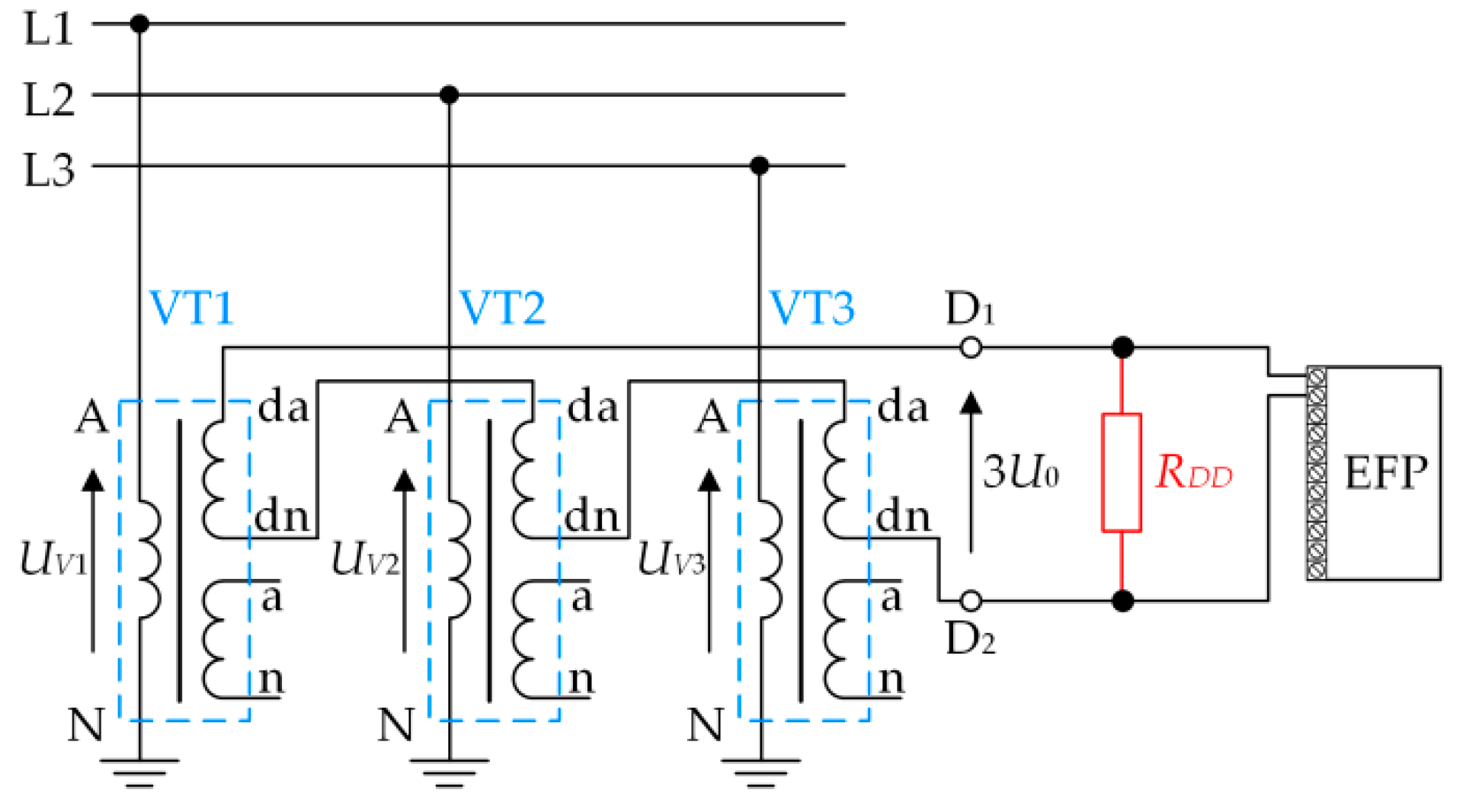
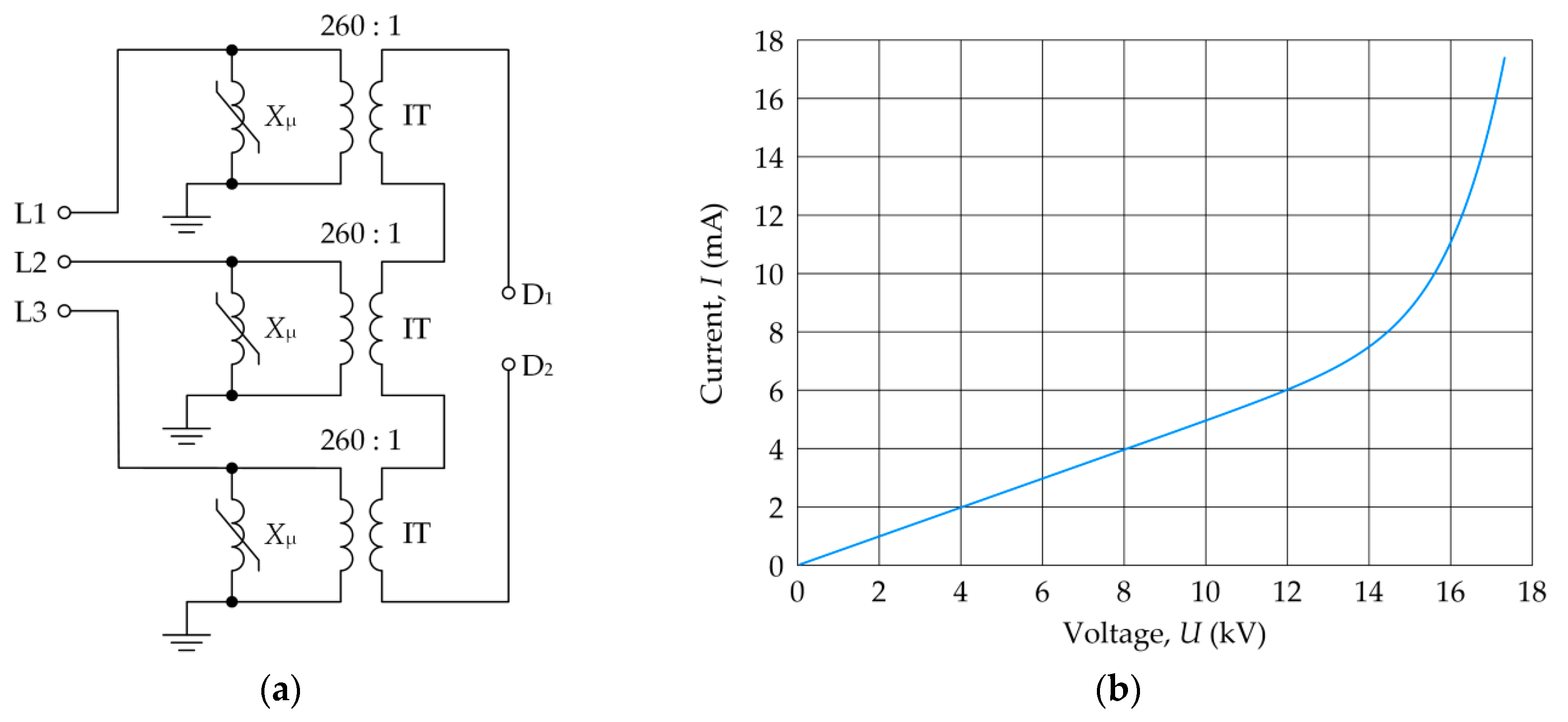
- The analyzed damping device (FDD) attached to terminals D1–D2 in a series of windings da-dn of voltage transformers (VTs) (open-delta connection);
- A digital recorder (DR) (class A portable power quality analyzer NP45 [24]) for measuring and recording analyzed currents and voltages.
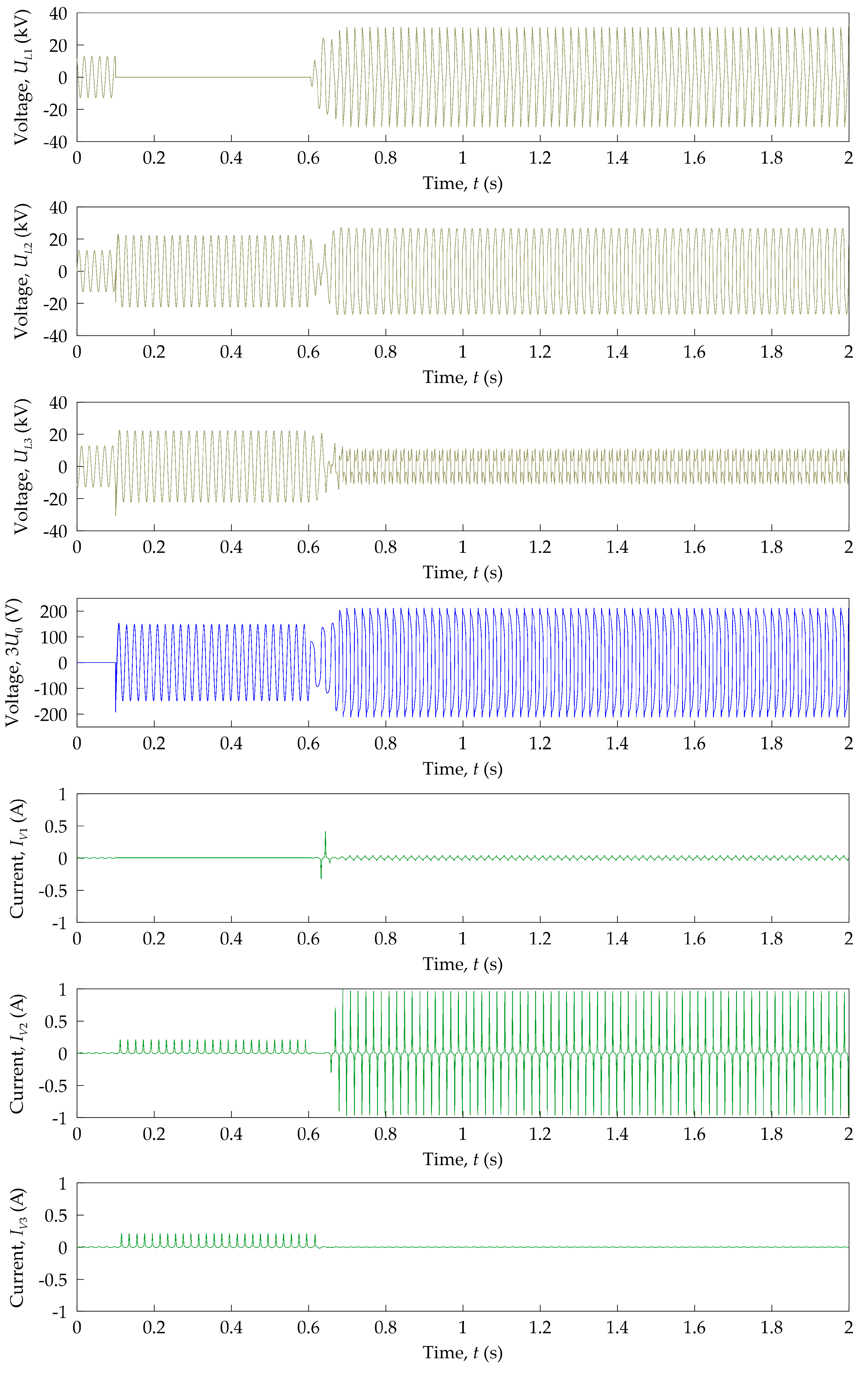
- Phase voltages UV1, UV2 and UV3 in the voltage transformer’s primary windings;
- Phase currents IV1, IV2 and IV3 in the voltage transformer’s primary windings;
- The tripled zero-sequence component of phase voltages 3U0 = UV1 + UV2 + UV3 (voltage in terminals D1–D2 of open-delta);
- The current IDD in the open-delta connection–current of the FDD.
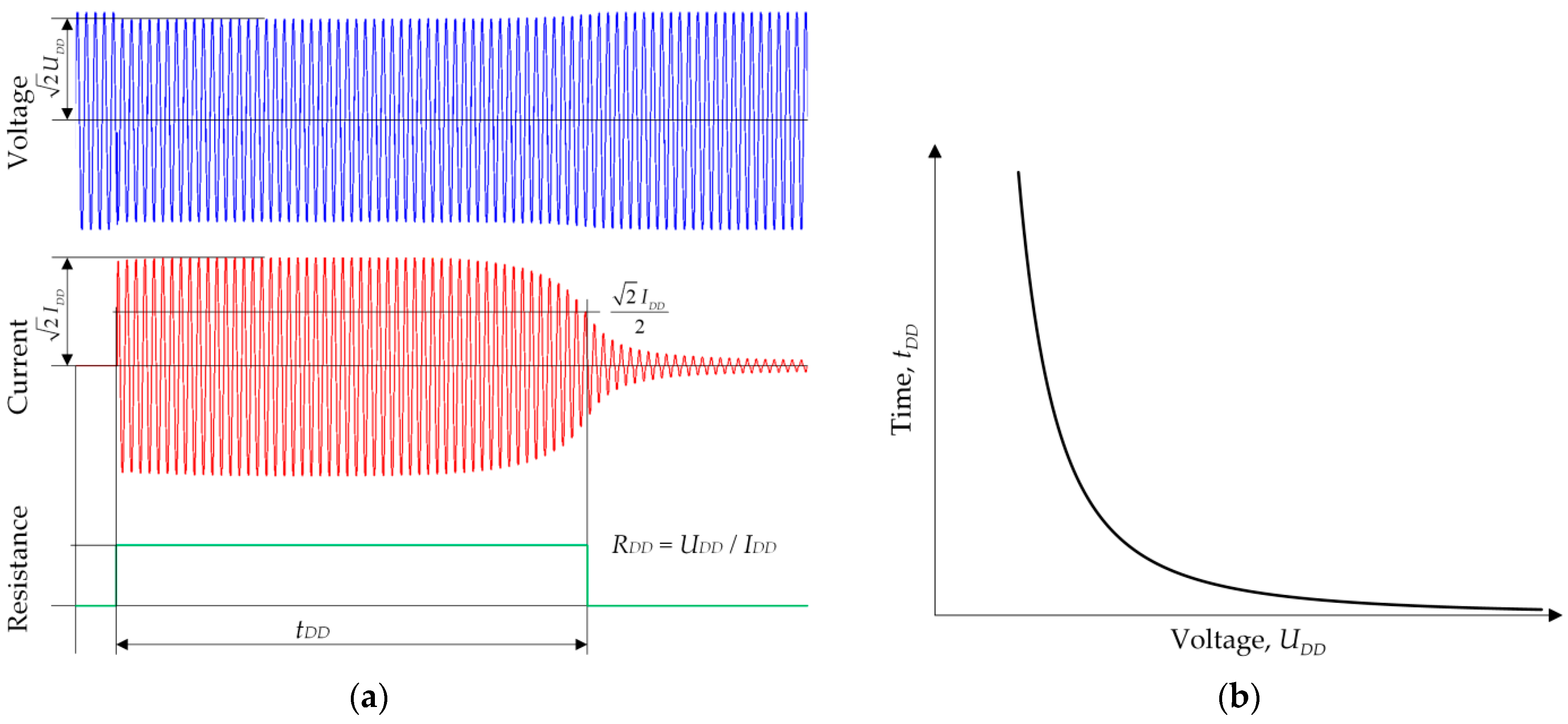
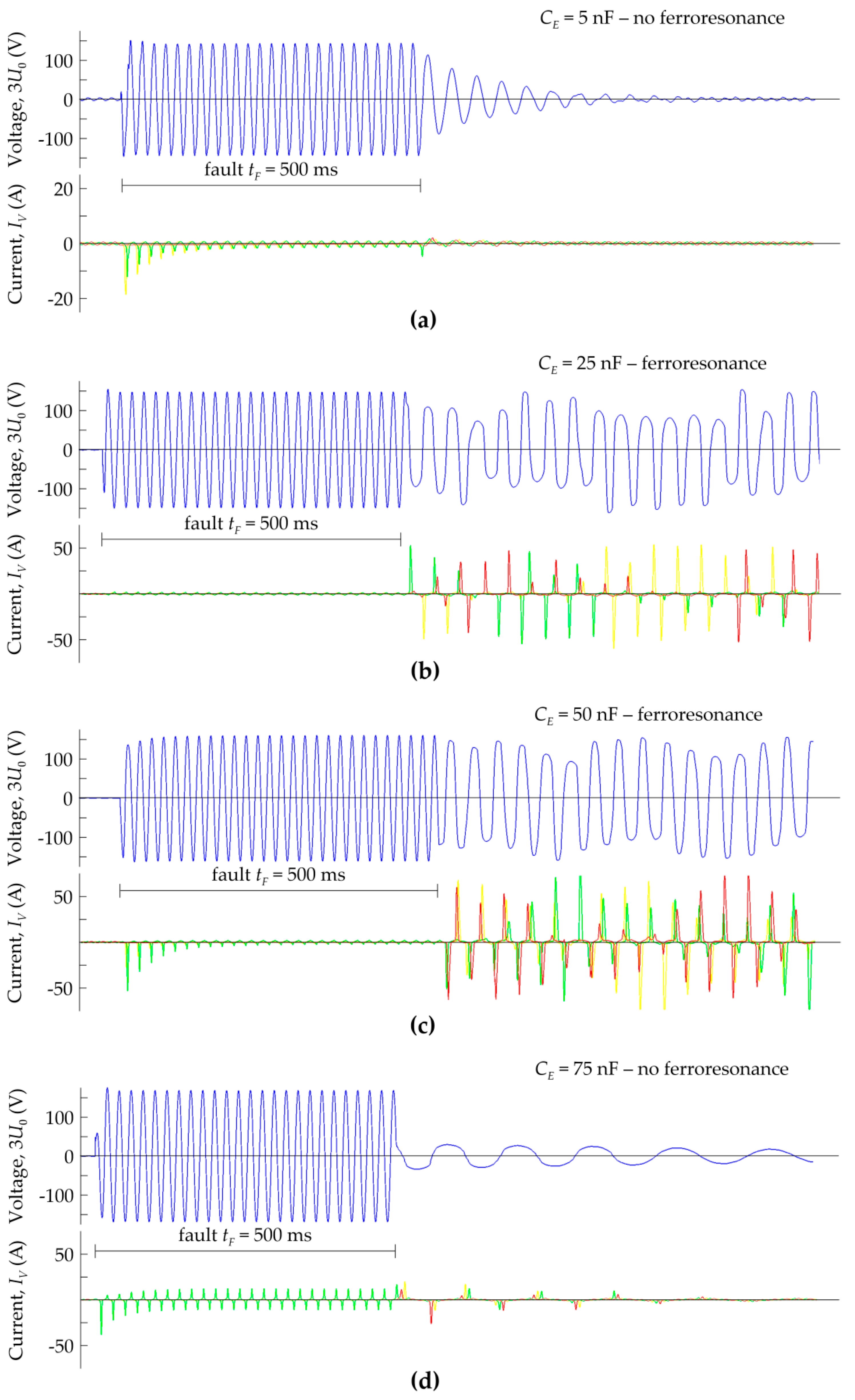
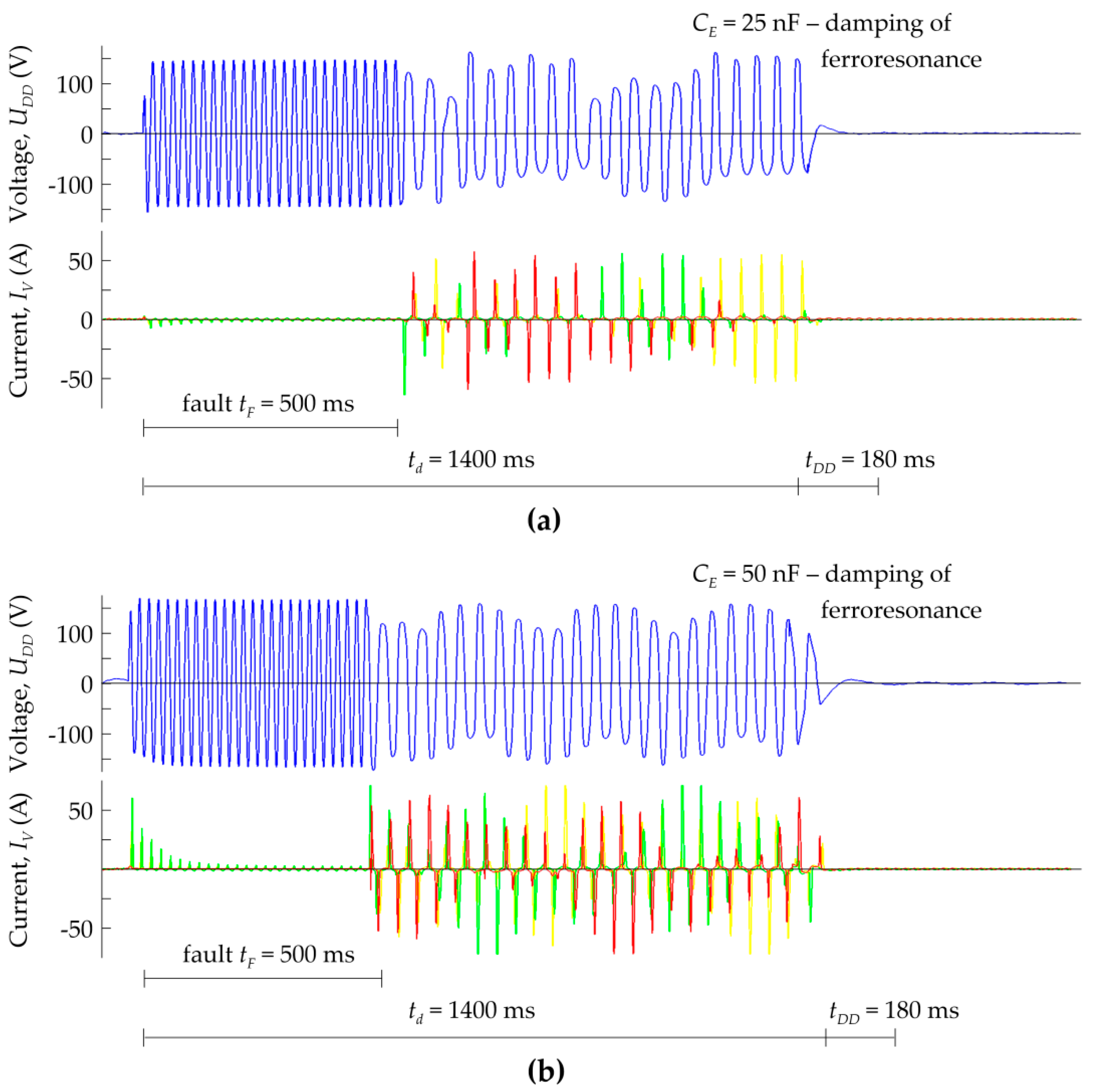
- The recorded voltages and currents waveforms created bases for determining the possibility of the occurrence of ferroresonance in the analyzed system. Moreover, it was possible to assess the effectiveness of operation and ferroresonance damping by selected FDD devices.
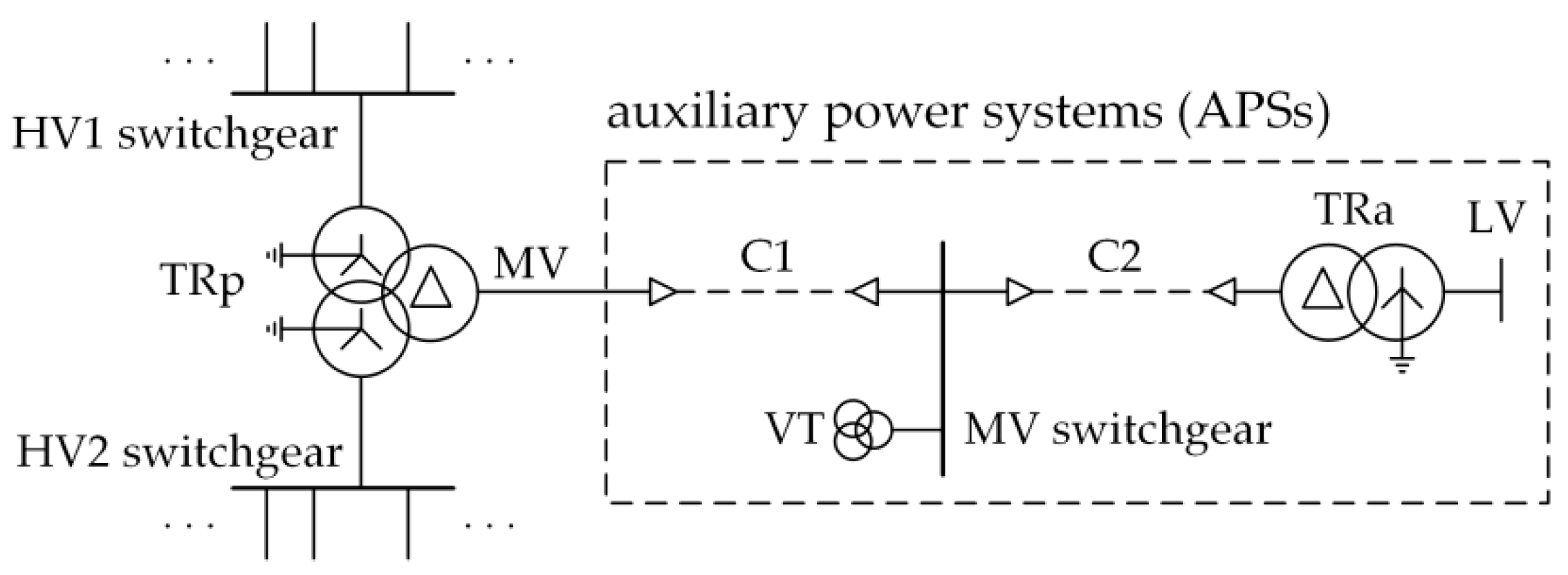
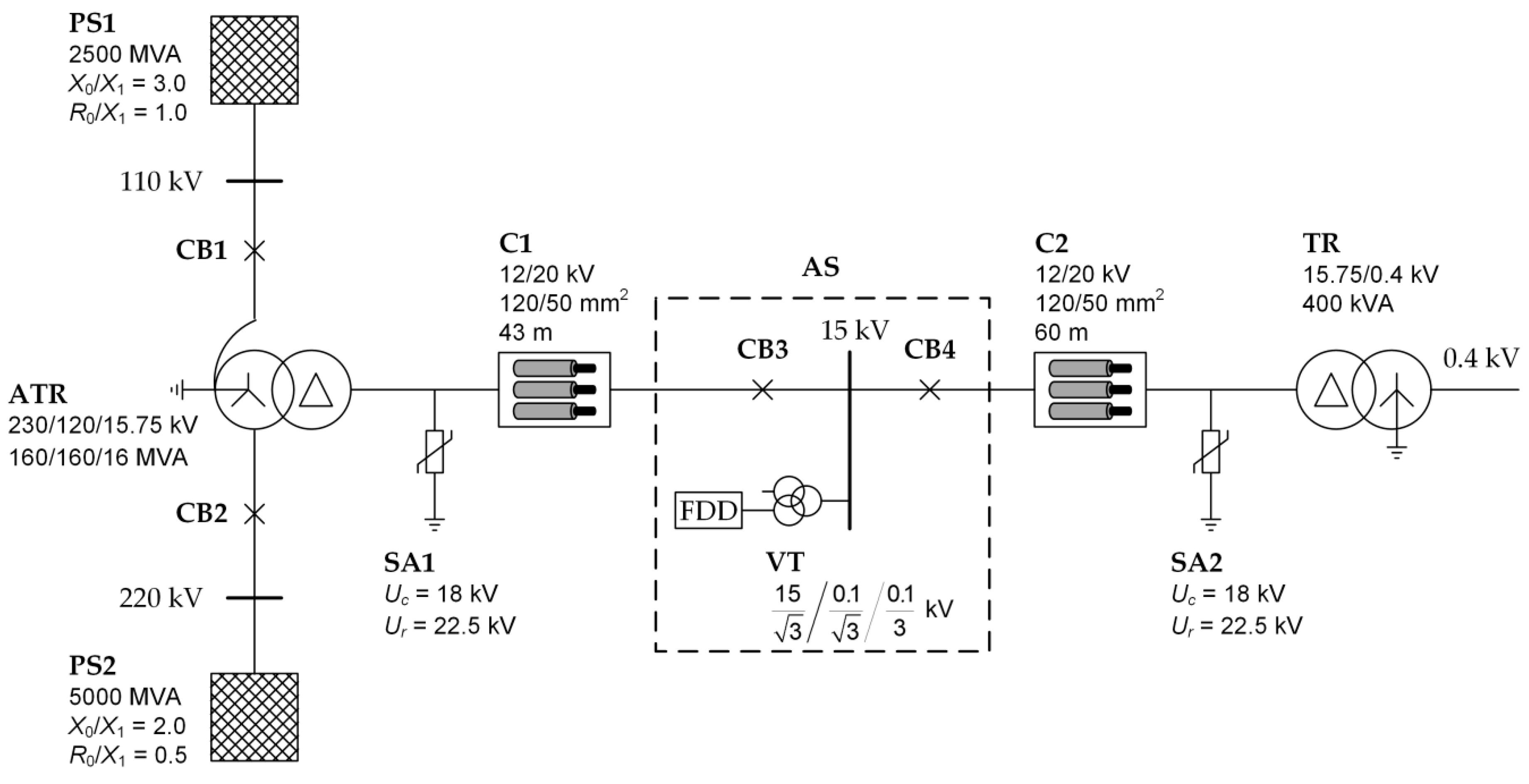
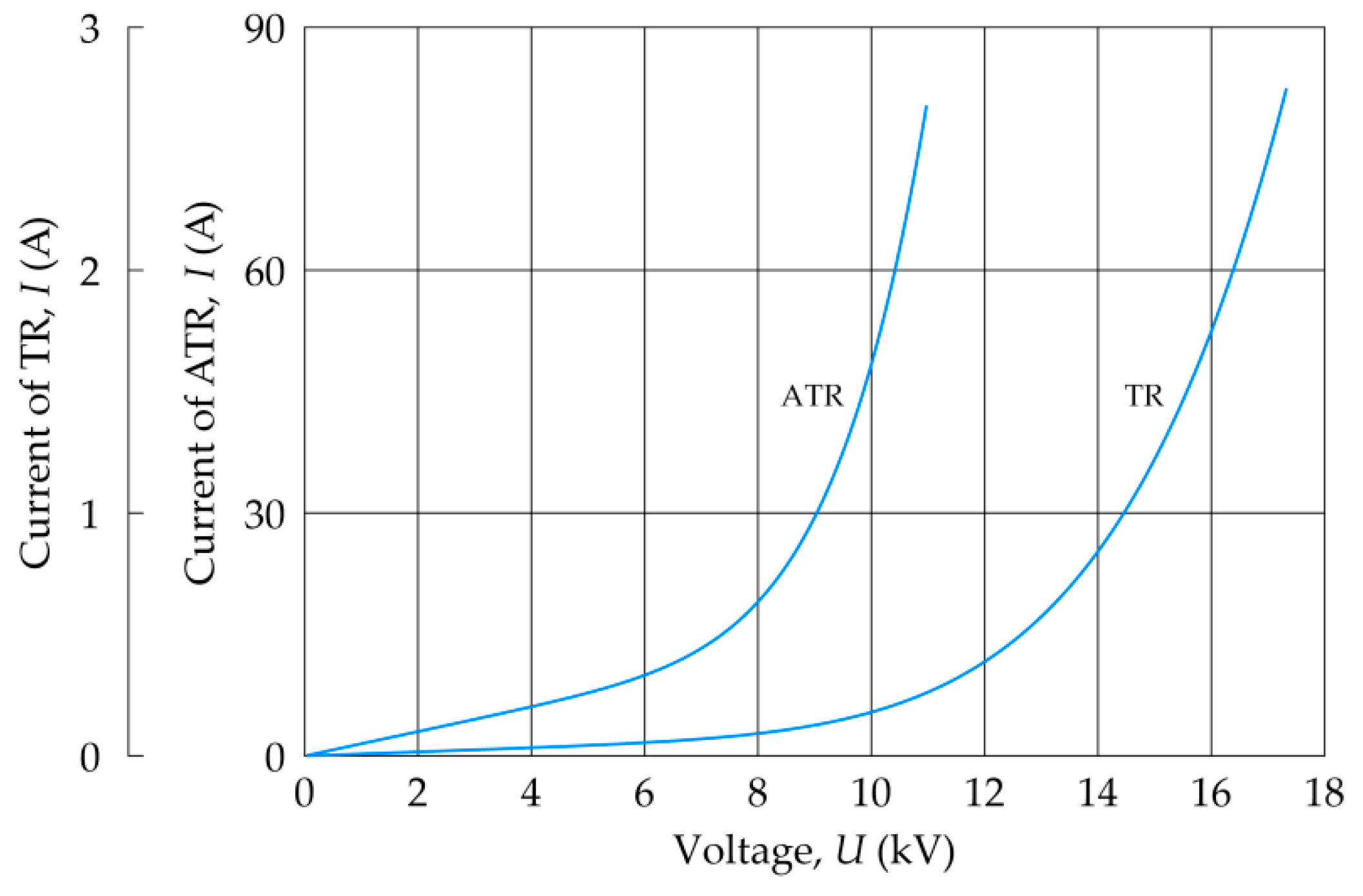
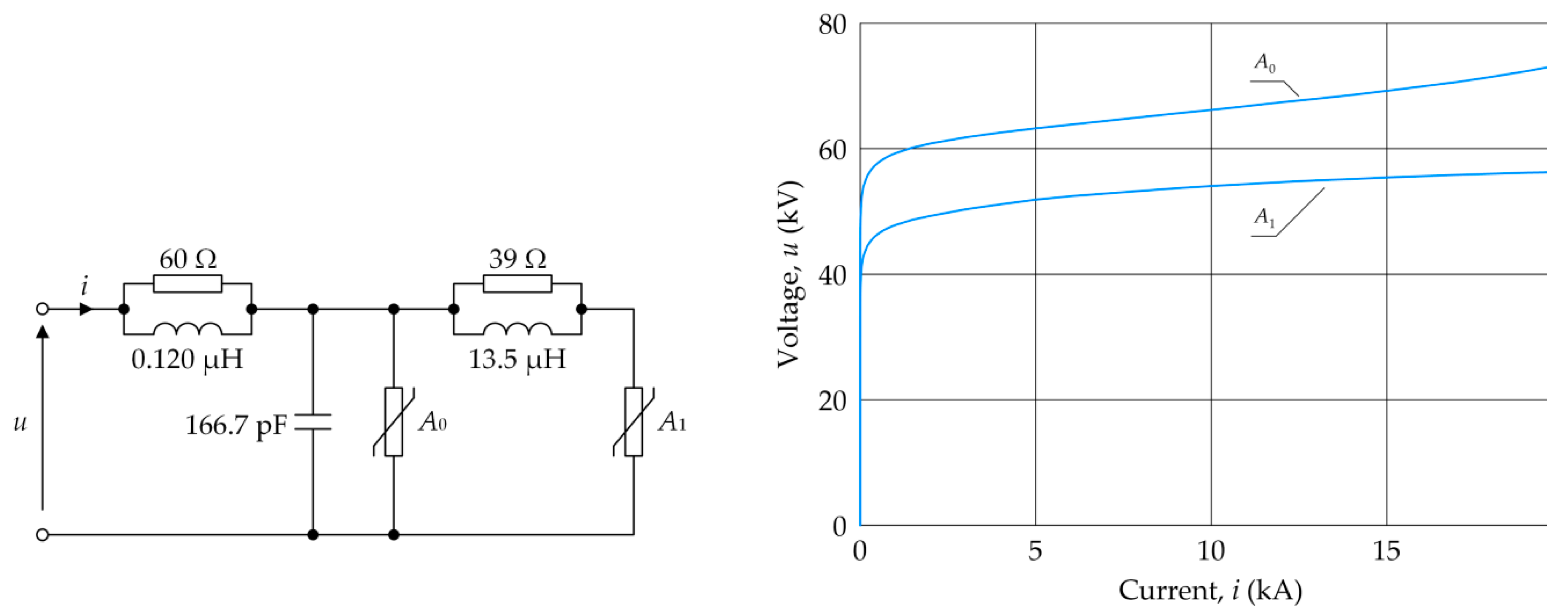
3. Simulation Studies of Ferroresonance Damping Efficiency in an Auxiliary Power System of a 220/110 kV Substation
- A 230/120/15.75 kV ATR autotransformer fed by systems PS1 and PS2;
- A TR 15.75/0.4 kV auxiliary transformer;
- Cable lines C1 and C2;
- Voltage transformers (VTs) with a ferroresonance damping device (FDD);
- Surge arresters SA1 and SA2.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rudenberg, R. Nonharmonic Oscillations as Caused by Magnetic Saturation. Trans. AIEE 1949, 68, 676–685. [Google Scholar] [CrossRef]
- Rudenberg, R. Transient Performance of Electric Power Systems; McGraw-Hill Book Company: New York, NY, USA, 1950. [Google Scholar]
- Barbisio, E.; Bottauscio, O.; Chiampi, M.; Crotti, G.; Giordano, D. Parameters Affecting Ferroresonance in LCR Electric Circuits. IEEE Trans. Magn. 2008, 44, 870–873. [Google Scholar] [CrossRef]
- Mork, B.A.; Stuehm, D.L. Application of nonlinear dynamics and chaos to ferroresonance in distribution systems. IEEE Trans. Power Del. 1994, 9, 1009–1017. [Google Scholar] [CrossRef]
- Van Craenenbroeck, T.; Michiels, W.; Van Dommelen, D.; Lust, K. Bifurcation analysis of three-phase ferroresonant oscillations in ungrounded power systems. IEEE Trans. Power Del. 1999, 14, 531–536. [Google Scholar] [CrossRef]
- Chen, L.; Yang, Q.; Wang, J.; Sima, W.; Yuan, T. Classification of Fundamental Ferroresonance, Single Phase-to-Ground and Wire Breakage Over-Voltages in Isolated Neutral Networks. Energies 2011, 4, 1301–1320. [Google Scholar] [CrossRef]
- Iravani, M.R.; Chaudhary, A.K.S.; Giesbrecht, W.J.; Hassan, I.E.; Keri, A.J.F.; Lee, K.C.; Martinez, J.A.; Morched, A.S.; Mork, B.A.; Parnian, M.; et al. Modeling and analysis guidelines for slow transients. III. The study of ferroresonance. IEEE Trans. Power Del. 2000, 15, 255–265. [Google Scholar] [CrossRef]
- International Council on Large Electric Systems. Working Group C4.307. TB 569. Resonance and Ferroresonance in Power Networks; CIGRE: Paris, France, 2014. [Google Scholar]
- Thanomsat, N.; Plangklang, B.; Ohgaki, H. Analysis of Ferroresonance Phenomenon in 22 kV Distribution System with a Photovoltaic Source by PSCAD/EMTDC. Energies 2018, 11, 1742. [Google Scholar] [CrossRef]
- Kutija, M.; Pravica, L. Effect of Harmonics on Ferroresonance in Low Voltage Power Factor Correction System—A Case Study. Appl. Sci. 2021, 11, 4322. [Google Scholar] [CrossRef]
- Staruhina, E.A.; Syutkin, A.V.; Evdokunin, G.A. Investigation of Ferroresonance Processes Leading to Thermal Damage of Cast-Insulated Transformers. In Proceedings of the International Ural Conference on Electrical Power Engineering (UralCon) 2022, Magnitogorsk, Russia, 23–25 September 2022; pp. 213–217. [Google Scholar] [CrossRef]
- Mikhak-Beyranvand, M.; Faiz, J.; Rezaei-Zare, A.; Rezaeealam, B. Electromagnetic and thermal behavior of a single-phase transformer during ferroresonance considering hysteresis model of core. Electr. Power Energy Syst. 2020, 121, 106078. [Google Scholar] [CrossRef]
- Torres-García, V.; Solís-Ramos, N.; González-Cabrera, N.; Hernández-Mayoral, E.; Guillen, D. Ferroresonance Modeling and Analysis in Underground Distribution Feeders. IEEE Open Access J. Power Energy 2023, 10, 583–592. [Google Scholar] [CrossRef]
- Pordanjani, I.R.; Liang, X.; Wang, Y.; Schneider, A. Single-Phase Ferroresonance in an Ungrounded System during System Energization. IEEE Trans. Ind. Appl. 2021, 57, 3530–3537. [Google Scholar] [CrossRef]
- Rezaei, S. Impact of Ferroresonance on protective relays in Manitoba Hydro 230 kV electrical network. In Proceedings of the IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 1694–1699. [Google Scholar] [CrossRef]
- International Council on Large Electric Systems, Working Group 23.04. TB 197. Design Guidelines for Power Station Auxiliaries and Distribution Systems; CIGRE: Paris, France, 2002. [Google Scholar]
- Ferracci, P. Ferroresonance. Cahier Technique ECT190; Group Schneider: Rueil-Malmaison, France, 1998. [Google Scholar]
- Dedović, M.M.; Mujezinović, A.; Turković, N.; Dautbašić, N.; Turković, I.; Tokić, A.; Bajramović, Z. Experimental investigation of ferroresonance and mitigation measures in 35 kv isolated networks. In Proceedings of the 25th International Conference on Electricity Distribution, Madrid, Spain, 3–6 June 2019. [Google Scholar] [CrossRef]
- Piasecki, W.; Florkowski, M.; Fulczyk, M.; Mahonen, P.; Nowak, W. Mitigating Ferroresonance in Voltage Transformers in Ungrounded MV Networks. IEEE Trans. Power Del. 2007, 22, 2362–2369. [Google Scholar] [CrossRef]
- Peng, G.; Yuan, S.; Gao, X.; Sun, H. Compound Elimination Method of Potential Transformer Ferroresonance in Distribution Network. In Proceedings of the 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, China, 4–6 November 2022. [Google Scholar] [CrossRef]
- Piasecki, W.; Florkowski, M.; Fulczyk, M.; Mahonen, P.; Luto, M.; Nowak, W.; Preiss, O. Ironing out resonance Ferroresonance prevention in MV voltage transformers. ABB Rev. 2005, 4, 42–46. Available online: https://library.e.abb.com/public/6ca5a3f4bb0ee0ecc1257beb002ba3e3/VT%20Guard-Ironing%20out%20resonance.pdf (accessed on 19 January 2024).
- ABB, Medium Voltage Product VT Guard Solution for Ferroresonance Elimination. Available online: https://library.e.abb.com/public/ccc4583980cbdabfc1257beb002bc276/VT%20Guard.pdf (accessed on 19 January 2024).
- Orion EE. Ferro-Damp Ferroresonance Solutions. Available online: https://orionee.com/application/files/1816/9409/6135/EN_Ferro-Damp.pdf (accessed on 10 March 2024).
- Lumel, S.A.; Góra, Z. NP45—Portable Power Quality Analyzer. Poland. Available online: https://www.lumel.com.pl/resources/Pliki%20do%20pobrania/NP45/NP45_data_sheet.pdf (accessed on 10 March 2024).
- IEC 60255-1:2022; Measuring Relays and Protection Equipment—Part 1: Common Requirements. ISO: Geneva, Switzerland, 2023.
- IEEE Working Group 3.4.11. Modeling of metal oxide surge arresters. IEEE Trans. Power Del. 1992, 7, 302–309. [Google Scholar] [CrossRef]
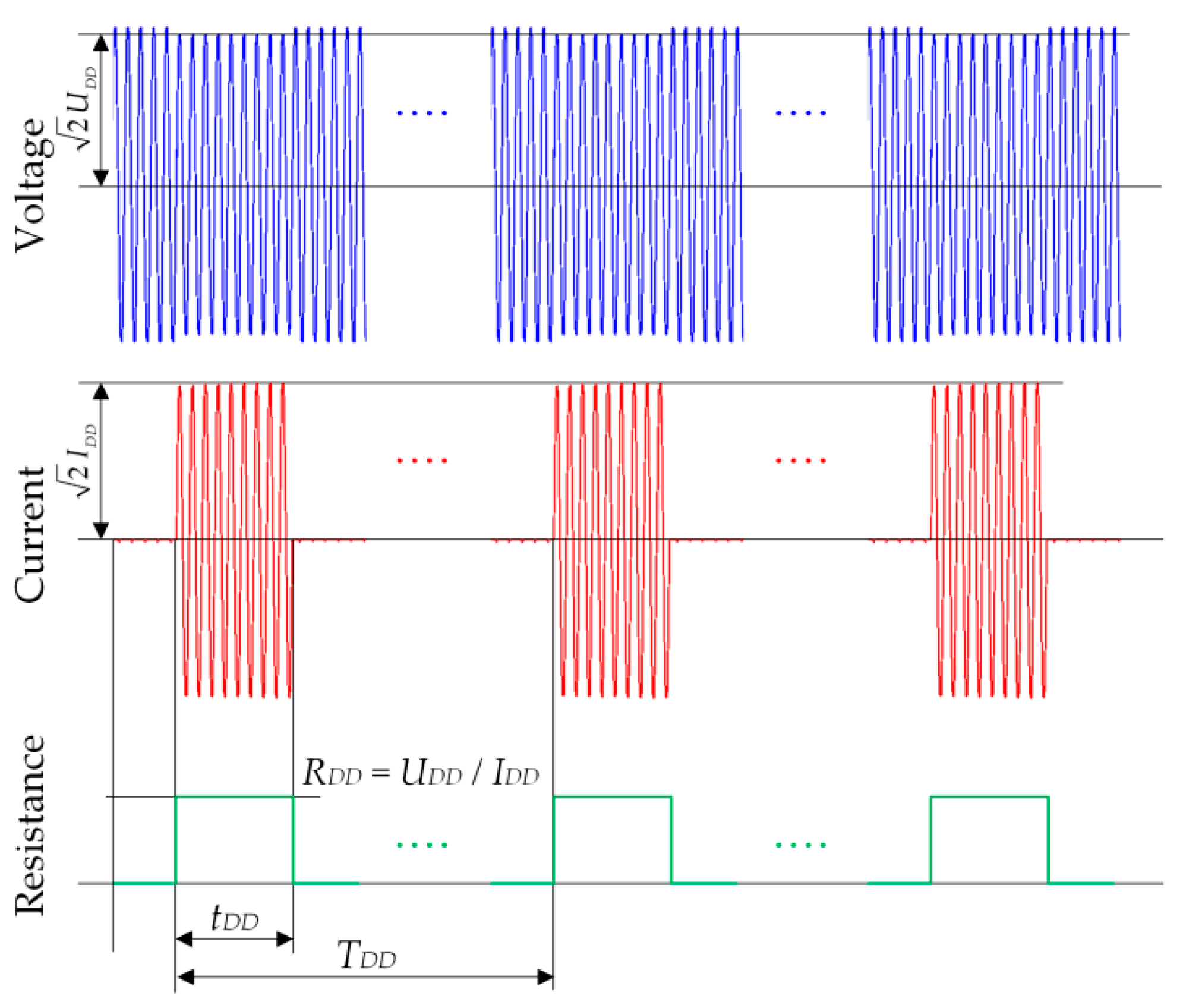

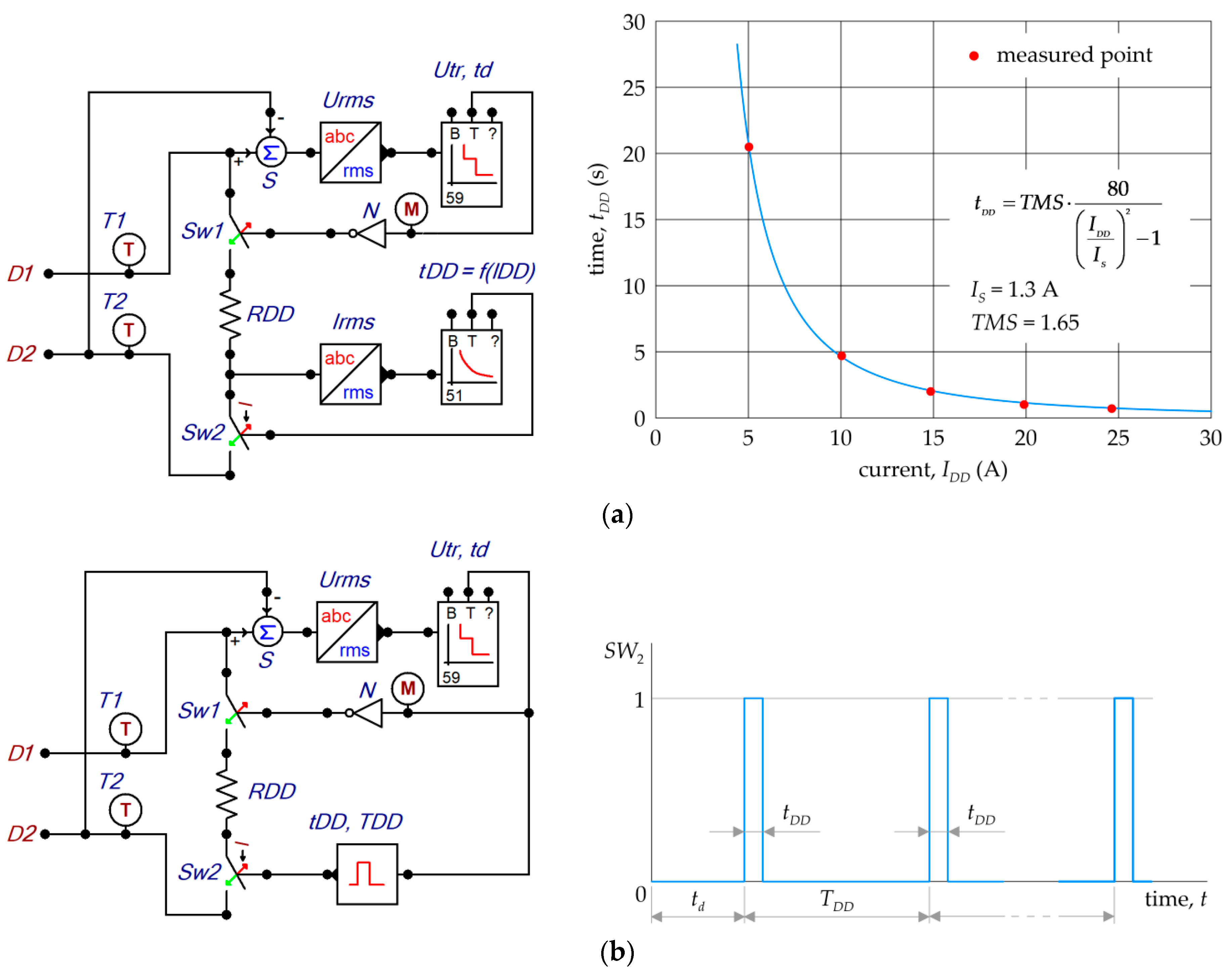
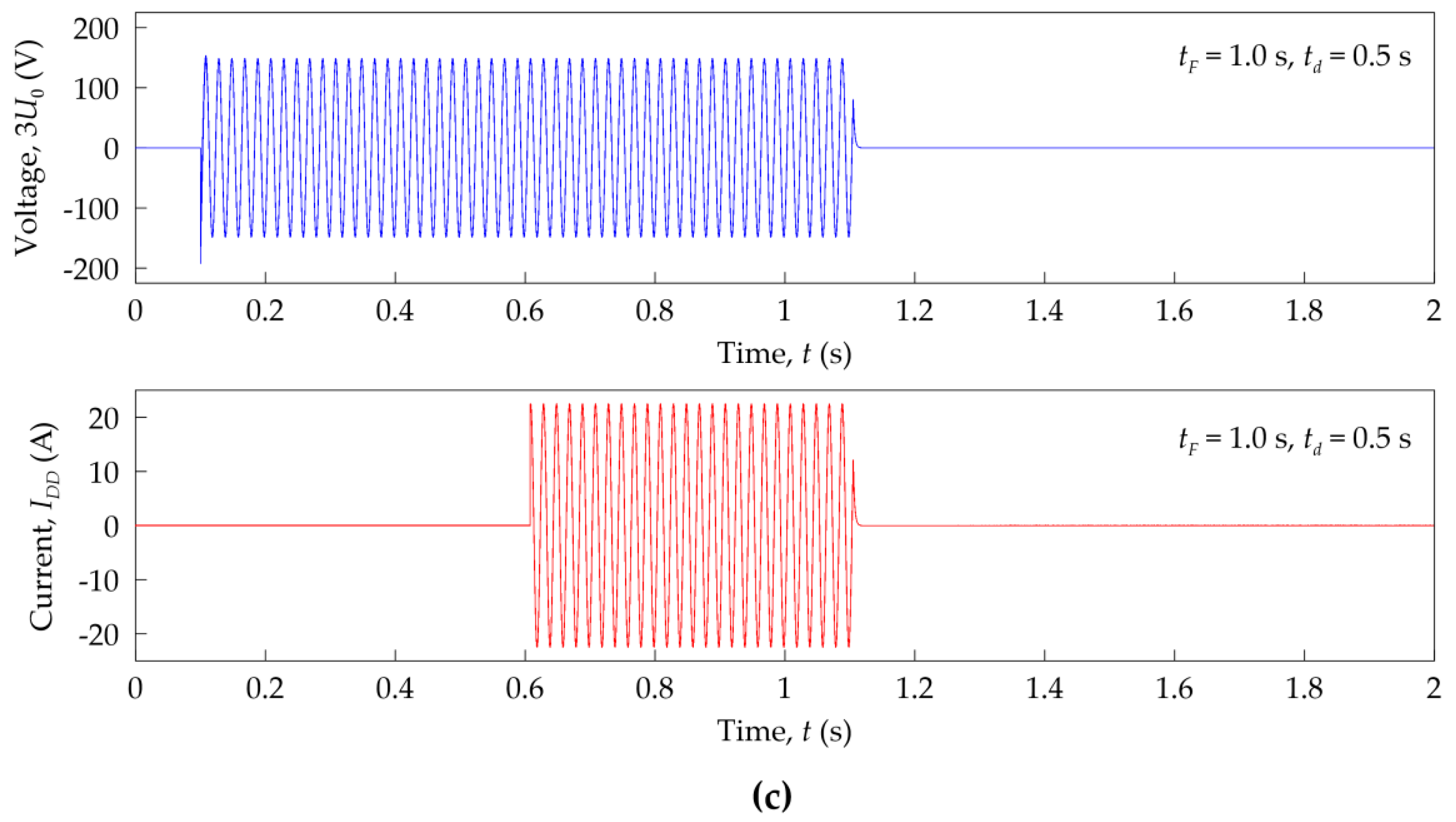
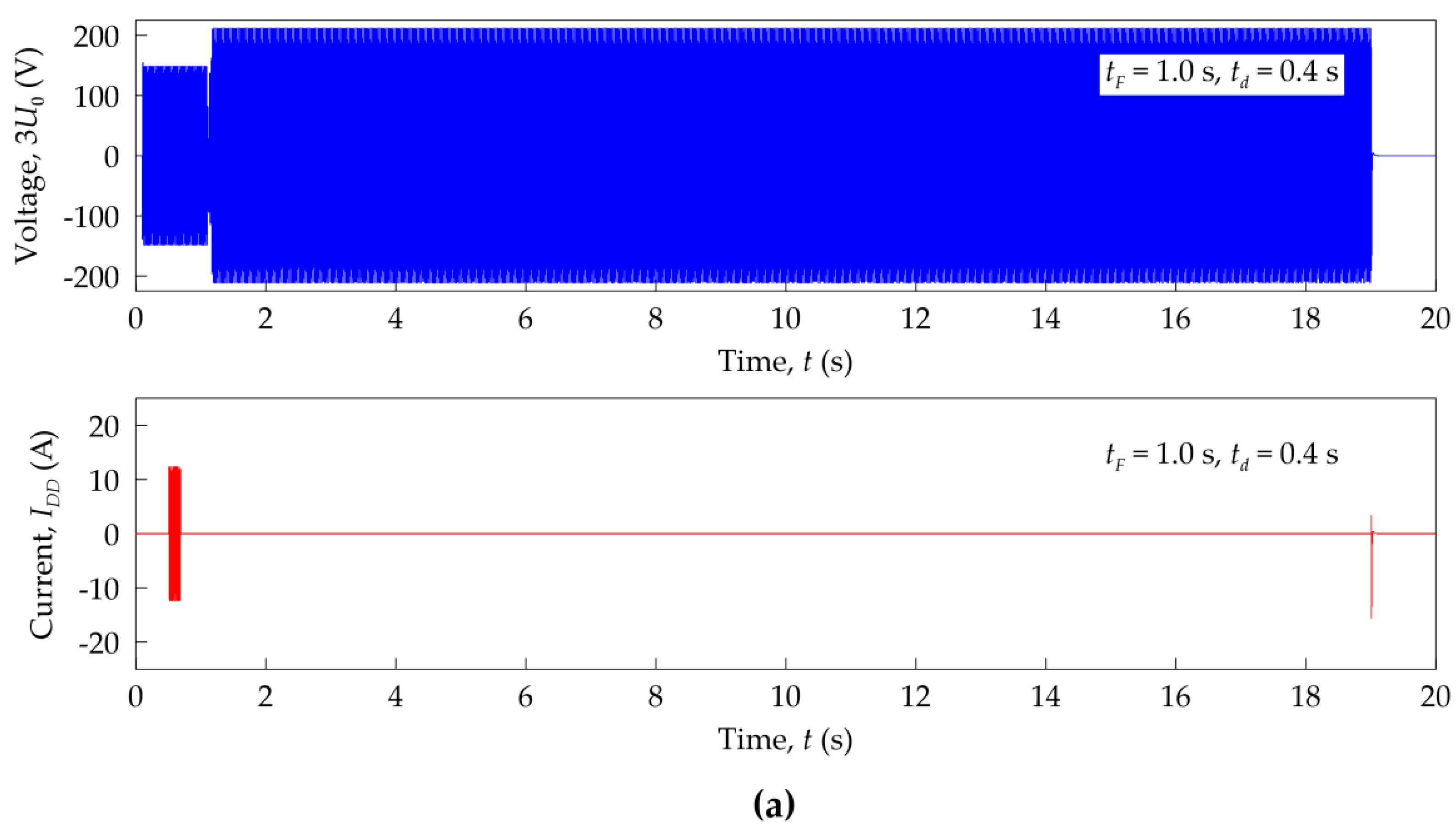
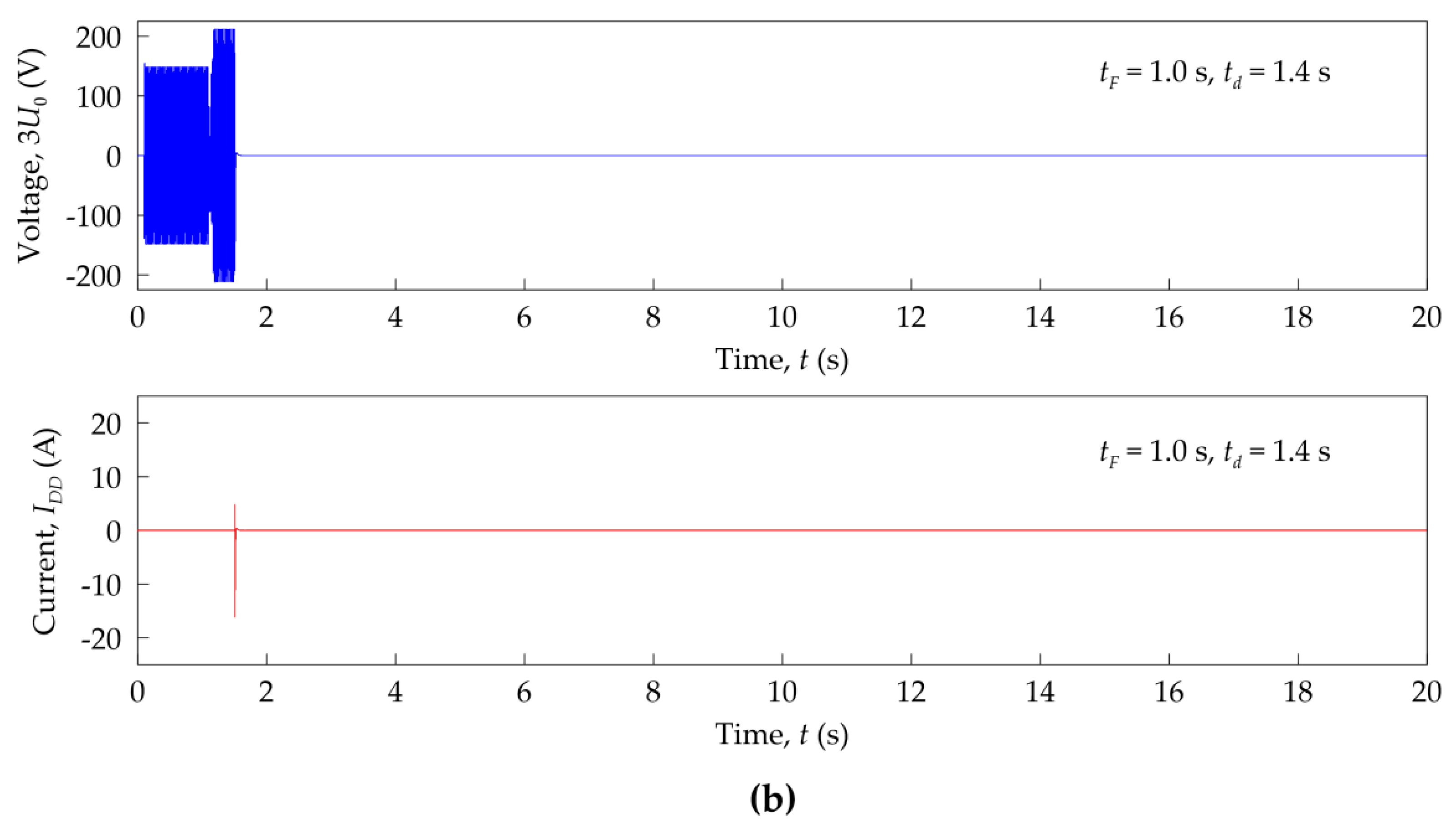
| Parameter | FDD Type A | FDD Type B |
|---|---|---|
| RDD (Ω) | 6.6 | 12.0 |
| tDD (s) | tDD = 22,130 × (UDD)−2.2 | 0.18 |
| TDD (s) | N/A | 18.5 |
| td (s) | 0 | 0.4; 1.4; 2.4; 3.4 |
| Utr (V) | 30 | 20; 25; 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarko, R.; Nowak, W.; Gajdzica, J.; Czapp, S. Analysis of Ferroresonance Mitigation Effectiveness in Auxiliary Power Systems of High-Voltage Substations. Energies 2024, 17, 2423. https://doi.org/10.3390/en17102423
Tarko R, Nowak W, Gajdzica J, Czapp S. Analysis of Ferroresonance Mitigation Effectiveness in Auxiliary Power Systems of High-Voltage Substations. Energies. 2024; 17(10):2423. https://doi.org/10.3390/en17102423
Chicago/Turabian StyleTarko, Rafał, Wiesław Nowak, Jakub Gajdzica, and Stanislaw Czapp. 2024. "Analysis of Ferroresonance Mitigation Effectiveness in Auxiliary Power Systems of High-Voltage Substations" Energies 17, no. 10: 2423. https://doi.org/10.3390/en17102423
APA StyleTarko, R., Nowak, W., Gajdzica, J., & Czapp, S. (2024). Analysis of Ferroresonance Mitigation Effectiveness in Auxiliary Power Systems of High-Voltage Substations. Energies, 17(10), 2423. https://doi.org/10.3390/en17102423







