Sizing Energy Storage Systems to Dispatch Wind Power Plants
Abstract
1. Introduction
- The problem of wind power dispatchability with the aid of ESSs is first presented in the framework of a DRO, which is different and novel from the widely studied problem of minimizing the wind power curtailment.
- The DRO formulation based on the moment-based ambiguity set to size ESSs has been converted to several sufficient finite-dimensional convex optimization problems.
- The problem formulation is straightforward. The SOC dynamics and power limits of ESSs have been removed; both can be realized after the solutions of the proposed optimal problems.
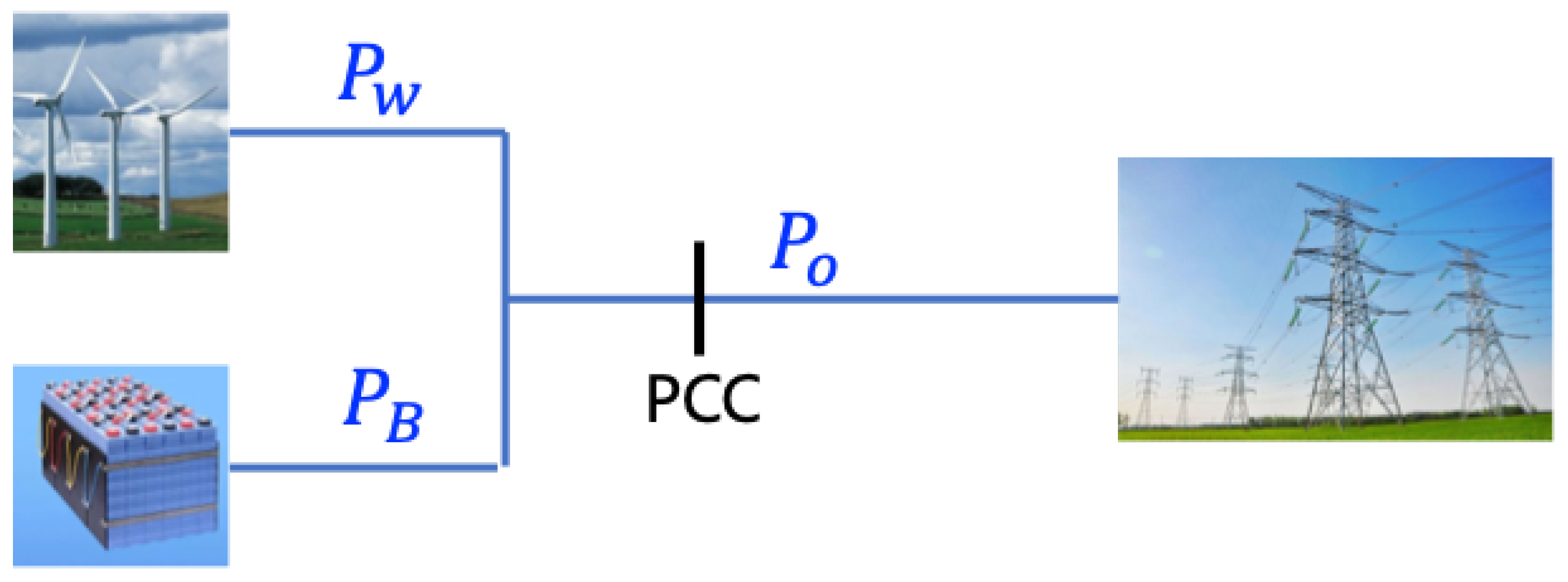
2. Problem Formulation
2.1. Power Balancing
2.2. Energy Constraints
2.3. Ambiguity Set
2.4. Dispatching Objective
3. Main Results
4. Disscussion
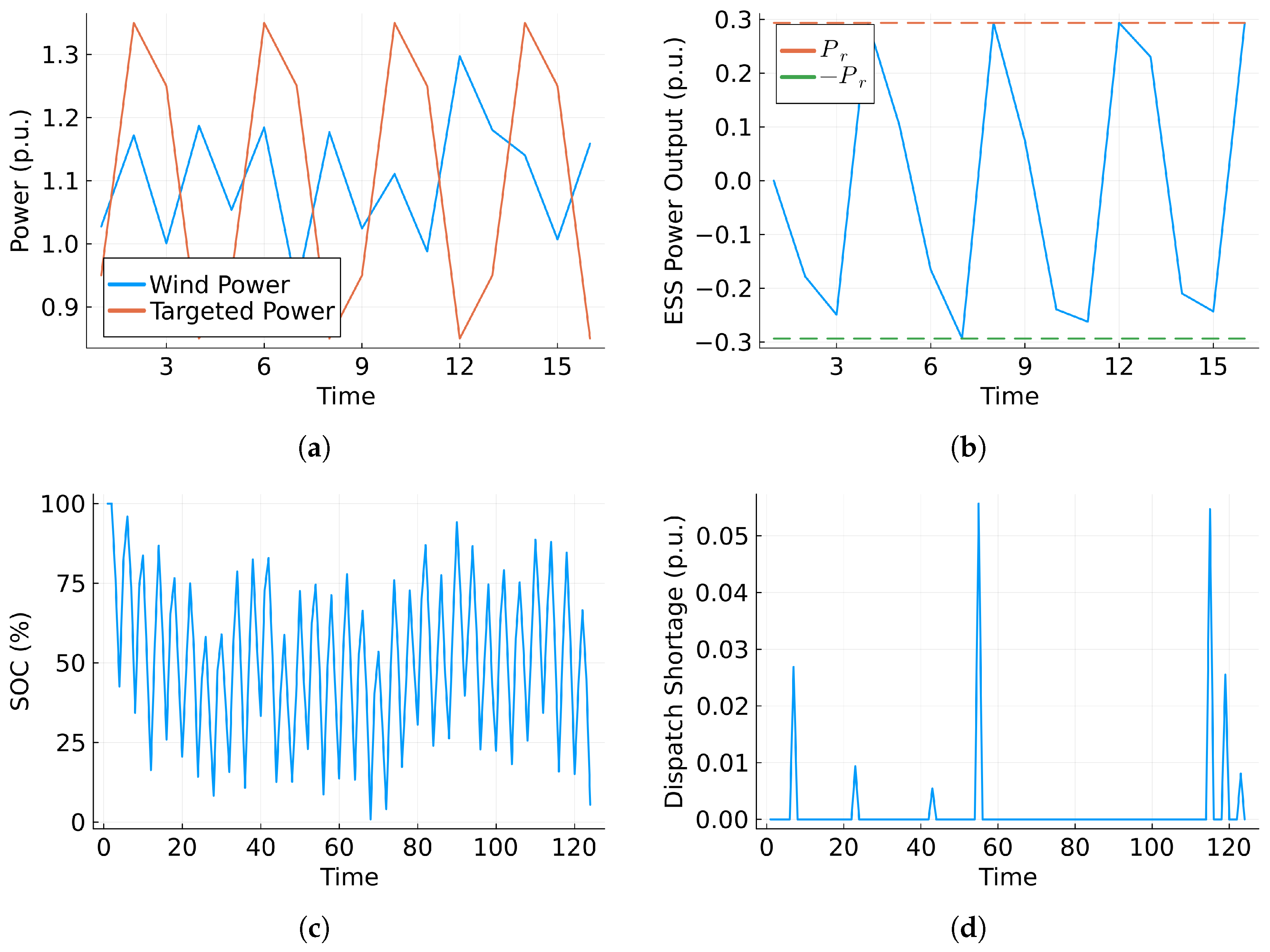
5. Numerical Study
5.1. The Case of
5.2. The Case of
5.3. Optimal Dispatch Power
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs
Appendix A.1. Proof of Lemma 1
Appendix A.2. Proof of Lemma 2
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Holttinen, H.; Tuohy, A.; Milligan, M.; Lannoye, E.; Silva, V.; Muller, S.; So, L. The flexibility workout: Managing variable resources and assessing the need for power system modification. IEEE Power Energy Mag. 2013, 11, 53–62. [Google Scholar] [CrossRef]
- Korpaas, M.; Holen, A.T.; Hildrum, R. Operation and sizing of energy storage for wind power plants in a market system. Int. J. Electr. Power Energy Syst. 2003, 25, 599–606. [Google Scholar] [CrossRef]
- Bitaraf, H.; Rahman, S.; Pipattanasomporn, M. Sizing energy storage to mitigate wind power forecast error impacts by signal processing techniques. IEEE Trans. Sustain. Energy 2015, 6, 1457–1465. [Google Scholar]
- Wu, J.; Zhang, B.; Li, H.; Li, Z.; Chen, Y.; Miao, X. Statistical distribution for wind power forecast error and its application to determine optimal size of energy storage system. Int. J. Electr. Power Energy Syst. 2014, 55, 100–107. [Google Scholar]
- Knap, V.; Chaudhary, S.K.; Stroe, D.I.; Swierczynski, M.; Craciun, B.I.; Teodorescu, R. Sizing of an energy storage system for grid inertial response and primary frequency reserve. IEEE Trans. Power Syst. 2016, 31, 3447–3456. [Google Scholar] [CrossRef]
- Liu, Y.; Du, W.; Xiao, L.; Wang, H.; Cao, J. A method for sizing energy storage system to increase wind penetration as limited by grid frequency deviations. IEEE Trans. Power Syst. 2016, 31, 729–737. [Google Scholar] [CrossRef]
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of energy storage for microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
- Khorramdel, H.; Aghaei, J.; Khorramdel, B.; Siano, P. Optimal battery sizing in microgrids using probabilistic unit commitment. IEEE Trans. Ind. Inform. 2016, 12, 834–843. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, J.; Dai, Y. Capacity allocation of a hybrid energy storage system for power system peak shaving at high wind power penetration level. Renew. Energy 2015, 75, 541–549. [Google Scholar] [CrossRef]
- Wang, X.Y.; Vilathgamuwa, D.M.; Choi, S.S. Determination of battery storage capacity in energy buffer for wind farm. IEEE Trans. Energy Convers. 2008, 23, 868–878. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, X.; Ju, P.; Qian, K.; Fu, Z. Applications of battery energy storage system for wind power dispatchability purpose. Electr. Power Syst. Res. 2012, 93, 54–60. [Google Scholar] [CrossRef]
- Teleke, S.; Baran, M.E.; Bhattacharya, S.; Huang, A.Q. Optimal control of battery energy storage for wind farm dispatching. IEEE Trans. Energy Convers. 2010, 25, 787–794. [Google Scholar] [CrossRef]
- Tarca, S.; Roughan, M.; Ertugrul, N.; Bean, N. Dispatchability of wind power with battery energy storage in south australia. Energy Procedia 2017, 110, 223–228. [Google Scholar] [CrossRef]
- Gholami, M.; Fathi, S.H.; Milimonfared, J.; Chen, Z.; Deng, F. A new strategy based on hybrid battery–wind power system for wind power dispatching. IET Gener. Transm. Distrib. 2018, 12, 160–169. [Google Scholar] [CrossRef]
- Bakhtvar, M.; Al-Hinai, A. Robust Operation of Hybrid Solar–Wind Power Plant with Battery Energy Storage System. Energies 2021, 14, 3781. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S.; O’Neill, R.P. Reserve requirements for wind power integration: A scenario-based stochastic programming framework. IEEE Trans. Power Syst. 2011, 26, 2197–2206. [Google Scholar] [CrossRef]
- Xia, S.; Luo, X.; Chan, K.W.; Zhou, M.; Li, G. Probabilistic transient stability constrained optimal power flow for power systems with multiple correlated uncertain wind generations. IEEE Trans. Sustain. Energy 2016, 7, 1133–1144. [Google Scholar] [CrossRef]
- Bian, J.; Wang, H.; Wang, L.; Li, G.; Wang, Z. Probabilistic optimal power flow of an ac/dc system with a multiport current flow controller. CSEE J. Power Energy Syst. 2021, 7, 744–752. [Google Scholar]
- Wu, W.; Chen, J.; Zhang, B.; Sun, H. A robust wind power optimization method for look-ahead power dispatch. IEEE Trans. Sustain. Energy 2014, 5, 507–515. [Google Scholar] [CrossRef]
- Peng, C.; Xie, P.; Pan, L.; Yu, R. Flexible robust optimization dispatch for hybrid wind/photovoltaic/hydro/thermal power system. IEEE Trans. Smart Grid 2016, 7, 751–762. [Google Scholar] [CrossRef]
- Lin, Z.; Wu, Q.; Chen, H.; Ji, T.; Xu, Y.; Sun, H. Scenarios-oriented distributionally robust optimization for energy and reserve scheduling. IEEE Trans. Power Syst. 2023, 38, 2943–2946. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, T.; Qu, M. An algorithmic approach for inner max-min model under norm-2 type uncertainty set in data-driven distributionally robust optimization. IEEE Trans. Power Syst. 2023, 8, 1755–1758. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Mei, S. Distributionally robust co-optimization of energy and reserve dispatch. IEEE Trans. Sustain. Energy 2016, 7, 289–300. [Google Scholar] [CrossRef]
- Cui, S.; Zhu, R.; Gao, Y. Distributionally Robust Optimization of an Integrated Energy System Cluster Considering the Oxygen Supply Demand and Multi-Energy Sharing. Energies 2022, 15, 8723. [Google Scholar] [CrossRef]
- Guo, Z.; Wei, W.; Chen, L.; Xie, R.; Mei, S. Sizing energy storage to reduce renewable power curtailment considering network power flows: A distributionally robust optimisation approach. IET Renew. Power Gener. 2020, 14, 3273–3280. [Google Scholar] [CrossRef]
- Ghaoui, L.; Oks, M.; Oustry, F. Worst-Case Value-At-Risk and Robust Portfolio Optimization: A Conic Programming Approach. Opertaions Res. 2003, 51, 543–556. [Google Scholar] [CrossRef]
- Yıldıran, U. Robust multi-stage economic dispatch with renewable generation and storage. Eur. J. Oper. Res. 2023, 9, 890–909. [Google Scholar] [CrossRef]
- Mora, C.A.; Montoya, O.D.; Trujillo, E.R. Mixed-Integer Programming Model for Transmission Network Expansion Planning with Battery Energy Storage Systems (BESS). Energies 2020, 13, 4386. [Google Scholar] [CrossRef]



| Model | R-DROM | E-DROM | No ESS | ||
|---|---|---|---|---|---|
| 1 | 2.5 | 4 | – | – | |
| Optimal value | 0.086 | 0.215 | 0.343 | 0.105 | – |
| ESS power | −0.154 | −0.154 | −0.154 | −0.153 | 0 |
| ESS power | 0.19 | 0.19 | 0.19 | 0.2 | 0 |
| ESS power | 0.24 | 0.24 | 0.24 | 0.246 | 0 |
| ESS power | −0.277 | −0.277 | −0.277 | −0.294 | 0 |
| ESS rated power | 0.277 | 0.277 | 0.277 | 0.294 | 0 |
| ESS capacity | 0.718 | 0.718 | 0.718 | 0.744 | 0 |
| Total dispatch shortage with fixed | 2.872 | 2.872 | 2.872 | 2.811 | 13.558 |
| Total dispatch shortage with variable | 0.474 | 0.474 | 0.474 | 0.186 | – |
| Model | R-DROM | Optimal SAAM | Without ESS |
|---|---|---|---|
| (a) Over the span of December 2021 | |||
| ESS rated power (p.u.) | 0.656 | 0.687 | 0 |
| ESS capacity (p.u.) | 5.761 | 5.328 | 0 |
| Total dispatch shortage with variable (p.u.) | 22.272 | 22.61 | 90.823 |
| (b) Over the span of 2021 | |||
| ESS rated power (p.u.) | 0.558 | 0.553 | 0 |
| ESS capacity (p.u.) | 4.91 | 4.987 | 0 |
| Total dispatch shortage with variable (p.u.) | 912.896 | 911.018 | 1649.123 |
| Expected Dispatch Shortage | The Optimal Value (p.u.) | Average Daily Dispatch Shortage (p.u.) | |
|---|---|---|---|
| 12 | 7 | 15.152 | 1.348 |
| 10 | 22.141 | 4.711 | |
| 15 | 32.64 | 13.761 | |
| 20 | 42.822 | 23.943 | |
| 24 | 7 | 2.079 | 0 |
| 10 | 9.153 | 0.263 | |
| 15 | 16.41 | 1.771 | |
| 20 | 22.141 | 4.713 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, B.; Wu, M.; Yang, W.; Chen, Q.; Xiang, J. Sizing Energy Storage Systems to Dispatch Wind Power Plants. Energies 2024, 17, 2379. https://doi.org/10.3390/en17102379
Xia B, Wu M, Yang W, Chen Q, Xiang J. Sizing Energy Storage Systems to Dispatch Wind Power Plants. Energies. 2024; 17(10):2379. https://doi.org/10.3390/en17102379
Chicago/Turabian StyleXia, Bingqing, Mingqi Wu, Wenbin Yang, Qing Chen, and Ji Xiang. 2024. "Sizing Energy Storage Systems to Dispatch Wind Power Plants" Energies 17, no. 10: 2379. https://doi.org/10.3390/en17102379
APA StyleXia, B., Wu, M., Yang, W., Chen, Q., & Xiang, J. (2024). Sizing Energy Storage Systems to Dispatch Wind Power Plants. Energies, 17(10), 2379. https://doi.org/10.3390/en17102379







