Open-Circuit Voltage Variation in LiCoO2 Battery Cycled in Different States of Charge Regions
Abstract
1. Introduction
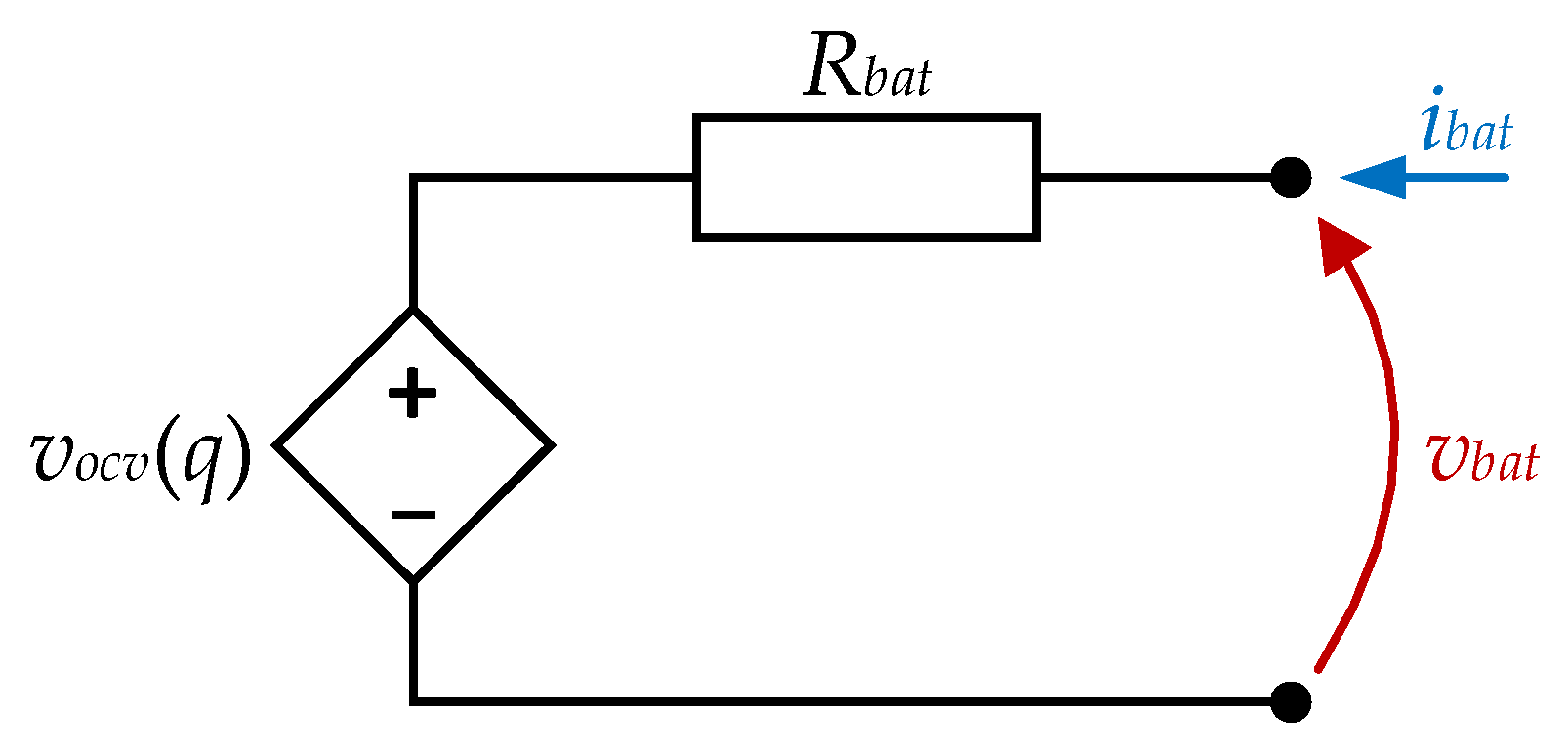
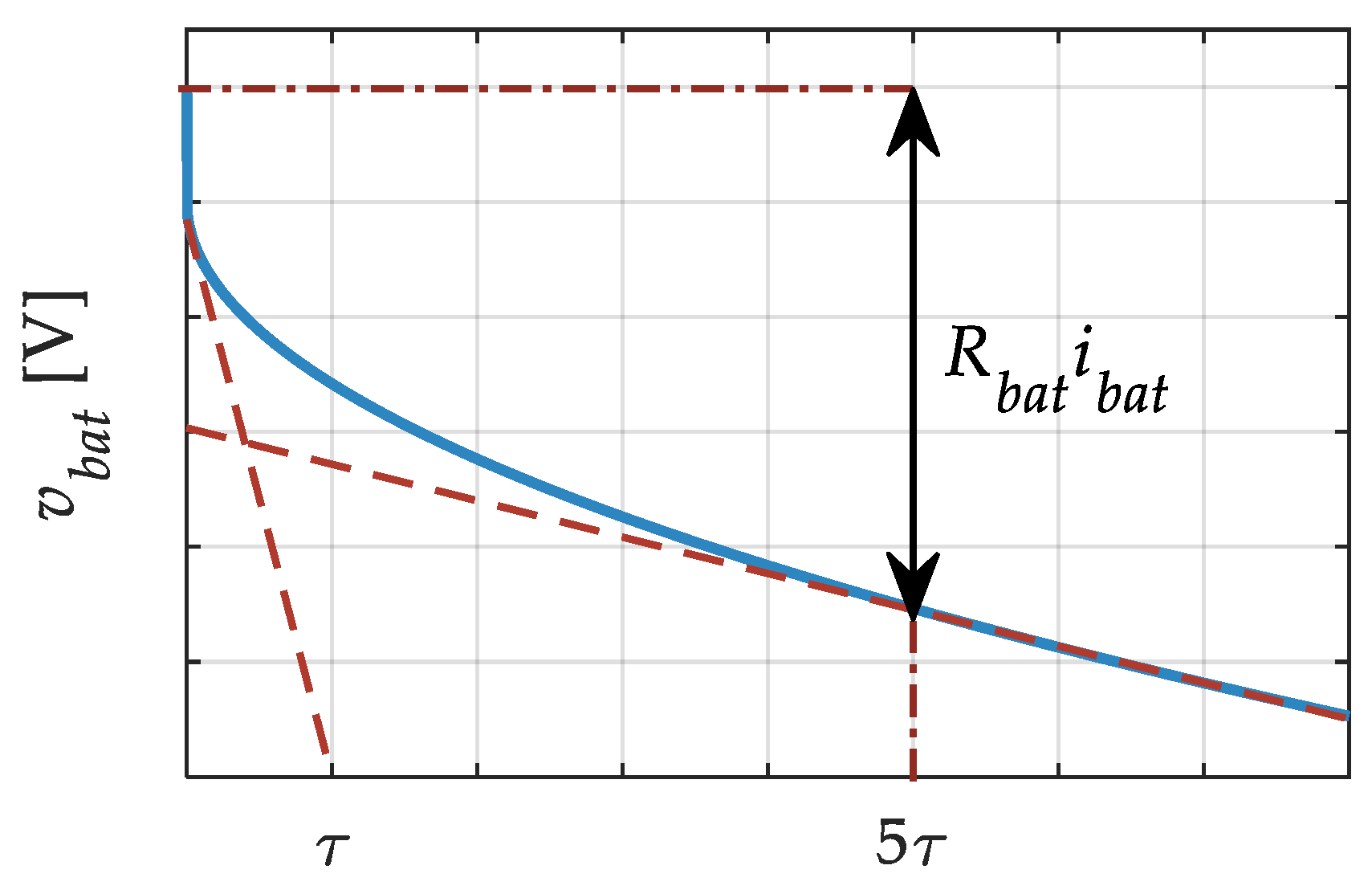
2. Battery Model
3. Test Procedure and Setup
3.1. Experimental Setup
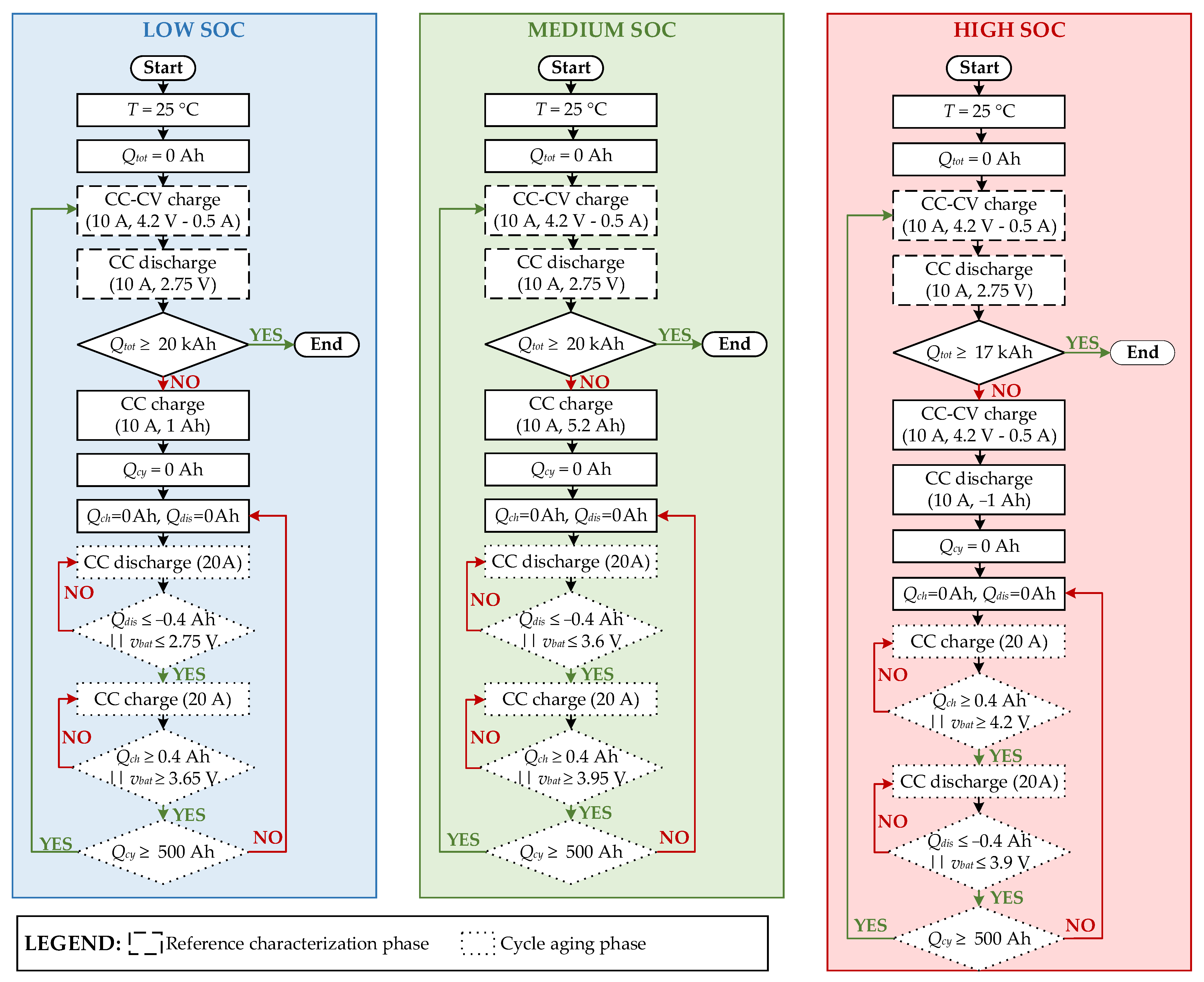
3.2. Experimental Procedure
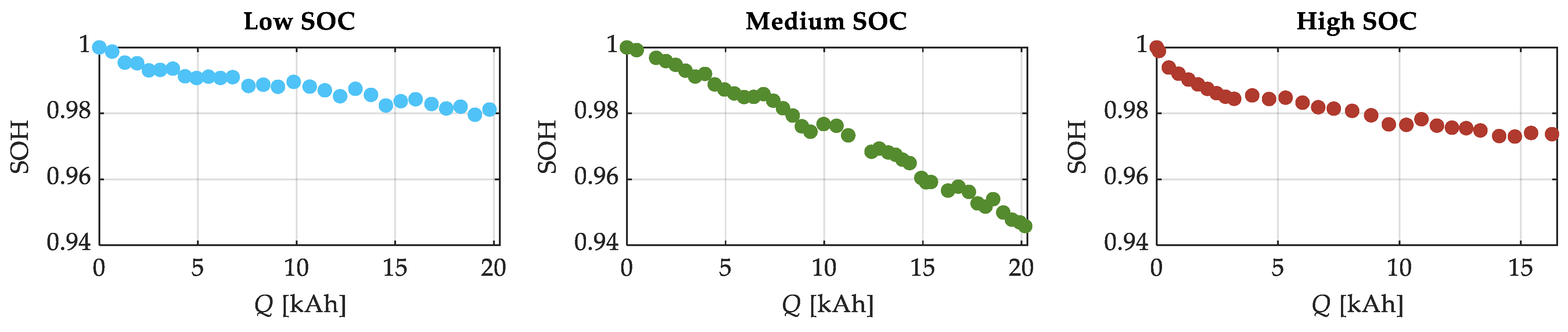
4. Discussion
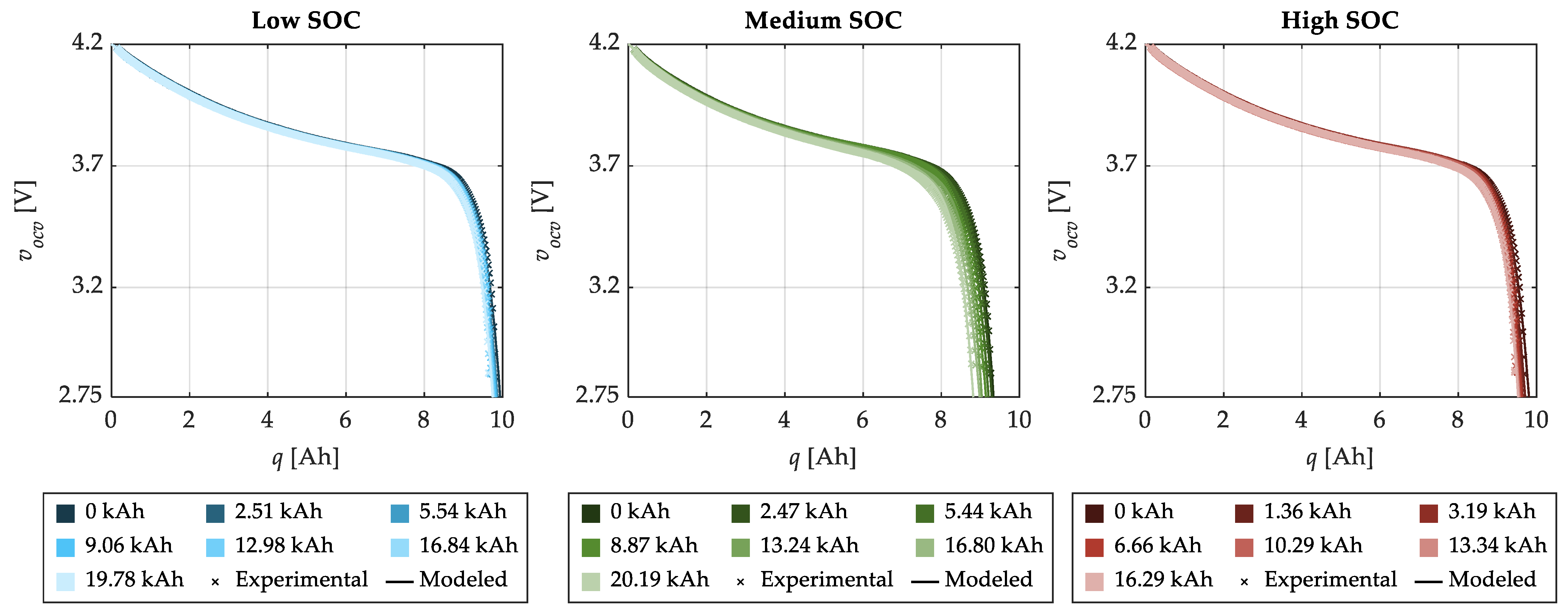
4.1. Model Characterization
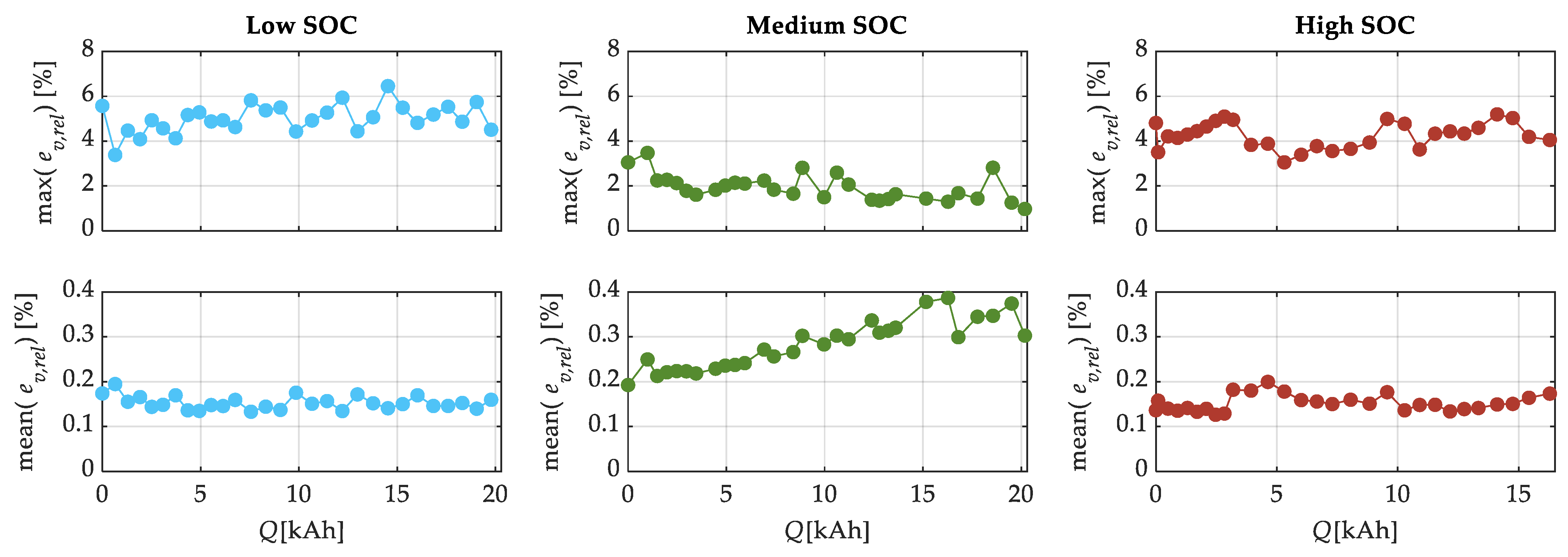
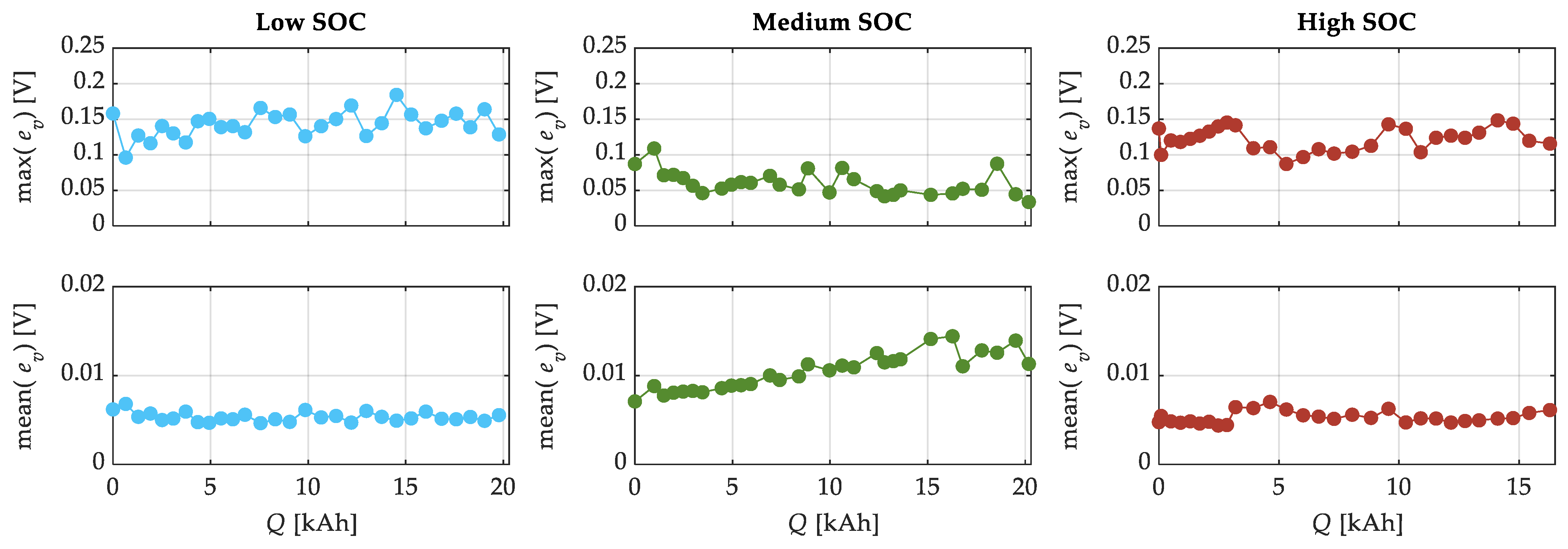
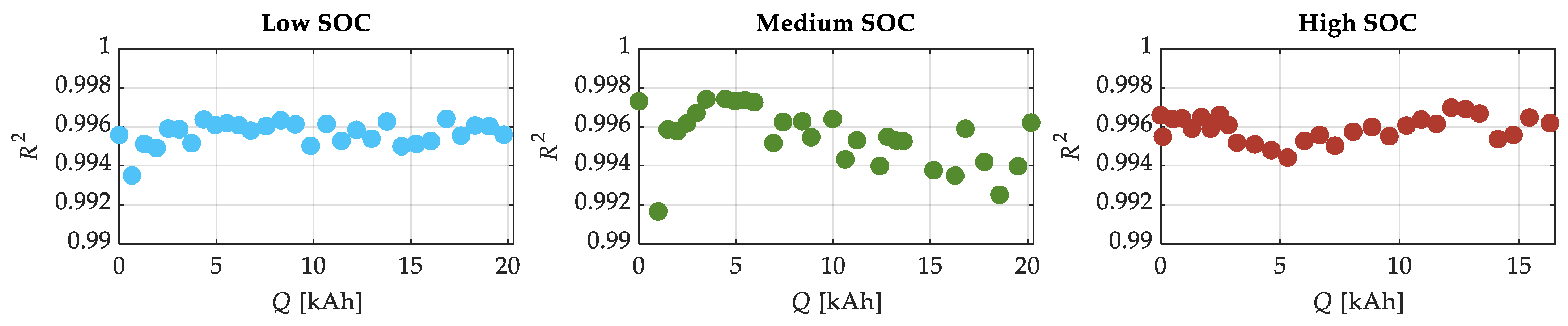
4.2. Model Validation
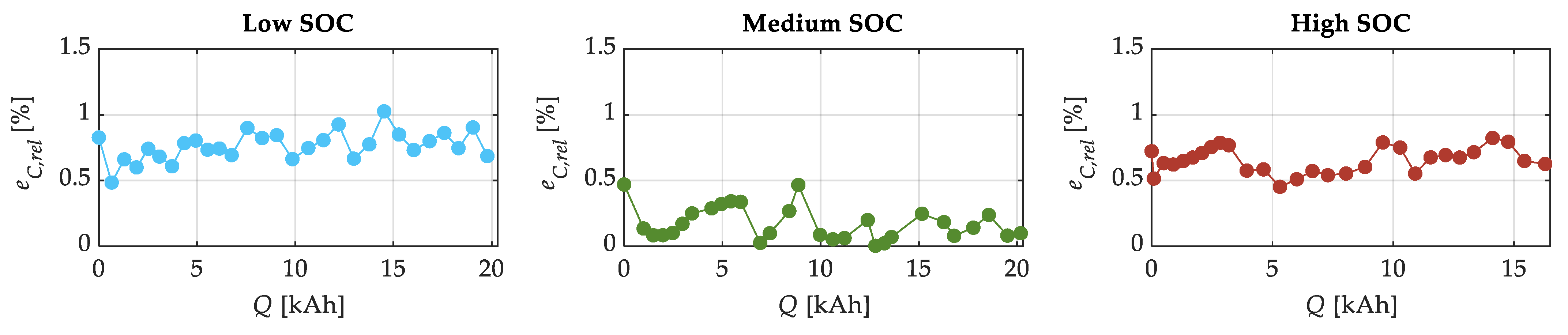
4.3. Actual Capacity Estimation of the Battery
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mitali, J.; Dhinakaran, S.; Mohamad, A.A. Energy Storage Systems: A Review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Krishan, O.; Suhag, S. An Updated Review of Energy Storage Systems: Classification and Applications in Distributed Generation Power Systems Incorporating Renewable Energy Resources. Int. J. Energy Res. 2019, 43, 6171–6210. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped Hydro Energy Storage System: A Technological Review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Aneke, M.; Wang, M. Energy Storage Technologies and Real Life Applications—A State of the Art Review. Appl. Energy 2016, 179, 350–377. [Google Scholar] [CrossRef]
- Berrada, A.; Loudiyi, K.; Zorkani, I. System Design and Economic Performance of Gravity Energy Storage. J. Clean. Prod. 2017, 156, 317–326. [Google Scholar] [CrossRef]
- Hossain, E.; Faruque, H.; Sunny, M.; Mohammad, N.; Nawar, N. A Comprehensive Review on Energy Storage Systems: Types, Comparison, Current Scenario, Applications, Barriers, and Potential Solutions, Policies, and Future Prospects. Energies 2020, 13, 3651. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on Thermal Energy Storage with Phase Change Materials and Applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Clelland, I.; Price, R.; Sarjeant, W.J. Advances in Capacitor Technology for Modern Power Electronics. In Proceedings of the Conference Record of the 2000 Twenty-Fourth International Power Modulator Symposium, Norfolk, VA, USA, 26–29 June 2000; pp. 145–148. [Google Scholar]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of Current Development in Electrical Energy Storage Technologies and the Application Potential in Power System Operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Boom, R.; Peterson, H. Superconductive Energy Storage for Power Systems. IEEE Trans. Magn. 1972, 8, 701–703. [Google Scholar] [CrossRef]
- Torre, W.V.; Eckroad, S. Improving Power Delivery through the Application of Superconducting Magnetic Energy Storage (SMES). In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.01CH37194), Columbus, OH, USA, 28 January–1 February 2001; Volume 1, pp. 81–87. [Google Scholar]
- Rey, S.O.; Romero, J.A.; Romero, L.T.; Martínez, À.F.; Roger, X.S.; Qamar, M.A.; Domínguez-García, J.L.; Gevorkov, L. Powering the Future: A Comprehensive Review of Battery Energy Storage Systems. Energies 2023, 16, 6344. [Google Scholar] [CrossRef]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy Storage Systems for Transport and Grid Applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef]
- Tsais, P.-J.; Chan, L.I. Nickel-Based Batteries: Materials and Chemistry. In Electricity Transmission, Distribution and Storage Systems; Elsevier: Amsterdam, The Netherlands, 2013; pp. 309–397. [Google Scholar]
- Arun, V.; Kannan, R.; Ramesh, S.; Vijayakumar, M.; Raghavendran, P.S.; Siva Ramkumar, M.; Anbarasu, P.; Sundramurthy, V.P. Review on Li-Ion Battery vs Nickel Metal Hydride Battery in EV. Adv. Mater. Sci. Eng. 2022, 2022, 1–7. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, Y.-L.; Cao, P.-F.; Lin, M.-C. Energy Storage System: Current Studies on Batteries and Power Condition System. Renew. Sustain. Energy Rev. 2018, 82, 3091–3106. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Calendar and Cycling Ageing Combination of Batteries in Electric Vehicles. Microelectron. Reliab. 2018, 88–90, 1212–1215. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A Review on Lithium-Ion Battery Ageing Mechanisms and Estimations for Automotive Applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Jiang, Y. Aging Mechanisms under Different State-of-Charge Ranges and the Multi-Indicators System of State-of-Health for Lithium-Ion Battery with Li(NiMnCo)O2 Cathode. J. Power Sources 2018, 400, 641–651. [Google Scholar] [CrossRef]
- Vermeer, W.; Chandra Mouli, G.R.; Bauer, P. A Comprehensive Review on the Characteristics and Modeling of Lithium-Ion Battery Aging. IEEE Trans. Transp. Electrif. 2022, 8, 2205–2232. [Google Scholar] [CrossRef]
- Gabbar, H.; Othman, A.; Abdussami, M. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Lelie, M.; Braun, T.; Knips, M.; Nordmann, H.; Ringbeck, F.; Zappen, H.; Sauer, D. Battery Management System Hardware Concepts: An Overview. Appl. Sci. 2018, 8, 534. [Google Scholar] [CrossRef]
- Luo, X.; Kang, L.; Lu, C.; Linghu, J.; Lin, H.; Hu, B. An Enhanced Multicell-to-Multicell Battery Equalizer Based on Bipolar-Resonant LC Converter. Electronics 2021, 10, 293. [Google Scholar] [CrossRef]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of Different Open Circuit Voltage Tests on State of Charge Online Estimation for Lithium-Ion Batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Yang, F.; Xing, Y.; Wang, D.; Tsui, K.-L. A Comparative Study of Three Model-Based Algorithms for Estimating State-of-Charge of Lithium-Ion Batteries under a New Combined Dynamic Loading Profile. Appl. Energy 2016, 164, 387–399. [Google Scholar] [CrossRef]
- Ren, X.; Liu, S.; Yu, X.; Dong, X. A Method for State-of-Charge Estimation of Lithium-Ion Batteries Based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Wang, L.Y.; Lin, C. A Novel Method to Obtain the Open Circuit Voltage for the State of Charge of Lithium Ion Batteries in Electric Vehicles by Using H Infinity Filter. Appl. Energy 2017, 207, 346–353. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Elfouly, T.; Alouani, A.; Massoud, A.M. A Comprehensive Review of Lithium-Ion Batteries Modeling, and State of Health and Remaining Useful Lifetime Prediction. IEEE Access 2022, 10, 119040–119070. [Google Scholar] [CrossRef]
- Lavigne, L.; Sabatier, J.; Francisco, J.M.; Guillemard, F.; Noury, A. Lithium-Ion Open Circuit Voltage (OCV) Curve Modelling and Its Ageing Adjustment. J. Power Sources 2016, 324, 694–703. [Google Scholar] [CrossRef]
- Sundaresan, S.; Devabattini, B.; Kumar, P.; Pattipati, K.; Balasingam, B. Tabular Open Circuit Voltage Modelling of Li-Ion Batteries for Robust SOC Estimation. Energies 2022, 15, 9142. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar] [CrossRef]
- Sun, D.; Yu, X.; Wang, C.; Zhang, C.; Huang, R.; Zhou, Q.; Amietszajew, T.; Bhagat, R. State of Charge Estimation for Lithium-Ion Battery Based on an Intelligent Adaptive Extended Kalman Filter with Improved Noise Estimator. Energy 2021, 214, 119025. [Google Scholar] [CrossRef]
- Zhao, S.; Duncan, S.R.; Howey, D.A. Observability Analysis and State Estimation of Lithium-Ion Batteries in the Presence of Sensor Biases. IEEE Trans. Control Syst. Technol. 2017, 25, 326–333. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Guo, H.; Ding, Y. Modeling for Lithium-Ion Battery Used in Electric Vehicles. Procedia Eng. 2011, 15, 2869–2874. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach. Energies 2012, 5, 1455–1469. [Google Scholar] [CrossRef]
- Ta, K.P.; Newman, J. Proton Intercalation Hysteresis in Charging and Discharging Nickel Hydroxide Electrodes. J. Electrochem. Soc. 1999, 146, 2769–2779. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Amara, N. Improved OCV Model of a Li-Ion NMC Battery for Online SOC Estimation Using the Extended Kalman Filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P. A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. A Study on the Open Circuit Voltage and State of Charge Characterization of High Capacity Lithium-Ion Battery Under Different Temperature. Energies 2018, 11, 2408. [Google Scholar] [CrossRef]
- Weng, C.; Sun, J.; Peng, H. A Unified Open-Circuit-Voltage Model of Lithium-Ion Batteries for State-of-Charge Estimation and State-of-Health Monitoring. J. Power Sources 2014, 258, 228–237. [Google Scholar] [CrossRef]
- Wang, L.; Lu, D.; Liu, Q.; Liu, L.; Zhao, X. State of Charge Estimation for LiFePO4 Battery via Dual Extended Kalman Filter and Charging Voltage Curve. Electrochim. Acta 2019, 296, 1009–1017. [Google Scholar] [CrossRef]
- Klintberg, A.; Klintberg, E.; Fridholm, B.; Kuusisto, H.; Wik, T. Statistical Modeling of OCV-Curves for Aged Battery Cells. IFAC-PapersOnLine 2017, 50, 2164–2168. [Google Scholar] [CrossRef]
- Tong, S.; Klein, M.P.; Park, J.W. On-Line Optimization of Battery Open Circuit Voltage for Improved State-of-Charge and State-of-Health Estimation. J. Power Sources 2015, 293, 416–428. [Google Scholar] [CrossRef]
- Barcellona, S.; Codecasa, L.; Colnago, S.; Piegari, L. Cycle Aging Effect on the Open Circuit Voltage of Lithium-Ion Battery. In Proceedings of the International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Venice, Italy, 29–31 March 2023; Volume 16, p. 4869. [Google Scholar]
- Barcellona, S.; Grillo, S.; Piegari, L. A Simple Battery Model for EV Range Prediction: Theory and Experimental Validation. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–7. [Google Scholar]
- Barcellona, S.; Brenna, M.; Foiadelli, F.; Longo, M.; Piegari, L. Analysis of Ageing Effect on Li-Polymer Batteries. Sci. World J. 2015, 2015, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Barcellona, S.; Piegari, L. Effect of Current on Cycle Aging of Lithium Ion Batteries. J. Energy Storage 2020, 29, 101310. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, F.; Kang, J.; Du, C.; Zhang, C.; Turkson, R.F. Fading Analysis of the Li(NiCoMn)O2 Battery under Different SOC Cycle Intervals. Ionics 2017, 23, 1383–1390. [Google Scholar] [CrossRef]
- Wikner, E.; Björklund, E.; Fridner, J.; Brandell, D.; Thiringer, T. How the Utilised SOC Window in Commercial Li-Ion Pouch Cells Influence Battery Ageing. J. Power Sources Adv. 2021, 8, 100054. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and Cycle Life Study of Li(NiMnCo)O2-Based 18650 Lithium-Ion Batteries. J. Power Sources 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Zhu, J.; Knapp, M.; Sørensen, D.R.; Heere, M.; Darma, M.S.D.; Müller, M.; Mereacre, L.; Dai, H.; Senyshyn, A.; Wei, X.; et al. Investigation of Capacity Fade for 18650-Type Lithium-Ion Batteries Cycled in Different State of Charge (SoC) Ranges. J. Power Sources 2021, 489, 229422. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, B.; Sun, Q.; Wennersten, R. Analysis and Modeling of Calendar Aging and Cycle Aging of LiCoO2/Graphite Cells. J. Therm. Sci. 2024, 33, 1109–1118. [Google Scholar] [CrossRef]
- Gantenbein, S.; Schönleber, M.; Weiss, M.; Ivers-Tiffée, E. Capacity Fade in Lithium-Ion Batteries and Cyclic Aging over Various State-of-Charge Ranges. Sustainability 2019, 11, 6697. [Google Scholar] [CrossRef]

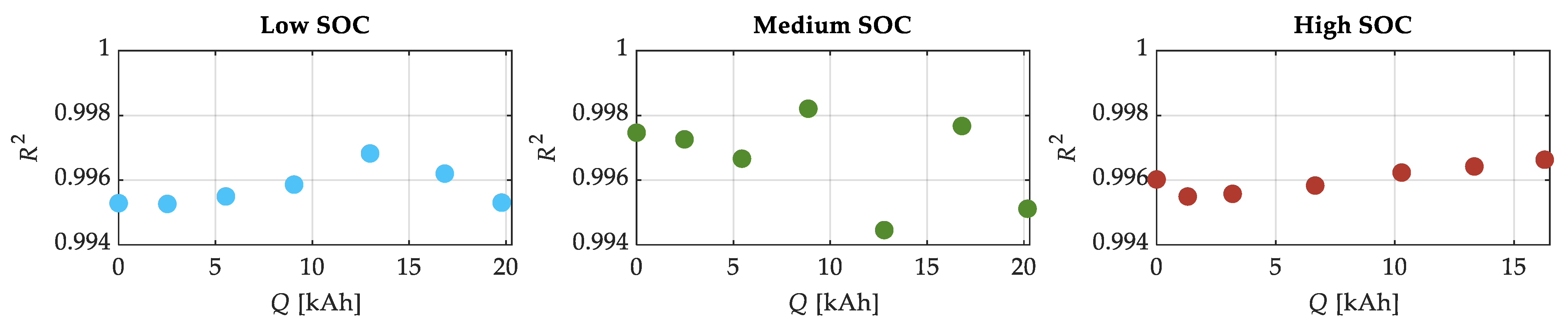
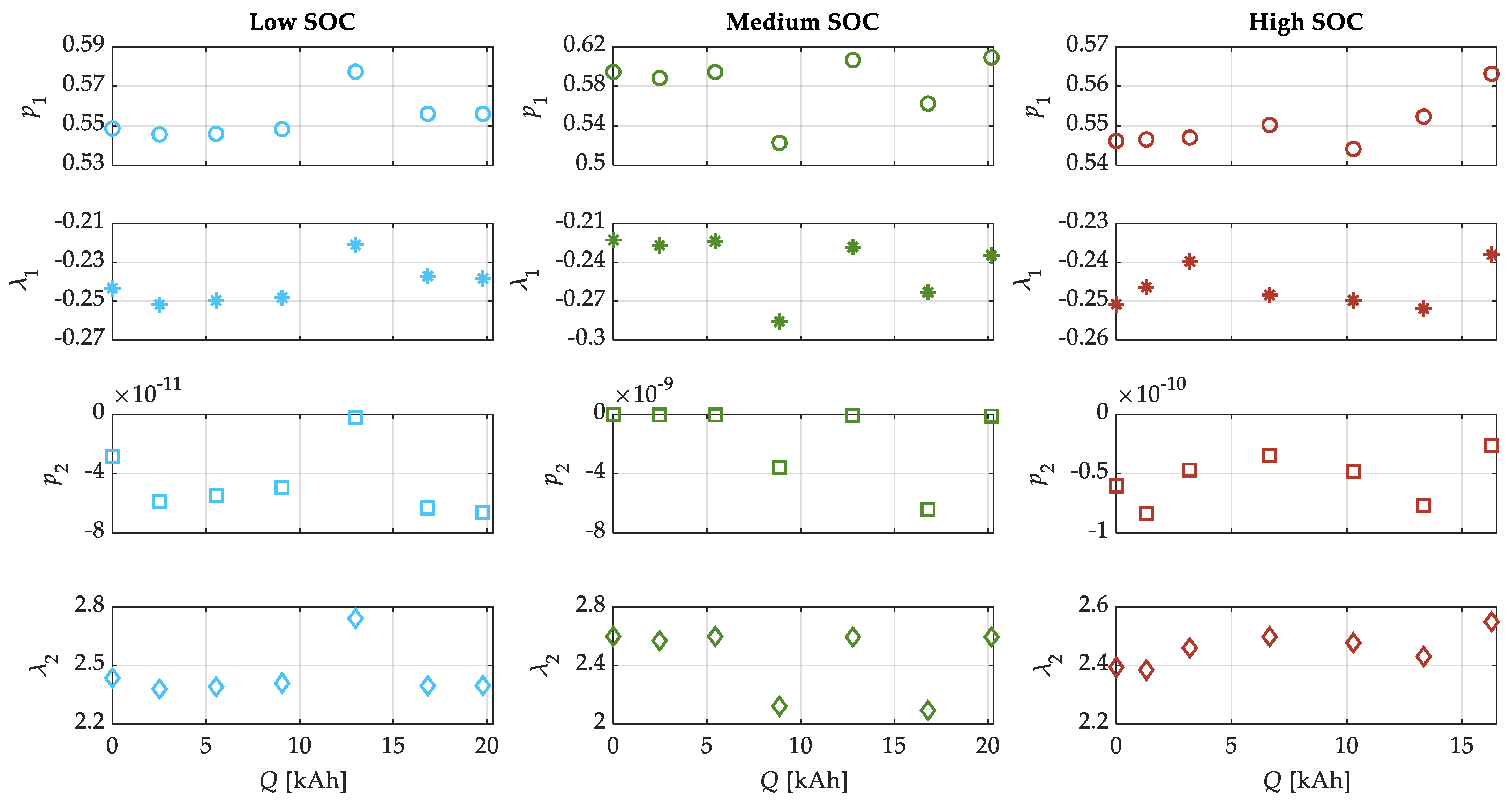
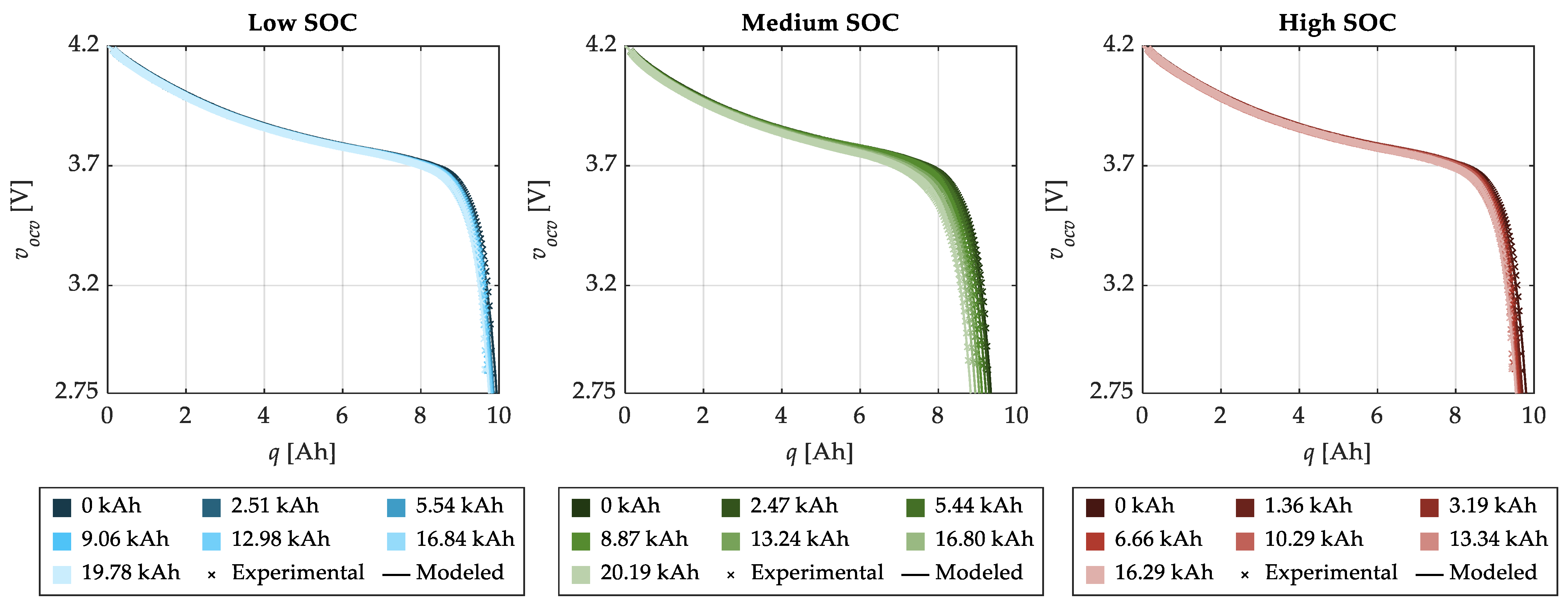

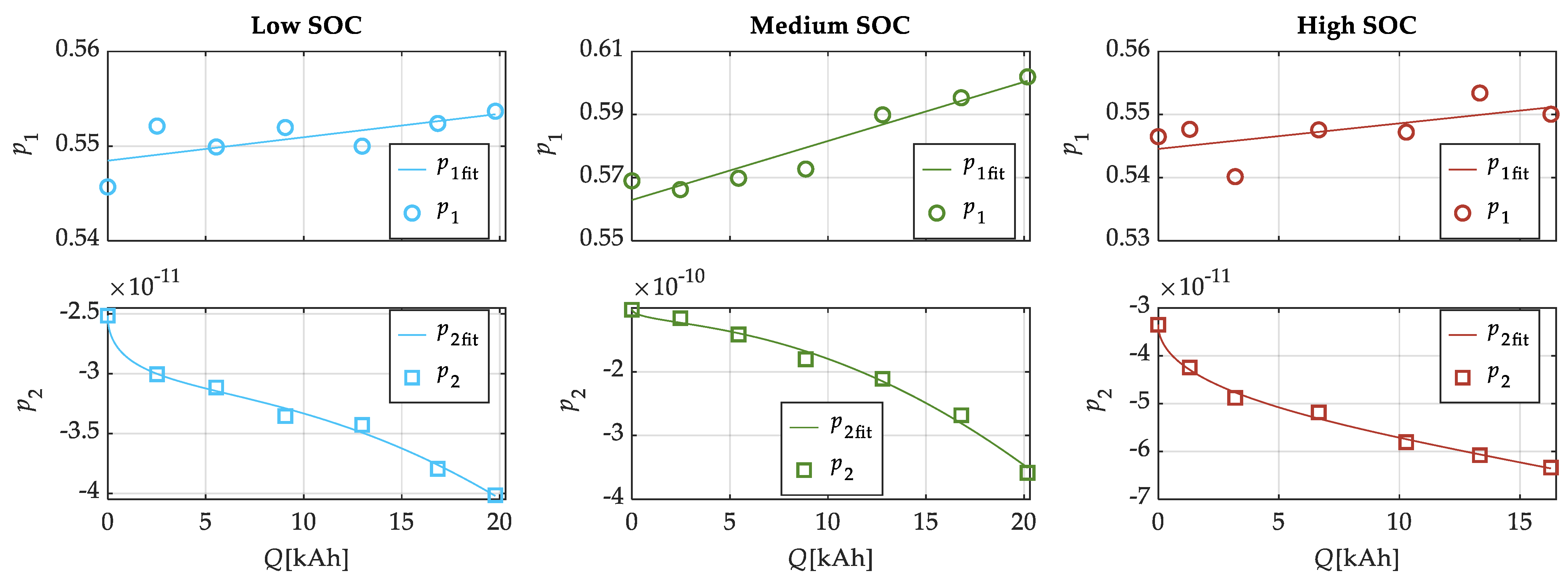
| SOC Level | Low SOC | Medium SOC | High SOC |
|---|---|---|---|
| λ1 [1/Ah] | −0.2413 | −0.2407 | −0.2464 |
| λ2 [1/Ah] | 2.451 | 2.454 | 2.457 |
| SOC Region | Low SOC | Medium SOC | High SOC |
|---|---|---|---|
| [V/Ah] | 2.479 × 10−7 | 1.872 × 10−6 | 4.05 × 10−7 |
| [V] | 0.5485 | 0.5629 | 0.5446 |
| [V/Ah0.5] | −1.39 × 10−13 | −5.408 × 10−13 | −2.831 × 10−13 |
| [V/Ah2] | −3.537 × 10−20 | −5.997 × 10−19 | −1.519 × 10−20 |
| [V/Ah] | 9.251 × 10−16 | 3.569 × 10−15 | 6.185 × 10−16 |
| [V] | −2.514 × 10−11 | −1.014 × 10−10 | −3.348 × 10−11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barcellona, S.; Codecasa, L.; Colnago, S.; Piegari, L. Open-Circuit Voltage Variation in LiCoO2 Battery Cycled in Different States of Charge Regions. Energies 2024, 17, 2364. https://doi.org/10.3390/en17102364
Barcellona S, Codecasa L, Colnago S, Piegari L. Open-Circuit Voltage Variation in LiCoO2 Battery Cycled in Different States of Charge Regions. Energies. 2024; 17(10):2364. https://doi.org/10.3390/en17102364
Chicago/Turabian StyleBarcellona, Simone, Lorenzo Codecasa, Silvia Colnago, and Luigi Piegari. 2024. "Open-Circuit Voltage Variation in LiCoO2 Battery Cycled in Different States of Charge Regions" Energies 17, no. 10: 2364. https://doi.org/10.3390/en17102364
APA StyleBarcellona, S., Codecasa, L., Colnago, S., & Piegari, L. (2024). Open-Circuit Voltage Variation in LiCoO2 Battery Cycled in Different States of Charge Regions. Energies, 17(10), 2364. https://doi.org/10.3390/en17102364







