Abstract
Location is crucial when it comes to reducing the energy demand of buildings. Deterministic mathematical models of the energy demand of a single-family building were developed for the cities of Wrocław and Suwałki, representing the mild and severe climatic conditions of Poland, respectively, and compared with energy demand for Białystok, representing medium conditions. Models include the windows area, heat transfer coefficient, solar radiation transmittance of glazing, and orientation of windows. For medium conditions (Białystok), the energy demand is 18.3% higher than for mild conditions (Wrocław) and 7.3% lower than for severe climate conditions (Suwałki). Location does not influence the nature of the effect of the factors on energy demand, which increases with an increase in heat transfer coefficient and a decrease in window area, glazing solar radiation transmittance, and orientation change from north to south. The large impact of solar gains was proved. The optimisation procedure was performed and mathematical descriptions of recommended parameters were created to ensure the equivalent energy efficiency of windows for each orientation and location. For Bialystok, north-facing windows can have an area 1.32 times larger and south-facing windows 1.48 times smaller than east-facing windows to ensure a building’s energy demand remains constant.
1. Introduction
The world’s building sector accounts for 40% of final energy consumption and 36% of greenhouse gas emissions [1]. Considering that up to 75% of buildings are energy inefficient, there is great potential to introduce activities in the building sector that will result in reducing the consumption of primary energy from fossil fuels, and thus contribute to decarbonisation.
In order to reduce the negative impact on the environment, various scenarios are being studied, the aim of which is to indicate what actions should be taken to achieve the desired degree of decarbonisation of the building sector in the future. Zhang et al. [2], as a result of simulations with the method of decomposing structural decomposition (DSD) and the Monte Carlo method, indicated the most important actions that can reduce CO2 emissions. These include a nationwide increase in the share of clean energy and investing in building-integrated energy sources (e.g., PV). It is also necessary to increase the level of electrification of households [3], which will enable an increase in the use of renewable energy sources, including heat pumps and energy storage facilities.
Many authors [2,3,4] also emphasised the role of the end-up activities in the process of intensifying the decarbonisation process. Important factors include patterns of operation of heating, cooling systems, and domestic hot water (e.g., usable temperature, use of local temperature control—thermostats), lighting, way of cooking, and equipping the building with appliances. The impact of these factors on the intensification of the decarbonisation process strictly depends on the household expenditure index, the household expenditure-related energy intensity of the current end-use structure, and the ratio of energy use from fossil fuels (emission factors) and household size [3]. The potential for decarbonisation is also influenced by the economic situation of the country, including GDP per capita [5], as well as the degree of urbanisation and population size [6].
Zhang et al. [2] emphasised that the greatest ratio of decarbonisation can be achieved by introducing improvements in heating systems and appliances. The results of Yan et al.’s research [3] also indicate the important role of building heating and, additionally, water heating systems. As Lee and Song [4] pointed out, heating is mostly influenced by the physical factors of the building.
The building energy balance depends in particular on architectural factors, construction, technical equipment, climatic conditions, and indoor air parameters. In terms of architecture, the shape of the building and its compactness, the arrangement of rooms in the building, and its orientation are crucial [7]. With regard to construction, the influence of airtightness and building technology has been proved [8]. For technical equipment, the energy consumption is influenced by the heating, ventilation, and air conditioning systems used, the type of heating/cooling source, the presence of a building management system, and systems for automatic control and regulation. One of the most important aspects is the thermal properties of buildings’ insulation, which determine the amount of heat transferring to the envelope, both in the form of energy losses and energy gains. In addition, the level of thermal protection affects the thermal comfort of the occupants and the thermal and moisture characteristics of the envelope.
There is a dualism in Polish legislation regarding thermal insulation requirements for residential buildings. The requirements to be met by new buildings relate to the maximum allowable value of the heat transfer coefficient Umax of the building partitions and the value of the primary energy demand EP [9]. Both parameters are strongly dependent on the thermal resistance of the insulation, as well as the technology of the transparent partitions, i.e., the windows.
Windows represent a critical part of the building envelope. This is due to high values of heat transfer coefficients in comparison with nontransparent partitions [10]. Simultaneously, windows affect the magnitude of heat losses and gains [11]. In modern buildings, windows are designed to have a large surface area relative to the surface area of the building envelope, even though there is no energy justification for this. This increases their share of the energy balance of the building [12]. Windows can be responsible for up to 45–50% of the total heat losses through the building envelope [11,13,14].
Windows also affect the comfort of building occupants by providing access to natural light, fresh air, and views, which are essential for physical and mental health [15]. Properly sized windows, taking into account solar conditions, reduce the number of hours of artificial lighting, which brings health benefits, while reducing the energy demand to power building lighting [16]. Pathirana et al. [7] showed that using the optimal window area relative to the envelope area resulted in changes of 1.5–9.5% in electricity consumption for lighting in residential buildings. Too much glazed area in offices can have a negative impact on occupant comfort as a result of too much sunlight for many working hours, uncomfortable lighting, and too much heat gain [17].
When analysing how windows contribute to building energy needs, it is important to mention the parameters related to the window construction, including the thermal transmittance [11], which depends on the insulation of the glazing and the frame [14]. Also relevant are the type and quality of installation [18], airtightness [13], and the use of shading elements [19]. Of particular importance is the position of windows in relation to the thermal insulation layer and the resultant thermal bridging, which can significantly affect the ratio of heat losses. Heat losses through thermal bridges around the windows can account for up to 40% of all heat losses through thermal bridges in a building [20].
An important window parameter that affects the thermal transmittance is the type and number of glazing units. The most common commercial solution is double glazing, with the cavity filled with a gas to improve the thermal properties of the window, such as argon [21] or krypton [22]. Increasing energy efficiency requirements for buildings have forced manufacturers to use triple glazing to achieve thermal transmittance values of up to 0.5 W/m2K [22]. A study by Djamel and Noureddine [12] for the climate of southern Algeria found that the use of double- and triple-glazed windows can significantly reduce energy consumption in office buildings. Similar conclusions were reached by Aste et al. [17], who determined that the use of triple glazing is extremely important in cold climates and contributes to lower building energy consumption. For the climate of Poznań, Poland, Błaszkiewicz and Kneblewski [23] showed that increasing the number of glazings reduces heat gains in summer. Thalfeldta et al. [24] studied triple, quadruple, and quintuple glazing, concluding that the greatest changes in a building’s cooling and heating demand occur when triple and quadruple glazing are used. In industrial buildings, an interesting solution is the vacuum tube window technology presented by Cuce and Riffat [25], which reduces a window’s heat transfer coefficient to 0.40 W/m2K, making this product competitive with the commercial solution of double-glass windows with argon filling. The disadvantage of this solution is the limited transparency of the window.
In addition to the number of glazing units, the type of glazing is also important. Kumar et al. [26] studied how parameters of glazing influence the building energy demand for five cities in India, representing cold, moderate, warm–humid, hot–dry, and composite climates. The analysis considered clear, bronze, green and bronze-reflective glazing, which differ in their spectral properties (solar transmittance and reflectance). It was found that using clear glass, which is most transmissive, compromises a building’s energy efficiency. Yoo et al. [27] showed that the use of double-skin windows, superwindows, or single- and double-low-e-coated windows instead of standard windows reduced the energy demand of the building by 15.2 to 19.2%.
One of the more interesting design solutions are so-called ‘smart windows’, which have the ability to change their optical properties to adapt to temporary climatic conditions. These windows can reduce a building’s heating, cooling, and lighting energy requirements compared with standard window solutions, but they usually require a very large investment [28]. As a result, this technology is often used in commercial buildings with large areas of glazing, where the benefits of using smart technology can compensate for the investment [29]. The change in light transmission of smart windows is due to the interaction of light, heat, or electricity [28]. One type of smart window is thermochromic, which changes from a transparent to a translucent or opaque state under solar radiation. This blocks the inflow of solar radiation and reduces the heat exchange between the building and the environment [30]. Other smart technologies cover electrochromic windows [31,32], gasochromic windows, microblinds, or liquid crystal glazing [28]. Different coatings are used in smart windows to modulate solar radiation, e.g., vanadium dioxide (VO2) thin films, sol–gel-synthesised titania–vanadium nanocrystalline films [33], Fe3O4 nanoparticles [34], or a mixture of adhesives and silica [35].
One of the key parameters with an impact on the level of heat losses or gains through windows is their size. However, the contribution of windows to the thermal balance of a building strongly depends on the window-to-wall ratio (WWR). This coefficient is closely related to the orientation of the windows, which determines the optimal window size [36]. The tilt angle of the windows is also important [23].
The influence of window size and WWR ratio on the building energy demand is closely related to the climatic conditions of the building’s location. In cold climates, the main concern is to reduce heat losses, while taking advantage of solar heat gains. For this reason, windows with a larger area are located on the south side, while window area is minimised on the north side [37]. In warm climates, on the other hand, the orientation and size of windows are chosen to minimise excessive heat gains and reduce the cooling load [17].
The orientation of windows and their window-to-wall ratios have been the subject of many research papers.
Djamel and Noureddine [12] analysed how the change in window orientation and WWR ratio (25, 50, 75, and 100%) influences the energy demand of office buildings located in southern Algeria. Based on simulations in EnergyPlus software version (8.4.0), they found that increasing window area increases the heating and cooling load. Sudan et al. [38] studied the effect of the ratio of window glazing area to floor area on the potential of energy demand reduction for different climatic conditions in India. The higher the WWR ratio, the higher the heat losses. This relationship has also been confirmed by Poirazis [39], who analysed the WWR ratio in an office building located in the cold climate of Gothenburg.
Alghoul et al. [40] used EnergyPlus software to study the effect of a change in WWR ratio and window orientations on energy demand in an office building in Tripoli, Libya. It was found that the addition of windows to the facade increases the total energy demand from 6 to 181%, depending on the orientation and window area. The analysis also confirmed that the WWR ratio contributes more to the cooling demand than to the heating demand.
Feng et al. [41] pointed out the need to optimise the WWR ratio, especially in near-zero-energy buildings. The analysis was carried out for an office building for the climatic conditions of the severe cold city of Shenyang, China, and showed that the most optimal WWR is 10–15% for the east (west) elevation and 10–22.5% for the south elevation. The WWR in the north orientation should be as low as possible, taking into account the need for daylight and ventilation. The optimal WWR values determined by Feng et al. [41] are only valid for the climatic conditions analysed. A review of the literature in this area confirms that the optimal WWR value is highly dependent on the climate. For example, in the cold conditions of Lithuania, the optimal WWR value for an air-conditioned office building was 20% for a south orientation and 20–40% for a north orientation [42]. Alwetaishi [43], for an educational building in Saudi Arabia, indicated that the most energy-optimal WWR is 10%.
As can be noticed, a large part of the research in this field is focused on office buildings. This is due to the fact that they are usually characterised by a very high proportion of windows on the facade, and at the same time, changes to the windows have the greatest impact on energy consumption. Residential buildings were also studied. One example is the analysis by Pathirana et al. [1] for a building located in the tropical hot and humid climate of Sri Lanka. Another is the analysis of the WWR ratio in passive solar houses in the Qinghai–Tibet region [44]. The authors concluded that the determination of the optimal WWR should always be based on the climatic conditions of the location, due to the variability of important parameters such as solar radiation. Błaszkiewicz and Kneblewski [23] also emphasised the need to carry out analyses for each building individually.
The majority of the analyses presented on the impact of windows are related to climate zones other than Poland. In addition, the vast majority of the analysis concerns office buildings. Office buildings differ from residential buildings in terms of permissible indoor air temperatures and, above all, in terms of requirements for ventilation airflow. Therefore, the results presented in the literature for office buildings are not applicable to residential buildings.
A number of directions for further research can be identified from the literature review. First of all, window technologies should be developed to achieve the lowest possible heat transfer coefficients. At the same time, attention should be paid to the glazing parameters, which affect the transmittance of solar radiation, thus influencing undesirable heat gains in the summer and desired gains in the heating season. The literature review shows that windows are a critical part of the building envelope. Due to the higher values of heat transfer coefficients compared with the opaque part of the building envelope, their surface area is extremely important—the larger it is, the more negative of an impact it has on the heat load or cooling demand. Taking into account the above, it should be noted that when analysing the impact of windows on the energy consumption of the building, many parameters should be analysed simultaneously, as they are interdependent.
Based on the literature review, there is also a need to perform more research on single-family houses due to their significant share in the final energy consumption. As highlighted by many researchers, it is also important to analyse the impact of window parameters on energy demand depending on the location of the building.
As a response to the current knowledge gap, a multicriteria analysis of the impact of window parameters on the energy consumption of a single-family building was carried out, taking into account the variability of climatic conditions.
The aim of this case study is to optimise the main parameters characterising the energy demand of a single-family building in Polish climatic conditions according to the energy criterion. This was conducted by analysing the dependence of the usable energy demand of a model building on the window surface area, heat transfer coefficient, solar radiation transmittance of glazing, and orientation. In order to fill the existing research gap, the ratio of the interaction between the analysed factors was determined.
This work applies a deterministic mathematical model with polynomial functions to describe the influence of the analysed parameters on the output value and to determine the nature of the interactions between them. Metamodeling with polynomial functions is one of the methods used to assess the energy demand and consumption of buildings. This method allows a quick sensitivity analysis or optimisation of the parameters studied, without the need to carry out a very large number of simulations [45]. Examples of the use of this method can be found in many publications. Asadi et al. demonstrated the usefulness of the multilinear response method for determining the energy demand in commercial buildings [46] and for attics in single-family buildings [47] at the early stages of their design. Romani et al. [48] developed and validated a metamodel for determining the heating and cooling load for low-energy buildings. The authors emphasised the advantages of using the design of the experiment method as a method reducing the number of simulations necessary to perform. Hester et al. [49] proposed a regression-based energy metamodel as a tool supporting the selection of parameters to ensure the lowest possible thermal energy consumption in the building. Jaffal and Inard [50] developed a general model with the use of a polynomial function to determine the building energy performance. The proposed model allows for taking into account a large number of parameters (including interactions between building components, as well as CO2 emissions and energy prices) and is characterised by high compliance with the results of dynamic simulations (R2 approximately 1). Novel et al. [51] used a second-degree polynomial to estimate the monthly energy heating and cooling load in cultural buildings. The authors demonstrated the usefulness of the metamodel for determining energy consumption depending on how buildings are used and HVAC operating parameters.
This article is an extension of the authors’ previous research on the city of Białystok, including the determination of the influence of window parameters and orientation on the coefficient of the usable energy demand of a single-family building [52,53]. Compared with previous publications, this article extends the analysis to other representative cities in Poland: Wrocław (mild climatic conditions) and Suwałki (severe climatic conditions). For the first time, it was planned to introduce the concept of a window with equivalent energy efficiency. Based on the three deterministic mathematical models developed, the authors created mathematical descriptions of the recommended parameters ensuring the equivalent energy efficiency of building windows in different locations.
2. Materials and Methods
2.1. Characteristics of a Model Residential Building
A two-storey building with a compact shape, a floor area of 165.53 m2, and a cubature of 446.93 m3 was used for the analysis. The building was constructed using traditional brick technology. The plans of the building, cross-section, and the values of the heat transfer coefficients of the partitions are presented in Figure 1. Natural ventilation was used to determine ventilation heat losses. Air supply was provided by hygro-controlled vents in the windows, while exhaust was provided by ventilation ducts in the kitchen and bathrooms. A gas boiler was used as the heat source for heating and preparing domestic hot water. Number of residents in the building—4. For research purposes, the concept of arranging 6 windows only on one facade was adopted [52,53].
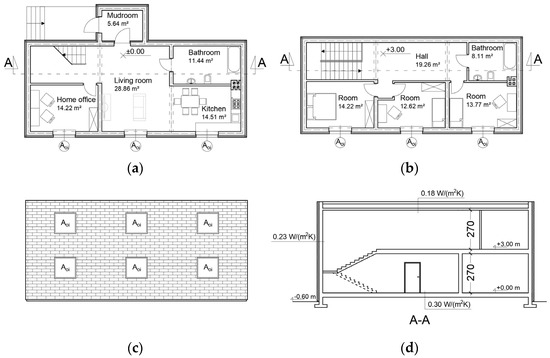
Figure 1.
Scheme of a model building: (a) ground floor plan; (b) first-floor plan; (c) glass elevation; (d) cross-section with heat transfer coefficient values of building partitions [52,53].
2.2. Mathematical Model of the Annual Usable Energy Demand in Single-Family Building
As a research method, mathematical modelling was adopted. This method uses mathematical relationships to describe the operation of the analysed object, determine the output parameters, and determine the optimal values of the object’s input parameters. Mathematical modelling makes it possible to dispense with physical modelling and reduces the number of samples and the research effort in comparison with a physical experiment [54]. The main component of such a system is the mathematical model. The usefulness, effectiveness, and practicality of a mathematical model can be ensured by developing short models that use the key factors that define the properties under investigation and provide information of interest to the recipients.
In accordance with the aim of this study, the annual usable energy demand for heating and ventilation in the building QH,nd [kWh/a] was selected as the objective function Y. The energy demand was calculated as the sum of the demands QH,nd,s,n for each of the s heated zones in the building and for each of the n months of the year. The QH,nd,s,n value was calculated taking into account heat losses and gains according to the Formulas (1)–(5) [55]:
where QH,ht,s,n is total heat transferred from the heated zone s in the n-th month of the year, QH,gn,s,n is total heat gains in the heated zone s in the n-th month of the year, and the ηH,gn,s,n coefficient is for the use of heat gains in the heated zone s in the n-th month of the year.
where Qtr,s,n is the total amount of heat transferred from the heated zone s by transmission in the n-th month of the year; Qv,e,s,n is the total heat transferred from the heated zone s by the ventilation in the n-th month of the year.
where Qsol,H is the monthly heat gains from solar radiation through windows and glazed surfaces; Qint,H is the monthly internal heat gains.
where Ci is the proportion of the glazing area to the total window area; Aoi is the surface area of windows; Ii is the radiant energy of the sun falling on a plane with a window in a given month; Fsh is the reduction coefficient due to shading from the building envelope; ggl is the solar radiation transmittance of the glazing.
where tm is the number of hours per month; qint is the internal heat load of the room; Af is the heated area of the building.
QH,nd,s,n = QH,ht,s,n − ηH,gn,s,n∙QH,gn,s,n,
QH,ht,s,n = Qtr,s,n + Qv,e,s,n,
QH,gn,s,n = Qsol,H + Qint,H,
Qsol,H = ∑Ci Aoi Ii Fsh ggl,
Qint,H = qint Af tm,
Based on Formulas (1)–(5) and the methodology in [54], the authors created an algorithm for calculating the required energy demand (Figure 2) by changing the values of each factor, which was used as a basis for developing an original computer program in Microsoft Excel.
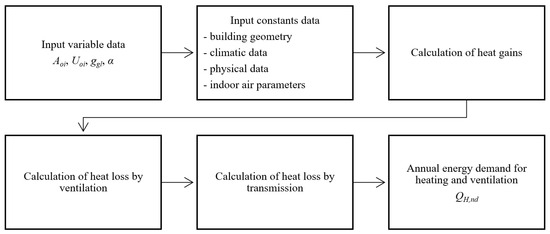
Figure 2.
Block diagram of QH,nd calculations.
The aim of this study is to determine the dependence of the annual usable energy demand for heating and ventilation QH,nd (Y) for the variable building location on four factors characterising the windows: surface area Aoi [m2] (factor X1), heat transfer coefficient Uoi [W/(m2K)] (factor X2), total solar radiation transmittance of the glazing ggl [-] (factor X3), and orientation of the windows α [°] (factor X4). All selected factors are controllable, measurable, independent, clear, and consistent, so they meet the requirements of mathematical modelling [56]. Climatic conditions cannot be included in the model as a fifth factor because they are represented as a set of different parameters (Table 1) [57], which are difficult to describe by a single factor. For this reason, mathematical models were developed separately for each of the climatic conditions analysed.

Table 1.
Average climatic characteristics in selected cities of Poland [57].
It was assumed that the desired relationship Y = f(X1,X2,X3,X4) can be described by a second-degree algebraic polynomial in the form of (6):
Y = a0 + a1×1 + a2X2 + a3X3 + a4X4 + a12X1X2 + a13X1X3 + a14X1X4 + a23X2X3 + a24X2X4 + a34X3X4 + a11X12 + a22X22 + a33X32 + a44X42
In order to obtain data to describe the relationship (6), a 4-factor computational experiment was conducted according to the second-stage plan (Table 2). A compositional symmetric three-level D-optimal design containing 24 trials was applied [58]. An original program in Microsoft Excel was developed to calculate the Yi value in the 24 lines of the plan.

Table 2.
Natural Ẋi and normalised Xi values of selected factors [52,53].
The calculation method requires the assumption of the range of variability of the analysed window parameters. This was determined by three levels (natural values for Ẋi factors). The levels are characterised by Xi normalised values as −1 (lower level), 0 (middle level), and 1 (upper level). Specific values of the analysed parameters were assigned to each level, i.e., the area of a single window (X1 factor), the window heat transfer coefficient (X2 factor), the total solar radiation transmittance of the glazing (X3 factor), and the window orientation (X4 factor). In the analysis, the authors assumed that there is no correlation between the total solar transmittance of the glazing and the value of the U-coefficient of the window, which makes it possible to extend the analysis to the search for optimal window parameters.
Due to the method used to plan the experiment, it was necessary to adopt an equal number of levels for each of the analysed factors. For this reason, the western orientation was eliminated from the analysis, assuming that its effect is close to the eastern orientation. The remaining input variables, i.e., geometric parameters of the building, physical properties, and characteristics of the heat source, were assumed constant.
The conversion from natural Ẋi to normalised Xi values of factors according to [56] is expressed by the Formula (7):
where Ẋi, Ẋimax, Ẋimin are the current, maximum, and minimum natural values of the i-th factor, respectively [59].
Xi = [2 Ẋi − (Ẋimax + Ẋimin)]/(Ẋimax − Ẋimin),
The natural and normalised values of the factors analysed are given in Table 2.
For the assumed levels of variability of the factors, calculations were made for the usable energy demand. The results for Suwałki, Wrocław, are presented in Table 3. For comparison, the results for Białystok are also presented.

Table 3.
Planning matrix and calculation results QiH,nd (the numerator represents the natural values of the factors, in the nominative—standardised).
In order to validate the correctness of calculations of usable energy demand with the original program, ArCADia software version 10 was used, which is software that is known and used in Poland, based on the procedures used in Poland for calculating the heat demand of buildings. Validation was performed for variants no. 1, 10, and 20, taking into account three building locations, for which the range of factor variability is presented in Table 3. The validation results are presented in Figure 3. It was found that the calculated values of usable energy demand are close to the values determined with the ArCADia software (maximum difference of up to 3%). Hence, the data presented in Table 3 can be used in further mathematical modelling processes.
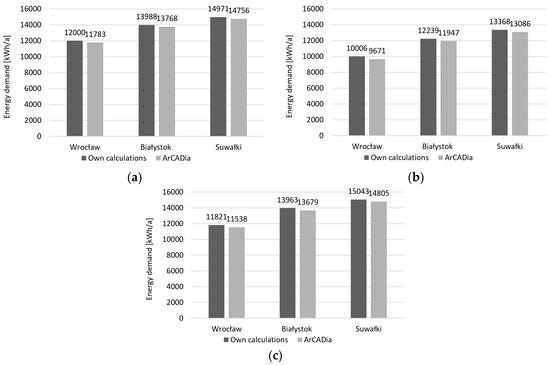
Figure 3.
Comparison of usable energy demand QH,nd calculated with the Microsoft Excel program and ArCADia software: (a) variant no. 1; (b) variant no. 10; (c) variant no. 20 according to Table 3.
Based on the calculation results (Table 3) and applying the method of least squares [60], three models were derived in the form of regression equations Y = f(X1,X2,X3,X4):
for Wrocław (8):
and for Suwałki (9):
ŶI = 11,386.12 − 522.43X1 + 435.56X2 − 349.98X3 − 502.69X4 + 137.70X1X2 − 102.98X1X3 − 160.26X1X4 − 4.49X2X3 − 3.57X2X4 − −66.59X3X4 + 32.35 X12 − 0.31X22 + 8.17X32 − 198.31X42,
ŶIII = 14,534.30 − 400.20X1 + 514.10X2 − 319.99X3 − 377.61X4 + 159.23X1X2 − 85.19X1X3 − 109.48X1X4 − 4.62X2X3 − 4.01X2X4 − 54.41X3X4 + 46.08 X12 − 2.93X22 + 7.88X32 − 131.32X42.
The model developed for Bialystok, which is the basis for comparing the results for the climatic conditions of Wrocław and Suwałki, is presented in the author’s Equation (10) [53]:
ŶII = 13,472.08 − 450.83X1 + 493.24X2 − 333.49X3 − 416.63X4 + 155.05X1X2 − 96.50X1X3 − 128.84X1X4 − 5.88X2X3 − 5.50X2X4 − 49.89X3X4 + 34.90 X12 − 5.18X22 + 11.05X32 − 122.89X42.
Deterministic models are characterised by a mutually unambiguous agreement between the external impact and the response to that impact. This was considered when testing the models [59]. At each point in the plan, only one experiment was performed. In the absence of repetitions and measurement imprecision variance, the adequacy of the resulting equation was evaluated by comparing the variance of the mean S2y and the residual variance S2r determined from Formulas (11) and (12) [60]:
where N is the number of calculations performed, and Nb is the number of coefficients in the regression equation.
S2y = Σ(Yi − Ȳ)2/(N − 1),
S2r = Σ(Ŷi − Yi)2/(N − Nb),
Fisher’s criterion was used for verification, which describes how much the spread is reduced with respect to the regression equation compared with the spread with respect to the average (13) [60]:
where f1, f2 are the number of degrees of freedom; f1 = (N − 1) = 24 − 1 = 23; f2 = (N − Nb) = 24 − 15 = 9.
F = S2y(f1)/S2r(f2),
The regression equation adequately describes the results of the calculation if the F value is significantly greater than the tabular value Ft at the significance level p and degrees of freedom f1 and f2, in the analysis Ft = F0.05; 23;9 = 2.910 [60]. The calculated F value of model (8), developed for Wrocław, is 351.840, and for model (10), for Suwałki, FIII = 434.465. For model (9), for Białystok, FII = 635.739 [40]. Since the values of FI, FII, and FIII are many times greater than Ft, the developed models are adequate. This is also confirmed by the values of the coefficient of determination R2, which for the three designated models are in the range of 0.9989–0.9994.
The t-criterion was then used to verify the significance of the coefficients of Equations (8)–(10). Since, at each point of the plan, we have one result without repetitions, the methodology proposed in [60] was applied. As a result, the following parameter was calculated for each coefficient (14):
where bj is the values of the coefficients of the regression equation; Sbj is the standard deviation of the j-th coefficient.
tj = |bj|/Sbj,
The residual variance Sr2 based on the sum of squared deviations (Ŷi − Yi)2 was used to determine Sbj. The values of tj were compared with the critical value t0.05;9 = 1.83 [60]. At tj < t0.05;9, the coefficient is considered insignificant. The final form of Equations (8)–(10) was adopted with k + 1 = 15 coefficients. The results confirm the models’ adequacy; thus, the models can be used for further analysis.
3. Results and Discussion
3.1. Analysis of the Impact of Window Parameters on Usable Energy Demand
The analysis of the impact of four factors on the usable energy demand QH,nd of the considered building under selected climatic conditions was carried out on mathematical models (8)–(10). For better understanding, the discussion of the results was made on natural variables of the factors. It should be noted that the word combinations ‘favourable effect’ or ‘favourable factor’ used hereafter mean that with a change in factor from a lower to an upper level, the value of usable energy QH,nd was decreased. The effect or factor is unfavourable if the QH,nd was increased. In the optimisation, parameter values were sought to ensure a minimum usable energy requirement QH,nd.
Analysing the developed models for varying climatic conditions, it was detected that in the centre Gp of the multifactor space, which is characterised by coordinates corresponding to the average level of the factors, namely window area Aoi (X1) = 2.73 m2; window heat transfer coefficient Uoi (X2) = 0.80 W/(m2K); total solar radiation transmittance of glazing ggl (X3) = 0.6 [-]; and window orientation α (X4) = 90°, the magnitudes of the usable energy demand QiH,nd of the considered building for selected groups of climatic conditions are as follows: for Wrocław (I group), QI, H,nd = 11,386, and for Suwałki (III group), QIII, H,nd = 14,534 kWh/a. For Białystok (II group), the demand is 18.3% higher than that of Wrocław and 7.3% lower than that of Suwałki. At the same time, it can be observed that a change in climatic conditions from the mildest to the most severe results in an increase in the energy demand of the same building by as much as 27.6%. This is due to changes in climatic indicators, mainly solar radiation (Table 1), which is the highest in Wroclaw and the lowest in Suwałki. As it can be observed, the approach to ensuring the thermal protection of buildings cannot be the same for the whole of Poland but must vary, taking into account the climatic conditions of the building’s location.
The influence of each factor on the value of the usable energy demand of the building in the locations analysed was then estimated. In each model, the degree of their influence varies greatly. When the selected factors are changed from the lower to the upper level (Table 2), the value of QiH,nd fluctuates significantly: it increases with an increase in the factor Uoi (X2) and decreases with an increase in the factors Aoi (X1), ggl (X3), and α (X4). The calculated ∆QiH,nd effects (natural and percentage) of the factors for the climatic conditions of Wrocław and Suwałki are given in Table 4. For comparison, Table 4 also shows the effects for Bialystok.

Table 4.
Effects ∆QiH,nd when changing the factors Aoi (X1), Uoi (X2), ggl (X3), α (X4) from the lower to the upper level in various climatic conditions.
The analysis of the results from Table 4 allows us to conclude that increasing the window area Aoi from 1.82 to 3.64 m2 causes a decrease in QiH,nd, which also depends on the group of climatic conditions. The largest decrease of −8.75% was detected in mild conditions (Wrocław) and the smallest of −5.3% in severe conditions (Suwałki). The nature of the influence of the Aoi factor confirms the important role of heat gains from solar radiation in the energy balance of the analysed building.
Then, it was found that increasing the heat transfer coefficient of windows Uoi from 0.50 to 1.10 W/(m2K) increases QiH,nd and has the only unfavourable effect among the factors considered. The natural values of this increase vary greatly in different climatic conditions, but the percentage increase in all locations is approximately 7–8%. Conversely, it was found that increasing the total solar radiation transmittance of the glazing ggl from 0.5 to 0.7 [-] reduces the energy demand QiH,nd. In the considered climatic conditions, the effect of this factor ranges from −4.3% (Suwałki) to −6.0% (Wrocław).
Changing the orientation of windows according to the sides of the horizon α from 0 to 180° also reduces QiH,nd, with the highest beneficial effect in group I of climatic conditions (Wrocław). The effects of this factor in the selected locations range from −5.1 to −8.6%.
The total effect of changes from the lower to the upper level of all factors simultaneously causes a significant decrease in QiH,nd for the considered building: from 7.8% for the mildest climatic conditions to −15.7% for the most severe of the analysed climatic conditions. In relation to the mild climate (Wrocław), the total beneficial effect increased by 21.3% for the medium climate of Białystok and by 60.9% for the severe climate of Suwałki.
It was noticed that in models (8)–(10), the signs of the coefficients are the same for all selected locations. This means that climatic conditions did not change the nature of the influence of the factors considered, but they did significantly change the magnitude of that influence.
For professionals, the most valuable is information about co-interactions of factors. Analysing the signs and values of the coefficients for double interactions in models (8)–(10), the following regularities were found, which apply directly to these three models.
With regard to the Aoi (X1) factor, it was found that the favourable negative effect of this factor weakens with an increase in the Uoi (X2) factor but strengthens with an increase in ggl (X3) and α (X4). At the same time, for the factors ggl (X3) and α (X4), there is a phenomenon of synergism with the factor Aoi (X1), as each of them, when increased together, has a stronger effect than would be the case if they were increased separately.
The large unfavourable positive effect of the factor Uoi (X2) strengthens with an increase in the factors Aoi (X1) but weakens with an increase in ggl (X3) and α (X4).
For the ggl (X3) factor, the favourable negative effect significantly increases with an increase in the Aoi (X1) and α (X4) factors, as these two factors are synergistic with the ggl (X3) factor.
It was also observed that the favourable negative effect of the factor α (X4) in the models increases with an increase in the factors Aoi (X1) and ggl (X3), due to their synergy with α (X4). If each of them is increased together, the effect is greater than if they are increased separately. These described regularities have important practical implications for designers of similar systems, as they reveal internal commonalities between the factors.
At the final stage of this study, an optimisation procedure for selected parameters according to the energy criterion was carried out on models (8)–(10). For the three analysed climatic conditions, the optimal parameter values turned out to be on the border of the factor space of four factors (Table 3). The best energy parameters of the building were obtained for the extreme values of the factors, i.e., the largest assumed area of a single window X1 = +1 (Aoi = 3.64 m2); the smallest value of the heat transfer coefficient X2 = −1 (Uoi = 0.5 W/(m2K)); the largest value of the total solar radiation transmittance of the glazing X3 = +1 (ggl = 0.7); and for the southern orientation X4 = +1 (α = 180°). The results obtained differ for each of the locations analysed.
For the mildest climatic conditions in Wrocław, the usable energy demand is the lowest at YImin = 8927 kWh/a, and for the most severe, i.e., Suwałki, it is the highest at YIIImin = 12,418 kWh/a. The results for Białystok are in between and are 26% higher than the demand in Wrocław and 9% lower than the demand in Suwałki (Table 4). This shows that the optimal values of the considered building parameters in each location turned out to be the same, while the extreme values of the energy demand are significantly dependent on the climatic conditions of the building location.
The maximum usable energy demand for heating and ventilation was also achieved at constant extreme factor values but with their mirror image. This means that the building with the highest energy demand is the one with the smallest window area X1 = −1 (Aoi = 1.82 m2) but with the highest values of the heat transfer coefficient X2 = +1 (Uoi = 1.10 W/(m2K)); the lowest value of the total solar radiation transmittance of the glazing X3 = −1(ggl = 0.5); and the northern orientation of the windows X4 = −1 (α = 0°). The maximum value of the function for the climatic conditions of Wrocław was YImax = 12,606 kWh/m2, and for Suwałki, it was YIIImax = 15,683 kWh/m2. The most unfavourable usable energy demand for Bialystok was 16% higher than that for Wrocław and 6.5% lower than that for Suwałki (Table 4).
As we can see, the spread of maximum and minimum values strictly depends on climatic conditions. The largest dispersion is observed for the mildest of the analysed climatic conditions, i.e., for Wrocław 3679 kWh/a (41.2% compared with the minimum value), and the smallest for Suwałki, 3265 kWh/a (26.3%). Such a large variation in results proves the very diverse contribution of selected factors to changes in the energy demand of the building under consideration in various climatic conditions.
The developed models made it possible to analyse the dependence of the demand for usable energy for heating and ventilation of a single-family building QH,nd on four selected factors, taking into account climatic conditions. Based on the models, the effect of the influence of each factor was estimated, and the optimal values of the analysed window parameters were determined. Note that these factors are the most important and directly affect solar gains because they characterise the properties of windows.
3.2. Analysis of Equivalent Energy Efficiency of Windows
From a practical point of view, in order to ensure the required inside temperature in the building, it makes sense to determine the equivalent energy efficiency of windows for each of their selected orientations. The easiest way to achieve the equivalent energy efficiency of windows is to change their surfaces on different facades. The exact determination of the area of windows of different orientations requires mathematical calculations. A mathematical description of windows with equivalent energy efficiency can be obtained from the obtained models of the dependence of the demand for usable energy for heating and ventilation of a single-family building on selected factors. For example, for Białystok, using the original model (10) and assuming the value QH,nd = 13,472 kWh/a in the Gp centre of the multivariate space, a mathematical description of the recommended window parameters ensuring equivalent energy efficiency of windows was created using appropriate algebraic simplifications (15):
34.90X12 − 5.18X22 + 11.05X32 − 122.89X42 + 155.05X1X2 − 96.50X1X3 − 128.84X1X4 − 5.88X2X3 − 5.50X2X4 − 49.89X3X4 − 450.83X1 + 493.24X2 − 333.49X3 − 416.63X4 = 0.
This description (15) answers the question of what window parameters should be recommended for the selected building in Bialystok, ensuring for each orientation of the windows equal heat losses and gains in the building at a level of QH,nd = 13,472 kWh/a.
The description (15) can be used as an operative tool to estimate window parameters in the building design process taking into account the location and orientation of the building. We now show how to use the presented description.
For example, for the selected building, we assume the heat transfer coefficient of the windows Uoi = 0.80 W/(m2K) (factor X2 = 0); solar radiation transmittance of glazing ggl = 0.6 (factor X3 = 0); and the orientation of the windows according to the sides of the horizon α = 90° (factor X4 = 0). After substituting X2, X3, and X4 into Equation (10) and after performing the appropriate calculations and algebraic simplifications, we received Equation (16), which is already a mathematical description of the recommended values of the window area with the physical parameters defined above and their orientation α = 90°:
34.90X12 − 450.83X1 = 0,
We have a second-degree equation and one unknown, which allows us to determine the value of the unknown: X1(1) = 12.92; X1(2) = 0. The value of X1(1) = 12.92 is outside the range of factor variability, i.e., we take X1 = 0. Using Formula (7), we perform the reverse procedure, and obtain the searched value of the window area: Aoi = 2.73 m2 (1.48 m × 1.84 m). Further, changing the orientation from eastern to northern (X4 = −1) and southern (X4 = 1) and substituting these values into Equation (10), we obtained mathematical descriptions (17) and (18) of the recommended window area values with the physical parameters specified above for north (17) and south (18) orientations, respectively:
34.90X12 − 321.99X1 +293.74 = 0,
Hence, X1 = 1.02. The value of X1 = 1.02 is almost at the limit of the factors’ variability range, i.e., X1 = 1.00. After decoding, this gives Aoi = 3.60 m2 (e.g., 1.48 m × 2.43 m).
34.90X12 − 560.31X1 − 579.67 = 0,
Therefore, X1 = −0.975; after decoding, Aoi = 1.84 m2 (e.g., 1.48 m × 1.24 m).
These area values, together with the other parameters adopted above, ensure the equivalent energy efficiency of windows for each orientation and the same energy demand in the building at the level of QH,nd = 13,472 kWh/a. Therefore, the required design inside temperature will be provided in each room in this building. This can be achieved by increasing the area of the northern windows by a factor of 1.32 and reducing the area of the southern windows by a factor of 1.48 in relation to the area of the windows facing east.
It should be noted that the influence of direct sunlight is large and determines the amount of external gain for different window orientations. This requires a significant adjustment of window sizes. The spread of the values for the north and south window areas for Bialystok is 3.6 − 1.84 = 1.76 m2. Despite the fact that these are opposite elevations, in some cases, this may negatively affect the architectural composition of the building. Therefore, a differentiated approach can be proposed to achieve window parameters of equivalent energy efficiency. The idea is to adjust several window parameters. This will reduce the need to change their area and also reduce their negative impact on the building’s composition. We demonstrate this approach in the example of medium climate conditions of Białystok, using mathematical description (15).
When analysing the northern windows α = 0° (X4 = −1) for the selected building, taking into account the nature of the influencing factors, we proposed the following values: window heat transfer coefficient Uoi = 0.70 W/(m2K) (X2 = −0.3333); glazing total solar transmittance ggl = 0.7 (X3 = +1). When analysing southern windows α = 180° (factor X4 = +1), other factor values were also adopted: window heat transfer coefficient Uoi = 0.90 W/(m2K) (X2 = +0.3333); total solar heat transmittance of glazing ggl = 0.6 (X3 = 0). After substituting X2, X3, and X4 into Equation (15) and performing the appropriate calculations and algebraic simplifications, we have equations that provide a mathematical description of the recommended values of the window area with the physical parameters changed above for their north (19) and south (20) orientations, respectively.
For X2 = −0.3333; X3 = +1; X4= −1:
34.90X12 − 470.16X1 − 143.66 = 0,
Hence, X1 = −0.298; after decoding, Aoi = 2.46 m2 (e.g., 1.48 m × 1.66 m).
For X2 = 0.3333; X3 = 0; X4 = +1:
34.90X12 − 527.98X1 − 377.53 = 0,
Hence, X1 = −0.684; after decoding, Aoi = 2.11 m2 (e.g., 1.48 m − 1.43 m).
According to the calculation results, in the case of correctly selected physical parameters, i.e., the heat transfer coefficient Uoi and solar radiation transmittance of glazing ggl, the area of the north windows can even be reduced by 0.90 times and the area of the south windows reduced by 0.77 times in relation to the area of the east-oriented windows at a constant level of the building’s energy demand QH,nd = 13,472 kWh/a.
In a similar way, based on the obtained models (8) and (10) of the dependence of the usable energy demand for heating and ventilation of a single-family building on selected factors, mathematical descriptions of equally energy-efficient windows for Wrocław and Suwałki were created. Using appropriate algebraic simplifications of models (8) and (9), the mathematical descriptions of the recommended window parameters ensuring equal energy efficiency of windows have the following form:
For Wrocław (21):
32.35X12 − 0.31X22 + 8.17X32 − 198.31X42 + 137.70X1X2 − 102.98X1X3 − 160.26X1X4 − 4.49X2X3 − 3.57X2X4 − 66.59X3X4 − 522.43X1 + 435.56X2 − 349.98X3 − 502.69X4 = 0.
For Suwałki (22):
46.08X12 − 2.93X22 + 7.88X32 − 131.32X42 + 159.23X1X2 − 85.19X1X3 − 109.48X1X4 − 4.62X2X3 − 4.01X2X4 − 54.41X3X4 − 400.20X1 + 514.10X2 − 319.99X3 − 377.61X4 = 0.
These descriptions answer the question of what window parameters should be recommended for the chosen building, ensuring for each orientation the same heat losses and gains in the building located in Wrocław at QH,nd = 11,386 kWh/a and in Suwałki at QH,nd = 14,534 kWh/a.
4. Conclusions
Based on the results of the calculation experiment for the mild (Wrocław), medium (Białystok), and severe (Suwałki) climatic conditions of Poland, three deterministic mathematical models of the dependence of the usable energy demand for heating and ventilation of a single-family building QH,nd (function Y) on four factors were presented: window area Aoi (factor X1), heat transfer coefficient Uoi (factor X2), solar radiation transmittance of glazing ggl (factor X3), and orientation of windows α (factor X4). The magnitude and the nature of the influence of the analysed factors on energy demand were estimated. Then, the optimisation procedure was performed for the parameters studied according to the energy criterion.
The change in the factors level from the lower to the upper value showed significant fluctuations in the influence effects for each analysed factor and for the climatic conditions considered. However, the nature of the effect of these factors on the energy demand in the different locations did not change. Only the window heat transfer coefficient Uoi showed an unfavourable effect on the function examined. With a change from the lower (0.5 W/(m2K)) to the upper (1.1 W/(m2K)) level of this factor, the energy demand of the building QH,nd increased by 7.3–8.0%, depending on the climatic conditions. The favourable influence of the other factors Ao, ggl, and α on the locations considered was recorded at levels ranging from 4.3 to 8.75%.
As a result of the optimisation procedure carried out for the selected parameters according to the energy criterion, it was detected that for the three models obtained, the optimal parameter values turned out to be at the limit of the factor space. The minimum of the tested functions was reached at constant extreme values of the factors X1 = +1 (Aoi = 3.64 m2); X2 = −1 (Uoi = 0.5 W/(m2K)); X3 = +1 (ggl = 0.7); and X4 = +1 (α = 180°). It was found that for medium climatic conditions (Białystok), the demand is 18.3% higher than for mild conditions (Wrocław), and a change in climatic conditions from mild to severe resulted in an increase in the usable energy demand of the building by as much as 27.6%. This means that the optimal values of the considered building parameters, in each location, turned out to be the same, while the extreme values of the energy demand were significantly dependent on the climatic conditions of the building location.
The notion of window equivalent energy efficiency at each of the selected orientations was proposed. Based on the developed mathematical models, mathematical descriptions were created of the recommended parameters ensuring equivalent energy efficiency of the building windows at each of the selected locations. A method for correcting the parameters of windows of different orientations to ensure a constant level of energy demand in the building was proposed for the descriptions. As a result, it was concluded that north-facing windows can have an area 1.32 times larger and south-facing windows 1.48 times smaller than east-facing windows to ensure a building’s energy needs remain constant.
The limitations of the proposed models result from the structural and architectural solutions of the building and the climatic conditions adopted for analysis. The presented mathematical models are adequate for the range of variability of the analysed window parameters: surface area, heat transfer coefficient, orientation, and solar radiation transmittance of the glazing. However, it should be stressed that the presented results are also universal. This is shown by the fact that the nature of the influence of the analysed factors was demonstrated to be unchanged for each of the three locations. Hence, the general conclusions drawn from the analysis may be applicable to the design of other single-family buildings.
The authors plan to extend the research to other locations of buildings. From a cognitive point of view, it will be important to conduct research on subsequent configurations of the arrangement of windows of a specific area on individual building facades. As window technology evolves, the analysis may be extended to include the latest solutions in the future. The authors intend to combine the research with an economic evaluation. In order to include more climate parameters, advanced building energy simulation software such as Design Builder or TRNSYS can also be applied.
Author Contributions
Conceptualisation, W.J. and A.Ś.; methodology, W.J.; software, W.J.; validation, W.J.; formal analysis, W.J.; resources, A.Ś.; writing—original draft preparation, W.J. and A.J.W.-J.; writing—review and editing, A.J.W.-J.; visualisation, A.Ś. and A.J.W.-J.; project administration, W.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Bialystok University of Technology and financed by the Ministry of Science and Higher Education of the Republic of Poland (grant number WZ/WB-IIL/2/2023).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Af | heated area of the building [m2]. |
| Aoi | surface area of window [m2] |
| bj | values of the coefficients of the regression equation [-] |
| Ci | the proportion of the glazing area to the total window area [-] |
| EP | primary energy demand [kWh/(m2∙a)] |
| F | value of the Fisher’s criterion [-] |
| Fsh | reduction factor due to shading from the building envelope [-] |
| Ft | tabular value of the Fisher’s criterion [-] |
| f1 | number of degrees of freedom [-] |
| f2 | number of degrees of freedom [-] |
| ggl | solar radiation transmittance of the glazing [-] |
| Ii | the radiant energy of the sun falling on a plane with a window in a given month [W/m2] |
| n | number of the month in the year [-] |
| N | number of calculations performed [-] |
| Nb | number of coefficients in the regression equation [-] |
| p | significance level [-] |
| qint | internal heat load of the room [kWh/a] |
| QH,gn,s,n | total heat gains in the heated zone s in the n-th month of the year [kWh/a] |
| QH,ht,s,n | total heat transferred from the heated zone s in the n-th month of the year [kWh/a] |
| QH,nd | annual demand for usable energy for heating and ventilation of the building [kWh/a] |
| QiH,nd | annual demand for usable energy for heating and ventilation of the building in specific climatic conditions [kWh/a] |
| Qint,H | monthly internal heat gains [kWh/month] |
| Qtr,s,n | the total amount of heat transferred from the heated zone s by transmission in the n-th month of the year [kWh/month] |
| Qsol,H | monthly heat gains from solar radiation through windows and glazed surfaces [kWh/month] |
| Qv,e,s,n | the total heat transferred from the heated zone s by the ventilation in the n-th month of the year [kWh/month] |
| R2 | coefficient of determination [-] |
| s | number of the heated zone [-] |
| Sbj | standard deviation of the j-th coefficient [-] |
| S2r | the residual variance [-] |
| S2y | the mean variance [-] |
| tj | value of the t-criterion [-] |
| tm | number of hours per month [-] |
| Uoi | heat transfer coefficient of the window [W/(m2K)] |
| Umax | maximum permissible value of heat transfer coefficient [W/(m2K)] |
| WWR | window-to-wall ratio [-] |
| Xi | the normalised values of the i-th factor |
| Ẋi | current natural value of the i-th factor |
| Ẋimax | maximum natural value of the i-th factor |
| Ẋimin | minimum natural value of the i-th factor |
| Y | objective function |
| α | orientation [°] |
| θi | annual average outdoor temperature [°C] |
| ηH,gn,s,n | coefficient for the use of heat gains in the heated zone s in the n-th month of the year [-] |
References
- European Commission, Clean Energy for All Europeans Package. 2019. Available online: https://ec.europa.eu/energy/topics/energy-strategy/clean-energy-all-europeans_en (accessed on 5 November 2023).
- Zhang, S.; Zhou, N.; Feng, W.; Ma, M.; Xiang, X.; You, K. Pathway for decarbonizing residential building operations in the US and China beyond the mid-century. Appl. Energy 2023, 342, 121164. [Google Scholar] [CrossRef]
- Yan, R.; Ma, M.; Zhou, N.; Feng, W.; Xiang, H.; Mao, C. Towards COP27: Decarbonization patterns of residential building in China and India. Appl. Energy 2023, 352, 122003. [Google Scholar] [CrossRef]
- Lee, S.-J.; Song, S.-Y. Time-series analysis of the effects of building and household features on residential end-use energy. Appl. Energy 2022, 312, 118722. [Google Scholar] [CrossRef]
- Xiang, X.; Zhou, N.; Ma, M.; Feng, W.; Yan, R. Global transition of operational carbon in residential buildings since the millennium. Adv. Appl. Energy 2023, 11, 100145. [Google Scholar] [CrossRef]
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- Pathirana, S.; Rodrigo, A.; Halwatura, R. Effect of building shape, orientation, window to wall ratios and zones on energy efficiency and thermal comfort of naturally ventilated houses in tropical climate. Int. J. Energy Environ. Eng. 2019, 10, 107–120. [Google Scholar] [CrossRef]
- Hassouneh, K.; Alshboul, A.; Al-Salaymeh, A. Influence of infiltration on the energy losses in residential buildings in Amman. Sustain. Cities Soc. 2012, 5, 2–7. [Google Scholar] [CrossRef]
- Polish Ministry of Development and Technology. Announcement by the Minister of Development and Technology of 15 April 2022 on the Announcement of the Consolidated Text of the Regulation of the Minister of Infrastructure on the Technical Conditions to Be Met by Buildings and Their Locations; Polish Ministry of Development and Technology: Warsaw, Poland, 2022. (In Polish)
- Cuce, E.; Young, C.-H.; Riffat, S.B. Performance investigation of heat insulation solar glass for low-carbon buildings. Energy Convers. Manag. 2014, 88, 834–841. [Google Scholar] [CrossRef]
- Grynning, S.; Gustavsen, A.; Time, B.; Jelle, B.P. Windows in the buildings of tomorrow: Energy losers or energy gainers? Energy Build. 2013, 61, 185–192. [Google Scholar] [CrossRef]
- Djamel, Z.; Noureddine, Z. The Impact of Window Configuration on the Overall Building Energy Consumption under Specific Climate Conditions. Energy Procedia 2017, 115, 162–172. [Google Scholar] [CrossRef]
- Cuce, E. Role of airtightness in energy loss from windows: Experimental results from in-situ tests. Energy Build. 2017, 139, 449–455. [Google Scholar] [CrossRef]
- Gustavsen, A.; Grynning, S.; Arasteh, D.; Jelle, B.P.; Goudey, H. Key elements of and material performance targets for highly insulating window frames. Energy Build. 2011, 43, 2583–2594. [Google Scholar] [CrossRef]
- Assimakopoulos, M.N.; Tsangrassoulis, A.; Santamouris, M.; Guarracino, G. Comparing the energy performance of an electrochromic window under various control strategies. Build. Environ. 2007, 42, 2829–2834. [Google Scholar] [CrossRef]
- Ghisi, E.; Tinker, J.A. An Ideal Window Area concept for energy efficient integration of daylight and artificial light in buildings. Build. Environ. 2005, 40, 51–61. [Google Scholar] [CrossRef]
- Aste, N.; Buzzetti, M.; Del Pero, C.; Leonforte, F. Glazing’s techno-economic performance: A comparison of window features in office buildings in different climates. Energy Build. 2018, 159, 123–135. [Google Scholar] [CrossRef]
- Cappelletti, F.; Gasparella, A.; Romagnoni, P.; Baggio, P. Analysis of the influence of installation thermal bridges on windows performance: The case of clay block walls. Energy Build. 2011, 43, 1435–1442. [Google Scholar] [CrossRef]
- Van Den Wymelenberg, K. Patterns of occupant interaction with window blinds: A literature review. Energy Build. 2012, 51, 165–176. [Google Scholar] [CrossRef]
- Misiopecki, C.; Bouquin, M.; Gustavsen, A.; Jelle, B.P. Thermal modeling and investigation of the most energy-efficient window position. Energy Build. 2018, 158, 1079–1086. [Google Scholar] [CrossRef]
- Cuce, E. Toward multi-functional PV glazing technologies in low/zero carbon buildings: Heat insulation solar glass—Latest developments and future prospects. Renew. Sustain. Energy Rev. 2016, 60, 1286–1301. [Google Scholar] [CrossRef]
- Manz, H.; Brunner, S.; Wullschleger, L. Triple vacuum glazing: Heat transfer and basic mechanical design constraints. Sol. Energy 2006, 80, 1632–1642. [Google Scholar] [CrossRef]
- Błaszkiewicz, Z.; Kneblewski, P. The identification of selected window energy parameters in winter and summer periods in the Greater Poland region. J. Agric. Eng. 2018, 63, 8–12. [Google Scholar]
- Thalfeldta, M.; Kurnitskia, J.; Voll, H. Comparison of simplified and detailed window models in office building energy simulations. Energy Procedia 2015, 78, 2076–2081. [Google Scholar] [CrossRef]
- Cuce, E.; Riffat, S.B. Vacuum tube window technology for highly insulating building fabric: An experimental and numerical investigation. Vacuum 2015, 111, 83–91. [Google Scholar] [CrossRef]
- Kumar, G.K.; Saboor, S.; Babu, T.P.A. Study of Various Glass Window and Building Wall Materials in Different Climatic Zones of India for Energy Efficient Building Construction. Energy Procedia 2017, 138, 580–585. [Google Scholar] [CrossRef]
- Yoo, S.; Jeong, H.; Ahn, B.-L.; Han, H.; Seo, D.; Lee, J.; Jang, C.-Y. Thermal transmittance of window systems and effects on building heating energy use and energy efficiency ratings in South Korea. Energy Build. 2013, 67, 236–244. [Google Scholar] [CrossRef]
- Fazel, A.; Izadi, A.; Azizi, M. Low-cost solar thermal based adaptive window: Combination of energy-saving and self-adjustment in buildings. Sol. Energy 2016, 133, 274–282. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.J.; Gustavsen, A. Properties, requirements and possibilities of smart windows for dynamic daylight and solar energy control in buildings: A state-of-the-art review. Sol. Energy Mater. Sol. Cells 2010, 94, 87–105. [Google Scholar] [CrossRef]
- Chen, G.; Wang, K.; Yang, J.; Huang, J.; Chen, Z.; Zheng, J.; Wang, J.; Yang, H.; Li, S.; Miao, Y.; et al. Printable Thermochromic Hydrogel-Based Smart Window for All-Weather Building Temperature Regulation in Diverse Climates. Adv. Mater. 2023, 35, 2211716. [Google Scholar] [CrossRef] [PubMed]
- Granqvist, C.G. Electrochromics for smart windows: Oxide-based thin films and devices. Thin Solid Film. 2014, 564, 1–38. [Google Scholar]
- Granqvist, C.G.; Arvizu, M.A.; Bayrak Pehlivan, İ.; Qu, H.-Y.; Wen, R.-T.; Niklasson, G.A. Electrochromic materials and devices for energy efficiency and human comfort in buildings: A critical review. Electrochim. Acta 2018, 259, 1170–1182. [Google Scholar] [CrossRef]
- Wu, S.-Y.; Su, S.-K.; Chang, C.-J.; Huang, C.-H.; Chen, J.-K. Sol-gel-synthesized titania-vanadia nanocrystal films for triple-functional window coatings. Ceram. Int. 2016, 42, 17610–17619. [Google Scholar] [CrossRef]
- Zhao, Y.; Sadat, M.E.; Dunn, A.; Xu, H.; Chen, C.-H.; Nakasuga, W.; Ewing, R.C.; Shi, D. Photothermal effect on Fe3O4 nanoparticles irradiated by white-light for energy-efficient window applications. Sol. Energy Mater. Sol. Cells 2017, 161, 247–254. [Google Scholar] [CrossRef]
- Cha, J.; Kim, S.; Park, K.-W.; Lee, D.R.; Jo, J.-H.; Kim, S. Improvement of window thermal performance using aerogel insulation film for building energy saving. J. Therm. Anal. Calorim. 2014, 116, 219–224. [Google Scholar] [CrossRef]
- Gomez-Mejia, D.; Balkin, L. Optimisation of building shape and orientation for better energy efficient architecture. J. Manag. Dev. 2007, 23, 635–648. [Google Scholar]
- Persson, M.-L.; Roos, A.; Wall, M. Influence of window size on the energy balance of low energy houses. Energy Build. 2006, 38, 181–188. [Google Scholar] [CrossRef]
- Sudan, M.; Tiwari, G.N.; Al-Helal, I.M. Dynamic analysis of daylight metrics and energy saving for rooftop window integrated flat roof structure of building. Sol. Energy 2015, 122, 834–846. [Google Scholar] [CrossRef]
- Poirazis, H.; Blomsterberg, Ĺ.; Wall, M. Energy simulations for glazed office buildings in Sweden. Energy Build. 2008, 40, 1161–1170. [Google Scholar] [CrossRef]
- Alghoul, S.K.; Rijabo, H.G.; Mashena, M.E. Energy consumption in buildings: A correlation for the influence of window to wall ratio and window orientation in Tripoli, Libya. J. Build. Eng. 2017, 11, 82–86. [Google Scholar] [CrossRef]
- Feng, G.; Chi, D.; Xu, X.; Dou, B.; Sun, Y.; Fu, Y. Study on the Influence of Window-wall Ratio on the Energy Consumption of Nearly Zero Energy Buildings. Procedia Eng. 2017, 205, 730–737. [Google Scholar] [CrossRef]
- Motuziene, V.; Juodis, E.S. Simulation based complex energy assessment of office building fenestration. J. Civ. Eng. Manag. 2010, 16, 345–351. [Google Scholar] [CrossRef]
- Alwetaishi, M. Impact of glazing to wall ratio in various climatic regions: A case study. J. King Saud Univ. Eng. Sci 2017, 31, 6–18. [Google Scholar] [CrossRef]
- Zhijian, L.; Di, W.; Junyang, L.; Hancheng, Y.; Baojie, H. Optimizing Building Envelope Dimensions for Passive Solar Houses in the Qinghai-Tibetan Region: Window to Wall Ratio and Depth of Sunspace. J. Therm. Sci. 2019, 28, 1115–1128. [Google Scholar]
- Østergård, T.; Jensen, R.L.; Maagaard, S.E. A comparison of six metamodeling techniques applied to building performance simulations. Appl. Energy 2018, 211, 89–103. [Google Scholar] [CrossRef]
- Asadi, S.; Amiri, S.S.; Mottahedi, M. On the development of multi-linear regression analysis to assess energy consumption in the early stages of building design. Energy Build. 2014, 85, 246–255. [Google Scholar] [CrossRef]
- Asadi, S.; Hassan, M.; Beheshti, A. Development and validation of a simple estimating tool to predict heating and cooling energy demand for attics of residential buildings. Energy Build. 2012, 54, 12–21. [Google Scholar] [CrossRef]
- Romani, Z.; Draoui, A.; Allard, F. Metamodeling the heating and cooling energy needs and simultaneous building envelope optimization for low energy building design in Morocco. Energy Build. 2015, 102, 139–148. [Google Scholar] [CrossRef]
- Hester, J.; Gregorya, J.; Kirchain, R. Sequential early-design guidance for residential single-family buildings using a probabilistic metamodel of energy consumption. Energy Build. 2017, 134, 202–211. [Google Scholar] [CrossRef]
- Jaffal, I.; Inard, C. A metamodel for building energy performance. Energy Build. 2017, 151, 501–510. [Google Scholar] [CrossRef]
- Novel, A.; Allard, F.; Joubert, P. Metamodeling of building energy consumption focused on climate, operation, space use and users related factor. In Proceedings of the E3S Web of Conferences, CLIMA 2019, Bucharest, Romania, 26–29 May 2019; Volume 111, p. 04027. [Google Scholar]
- Jezierski, W.; Święcicki, A. The dependence of the seasonal demand indicator for usable energy of a single-family residential building on the parameters and orientation of windows. District Heating, Heat. Vent. 2018, 49, 400–403. (In Polish) [Google Scholar]
- Jezierski, W.; Święcicki, A.; Kadłubowski, A. Influence of parameters and orientation of windows on the demand for usable energy of a residential building. Build. Mater. 2018, 8, 46–47. (In Polish) [Google Scholar] [CrossRef]
- Gutenbaum, J. Mathematical Modeling of Systems; EXIT: Warsaw, Poland, 2003. (In Polish) [Google Scholar]
- Polish Ministry of Infrastructure and Development. Regulation of the Minister of Infrastructure and Development of 3 June 2014 on the Methodology for Calculating the Energy Performance of a Building and a Dwelling or Part of a Building Constituting a Separate Technical and Utilitarian Unit, as well as the Method of Drawing Up and Models of Energy Performance Certificates; Polish Ministry of Infrastructure and Development: Warsaw, Poland, 2014. (In Polish)
- Korzyński, M. Methodology of the Experiment. Planning, Implementation, and Statistical Analysis of the Results of Technological Experiments; WNT: Warsaw, Poland, 2006. (In Polish) [Google Scholar]
- Data for Building Energy Calculations. Available online: https://www.gov.pl/web/archiwum-inwestycje-rozwoj/dane-do-obliczen-energetycznych-budynkow (accessed on 10 March 2024).
- Rafajłowicz, E. Algorithms for Planning an Experiment with Implementations in the Mathematica Environment; Academic Publishing House PLJ: Warsaw, Poland, 1996. (In Polish) [Google Scholar]
- Jezierski, W.; Sadowska, B. Optimization of the Selected Parameters of Single-Family House Components with the Estimation of Their Contribution to Energy Saving. Energies 2022, 15, 8810. [Google Scholar] [CrossRef]
- Brandt, S. Data Analysis; Scientific Publishers PWN: Warsaw, Poland, 1999. (In Polish) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).