Abstract
Reductions in energy consumption and greenhouse gas emissions are required globally. Under this background, the Multilayer Perceptron machine-learning algorithm was used to predict liquid natural gas consumption to improve energy consumption efficiency. Setting hyperparameters remains challenging in machine-learning-based prediction. Here, to improve prediction efficiency, hyperparameter autotuning via Bayesian optimization was used to identify the optimal combination of the eight key hyperparameters. The autotuned model was validated by comparing its predictive performance with that of a base model (with all hyperparameters set to the default values) using the coefficient of variation of root-mean-square error (CvRMSE) and coefficient of determination (R2) based on the Measurement and Verification Guideline evaluation metrics. To confirm the model’s industrial applicability, its predictions were compared with values measured at a small-to-medium-sized food factory. The optimized model performed better than the base model, achieving a CvRMSE of 12.30% and an R2 of 0.94, and achieving a predictive accuracy of 91.49%. By predicting energy consumption, these findings are expected to promote the efficient operation and management of energy in the food industry.
1. Introduction
As energy consumption has become a major global issue, interest in reducing energy consumption and greenhouse gas emissions has increased in various sectors. According to the Energy Demand Forecast Report [,] published by the Korea Energy Economics Institute and data from the Korea Energy Statistical Information System [], total energy consumption in the first half of 2023 was expected to decrease by approximately 2.2%, with this change mainly attributed to industry because of the economic slowdown in South Korea and other countries caused by the COVID-19 pandemic. This slowdown began in the second half of 2022 and reduced manufacturing production. However, production is expected to rebound by 2.0% in 2024, reaching approximately 305.4 million tons of oil equivalent (TOE), potentially driven by export recovery. Production is expected to increase by an annual average of 1.0% from 2022 to 2027, reaching 319.3 million TOE. Table 1 presents the trends and forecasts for total energy consumption and final consumption (coal, oil, gas, electricity, thermal energy, nuclear, renewables, and others).

Table 1.
Energy consumption trends and forecasts.
In many advanced countries, the food industry accounts for approximately 20% of total energy consumption, which is quite high; moreover, the energy consumption of domestic food factories accounted for 1,331,000, 1,373,000, and 1,398,000 TOE in 2020, 2021, and 2022, respectively, thus showing a continuously increasing trend. Accordingly, methods to reduce energy consumption and improve energy efficiency in the food industry are urgently required. Analysis of energy use in food factories has revealed high levels of thermal energy use, with 59% used for heating, 16% used for cooling, 12% used for mechanization, 8% used for infrastructure, and 5% used for other purposes. Although thermal energy accounts for more than half of the energy sources in the Korean food industry, the energy-saving performance of the industry depends on the electricity sector []. Moreover, heat energy consumption in the food industry accounts for a large portion of energy consumption both domestically and globally (e.g., the United States and Denmark) [], and liquid natural gas (LNG) is a representative thermal energy in food factories.
The continuous increase in energy consumption is expected to lead to many issues and risks, and diverse policies and technologies have been discussed to address such problems. Historically, the focus was on increasing supply; however, the focus has now shifted to decreasing consumption. Energy management and optimization are important for reducing energy consumption. Consequently, technologies for energy analysis and prediction have attracted attention. An effective method for energy prediction involves employing thermodynamic analysis utilizing the physical information of a building. Representative examples of such methods include EnergyPlus (https://energyplus.net) and TRNSYS (https://www.trnsys.com), which are energy simulation tools [,]. Although these methods can provide sophisticated and abundant prediction results, the models can be time-consuming and costly to construct and analyze because they require detailed input data and researcher experience to achieve accuracy. In contrast, machine learning using existing building-operation data can identify patterns and relationships in the data that are difficult for researchers to identify. Machine-learning techniques, known for their practicality and efficient performance in terms of time and cost, enable automated prediction and decision-making processes by leveraging available data. Furthermore, these techniques exhibit high adaptability to new data and versatility across various scenarios. Notably, their performance can be continuously enhanced through feedback mechanisms. Therefore, they have been increasingly applied in energy-related prediction research.
Ji et al. [] developed a deep neural network (DNN) model to predict hot water heating energy consumption in apartment buildings considering various independent variables; their model considering holidays as well as climatic factors achieved the best predictive performance, followed by a model considering climatic factors and one considering outdoor temperatures. Kim et al. [] utilized Multi Linear Regression (MLR) and the Multilayer Perceptron (MLP), Support Vector Machine (SVM), and Random Forest (RF) algorithms to predict the electricity consumption of buildings, addressing temporal resolution and comparing algorithms to improve predictive accuracy. Bekdaş et al. [] utilized five foundational regression algorithms and five ensemble algorithms to predict cooling loads (the amount of energy that must be removed from or consumed in a space to keep its temperature at an acceptable level or within an acceptable range) based on the basic architectural and structural characteristics of low-rise buildings in the tropics and found that the Histogram Gradient Boosting algorithm and stacking models efficiently modeled the relationship between the predictors and cooling load. Matos et al. [] suggested a method to manage community energy balance through electricity consumption forecasts via eXtreme Gradient Boosting (XGBoost) and used a decision algorithm for energy trading with the public grid based on solar production and energy consumption forecasts, storage levels, and market electricity prices. Son et al. [] suggested an algorithm for short- and medium-term electricity consumption forecasts by combining the Gated Recurrent Unit (GRU) model (which achieves accurate long-term forecasts) with the Prophet model (which is appropriate for modeling seasonal events), and their proposed model reduced forecasting errors and provided insights into electricity consumption patterns. Consequently, the application of machine learning in predicting energy consumption is continuously increasing, with the effectiveness of machine learning relying heavily on the optimization of hyperparameter settings. It is therefore important to identify the optimal hyperparameters for each model [].
This study aims to evaluate the usefulness of hyperparameter autotuning in predicting LNG consumption by applying it to an MLP-based model with default settings, deriving predicted values, and confirming its predictive accuracy via comparison with values measured in a food factory. Setting the hyperparameters in machine-learning-based prediction remains challenging []. Therefore, this study utilizes Bayesian optimization, an efficient approach for hyperparameter tuning. The optimized model performed better than the base model, achieving a coefficient of variation of root-mean-square error (CvRMSE) of 12.30%, a coefficient of determination (R2) of 0.94, and a predictive accuracy of 91.49%. These findings provide reference data for performing machine-learning-based predictions of food factory energy consumption and identifying the hyperparameter search range. Energy consumption characteristics are affected by various factors, such as differences in the operation characteristics of different building types (e.g., commercial, residential, or school) and differences in how occupants use the building, which means that the data required to predict energy consumption will differ for each building type. Few previous studies have focused on food factory energy. In particular, to our best knowledge, no research has been conducted on improving the efficiency of LNG use in food factories. Therefore, this study can be used as a reference for datasets required to predict food factory energy consumption, especially LNG, using machine learning. In addition, this study targets a wider variety of hyperparameters than previous studies, furthering its usefulness as reference material. The search interval for each hyperparameter and visualization data for the research results provided in this work will aid future researchers in selecting hyperparameter types and setting search intervals.
As energy improvement in the Korean food industry typically focuses on the electricity sector, this study aims to contribute to energy efficiency in the thermal energy sector by predicting LNG consumption. Food factories use LNG in several ways. Boilers use LNG as fuel to heat water and generate steam, which, in turn, is used for various heating and cooling processes. Further, it is used to heat or cook food in gas and steam ovens, in cooling and freezing processes when storing and transporting food, and as a packaging material for food preservation. Therefore, predicting the LNG requirements and consumption can help enhance energy efficiency in food factories. Energy consumption prediction can contribute substantially to optimizing energy-system operations by reducing energy waste, costs, and carbon emissions. Thus, by predicting LNG consumption and evaluating the performance of the prediction model based on actual food factory data, the results of this study can be used in practical applications for industrial sites through Factory Energy Management Systems (FEMSs). Applying the LNG consumption prediction function to the FEMS of a food factory can determine the LNG demand and supply status in real time, and changes can be addressed. These findings are expected to provide practical value to food factory operators and energy managers by enabling energy consumption predictions based on machine learning. In addition, the prediction function could also be applied to the overall energy management of food factories by predicting the consumption of not only LNG but also other energy sources. Furthermore, by following the series of research processes in this paper (selecting the type of building and energy for research, securing the data necessary for prediction, building a base model using machine learning, setting a hyperparameter search interval, upgrading the prediction model through the application of autotuning techniques, verifying the prediction performance of the prediction mode, and so on), this can be applied not only to food factories but also to other building types.
The remainder of this paper is organized as follows: Section 2 describes machine learning and various applied conditions and methods, such as algorithms, hyperparameters, and Bayesian optimization. Section 3 outlines the results of autotuning based on Bayesian optimization. Section 4 presents the conclusions and highlights future research plans.
2. Materials and Methods
2.1. Machine Learning and MLP
Machine learning is a specific subset of Artificial Intelligence (AI), which refers to technology (or the relevant research field) for computer-based learning, reasoning, and perception. Machine learning, a representative AI method, refers to algorithms or technology that enable computers to learn in the same way as humans do.
Machine learning has been applied in various fields, including image and text classification, text summarization, regression analysis, voice recognition, outlier detection, data visualization, and reinforcement learning. It can identify complex patterns and features in data and handle various data formats, as well as dynamic, large, and complex datasets. Once it has been set up, it does not require further human intervention, and it can generate more accurate results over time via the accumulation of data. There are four types of machine learning: supervised learning, which involves training by providing a problem and an answer; unsupervised learning, which involves training without providing an answer; semi-supervised learning, a combination of supervised and unsupervised learning; and reinforcement learning, which involves training by trial and error, using rewards and punishments.
MLP, which is used in classification and regression problems, is a supervised learning algorithm. The MLP algorithm is a Feed-Forward DNN (FFDNN), a network with multiple layers, comprising input, hidden, and output layers. An FFDNN overcomes the limitations of the single-layer perceptron model by training a network after adjusting the layer weights via backpropagation. An FFDNN has a similar structure to an MLP, although it includes a hidden layer and uses nonlinear functions for the inputs and outputs of each node, enhancing its ability to model complex nonlinear relationships. The FFDNN has been frequently utilized in prediction and classification due to such features [].
Artificial Neural Network (ANN) and Support Vector Regression (SVR) algorithms are commonly utilized for prediction in the energy and environmental sectors, and MLP is one of the most frequently utilized ANN algorithms [,]. The performance of the MLP algorithm was compared with a linear SVR model, an SVR Radial Basis Function (RBF) model, and an SVR polynomial model in the previously published findings. Of these, the MLP model achieved better performance. This study aimed to further examine the performance of the MLP algorithm [].
2.2. Hyperparameters
In machine learning, hyperparameters are variables that are set for optimal model implementation; for these parameters, no absolute optimal values exist; hence, researchers must manually adjust them during model design. Each hyperparameter determines a different machine-learning model, and model performance depends on the hyperparameter values; using inappropriate values leads to extremely poor performance []. However, machine-learning algorithms are complex (the ‘black box’ problem), hyperparameter tuning is difficult, and some combinations of hyperparameters are incompatible []. While the optimized hyperparameters should ideally be selected after confirming all combinations, this is practically impossible owing to the extremely large number of potential combinations. Machine-learning algorithms typically involve not only continuous variables, but also categorical and integer variables, resulting in discrete changes. As the hyperparameter space is often discrete, it is difficult to predict the impact of a change in a particular value on model performance. Random initialization of hyperparameters and features of the data can result in different training results; hyperparameters are therefore non-deterministic, making it more difficult to determine their optimal values.
Various autotuning techniques have been investigated for deriving the optimal combination of hyperparameters. Ko [] utilized SVM, RF, Boosted Regression Trees (BRTs), XGBoost, and MLP algorithms to predict the emergence probability of several insects. Bayesian optimization was applied to optimize the MLP hyperparameters. The ‘number of nodes in the hidden layer’, ‘activation function’, ‘batch size’, ‘epoch’, and ‘learning rate’ were selected as the target hyperparameters. Cho [] performed hyperparameter tuning by using the grid-search method on the MLP algorithm to determine the optimal combination of explanatory factors and to improve the modeling accuracy of public office cost estimates. ‘Node and hidden layers’ were targeted for tuning; the numbers of nodes were set to 4, 8, 16, 32, 64, and 128, and the numbers of hidden layers were set to 1, 2, 3, and 4. Jafar [] conducted research on hyperparameter optimization of RF, XGBoost, SVM, and Convolutional Neural Network (CNN) algorithms using hyperparameter optimization frameworks. The utilized hyperparameter optimization framework consisted of Bayesian optimization, Optuna, HyperOpt, and the Keras tuner. In the case of RF in research, ‘n_estimators’, ‘max_depth’, ‘min_samples_split’, ‘min_samples_leaf’, ‘max_features’, and ‘criterion’ were the research subjects for hyperparameter optimization. For XGBoost, ‘colsample_bytree’, ‘gamma’, ‘max_depth’, ‘min_child_weight’, ‘n_estimators’, and ‘subsample’ were studied for hyperparameter optimization. In the case of SVM, the research subjects were ‘C’, ‘degree’, ‘kernel’, and ‘gamma’. In the case of CNN, ‘learning_rate’, ‘dense_layers’, ‘conv_layers’, ‘num_nodes’, and ‘batch_size’ were the research subjects. Kim [] developed an artificial intelligence model that can classify eight representative military movements using the LSTM algorithm. Hyperparameter tuning was performed by applying the Bayesian optimization method to hyperparameters including the initial learning rate, minibatch size, max epochs, and number of hidden units.
Machine-learning-based prediction has been applied in multiple fields. Specific hyperparameters have been selected, and autotuning has been utilized in several studies. Hyperparameter autotuning provides an effective approach to maximizing model performance. This study attempts to test the autotuning of eight hyperparameters (‘hidden_layer_sizes’, ‘alpha’, ‘learning_rate_init’, ‘activation’, ‘learning rate’, ‘max_iter’, ‘momentum’, and ‘solver’) in the base model to predict LNG consumption in a food factory. These hyperparameters are considered tuning targets when constructing an MLP model, as they determine the model’s structure and learning method, thus substantially affecting its learning process and performance. Although there are other hyperparameters in an MLP, model tuning can become too complicated if too many hyperparameters are considered, thereby increasing computational costs. Therefore, this study selected eight key hyperparameters that significantly impact predictive performance.
The eight hyperparameters are described as follows: (1) ‘Hidden_layer_size’ refers to the number of neurons included in each hidden layer and determines how many neurons are placed in each layer. (2) ‘Alpha’ controls model complexity by imposing penalties on the weights, thereby helping to reduce overfitting. (3) The ‘initial learning rate’ is used when the optimization algorithm updates the weights. (4) ‘Activation’ describes the function that calculates the output of each neuron (the most frequently used activation functions are Rectified Linear Unit (ReLU) and Sigmoid). (5) ‘Learning rate’ determines the frequency at which the weights are updated in each iteration—if updating is too frequent, divergence may occur, whereas if it is too infrequent, convergence may be slow. (6) ‘Max iteration’ refers to the number of times that the optimization algorithm repeatedly uses the training data. (7) ‘Momentum’ is used in the gradient-descent method to update the weights to reflect previous movements by adding the current gradient update while partially maintaining previous gradient updates. (8) ‘Solver’ selects an optimization algorithm, with ‘Adam’ and ‘stochastic gradient descent’ being representative cases.
2.2.1. Hyperparameter Autotuning
Many methods for hyperparameter autotuning exist, with the primary methods being grid search, random search, Bayesian optimization, genetic algorithms, and hyperband []. Grid search, which resolves the instability associated with manual searching, finds an optimal combination after trying all possible combinations of hyperparameter values for prespecified values. While this method is explicit, intuitive, and simple, its computational costs increase exponentially along with the expanded search space []. Random search randomly selects some of the hyperparameter values and tests them. While it has a lower computational cost than that of grid search, it may be time-consuming to find optimal combinations, and it is less reliable as it may not explore some search spaces in detail; finally, it does not consider correlations between hyperparameter combinations. Bayesian optimization finds the optimal combinations while updating the probability distribution of the hyperparameter values to be tested next, based on previous attempts; it can achieve relatively good results with fewer attempts by efficiently exploring the search spaces. Though it may initially exhibit unstable performance, Bayesian optimization typically improves over subsequent iterations, demonstrating its effectiveness in hyperparameter tuning. The genetic algorithms method utilizes the concept of genetics to evolve hyperparameters over multiple generations and find optimal combinations by genetically propagating successful hyperparameter combinations in each generation. While this method can maintain diversity by exploring various combinations, it may initially perform in a similar manner to the random search method, and determining its optimization process may be time-consuming. The hyperband method, which efficiently uses computational resources, trains a model using various hyperparameter combinations and selects those combinations with good performance. The hyperband method may be unstable initially, and the results can significantly vary depending on the hyperparameter settings.
Among the above methods, Bayesian optimization conducts an efficient probabilistic search in the hyperparameter space. In addition, it enables efficient and fast searching by using previously obtained results to determine the next point to search. It has the flexibility to combine various search algorithms and modeling techniques and can be applied to various types of problems. In particular, this method can be applied to any function for obtaining current information and can be used for a black box-type objective function, which is expensive and whose shape is unknown [,,]. This study used Bayesian optimization because of its efficiency.
2.2.2. Bayesian Optimization
Optuna, a hyperparameter optimization library based on Bayesian optimization [], was used for hyperparameter autotuning. Optuna finds optimal hyperparameter combinations that minimize or maximize the values of objective functions in given hyperparameter spaces. Unlike other methods, this method evaluates the objective function through a series of attempts and selects the next hyperparameter combinations to try based on the results of the previous attempts. This method, known as sequential model-based global optimization, functions by utilizing the estimates of the objective function obtained from previous hyperparameters to select the next hyperparameter values in a sequential and iterative search process. Bayesian optimization utilizes a surrogate model and an acquisition function. In the surrogate model, which is used to improve the optimal function model, the acquisition function recommends the optimal input values. The surrogate model estimates the objective function based on the data secured so far, primarily using a Gaussian function [,]. Using the acquisition function, the surrogate model probabilistically calculates the next value to be investigated based on the actual data for the objective function []. Here, ‘objective function’ refers to the optimal function being sought, also referred to as a ‘black-box function’. The Bayesian optimization process is illustrated in Figure 1.
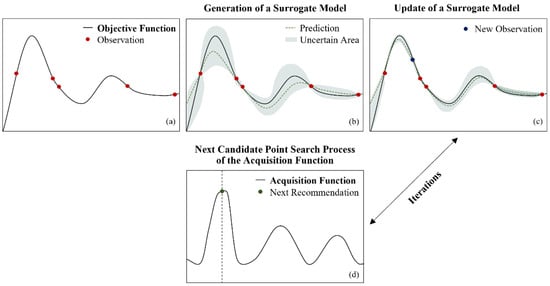
Figure 1.
Bayesian optimization process. The black line in (a) indicates the unknown objective function, which makes it possible to obtain results after the initial random hyperparameter sampling. Based on the observed values, the surrogate model estimates the optimum function (green line in (b)), and the acquisition function finds the candidate hyperparameter combinations to observe the next value (d). The surrogate model then again estimates the optimal function (green line in (c)), and the process is repeated to find a hyperparameter combination, with the values approaching the objective function.
2.3. Data Collection and Utilization
The research target for the prediction model was a small-to-medium-sized food factory in South Korea. It manufactures, processes, and sells food products, such as ham, sausages, and pork cutlets, and its main processes include raw material pretreatment, processing, smoking, grilling, and sterilization. There is no systematic energy management, and operations are managed based on employee experience. Here, it was assumed to be necessary to analyze and predict energy consumption to improve the factory’s energy utilization efficiency.
Production per factory building, total production, LNG temperature and pressure data for each factory building, and outside temperature and humidity data were utilized as independent variables to predict LNG consumption. LNG consumption, LNG temperature and pressure, and production data were obtained from boiler logs, which are manually written and managed by the factory, as well as from human–machine interface data and details of production logs maintained in a database. The data period utilized was 6 December 2021 to 19 March 2022. All conditions of the model except hyperparameter settings were the same as the predeveloped base model, including the data period used for analysis [].
2.4. Base Prediction Model
The MLP algorithm, used here for prediction, was developed and analyzed using Python 3.9.7, Tensorflow 2.3.0, Keras 2.4.3, Sklearn 1.0.2, Pandas 1.4.1., Numpy 1.19.5, and Matplotlib 3.5.1. The data, comprising training and testing datasets at a 9:1 ratio, were preprocessed using minmax and standard scaling.
2.4.1. Hyperparameter Settings for the Base Prediction Model
Default values were applied to the hyperparameters of the base prediction model (hidden layer size = 100; alpha = 0.0001; initial learning rate = 0.001; activation function, ReLU; learning rate, constant; max iteration = 200; momentum = 0.9; solver, Adam).
2.4.2. Predictive Performance Criteria
Machine-learning-based prediction studies typically evaluate predictive performance based on the Measurement and Verification (M & V) Guidelines of the American Society of Heating, Refrigerating, and Air-Conditioning Engineers (ASHRAE) [], the United States Department of Energy’s Federal Energy Management Program (FEMP) [], and the International Performance Measurement and Verification Protocol [,,]. Each of these sources suggests measurement and verification protocols and predictive performance criteria for prediction models.
This study uses the reference values suggested by AHSRAE and FEMP, and the CvRMSE and R2 were used to evaluate predictive performance. ASHRAE and FEMP suggest requirements of CvRMSE < 15% for monthly data and CvRMSE < 30% for hourly data. As this study utilizes daily data, 20%, the median value, was set as the target. ASHRAE suggests using R2 > 0.75, and this study used this value as the target (Table 2).

Table 2.
Evaluation metrics of the prediction model.
2.5. Prediction Model Applying Autotuning Based on Bayesian Optimization
This study applied autotuning based on the base model. The hidden layer size was set to search integer values of 50–500. Alpha was set to search from 1 × 10−6 to 1 × 10−2 using a log-uniform distribution. The initial learning rate was set to search from 1 × 10−6 to 1 × 10−1 using a log-uniform distribution, ensuring that the potential values were evenly spaced on the log scale. The activation function was set to search after selecting among the identity, logistic, tanh, and ReLU functions. The learning rate was set to search after selecting among the constant, invscaling, and adaptive configuration values. The maximum iteration was set to search integer values of 50–500. Momentum was set to search after selecting values with a uniform distribution of 0.1–0.9. Solver was set to search after choosing between the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) and Adam algorithms. Table 3 summarizes the search range of each hyperparameter.

Table 3.
Evaluation metrics of the predictive model.
The search range for each hyperparameter can be categorized as discrete, continuous, or categorical. The hidden layer size and max iteration are discrete hyperparameters; alpha, initial learning rate, and momentum are continuous; and the activation function, learning rate, and solver are categorical. For the hidden layer size, activation function, learning rate, max iteration, and solver, there were 451, 4, 3, 451, and 2 cases, respectively. However, the number of searches cannot be determined for the continuous hyperparameters (alpha, initial learning rate, and momentum). As alpha and learning rate increase on a log scale, it is not possible to determine the number of searches as a discrete value. For momentum, the interval between each value is not clearly defined, so the number of searches cannot be determined. While the total number of searches can be calculated by multiplying the number of searches for each of the eight hyperparameters, it cannot be determined here, as this is unknown for alpha, learning rate, and momentum.
3. Results and Discussion
3.1. Hyperparameter Autotuning Based on Bayesian Optimization
Bayesian optimization-based autotuning essentially uses a probabilistic model to search for points with high possibilities in the hyperparameter space, making it possible to efficiently find optimal hyperparameter combinations. However, it is only possible to confirm the final optimal combinations, and it is impossible to precisely determine the process (that is, to identify the combinations tested during the optimization process and the results for each attempted combination). Instead, the optimization process can be visualized and thus confirmed using contour, slice, and parallel coordinate plots, revealing how each hyperparameter influences model performance.
Figure 2 presents a contour plot visualizing the hyperparameter autotuning process. Each contour plot visualizes the interactions between two hyperparameters (on the x- and y-axes), with model performance (mean-squared error [MSE], the value of the objective function) represented as a contour. The top panel presents all the contour plots, while the bottom panel presents two zoomed-in examples, i.e., the hidden layer size–max iteration and hidden layer size–momentum. Closer contour spacing reflects a substantial change in objective function value, and the darker contour represents lower objective function values. Contours with closer spacing and darker colors can thus be interpreted as areas of optimal hyperparameter combinations, whereas those with wider spacing and lighter colors can be interpreted as areas with suboptimal hyperparameters. Although it is impossible to directly confirm optimal combinations within the entire hyperparameter search space of the contour plot, the interactions between two combinations can be confirmed visually, and the tendency of each combination in each section can thus be confirmed. In the hidden layer size–max iteration combination, when the hidden layer sizes are approximately 110–130 and the max iteration is approximately 470–490, there is a high probability of a low objective function result, that is, an optimal combination. Similarly, in the hidden layer size–momentum combination, when the hidden layer sizes are approximately 110–130 and the momentum is approximately 0.1–0.15, there is a high probability of a low objective function result; that is, an optimal combination.
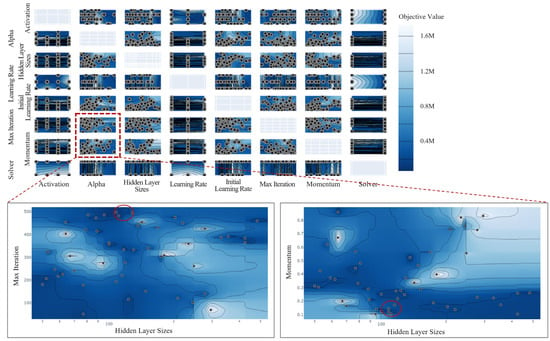
Figure 2.
Contour plots of the hyperparameters.
Figure 3 presents a slice plot illustrating the effect of each hyperparameter in one dimension, making it possible to confirm that the objective function values change along with the values of each hyperparameter. Each subplot shows the changes in the objective function values in line with the values of the other hyperparameters, besides the corresponding hyperparameters. The x-axis indicates the set value of the corresponding hyperparameter, and the y-axis is the objective function; this makes it possible to confirm the MSE values. A darker color and lower y-axis value indicate areas with lower objective-function values; the optimal value will likely be obtained by moving toward the point with the lower objective function value. It is likely that the optimal value will not be found in areas of the plot with low y-axis values and lighter colors or high y-axis values and darker colors. In summary, it is possible to confirm the relative performance of hyperparameter combinations by comprehensively considering values on the y-axis and the colors of the dots. For instance, for the solver hyperparameter, which exhibited the clearest pattern, there were more searches in L-BFGS (which exhibited more points with darker colors) than in the Adam algorithm, and the points with darker colors were located lower on the y-axis. Thus, for the solver, the optimal points are more likely to be found in L-BFGS than in Adam.
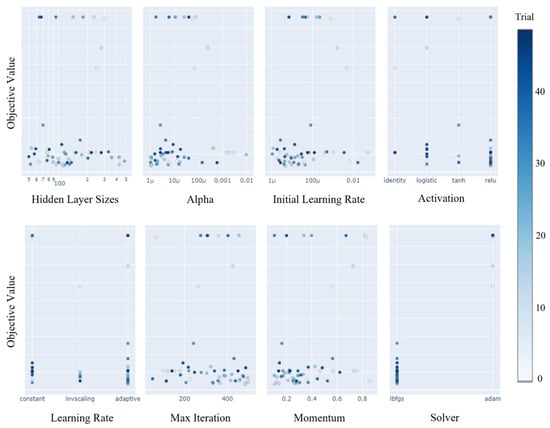
Figure 3.
Slice plot of hyperparameters.
Figure 4 presents a parallel coordinate plot illustrating the model’s performance for various hyperparameter combinations, visualizing model performance in multidimensional space. This plot can intuitively confirm the impact of each hyperparameter on the objective function, because the values of multiple observations are connected by a line, thus indicating that Bayesian optimization effectively searches for the optimal hyperparameter []. A darker line indicates a lower value of the objective function at the corresponding point, and the optimal hyperparameter combination minimizing the objective function will likely be found. For example, activation, alpha, learning rate, initial learning rate, and solver are relatively visible in the figure. For activation, a dark line is distributed toward ReLU, and for both alpha and initial learning rate, a dark line is distributed toward the bottom near 1 × 10−6. In the case of learning rate, a dark line is distributed toward adaptive. Finally, the solver can confirm that a dark line is distributed toward L-BFGS (Figure 4).
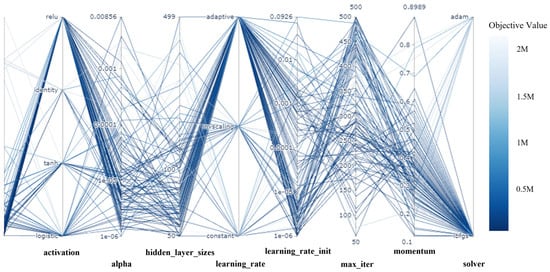
Figure 4.
Parallel coordinate plot of hyperparameters.
Figure 5 presents the CvRMSE and R2 results based on the hyperparameter settings; the red dots indicate the optimal values, while the blue dots represent the model performance obtained by changing specific hyperparameter values in each trial. Each dot has a CvRMSE or R2 value corresponding to the hyperparameter values. The distribution of these dots enables visual identification of how each hyperparameter affects the model’s performance. The red dots reflect trials obtained using hyperparameter combinations with the best performance identified during optimization. For instance, for the initial learning rate, many trials were conducted when the setting was ‘adaptive’, indicating that the optimal combination was found using this setting.
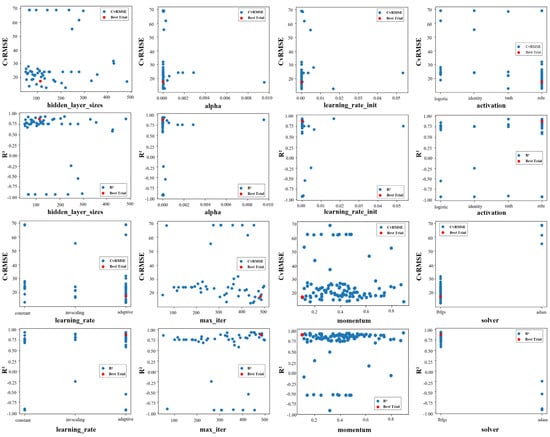
Figure 5.
CvRMSE and R2 in line with hyperparameter settings.
Using the MLP algorithm with Bayesian optimization-based autotuning revealed the following optimal hyperparameter combinations for predicting the target factory’s LNG consumption: hidden layer size, 112; alpha, 1.0721554206232144 × 10−6; initial learning rate, 4.606358642703309 × 10−6; activation function, ReLU; learning rate, adaptive; max iteration, 482; momentum, 0.10528239434765554; and solver, L-BFGS (Table 4).

Table 4.
Combinations of the optimal hyperparameter setting.
3.2. Comparison of Predictive Performance
In terms of the model’s predictive performance applying the optimal hyperparameter settings, CvRMSE was 12.2965% and R2 was 0.9384. These results are consistent with the target values of CvRMSE = 20% and R2 = 0.75, indicating that the optimized predictive model performed better than the base model with default values (Table 5). The CvRMSE and R2 values are averages obtained after running each model’s prediction 10 times.

Table 5.
Predictive performance of the base model and autotuning model.
3.3. Predictive Accuracy
The predicted values were obtained for the period of 1–31 January 2022, excluding weekends (owing to the irregular operating schedule on weekends of each factory building) and were compared with the measured values (24 January was excluded as the values were not measured on this day). Table 6 compares the measured and predicted values.

Table 6.
Comparison of the measured and predicted values.
Error rates were calculated by comparing the predicted values with the measured values, and the predictive accuracy of the model was derived based on the average error rate. The average error rate of the model was 8.5086%, with a high predictive accuracy of 91.4914%, confirming the usefulness of this predictive model by applying Bayesian optimization-based autotuning.
The error rate was calculated as follows:
Predictive accuracy was derived based on the calculated average error rate.
Figure 6 compares the measured and predicted values.
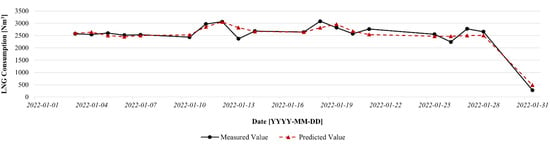
Figure 6.
Comparison of measured and predicted values.
4. Conclusions
This study utilized a machine-learning MLP algorithm to predict daily LNG consumption at a food factory. First, a base model with default values for the key hyperparameters was developed. Bayesian optimization, an autotuning technique, was applied to the predeveloped prediction model. The targeted hyperparameters for autotuning were the hidden layer size, alpha, initial learning rate, activation function, learning rate, max iteration, momentum, and solver. Autotuning was used to determine the optimal combinations of hyperparameters, which were then saved as the updated model. By comparing and analyzing the measured and predicted values for a given period, the updated model’s predictive performance (in terms of CvRMSE and R2) was verified, thus confirming its applicability. Autotuning improved the model’s predictive performance, with its predictive accuracy exceeding 90%. Although this is a relatively simple model with autotuning applied to the base model, it performed well in predicting LNG consumption. The findings suggest that machine-learning-based prediction can be used to monitor and manage energy consumption at industrial sites. This predictive model may be particularly useful in predicting thermal energy use, which accounts for a large proportion of the food industry.
Although these findings cannot be generalized (because the model can generate different outcomes depending on factors such as research targets and data characteristics), they provide insights into the types of data that should be collected depending on the research targets and the ranges that should be considered for tuning hyperparameters. In this study, hyperparameter tuning was applied only to the base model. Additional enhancements are anticipated with further improvements to the model. Given that this study is focused on a comparison with the predeveloped base model, we utilized available data types from the initial research phase to construct the base model, such as product production and LNG temperature. Specifically, data from a relatively shorter period—daily data from 6 December 2021 to 19 March 2022—were utilized. However, there is potential to enhance this study by broadening the scope of the data categories and extending the duration of future investigations. Additionally, we intend to integrate this predictive function into FEMSs to enhance its efficiency in industrial settings. This integration will include a mechanism to automatically retrain the model when prediction performance declines below a certain threshold, along with features to automatically generate prediction values and assess prediction accuracy. In addition, although the current study focuses on LNG, we plan to expand and apply the results of this study to research on various other energies, thereby contributing to improving energy efficiency across the industrial sector.
Author Contributions
Conceptualization, H.L., W.C. and J.-h.G.; Methodology, H.L., W.C. and J.-h.P.; Software, H.L.; Writing—original draft preparation, H.L.; Writing—review and editing, H.L. and J.-h.P.; Visualization, H.L. and J.-h.P.; Supervision, J.-h.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (20202020800290).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available, owing to the funding institution’s research data-security commitments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Korea Energy Economics Institute. The 2024 Energy Demand Forecast (Second Half of 2023); Korea Energy Economics Institute: Ulsan, Republic of Korea, 2024; pp. 7–9. ISSN 1599-9009. Available online: https://www.kesis.net/FileDownloadAction.do?file=/admin/admin_RegList.jsp/20240110/704451704875652202_01.pdf&oldFile=_2024%EB%85%84_%EC%97%90%EB%84%88%EC%A7%80%EC%88%98%EC%9A%94%EC%A0%84%EB%A7%9D(2023_%ED%95%98%EB%B0%98%EA%B8%B0%ED%98%B8).pdf (accessed on 1 May 2024).
- Korea Energy Economics Institute. Nov. Mid-Term Energy Demand Forecast (2022–2027); Korea Energy Economics Institute: Ulsan, Republic of Korea, 2023; pp. 7–10. ISSN 2287-2841. Available online: https://www.keei.re.kr/web_keei/d_results.nsf/0/BA9D951CBD18E3CB492583940025A4F5/$file/MOL18.PDF (accessed on 1 May 2024).
- Korea Energy Statistical Information System, Energy Demand Forecast. Available online: https://www.kesis.net/sub/sub_0005_01.jsp (accessed on 22 January 2024).
- Korea Energy Agency. 2022 Energy Usage Statistics—Companies Reporting Energy Usage, 2023, 28–49. Available online: https://www.data.go.kr/data/15004793/fileData.do (accessed on 1 May 2024).
- Pereira, R.N.; Vicente, A.A. Environmental impact of novel thermal and non-thermal technologies in food processing. Food Res. Int. 2010, 43, 1936. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Beckman, W.A.; Broman, L.; Fiksel, A.; Klein, S.A.; Lindberg, E.; Schuler, M.; Thornton, J. TRNSYS the most complete solar energy system modeling and simulation software. Renew. Energy 1994, 5, 486–488. [Google Scholar] [CrossRef]
- Ji, H.-Y.; Kang, C.-D.; Park, D.-H. Heat consumption prediction models based on machine learning for district heating-applied apartment houses. J. Mech. Sci. Technol. B 2023, 47, 663–672. [Google Scholar] [CrossRef]
- Kim, J.-W.; Kwak, Y.-H.; Mun, S.-H.; Huh, J.-H. Electric energy consumption predictions for residential buildings: Impact of data-driven model and temporal resolution on prediction accuracy. J. Build. Eng. 2002, 62, 105361. [Google Scholar] [CrossRef]
- Bekdaş, G.; Aydın, Y.; Isıkdağ, Ü.; Sadeghifam, A.N.; Kim, S.-H.; Geem, Z.-W. Prediction of cooling load of tropical buildings with machine learning. Sustainability 2023, 15, 9061. [Google Scholar] [CrossRef]
- Matos, M.; Almeida, J.; Gonçalves, P.; Baldo, F.; Braz, F.J.; Bartolomeu, P.C. A machine learning-based electricity consumption forecast and management system for renewable energy communities. Energies 2024, 17, 630. [Google Scholar] [CrossRef]
- Son, N.-R.; Shin, Y.-J. Short- and medium-term electricity consumption forecasting using Prophet and GRU. Sustainability 2023, 15, 15860. [Google Scholar] [CrossRef]
- Won, J.-H.; Shin, J.-M.; Kim, J.-H.; Lee, J.-W. A survey on hyperparameter optimization in machine learning. J. Kor. Inst. Commun. Inf. Sci. 2023, 48, 733–747. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Bengio, Y.; Courvile, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.-B.; Seo, B.-M.; Han, J.-M.; Lee, K.-H.; Cho, S.-Y. Trends of research on building energy efficiency utilizing artificial intelligence technologies: Focused on international journal papers. KIEAE J. 2020, 20, 169–176. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting energy use in buildings using artificial neural networks: A review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef]
- Lee, H.-A.; Kim, D.-J.; Gu, J.-H. Prediction of food factory energy consumption using MLP and SVR algorithms. Energies 2023, 16, 1550. [Google Scholar] [CrossRef]
- Moon, Y.-H.; Ikhee, Y.-J.L.; Min, O. Recent research & development trends in automated machine learning. Electron. Telecommun. Trends 2019, 34, 32–42. [Google Scholar]
- Koch, P.; Golovidov, O.; Gardner, S.; Wujek, B.; Griffin, J.; Xu, Y. Autotune: A derivative-free optimization framework for hyperparameter tuning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 443–452. [Google Scholar] [CrossRef]
- Ko, B.-G. Development of Optimal Species Distribution Models Using the Bayesian Optimization and Model Interpretation. Master’s Thesis, University of Seoul, Seoul, Republic of Korea, 2021. [Google Scholar]
- Cho, Y.-H. Development of a Prediction Model for a Conceptual Cost Estimate of Public Offices Based on Machine Learning and Regression Analysis. Master’s Thesis, Gyeongsang National University, Gyeongsangnam-do, Republic of Korea, 2021. [Google Scholar]
- Jafar, A.; Lee, M.-H. Comparative performance evaluation of state-of-the-art hyperparameter optimization frameworks. Trans. Korean Inst. Electr. Eng. 2023, 72, 607–620. [Google Scholar] [CrossRef]
- Kim, J.-H.; Chae, G.-J.; Park, J.-M.; Park, K.-W. A data-driven classifier for motion detection of soldiers on the battlefield using recurrent architectures and hyperparameter optimization. J. Intell. Inform. Syst. 2023, 29, 107–119. [Google Scholar] [CrossRef]
- Feurer, M.; Hutter, F. Hyperparameter optimization. In Automated Machine Learning: Methods, Systems, Challenges; Hutter, F., Kotthoff, L., Vanschoren, J., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 3–33. [Google Scholar] [CrossRef]
- Bellman, R.E. Adaptive Control Processes: A Guided Tour; Princeton University Press: Princeton, NJ, USA, 1961. [Google Scholar]
- Klein, A.; Falkner, S.; Bartels, S.; Henning, P.; Hutter, F. Fast Bayesian optimization of machine learning hyperparameters on large datasets. Proc. Mach. Learn. Res. 2017, 54, 528–536. [Google Scholar] [CrossRef]
- Li, H.-S.; Yang, W.-Y.; Yong, X.-S. Deep learning for ground-roll noise attenuation. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2018; pp. 1981–1985. [Google Scholar] [CrossRef]
- Choi, Y.-U.; Yoon, D.-U.; Choi, J.-W.; Byun, J.-M. Hyperparameter search for facies classification with Bayesian optimization. Geophys. Geophys. Explor. 2020, 23, 157–167. [Google Scholar]
- Brochu, E.; Cora, V.M.; de Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv 2010, arXiv:1012.2599. Available online: https://arxiv.org/pdf/1012.2599.pdf (accessed on 1 May 2024).
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural. Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar] [CrossRef]
- ASHRAE (American Society of Heating, Refrigerating and Air Conditioning Engineers). ASHRAE Guideline 14: Measurement of Energy and Demand Savings; ASHRAE: Atlanta, GA, USA, 2022; pp. 4–165. [Google Scholar]
- Webster, L.J.; Bradford, J. M&V Guidelines: Measurement and Verification for Federal Energy Projects, Version 3.0; Technical Report; U.S. Department of Energy Federal Energy Management Program: Washington, DC, USA, 2008.
- Efficiency Valuation Organization. International Performance Measurement & Verification Protocol; EVO: North Georgia, AL, USA, 2016. [Google Scholar]
- Fernández Bandera, C.; Ramos Ruiz, G. Towards a new generation of building envelope calibration. Energies 2017, 10, 2102. [Google Scholar] [CrossRef]
- Seong, N.-C.; Hong, G.-Y. Comparative evaluation of building cooling load prediction models with multi-layer neural network learning algorithms. KIEAE J. 2022, 22, 35–41. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).