A Predictive Energy Management Strategy for Heavy Hybrid Electric Vehicles Based on Adaptive Network-Based Fuzzy Inference System-Optimized Time Horizon
Abstract
1. Introduction
- To further optimize the predictive energy management strategy and improve the fuel economy of HEVs, a predictive energy management strategy based on ANFIS optimization was proposed.
- The RBF neural network is applied to predict vehicle velocity in MPC, aiming at optimal fuel consumption; DP is used to solve the optimal diesel genset output power in the forecast time domain.
- The performance is verified through comparison among different methods.
2. The Plant Model of HEV
2.1. Vehicle Dynamics
2.2. Diesel Genset Model
2.3. Battery Model
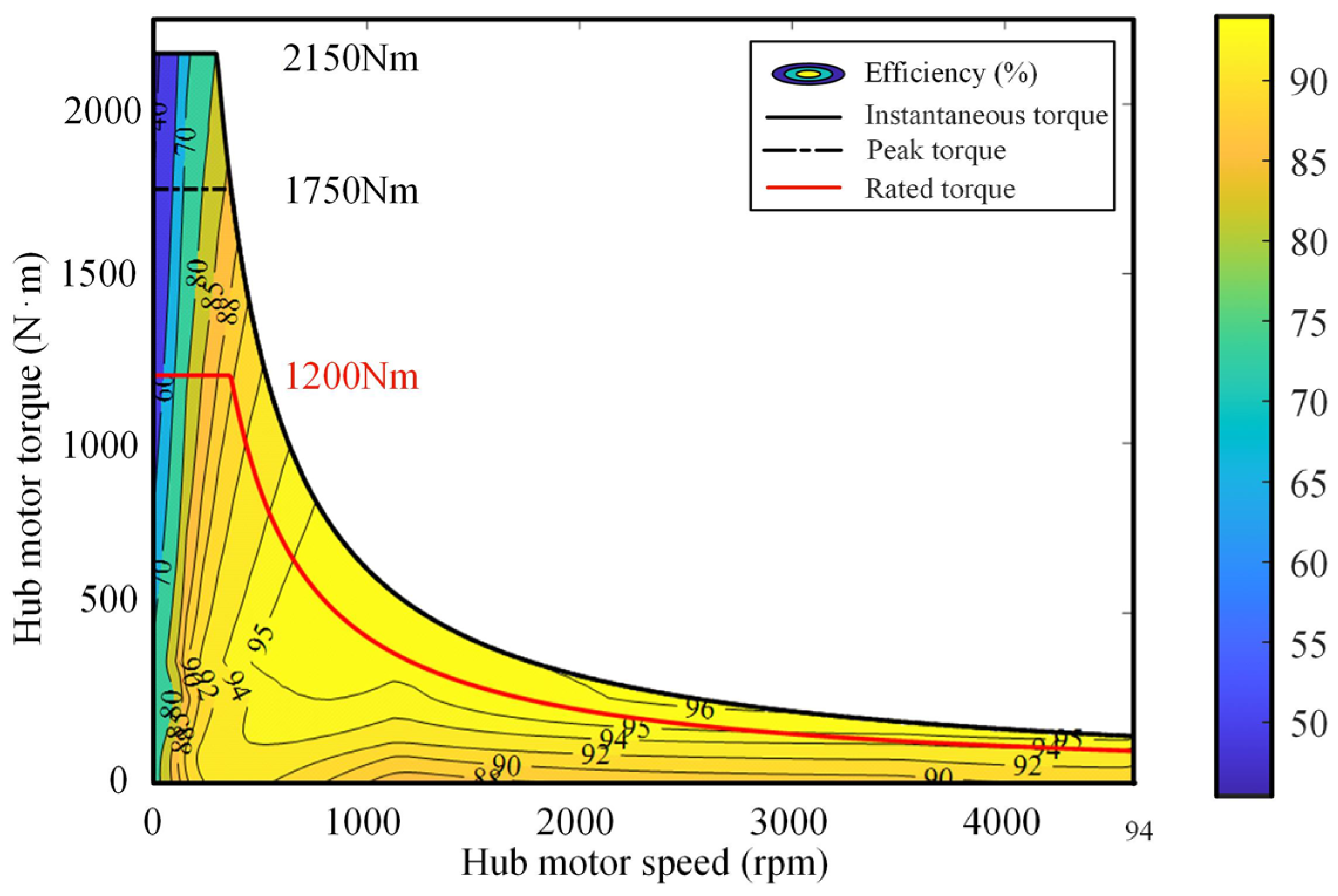
2.4. Hub Motor Model
3. Architecture of Control System
3.1. Prediction Model
3.2. Tables and Schemes B. Time Horizon Optimization Based on ANFIS
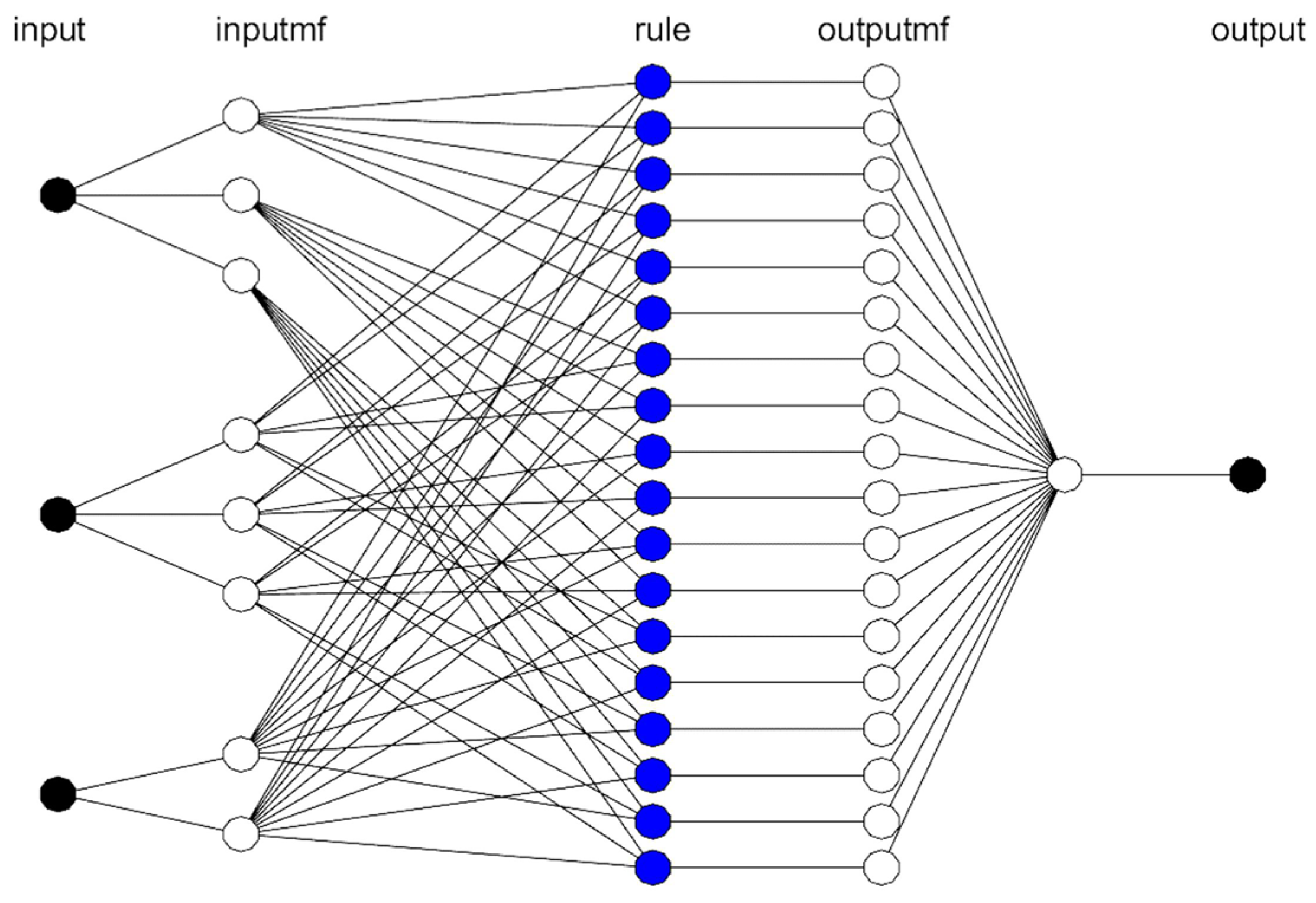
3.2.1. Fuzzy Neural Network Structure
3.2.2. Learning Algorithms for Fuzzy Neural Networks
3.2.3. Training Results
3.3. Cost Function and Limitations
3.4. Optimization Based on DP Algorithm
4. Simulation Results and Analysis
4.1. Training Setting
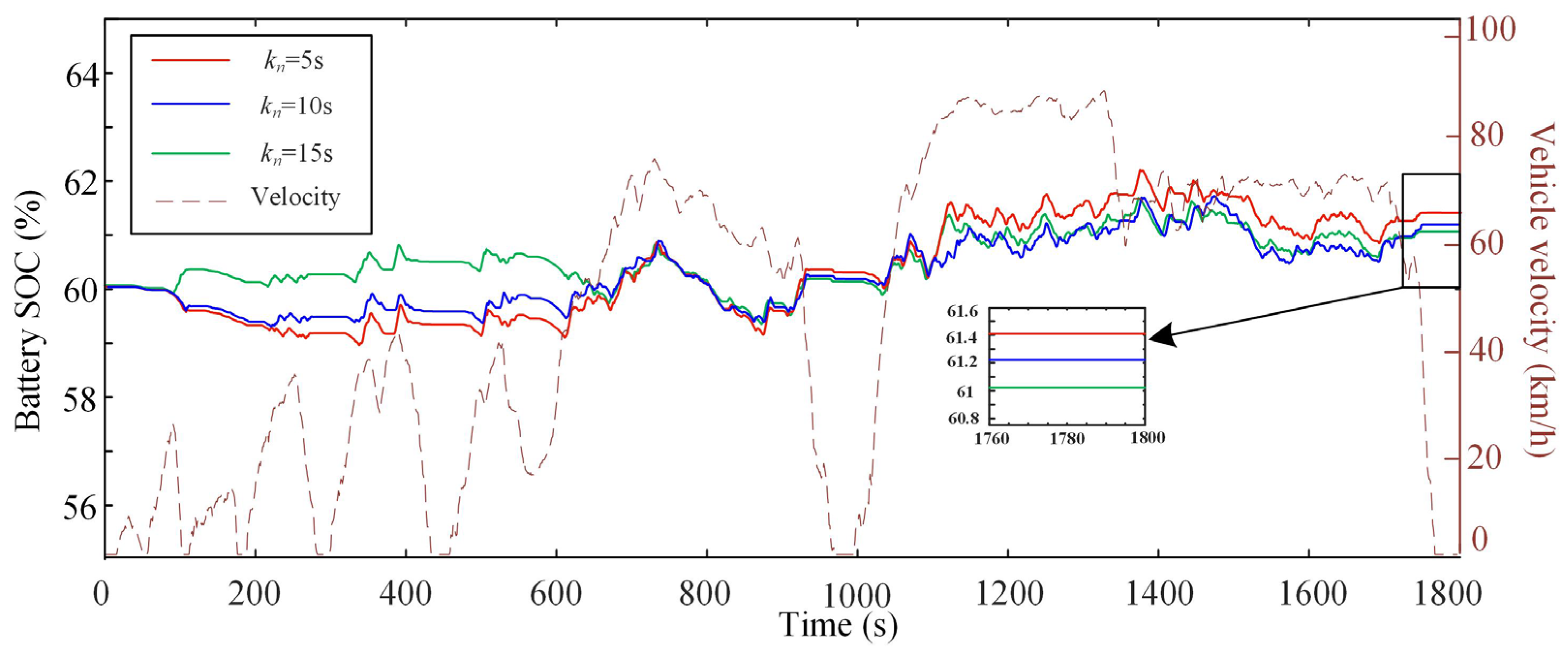
4.2. Simulation Analysis of RBF–MPC
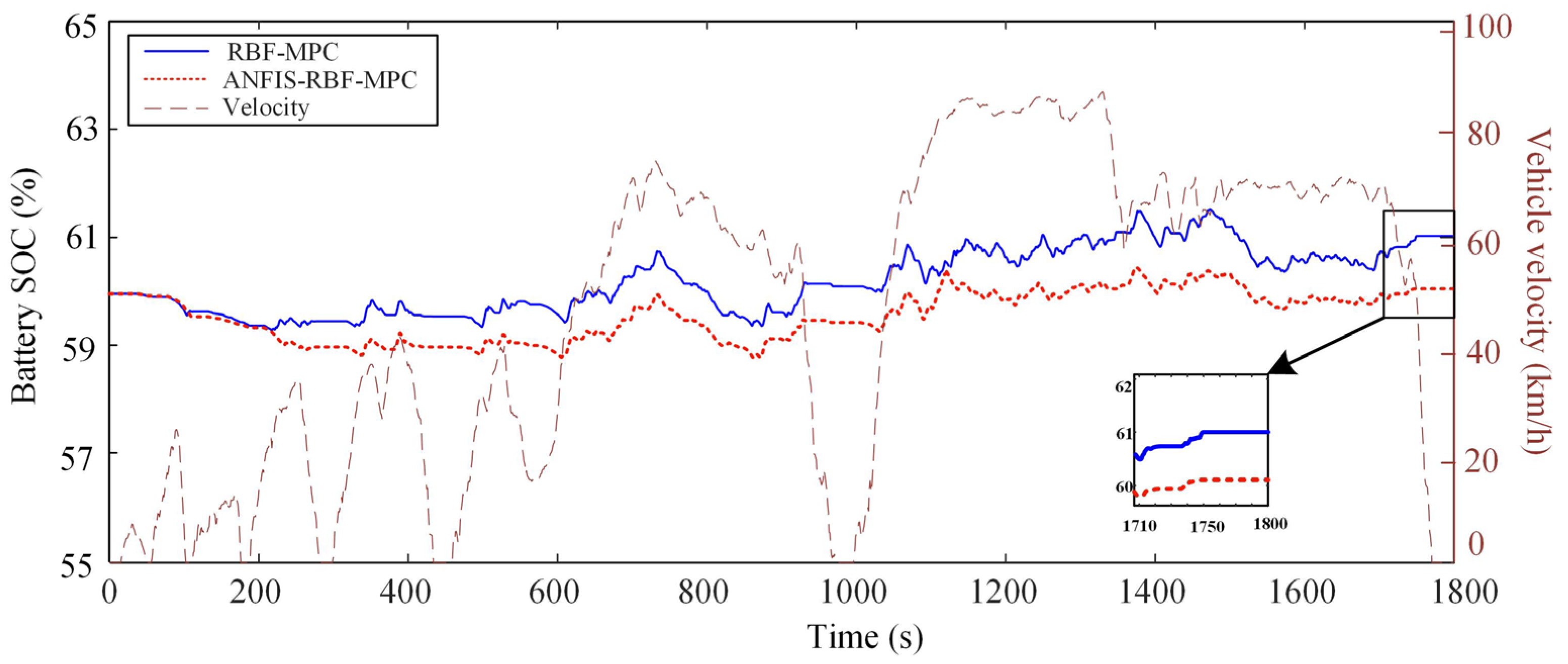
4.3. Simulation Analysis of RBF–ANFIS–MPC
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, C.; Du, X.; Wang, W.; Yang, L.; Zha, M. A Rolling Convergent Equivalent Consumption Minimization Strategy for Plug-in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2024, 73, 3340–3353. [Google Scholar] [CrossRef]
- Tang, X.; Jia, T.; Hu, X.; Huang, Y.; Deng, Z.; Pu, H. Naturalistic Data-Driven Predictive Energy Management for Plug-In Hybrid Electric Vehicles. IEEE Trans. Transp. Electrif. 2021, 7, 497–508. [Google Scholar] [CrossRef]
- Biswas, A.; Emadi, A. Energy Management Systems for Electrified Powertrains: State-of-the-Art Review and Future Trends. IEEE Trans. Veh. Technol. 2019, 68, 6453–6467. [Google Scholar] [CrossRef]
- Nguyen, N.-D.; Yoon, C.; Lee, Y.I. A Standalone Energy Management System of Battery/Supercapacitor Hybrid Energy Storage System for Electric Vehicles Using Model Predictive Control. IEEE Trans. Ind. Electron. 2023, 70, 5104–5114. [Google Scholar] [CrossRef]
- Chatterjee, D.; Biswas, P.K.; Sain, C.; Roy, A.; Ahmad, F. Efficient Energy Management Strategy for Fuel Cell Hybrid Electric Vehicles Using Classifier Fusion Technique. IEEE Access 2023, 11, 97135–97146. [Google Scholar] [CrossRef]
- Chang, C.; Fan, Z.; Wang, Z.; Liu, H. Research on Adaptive Two-Point Energy Management Strategy and Optimization for Range-Extended Electric Vehicle. IEEE Access 2023, 11, 90201–90213. [Google Scholar] [CrossRef]
- Jia, C.; Qiao, W.; Cui, J.; Qu, L. Adaptive Model-Predictive-Control-Based Real-Time Energy Management of Fuel Cell Hybrid Electric Vehicles. IEEE Trans. Power Electron. 2023, 38, 2681–2694. [Google Scholar] [CrossRef]
- Banvait, H.; Anwar, S.; Chen, Y. A rule-based energy management strategy for Plug-in Hybrid Electric Vehicle (PHEV). In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3938–3943. [Google Scholar]
- Li, Q.; Chen, W.; Li, Y.; Liu, S.; Huang, J. Energy management strategy for fuel cell/battery/ultracapacitor hybrid vehicle based on fuzzy logic. Int. J. Electr. Power Energy Syst. 2012, 43, 514–525. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Z.; Huang, D.; Lin, T. Model prediction and Rule Based energy management strategy for a plug-in hybrid electric vehicle with hybrid energy storage system. IEEE Trans. Power Electron. 2021, 36, 5926–5940. [Google Scholar] [CrossRef]
- Tao, F.; Zhu, L.; Ji, B.; Si, P.; Fu, Z. Energy management strategy using equivalent consumption minimization strategy for hybrid electric vehicles. Secur. Commun. Netw. 2020, 2020, 6642304. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.D.; Xu, M.; Liu, Y.G. A real-time optimization energy management of range extended electric vehicles for battery lifetime and energy consumption. J. Power Sources 2021, 498, 229939. [Google Scholar] [CrossRef]
- Wieczorek, M.; Lewandowski, M. A mathematical representation of an energy management strategy for hybrid energy storage system in electric vehicle and real time optimization using a genetic algorithm. Appl. Energy 2017, 192, 222–233. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Wang, Y.; Jiao, X. An Intelligent Logic Rule-Based Energy Management Strategy for Power-Split Plug-in Hybrid Electric Vehicle. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 7668–7672. [Google Scholar]
- Tao, F.; Zhu, L.; Fu, Z.; Si, P.; Sun, L. Frequency Decoupling-Based Energy Management Strategy for Fuel Cell/Battery/Ultracapacitor Hybrid Vehicle Using Fuzzy Control Method. IEEE Access 2020, 8, 166491–166502. [Google Scholar] [CrossRef]
- Erdinc, O.; Vural, B.; Uzunoglu, M. A wavelet-fuzzy Logic Based energy management strategy for a fuel cell/battery/ultra-capacitor hybrid vehicular power system. J. Power Sources 2009, 194, 38–44. [Google Scholar] [CrossRef]
- Hamlat, A.; Sekkour, M.; Mankour, M.; Khalfaoui, M. An improved energy management system for fuel cell/ultra-capacitor electric vehicle based fuzzy logic control. In Artificial Intelligence and Heuristics for Smart Energy Efficiency in Smart Cities; Springer: Cham, Switzerland, 2021; Volume 361, pp. 183–189. [Google Scholar]
- Li, L.; Yang, C.; Zhang, Y.; Zhang, L.; Song, J. Correctional DP-Based Energy Management Strategy of Plug-In Hybrid Electric Bus for City-Bus Route. IEEE Trans. Veh. Technol. 2015, 64, 2792–2803. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2016, 185, 1633–1643. [Google Scholar] [CrossRef]
- Zou, Y.; Hou, S.; Han, E.; Liu, L.; Chen, R. Dynamic Programming-based Energy Management Strategy Optimization for Hybrid Electric Commercial Vehicle. Automot. Eng. 2012, 34, 663–668. [Google Scholar]
- Fan, L.; Wang, Y.; Wei, H.; Zhang, Y.; Zheng, P.; Huang, T.; Li, W. A GA-based online real-time optimized energy management strategy for plug-in hybrid electric vehicles. Energy 2021, 241, 122811. [Google Scholar] [CrossRef]
- Ding, N.; Prasad, K.; Lie, T.T. Design of a hybrid energy management system using designed rule-based control strategy and genetic algorithm for the series-parallel plug-in hybrid electric. Int. J. Energy Res. 2021, 45, 1627–1644. [Google Scholar] [CrossRef]
- Yuan, H.B.; Zou, W.J.; Jung, S.; Kim, Y.B. Optimized rule-based energy management for a polymer electrolyte membrane fuel cell/battery hybrid power system using a genetic algorithm. Int. J. Hydrogen Energy 2021, 47, 7932–7948. [Google Scholar] [CrossRef]
- Tian, X.; He, R.; Sun, X.; Cai, Y.; Xu, Y. An ANFIS-Based ECMS for Energy Optimization of Parallel Hybrid Electric Bus. IEEE Trans. Veh. Technol. 2020, 69, 1473–1483. [Google Scholar] [CrossRef]
- Rezaei, A.; Burl, J.B.; Zhou, B.; Rezaei, M. A New Real-Time Optimal Energy Management Strategy for Parallel Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2019, 27, 830–837. [Google Scholar] [CrossRef]
- Zhou, B.; Burl, J.B.; Rezaei, A. Equivalent Consumption Minimization Strategy with Consideration of Battery Aging for Parallel Hybrid Electric Vehicles. IEEE Access 2020, 8, 204770–204781. [Google Scholar] [CrossRef]
- Zhou, Y.; Ravey, A.; Péra, M.-C. Multi-mode predictive energy management for fuel cell hybrid electric vehicles using Markov driving pattern recognizer. Appl. Energy 2019, 258, 114057. [Google Scholar] [CrossRef]
- Li, T.; Liu, H.; Wang, H.; Yao, Y. Hierarchical predictive control-based economic energy management for fuel cell hybrid construction vehicles. Energy 2020, 198, 117327. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Qi, S.; Tang, X.; Lang, K.; Xin, Z.; Brighton, J. Model predictive energy management for plug-in hybrid electric vehicles considering optimal battery depth of discharge. Energy 2019, 173, 667–678. [Google Scholar] [CrossRef]
- Hao, J.; Ruan, S.; Wang, W. Model Predictive Control Based Energy Management Strategy of Series Hybrid Electric Vehicles Considering Driving Pattern Recognition. Electronics 2023, 12, 1418. [Google Scholar] [CrossRef]
- Xiang, C.; Ding, F.; Wang, W.; He, W. Energy management of a dual-mode power-split hybrid electric vehicle based on velocity prediction and nonlinear model predictive control. Appl. Energy 2016, 181, 640–653. [Google Scholar] [CrossRef]
- Kohut, N.J.; Hedrick, J.K.; Borrelli, F. Integrating Traffic Data and Model Predictive Control to Improve Fuel Economy. IFAC Proc. Vol. 2009, 42, 155–160. [Google Scholar] [CrossRef]
- Yu, K.; Xu, X.; Hu, Z. Predictive control strategies for energy saving of hybrid electric vehicles based on traffic light information. J. Hebei Univ. Sci. Technol. 2015, 36, 480–486. [Google Scholar]
- Shu, H.; Nie, T.; Deng, L.; Qiao, J. Model predictive control for a plug-in hybrid electric vehicle. J. Chongqing Univ. 2011, 34, 36–41. [Google Scholar]
- Zhang, J.; Shen, T. Real-Time Fuel Economy Optimization with Nonlinear MPC for PHEVs. IEEE Trans. Control Syst. Technol. 2016, 24, 2167–2175. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust Optimal Demand Response of Energy-efficient Commercial Buildings. In Proceedings of the European Control Conference (ECC), London, UK, 12–15 July 2022; pp. 1–6. [Google Scholar]
- Lu, L.; Zhao, H.; Liu, X.; Sun, C.; Zhang, X.; Yang, H. MPC-ECMS Energy Management of Extended-Range Vehicles Based on LSTM Multi-Signal Speed Prediction. Electronics 2023, 12, 2642. [Google Scholar] [CrossRef]
- Xu, E.; Ma, M.; Zheng, W.; Huang, Q. An Energy Management Strategy for Fuel-Cell Hybrid Commercial Vehicles Based on Adaptive Model Prediction. Sustainability 2023, 15, 7915. [Google Scholar] [CrossRef]
- Liu, C.; Li, X.; Chen, Y.; Wei, C.; Liu, X.; Li, K. Real-time energy management strategy for fuel cell/battery vehicle based on speed prediction DP solver model predictive control. J. Energy Storage 2023, 73, 109288. [Google Scholar] [CrossRef]
- Liu, J.; Liang, Y.; Chen, Z.; Yang, H. An ECMS Based on Model Prediction Control for Series Hybrid Electric Mine Trucks. Energies 2023, 16, 3942. [Google Scholar] [CrossRef]
- Yang, X.P.; Jiang, C.Y.; Zhou, M.; Hu, H. Bi-level energy management strategy for power-split plug-in hybrid electric vehicles: A reinforcement learning approach for prediction and control. Front. Energy Res. 2023, 11, 1153390. [Google Scholar] [CrossRef]
- Yao, Z.Y.; Shao, R.P.; Zhan, S.N.; Mo, R.; Wu, Z. Energy management strategy for fuel cell hybrid electric vehicles using Pontryagin’s minimum principle and dynamic SoC planning. Energy Sources Part A-Recovery Util. Environ. Eff. 2023, 46, 5112–5132. [Google Scholar] [CrossRef]
- Chen, Z.; Gu, H.; Shen, S.; Shen, J. Energy management strategy for power-split plug-in hybrid electric vehicle based on MPC and double Q-learning. Energy 2022, 245, 123182. [Google Scholar] [CrossRef]
- Cao, J.; Peng, J.; He, H. Research on Model Prediction Energy Management Strategy with Variable Horizon. Energy Procedia 2017, 105, 3565–3570. [Google Scholar] [CrossRef]
- Kong, Y.; Xu, N.; Liu, Q.; Sui, Y.; Jia, Y. Variable horizon-based predictive energy management strategy for plug-in hybrid electric vehicles and determination of a suitable predictive horizon. Energy 2024, 294, 130809. [Google Scholar] [CrossRef]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics, 1st ed.; Tsinghua University Press: Beijing, China, 2006. [Google Scholar]
- Bo, L.; Han, L.; Xiang, C.; Liu, H.; Ma, T. A Q-learning fuzzy inference system based online energy management strategy for off-road hybrid electric vehicles. Energy 2022, 252, 123976. [Google Scholar] [CrossRef]
- Badreddine, B.; Amar, B.; Noureddine, H. Design and real-time implementation of an adaptive fast terminal synergetic controller based on dual RBF neural networks for voltage control of DC–DC step-down converter. Electr. Eng. 2022, 104, 945–957. [Google Scholar]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Djukanovic, M.B.; Calovic, M.S.; Vesovic, B.V.; Sobajic, D.J. Neuro-fuzzy controller of low head hydropower plants using adaptive-network based fuzzy inference system. IEEE Trans. Energy Convers. 1997, 12, 375–381. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Bardhan, A.; Kardani, N.; Samui, P.; Hu, J.W.; Ramzy, A. Novel application of adaptive swarm intelligence techniques coupled with adaptive network-based fuzzy inference system in predicting photovoltaic power. Renew. Sustain. Energy Rev. 2021, 148, 111315. [Google Scholar] [CrossRef]
- Niasar, A.H.; Vahedi, A.; Moghbelli, H. ANFIS-based controller with fuzzy supervisory learning for speed control of 4-switch inverter brushless DC motor drive. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; pp. 1–5. [Google Scholar]
















| Component | Item | Value |
|---|---|---|
| Vehicle | Curb weight (kg) | 16,000 |
| Wheel radius (m) | 0.56 | |
| Wind area (m2) | 3.2 | |
| Coefficient of rolling resistance | 0.008 | |
| Air drag coefficient | 0.35 | |
| Gravity acceleration (m/s2) | 9.8 | |
| Diesel genset | Peak power (kW) | 260 |
| Rated power (kW) | 150 | |
| Engine rotational inertia (kg⋅m2) | 92.77 | |
| Generator rotational inertia (kg⋅m2) | 3.297 | |
| Hub motor | Peak power (kW) | 66 |
| Rated power (kW) | 46 | |
| Maximum speed (rpm) | 5000 | |
| Peak torque (Nm) | 1750 | |
| Rated torque (Nm) | 1200 | |
| Battery | Type | Lithium battery |
| Capacity (Ah) | 75 | |
| Rate Voltage (V) | 601.2 | |
| Hub motor transmission | Gear Ratio | 7.885 |
| Hub motor controller | Efficiency (%) | 90 |
| Cycle | Velocity Max (km/h) | Average Velocity (km/h) | During Time (s) | Distance (km) |
|---|---|---|---|---|
| CHTC-TT | 88 | 46.44 | 1800 | 21.3 |
| UDDS | 91.2 | 31.5 | 1370 | 12.07 |
| NEDC | 120 | 24.7 | 1180 | 11.02 |
| HWFET | 96.37 | 77.7 | 765 | 16.45 |
| SFTP-US06 | 129.2 | 77.9 | 596 | 12.8 |
| WLTP | 131.3 | 46.5 | 1800 | 23.27 |
| Time Horizon (s) | RMSE | Initial SOC | Final SOC | Fuel (L/100 km) | Calculation Time (s) |
|---|---|---|---|---|---|
| 5 | 0.061 | 60 | 61.42 | 17.85 | 0.016 |
| 10 | 1.326 | 60 | 61.26 | 17.16 | 0.034 |
| 15 | 2.595 | 60 | 61.15 | 17.23 | 0.059 |
| Method | Initial SOC | Final SOC | Fuel (L/100 km) | Calculation Time (s) |
|---|---|---|---|---|
| RBF–MPC | 60 | 61.26 | 17.16 | 0.034 |
| RBF–ANFIS–MPC | 60 | 60.51 | 16.11 | 0.026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, B.; Wei, C.; Feng, F.; Liu, T. A Predictive Energy Management Strategy for Heavy Hybrid Electric Vehicles Based on Adaptive Network-Based Fuzzy Inference System-Optimized Time Horizon. Energies 2024, 17, 2288. https://doi.org/10.3390/en17102288
Lin B, Wei C, Feng F, Liu T. A Predictive Energy Management Strategy for Heavy Hybrid Electric Vehicles Based on Adaptive Network-Based Fuzzy Inference System-Optimized Time Horizon. Energies. 2024; 17(10):2288. https://doi.org/10.3390/en17102288
Chicago/Turabian StyleLin, Benxiang, Chao Wei, Fuyong Feng, and Tao Liu. 2024. "A Predictive Energy Management Strategy for Heavy Hybrid Electric Vehicles Based on Adaptive Network-Based Fuzzy Inference System-Optimized Time Horizon" Energies 17, no. 10: 2288. https://doi.org/10.3390/en17102288
APA StyleLin, B., Wei, C., Feng, F., & Liu, T. (2024). A Predictive Energy Management Strategy for Heavy Hybrid Electric Vehicles Based on Adaptive Network-Based Fuzzy Inference System-Optimized Time Horizon. Energies, 17(10), 2288. https://doi.org/10.3390/en17102288






