1. Introduction
Crosslinked polyethylene (XLPE) cables are widely used in urban distribution networks [
1]. However, under long-term high-temperature operating conditions, the XLPE insulation material of power cables will inevitably undergo thermal aging, leading to deterioration in electrical, mechanical, and thermal performance, and even cable failures [
2,
3,
4]. Since thermal aging often occurs throughout the entire cable, it may cause a decrease in the performance of the entire cable line, and ultimately lead to multiple points of breakdown [
5]. Therefore, a timely and accurate detection of the thermal aging degree of the cable is crucial for the safe and stable operation of the power system.
The polarization and depolarization current (PDC) measurement has been increasingly applied in the evaluation of the insulation condition in recent years due to its advantages of fewer measurement modules, lightweight equipment, lower cost, and shorter measurement time [
6,
7,
8]. Researchers have extracted various diagnostic parameters such as the polarization current, aging factor, PDC slope, relationship between the depolarization current and time, DC conductivity and its non-linear coefficient, 0.1 Hz dielectric loss and its non-linear coefficient, etc., from PDC measurement results, to diagnose the insulation condition of cables [
9,
10,
11,
12]. These parameters can reflect the overall electrical performance of the cable. However, there has been limited research on how to use PDC measurement results to determine the thermal aging degree of cables. It is worth noting that according to the extended Debye theory, the dielectric process of thermal-aged cables can usually be equivalent to a three-branch model, with each branch representing different polarization and depolarization types [
13]. Thermal aging will cause changes in the PDC characteristics of the cable, leading to changes in the branch parameters of the extended Debye model [
14]. If the information reflecting the degree of thermal aging of the cable can be separated from the extended Debye model, the accuracy of insulation diagnoses for thermal-aged cables can be greatly improved. However, it is still unclear what the correlation is between the three-branch parameters of the extended Debye model of thermal-aged cables and the degree of thermal aging. Meanwhile, the physical mechanism of thermal-aging-induced changes in XLPE dielectric properties also lacks sufficient investigations.
To address the aforementioned issues, this study artificially prepared short cable samples with different durations of thermal aging, and conducted PDC measurement on the samples. The variations of the cable DC conductivity, dielectric loss factor, and other parameters with thermal aging time were analyzed. The corresponding relationship between Debye model branch parameters and cable thermal aging time was determined. Additionally, differential scanning calorimetry (DSC) testing and scanning electron microscopy (SEM) testing were employed to analyze the influence of thermal aging duration on the structural parameters of XLPE insulation materials, based on which the physical mechanism of the changes in dielectric parameters of XLPE materials caused by thermal aging was analyzed from the perspective of the aggregated structure of XLPE.
2. Materials and Methods
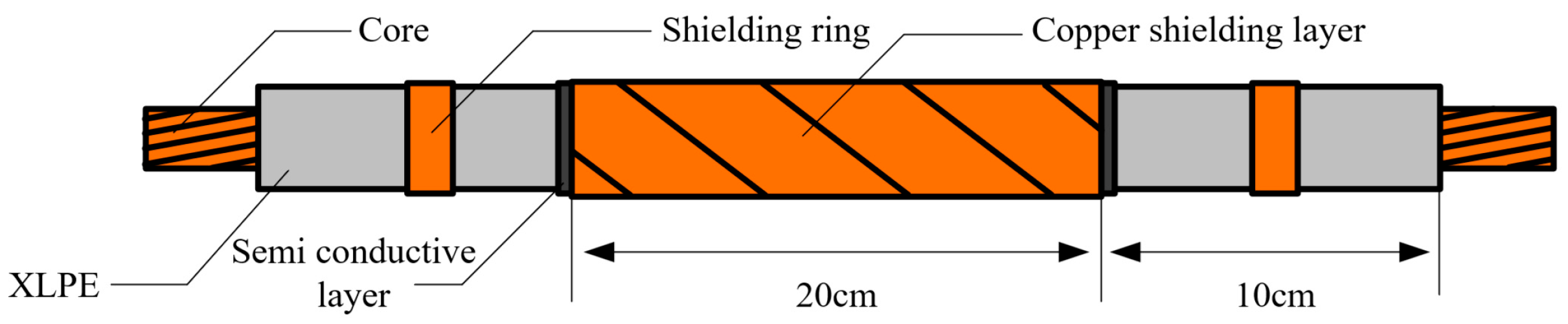
To conduct research on the thermal aging characteristics of cables, samples of short cables with different degrees of thermal aging were first prepared. These short cable samples were cut from XLPE long cables with a model of YJV22-3×95, rated at 8.7/10 kV. Each short cable sample was 50 cm long, as illustrated in
Figure 1. A total of 25 short cable samples were cut. Subsequently, the short cable samples were divided into five groups, G0, G1, G2, G3, and G4, with each group containing five cables. The short cable samples in groups G1, G2, G3, and G4 were placed in an oven for thermal aging, with aging temperatures set at 140 °C and aging durations of 108 h, 216 h, 324 h, and 432 h, respectively. The short cable samples in group G0 were not subjected to thermal aging and served as the control group for new cables.
After the thermal aging, PDC measurements were performed on the short cable samples, with the platform shown in
Figure 2. The DC power supply used was the ZGF-120 DC high-voltage generator, with an output DC voltage range of 0–5 kV, voltage ripple coefficient less than 0.1%, and maximum output current of 20 mA. The cable core was connected to the DC high-voltage generator, while the copper tape was connected to the ammeter current input port. Additionally, a shielding ring was added and grounded on the exposed insulation layer at both ends of the cable to avoid the influence of the surface current on the PDC measurement results. During the measurement, the switch S was toggled to positions S1 and S2 to measure the polarization current
ipol and depolarization current
idepol of the sample, respectively. The measurement voltage was set at 1 kV, with polarization and depolarization times both set to 90 s.
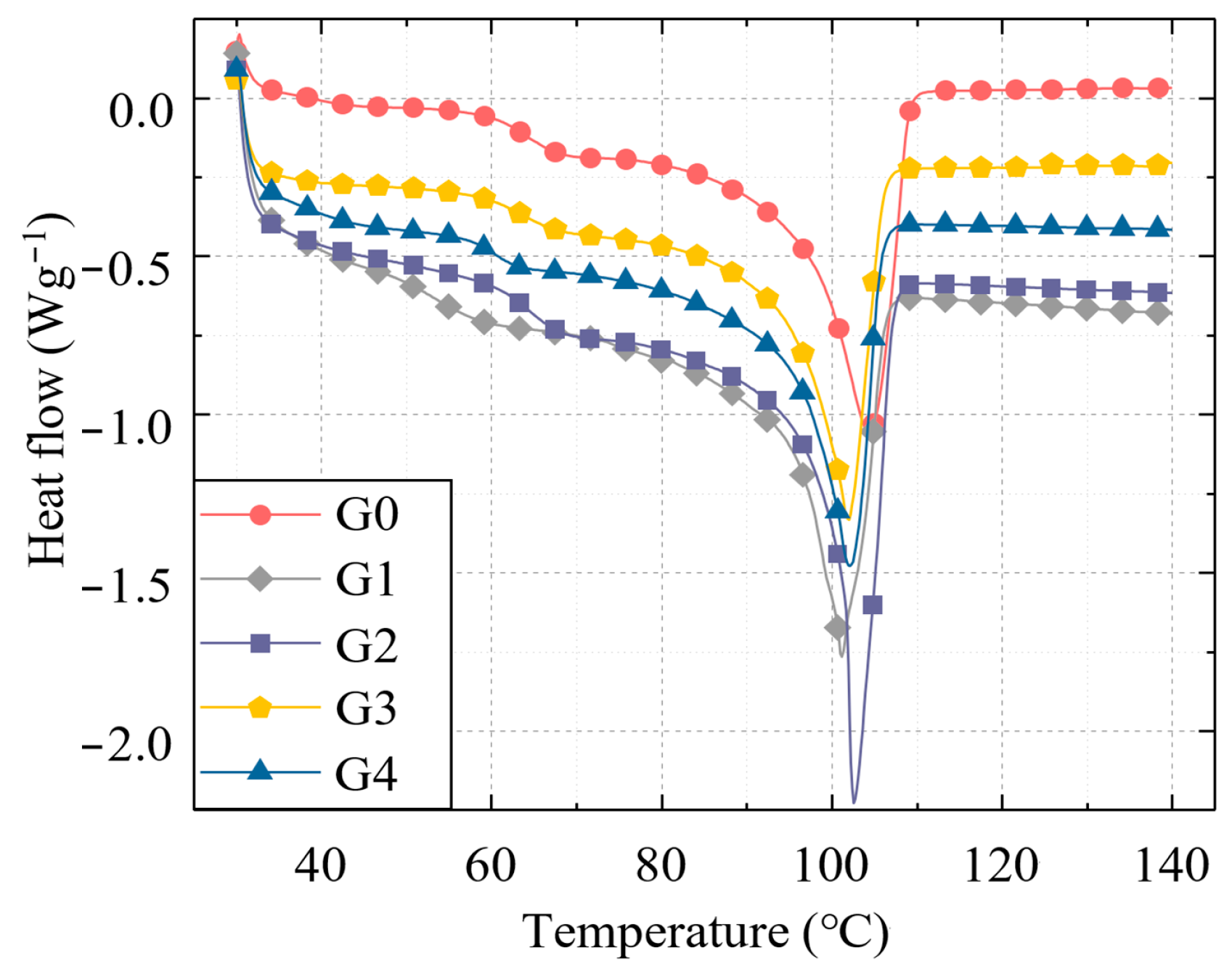
To comprehensively understand the changes in the mechanical properties and microstructure of samples before and after thermal aging, this study sliced the thermal-aged samples and conducted differential scanning calorimetry (DSC) tests and scanning electron microscopy (SEM) observations on the samples.
The DSC test can reflect the material’s elastic modulus [
15]. Before DSC testing, the semiconductor layers on both sides of the aged samples were removed to prevent other materials from mixing into the XLPE. Afterwards, the samples were cut into small pieces, with individual sample weights ranging from 3 mg to 8 mg. The cut block samples were placed in crucibles, with nitrogen gas being introduced into the entire testing environment as a protective gas. The samples were heated according to the programmed heating rate and temperature (30~140 °C, with a heating rate of 10 °C/min), during which the thermal flow changes in the sliced samples were recorded.
The SEM test can reflect the material’s microstructure [
16]. Before SEM testing, liquid nitrogen was used to quench the samples. The quenched sample surfaces were then gold-sputtered and observed under the SEM. The SEM testing instrument used in this experiment was the JSM-7500F scanning electron microscope, with an acceleration voltage range of 0.1 kV to 30 kV, an adjustable resolution range of 1.0 nm (15 kV) to 1.4 nm (1 kV), and an adjustable magnification range of 25 to 800,000 times. Since the cable samples underwent overall thermal aging, the observation area could be randomly selected.
3. Extraction Method of Electrical Parameters Based on PDC
PDC measurement can reflect various polarization and relaxation information inside the measured material. Based on the current obtained from the measurement, parameters such as the conductivity, dielectric loss factor, etc., can be calculated. Additionally, an extended Debye model reflecting the polarization type of the material can be constructed.
3.1. Extraction of Conventional Electrical Parameters
After applying a step voltage excitation to the cable, various electrical conduction and polarization processes begin within the XLPE insulation of the cable. This is the response of the insulation to the step voltage excitation applied, which can be manifested as a polarization current response. Since the capacitive current component decays rapidly, the influence of the capacitive current will be neglected in investigating the polarization process. At this point, the polarization current is mainly composed of the absorption current and conduction current.
The absorption current component is related to the polarizability of the insulating material of the cable. After applying an external electric field, the current response density
J(
t) within the insulation can be expressed as
In Equation (1), σ represents the conductivity of the insulating material; E(t) is the electric field strength applied to the material; and D(t) is the electric induction intensity of the material.
If the insulation layer of an XLPE cable is isotropic, the induced electric field strength inside the insulation when an external electric field is applied is related to the applied electric field strength and the polarization strength of the insulation material, as
In the equation,
ε0 represents the vacuum permittivity;
ε∞ is the relative dielectric constant of the insulating material at optical frequencies; and ∆
P(
t) is the rate of change of the polarization intensity of the material, which can be represented as
where
f(
t) represents the dielectric response function of the insulating material.
Therefore, the current response density
J(
t) can be expressed as follows:
The three components on the right side of Equation (4) are the conductive current density, the capacitive current density, and the absorption current density, respectively. When the insulating material is in a planar structure, the polarization process is characterized by the polarization current flowing through the interior of the material:
where
U(
t) represents the applied voltage.
Since an XLPE cable is of a coaxial structure, its geometric capacitance can be expressed as
In the equation, Di represents the outer diameter of the cable insulation layer; L represents the cable length; and DC represents the inner diameter of the cable insulation layer.
Due to the rapid decay of the capacitive current, it is often ignored. The polarized current after ignoring the capacitive current can be expressed as follows:
In the equation,
U0 represents the constant polarization voltage. Similarly, the depolarization current can be expressed as follows:
where
tc represents the polarization time.
Based on Equations (7) and (8), the conductivity of XLPE cable insulation can be inferred as
On the other hand, due to the limited information contained in the time-domain signal results measured by the PDC, it is necessary to perform a frequency-domain diagnosis of XLPE cable insulation aging. The current signal measured by the PDC can be transformed from the time domain to the frequency domain, typically using the Fourier transform, with the following specific method:
Equation (10) can also be expressed as
According to the definition of the dielectric loss factor, the dielectric loss factor of insulation materials can be calculated by the following equation:
In the equation, IR(ω) is the frequency domain expression of the resistive current, where IR(ω) = ωUC′(ω); IC(ω) is the frequency domain expression of the capacitive current, where IC(ω) = jωUC″(ω); C′ is the real part of complex capacitance; C″ is the imaginary part of complex capacitance; and ε′ and ε″ are the real and imaginary parts of the complex dielectric constant, respectively. It is worth mentioning that in the expressions of IR(ω) and IC(ω), U(ω) represents the frequency domain expression of the applied voltage signal, which is generally considered a step signal due to the high resistance of the XLPE cable.
3.2. Extraction of Extended Debye Model Branch Parameters
Dielectric molecules will undergo polarization under the action of an electric field. On the one hand, the positive and negative charge centers of the dielectric molecules will separate, forming electric dipoles. The orientation and distribution of electric dipoles vary with the variation of the electric field, thereby affecting the dielectric constant and other electrical properties of the dielectric molecules. On the other hand, when the dielectric molecules undergoes aging, there may be interfaces between structures with different degrees of aging [
17]. After applying an external DC electric field to the dielectric molecules, the electric fields on both sides of the interface transition from capacitive distribution to resistive distribution, during which charges accumulate at the interface, triggering the interface polarization process. Different dielectric structures or material types can correspond to different polarization processes, the dynamic characteristics of which can be described by the extended Debye model. Therefore, the extended Debye model is an effective method for studying the phenomenon of dielectric aging [
18,
19,
20,
21].
The extended Debye model mainly consists of three parts: the resistance branch corresponding to the resistance value of the dielectric molecules, the capacitance branch corresponding to the geometric capacitance of the dielectric molecules, and multiple
RC series branches, corresponding to different polarization processes within the dielectric molecules [
21]. The model is shown in
Figure 3.
In
Figure 3,
R0 represents the insulation resistance of the dielectric molecules; in other words, this branch corresponds to the conductivity process inside the dielectric molecules. The current flowing through
R0 is the conductance current during polarization.
C0 represents the geometric capacitance of the dielectric molecules, which corresponds to the capacitive charging process inside the dielectric molecules just after an externally applied DC voltage is applied to the dielectric molecules. The current flowing through
C0 is the capacitive current during polarization. And since the
RC series branch corresponds to the polarization process, the current flowing through each
RC series branch is the various types of polarization absorption currents.
In the extended Debye model, the complex dielectric constant of the dielectric molecules is given by the following equation:
Among which εs represents the dielectric constant of the dielectric molecules under the direct current voltage; ε∞ represents the dielectric constant of the dielectric molecules under the optical frequency voltage; and n represents the various polarizations and processes that may occur in the dielectric molecules.
After removing the external electric field, the polarized structures in the dielectric molecules gradually relax. This is reflected in multiple parallelled
RC series branches, where the discharge current of the capacitor
Ci is formed, representing the depolarization current, which can be expressed by the following equation:
Therefore, solving the depolarization current curve can obtain the parameter values of each branch in the extended Debye model, and an electrical performance evaluation of XLPE insulation can be carried out.
5. Discussion
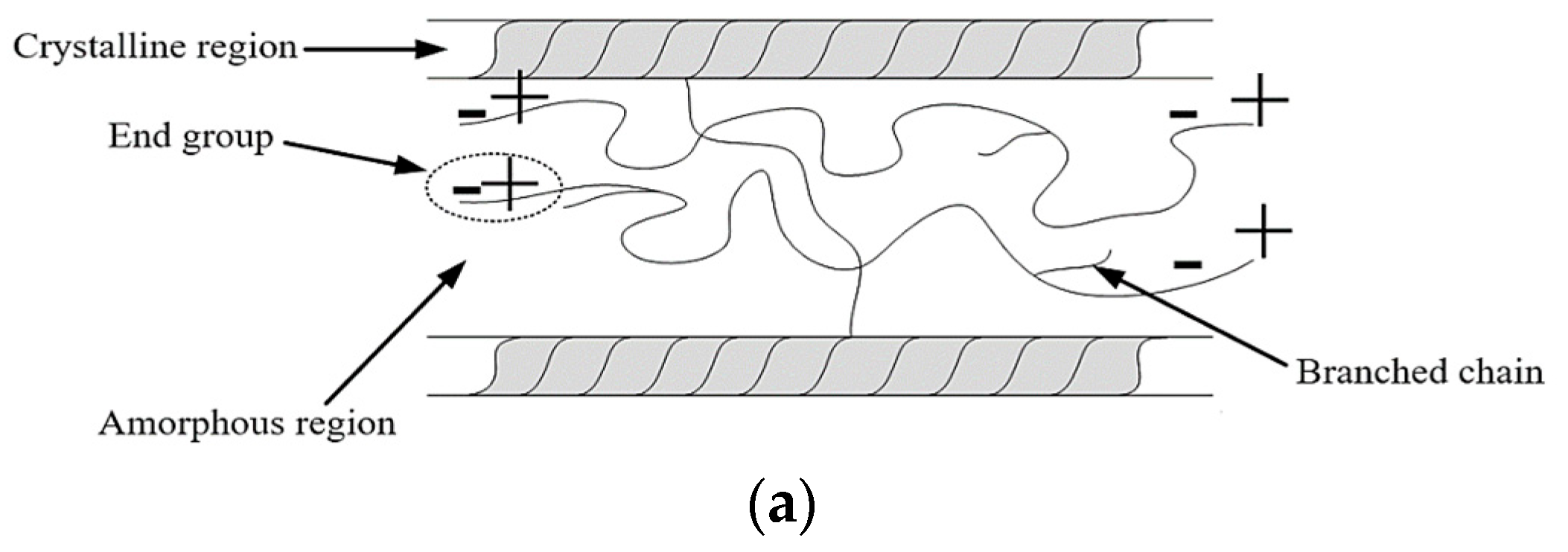
XLPE is a polymer composed of crystalline and amorphous regions, with the molecular chain segments in the amorphous region arranged in a random manner, while the molecular chain segments in the crystalline region are arranged in an ordered manner, as illustrated in
Figure 11a. During thermal aging, localized thermal oxidative aging will occur in the amorphous region of XLPE material, leading to molecular chain breakage, and the broken molecular chain segments will be oxidized to form polar groups such as carbonyl groups. At the same time, due to the structural heterogeneity of the material itself, as well as the differences in density between the amorphous and crystalline regions, the material experiences uneven heating and aging during the thermal aging process.
The unevenness of thermal aging is mainly manifested in two aspects: On one hand, the inner temperature of the operating cable is higher while the outer temperature is lower; thus, the insulation inside the cable is usually more severely thermal-aged, as illustrated in
Figure 11b. On the other hand, due to the unevenness of the material structure, under high-temperature conditions, some crystalline regions in the material will melt and transform into amorphous regions, leading to the formation of more “crystal region–amorphous region” interfaces. Additionally, thermal-aging-induced material oxidation and material decomposition will also create micropore voids within the XLPE material, resulting in “void–XLPE” interfaces. Under the action of an electric field, these interfaces will undergo dipole polarization and interface polarization, as illustrated in
Figure 11c.
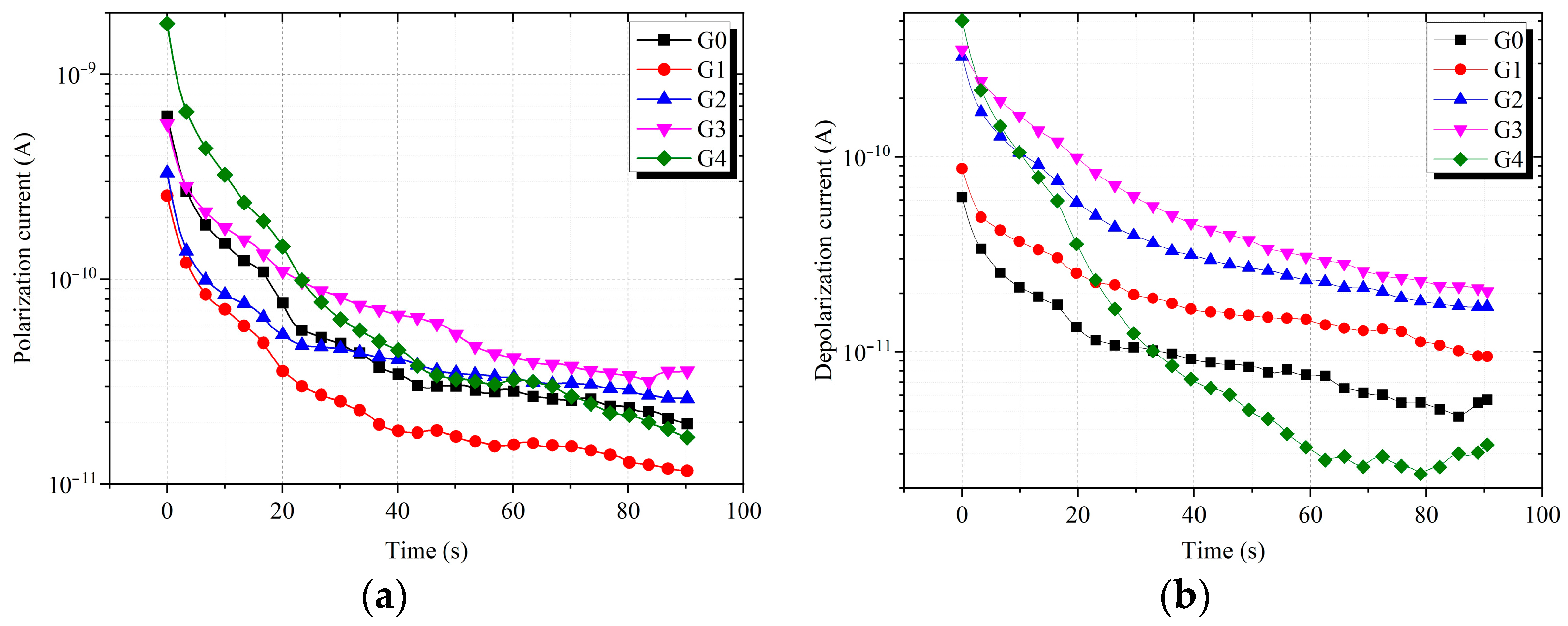
During the thermal aging process, the sample will undergo molecular chain segment breakage and generate polar functional groups. In addition, new interfaces (“crystal region–amorphous region” interfaces, “air–XLPE” interface, etc.) will also be generated, which will cause an increase in the dipole polarization and interface polarization degree of the sample, resulting in an increase in the polarization current and depolarization current of the sample shown in
Figure 7. In the figure, the polarization and depolarization curves of G4 samples have a larger slope, indicating more polar aging products and a severe degree of aging of the sample, therefore leading to a severe polarization process inside the insulation material of the cable. Meanwhile, the phenomenon of recrystallization, indicated by the results in
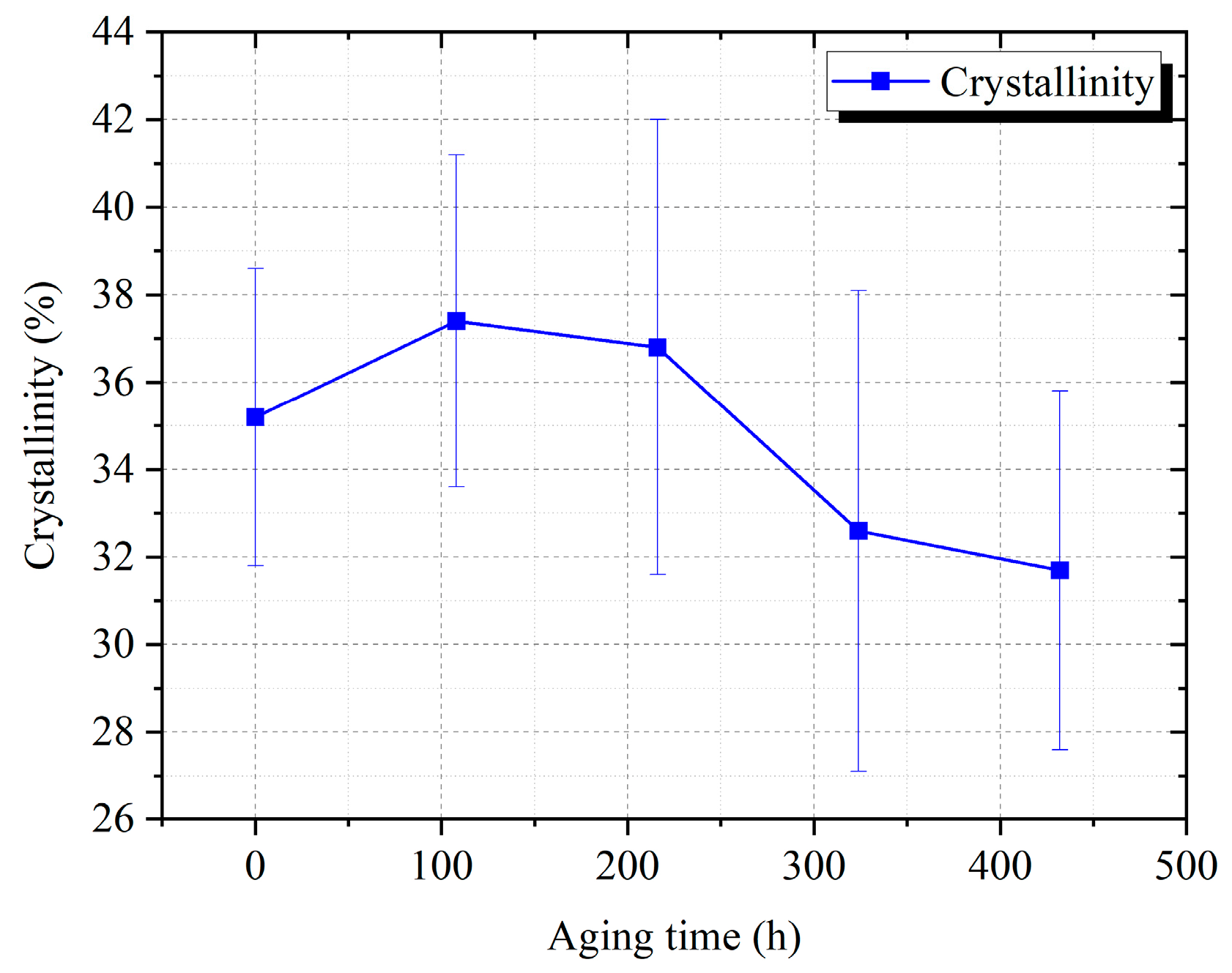
Figure 5, causes the initial part of the polarization current to show a trend of first decreasing and then increasing with the thermal aging time (G0 to G4).
On the other hand, due to the absence of new charge migration pathways in the material, the increase in DC conductivity of the thermal-aged samples is not significant (as shown in
Figure 8). In the early stage of thermal aging (before 108 h of aging), the oxidation process of XLPE molecular chains is inhibited by the antioxidant in the insulation material, preventing thermal oxidation degradation. At the same time, recrystallization phenomena gradually transform some amorphous regions into crystalline regions, resulting in a more regular arrangement of XLPE molecular chains and a decrease in the charge migration rate, leading to a decrease in DC conductivity in the early stage of thermal aging as aging progresses. Before 216 h of thermal aging of the cable samples, the DC conductivity is even lower than that of the samples that have not undergone thermal aging. With increasing thermal aging time, the crystal zones of the cable samples gradually deteriorate, leading to a gradual increase in DC conductivity.
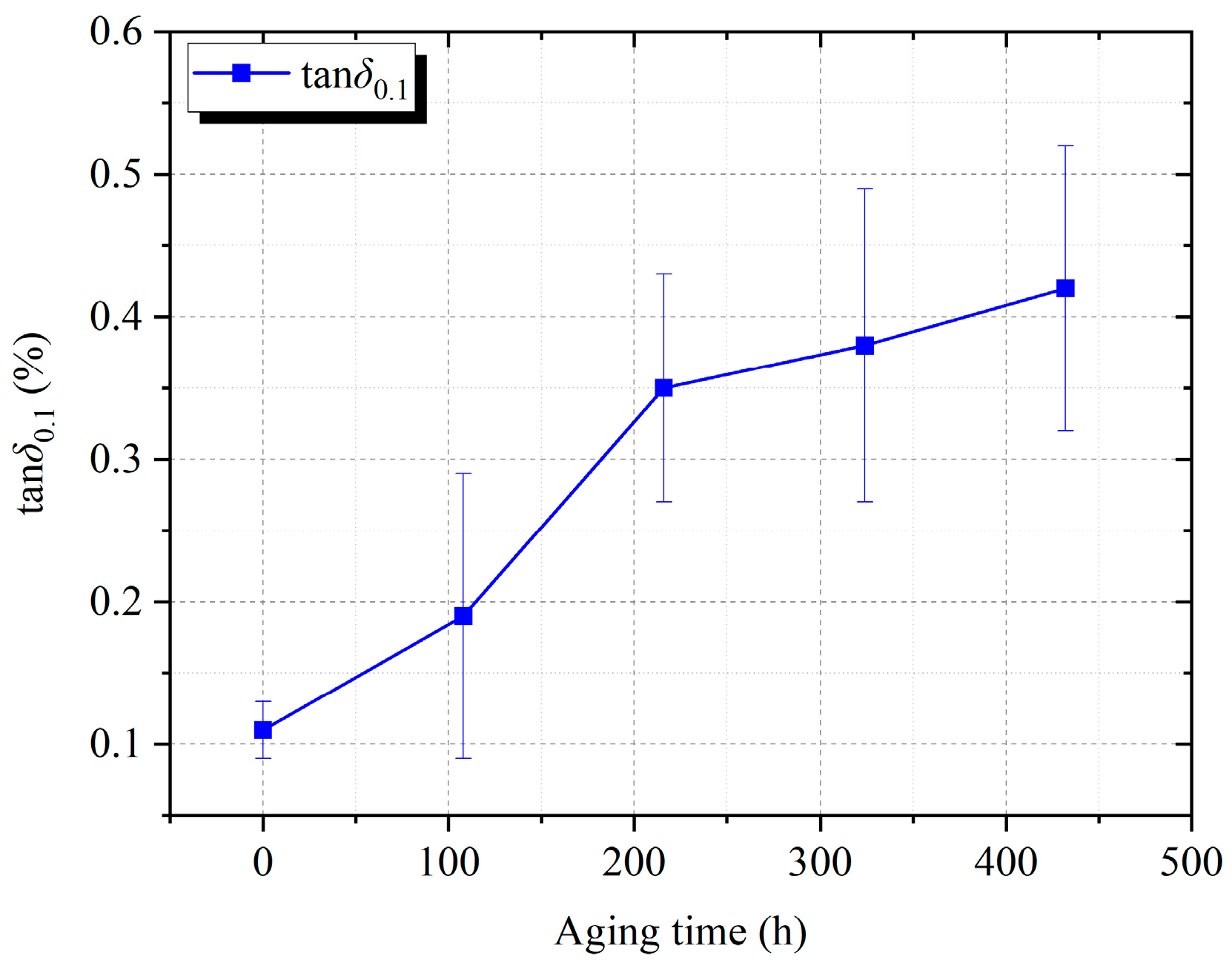
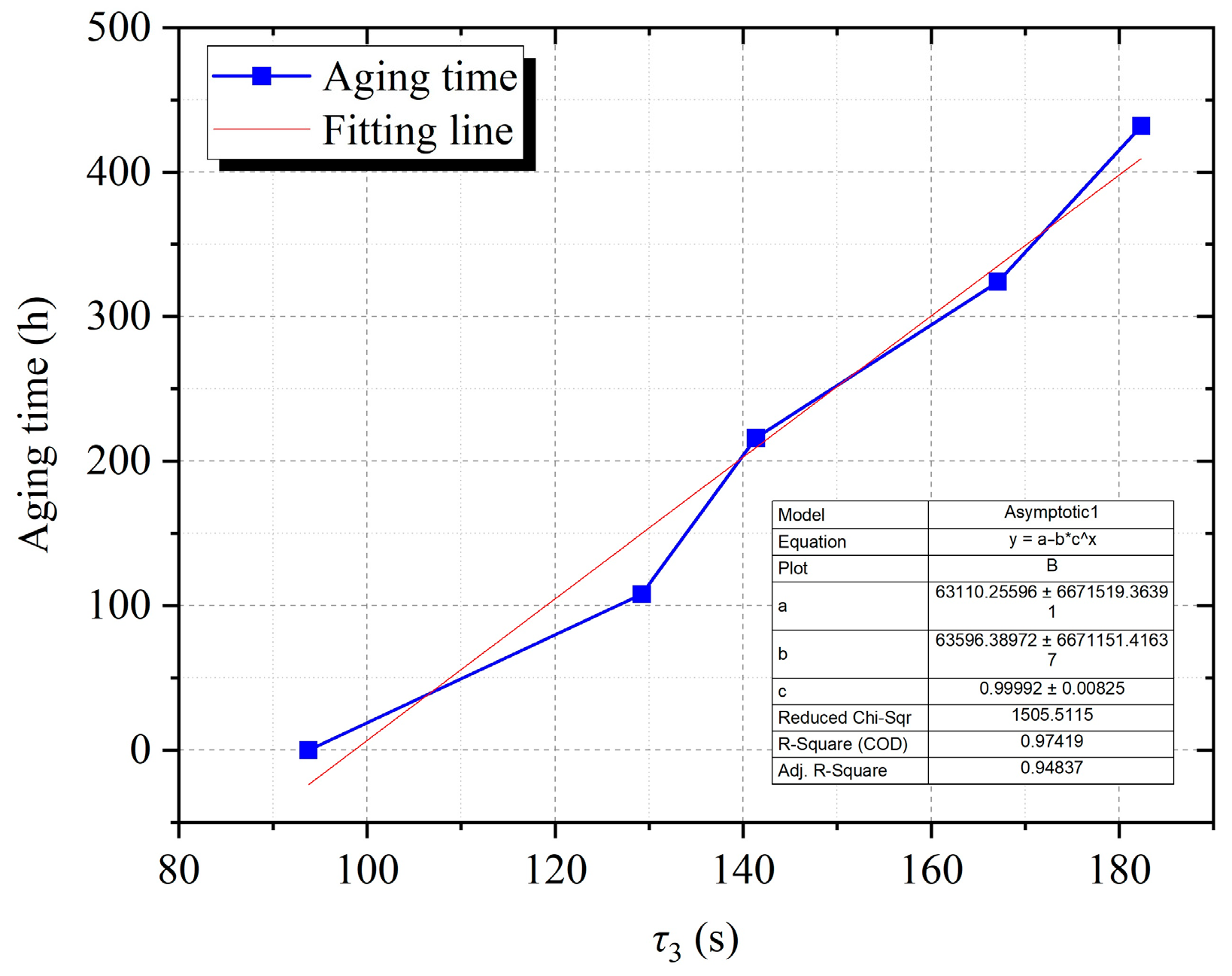
In addition, the aging process is accompanied by molecular chain breakage and an increase in the number of interfaces, which will lead to a gradual increase in the loss factor tanδ0.1. The formation of new interfaces can simultaneously create isolated microvoids within the XLPE, and as the aging time increases, the degree of interface polarization increases. Since isolated microvoids do not provide a channel for charge movement, the increase in sample conductivity is not significant with increasing aging time. However, aging will result in the formation of a large number of polar groups such as carbonyl groups, combined with the new interfaces, which will increase the dielectric constant and capacitance of the sample. The increase in capacitance is greater relative to the decrease in resistance, and the third time constant is the product of capacitance and resistance. This leads to an overall increase in the third time constant τ3 of the sample with increasing aging time.
Also, it should be noted that for this study, as the experimental subjects used 8.7/10 kV AC cables, the conclusions regarding thermal aging mainly apply to this type of cable. For cables used under the DC voltage, although their dielectric loss factor and conductivity also tend to increase under thermal aging according to previous research, the amplitude of changes in dielectric parameters may vary due to different specific components of insulation materials. Meanwhile, when adopting the PDC method to study the dielectric properties of thermal-aged cable samples, it is necessary to use the DC voltage to effectively distinguish the polarization process and the conductivity process for a better analysis. Since the detected results, such as dielectric loss, conductivity, etc., belong to the intrinsic properties of the material, the PDC result under the DC voltage can also reflect the insulation state of the AC cable samples after thermal aging.
In future research, we will refer to previous research methods and conduct X-ray diffraction and infrared absorption spectroscopy tests on samples of thermally aged cables, therefore establishing a deeper understanding of the interrelationship between the microstructure and the dielectric parameters of insulation materials for thermally aged cables, and to deepen our understanding of the thermal aging mechanism of power cables [
22].
6. Conclusions
In this paper, the thermal aging characteristics and mechanisms of XLPE cables based on polarization–depolarization current measurement are investigated. Conclusions are drawn as follows:
During the thermal aging process, microvoids, melted crystalline regions, and increased dipole polarization will be formed in XLPE materials, leading to an increase in the polarization current and depolarization current with aging time.
The DC conductivity and 0.1 Hz dielectric loss factor of thermal-aged cable samples both show an overall increasing trend with the aging time. However, due to that, no new charge transfer channels are formed in the material during aging; the increase in conductivity of thermal-aged samples is not significant. Meanwhile, the aging process will generate interfaces within XLPE, leading to a gradual increase in the material’s dielectric loss factor.
Thermal aging will cause the molecular chain segments of materials to break and generate new “crystal region–amorphous region” interfaces. Meanwhile, due to the isolation of most microvoids within the material, the movement of charges is restricted. The decrease in sample resistance is smaller than the increase in capacitance. Therefore, the third branch time constant of the material’s extended Debye model will increase, and its magnitude can reflect the degree of thermal aging of the material.