Abstract
This research emphasizes a meta-heuristic modified ant lion optimizer (MALO) optimization approach for the simultaneous utilization of DSTATCOM devices and distributed photovoltaic (PV) sources with network reconfiguration in a radial power distribution scheme. In a radial power distribution network with network reconfiguration, the majority of the research is based on constant power model analysis. However, it is noticed that load models have a substantial impact on the distributed PV sources and the DSTATCOM device’s optimal size and position. The effect of the constant power (CP) and polynomial (ZIP) with load growth load models for the simultaneous insertion of distributed PV sources and DSTATCOM devices with network reconfiguration is examined in this research work for power system planning. The penetration levels of distributed PV sources considered for the investigation are 25%, 50%, 75%, and 100%. The principal objective of this research is to reduce network total power losses, enhance the voltage magnitude profile at all buses, and reduce the overall operating cost while adhering to equality and inequality constraints. The proposed algorithm is verified on 118-node test systems. The investigation is carried out for planning network upgrading to a high-voltage distribution system (HVDS) on 317 nodes in the rural Bangalore Electricity Supply Company Limited (BESCOM) radial distribution scheme. The simulated results obtained with this method are validated with the BAT algorithm and techniques available in the literature. It is observed that in the IEEE 118-bus system, via the simultaneous placement and sizing of PV sources considering a 25% penetration level and DSTATCOM devices during network reconfiguration, the total power loss reduction is 41.47% and 42.98% for the constant power model and ZIP with the load growth model. For the 317-bus system, the total power loss reduction observed for 11 kV is 49.77% and 59.34% for the constant power model and ZIP model with load growth. Similarly, for the 22 kV system, the power loss reduction observed is 51.69% and 55.75% for the constant power model and ZIP with the load growth model.
1. Introduction
The distribution network is a complex network incorporating many devices and different consumer categories. Distribution companies should redesign networks to optimize their operation procedure, voltage magnitude profile, energy loss, and voltage stability. Utility companies are implementing recent technologies to mitigate these issues by equilibrating reactive power in the distribution scheme. Reactive power compensator schemes like capacitor positioning, their incorporation of DG, the and allotment of customer power devices reduce total power loss and allow an improvement in the voltage magnitude profile and stability index [1].
To bring down total real power losses, enhance the voltage stability indicator, and improve the voltage profile, the BAT method is developed in this study for the ideal position and rating of DG sources in radial power distribution systems. In this work, various DG (single/multiple) unit types are considered for optimization [2]. The author of this paper [3] examines the most current publications and several authors’ methodologies, and conceptualizes problems, particularly objective formulation and constraints.
Studies on simultaneous reconfiguration, DG sources, and capacitor placement in the distribution scheme demonstrated their capacity to reduce total power loss, which can increase system performance and efficiency [4]. A binary genetic algorithm is applied by the authors of [5] to position multi-DG units and capacitors simultaneously in an intelligence-driven, automatic reconfigured radial network to reduce power loss. In [6], an improved equilibrium optimization formulation is exploited to examine the issue of DG source allocation in a reconfigured scheme. This study proposes a Max–Min-supported multi-subjective formulation optimization strategy for the best arrangement of dispersed generators with the best power distribution reconfigured scheme [7].
To maximize the techno-economic potential of the system, it is now a common practice to deploy both DG sources and DSTATCOM devices concurrently in distribution networks. The PSO approach was employed to minimize loss by assigning the DG source and distributed STATCOM device in the power distribution topology. It has the drawback of having convergence properties [8]. This paper reports the simultaneous network reconfiguration and location of distributed STATCOM devices and solar arrays in a power distribution scheme utilizing the Fuzzy-Ant colony optimization method [9]. Loss sensitivity analysis was employed to assign DG and the bacterial foraging optimizing algorithm in the distribution network to size the DG source and DSTATCOM device for various load levels. This research intends to bring down overall total power losses and enhance voltage magnitude profiles [10]. The cuckoo search method presented by the authors demonstrates the best allocation and rating of DG sources and DSTATCOM devices in the power distribution scheme in the same instance [11]. The water cycle algorithm is used to allocate the DG source and distributed STATCOM device in the power distribution scheme; the author obtained environmental, technical, and economic benefits [12]. The author presented a meta-heuristic approach for network reconfiguration using DG (photovoltaic) and distributed STATCOM for total power loss mitigation and voltage magnitude profile enhancement [13]. A grasshopper optimization method is employed in this document due to the existence of distributed STATCOM devices and the PV arrangement in the power distribution network under reconfiguration. The essential goal of this effort is to decrease total power losses and improve voltage magnitude profiles under varied loading scenarios [1]. The authors in [14] utilized a composite firefly algorithm and particle swarm optimization techniques, considering various technical, financial, and environmental indicators in a multi-objective problem formation for the best distribution of PV-DG sources and DSTATCOM devices. The best DG and DSTATCOM rating and placement were computed by implementing hybrid lightning search, the simplex method, and the loss sensitivity factor to reduce total power losses [15]. To improve the accuracy of the photovoltaic power prediction, the PSO-GWO-BP prediction model was proposed [16]. With due respect to reducing total power loss, the simultaneous assignment of DG sources and several shunt compensators, considering the static VAR compensator, is performed, and distributed STATCOM devices are proposed in [17].
A unique method is built on the Coyote algorithm rule for the synchronized distributed generation unit’s allotment and the rearrangement of networks to reduce total power loss. The analysis revealed that network topology is less successful at reducing power loss than networks with DG systems [18]. The proposed MMPO is employed to aid in simultaneous network reconfiguration and DG allotment. A reduction in overall power loss and enhancing voltage stability improves the performance of the distribution scheme [19]. An innovative chaotic search group algorithm was introduced by the authors in [20] for the synchronized operation of distributed generation allotment and network reconfiguration to reduce power loss. The CSGA was verified on IEEE buses 118, 84, 69, and 33 under three diverse load conditions. The voltage profile and real power loss of the system were significantly enhanced utilizing the SNR-DG approach. The Archimedes optimization method allowed the optimum planning of solar photovoltaic systems under deterministic situations, reducing reliance on the grid and greenhouse gas emissions from traditional power-producing plants [21].
The majority of the researchers reported low precision, sluggish assembly, and high CPU improvement needs. The basic BAT algorithm combines a population-based algorithm and local search strategy to produce a better-performing metaheuristic algorithm that can be employed for both local and global exploration [22]. BAT has shown effectiveness in resolving a variety of optimization issues in various contexts, including the power and energy system, economic load dispatch, engineering designs, image processing, and medical applications. The problem confined to the actual world and the first solution that fulfills all the constraints are unknown. The ease of hybridization with other optimization methods, simplicity, and search speed are some of its advantages over other optimization techniques [23].
Goldberg demonstrated that when compared with PSO and GA, several benchmark unimodal and multimodal functions performed well for BAT. This algorithm is employed to tackle extremely difficult problems from the real world that are difficult to solve using more traditional calculus-based techniques. The emphasis turned to BAT variations, such as Chaotic BAT, Directional BAT, BAT with mutation, BAT with differential evolution (DE) mutation and crossover, BAT with DE mutation, and Levy flight trajectories, which further improved and were used to solve real-world optimization problems for better outcomes. The majority of BAT variants involve tiny adjustments to the loop’s basic system of evolution [24]. The nonconvex, nonlinear, multiobjective, multivariant, and constrained optimization issue was successfully handled using the conventional form of the BAT algorithm [25].
An effective method, the Ant Lion Optimizer (ALO), was built based on the hunting habits of ant lions. The ALO algorithm combines the two essential techniques, namely the population-based search strategy and local-based search strategy, to create an intelligent technique that can search efficiently via the two primary search strategies (global exploration and local exploitation). The ALO algorithm is less complicated, easier to use, and more customizable than other meta-heuristic techniques. As a result, numerous optimization issues have been resolved using ALO [26,27,28]. Despite sometimes experiencing a standstill, the ALO is capable of resolving several optimization issues. The ALO has since undergone several modifications and improvements to increase its search capabilities.
A modified ALO that uses Lévy flying to optimize feature selection is presented in [29]. A modified form of the ALO based on opposition learning with Lévy flight was introduced [30]. The Levy flight distribution (LFD) application has already been offered. The LFD is commonly used, nevertheless, to improve the exploration of optimization algorithms, since it allows people to move to new locations and prevent optimization algorithms from becoming stagnant. A useful method for improving the search and exploitation phases of several optimization algorithms is the spiral movement of populations around the optimal solution [31,32,33].
Thus, a modified Ant Lion Optimizer (MALO) is suggested in this article to increase the basic ALO’s exploration and exploitation by improving the basic ALO’s seeking capabilities using Levy flight distribution (LFD) and the spiral population direction. The proposed method statistically outperforms the elementary ALO algorithm [34].
The best location for DSTATCOM devices and PV DG sources is continuous, while the solution to the network reconfiguration problem is discrete. As a result, this is a complicated, multi-objective, nonlinear optimization problem. Only a few studies in the literature have focused on network reconfiguration with DSTATCOM devices and DG sources by considering the constant power load model. In the mentioned survey of the literature on the simultaneous installation of DG sources and DSTATCOM devices, authors have not considered the effect of the DG penetration level. Hence, the author of the current research work investigates the influence of the CP and ZIP load models, including load increase on a radial distribution system with a reconfigured network, by simultaneously installing distributed PV sources and DSTATCOM devices, considering the PV penetration level using MALO and BAT algorithms. Load models were found to have a substantial impact on the sizing and positioning of distributed PV sources and DSTATCOM devices. The novelty of the research work presented in this paper is as follows:
- (i)
- The three objectives considered are (a) the minimization of total power loss, (b) voltage magnitude profile enhancement, and (c) overall operating cost reduction during network reconfiguration achieved by simultaneously installing distributed PV sources and DSTATCOM devices.
- (ii)
- Three operational scenarios considered are (a) a network without reconfiguration and additional distributed PV sources/DSTATCOM devices, (b) network reconfiguration without additional distributed PV sources/DSTATCOM devices, and (c) a combined assignment of DSTATCOM device and distributed PV source allocation with network reconfiguration considering penetration levels 0.25, 0.5, 0.75, and 1.0 in radial distribution topology using the MALO and BAT method.
- (iii)
- An evaluation of the positioning and capacity of the distributed PV sources, DSTATCOM devices, and network reconfiguration, considering the influence of load models and PV penetration levels, is conducted.
- (iv)
- The recommended MALO method is well tried on standard IEEE 118-node test systems.
- (v)
- The real-time data of State Utility 317 nodes in the rural BESCOM radial distribution scheme are also considered for testing by utilizing MALO and BAT. The investigations were carried out to assess the total power losses, voltage profile, capacity, and positioning of PV sources and DSTATCOM devices along with network reconfiguration in rural feeder BESCOM for high-voltage (22 kV) distribution systems under Deendayal Upadhyaya Gram Jyoti Yojana (DDUGJY) launched by the Government of India for planning network.
This scheme intends to provide 24 h of continuous power to rural areas for agricultural needs through a high-voltage distribution system (HVDS) by upgrading infrastructure to handle 22 kV including feeder segregation. HVDS is a practice where the HV line extends up to the load point. This planning reduces the length of the LT line to a level sufficient for the service cable. Also, the HV line can manage extra peak hour load demand, reducing tripping due to overloading.
The layout of the current research is as follows: The objective function problem formulation for minimizing power loss is explained in Section 2. Load models are discussed in Section 3. The MALO approach is presented in Section 4. The results and analysis of the IEEE 118 node test systems and State Utility 317 nodes in the rural BESCOM radial distribution scheme are explained in Section 5, and the resulting outcomes are compared with those of various methodologies published in the available literature. The findings of the present MALO and BAT approach are summarized in Section 6.
2. Problem Formulation
The suggested MALO algorithm’s objective is to determine the best design for the radial power distribution network topology, DSTATCOM devices, and distributed PV source allotment simultaneously during reconfiguration. The intention is to reduce total power loss and the overall operating costs and to improve the voltage magnitude profile under limitations represented by Equation (4) for the load models and DG penetration levels considered.
2.1. Power Flow Study for Distribution Network
A direct method for the distribution scheme for the load flow solution is applied in this research to achieve a superior outcome [35]. Figure 1 shows the schematic representation of a simple distribution strategy. Equation (1) is utilized to calculate the equivalent injected current at node ‘t’:

Figure 1.
Schematic diagram of distribution scheme.
Kirchhoff’s current law is adapted to compute the branch current in the feeder section connected between buses ‘t’ and ‘t + 1’, mentioned in Equation (2)
This is achieved by using the bus injected to branch current matrix (BIBC) shown in Equation (3):
Kirchhoff’s voltage law is implemented to compute the voltage at bus ‘t + 1’, indicated by Equation (4):
The power loss in the distribution line segment connected between buses ‘t’ and ‘t + 1’ is computed in Equation (5):
The overall power loss (PTLoss) of the power distribution scheme is estimated via the summation of losses in all distribution line segments [36], specified by Equation (6):
2.2. Network Reconfiguration
Changing the status of normally open tie switches and normally closed sectionalizing switches, the distribution system’s topology is altered. Opening sectionalizing switches lowers active power losses, and closing tie switches will transfer voltage between feeders. The radiality of the network is considered to resolve the reconfiguration issue.
In a radial power distribution scheme, the network reconfiguration issue is resolved by fulfilling the enforced system’s operating constraints such as those on the voltage magnitude profile, feeder current carrying capability, and radial power distribution topology. This ideal network structure delivers the lowest total power loss. Equation (7) is utilized to calculate the power loss in the feeder line segment connected between “t” and “t + 1” following reconfiguration:
The reconfigured scheme’s overall power loss is calculated by summing up line losses in all line segments indicated in Equation (8):
The structure net power loss, , obtained via the difference in power loss before and after network reconfiguration [13], is represented in Equation (9):
2.3. DSTATCOM Modeling
DSTATCOM is a voltage source converter, a shunt connected to the utility network through an injection transformer. DSTATCOM can mitigate current-related power quality issues. The magnitude of the generated voltage of DSTATCOM is controlled to modify the amount of reactive power [9]. The real power is adjusted to zero, and the reactive power of the network after DSTATCOM device distribution can be computed using Equation (10):
where Vt = utility bus voltage; Vs = DSTATCOM bus voltage; XL = reactance of the power distribution line; α = phase angle displacement between Vt and VS.
2.4. PV Modeling
The distributed PV sources considered here are based on the solar irradiance model represented by Equations (11)–(13):
where P − PV = PV output power (MW); GSTD = solar irradiance in the standard conditions, typically fixed to 1000 W/m2; XC = a certain radiation point, generally fixed to 150 W/m2; Gs = solar irradiance at a selected location; and P − PV rated = PV-rated power (MW) [34].
2.5. Total Operating Cost Minimization
The total operating Cost (TOC) of real/reactive power generated by the connected distributed PV sources/DSTATCOM devices and the cost of real power losses after reconfiguration [37] are computed using Equation (14):
where
Pcj = PV DG source real power size (kW); Qck = DSTATCOM device size (kVAr); Ap = energy cost (USD/kWh);
Ac = DSTATCOM device cost ($/kVAr); Ad = PV DG source real power supplied cost (USD/kW); H = total number of hours per annum.
2.6. Objective Function
The objective of the allocation procedure is to minimize power loss, resulting in lower annual operating costs and enhanced voltage profiles across the radial distribution network, implementing all restrictions [38]. The following is the formulation of the objective function (15):
where
and = net real and reactive power injection at bus
= line resistance between and
= voltage and angle at the bus .
2.6.1. Equality Constraints
The equality restrictions pertain to the distribution system’s actual and reactive power flow balance shown in Equations (18) and (19):
2.6.2. Inequality Constraints
- 1.
- Node voltage limit
Equation (20) refers to the magnitude of node voltages that must be between Vmin = 0.95 p.u. and Vmax =1.05 p.u. at all buses to maintain power quality.
- 2.
- Feeder capacity limits
The size of the branch current Ii should not exceed Imax flowing in the branch to prevent the insulation failure mentioned in [13] in Equation (21):
- 3.
- DG constraints
The minimum and maximum real power generation from distributed PV sources are restricted, as shown in Equation (22):
- 4.
- DSTATCOM constraints
The minimum and maximum reactive power generation from distributed static compensator devices are represented by Equation (23):
- 5.
- Rule to retain the radial topology
A radial arrangement is favored as it comes with simple operation and power distribution grid protection with reasonable cost. All loops should comprise a tie line switch and a sectionalizing switch, owing to the specification. Accordingly, a single switch should be permitted to open in a loop when a tie switch is closed [39,40]. The subsequent rule should be practiced to retain the radial topology
Closing entire tie lines revealed the total number of focal loops, obtained utilizing Equation (24):
where Nbr = overall number of branches;
Nb = overall number of nodes
The overall number of sectionalizing switches is calculated via Equation (25).
The overall sum of tie switches and focal loops should be identical.
3. Load Model
Constant Power: The amount of power used in power systems always remains the same. Induction motors and air conditioners are load devices that maintain constant power by either increasing voltage or decreasing current, or vice versa.
Constant Current: To maintain the current, the constant voltage can either be increased or decreased by load devices such as those used for electroplating, smelting, and welding.
Constant Impedance: Constant impedance is a characteristic of some loads, such as resistive water heaters and incandescent light bulbs. The impedance in a load remains constant despite changes in voltage or current.
In an exponential form represented in Equations (26) and (27), the real and reactive powers of the static load models are as follows:
The actual and reactive powers at the node’s nominal voltage V0 are P0 and Q0, respectively. The bus load voltage is denoted by V, and the load exponents are denoted by np and nq [41]. Both np and nq have the following values:
and = ‘0’ value for the “Constant Power load model” (CP).
and = ’1’ value for the “Constant Current load model” (CI).
and = ‘2’ value for the “Constant Impedance load model” (CZ).
3.1. Polynomial (ZIP) Load Model
Each load in the ZIP model is modeled by three parameters: constant power (P), constant current (I), and constant impedance (Z). This model provides a more realistic representation of load behavior than straightforward constant power, current, or impedance models do because it considers the dynamic nature of real-world loads.
Comprehending load characteristics is crucial for power system analysis to construct and manage stable and effective electrical networks. In particular, to ensure reliable and effective operation, the ZIP model supports the study and the modeling of power systems with fluctuating loads.
The entire ZIP load constant for both real and reactive loads denoted by Equation (28) is 1. As a result, aq + bq + cq = 1 and ap + bp + cp = 1. The simulation parameters considered are ap = aq = 0.1, bp = bq = 0.1, and cp = cq = 0.8. At nominal voltage, V0, P0, and Q0 represent actual and reactive power.
3.2. Load Growth Model
“Load growth” is reflected in Equation (29) for the planning of the power distribution scheme [41]:
R = annual load growth rate (7%)
T = period (5 years)
4. MALO Algorithm
Table 1 lists the parameters utilized for the MALO technique, and Table 2 shows the cost factors that were chosen. MALO focused on improving the exploration and exploitation process to increase the fundamental ALO’s searching capability. Applying Levy flight distribution (LFD) improves the exploration phase by allowing the algorithm to jump to different regions to abstain from the primitive ALO’s stagnation [34].
where signifies a random step parameter; respresents the entry-wise multiplication. symbolizes a parameter related to the LFD. The step size is as follows:
where u and v indicate variables achieved by normal distribution,
where = standard gamma function;

Table 1.
Parameters for MALO algorithm.

Table 2.
Cost factors.
The exploitation phase of the algorithm is improved by moving the ants in a spiral manner around the elite (best) solution as follows:
The shape of the logarithmic spiral is defined by the constant ‘b’. An adaptive operator is employed for this purpose in order to strike a balance between exploitation and exploration, as seen in the following:
where Amax and Amin are the highest and lowest allowed values for A. Amax to Amin represent a significant change in this number. When the value of A is close to Amin, the position of the populations will be updated in Equation (32) to enhance the exploration of this technique, whereas when the value of A is close to Amax, the position of the populations will be updated in Equation (36), which enhances the exploitation of this technique, as shown in Figure 2.

Figure 2.
Flow chart of MALO algorithm.
Pseudo code of checking system radiality is shown in Algorithm 1.
| Algorithm 1: Pseudo code of checking system radiality [42] |
| Input: a candidate configuration with set of open branches Output: a candidate configuration is a radial configuration or not Determine connection matrix A for the network, which involves initial open branches. Remove the first column of matrix A Remove the rows of matrix A corresponding to open branches in candidate configuration If (matrix A is a square matrix) Calculate determinant of square matrix A If (determinant of square matrix A = 1 or −1) Output: = a candidate configuration is a radial configuration Else Output: = a candidate configuration is not a radial configuration End if Else Output: = a candidate configuration is not a radial configuration End if |
The reconfiguration with DSTATCOM (distribution static synchronous compensator) and PV (photovoltaic) placement using a modified ant lion optimizer aims to enhance the performance and efficiency of the power distribution system. The steps are as follows:
- Initially conduct a thorough analysis of the existing power distribution system (before reconfiguration) to understand the load requirements, voltage profiles, and power flow patterns.
- Collect the PV data, load profiles, and other parameters that affect the power system.
- Reconfigure the system, which involves changing the topology of the distribution network, which in this process are the input data, comprising the network configuration, the row and line data, and the parameter setting of the MALO.
- To find the number of dimensions (dn), use the number of dimensions found from the closure of entire interconnection switches existing in the distribution system. The number of meshes created via the closing of switches will be equivalent to the number of dimensions.
- To determine the search space for every dimension: Close all interconnecting switches creating meshes; branches not part of the mesh are less important. The search space of every dimension will contain the branches that fit into the mesh that signifies it; branches belonging to more than single mesh must form part of a single dimension. This selection is completed randomly at every iteration.
- This could include changing the status of switches, re-routing power flows, and optimizing the placement of DSTATCOM and PV units.
- The modified ant lion optimizer applies the objective function to minimize power losses, improving voltage stability to integrate the DSTATCOM and PV into the system for optimal placement and sizing.
5. Results
The impact of various load models is evaluated for the concurrent deployment of multiple PV sources and distributed STATCOM devices with network reconfiguration for power distribution networks in this research work. The MALO and BAT technique is applied to solve network reconfiguration issues using MATLAB software 2022. The direct load flow algorithm calculates base case power flows, power losses, voltage values in the power distribution scheme, and the ideal location and size of distributed PV sources /DSTATCOM devices considering PV penetration levels of 0.25, 0.5, 0.75, and 1.0. The recommended technique is proven in the IEEE 118-node test scheme and State Utility 317 nodes in the rural BESCOM radial distribution scheme to validate algorithm performance. Three contrasting situations were investigated to evaluate the effectiveness of the proposed strategy.
The parameters utilized in the BAT algorithm for validating results obtained by the MALO are number of populations = 10; number of Iterations = 10; loudness = 0.5; emission rate = 0.5; and frequency = 0.2;
For the standard arrangement in Scenario 1, total power losses, total voltage variation, and total running costs were assessed for the load models considered. In Scenario 2, the best network reconfiguration design was performed. Additionally, estimates were made for total power losses, total voltage variation, and total operating costs. The optimal design for network reconfiguration in Scenario 3 is assessed for load models, considering factors like size, the location of PV DG sources, DSTATCOM devices, total power losses, the total voltage profile, and total operating costs. In this instance, the PV DG penetration level is evaluated at 0.25, 0.5, 0.75, and 1.0.
On a rural feeder real-time network, the MALO and BAT method is applied for high-voltage distribution network planning. Investigations are conducted on 11 kV and 22 kV feeders to determine the size, position, and PV penetration level at 0.25, 0.5, 0.75, and 1.0, as well as to estimate total power losses, the total voltage profile, total operating costs, and DSTATCOM device sizing and location.
Scenario 1—System with uncompensated condition and standard configuration.
Scenario 2—System with network reconfiguration and without compensation.
Scenario 3—System with simultaneous positioning of multiple distributed PV sources and DSTATCOM devices with network reconfiguration.
Load increase is considered while planning the power distribution scheme. For the next five years, a 7% increment in load is anticipated. Network load models in the distribution system are sensitive to voltage levels. The load is modeled using a distinct model to examine the real condition.
Case 1: Network under the constant power model (CP)
Case 2: Network under the ZIP model with load growth
Test system 1: IEEE 118-node radial power distribution scheme
The second test scheme is a radial power distribution scheme with 118 buses, 15 tie switches, and 117 sectionalizing switches, as depicted in Figure 3. The overall actual and reactive power needs of the scheme are 22.7 MW and 17 MVAr, respectively. The network power flow study is executed utilizing S base = 100 MVA along with V base = 11 kV. A reference paper [43] is cited for the power distribution scheme feeder line data and load data. The total number of distributed PV sources evaluated for simulation is three, with sizes ranging from 10 to 2000 kW considering a penetration level of 0.25. Two DSTATCOMs being examined, with sizes ranging from 10 to 1900 kVAr. Table 3. shows the outcomes of 10 iterations of solving all situations of a 118-bus system. Load growth is assumed to be 7% for a span of over five years for planning purposes.

Figure 3.
IEEE 118-node radial power distribution scheme.

Table 3.
Assessment of IEEE 118 test scheme for load models considered with network reconfiguration considering PV penetration level = 0.25.
The total actual power loss estimated using the constant power model is for scenarios 1 to 3 is 1298.14, 800.62, and 759.75. Similarly, for situations 1 to 3, the total reactive power loss estimated is 978.90, 925.50, and 856.01, respectively. Figure 4 shows that the voltage profile improved from scenarios 1 to 3, with V min 0.86 (77), 0.95(33), and 0.95(48) p.u. The percentage losses estimated utilizing the MALO algorithm for scenarios 2 to 3 are 38.32 and 41.47. The optimal system configuration for the constant power model is found in Scenario 3 using the MALO method by modifying tie lines 132, 120, 128, 124, 121, 102, 126, 51, 118, 55, 125, 127, 129, and 119 as an alternative for 118 to 132. Three PV sources are sized and located at 1993 (65), 604(84), and 621(102) considering a PV penetration level of 0.25. Two DSTATCOM devices are sized and located at 382(106) and 1317(47).

Figure 4.
Bus voltage magnitude profile (p.u.) of IEEE118 nodes for CP model.
The total actual power loss predicted for scenarios 1–3 using the ZIP model with load increase is 2631.08, 1603.08, and 1500.13 when utilizing the MALO method. Similarly, the total reactive power loss estimated for situations 1 through 3 is 1979.25, 1162.50, and 1145.64. As indicated in Figure 5, the voltage profile improved from Scenario 1 to Scenario 3, with V min 0.81 (77), 0.95(42), and 0.95(42) (p.u.). The percentage losses estimated for scenarios 2 to 3 are 39.07 and 42.98. Similarly, for the ZIP model with load growth in Scenario 3 with the assistance of the MALO algorithm, the optimal system structure is established by modifying timelines 129, 121, 132, 120, 130, 118, 124, 72, 128, 123, 106, 125, 126, 49, and 119 as a substitute for 118 to 132. Three PV sources are sized and located at 2000(11), 2000(118), and 1858(118) considering a PV penetration level of 0.25. Two DSTATCOM devices are sized and located at 1900(118) and 1900(118).
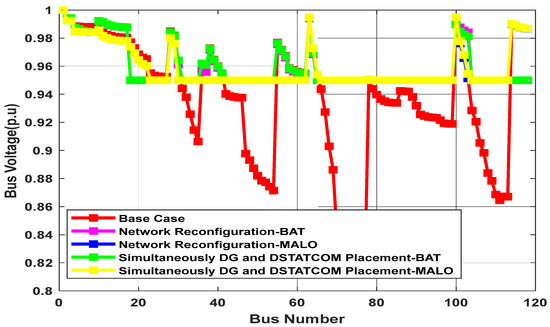
Figure 5.
Bus voltage magnitude profile (p.u.) of IEEE118 node for ZIP model with load growth.
The total actual power loss estimated for scenarios 1 to 3 is 1298.14, 935.48, and 871.34 for the constant power model. Similarly, for situations 1 to 3, the total reactive power loss estimated is 978.70, 1054.14, and 887.01, respectively. Figure 4 shows that the voltage profile improved from scenarios 1 to 3, with V min 0.86 (77), 0.95 (40), and 0.95 (40) p.u., respectively. The percentage loss reduction computed for scenarios 2 to 3 is 27.93 and 32.87 when utilizing the BAT algorithm. The optimal system configuration for the constant power model is found in Scenario 3 using the BAT method by modifying tie lines 130, 122, 128, 101, 131, 21, 47, 126, 125, 132, 123, 119, 124, 118, and 127 as an alternative for 118 TO 132. Three PV sources are sized and located at 871 (81), 1014 (72), and 1193 (3) considering a PV penetration level of 0.25. Two DSTATCOM devices are sized and located at 274 (26) and 1864 (84).
The total actual power loss predicted for scenarios 1–3 using the ZIP model with load increase is 2631.08, 1611.99, and 1447.85 when utilizing the BAT method. The total reactive power loss estimated for situations 1 through 3 is 1979.25, 1385.87, and 1393.75. As indicated in Figure 5, the voltage profile improved from Scenario 1 to Scenario 3, with V min 0.81 (77), 0.95 (22), and 0.95 (22) (p.u.). The percentage loss estimated for scenarios 2 to 3 is 38.73 and 37.36. Similarly, for the ZIP model with load growth in Scenario 3 with the assistance of the BAT algorithm, the optimal system structure is established by modifying tie lines 129, 130, 128, 125, 119, 132, 120, 126, 124, 21, 103, 40, 122, and 127 as a substitute for 118 to 132. Three PV sources are sized and located at 1336 (90), 984 (41), and 1418 (76) considering a PV penetration level of 0.25. Two DSTATCOM devices are sized and located at 1367 (101) and 1463 (27).
The results presented in Figure 6 and Figure 7 demonstrate that for the IEEE 118-bus system under the constant power model, the MALO method minimizes power loss at penetration levels 25% greater than those in the BAT approach. For penetration levels of 50% and 75%, the BAT algorithm predicts a higher power loss reduction than the MALO method does.

Figure 6.
IEEE 118-bus power loss reduction considering 3 PV DG = 2000 kW and 3 DSTATCOM = 1900 kVAr (constant power model).

Figure 7.
IEEE 118-bus power loss reduction considering single PV DG = 2000 kW and single DSTATCOM = 1900 kVAr (constant power model).
Similar findings were observed for the IEEE 118-bus system ZIP with the load growth model (Figure 8 and Figure 9). When estimating power loss reduction at a 25% penetration level, the MALO algorithm performed better than the BAT approach. Nevertheless, the BAT algorithm yielded a better-predicted power loss reduction for penetration levels of 50% and 75% than the MALO algorithm did.

Figure 8.
IEEE 118-bus power loss reduction considering 3 PV DG = 2000 kW and 3 DSTATCOM = 1900 kVAr (ZIP power model with load growth).

Figure 9.
IEEE 118-bus power loss reduction considering single PV DG = 2000 kW and single DSTATCOM = 1900 kVAr (ZIP power model with load growth).
Table 4 shows the performance of the suggested MALO and BAT algorithm for the IEEE 118-node test scheme compared with the results of other approaches for the constant power load model available in the literature. According to the observed results, a considerable reduction in overall actual power loss and reactive power loss and an improvement in the voltage magnitude profile for Scenario 3 are achieved when placed concurrently in a reconfigured network considering the PV penetration level.

Table 4.
Comparative analysis of the BAT and MALO algorithm for the IEEE 118-node test scheme.
Test system 2: 317-node rural BANGALORE ELECTRICITY SUPPLY COMPANY LIMITED radial distribution scheme
The real-time rural (BESCOM) radial distribution scheme consists of 317 buses, 3 tie switches that are initially open (317, 318, and 319), and 316 sectional switches that are initially closed. The overall actual and reactive power needs of the scheme are 660.69 MW and 773.73 MVAr, respectively. The network power flow study was executed using S base = 100 MVA along with V base = 11 kV (for the present system) and 22 kV (planned HVDS). The system uses a Rabbit conductor type, and its specifications are as follows: C/S area = 50 mm2 (aluminum); DC resistance = 0.5524 ohm per kilometer; current rating = 185 A; diameter of wire = 6/3.35 mm; and diameter of steel = 1/3.35 mm. The total number of distributed PV sources evaluated for simulation is three, with sizes ranging from 10 to 5000 kW considering a penetration level of 0.25. Two DSTATCOMs are examined, with sizes ranging from 10 to 10,000 kVAr. Table 5 shows the outcomes of five iterations of solving all situations of a 317-bus scheme for the present system at 11kV. For planning purposes, load growth is assumed to be 7% over five years.

Table 5.
Assessment of 317-node rural BANGALORE ELECTRICITY SUPPLY COMPANY LIMITED radial distribution scheme for load models with network reconfiguration considering a PV penetration level of 0.25 in an 11 kV power distribution network.
The total actual power loss estimated for scenarios 1 to 3 is 3.5 × 105, 3.25 × 105, and 1.75 × 105considering the constant power model employing the MALO algorithm. Similarly, for situations 1 to 3, the total reactive power loss estimated is 2.0 × 105, 1.83 × 105, and 0.95 × 105, respectively. Figure 10. shows that the voltage profile improved from scenarios 1 to 3, with Vmin 0.95 (12), 0.95 (14), and 0.95 (10) p.u., respectively. The percentage loss estimated for scenarios 2 to 3 is 7.11 and 49.77 utilizing the MALO algorithm. The optimal system configuration for the constant power model is found in Scenario 3 using the MALO method by modifying tie lines 45, 59, and 76 instead of 317, 318, and 319. Three PV sources are sized and located at 2142 (258), 3022 (27), and 2568 (317) considering a PV penetration level of 0.25. Two DSTATCOM devices are sized and located at 5355 (190) and 8878 (101).

Figure 10.
Bus voltage magnitude profile of 317-bus scheme at 11 kV (constant power model).
The total actual power loss predicted for scenarios 1–3 using the ZIP model with load increase is 3.05 × 105, 2.68 × 105, and 1.24 × 105, respectively, utilizing the MALO method. Similarly, the total reactive power loss estimated for situations 1 through 3 is 1.78 × 105, 1.51 × 105, and 1.77 × 105. As indicated in Figure 11, the voltage profile improved from Scenario 1 to Scenario 3, with V min 0.95 (12), 0.95 (12), and 0.95 (12) (p.u.). The percentage losses estimated for scenarios 2 to 3 are 12.30 and 59.34. Similarly, for the ZIP model with load growth in Scenario 3 with the assistance of the MALO algorithm, the optimal system structure is established by modifying tie lines 45, 73, and 56 as a substitute for 317, 318, and 319. Three PV sources are sized and located at 5000 (294), 5000 (317), and 5000 (317) a considering PV penetration level of 0.25. Two DSTATCOM devices are sized and located at 10,000 (97) and 10,000 (317).
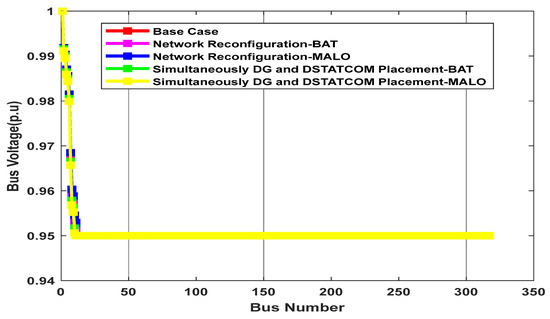
Figure 11.
Bus voltage magnitude of 317-bus scheme at 11 kV (ZIP power model with load growth).
The overall real power loss for the 11 kV system from scenarios 1 to 3 is 3.5 × 105, 3.1 × 105, and 2.57 × 105according to the results of the 317-node utility scheme for the constant power load model utilizing the BAT algorithm. The overall reactive power loss from situations 1 through 3 is 2.0 × 105, 1.77 × 105, and 1.40 × 105. The minimum voltage from scenarios 1 to 3 is 0.95 (12), 0.95 (15), and 0.95 (10) (p.u.), and the voltage profile is illustrated in Figure 10. The percentage loss reduction estimated for scenarios 2 and 3 are 9.65 and 26.56. In the constant power model for Scenario 3, the optimal system configuration is determined using the BAT method by modifying tie lines 50, 318, and 44 instead of 317, 318, 319 and placing three distributed PV source sizes at bus 2013 (117), 2113 (76), and 1021 (23). Two DSTATCOM devices are sized and located on buses 6765 (122) and 2000 (192).
The overall real power loss from scenarios 1 to 3 is 3.05 × 105, 2.83 × 105, and 1.10 × 105according to the results of the 317-node utility scheme for the ZIP load with a load growth model utilizing the BAT algorithm. The overall reactive power loss from scenarios 1–3 is 1.78 × 105, 1.60 × 105, and 0.54 × 105. The improved voltage profile from scenarios 1 to 3 is illustrated in Figure 11, and V min is 0.95 (12), 0.95 (12), and 0.95 (11) (p.u.). The percentage loss reduction computed for scenarios 2 and 3 are 7.36 and 63.78. In the ZIP model with load increase, the optimal system configuration is produced in Scenario 3 using the BAT method by modifying the lines 75, 45, and 63 instead of 317, 318, and 319 by placement of three distributed PV sources sized and placed are 3033 (294), 3432 (6), and 378 (229). Two DSTATCOM devices are sized and placed at 9173 (136) and 7979 (85).
Table 6 shows the outcomes of the investigation carried out on the planned high-voltage distribution system (22 kV) to assess the feeder line losses and voltage magnitude profile (Figure 12 and Figure 13) in the rural BESCOM feeder. This investigation is carried out to analyze the simultaneous placement of distributed PV sources and D- STATCOM devices along with network reconfiguration considering PV penetration levels of 0.25, 0.5, 0.75, and 1.0. Figure 14 and Figure 15 show the fitness function for the 317-bus utility system (ZIP model) at 11 kV and 22 kV.

Table 6.
Assessment of 317-node rural BANGALORE ELECTRICITY SUPPLY COMPANY LIMITED radial distribution scheme for load models with network reconfiguration considering a PV penetration level of 0.25 in a 22 kV power distribution network.

Figure 12.
Bus voltage magnitude profile of 317-bus system at 22 kV (constant power model).

Figure 13.
Bus voltage magnitude of 317-bus system at 22 kV (ZIP power model with load growth).

Figure 14.
Fitness function of 317-bus scheme for the utility power distribution ZIP model with load growth (11 kV).

Figure 15.
Fitness function of 317-bus scheme with utility power distribution with load growth (22 kV).
It can be observed from Table 6 that when upgrading the present system from a 11 kV to HVDS 22 kV system for the constant power model considering penetration levels of 0.25, 0.5, 0.75, and 1.0, the real power loss reduction achieved is 55.21%, 60.29%, 24.74%, and 36.25%, respectively. Similarly, as can be observed from Table 6 for the ZIP load model with load growth, considering penetration levels of 0.25, 0.5, 0.75, and 1.0, the real power loss reduction is 38.42%, 51.45%, 16.60%, and 43.84%, which is achieved by utilizing the BAT algorithm. Also, the minimum bus voltage magnitude remains the same for all situations considered. From Table 6, it can be seen that, by employing the MALO algorithm, when upgrading the present system from a 11 kV to HVDS 22 kV system for the constant power model considering penetration levels of 0.25, 0.5, 0.75, and 1.0, the real power loss reduction achieved is 51.69%, 21.76%, 59.67%, and 44.30%, respectively. Similarly, for the ZIP load model with load growth considering penetration levels of 0.25, 0.5, 0.75, and 1.0, real power loss reductions of 55.75%, 55.29%, 35.87%, and 56.35% are achieved. Also, the minimum bus voltage magnitude remains the same for all situations considered. The total technical losses are reduced, as observed from the results, and upgrading to an HVDS (22 kV) system will prevent pilferage, tampering, and hooking on the feeder (non-technical losses). The primary objective of Ujjwal DISCOM Assurance Yojana (UDAY) of to reducing AT and C losses by less than 12 to 15% could be achieved.
Limitation of Current Approach
Optimizing DSTATCOM device and photovoltaic (PV) source planning with network reconfiguration has numerous advantages. Increased distribution system dependability, stability, and efficiency are some of these advantages. Like any technological solution, it does have certain limitations:
- Complexity due to the dynamic nature of the distribution system and the interdependencies between PV sources, DSTATCOM devices, and network reconfiguration, so optimizing these operations can be challenging.
- Reliable information on solar radiation, load profiles, weather patterns, system topology, and other aspects is required for efficient planning.
- It is critical to carefully weigh the initial costs of installing DSTATCOM equipment and PV sources against the continuing costs of maintenance and operation. PV generation is prone to variability and sporadic power outages.
6. Conclusions
The MALO optimization method is applied in this research work to optimize the simultaneous allotment and sizing of distributed PV sources and DSTATCOM devices in the redesigned power distribution scheme. The main intention is to minimize overall power losses, enhance the voltage magnitude profile, and reduce overall operating costs. We discussed the influence of load models, the sizing and positioning of distributed PV sources, and DSTATCOM device analysis applied to the IEEE 118-node test schemes and State Utility 317 bus Bangalore Rural Distribution system. The suggested technique considered three scenarios: the base case, network reconfiguration, and the simultaneous integration of distributed PV sources and distributed STATCOM devices in a radial power distribution scheme for the redesigned network with PV penetration levels of 0.25, 0.5, 0.75, and 1.0. The suggested method’s results obtained for standard IEEE 118 power distribution systems were validated with the BAT algorithm and the results available in the literature for the constant power model. Also, this technique proved to be effective in solving real-time the State Utility 317-node scheme in rural Bangalore distribution power system problems for planning purposes. The investigation carried out on planned HVDS (22 kV) demonstrates that total line losses are reduced substantially. In addition, computational findings demonstrated that the MALO and BAT algorithm outperformed other approaches in Scenario 2 and gave promising results in Scenario 3. The suggested technique produces better outcomes concerning total actual power reduction, voltage magnitude profile enhancement, and overall operating cost reduction. It was revealed that the size and positioning of DG sources/DSTATCOM devices change with the load models considered. Further research work can be extended for planning PV-DG systems with energy storage systems and DSTATCOM devices to maximize efficiency.
Author Contributions
Conceptualization, S.B.C.; methodology, S.B.C.; validation, S.B.C.; formal analysis, S.B.C.; investigation, S.B.C.; resources, S.B.C.; data curation, S.B.C.; writing—original draft preparation, S.B.C.; writing—review and editing, S.B.C.; visualization, S.B.C.; supervision, U.A. and G.R.S.; project administration, U.A. and G.R.S.; All authors have read and agreed to the published version of the manuscript.
Funding
The authors state that no funds, grants, or other financial support were received during preparation of the manuscript.
Data Availability Statement
The data that support the findings of current research are available on request from the corresponding author, SUJATHA B. C.
Acknowledgments
The authors wish to thank the authorities of BESCOM, KPTCL, Bangalore, Karnataka, India, and Parimala R V, MIT, Mysore, for providing the relevant distribution network data for the activities in the current investigation.
Conflicts of Interest
The authors declare no conflicts of interest with respect to the publication of this research work.
Abbreviations
| ALO | Ant Lion Optimizer |
| BIBC | Bus Injected to Branch Current Matrix |
| CP | Constant Power |
| CGSA | Chaotic Search Group algorithm |
| DDUGJY | Deendayal Upadhyaya Gram Jyoti Yojana |
| DG | Distributed Generation |
| DSTATCOM | Distributed Static Compensator |
| GA | Genetic Algorithm |
| LFD | Levy Flight Distribution |
| MALO | Modified Ant Lion Optimizer |
| MMPO | Modified Marine Predators Optimizer |
| PV-DG | Photovoltaic Distributed Generation |
| PV | Photovoltaic |
| SNR | Simultaneous Network Reconfiguration |
| TOC | Total Operating Cost |
Symbol
| kV | Kilovolt |
| kW | Kilowatt |
| kVAr | Kilovolt–Ampere Reactive |
| Power Loss | |
| Pu | Per Unit |
| Real Power Injection | |
| Reactive Power Injection | |
| Voltage at the bus | |
| Voltage Minimum | |
| Voltage Maximum | |
| Angle at the Bus |
References
- Sambaiah, K.S.; Jayabharathi, T. Optimal reconfiguration of Distribution Network in presence of D-STATCOM and Pho-tovoltaic array using Metaheuristic algorithm. Eur. J. Electr. Eng. Comput. Sci. 2020, 4. [Google Scholar]
- Prakash, R.; Sujatha, B. Optimal placement and sizing of DG for power loss minimization and VSI improvement using BAT algorithm. In Proceedings of the IEEE Conference NPSC 2016, IIT Bhubaneshwar, Bhubaneshwar, India, 19–21 December 2016; pp. 1–6. [Google Scholar]
- Moura, A.; Salvadorinho, J.; Soares, B.; Cordeiro, J. Comparative study of distribution networks reconfiguration problem approaches. RAIRO Oper. Res. 2021, 55, 2083–2124. [Google Scholar] [CrossRef]
- Ben Hamida, I.; Salah, S.B.; Msahli, F.; Mimouni, M.F. Optimal network reconfiguration and renewable DG integration considering time sequence variation in load and DGs. Renew. Energy 2018, 121, 66–80. [Google Scholar] [CrossRef]
- Shuaibu Hassan, A.; Sun, Y.; Wang, Z. Optimization techniques applied for optimal planning and integration of renewable energy sources based on distributed generation: Recent trends. Cogent Eng. 2020, 3, 1766394. [Google Scholar] [CrossRef]
- Shaheen, A.; Elsayed, A.; El-Sehiemy, R.A.; Abdelaziz, A.Y. Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems. Appl. Soft Comput. 2021, 98, 106867. [Google Scholar] [CrossRef]
- Thunuguntla, V.K.; Injeti, S.K. Butterfly optimizer assisted Max–Min based multi-objective approach for optimal connection of DGs and optimal network reconfiguration of distribution networks. J. Electr. Syst. Inf. Technol. 2022, 9, 1–25. [Google Scholar] [CrossRef]
- Devi, S.; Geethanjali, M. Optimal location and sizing determination of Distributed Generation and DSTATCOM using Particle Swarm Optimization algorithm. Int. J. Electr. Power Energy Syst. 2014, 62, 562–570. [Google Scholar] [CrossRef]
- Tolabi, H.B.; Ali, M.H.; Rizwan, M. Simultaneousreconfiguration, optimal placement of DSTATCOM, and photovoltaic array in a distribution system based on fuzzy-ACO approach. IEEE Trans. Sustain. Energy 2015, 6, 210–218. [Google Scholar] [CrossRef]
- Devabalaji, K.; Ravi, K. Optimal size and siting of multiple DG and DSTATCOM in radial distribution system using Bacterial Foraging Optimization Algorithm. Ain Shams Eng. J. 2016, 7, 959–971. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Ravi, K. Multi-objective simultaneous DG and DSTATCOM allocation in radial distribution networks using Cuckoo Searching Algorithm. Alex. Eng. J. 2018, 57, 2729–2742. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal Placement and Sizing of Distributed Generation and Capacitor Banks in Distribution Systems Using Water Cycle Algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Ganesh, S.; Kanimozhi, R. Meta-heuristic technique for network reconfiguration in distribution system with photovoltaic and D-STATCOM. IET Gener. Transm. Distrib. 2018, 12, 4524–4535. [Google Scholar] [CrossRef]
- Zellagui, M.; Lasmari, A.; Settoul, S.; El-Sehiemy, R.A.; El-Bayeh, C.Z.; Chenni, R. Simultaneous allocation of photovoltaic DG and DSTATCOM for echno-economic and environmental benefits in electrical distribution systems at different loading conditions using novel hybrid optimization algorithms. Int. Trans. Electr. Energy Syst. 2021, 31, 12992. [Google Scholar] [CrossRef]
- Chinnaraj, S.G.R.; Kuppan, R. Optimal sizing and placement of multiple renewable distribution generation and DSTATCOM in radial distribution systems using hybrid lightning search algorithm-simplex method optimization algorithm. Comput. Intell. 2021, 37, 1673–1690. [Google Scholar] [CrossRef]
- He, P.; Dong, J.; Wu, X.; Yun, L.; Yang, H. Photovoltaic power prediction based on improved grey wolf algorithm optimized back propagation. Arch. Electr. Eng. 2023, 72, 613–628. [Google Scholar]
- Eid, A.; Kamel, S.; Zawbaa, H.M.; Dardeer, M. Improvement of active distribution systems with high penetration capacities of shunt reactive compensators and distributed generators using Bald Eagle Search. Ain Shams Eng. J. 2022, 13, 101792. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T.; Nguyen, N.A.; Duong, T.L. A novel method based on coyote algorithm for simultaneous network reconfiguration and distribution generation placement. Ain Shams Eng. J. 2021, 12, 665–676. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; El-Sehiemy, R.A.; Kamel, S.; Ghoneim, S.S.M. A modified marine predators optimization algorithm for simultaneous network reconfiguration and distributed generator allocation in distribution systems under different loading conditions. Eng. Optim. 2020, 54, 687–708. [Google Scholar] [CrossRef]
- Huy, T.H.B.; Van Tran, T.; Vo, D.N.; Nguyen, H.T.T. An improved metaheuristic method for simultaneous network reconfiguration and distributed generation allocation. Alex. Eng. J. 2022, 61, 8069–8088. [Google Scholar] [CrossRef]
- Janamala, V.; Radha Rani, K. Optimal allocation of solar photovoltaic distributed generation in electrical distribution networks using Archimeds optimization algorithm. Clean Energy 2022, 6, 271–287. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspired Comput. 2013, 5, 141. [Google Scholar] [CrossRef]
- Shehab, M.; Abu-Hashem, M.A.; Shambour, M.K.Y.; Alsalibi, A.I.; Alomari, O.A.; Gupta, J.N.D.; Alsoud, A.R.; Abuhaija, B.; Abualigah, L. A Comprehensive Review of Bat Inspired Algorithm: Variants, Applications, and Hybridization. Arch. Comput. Methods Eng. 2023, 30, 765–797. [Google Scholar] [CrossRef]
- Jayabarathi, T.; Raghunathan, T.; Gandomi, A.H. The Bat Algorithm, Variants and Some Practical Engineering Applications: A Review. In Nature-Inspired Algorithms and Applied Optimization, Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2017; Volume 744. [Google Scholar]
- Alyasseri, Z.A.A.; Alomari, O.A.; Al-Betar, M.A.; Makhadmeh, S.N.; Abu Doush, I.; Awadallah, M.A.; Abasi, A.K.; Elnagar, A. Recent advances of bat-inspired algorithm, its versions and applications. Neural Comput. Appl. 2022, 34, 16387–16422. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Mirjalili, S.; Aljarah, I.; Mafarja, M. Ant lion optimizer: Theory, literature review, and application in multi-layer perceptron neural networks. In Nature-Inspired Optimizers; Springer: Berlin/Heidelberg, Germany, 2020; pp. 23–46. [Google Scholar]
- Assiri, A.S.; Hussien, A.G.; Amin, M. Ant lion optimization:Variants, hybrids, and applications. IEEE Access 2020, 8, 77746–77764. [Google Scholar] [CrossRef]
- Wang, M.; Wu, C.; Wang, L.; Xiang, D.; Huang, X. A feature selection approach for hyperspectral image based on modified ant lion optimizer. Knowledge-Based Syst. 2019, 168, 39–48. [Google Scholar] [CrossRef]
- Dinkar, S.K.; Deepa, K. An efficient opposition based Lévy flight antlion optimizer for optimization problems. J. Comput. Sci. 2018, 29, 119–141. [Google Scholar] [CrossRef]
- Barshandeh, S.; Haghzadeh, M. A new hybrid chaotic atom search optimization based on tree-seed algorithm and Levy flight for solving optimization problems. Eng. Comput. 2020, 37, 3079–3122. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, Y.; Liu, C.; Hu, P.; Li, Y.; Li, H.; Yuan, C. Selfish herd optimizer with levy-flight distribution strategy for global optimization problem. Phys. A Stat. Mech. Appl. 2020, 538, 122687. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, B. A Novel Ant Colony Optimization Algorithm With Levy Flight. IEEE Access 2020, 8, 67205–67213. [Google Scholar] [CrossRef]
- Oda, E.S.; Abd El Hamed, A.M.; Ali, A.; Elbaset, A.A.; Abd El Sattar, M.; Ebeed, M. Stochastic optimal planning of distribution system considering integrated photovoltaic-based DG and DSTATCOM under uncertainties of loads and solar irradiance. IEEE Access 2021, 9, 26541–26555. [Google Scholar] [CrossRef]
- Teng, J.-H. A direct approach for distribution system load flow solutions. IEEE Trans. Power Deliv. 2003, 18, 882–887. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.R.; Prabaharan, N.; Alhelou, H.H.; Manju, A.; Pal, P.; Siano, P. Optimal Integration of Capacitor and Distributed Generation in Distribution System Considering Load Variation Using Bat Optimization Algorithm. Energies 2021, 14, 3548. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.R.; Ravi, K. Optimal placement and sizing of STATCOM using harmony search algorithm. Energy Procedia 2015, 79, 759–765. [Google Scholar] [CrossRef]
- Bhumkittipich, K.; Phuangpornpitak, W. Optimal placement and sizing of distributed Generation for power loss redution using Particle Swarm Optimization. Energy Procedia 2013, 34, 307–317. [Google Scholar] [CrossRef]
- Gupta, A.R.; Kumar, A. Energy saving using D-STATCOM placement in radial distribution system under reconfigured network. Energy Procedia 2015, 90, 124–136. [Google Scholar] [CrossRef]
- Pegado, R.; Naupari, Z.; Molina, Y.; Castillo, C. Radial distribution network reconfiguration for power losses reduction based on improved selective BPSO. Electr. Power Syst. Res. 2019, 169, 206–213. [Google Scholar] [CrossRef]
- Gupta, A.R.; Kumar, A. Impact of various load models on D-STATCOM allocation in DNO operated distribution network. Procedia Comput. Sci. 2018, 125, 862–870. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Truong, A.V.; Phung, T.A. A novel method based on adaptive cuckoo search for optimal network reconfiguration and distributed generation allocation in distribution network. Electr. Power and Energy Syst. 2016, 78, 801–815. [Google Scholar] [CrossRef]
- Zhang, D.; Fu, Z.; Zhang, L. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems, Electr. Power Syst. Res. 2007, 77, 685–694. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).