Application of Neural Network Feedforward in Fuzzy PI Controller for Electric Vehicle Thermal Management System: Modeling and Simulation Studies
Abstract
1. Introduction
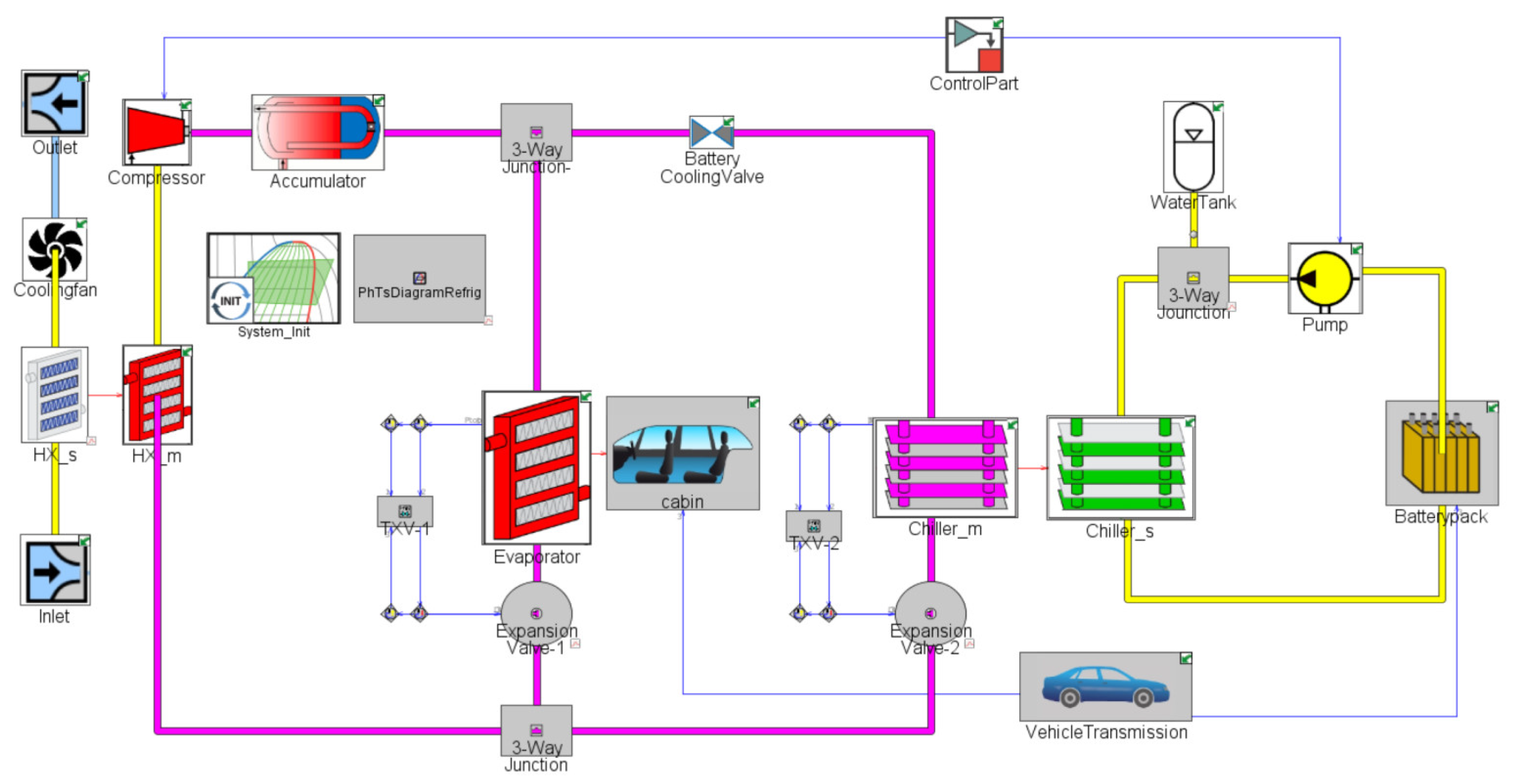
2. Physical Model
2.1. Cabin AC Circuit Model
2.1.1. Compressor Model
2.1.2. Expansion Valve Model
2.1.3. Heat Exchanger Model
2.1.4. Cabin PMV Model
2.2. Battery Cooling Circuit Model
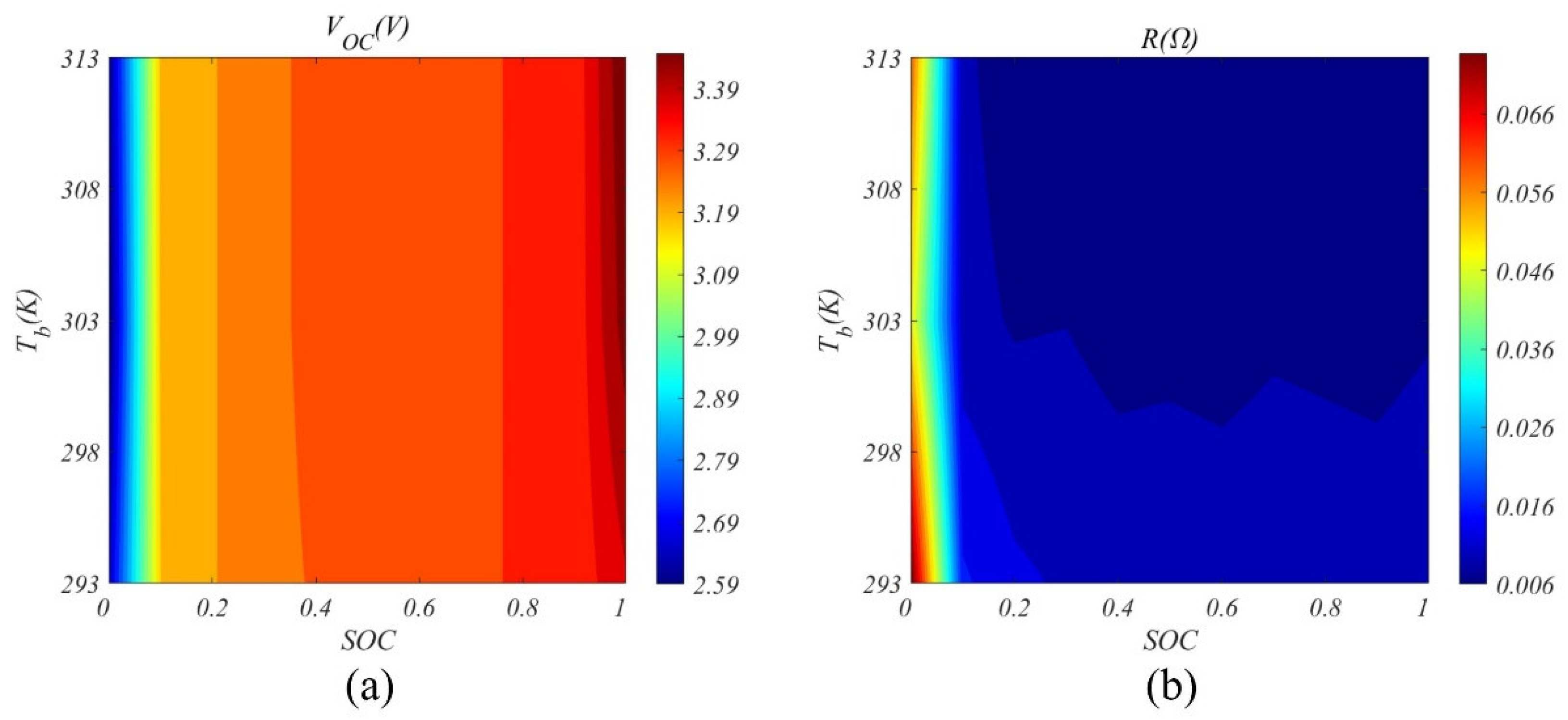
2.2.1. Battery Pack Model
2.2.2. Pump Model
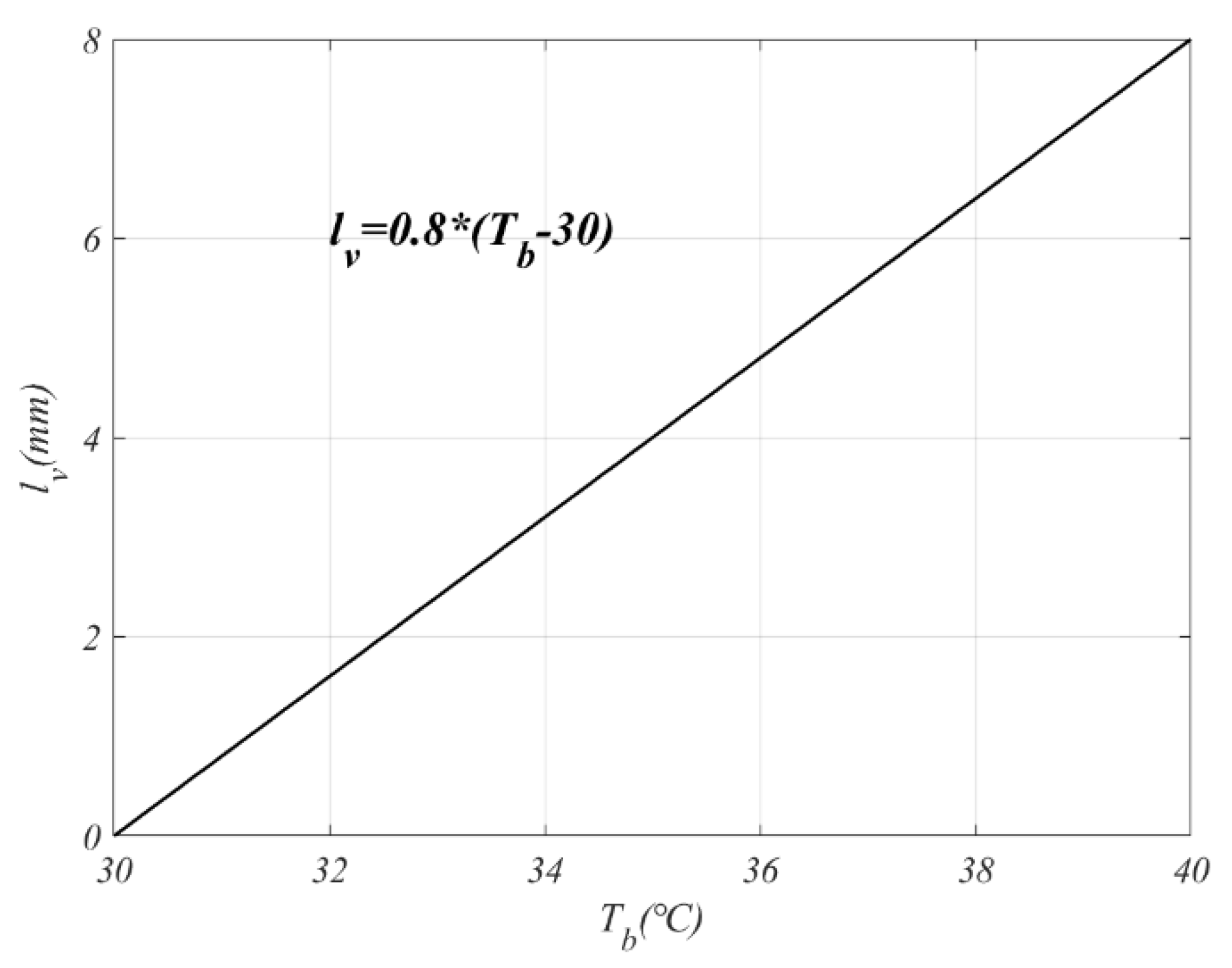
2.2.3. Battery Cooling Valve
2.3. Vehicle Dynamic Model
2.4. Discrete Fluid Model
2.5. Equilibrium Points
3. Control Model
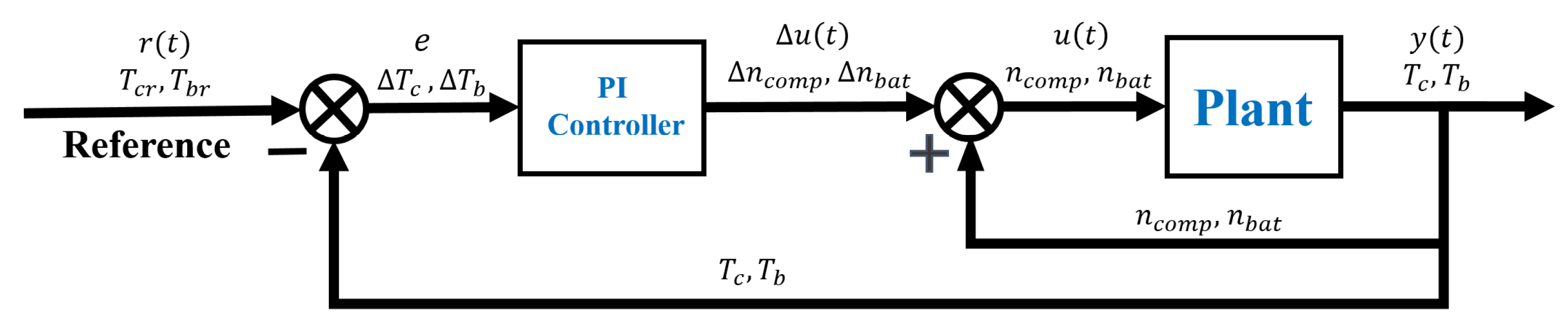
3.1. PI Controller
3.2. Model Predictive Control (MPC)
- Prediction Model: Based on the current information of the system and future control inputs, the prediction model forecasts the system’s future output;
- Rolling Optimization: This refers to the continuous forward movement in a finite time horizon, where the optimization problem is repeatedly solved;
- Feedback Correction: At each step of rolling optimization, the current system output is compared with the predicted output within the prediction horizon. The error is calculated, and the feedback difference is used for correction.
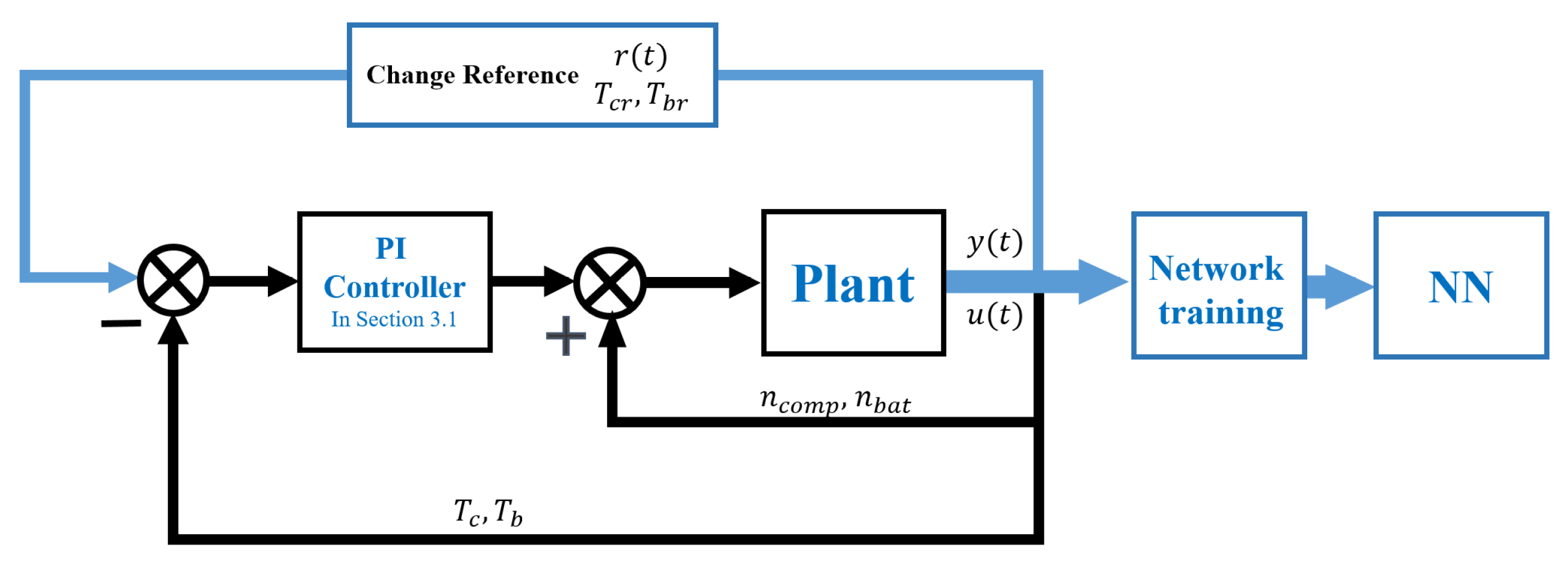
3.2.1. System Identification Simulation
3.2.2. State-Space Model
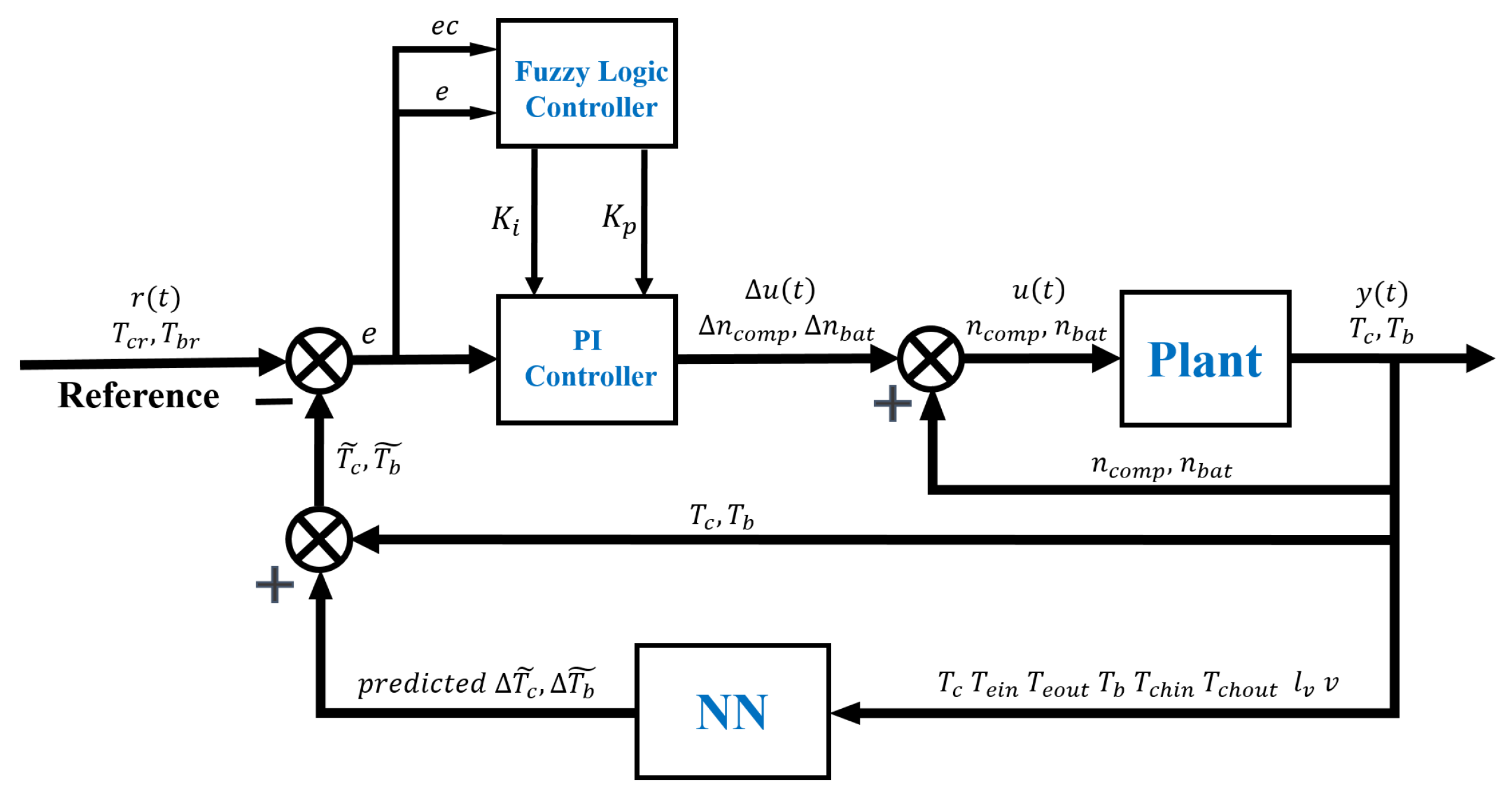
3.3. NN-Fuzzy PI Controller
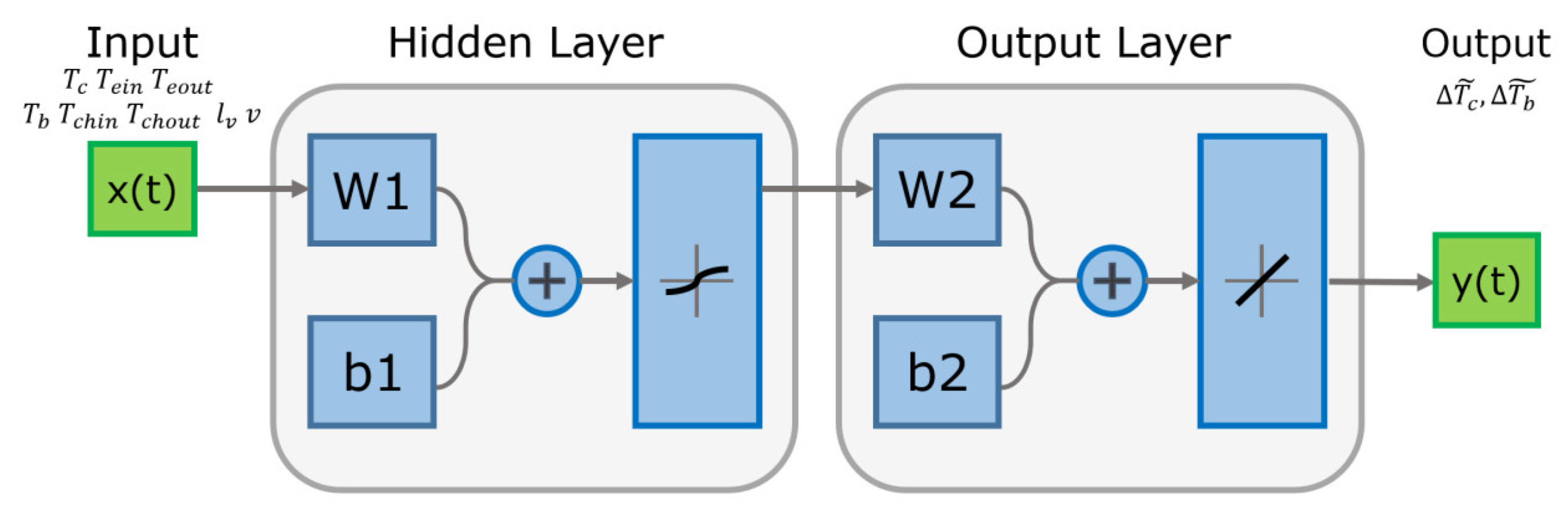
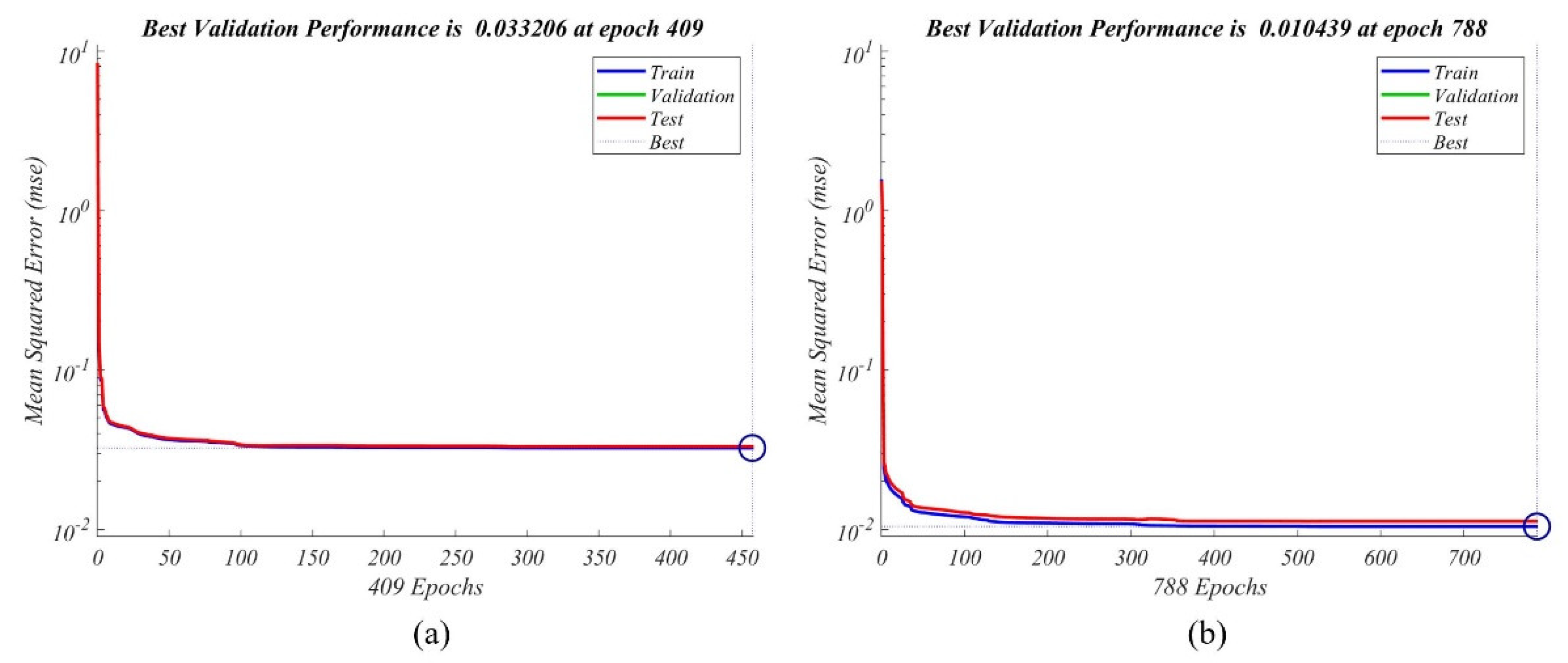
3.3.1. BP Neural Network Model
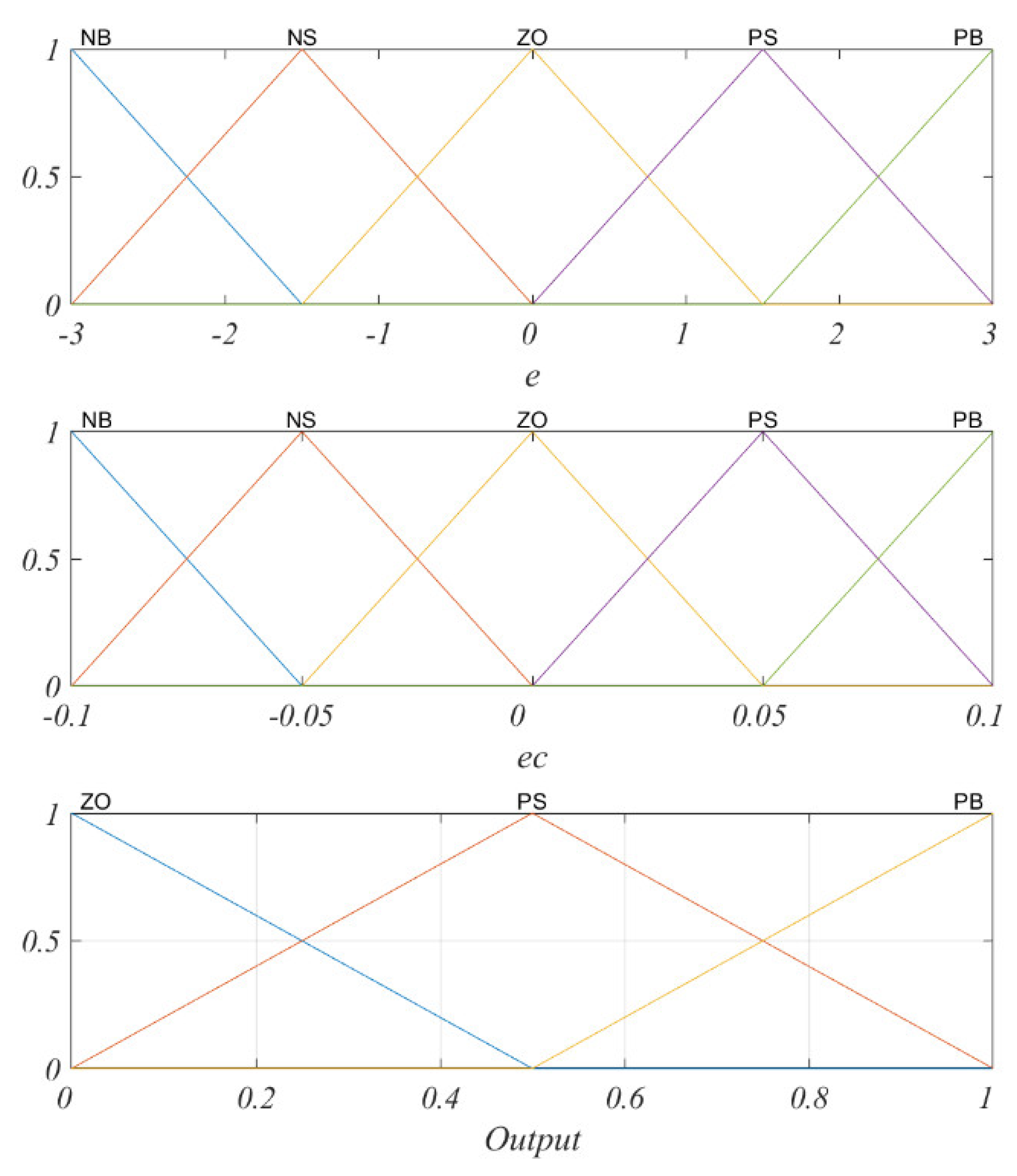
3.3.2. Fuzzy PI Controller
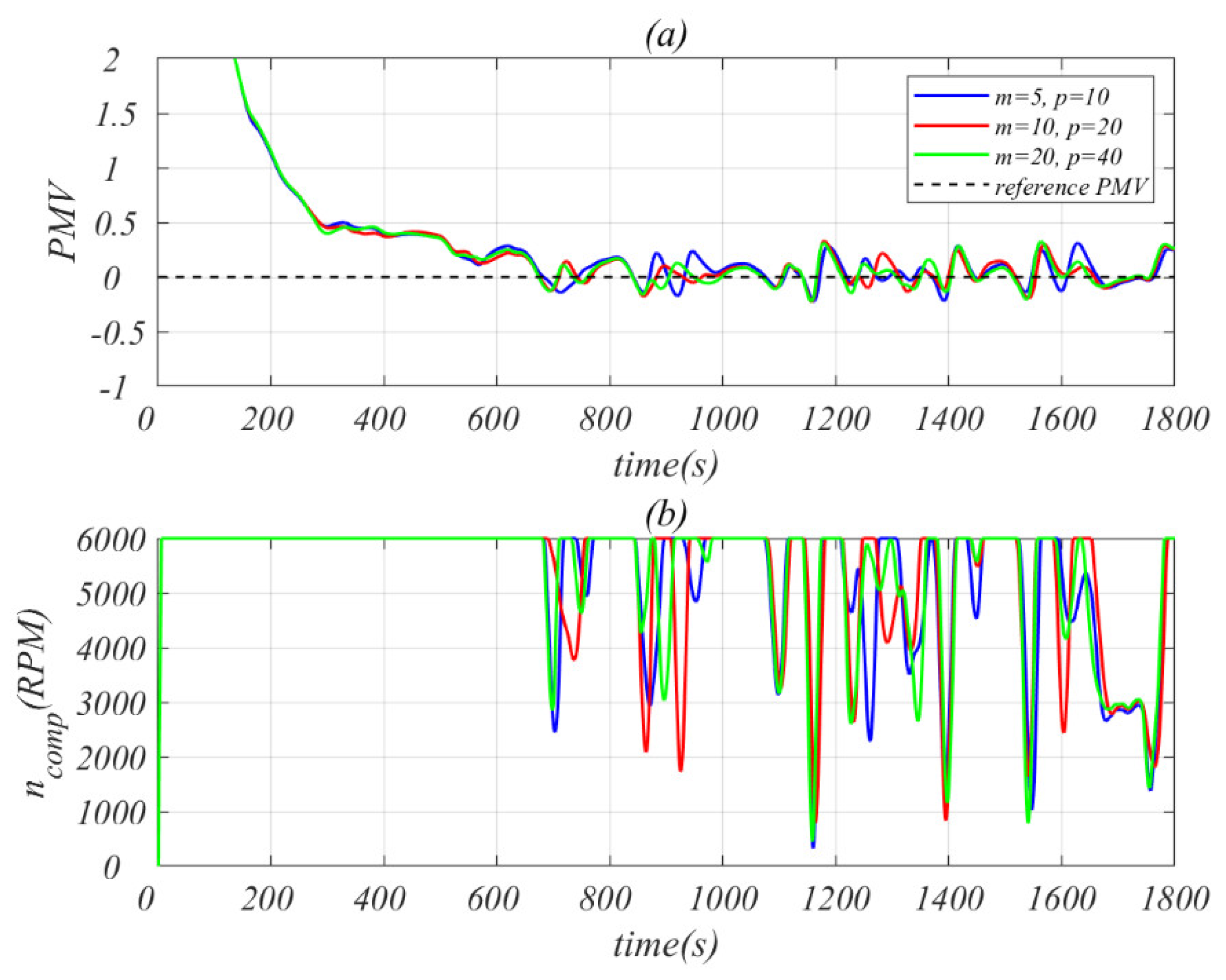
3.4. Controller Parameters
4. Result and Analysis
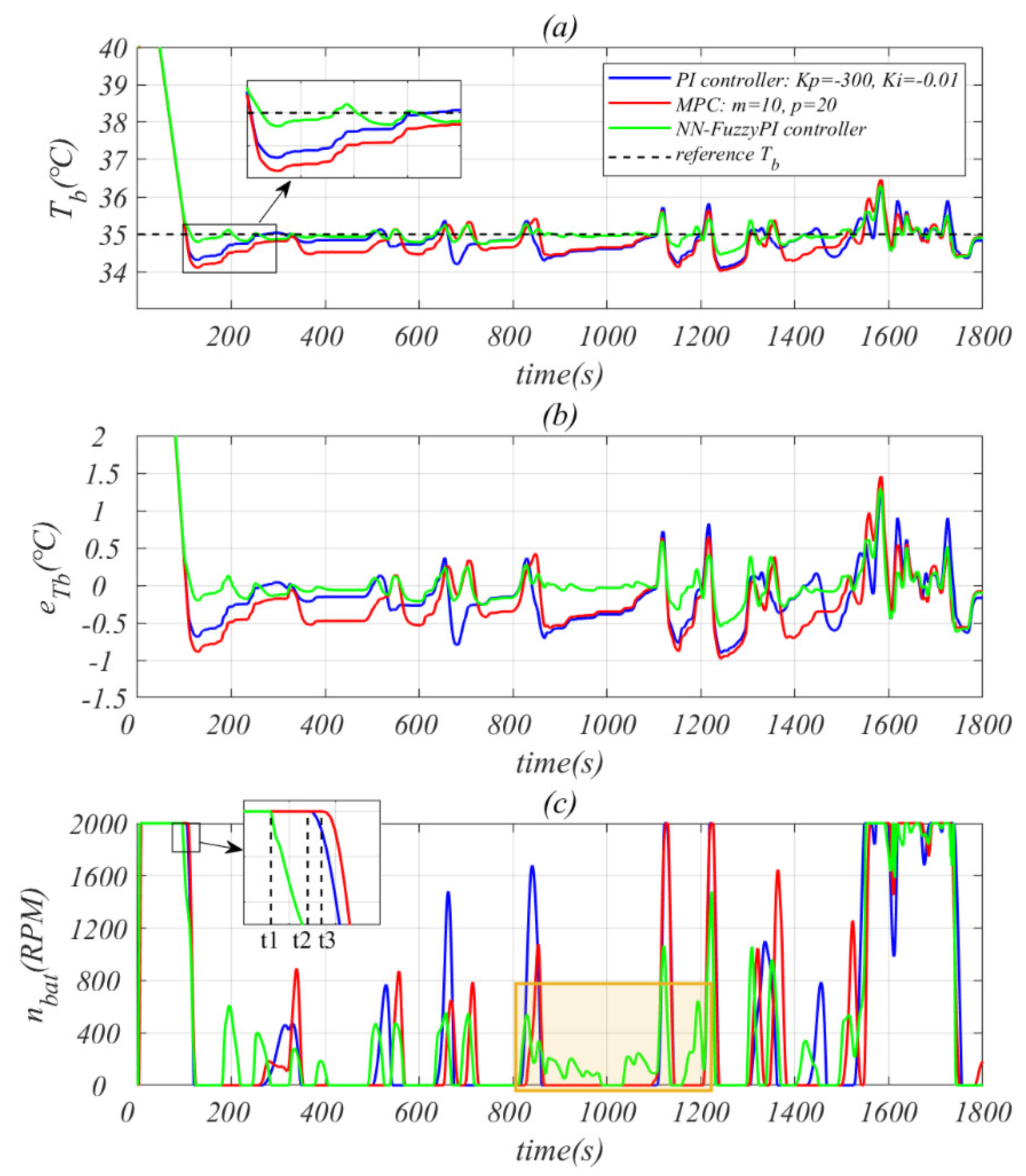
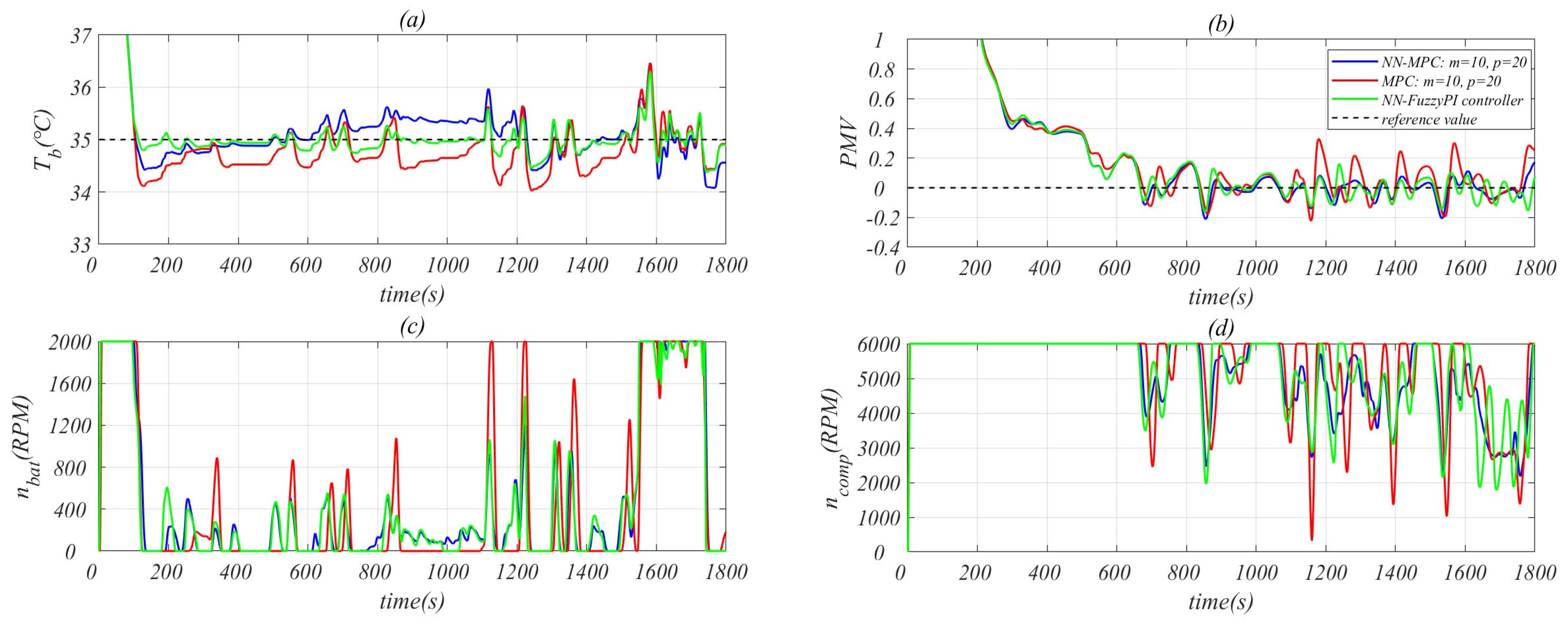
4.1. Battery Pack Temperature Control Effect
4.2. PMV Control Effect
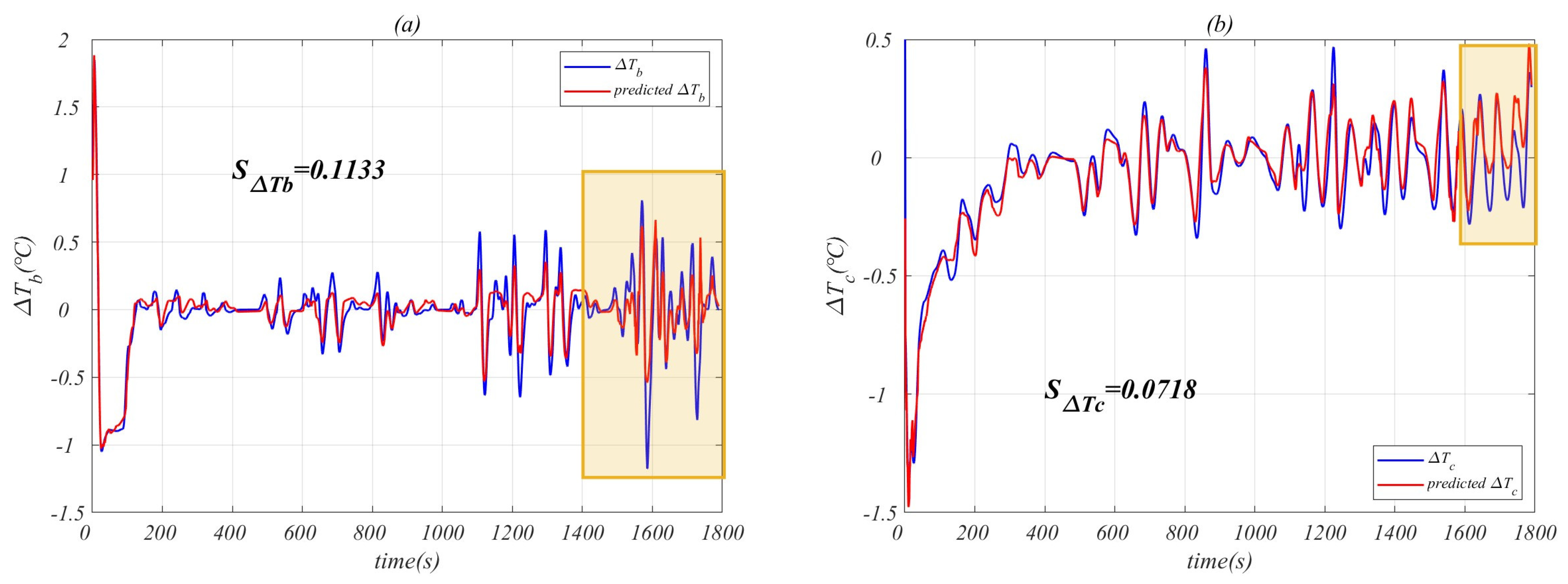
4.3. Performance of Neural Network Feedforward
5. Conclusions
- 1.
- Under WLTC condition, the NN-Fuzzy PI controller can accurately predict the nonlinear and time delay characteristics of the EVTMS and provide advanced feedforward to the system, resulting in better control performance and lower energy consumption compared to PI controller and MPC;
- 2.
- The fluctuations under NN-Fuzzy PI controller are within the range of [−0.5, 0.5], while the fluctuations are within the range of [−0.1, 0.1];
- 3.
- Compared to PI controller, the NN-Fuzzy PI controller reduces by 70% to 150% and by 17% to 22%; compared to MPC, it reduces by 106% to 173% and by 13% to 18%;
- 4.
- Compared to PI controller, the NN-Fuzzy PI model reduces by 107% to 164% and by 2.58% to 3.16%; compared to MPC, it reduces by 43% to 58% and by 1.98% to 2.68%;
- 5.
- When NN feedforward is added to MPC, , and the energy consumption are also significantly reduced, which indicates the effectiveness of NN feedforward in different controllers.
- Factors that may affect the EVTMS performance, such as the battery arrangement and consistency, are not considered, which can be further studied by CFD simulation to establish a more accurate battery model;
- Some algorithms, such as nonlinear model predictive control (NMPC), genetic algorithms (Gas) and particle swarm optimization (PSO), can be used to control all variables inside EVTMS instead of only pump and compressor speed;
- Parameters and hyperparameters in the controllers can be further optimized;
- The robustness and performance of controllers under heating conditions in the winter can be further tested.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Effective heat transfer area () | Root-mean-square error | ||
| Maximum cross-sectional area () | Root-mean-square error of NN-Fuzzy PI controller | ||
| Refrigerant flow coefficient | Root-mean-square error of battery temperature () | ||
| Constant pressure specific heat capacity () | Root-mean-square error of | ||
| Battery capacity | State of charge | ||
| Maximum battery capacity | Initial state of charge | ||
| Characteristic diameter () | Temperature () | ||
| Difference | Air temperature () | ||
| Difference change rate | Battery pack temperature () | ||
| Electromechanical conversion efficiency | Reference battery pack temperature () | ||
| Ratio of the surface area | Chiller inlet temperature () | ||
| Convective heat transfer coefficient () | Chiller outlet temperature () | ||
| Condenser convection heat transfer coefficient () | Comfortable temperature () | ||
| Evaporator convection heat transfer coefficient () | Reference cabin temperature () | ||
| Cabin convective heat transfer coefficient () | Clothes surface temperature () | ||
| Refrigerant enthalpy change | Evaporator inlet temperature () | ||
| Battery current () | Evaporator outlet temperature () | ||
| Instantaneous current () | Average radiation temperature () | ||
| Thermal resistance of clothes () | Reference temperature () | ||
| Integral coefficient | Wall temperature () | ||
| Proportional coefficient | Braking or acceleration torque () | ||
| Heat conductivity coefficient () | Braking friction torque () | ||
| Characteristic length () | Thickness of the heat exchanger pipe () | ||
| Battery cooling valve lift () | Manipulated variable | ||
| Metabolic rate () | Open-circuit voltage () | ||
| Mass () | Compressor displacement () | ||
| Control time horizon () | Wall material volume () | ||
| Nusselt number | Vehicle speed () | ||
| Pump speed () | Wind speed () | ||
| Compressor speed () | External absorbed work () | ||
| Compressor power consumption () | Compressor energy consumption () | ||
| Pump power consumption () | Pump energy consumption () | ||
| Relative humidity | Prediction time point () | ||
| Braking or acceleration power demand () | Output value | ||
| Required power demand () | Efficiency | ||
| Predicted mean vote | Refrigerant density at the expansion valve inlet | ||
| Prandtl number | Subscripts and acronyms | ||
| Prediction time horizon () | |||
| Critical pressure () | AC | Air conditioning | |
| Expansion valve inlet pressure () | EV | Electric vehicle | |
| Expansion valve outlet pressure () | DP | Dynamic programming | |
| Heat transfer of refrigerant | FSM | Finite state machine | |
| Heat transfer of slave fluid | FC | Fuzzy control | |
| Mass flow rate () | NN | Neural network | |
| Coulombic losses | NN-Fuzzy PI | Neural network fuzzy proportional-integral | |
| Reversible losses | PI | Proportional-Integral | |
| Ohmic and reaction losses | PID | Proportional-Integral-Derivative | |
| Pump volumetric flow rate () | PHEV | Plug-in hybrid electric vehicle | |
| Refrigerant mass flow rate () | PSO | Particle Swarm Optimization | |
| Weight matrix of the tracking error variable | TMS | Thermal management system | |
| Weight matrix of the control variable | WLTC | World light vehicle test cycle | |
| Battery resistance | Greek symbols | ||
| Reynolds number | |||
| Reference value | Difference | ||
References
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Hosen, M.S.; Youssef, R.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. Battery cycle life study through relaxation and forecasting the lifetime via machine learning. J. Energy Storage 2021, 40, 102726. [Google Scholar] [CrossRef]
- Sun, P.; Bisschop, R.; Niu, H.; Huang, X. A Review of Battery Fires in Electric Vehicles. Fire Technol. 2020, 56, 1411. [Google Scholar] [CrossRef]
- Yang, T.; Yang, N.; Zhang, X.; Li, G. Investigation of the thermal performance of axial-flow air cooling for the lithium-ion battery pack. Int. J. Therm. Sci. 2016, 108, 132–144. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1–R25. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Li, B.; Yan, Y. A critical review of thermal management models and solutions of lithium-ion batteries for the development of pure electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 106–128. [Google Scholar] [CrossRef]
- Yokoyama, A.; Osaka, T.; Imanishi, Y.; Sekiya, S. Thermal Management System for Electric Vehicles. SAE Int. J. Mater. Manuf 2011, 4, 1277–1285. [Google Scholar] [CrossRef]
- Kiss, T.; Chaney, L.; Meyer, J. A New Automotive Air Conditioning System Simulation Tool Developed in MATLAB/Simulink. SAE Int. J. Passeng. Cars-Mech. Syst. 2013, 6, 826–840. [Google Scholar] [CrossRef][Green Version]
- Kiss, T.; Lustbader, J. Comparison of the Accuracy and Speed of Transient Mobile A/C System Simulation Models. SAE Int. J. Passeng. Cars-Mech. Syst. 2014, 7, 739–754. [Google Scholar] [CrossRef][Green Version]
- Kiss, T.; Lustbader, J.; Leighton, D. Modeling of an Electric Vehicle Thermal Management System in MATLAB/Simulink. In Proceedings of the SAE 2015 World Congress & Exhibition, Detroit, MI, USA, 21–23 April 2015. [Google Scholar]
- Lee, S.; Chung, Y.; Kim, S.; Jeong, Y.; Kim, M.S. Investigation on the performance enhancement of electric vehicle thermal management system utilizing floating loop with finite heat exchanger size. Energy Convers. Manag. 2022, 255, 115265. [Google Scholar] [CrossRef]
- Yang, Q.; Zeng, T.; Zhang, C.; Zhou, W.; Xu, L.; Zhou, J.; Jiang, P.; Jiang, S. Modeling and simulation of vehicle integrated thermal management system for a fuel cell hybrid vehicle. Energy Convers. Manag. 2023, 278, 116745. [Google Scholar] [CrossRef]
- Shah, S.; Vijay, D.; Lehocky, M. Thermal Management of Electrified Vehicle by Means of System Simulation. In Proceedings of the Thermal Management Systems Conference 2020, Berlin, Germany, 21–22 January 2020. [Google Scholar]
- Dong, Y.Q.; Wu, H.; Zhou, J.; Ding, Y.; Wang, X.; Xu, S. Designing and Evaluating the Integrated Thermal Management System of a Plug-in Parallel Hybrid Electric Vehicle. In Proceedings of the SAE 2020 Vehicle Electrification and Autonomous Vehicle Technology Forum, Shanghai, China, 3–4 December 2020. [Google Scholar]
- Deng, L.; Li, S.; Tang, X.; Yang, K.; Lin, X. Battery thermal- and cabin comfort-aware collaborative energy management for plug-in fuel cell electric vehicles based on the soft actor-critic algorithm. Energy Convers. Manag. 2023, 283, 116889. [Google Scholar] [CrossRef]
- Asef, A.; Chitsaz, I.; Madan, N. Modeling and total cost optimization of battery thermal management system in a hybrid electric vehicle. J. Energy Storage 2022, 52 Pt A, 104844. [Google Scholar] [CrossRef]
- Wang, Z.R.; Huang, L.P.; He, F. Design and analysis of electric vehicle thermal management system based on refrigerant-direct cooling and heating batteries. J. Energy Storage 2022, 51, 104318. [Google Scholar] [CrossRef]
- Cen, J.; Jiang, F. Li-ion power battery temperature control by a battery thermal management and vehicle cabin air conditioning integrated system. Energy Sustain. Dev. 2020, 57, 141–148. [Google Scholar] [CrossRef]
- Yasaman, M.; Ahmad, M.; Nasser, L.A. Battery Thermal Management of Electric Vehicles: An Optimal Control Approach. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015. [Google Scholar]
- Chong, Z.; Fei, L.; Hua, Z.; Jing, S.; Chris, M.C. A Real-Time Battery Thermal Management Strategy for Connected and Automated Hybrid Electric Vehicles (CAHEVs) Based on Iterative Dynamic Programming. IEEE Trans. Veh. Technol. 2018, 67, 8077–8084. [Google Scholar]
- Min, H.; Zhang, Z.; Sun, W.; Min, Z.; Yu, Y.; Wang, B. A thermal management system control strategy for electric vehicles under low-temperature driving conditions considering battery lifetime. Appl. Therm. Eng. 2020, 181, 115944. [Google Scholar] [CrossRef]
- Shen, W.; Wang, N. Simulation and Control of Battery Thermal Management System for Electric Vehicle. In Proceedings of the Vehicle Electrification and Powertrain Diversification Technology Forum, Beijing, China, 23–24 August 2022. [Google Scholar]
- Şefkat, G.; Özel, M.A. Experimental and numerical study of energy and thermal management system for a hydrogen fuel cell-battery hybrid electric vehicle. Energy 2022, 238, 121794. [Google Scholar] [CrossRef]
- Wang, H.; He, F.; Ma, L. Experimental and modeling study of controller-based thermal management of battery modules under dynamic loads. Int. J. Heat Mass Transf. 2016, 103, 154–164. [Google Scholar] [CrossRef]
- Bauer, S.; Suchaneck, A.; León, F.P. Thermal and energy battery management optimization in electric vehicles using Pontryagin’s maximum principle. J. Power Sources 2014, 246, 808–818. [Google Scholar] [CrossRef]
- Zhang, Z.; Min, H.; Yu, Y.; Cao, Q.; Li, M.; Yan, K. An optimal thermal management system heating control strategy for electric vehicles under low-temperature fast charging conditions. Appl. Therm. Eng. 2022, 207, 118123. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, Z.; Liu, J.; Li, K.; Zhang, Y.; Wu, C.; Wang, P.; Wang, X. A Self-learning intelligent passenger vehicle comfort cooling system control strategy. Appl. Therm. Eng. 2020, 166, 114646. [Google Scholar] [CrossRef]
- Yasaman, M.; Nasser, L.A. MPC-based battery thermal management controller for Plug-in hybrid electric vehicles. In Proceedings of the IEEE 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017. [Google Scholar]
- Vermillion, C.; Jing Sun Butts, K. Predictive Control Allocation for a Thermal Management System Based on an Inner Loop Reference Model—Design, Analysis, and Experimental Results. IEEE 2011, 19, 772–781. [Google Scholar] [CrossRef]
- Tao, X.W.; Wagner, J. Cooling Air Temperature and Mass Flow Rate Control for Hybrid Electric Vehicle Battery Thermal Management. In Proceedings of the ASME 2014 Dynamic Systems and Control Conference, San Antonio, TX, USA, 22–24 October 2014. [Google Scholar]
- Tao, X.; Zhou, K.; Ivanco, A.; Wagner, J.R.; Hofmann, H.; Filipi, Z. A Hybrid Electric Vehicle Thermal Management System—Nonlinear Controller Design. In Proceedings of the SAE 2015 World Congress & Exhibition, Detroit, MI, USA, 21–23 April 2015. [Google Scholar]
- Lopez-Sanz, J.; Ocampo-Martinez, C.; Alvarez-Florez, J.; Moreno-Eguilaz, M.; Ruiz-Mansilla, R.; Kalmus, J.; Graeber, M.; Lux, G. Nonlinear Model Predictive Control for Thermal Management in Plug-in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2015, 66, 3632–3644. [Google Scholar] [CrossRef]
- Lopez-Sanz, J.; Ocampo-Martinez, C.; Alvarez-Florez, J.; Moreno-Eguilaz, M.; Ruiz-Mansilla, R.; Kalmus, J.; Graeber, M.; Lux, G. Thermal Management in Plug-In Hybrid Electric Vehicles: A Real-Time Nonlinear Model Predictive Control Implementation. IEEE Trans. Veh. Technol. 2016, 66, 7751–7760. [Google Scholar] [CrossRef]
- Ma, Y.; Ding, H.; Mou, H.; Gao, J. Battery thermal management strategy for electric vehicles based on nonlinear model predictive control. Measurement 2021, 186, 110115. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J. Self-adapting J-type air-based battery thermal management system via model predictive control. Appl. Energy 2020, 263, 114640. [Google Scholar] [CrossRef]
- García-Morales, J.; Cervantes-Bobadilla, M.; Hernández-Pérez, J.A.; Saavedra-Benítez, Y.I.; Adam-Medina, M.; Guerrero-Ramírez, G.V. Inverse artificial neural network control design for a double tube heat exchanger. Case Stud. Therm. Eng. 2022, 34, 102075. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- Farzaneh, Y.; Tootoonchi, A.A. Controlling automobile thermal comfort using optimized fuzzy controller. Appl. Therm. Eng. 2008, 28, 1906–1917. [Google Scholar] [CrossRef]
- Jang, M.S.; Koh, C.D.; Moon, I.S. Review of thermal comfort design based on PMV/PPD in cabins of Korean maritime patrol vessels. Build. Environ. 2007, 42, 55–61. [Google Scholar] [CrossRef]
- Toftum, J.; Jorgensen, A.S.; Fanger, P.O. Upper limits for indoor air humidity to avoid uncomfortably humid skin. Energy Build. 1998, 28, 1–13. [Google Scholar] [CrossRef]
- Atmaca, I.; Yigit, A. Predicting the effect of relative humidity on skin temperature and skin wittedness. J. Therm. Biol. 2006, 31, 442–452. [Google Scholar] [CrossRef]
- Euzébio, T.A.M.; Ramirez, M.A.P.; Reinecke, S.F.; Hampel, U. Energy Price as an Input to Fuzzy Wastewater Level Control in Pump Storage Operation. IEEE Access 2023, 11, 93701–93712. [Google Scholar] [CrossRef]
- Júnior, M.P.; da Silva, M.T.; Guimarães, F.G.; Euzébio, T.A.M. Energy savings in a rotary dryer due to a fuzzy multivariable control application. Dry. Technol. 2022, 40, 1196–1209. [Google Scholar] [CrossRef]
- Gopi, B.; Ramesh, G.; Logeshwaran, J. The Fuzzy Logical Controller Based Energy Storage and Conservation Model to Achieve Maximum Energy Efficiency In Modern 5G Communication. ICTACT J. Commun. Technol. 2022, 13, 2774–2779. [Google Scholar]
- Mann, G.K.I.; Hu, B.-G.; Gosine, R.G. Analysis of direct action fuzzy PID controller structures. IEEE Trans. Syst. Man Cybern. Part B 1999, 29, 371–388. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Q.; Zhang, R. Improved fuzzy PID controller design using predictive functional control structure. ISA Trans. 2017, 71 Pt 2, 354–363. [Google Scholar] [CrossRef]











| Parameter | Value |
|---|---|
| Maximum flow cross-sectional area () | 3.28 |
| Minimum flow cross-sectional area () | 0.27 |
| Time constant (s) | 3 |
| Pressure drop coefficient | 2 |
| Target superheat () | 3 |
| Parameters | Condenser | Evaporator | Chiller |
|---|---|---|---|
| Length (mm) | 375.5 | 220 | 85 |
| Width (mm) | 640 | 190 | 61 |
| Thickness (mm) | 26 | 34 | 53 |
| Connection diameter (mm) | 11 | 20 | 16 |
| Dry mass (kg) | 1 | 0.9 | 1 |
| Material | Aluminum | ||
| Parameter | Value |
|---|---|
| Cabin air volume (L) | 2800 |
| ) | 26.9 |
| ) | 14.5 |
| 1000 |
| Thermal Sensation | |
|---|---|
| Very cold | |
| Cold | |
| Cool | |
| Slightly cool | |
| Comfortable | |
| Slightly warm | |
| Warm | |
| Hot | |
| Very hot |
| Parameter | Value |
|---|---|
| Cell capacitance (A/h) | 57 |
| ) | 0.8 |
| Number of series cells | 96 |
| Number of parallel cells | 3 |
| Battery load type | Power request |
| ) | 1 |
| Material | Aluminum |
| Parameter | Value |
|---|---|
| ) | 1929 |
| ) | 2335 |
| Wind drag coefficient | 0.23 |
| Rolling resistance coefficient | 0.01 |
| ) | 3.4 |
| Length · Width · Height ) | 4750 · 1921 · 1624 |
| ) | 2890 |
| ) | 1636 |
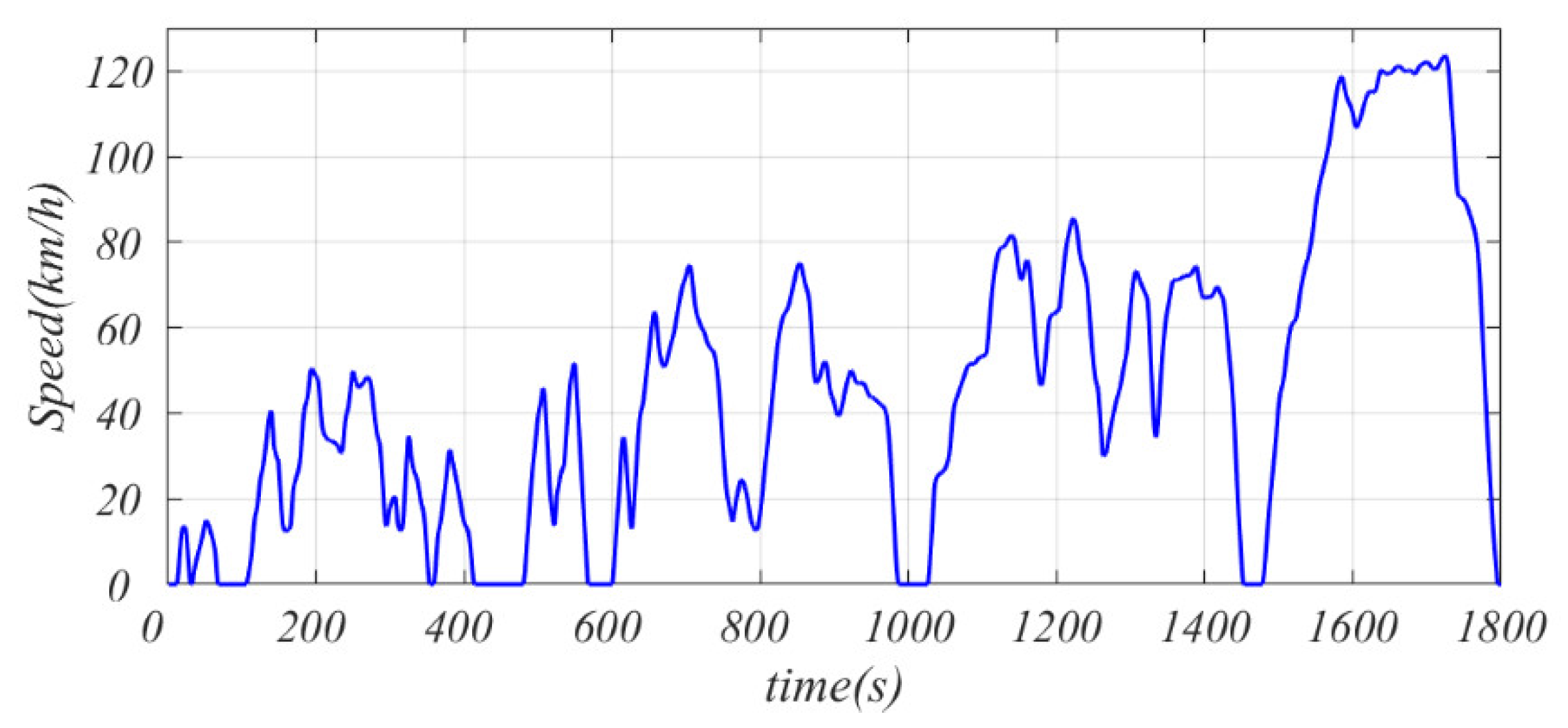
| Time (s) | Speed (km/h) * | (RPM) | (RPM) |
|---|---|---|---|
| 0–300 | 0 | 0 | 0 |
| 300–400 | 400 | 1000 | |
| 400–500 | 800 | 2000 | |
| 500–600 | 1200 | 3000 | |
| 600–700 | 1600 | 4000 | |
| 700–800 | 2000 | 5000 | |
| 800–2600 | 3 * WLTC | 0 | 0 |
| 2600–3320 | 400 | 1000 | |
| 3320–4040 | 800 | 2000 | |
| 4040–4760 | 1200 | 3000 | |
| 4760–5480 | 1600 | 4000 | |
| 5480–6200 | 2000 | 5000 |
| e ec | NB | NS | ZO | PS | PB |
|---|---|---|---|---|---|
| NB | PB | PB | PB | PB | PS |
| NS | PB | PS | PS | PS | ZO |
| ZO | PS | ZO | ZO | ZO | PS |
| PS | ZO | PS | PS | PS | PB |
| PB | PS | PB | PB | PB | PB |
| Controller | (%) | (%) | ||||
|---|---|---|---|---|---|---|
| PI Controller ( | 0.5845 | 0.3589 | 159.1 | 1.225 | 0.182 | 17.45 |
| PI Controller ( | 0.3873 | 0.1617 | 71.68 | 1.238 | 0.195 | 18.70 |
| PI Controller ( | 0.4264 | 0.2008 | 89.01 | 1.274 | 0.231 | 22.15 |
| MPC | 0.6158 | 0.3902 | 173.0 | 1.237 | 0.194 | 18.60 |
| MPC | 0.4571 | 0.2315 | 102.6 | 1.181 | 0.138 | 13.23 |
| MPC | 0.4647 | 0.2391 | 106.0 | 1.233 | 0.190 | 18.22 |
| NN-Fuzzy PI Controller | 0.2256 | 0 | 0 | 1.043 | 0 | 0 |
| Controller | (%) | (%) | ||||
|---|---|---|---|---|---|---|
| PI Controller ( | 0.2135 | 0.1287 | 151.8 | 3251.9 | 81.8 | 2.580 |
| PI Controller ( | 0.1760 | 0.0912 | 107.6 | 3269.5 | 99.4 | 3.136 |
| PI Controller ( | 0.2239 | 0.1391 | 164.0 | 3270.2 | 100.1 | 3.158 |
| MPC | 0.1343 | 0.0495 | 58.4 | 3245.3 | 75.2 | 2.372 |
| MPC | 0.1200 | 0.0352 | 41.5 | 3232.9 | 62.8 | 1.981 |
| MPC | 0.1221 | 0.0373 | 43.9 | 3253.9 | 83.8 | 2.643 |
| NN-Fuzzy PI Controller | 0.0848 | 0 | 0 | 3170.1 | 0 | 0 |
| Controller | (%) | (%) | ||||
|---|---|---|---|---|---|---|
| MPC | 0.4571 | 0.2315 | 102.6 | 1.181 | 0.138 | 13.23 |
| NN-MPC | 0.3651 | 0.1395 | 61.8 | 1.085 | 0.042 | 4.03 |
| NN-Fuzzy PI Controller | 0.2256 | 0 | 0 | 1.043 | 0 | 0 |
| Controller | (%) | (%) | ||||
|---|---|---|---|---|---|---|
| MPC | 0.1200 | 0.0352 | 41.5 | 3232.9 | 62.8 | 1.981 |
| NN-MPC | 0.0819 | −0.0029 | −3.4 | 3166.7 | −3.4 | −0.107 |
| NN-Fuzzy PI Controller | 0.0848 | 0 | 0 | 3170.1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, F.; Wang, D. Application of Neural Network Feedforward in Fuzzy PI Controller for Electric Vehicle Thermal Management System: Modeling and Simulation Studies. Energies 2024, 17, 9. https://doi.org/10.3390/en17010009
Fei F, Wang D. Application of Neural Network Feedforward in Fuzzy PI Controller for Electric Vehicle Thermal Management System: Modeling and Simulation Studies. Energies. 2024; 17(1):9. https://doi.org/10.3390/en17010009
Chicago/Turabian StyleFei, Fan, and Dong Wang. 2024. "Application of Neural Network Feedforward in Fuzzy PI Controller for Electric Vehicle Thermal Management System: Modeling and Simulation Studies" Energies 17, no. 1: 9. https://doi.org/10.3390/en17010009
APA StyleFei, F., & Wang, D. (2024). Application of Neural Network Feedforward in Fuzzy PI Controller for Electric Vehicle Thermal Management System: Modeling and Simulation Studies. Energies, 17(1), 9. https://doi.org/10.3390/en17010009








