Short-Term Photovoltaic Power Generation Prediction Model Based on Improved Data Decomposition and Time Convolution Network
Abstract
:1. Introduction
2. Optimization of Multivariate Variational Modal Decomposition
2.1. Common Data Decomposition Methods
2.2. Hybrid Whale Optimization Algorithm
2.2.1. Tent Mapping
2.2.2. Elite Reverse Learning Strategy
2.2.3. Nonlinear Adaptive Weight Strategy
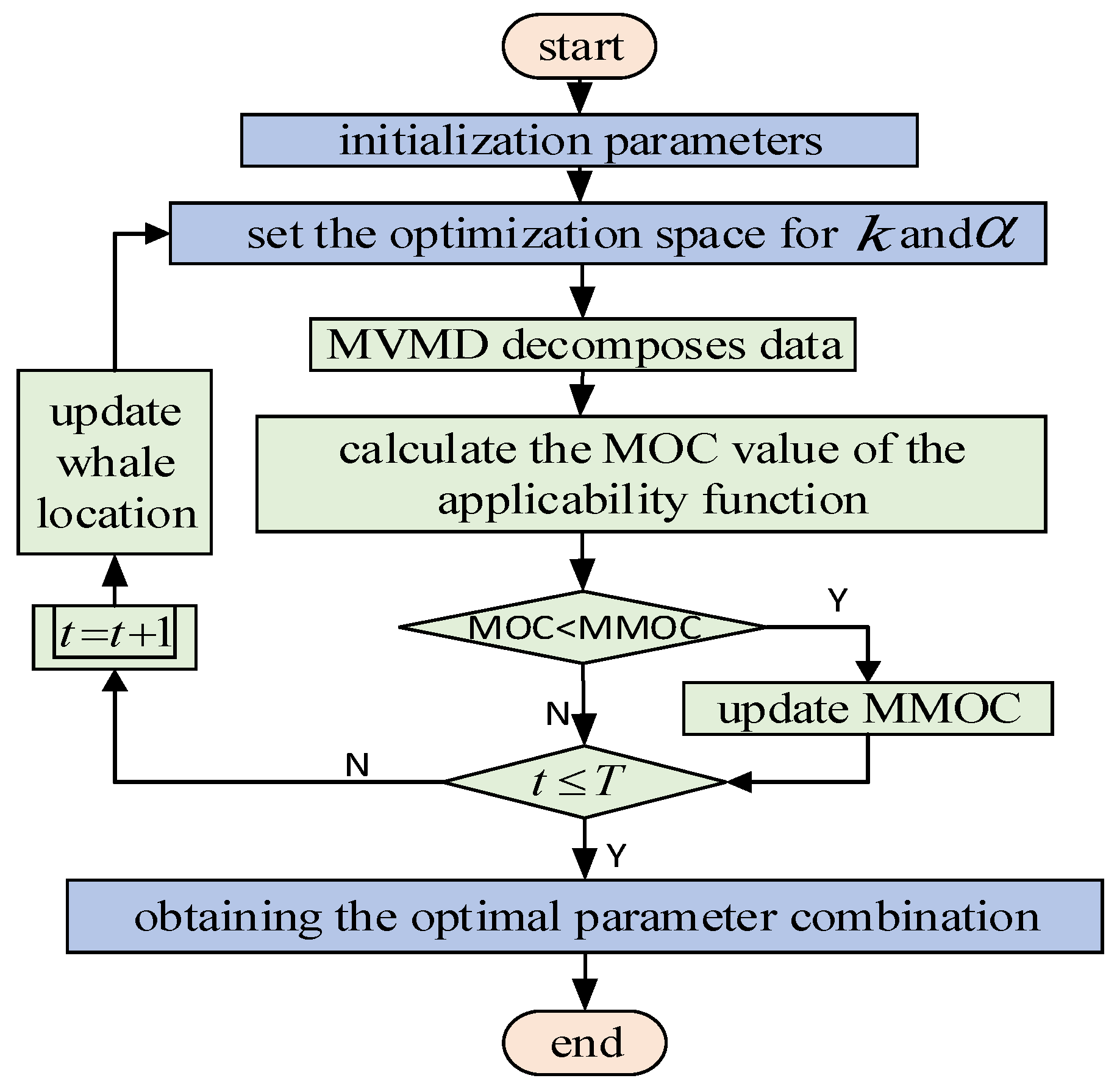
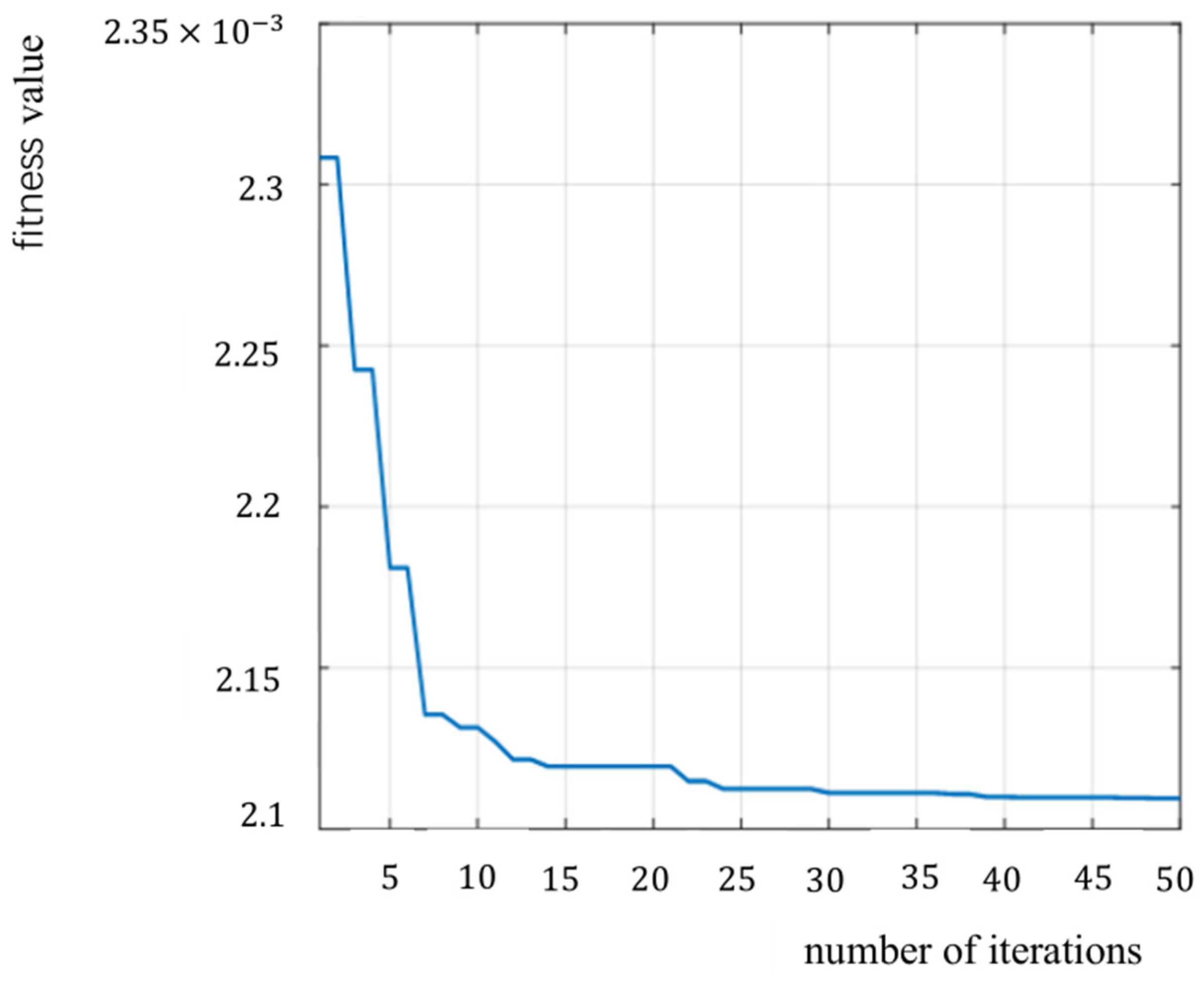
2.3. HWOA-MVMD Algorithm
- (1)
- Set the whale population size, maximum number of iterations, optimization parameter optimization space, and initialization population position;
- (2)
- Take the minimum modal overlap component as the fitness function, calculate the fitness value according to the position of the population, and save the current optimal value;
- (3)
- Search for the optimal individual update search area, and update the position of the whale’s next iteration according to the fitness value level;
- (4)
- Determine whether the termination conditions are met: if it is met, jump out of the loop to execute step (5); otherwise, re-execute steps (2)–(3);
- (5)
- Save the result of the final global optimal solution [, ]; HWOA-MVMD will decompose the original data according to the parameter optimal solution to obtain different modal components.
3. TPA-TCN Prediction Model
3.1. Analysis of Photovoltaic Power Generation Characteristics
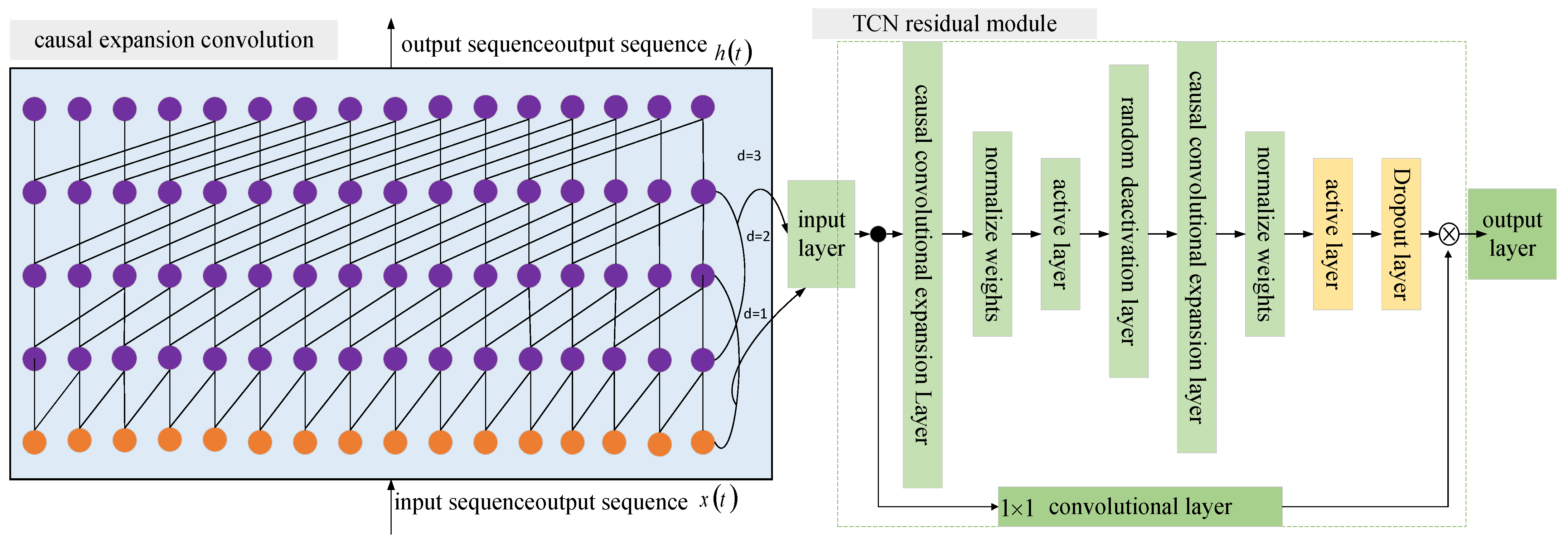
3.2. Time Convolutional Network
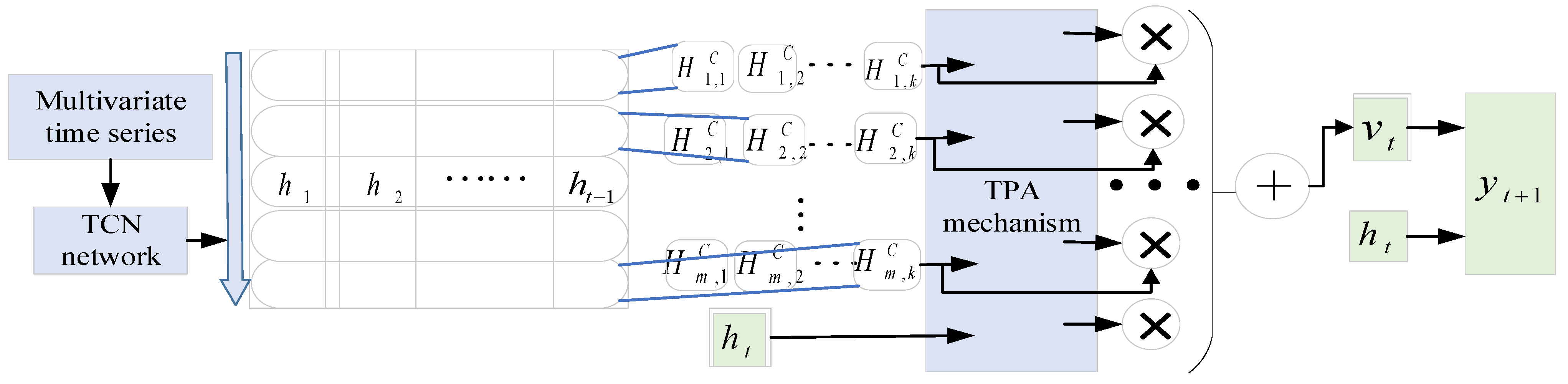
3.3. Temporal Convolutional Network Model Based on Time Pattern Attention
- (1)
- TCN layer
- (2)
- Time mode capture layer
- (3)
- Time Mode Attention Layer
4. Short-Term Photovoltaic Power Generation Prediction Model Based on HWOA-MVMD-TPA-TCN
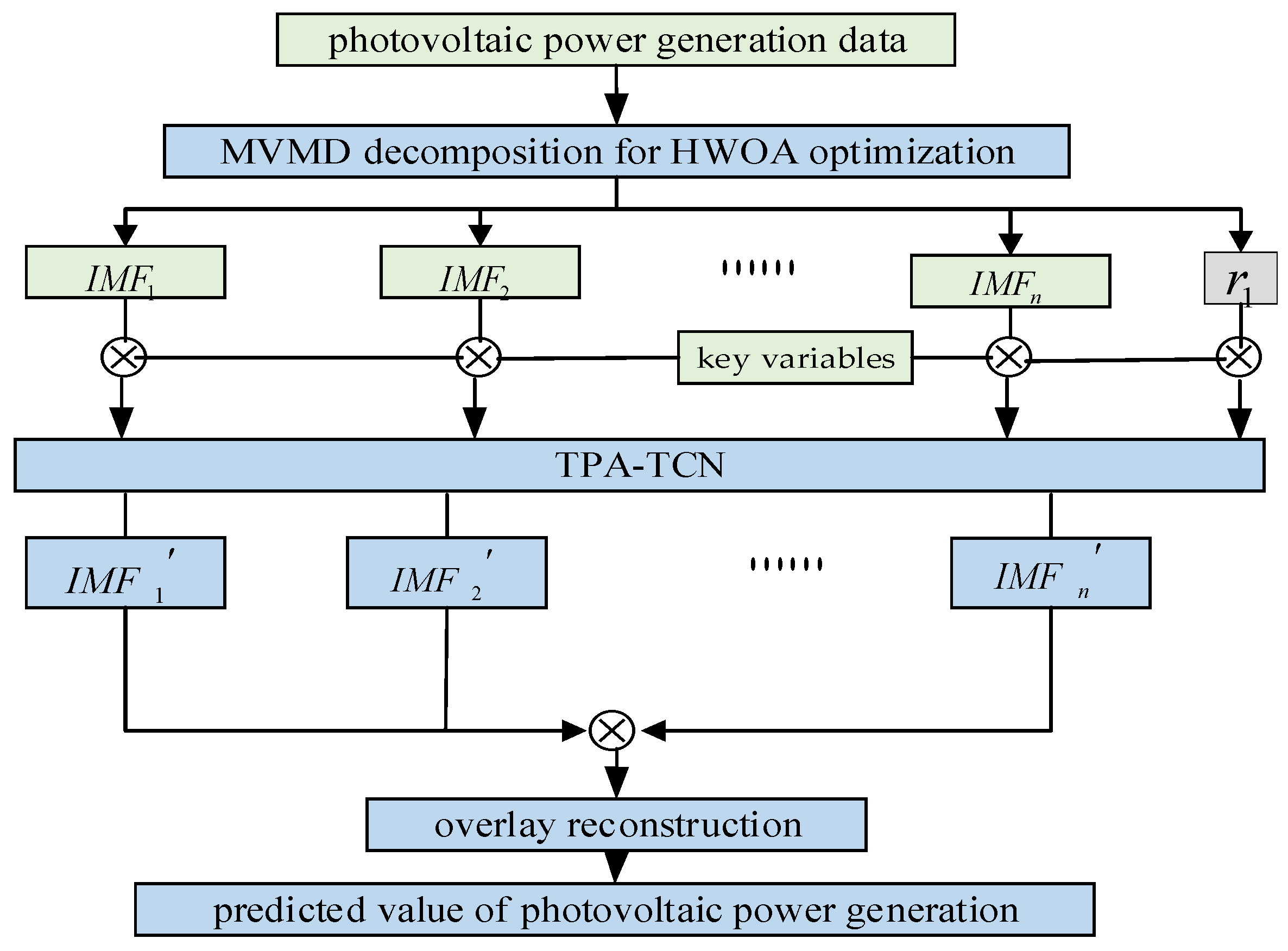
4.1. Prediction Model Process
- (1)
- Utilize the HWOA to optimize the modal number and penalty factor in MVMD, with the MMOC as the objective function, to obtain and save the optimal solution.
- (2)
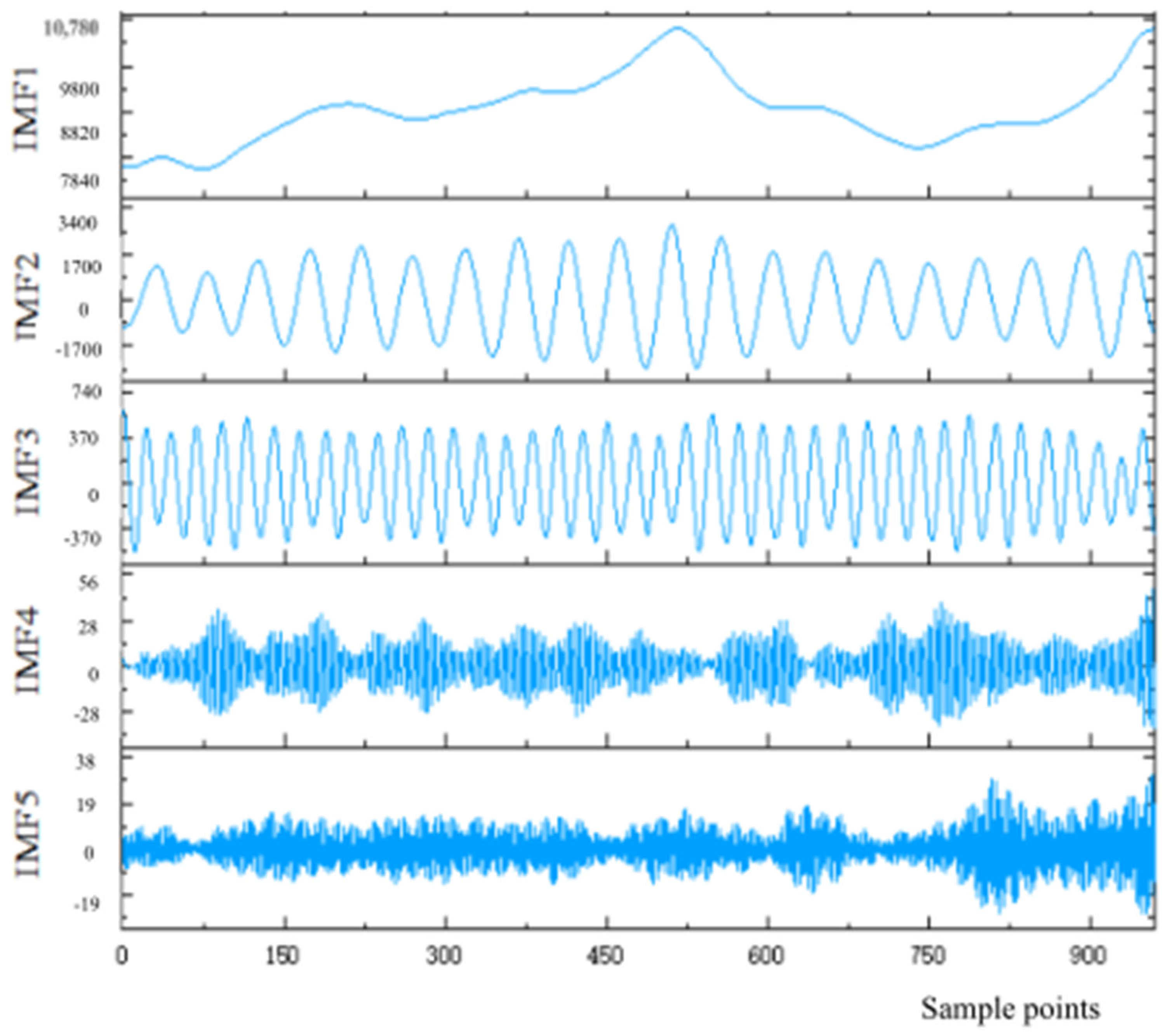
- According to the optimal solution in (1), the original photovoltaic power generation sequence is decomposed using the HWOA-optimized MAMD to obtain different IMF components and a residual component .
- (3)
- Each component of the original data after decomposition, different IMF components, and the key influencing factor variable data are combined into a training set and input into the TPA-TCN model to obtain different components.
- (4)
- The superposition and reconstruction of the predicted values of different components are performed to obtain the final predicted value of photovoltaic power generation.
- (5)
- The predicted photovoltaic power generation value is compared with the actual photovoltaic power generation data, and the error is analyzed.
4.2. Data Preprocessing
4.2.1. Normalization
4.2.2. Selection of Evaluation Indicators for Prediction Error
4.2.3. Preprocessing of the Photovoltaic Power Generation Sequence
5. Example Analysis
5.1. Parameter Settings for the Prediction Models
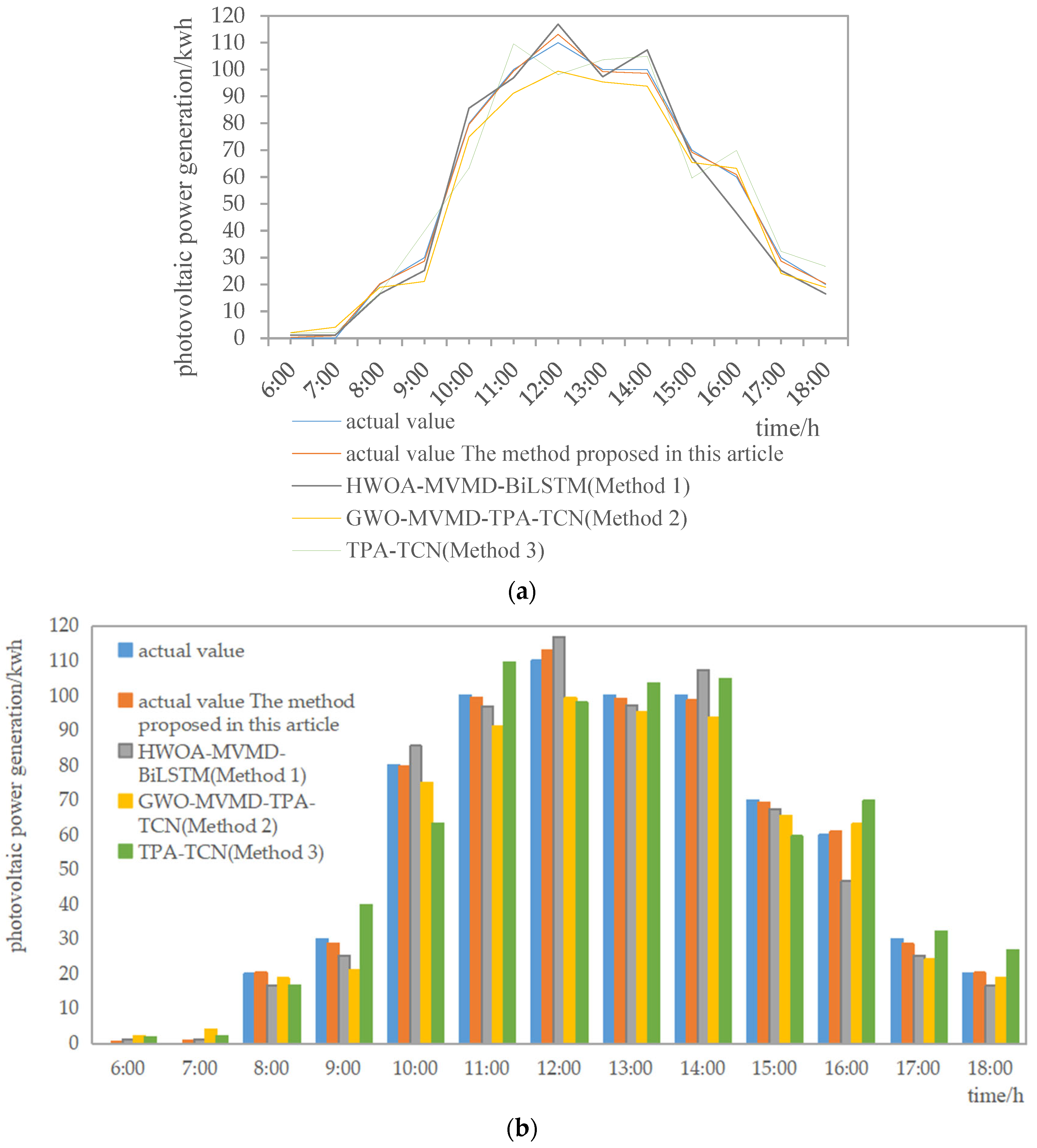
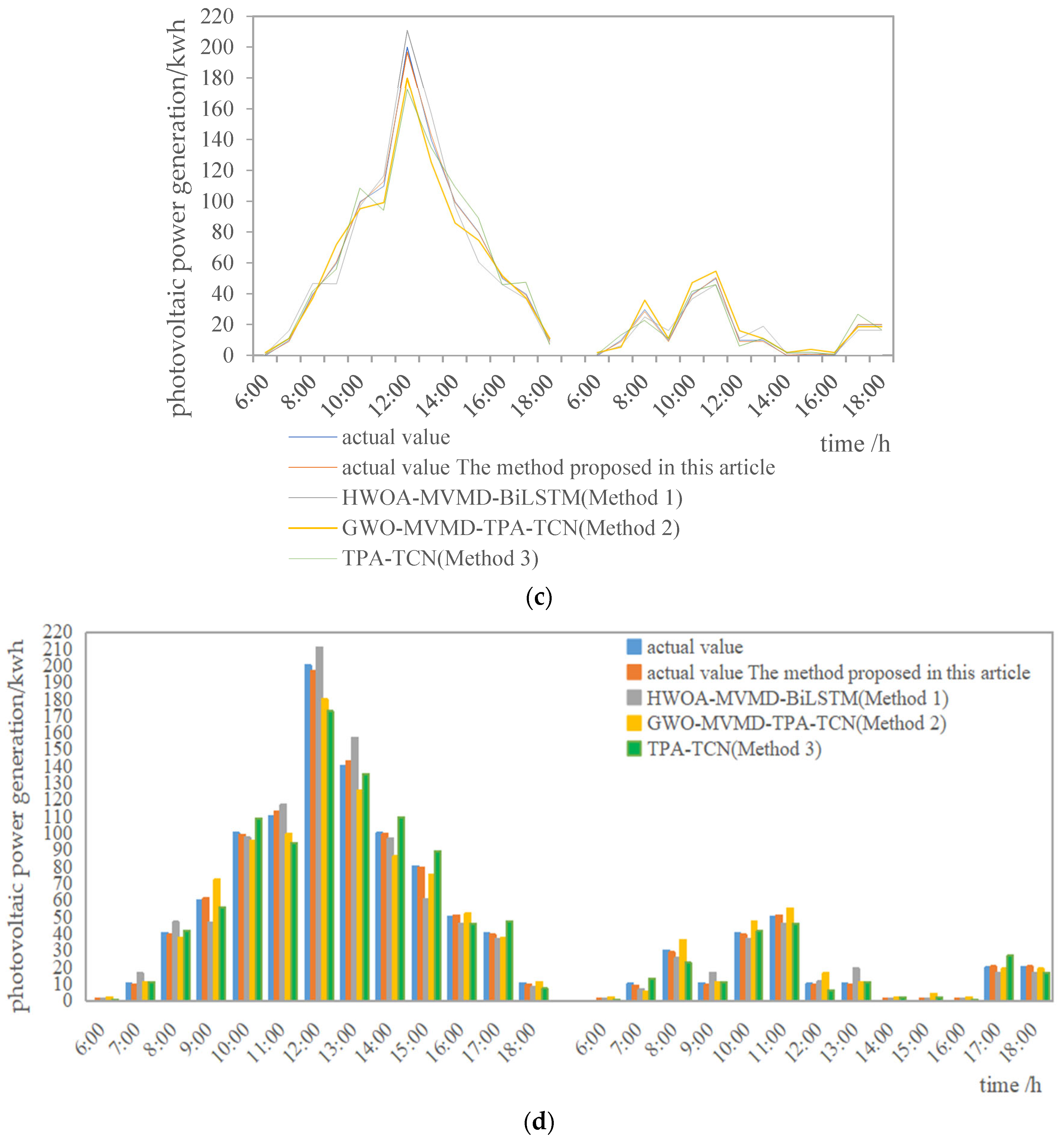
5.2. Photovoltaic Power Generation Prediction Based on TAP-TCN
5.3. Comparative Analysis of Prediction Methods
6. Conclusions
- (1)
- Using the actual data example analysis of a business center in Tianjin, the HWOA-MVMD-TPA-TCN model effectively reduces the prediction error of photovoltaic power generation, in which the MAE value is 1.95 MW and the RMSE value is 2.55 MW, which can be reduced by up to 33.74% and 38.85%, respectively. The effectiveness of the forecasting model proposed in this paper is proved, and the model has certain reference value in the field of time series forecasting.
- (2)
- The IMF components resulting from the decomposition of photovoltaic power generation possess distinct characteristic changes. Exploring more efficient prediction methods for these components requires further research. Additionally, analyzing error components and improving prediction accuracy through error correction should be considered. Future research can focus on these aspects to advance photovoltaic power generation prediction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, S.; Pan, T. Photovoltaic electricity generation power prediction based on similar day and LS-SVM with EP-SO. Transducer Microsyst. Technol. 2019, 38, 46–48+52. [Google Scholar]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.; Coimbra, C.F. History and trends in solar irradiance and PV power forecasting: A preliminary assessment and review using text mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, J.; Lan, K.; Huan, X.; Fan, C.; Xia, X. Prediction of power generation of photovoltaic power station based on data mining and genetic wavelet neural network. J. Sol. Energy 2021, 42, 375–382. [Google Scholar]
- Gigoni, L.; Betti, A.; Crisostomi, E.; Franco, A.; Tucci, M.; Bizzarri, F.; Mucci, D. Day-ahead hourly forecasting of power generaion from photovoltaic plants. IEEE Trans. Sustain. Energy 2018, 9, 831–842. [Google Scholar] [CrossRef]
- Liu, L.; Qiu, J.; Chen, X. Solar photovoltaic power prediction based on Ant colony optimization algorithms. Comput. Digit. Eng. 2021, 49, 2396–2401. [Google Scholar]
- Ni, A.; Wang, Y.; Xue, H. Prediction of ultra short term photovoltaic power generation output based on improved whale optimization algorithm based on chaotic characteristics—Relevance vector machine. Mod. Power 2021, 38, 268–276. [Google Scholar]
- Zhao, H.; Zhao, Z.; Wang, H.; Yue, Y. Short-term photovoltaic power prediction based on DE-GWO-LSTM. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020. [Google Scholar]
- Zhang, X.; Han, P.; Xu, L.; Zhang, F.; Wang, Y.; Gao, L. Research on bearing fault diagnosis of wind turbine gearbox based on 1DCNN-PSO-SVM. IEEE Access 2020, 8, 192248–192258. [Google Scholar] [CrossRef]
- Dai, B.; Hu, T.; Tan, J.; Sun, X.; Huang, Y.; Zhu, L.; Hu, T.; Yi, J. Prediction of photovoltaic power generation based on SWOA optimized BPNN. J. Hubei Univ. Natl. Nat. Sci. Ed. 2021, 39, 321–325+331. [Google Scholar]
- Ling, N.; An, W.; Zhou, Y.; Jiang, Z.; Li, S. Research on the photovoltaic power generation prediction model based on HBA-SVR. Electr. Appl. 2023, 42, 72–78. [Google Scholar]
- Li, P. Short term photovoltaic power generation prediction based on ISSA-SVR. Sci. Technol. Innov. 2023, 1, 34–37. [Google Scholar]
- Zhao, J.; Zhang, J.; Mao, L.; Qu, K.; Huang, C.; Jie, Y. Research on photovoltaic power generation prediction based on PSO Soft attention bidirectional LSTM algorithm. Smart Power 2022, 50, 1–7. [Google Scholar]
- Liu, C. Research on Photovoltaic Power Generation Prediction and FPGA Acceleration Based on QLSTM. Master’s Thesis, Nanchang University, Nanchang, China, 2022. [Google Scholar]
- Dai, B. Research and Implementation of Photovoltaic Power Generation Prediction Algorithm Based on BP Neural Network. Master’s Thesis, Hubei University for Nationalities, Enshi City, China, 2022. [Google Scholar] [CrossRef]
- Hai, T.; Wen, K.; Zhou, L.; Hu, X.; Zhang, C. Photovoltaic power generation prediction method based on meteorological similarity and Markov chain. J. Guangxi Univ. Nat. Sci. Ed. 2015, 40, 1452–1460. [Google Scholar]
- Tan, J.; Deng, C.; Yang, W.; Liang, N.; Li, F. Adaboost weather clustering ultra short term prediction method for microgrid photovoltaic power generation. Power Syst. Autom. 2017, 41, 33–39. [Google Scholar]
- Xi, F.; An, Y.; Yao, J. Prediction of photovoltaic power generation based on nonlinear combination models. In Proceedings of the 2016 Second International Conference on Electrical and Industrial Engineering, Shanghai, China, 11–12 December 2016. [Google Scholar]
- Jiao, C. Research on Short-Term Photovoltaic Power Prediction Method Based on Machine Learning. Master’s Thesis, Zhongyuan University of Technology, Zhengzhou, China, 2021. [Google Scholar] [CrossRef]
- Liu, F.; Ji, C.; Peng, Y.; Jiang, W. Photovoltaic power generation combination prediction model based on ACO-KF-GRU-EC. Comput. Simul. 2022, 39, 118–123+147. [Google Scholar]
- Zhang, F. Combined application of photovoltaic power generation prediction method based on historical data. Commun. Power Technol. 2020, 37, 190–191. [Google Scholar] [CrossRef]
- Wang, X.; Luo, D.; Sun, Y.; Li, C.; Li, J. Research on the combined prediction method of daily power generation in photovoltaic microgrids based on ABC-SVM and PSO-RF. J. Sol. Energy 2020, 41, 177–183. [Google Scholar]
- Gao, Q.; Lu, J. Short term photovoltaic power prediction based on CEEMDAN-LSSVM-ARIMA model. Sens. Microsyst. 2022, 41, 118–122. [Google Scholar]
- Zhang, M.; Han, Y.; Zalhaf, A.S.; Wang, C.; Yang, P.; Wang, C.; Zhou, S.; Xiong, T. Accurate ultra-short-term load forecasting based on load characteristic decomposition and convolutional neural network with bidirectional long short-term memory model. Sustain. Energy Grids Netw. 2023, 35, 101129. [Google Scholar] [CrossRef]
- Elboshy, B.; Alwetaishi, M.; Aly, R.M.; Zalhaf, A.S. A suitability mapping for the PV solar farms in Egypt based on GIS-AHP to optimize multi-criteria feasibility. Ain Shams Eng. J. 2022, 13, 101618. [Google Scholar] [CrossRef]
- Zhao, E.; Han, Y.; Lin, X.; Yang, P.; Blaabjerg, F.; Zalhaf, A.S. Impedance characteristics investigation and oscillation stability analysis for two-stage PV inverter under weak grid condition. Electr. Power Syst. Res. 2022, 209, 108053. [Google Scholar] [CrossRef]
- Zhao, E.; Han, Y.; Lin, X.; Liu, E.; Yang, P.; Zalhaf, A.S. Harmonic characteristics and control strategies of grid-connected photovoltaic inverters under weak grid conditions. Int. J. Electr. Power Energy Syst. 2022, 142, 108280. [Google Scholar] [CrossRef]
- Wen, B.; Chen, F.; Wang, H. Short-term wind power prediction based on data feature extraction and SSA-BiLSTM. Appl. Sci. Technol. 2023, 50, 71–78. [Google Scholar]
- Shi, P.; Zhang, H.; Yi, S.; Han, D. An improved method for extracting fault signal characteristics of adaptive multivariational modal decomposition bearings. J. Metrol. 2022, 43, 1326–1334. [Google Scholar]
- Liu, N.; Cai, G.; Yang, D.; Wang, B. Identification of low-frequency oscillation modes of power system based on adaptive multivariational mode decomposition. J. Northeast. Dianli Univ. 2020, 40, 1–7. [Google Scholar] [CrossRef]
- Wang, J. Research on Multi-Energy Microgrid Optimization Based on Improved Whale Algorithm. Master’s Thesis, Beijing University of Civil Engineering and Architecture, Beijing, China, 2023. [Google Scholar] [CrossRef]
- Xiao, Z.; Liu, S. Research on elite inverse golden sinusoidal whale algorithm and its engineering optimization. Acta Electron. Sin. 2019, 47, 2177–2186. [Google Scholar]
- Chen, D.; Chen, Z.; Li, Z.; Zhang, J. Permanent magnet synchronous motor control strategy based on improved whale optimization algorithm. Radio Eng. 2023, 1–8. Available online: http://kns.cnki.net/kcms/detail/13.1097.TN.20231016.0950.002.html (accessed on 22 October 2023).
- Li, J.; Li, M.; Yao, X.; Wang, H.; Yu, Q.; Wang, X. Rolling bearing fault diagnosis based on set empirical mode decomposition and K-neneneba singular value decomposition dictionary learning. J. Metrol. 2020, 41, 1260–1266. [Google Scholar]
- Wang, X. Research on All-Weather System and Output Prediction Method of Distributed Photovoltaic Power Generation. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2022. [Google Scholar] [CrossRef]
- Shih, S.; Sun, F.; Lee, H. Temporal pattern attention for multivariate time series forecasting. Mach. Learn. 2019, 108, 8–9. [Google Scholar] [CrossRef]


| File Number | Main Content | Areas of Shortcoming | |
|---|---|---|---|
| Establish a single predictive model | [5] | Using ant element data packets to probe the network environment, selecting information transmission links, constructing roaming paths, and enhancing predictive accuracy through iterative computations to search for optimal solutions. | Ignored the problem of poor population diversity and the tendency for the initialization to fall into local optima. |
| [6] | Optimizing the photovoltaic power output prediction algorithm based on the Whale Optimization Algorithm for Support Vector Machines. Optimizing time delay and embedding dimensions in the kernel function to improve generalization ability and convergence speed, resulting in better adaptability. | ||
| [7] | Optimizing the photovoltaic power prediction algorithm using the Grey Wolf Algorithm to optimize the weights of Long Short-Term Memory (LSTM) neural networks. Predicting power based on optimal weights, overcoming the drawbacks of backpropagation, and improving prediction accuracy. | ||
| [8,9,10,11,12] | Establishing optimization models using the Honey Badger Algorithm, Sparrow Algorithm, and PSO (Particle Swarm Optimization) Algorithm for predicting the power generation of photovoltaic power stations. Enhancing prediction accuracy. | ||
| [13,14] | Taking into account the impact of solar irradiance on photovoltaic power generation. Integrating variational quantum circuits with Long Short-Term Memory (LSTM) neural networks, forming a Quantum LSTM neural network applied in predictive research. Accelerating the prediction algorithm through an FPGA hardware platform to reduce computational complexity. | Required a large amount of historical data support. | |
| Combined forecasting method [4] | [15,16,17,18,19,20] | Pointing out the random fluctuations due to meteorological factors in ultra-short-term photovoltaic power generation forecasting. | Low prediction accuracy and did not comprehensively consider all meteorological factors. |
| [21] | Utilizing the Artificial Bee Colony Optimization Support Vector Machine (ABC-SVM) classification model, combined with the Particle Swarm Optimization Random Forest (PSO-RF) model, for classification training based on meteorological data. | Suitable for small sample analysis, but the time complexity increased with the growth of the sample size. | |
| [22] | Adopting the Complex Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) method to decompose the photovoltaic power sequence, reducing the impact of non-stationary features on the prediction. | There were challenges related to mode mixing and difficulty in determining the stopping conditions. | |
| [23,24,25,26] | Establishing a combined forecasting model to enhance the accuracy and stability of ultra-short-term load forecasting. | For nonlinear time series, it did not perform well in capturing nonlinearity. |
| Data Decomposition Method | Problems |
|---|---|
| Wavelet decomposition | Wavelet transform is limited by the need for the manual determination of wavelet bases and the Heisenberg uncertainty principle, which ultimately affects the accuracy of the prediction results. |
| Empirical mode decomposition (EMD) | There are problems such as modal aliasing, endpoint effects, and difficulty in determining the stopping conditions. |
| Variational mode decomposition (VMD) | VMD requires predefined modal numbers. Inaccurate modal numbers can lead to insufficient or excessive modal decomposition, and if the signal is long, the bandwidths may overlap. |
| Multivariate variational modal decomposition (MVMD) | The influencing parameters in its decomposition process are related to the number of intrinsic modes and the quadratic penalty factor, and these parameters must be preset. |
| Weight | b_Size | Ir | Dropout | d |
|---|---|---|---|---|
| 32, 64, 128 | 0.001 | 0.01 | 3, 4, 5, 6, 7 | |
| 32, 64, 128 | 0.001 | 0.00001 | 3, 4, 5, 6, 7 |
| Training Parameter | Value |
|---|---|
| k_size | 3 |
| Optimizer | Adam |
| Activation | Sigmoid |
| Epochs | 80 |
| Time | Standard/MW | Proposed Method | HWOA-MVMD- BiLSTM (Method 1) | GWO-MVMD-TPA-TCN (Method 2) | TPA-TCN (Method 3) |
|---|---|---|---|---|---|
| 29 July | MAE | 2.07 | 3.14 | 4.12 | 5.31 |
| RMSE | 2.20 | 4.21 | 5.83 | 6.83 | |
| 30 July | MAE | 2.74 | 4.75 | 6.01 | 11.22 |
| RMSE | 3.58 | 6.76 | 7.18 | 10.58 | |
| 31 July | MAE | 1.07 | 1.69 | 3.68 | 5.03 |
| RMSE | 1.31 | 2.09 | 4.53 | 7.12 | |
| 1 August | MAE | 2.46 | 3.32 | 5.08 | 6.38 |
| RMSE | 3.07 | 4.50 | 6.18 | 7.62 | |
| 2 August | MAE | 1.93 | 2.58 | 4.13 | 5.51 |
| RMSE | 2.59 | 3.56 | 5.67 | 6.79 | |
| average error | MAE | 1.95 | 3.10 | 4.60 | 6.69 |
| RMSE | 2.55 | 4.17 | 5.88 | 7.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Tian, H.; Li, D.; Feng, M.; Fan, H. Short-Term Photovoltaic Power Generation Prediction Model Based on Improved Data Decomposition and Time Convolution Network. Energies 2024, 17, 33. https://doi.org/10.3390/en17010033
Cao R, Tian H, Li D, Feng M, Fan H. Short-Term Photovoltaic Power Generation Prediction Model Based on Improved Data Decomposition and Time Convolution Network. Energies. 2024; 17(1):33. https://doi.org/10.3390/en17010033
Chicago/Turabian StyleCao, Ranran, He Tian, Dahua Li, Mingwen Feng, and Huaicong Fan. 2024. "Short-Term Photovoltaic Power Generation Prediction Model Based on Improved Data Decomposition and Time Convolution Network" Energies 17, no. 1: 33. https://doi.org/10.3390/en17010033
APA StyleCao, R., Tian, H., Li, D., Feng, M., & Fan, H. (2024). Short-Term Photovoltaic Power Generation Prediction Model Based on Improved Data Decomposition and Time Convolution Network. Energies, 17(1), 33. https://doi.org/10.3390/en17010033




