Wind Power Short-Term Time-Series Prediction Using an Ensemble of Neural Networks

Abstract

Short-term wind power forecasting has difficult problems due to the very large variety of speeds of the wind, which is a key factor in producing energy. From the point of view of the whole country, an important problem is predicting the total impact of wind power’s contribution to the country’s energy demands for succeeding days. Accordingly, efficient planning of classical power sources may be made for the next day. This paper will investigate this direction of research. Based on historical data, a few neural network predictors will be combined into an ensemble that is responsible for the next day’s wind power generation. The problem is difficult since wind farms are distributed in large regions of the country, where different wind conditions exist. Moreover, the information on wind speed is not available. This paper proposes and compares different structures of an ensemble combined from three neural networks. The best accuracy has been obtained with the application of an MLP combiner. The results of numerical experiments have shown a significant reduction in prediction errors compared to the naïve approach. The improvement in results with this naïve solution is close to two in the one-day-ahead prediction task.

1. Introduction

Interest in renewable energy generation has grown considerably in recent years, since it reduces the cost of energy and at the same time reduces greenhouse gas emissions. Wind power generation is the fastest-growing source of renewable energy. Wind energy generation is connected to the end of the conventionally generated (hydro, coal, gas, atomic) system or microgrid, which has a small inertia. However, wind power output depends heavily on the wind speed generating irregular power. After connecting irregular wind power to the grid, a system stability problem might occur. Therefore, to stabilize the system’s performance, it is essential to accurately forecast the total wind power in the country and calculate the reserve power. This should be conducted every day, taking into account the data from the previous day.

Different methods of forecasting wind-generated power have been proposed in the past. They are based mainly on the application of different forms of machine learning. All of them use the wind parameter’s information as the basic attributes input into the prognostic system. The authors in [1] discuss the use of the prognostic methods based on persistence (the last known value as the forecast for every future point), the gradient-boosting framework, light gradient-boosting machine (LightGBM) based on decision trees and the idea of a “weak” learner, and support vector regression, as well as the autoregressive integrated moving average with exogenous variable (ARIMAX) and a general additive model (GAMAR). All of them are arranged in the ensemble. The predictive models used as the input attribute 30 parameters associated with atmospheric turbulence as well as other types of nonlinear atmospheric phenomena. The models have been checked at the location of wind farms with the total average error measured in the form of normalized root-mean-square error (NRMSE). The best result was 11.59%. The authors of [2] compared classical and deep learning methods for time-series forecasting. The ratio of the obtained best value of RMSE to the naïve approach is interesting. Its value for different methods changes from 0.935 to 1.00. The authors in [3,4] used the classical multilayer perceptron as the forecasting tool, supplied by the parameters of the wind. The forecasting error is presented in the form of the normalized mean absolute error and root-mean-square error. In the case of [4], they are 8.76% and 13.03%. The authors in [5] present methods of tracking the maximum power point of the wind turbine related to a permanent magnet synchronous generator. It uses artificial neural networks and fuzzy logic systems. The authors in [6] validated the artificial neural network model on an onshore wind farm in Denmark, demonstrating that its mean absolute error is close to 6%. A hybrid approach combining a mode decomposition method and empirical mode decomposition with support vector regression was proposed in [7]. The results in the form of the root-mean-square error for the succeeding hours of the day are given for the Röbergsfjället wind farm, situated in the municipality of Vansbro in Sweden [8]. The authors in [9] presented the application of a spatial–temporal feature extraction neural network developed for short-term spatial and temporal wind power forecasts. The best results of MAPE are from 22.59% in 1-h-ahead forecasting to 60.26% in the 6-h-ahead approach.

The authors in [10] deal with the day-ahead wind power forecasting problem for a newly completed wind power generator using a deep-learning-based transfer learning model, comparing it with a deep learning model without learning from scratch and the light gradient-boosting machine (LGBM). The study shows the advantage of using the transfer learning technique. The LSTM model for the prediction of wind-generated power was proposed in [11]. Authors have shown its advantage in comparison to classical artificial neural networks and support vector regression techniques. The authors in [12] proposed an algorithm for day-ahead wind power prediction by applying fuzzy C-means clustering. This algorithm was used to classify turbines with similar power output characteristics into a few categories, and then a representative power curve was selected as the equivalent curve of the wind farm. The proposed model was validated using historical data taken from two different wind farms, showing improved performance. The authors in [13,14] presented a systematic review of the state-of-the-art approaches of wind power forecasting regarding physical, statistical (time series and artificial neural networks), and hybrid methods, including factors that affect the accuracy and computational time in predictive modeling efforts. They found that artificial neural networks are used more commonly for the forecasting of wind energy and provide increased accuracy of prediction compared with other methods. The authors in [15] show the short-term forecasting system based on the application of discrete wavelet transformation (DWT) and LSTM. The numerical results presented for the dataset containing hourly data of wind generation, solar generation, and inter-connector flow in the entire British area have shown high accuracy in terms of MAPE, MAE, and RMSE values. The authors in [16] presented the DWT-SARIMA-LSTM model, which provided the highest accuracy during testing, indicating it could efficiently capture complex time-series patterns from offshore wind power.

All these papers, proposing different approaches to wind power forecasting, use wind parameters as the key factors in forecasting the power generated by the farm. These approaches are not applicable if the information on wind parameters is not known, which is the case in our problem.

Our study aims to forecast the 24-h pattern of the total power generated by the wind for the whole country, based only on its history. The wind farms producing this type of energy are distributed in many regions of the country from the seacoast to the mountains. These regions differ significantly in terms of wind speed and direction. Dealing with only the dataset of the total energy generated by these wind farms in the whole country, we cannot use information on wind speed, since its values in a particular time instant change a lot, according to its location in the region, and are not known. Therefore, the forecasting problems considered by us are significantly different from those mentioned in the review. Moreover, the forecasting problem is very difficult due to the abrupt changes (from hour to hour) in the time-series values.

It is an important subject from the economic point of view of the power system since it allows one to control and plan the amount of higher-cost conventionally generated energy. The main question arises: how it is possible to predict the next day’s wind energy production in the whole country based on historical data without access to information concerning wind characteristics? This paper shows that this task can be effectively solved by applying the ensemble of a few types of properly integrated neural networks. The proposed MLP and PCA fusing methods have been found to be good tools for obtaining increased prediction accuracy.

Our solution is based on the generalization ability of the neural networks, trained on the available historical data. Using the dataset of the wind energy produced in the past, we develop a neural prediction model of the wind energy for the next day, which is based on the ensemble of individual predictors. The ensemble form in prediction problems solution was proved to be very effective [17]. A few types of predictors will be involved in the ensemble: the multilayer perceptron (MLP) neural networks applying the sigmoidal activation function, the radial basis function (RBF) network, and the recurrent long short-term memory (LSTM) network [18,19,20,21]. Their predicted values will be integrated into a final forecast for the next day. Different forms of fusing these results will be investigated and compared.

This paper is organized as follows: Section 2 is devoted to the dataset characteristics. Section 3 briefly introduces three structures of the individual neural networks and the ensemble of such networks in regression mode, all applied in the prediction of short-term wind power generation of the country. The results of numerical experiments are presented and discussed in Section 4. The last section represents the conclusions of the study.

2. Dataset Characteristics

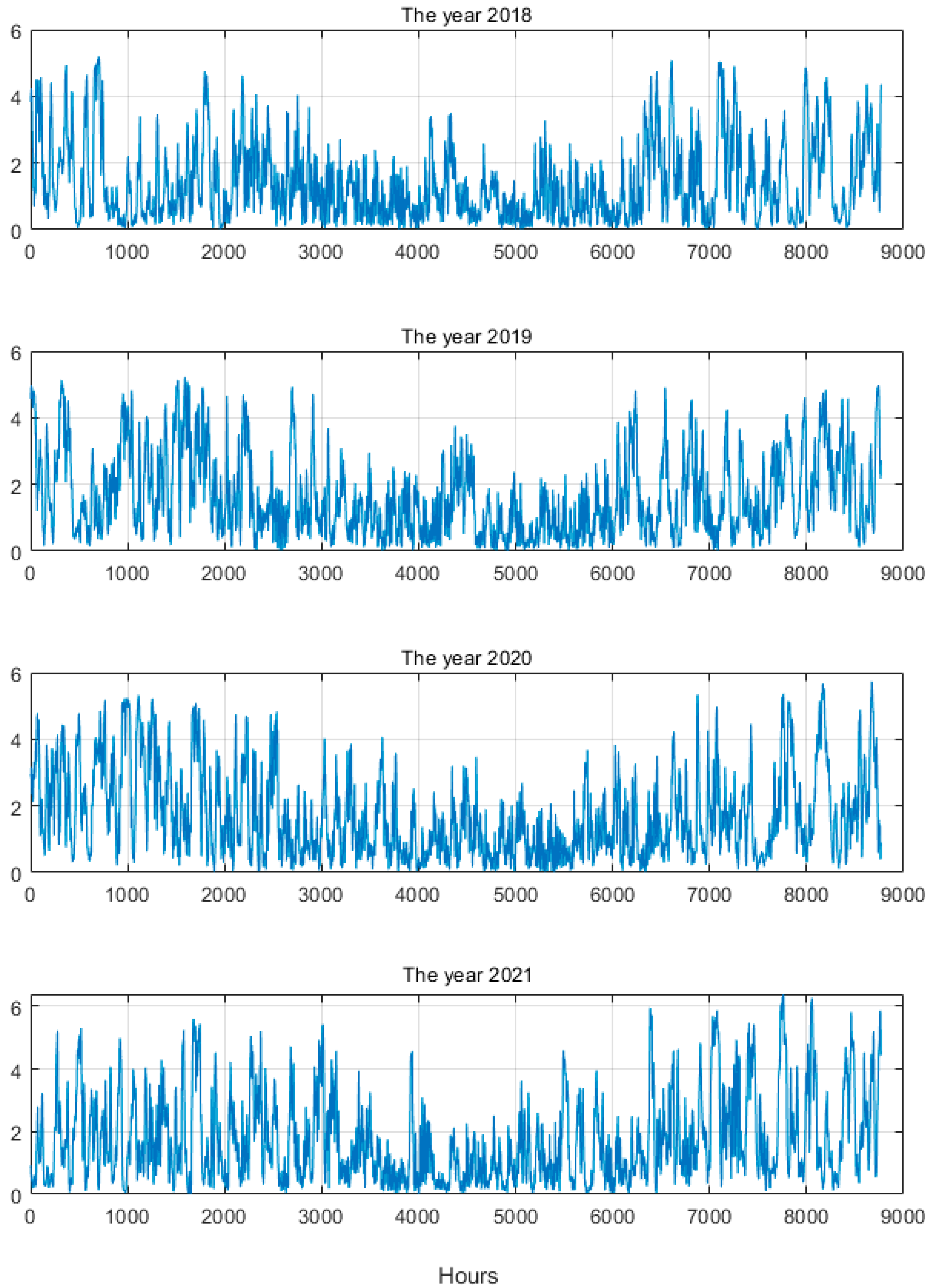
The dataset of wind-generated energy in Poland was collected within the years 2018–2021 [22]. The data records correspond to the total power generated by many farms and correspond to the succeeding hours of the day. The farms are distributed in the different regions of the country. Due to the large areas in which the farms are located, the wind conditions differ a lot. Therefore, the generated power has large variations at different hours of the day. Figure 1 presents the hourly values of the generated power in the succeeding years. Very large variations from hour to hour of the generated power are visible. Their changes are the results of changes in the wind.

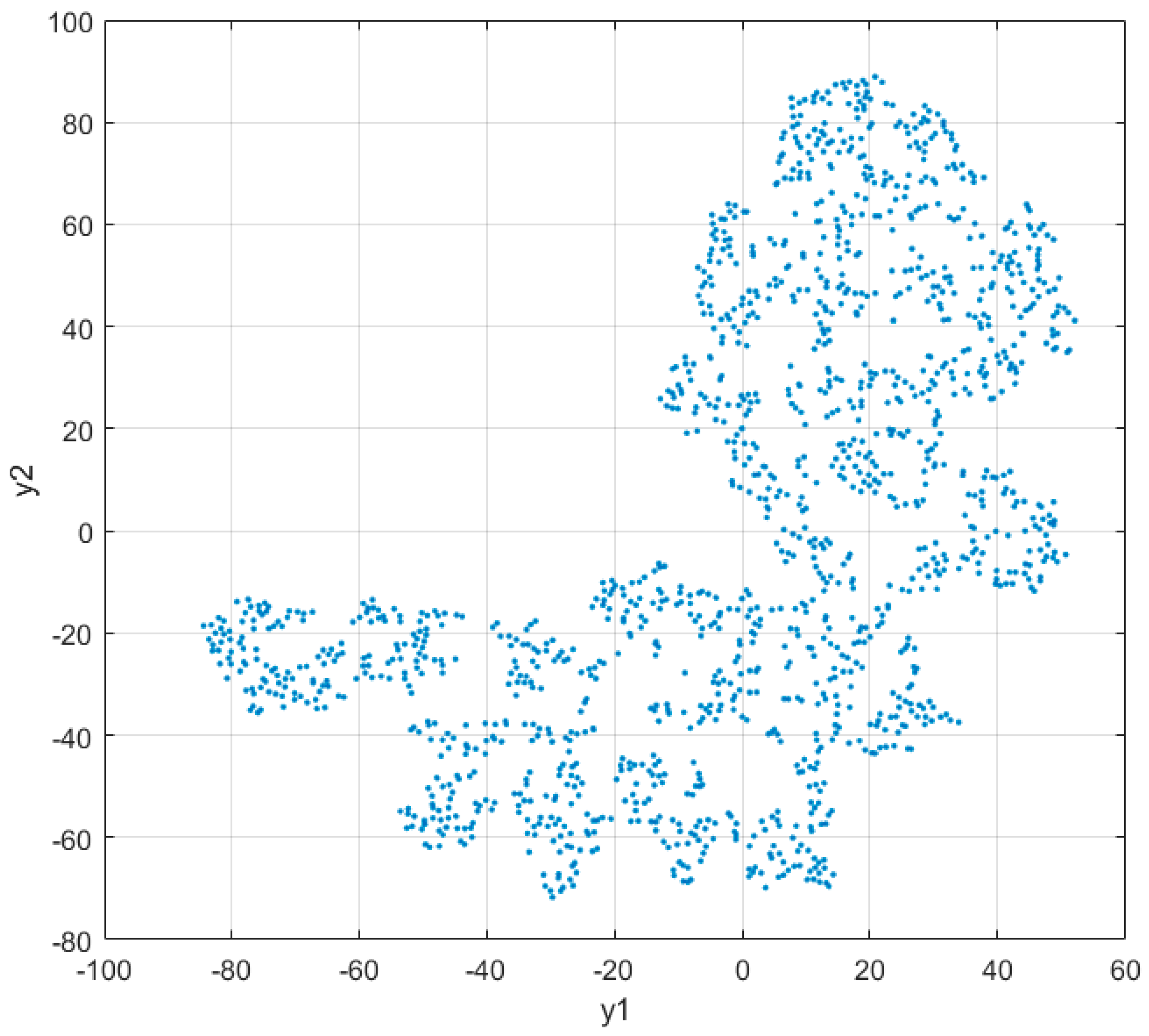
The large diversity of generated power is well seen in graphical form after mapping the 24-h data samples x into a two-dimensional system using t-distributed Stochastic Neighbor Embedding (tSNE) transformation, representing the nonlinear method y = f(x) = [y₁, y₂]^T of dimensionality reduction [23,24,25]. The method maps the high-dimensional data into a two- or three-dimensional space. Similar objects are modeled by neighboring points, and less similar objects are modeled by much distant points with high probability [25,26,27].

Van der Maaten and Hinton [25] explained the description of tSNE as follows: “The similarity of datapoint x_j to datapoint x_i is the conditional probability, p_j|i, that x_i would pick x_j as its neighbor if neighbors were picked in proportion to their probability density under a Gaussian centered at x_i (1)”.

$$p_{ij}=\frac{p_{j|i}+p_{i|j}}{2N}$$

(1)

The results of such mapping are presented in Figure 2. The samples of data are dispersed in large areas of space, proving the large variety of data patterns.

The farms’ capacity was increasing from year to year, leading to an increase in the total generated power value.

Table 1. The average power and its standard deviation generated in the considered four years.

Year	Average Power (MW)	The Standard Deviation of Power (MW)
2018	1408.7	1152.9
2019	1662.3	1226.2
2020	1731.7	1296.6
2021	1739.8	1393.2

shows the average power and its standard deviation generated during the four years under consideration.

The values of the average and standard deviation of generated power are very close to each other. This means a very high variation in the produced power in the succeeding hours. Even if the ratio std/mean is on the same level for the considered years, high difficulty in the prediction task is confirmed.

In our approach to forecasting, we will use the 24-h power vector of the previous day to predict its form for the next day. Therefore, it is interesting to show the correlation between these vectors for the neighboring days. Such relations are presented in Figure 3.

The correlation coefficients change a lot and have both positive and negative values. Their change is from −0.9798 to 0.9941 with a total mean of 0.1261. However, some repetitions of the patterns are observed in certain periods of the day. For example, within the periods of positive correlations, the mean is 0.5884, and within the negative values, the mean is 0.4116. The forecasting neural system considers these relations in predicting the next-day pattern of the generated power.

3. The Neural Prediction System

The next-day prediction system of the time series representing 24-h vectors of the wind-generated power is a challenging problem. To solve it, we will exploit the generalization ability of neural networks. Two types of networks will be applied: the classical feedforward neural networks of different activation functions and learning algorithms (MLP and RBF) [19] and the recurrent long short-term memory network (LSTM) [20,26]. They will be arranged in the form of an ensemble, which is responsible for the final forecast based on the predictions of the individual members.

3.1. Individual Neural Predictors Forming an Ensemble

Artificial neural networks, often called simulated neural networks of the classical type (so-called shallow architecture), represent the structure of one or sometimes two hidden layers and an output layer. The layers are composed of parallel artificial neurons. They are connected to other neurons in the next layer by the associated weights and using the activation function. In the case of feedforward structure, the flow of signals is from input to output without any feedback. The data are passed along to the next layer of the network up to the output. There are different types of feedforward structures, depending mainly on the activation function. The most typical is the multilayer perceptron (MLP) applying the sigmoidal (logistic) activation function f(u), where $f(u)=\frac{1}{1+\mathit{exp}(-u)}$ [18].

The output signal of the ith neuron depends on the actual excitation vector x and is defined by:

$$y_i(\mathbf{x})=f(u)=f\left(\sum _j{\mathbf{w}}_i^T\mathbf{x}\right)$$

(2)

where w_i is the weight vector of the ith neuron. The other type of activation used in radial basis function (RBF) networks is based on the Gaussian function:

$$y(\mathbf{x})=\mathit{exp}\left(-\frac{{‖\mathbf{x}-\mathbf{c}‖}^2}{{\sigma }^2}\right)$$

(3)

where c represents the center, and σ is the coefficient characterizing the width of the function. The networks applying such a form of activation also use different learning algorithms. In the case of a regression task, the output neurons of both (MLP and RBF) networks are usually linear [19].

The recurrent neural networks differ from feedforward by their feedback loops. The response of the neurons depends not only on the actual excitation x(t) but also on its previous state x(t − 1). The most efficient implementation of the recurrent neural network is now long short-term memory [22], which has a very good reputation in prediction tasks. Therefore, they are good candidates for time-series prediction of the future outcome.

LSTM contains only one hidden layer of mutual feedback between its neurons represented by the LSTM cells. The output layer is fed by the output signals from the hidden layer cells. The network contains many LSTM cells. The structure of the LSTM cell is presented in Figure 4 [19,20,28,29].

The cell is operating in two succeeding time points. The actual time point is marked as t, and the previous is t − 1. The cell takes three inputs and generates two outputs, which might be presented in the following form:

$$\left(h_t,c_t\right)=L\left(h_{t-1},c_{t-1},{\mathbf{x}}_t\right)$$

(4)

where x_t is a vector of input signals in the time points t, c_t−1 represents the memory signal (cell state) of the cell in the time point t − 1, and h_t−1 is the output signal of the cell in the preceding time point t − 1. The cell generates c_t and h_t of the memory cell and the output signal (at time point t). Both signals (c_t and h_t) leave the cell, and they are fed back to the cells in the hidden layer at a time t + 1.

The proposed three individual network structures, candidates for creating the ensemble in the forecasting problem, differ in many ways: type of activation functions (RBF and MLP), type of structures (recurrent in the case of LSTM and no feedback in MLP and RBF), and the significant differences in the way the signals in the neural cells within the networks are processed. Thanks to such factors, the probability of their independent performance is very high.

3.2. Ensemble of Predictors

It is well known that the results of individual predictors can be improved by proper fusing of their values in an ensemble [17,23]. Ensembles of predictors are now the most competitive form in time-series forecasting tasks. However, to obtain good performance from an ensemble, the independence of its members should be provided. Different ways to obtain maximum independence are applied. Such methods belong to the bagging technique with different random bootstrap samples applied in the training. They use different types and diversified parameters of the predicting units. Both approaches will be used in our system.

The other aspect that should be considered is providing efficient integration (fusion) of the results of its members. The typical approach is the simple or weighted averaging of the results generated by its members. The weighted averaging is usually implemented by applying the special weighted combiner of the individual results. The weights of the combiner are adapted using the learning data results. Only in the case of members of comparable prediction accuracy can good results be obtained by applying the ordinary mean of the individual results of the ensemble members.

An interesting approach to the integration of the ensemble is to apply principal component analysis (PCA). PCA is a dimensionality reduction method that is used to reduce the dimension of the datasets by transforming this set of variables into a smaller dimension that still contains most of the information in the large dimensionality set. Such a transformation reduces the complexity of the problem and in this way improves the generalization ability of the system.

The vectors predicted by all members of the ensemble are concatenated into one longer vector. This concatenated vector takes part in PCA decomposition [30,31] at the application of the limited number of principal components corresponding to the highest eigenvalues of the covariance matrix. The rejected components are associated with the noise contaminating the original time series. The principal components represent the input attributes to the MLP, responsible for the generation of the final forecast of the generated power.

4. Numerical Results of Experiments

The numerical experiments aim at the prediction of time series representing the total power generated by wind turbines in Poland [22]. The dataset presented in Section 2 was split into two parts. The records from the first three years were used in learning the neural networks, and the last (fourth) year is left only for testing. Ten percent of learning data was generated randomly and used only in the initial experiments to obtain the most efficient network structures (number of hidden neurons, type of activation, initial parameters of learning, etc.). Two tasks of prediction have been considered:

• Prediction of the 24-h power pattern generated by the wind for the next day (24 h ahead), based on the information from the previous day;
• Prediction of 1-h-ahead hourly power generation, assuming its knowledge from the previous hour.

Three types of neural networks are applied in the ensemble. The MLP architecture adjusted in the experiments was in the form: 24-n_h-24. In forecasting the 24-h vector of the next day’s power, we used the 24-h vector of power generated in the previous day and n_h hidden neurons of sigmoidal nonlinearity. The RBF network applying the Gaussian activation function has a similar architecture of n_h hidden neurons and can be presented as 24-n_h-24 (input formed by the elements of 24-h power pattern generated in the previous day, the output represents the corresponding vector for the day under prediction). In both cases, the value of n_h was adjusted in the initial stage of experiments, depending on the type of task.

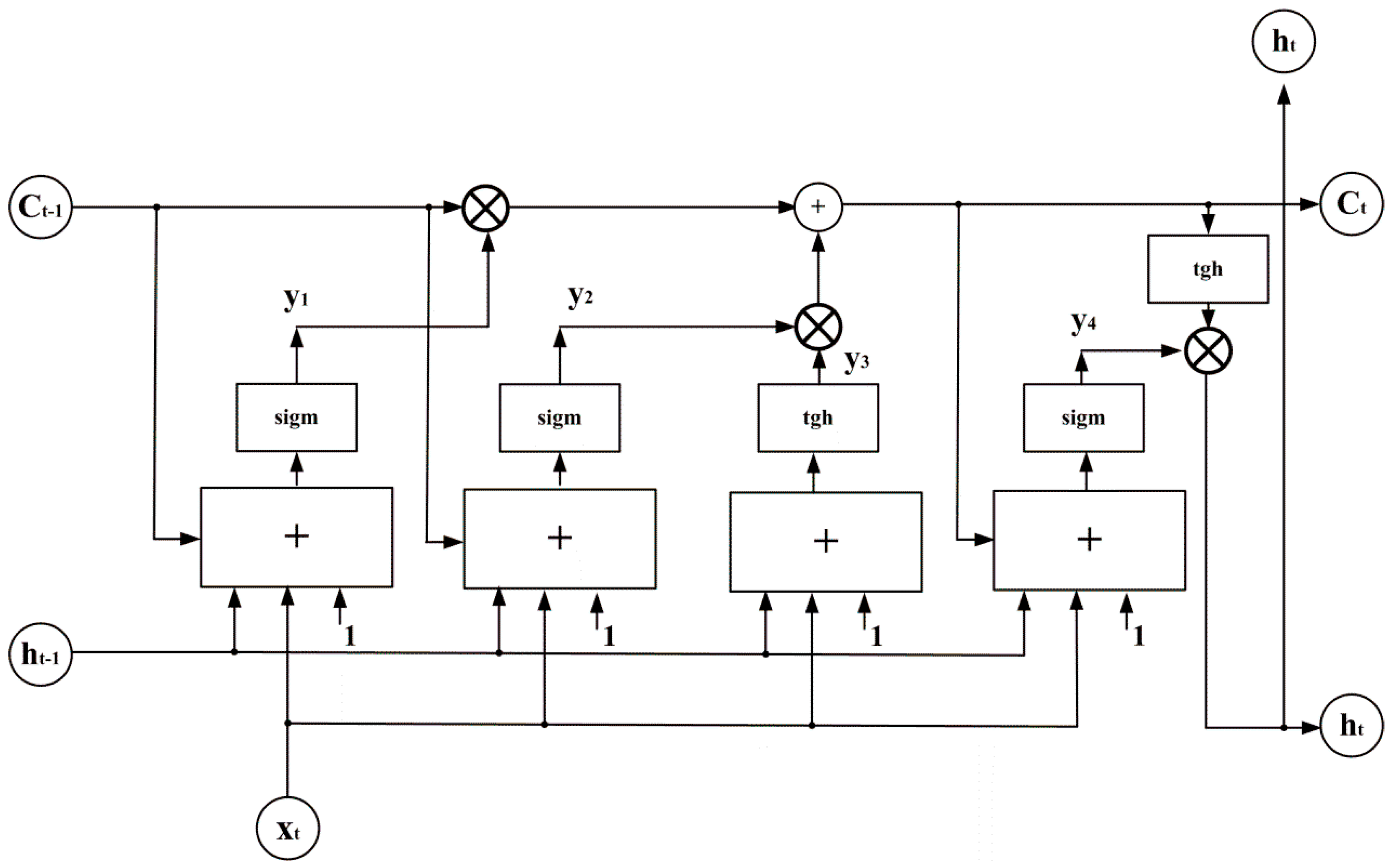
The LSTM network accepts the input data composed of 24-dimensional vectors x representing the 24-h patterns of the previous daily load. These samples are associated during the learning of the network with the target vector of the 24-h load pattern of the next day. The network is trained using the pairs of vectors: predicted input x(d) and known output x(d + 1). In the testing mode, the pattern of the 24-h vector for the next day is predicted by the learned network. It uses the supplied vector of the already-known pattern of the previous day. The structure of the LSTM network used in the experiments is 24-n_h-24, where n_h represents the number of LSTM cells. This number is also chosen in the introductory experiment phase. The results of individual units will be fused in an ensemble form using three approaches to their integration:

• Simple averaging of the results of individual units;
• Weighted averaging using the application of the MLP combiner;
• Application of PCA in the fusing phase.

The results of experiments will be presented for the individual units and, after their integration, the results of the ensemble. Different measures of quality are used. The typical is mean absolute error (MAE) defined as:

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n}\left(\sum _{h=1}^n\left|P\left(h\right)-\widehat{P}\left(h\right)\right|\right)$$

(5)

where P(h) represents the true value of the hth hour, $\widehat{P}\left(h\right)$ is the corresponding value predicted by the system, and n is the number of hours taking part in the testing stage. The other percentage quality measure used sometimes in the papers is the root-mean-square error (RMSE), defined as:

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{n}\sum _{h=1}^n{\left(P\left(h\right)-\widehat{P}\left(h\right)\right)}^2}\cdot 100\mathrm{\%}$$

(6)

The most demanding is the mean absolute percentage error (MAPE) defined by:

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=\frac{1}{n}\sum _{h=1}^n\frac{\left|P\left(h\right)-\widehat{P}\left(h\right)\right|}{P\left(h\right)}\cdot 100\mathrm{\%}$$

(7)

This measure is rarely used, because of the denominator P(h), which sometimes takes very small values (close to zero), especially in wind-generated power production.

To properly assess the results of prediction, we compared them with the so-called naïve approach, in which the true values of the last period are used as the forecast for the next period, without considering any special method of prediction. This measure can be performed for all three definitions of error. This form will be called the relative error. In this way, we can define three additional relative measures:

$$\mathrm{R}\mathrm{E}\mathrm{L}\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=\frac{\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}}{\mathrm{M}\mathrm{A}\mathrm{P}{\mathrm{E}}_{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$$

(8)

$$\mathrm{R}\mathrm{E}\mathrm{L}\mathrm{M}\mathrm{A}\mathrm{E}=\frac{\mathrm{M}\mathrm{A}\mathrm{E}}{\mathrm{M}\mathrm{A}{\mathrm{E}}_{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$$

(9)

$$\mathrm{R}\mathrm{E}\mathrm{L}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\frac{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}{\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{E}}_{\mathrm{n}\mathrm{a}\mathrm{i}\mathrm{v}\mathrm{e}}}$$

(10)

The smaller these values, the better the proposed solution concerning the naïve approach.

4.1. Prediction of the 24-h Power Pattern for the Next Day

The first considered task is the prediction of the 24-h vector of generated power for the day based on its pattern of the previous day (the 24-h-ahead forecasting). The learning task is adjusting the structure and parameter values of neural networks to create a model able to approximate learning data acceptably. The prediction philosophy of the neural network will apply its generalization ability to forecast the next day’s power pattern based on its previous day’s form. The introductory experiments were aimed at adjusting the proper number n_h of hidden neurons in the networks. The experiments have shown the best results for n_h = 12 in MLP, n_h = 16 in RBF, and n_h = 18 in LSTM networks.

These numbers have been used in further experiments. They have been repeated 10 times at different initial conditions and using randomly generated learning data (80% of the learning set). The prediction results of individual units in the form of mean value and standard deviation of MAE, RMSE, and MAPE for the testing data not taking part in the learning phase are shown in

Table 2. The MAE, RMSE, and MAPE of individual units in the prediction of the 24-h power pattern of the next day for testing data.

	MAE (Mean ± Std.) (MW)	RMSE (Mean ± Std.) (MW)	MAPE (Mean ± Std.) (%)
MLP	673.12 ± 9.90	932.43 ± 5.08	38.43 ± 0.12
RBF	681.47 ± 11.67	938.93 ± 8.83	38.82 ± 0.30
LSTM	708.55 ± 9.25	937.53 ± 5.24	38.00 ± 0.17

.

The relatively high value of MAPE can be observed in each forecasting method. On certain days, the generated power in some hours is very low, resulting in a high value of single errors taking part in the MAPE calculation. This kind of problem is not taking place for RMSE and MAE. Their definitions avoid the problem of temporary low values of generated power.

In the next step, the individual units are integrated into an ensemble. The integration of their results has been performed using the three methods mentioned above. The first was simple averaging. The second used the concatenated three 24-dimensional vectors (of dimension 72) generated by MLP, RBF, and LSTM as the input to the weighted MLP of form 72-16-24, responsible for the reconstruction of the predicted 24-h load pattern for the next day. Its general structure is presented in Figure 5.

The learning stage of the MLP combiner is organized on the learning dataset. The input is formed from the results predicted by three networks (MLP, RBF, and LSTM). The destination is the vector representing the true values. In the testing mode, the vectors predicted by MLP, RBF, and LSTM are the inputs for the trained combiner. Its output values form the forecasted 24-h power pattern.

The third integration system used principal component analysis. Three concatenated 24-dimensional vectors generated by the individual predictors are subjected to the PCA transformation. As a result, the N-dimensional input vector x (N = 72) is transformed into K-dimensional output vector z, defined as follows:

$$\mathbf{z}=\mathbf{W}\mathbf{x}$$

(11)

of K < N, where $\mathit{W}={\left[{\mathit{w}}_1,{\mathit{w}}_2,\dots ,{\mathit{w}}_K\right]}^T$ is the transformation matrix formed by K eigenvectors of the covariance matrix R_x associated with K largest eigenvalues. The vector z is composed of K principal components, starting from the most important z₁ and ending on the least important component z_K. The cut information can be associated with the noise of data. The vector z following from the PCA transformation is treated as the input to the MLP combiner of the structure like that presented in Figure 4. The introductory experiments have shown that the best results are obtained at the dimension of vector z equal to 35. The final forecasting for 24 h of the next day is performed by the MLP combiner of the structure 35-12-24 (35 elements following from PCA transformation, 12 hidden neurons, and 24 output signals representing the final forecast). PCA is explained well in [30,31]. The calculations were performed using a laptop with Windows 10 64-bit with the following parameters: Intel Core i7-6700HQ 2.60 GHz, RAM 16 GB, HDD 1 TB. All experiments were conducted using the MATLAB R2023a computation platform [24]. The detailed structures of these three members of the ensemble were adjusted using and accepting the introductory experiments, which provided the best results on the validation data (around 20% of the learning set).

Table 3. The MAE, RMSE, and MAPE of an ensemble in the prediction of the 24-h power pattern of the next day for testing data.

	MAE (Mean ± Std.) (MW)	RMSE (Mean ± Std.) (MW)	MAPE (Mean ± Std.) (%)
Simple averaging	665.68 ± 6.27	913.62 ± 4.59	37.60 ± 0.19
MLP combiner (nh = 16)	598.45 ± 4.87	835.08 ± 6.23	34.75 ± 0.27
PCA integration (K = 35)	611.38 ± 3.38	856.14 ± 6.17	35.60 ± 0.28

presents the average value of the MAE, RMSE, and MAPE of an ensemble after the application of these three methods of data fusion. They correspond to 10 repetitions of the experiments. The values of MAE and RMSE are expressed in MW, while MAPE is represented in percentages. The best results of an ensemble correspond to the application of weighted fusion organized in the form of MLP.

The best results were obtained for the ensemble applying the MLP combiner as the integration tool. They are better than the best individual units. For example, the best individual MAE corresponding to MLP (673.12 MW) has been reduced in an ensemble to 598.45 MW. Similar proportions of improvement have also been observed for other measures of quality (the best MAPE of individual units equal to 38% was reduced to 34.75%).

The comparison of the best-obtained results with those corresponding to the technique in which the true last period’s results are used as the prognosed period’s forecast (the naïve prediction) is interesting.

Table 4. The comparison of the proposed approach and the naïve methods of forecasting in terms of RELMAE, RELRMSE, and RELMAPE for 24-h-ahead forecasting.

Relative quality measures	RELMAE	RELRMSE	RELMAPE
	0.57	0.58	0.65

presents the values of the relative measures defined by RELMAE, RELRMSE, and RELMAPE.

In all cases, we observe the significant reduction in errors offered by our approach based on an ensemble concerning the naïve method. This result is useful for agents controlling and managing the production of electricity in the country. In planning the next day’s generation of power, they can substitute the naïve approach to forecasting with the proposed, more accurate method. Thanks to this, it is possible to save the natural materials (coal, oil, gas) used in conventional generating units.

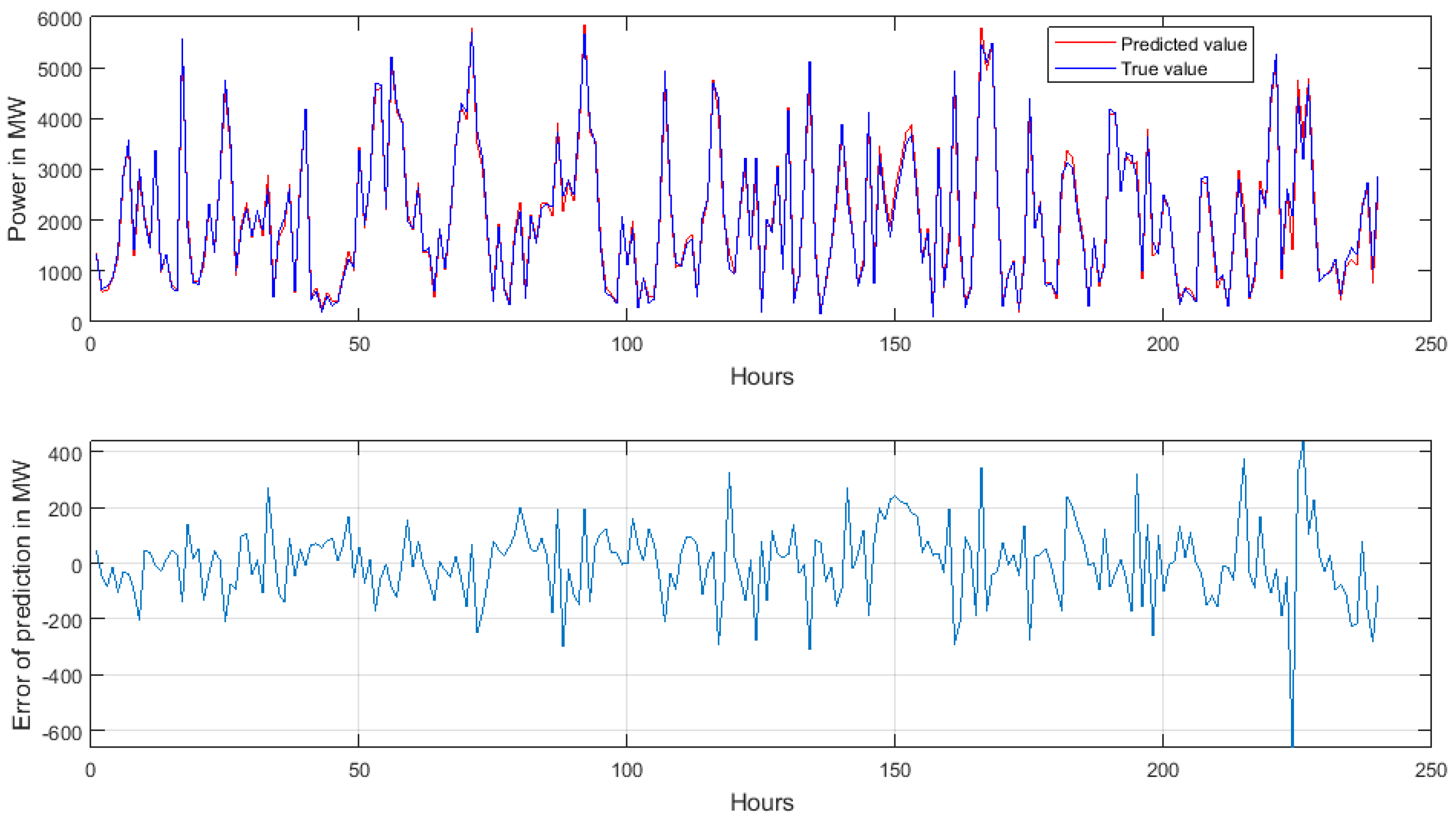
Figure 6 presents the true and predicted time series of the wind-generated power for 10 succeeding days in the country, chosen randomly from the records of the year not taking part in learning. The following values of errors have been estimated in this case: MAPE = 4.91%, RMSE = 136.15 MW, and MAE = 101.68 MW.

4.2. Prediction of 1-h-Ahead Hourly Power

The second task is the prediction of the 1-h-ahead wind-generated power, based on the knowledge of its previous hour’s result. The same three neural networks have been applied, however, to different numbers of hidden units. The input vector x used for prediction of the power value of the hth hour p(h) is also composed of 24 elements, representing powers corresponding to its past 24 h, x(h) = [p(h − 1) p(h − 2) … p(h − 24)]. Similar to the first task, the learning data were composed from the first three years, leaving the last (fourth) year only for testing.

The introductory experiments were performed once again to find the optimal number of hidden neurons in the networks. The best results of these experiments have shown n_h = 8 in MLP, n_h = 10 in RBF, and n_h = 30 in LSTM networks.

The experiments of learning and testing were repeated 10 times at various sets of hyperparameters. The individual neural networks were treated as the members of the ensemble, and their results were fused into one common forecasting output using the three integration methods mentioned above.

Table 5. The MAE, RMSE, and MAPE of the individual units and an ensemble in the prediction of the 1-h-ahead power value for testing data.

	MAE (Mean ± Std.) (MW)	RMSE (Mean ± Std.) (MW)	MAPE (Mean ± Std.) (%)
MLP	130.10 ± 0.97	182.67 ± 1.36	8.03 ± 0.06
RBF	130.79 ± 2.22	182.59 ± 1.29	8.02 ± 0.06
LSTM	114.49 ± 9.51	159.54 ± 12.74	6.90 ± 0.51
Simple averaging	119.78 ± 1.84	168.32 ± 2.96	7.39 ± 0.13
MLP combiner (nh = 2)	107.71 ± 5.57	152.42 ± 7.70	6.69 ± 0.33
PCA integration (K = 2)	107.70 ± 5.39	152.41 ± 7.61	6.69 ± 0.33

presents the mean and standard deviation values of MAE, RMSE, and MAPE obtained in these 10 repetitions of the experiments. They correspond to the testing data of the fourth year, not taking part in the learning procedure. All types of errors are now much smaller, since in forecasting the generated power in hth hour, we use its known information from the previous hour.

This time, the results of an ensemble approach are only slightly better than the best LSTM method. This is the expected result since LSTM is very effective if the time lag between two neighboring samples is very small (one hour in our case). Fusing its results with worse predictors (MLP and RBF) leads only to a small decrease in error. The best results correspond to the application of PCA combined with the MLP combiner in the role of integration.

Table 6. The comparison of the proposed approach and the naïve methods of forecasting in terms of RELMAE, RELRMSE, and RELMAPE for 1-h-ahead forecasting.

Relative quality measures	RELMAE	RELRMSE	RELMAPE
	0.83	0.84	0.84

presents the values of the relative measures defined by RELMAE, RELRMSE, and RELMAPE in 1-h-ahead forecasting.

Once again, we observe the reduction in errors offered by our approach concerning the naïve method.

5. Conclusions

This paper has presented a study concerning wind-generated power time-series prediction based on its historical values without knowledge of the wind parameters. The 24-h values of the power pattern considered in this paper represent the total power generated by the wind in the whole country. This is a significant difference from other forecasting methods presented in numerous papers, in which the wind parameters are the key factor in the forecasting method. Our method does not need information on wind parameters and can be applied to any region of the country if such information is not available. The methods based on wind information are not applicable in such cases. We are aware that including wind parameters will increase the accuracy of forecasting.

The proposed forecasting system is based on an ensemble composed of three different types of neural network: MLP, RBF, and LSTM. Thanks to the diversity of the member’s type, the high independence of units is obtained, which is very important from the ensemble performance point of view. Two types of forecasting tasks have been considered. The first is the prediction of the whole 24-h power-generated pattern for the next day in the 24-h-ahead mode. It is based on the hourly pattern of generated power corresponding to the previous day. The second task is the prediction of the 1-h-ahead power value. In both cases, a similar predictive system has been used, however, with different hyperparameters of the units.

The applied ensemble system has shown its superior performance concerning the individual units forming the ensemble and has allowed for a significant reduction in the values for all types of quality measures. The advantages of the proposed solution are very visible when we compare its results with those of naïve prediction. The prediction errors in the case of a 24-h-ahead forecast have been reduced almost twice. The proposed system might also find application for other types of production of renewable energy, for example photovoltaic.

Future studies will continue this direction of research concerning the prediction of wind power generation by expanding the number of members of the ensemble and the preparation method of the input attributes delivered to them. An interesting direction is to decompose the analyzed time series into simpler terms by applying wavelet transformation and arranging the ensemble composed of prediction units specializing in these terms. Future studies will also apply more advanced deep neural network models such as transformers or temporal convolutional neural networks [32,33].