Abstract
To develop reliable numerical models and better interpret monitoring campaigns experimental data of wind turbines, knowing the structure operation conditions, in particular the rotor angular velocity and blades’ pitch angle, is of paramount importance, but often not known due to confidentiality restrictions, or known with low time resolution (typically 10 min average values). In this work, it is shown analytically that blades accelerations measurements contain valuable information that allow for a better characterisation of the effective rotor shaft tilt and blades cone angle for different operating conditions. It is also shown that these measurements can be used to reconstruct the time history of the rotor angular velocity and blades’ pitch angle. After presented in an analytical framework, the methodology is validated with experimental data of two full scale wind turbines. The successful reconstruction of the rotor operating conditions shows that the method presented can be used to provide further insight into the dynamics of the structure that aids monitoring data analysis and provides an alternative method to monitor the SCADA systems themselves. The paper combines quite unique experimental data collected at two operating rotors with original data processing strategies that provide very valuable information to researchers and wind turbine operators.
1. Introduction
A proper knowledge of the rotor geometrical properties, namely the angle between the rotor rotation axis and the horizontal (tilt) and the blades’ angle with respect to a plane orthogonal to rotor rotation axis (cone angle), is important for many applications in wind turbine numerical modelling and structural health monitoring, as they impact the perceived loads in both the blades and the tower, but not always known with adequate uncertainty levels. In fact, recently proposed strain gauges calibration improved procedures try to explicitly include the impact on the rotor tilt and blade cone angles, as well as the blades pitch angle, in the internal forces originated at the tower basis, when a nacelle untwist event occurs [1]. More recently, a new method for computing the forces and bending moments on operating wind turbine blades using strain measurements at the blades’ root has also been presented [2]. In this case, the blades’ cone angle is neglected and the rotor tilt is assumed to be constant for any operating condition, which may not be realistic due to the tower deflection induced by the external applied loads. This will mimic an effective rotor tilt that may differ from its design value. Additionally, in the quest for increasingly more efficient wind turbines, recent studies have revealed that the rotor tilt angle has a non negligible effect not only in the internal loads experienced by both the blades and tower [3] but also in the aerodynamic performance [4,5] and even in the power production [6] of these structures. Finally, it should be noted that these angles are also of great importance to allow for the construction of reliable numerical models of wind turbines. In this case, not only their design value is relevant, but also, if truly digital twins are to be constructed, a methodology that can be used to compare it against experimental data is needed.
From a different perspective, condition and structural monitoring of wind turbines is essential to maximise the economic benefit of a given wind farm, as this information is used to optimise its behaviour as well as to predict necessary maintenance actions (see, for instance [7,8,9]). For these purposes, every installed and operating modern wind turbine is provided with its own Supervisory Control and Data Acquisition system, more commonly referred to as SCADA. This system registers key variables from both environmental (wind speed, turbulence intensity, wind direction, among others) and operational (rotor angular velocity, generator temperature, power production, blades’ pitch, among others) conditions that are not only a key feature for the operation strategies, as have also been used for the development of artificial intelligence and deep learning techniques for wind turbine condition monitoring (see, for instance, the work by Tautz-Weinert and Watson [10] concerning the mechanical and electrical parts of the rotor, Papatheou et al. [11] for identification of unhealthy wind turbines in a wind farm or refs. [12,13,14] as examples of non-intrusive methodologies that have also been developed over the years to identify different types of faults). Due to its importance, an independent methodology to estimate some of its variables is of significant importance. Furthermore, the SCADA available are often recorded with a low time resolution, typically 10 min, which is clearly insufficiency to fully characterise important transient events.
In this work, it is shown that the accelerations measurements obtained at the blades can be used for both purposes discussed above. Here, it should be noted that while the methodologies already mentioned use SCADA information or operation conditions parameters as inputs, in this work is proposed a new methodology to reconstruct the SCADA data itself. If traditional measurement systems are often associated with complex cable connections and significant dependence from an external power supply, making their application to wind turbines’ blades monitoring not feasible, recently available, microelectromechanical system (MEMS) based wireless nodes as the ones developed at the Faculty of Engineering of the University of Porto (FEUP) do not experience these limitations, making them highly suitable for this type of installations [15]. These sensors have already been applied successfully to monitor human-induced vibrations at a steel bridge [16], as well as to the continuous dynamic monitoring of Infante D. Henrique bridge, Portugal [17]. Here, it is proposed to extend the application of these sensors to bridge the gap between wind turbines’ numerical model and experimental data by using the blades’ accelerations time series to infer the rotor geometrical parameters and to study how they evolve with the operating conditions, as well as to reconstruct some key features of the SCADA systems, namely the rotor angular velocity and the blades pitch angle.
2. Analytical Considerations
2.1. Reference Frames and Rotation Matrix
The position of the sensors in the blades with respect to a fixed reference frame can be defined from 4 different angles:
- The inclination of the nacelle
- The angular position of the blade
- The precone angle
- The pitch plus structural twist over the blade axis
In the following calculations, the angles will be used in this order to transform vector quantities from one reference frame (RF) to another. The relevant reference frames, as represented in Figure 1, are a tower bounded RF (define by the unitary vectors ), a nacelle bounded RF (), a RF rotated over the rotor rotation axis by the azimuth angle of a reference blade (), a RF obtained by rotating the previously defined RF by the blade cone angle () and a blade-axis bounded RF that pitches with the blade ().
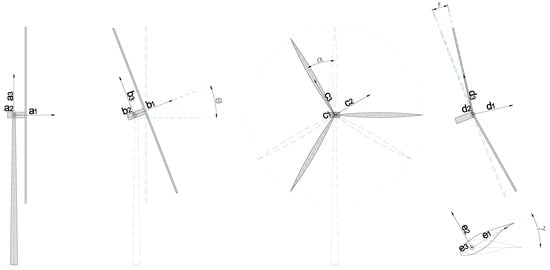
Figure 1.
Schematic representation of the angles used to define the position of a sensor. It should be noted that, as represented, . The sensor itself is assumed to oriented along the unitary vectors of the pitched reference frame, .
Since the accelerations and strain gauges should be expressed in the blades’ moving reference frame, in an approach similar to the one used by Tcherniak and Schwaab [18], the rotation matrices that relate a given reference frame to the next are needed, namely:
where the convention and have been introduced.
2.2. Accelerations Measurements
The gravitational force is more easily expressed in the reference frame such that, in the absence of any rotation, the measured acceleration of a given acceloremeter is simply:
where the index in the explicit vector representation has been included to clearly identify the reference frame and g is the gravitational acceleration. It is important to note that the accelerometer measurements (of sensors that are sensitive to gravity acceleration, as is being assumed to be the case) are recorded with respect to a free falling reference frame, such that a standing still accelerometer at the Earth’s surface pointing upwards will measure m/s, while a free falling one will register 0 m/s.
On the other hand, the centripetal and tangential accelerations due to the rotor rotation are more easily expressed in the reference frame that moves with the blade, :
where and R are the rotor angular velocity and the distance between the instrumented section and axis of rotation, respectively. The value measured by an accelerometer can then be obtained considering and transforming the different contributions as:
The sensitivity of these measurements to variations of the different parameters is represented in Figure 2, Figure 3 and Figure 4, where two out of the nacelle tilt, blade cone and blade pitch angles have been fixed and the remaining one varied within a certain range. It can be seen that the accelerations time series, when any combination of 2 channels is considered, describe an ellipsis that may be written, in its most general form, as:
where and are the centre point coordinates, is the rotation angle as measured from the positive x semi-axis and a and b are the ellipsis semi-axis associated to the axis obtained after the rotation by the angle . As will be seen, these parameters, that can be measured in the field, can be related with the rotor geometrical properties.
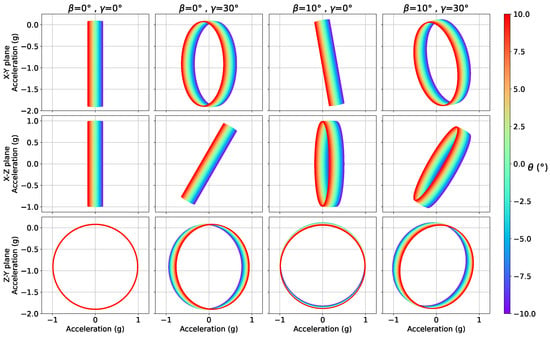
Figure 2.
Relation between different blades’ measurements over a full revolution as a function of the nacelle tilt (), considering different combinations of the blades’ pre-cone () and pitch () angles.
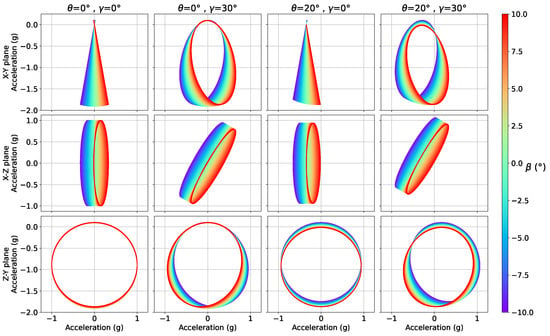
Figure 3.
Relation between different blades’ measurements over a full revolution as a function of the blade precone angle (), considering different combinations of the nacelle tilt () and blade pitch () angles.
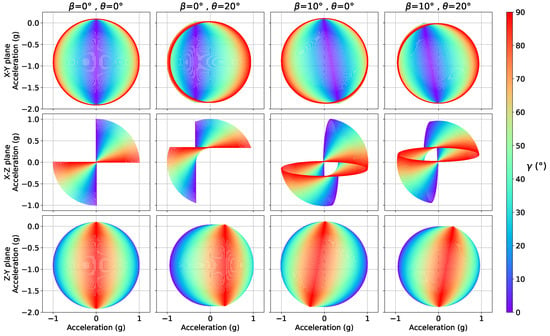
Figure 4.
Relation between different blades’ measurements over a full revolution as a function of the blade pitch angle, considering different combinations of the blades’ pre-cone () and nacelle tilt () angles.
3. Blades Measurements Relation with Operation and Structural Parameters
3.1. Model Calibration from Measurements
The first contribution based on the blades accelerations measurements that will be presented is the possibility of determining the rotor geometrical angles (nacelle tilt, blades precone and pitch) from experimental measurements alone. This is particular relevant for the development of numerical models of structures that are being instrumented when confidentiality issues limit the amount of data available. For this particular analysis, only setups with particular conditions (that may be identified from the measurements alone) will be used, a restriction that will then be relaxed.
By requiring the rotor to rotate with a constant angular velocity, a corresponding constant term is originated by the centripetal acceleration, given by:
where from now on the index in the vector explicit representation is omitted since it is implicitly assumed a representation in the local sensors reference frame. On the other hand, an additional constant term and a time varying component have their origin in the gravitational pull since:
Defining the constant terms, , as:
the ellipsis equation for the different directions measurements combinations can be derived. In what follows, this derivation will be detailed for the plane, while the equivalent expressions for the remaining planes will only be presented for completeness, without further derivations. For the plane, it may be written:
Matching the different terms with the ones in Equation (6), the different parameters can be constrained by requiring that the coefficients multiplying and must equal 1 independently and that the coefficients multiplying must vanish, leading to:
At this point a special remark should be made regarding the accelerometers uncertainties. The response of such an equipment can be parameterised as:
where S is the sensitivity and O the offset that map the real acceleration to the measured value . While it may be assumed that for well calibrated devices, it might not be that (as discussed by [19], it is common the existence of small variations of the sensor offset over time). From the equations above, it can be seen that the offset condition impacts the coordinates of the ellipsis centre, while the sensitivity impacts both the centre and the ellipsis parameters. Since only the errors on the sensitivity are being neglected, it can be seen that although the centre point coordinates could theoretically be used to estimate the needed parameters, these are not reliable, so only differential measurements should be used. Having set this clear, it can be noted that Equation (17) can readily be used to provide a direct estimate for since:
The pitch angle (plus the structural twist) is then simply the inclination of the ellipse when evaluated in the plane. Using this conclusion, Equations (15) and (16) above can be rewritten as:
that can be combined to yield another two direct estimates, this time for and :
The expressions above show that the precone angle can be obtained by the ratio between the major and minor axis of the plane ellipse, while the tilt can be computed from the ratio between one of the semi-axis and the gravitational acceleration.
As mentioned before, for completeness and without further derivation, the ellipsis parameters in the are related to the geometrical angles by:
while for plane it may be shown that:
respectively. As can be seen, both sets of equations are more cumbersome and do not provide as direct estimates as the ones in the plane. From this point on, only the latter will be used.
3.2. Operating Conditions Estimates
Once the geometrical angles are constrained (or known a priori), every time series may be used to recover the angular velocity and pitch angle. This information is once more hardly available (the more easily available SCADA data is limited to a time resolution of 10 min), but can be used to gain additional insight into the operation conditions of the wind turbine that can significantly enhance the interpretation of the monitoring data.
Firstly, let the data be cleaned such that only the component directly related to the rotor rotation is kept, which may be easily done by applying a calibrated low pass filter to the data. After this step, it can be noted that the following relations hold:
The difference between consecutive records measured at times and are given by:
where it has been used that and:
The expressions above can all be combined to give an estimate for the rotor angular velocity () and the blade’s pitch angle ():
Finally, it should be noted that Equation (38) can be used to identify constant RPM setups, or even parked rotor scenarios, even before fitting the value of any of the geometrical angles at play.
4. Results
4.1. Experimental Campaign Overview
The sensors used in this monitor campaign have been developed at FEUP and the description here presented mainly follows the extensive description provided in [17]. The data are saved locally in a microSD card. The files have a duration of 10 min each and are organised in a folder structure identified according to the date of the measurements.
The MEMS accelerometer is of digital type integrating a 20-bit ADC and includes internal antialiasing filters, programmable frequency rate and dynamic range. In this case, the frequency rate was fixed at 62.5 Hz, being the low-pass cut-off frequency set to 15.625 Hz (the sensor automatically sets the frequency of this filter to one-quarter of the sampling frequency to avoid aliasing errors). With this configuration, we ensure, with an adequate safety margin, an accurate characterisation of the signal frequency content between 0 Hz (DC) and 6 Hz.
This version of the wireless nodes is not equipped with any hardware for time synchronisation, each node containing a high-precision clock that works independently. In this solution, the autonomy is increased, the cost is reduced, and the flexibility of the system layout increased (no limitations on the sensors distance and no need to be installed in open sky, as it happens in systems synchronised by GPS).
The system is powered by nine batteries of 3400 mAh capacity each, enabling an autonomy of 6 months in continuous operation. The module contains an XBee radio transmission module, but in the present application, in order to extend the batteries’ life, the online data transmission is disabled. In order to optimise the size of sensor, the enclosure was customised, using for this purpose a 3D printer. One of the main advantages of this system is the possibility of developing monitoring solutions specially designed for a given experimental campaign.
The data that will be used in this work was obtained from the extensive monitoring campaign being conducted in the context of the WindFarmSHM project in a windfarm located in Tocha, Portugal. This windfarm included 5 VESTAS V100 wind turbines, labelled from WT1 to WT5, with a rated power of 1.8 MW. The experimental campaign, described in detail in [20] for which 10-min averaged SCADA data was also available, includes accelerometers and strain gauges installed in both the tower and the blades of WT1 and WT5 (WT1 with the 3 blades instrumented and WT5 with two blades instrumented), namely a set of fibre optic strain gauges at each blade’s root and the MEMS accelerometers described above placed at roughly 10m from the root, as represented in Figure 5. The methodology that will be presented in the following section will rely only on the latter.
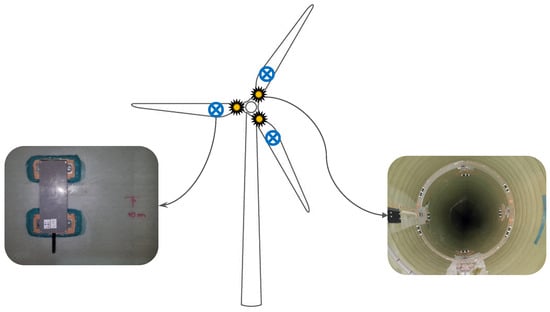
Figure 5.
Representation of the MEMS sensors (on the left) and the strain gauges (on the right) installed in wind turbine WT1 and WT5 of Tocha wind farm (adapted from Pacheco [21]).
4.2. Parameters Estimation
Firstly, time periods where the rotor was parked have been selected by identifying regions where the accelerations measurements were constant with a time length of at least 1 min. Additionally, it should be noted that, as long as the pitch angle is the same, all the selected time periods should be possible to fit within a single ellipse. The results are presented in Figure 6, while from the fitted parameters, the geometrical angles can be immediately estimated:
The pitch angle obtained above is not particularly relevant since it only represents the sensors particular position on the blade and should not be read as the SCADA equivalent pitch value.
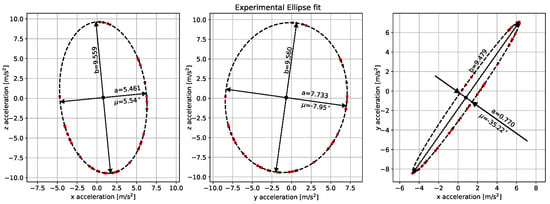
Figure 6.
Measured data (red points) and fitted ellipse (black dashed line) for parked time periods selected from WT5 Blade 2 data.
To study how these parameters evolve with the operating conditions, the parked rotor scenario has been dropped, while still demanding for constant angular velocities. The evolution of each angle with the rotor angular velocity are plotted in Figure 7, where have been included results for all the blades of both wind turbines and where have been plotted not the pitch angle value, but its variation, since the reference value has no particularly significant meaning as it is related to the sensors location on the blade. Although the expected pitch curve is successfully reproduced, the tilt and precone dependencies still need further explanations. In fact, it can be seen that for regions of constant pitch angle, the tilt increases with the rotor speed, and hence with the wind speed, while the precone decreases. Both these results are expected. However, some coupling between the pitch angle and both predictions can also be identified, in particular in the discontinuity between the estimations for very low wind speeds and operating conditions. This may be explained since the measurements are not being made on the blades centre, but on its surface. Nevertheless, the parameters needed for a numerical model can still be identified as the almost constant values obtained for parked conditions, since the wind induced behaviour should be properly reproduced when the structural response under different loading conditions is considered. Furthermore, small variations of about of the averaged pre-cone angle observed for different blades might be explained by the sensor installation (the sensor longitudinal axis might not be perfectly parallel with the blade longitudinal axis) and this will most certainly not have an important impact on the modelling results.
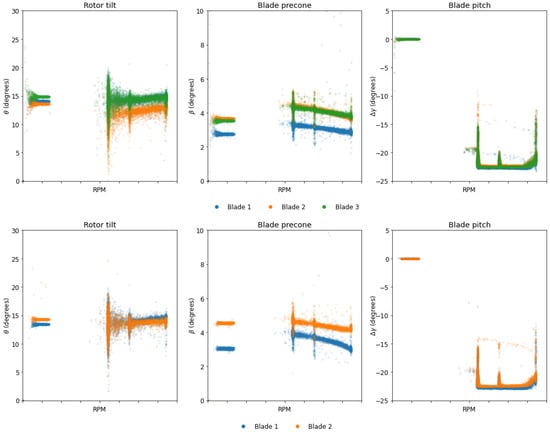
Figure 7.
Rotor tilt, blade precone and pitch angle for different values of the rotor angular velocity for WT1 (on top) and WT5 (on bottom). The rotor angular velocity values cannot be disclosed due to confidentiality constraints.
4.3. SCADA Data Reconstruction
Considering now a single setup where varying operating conditions could be easily identified. For this particular setup, the 10 min resolution SCADA data registered a rotor angular velocity between 2.3 and 10.1, with a mean value of 4.3 RPM, and a pitch angle between −3.6 and 20.1, with a mean value of 13.6. After applying Equations (38) and (39), the full pitch and rotor angular velocity time series have been reconstructed as represented in Figure 8, where it should be recalled that the absolute value of the pitch value is not significant, only its variation. The distinct operation conditions are easily identifiable in the accelerations time series, and are also present in the reconstructed SCADA time series. The maximum and minimum values of the RPM are validated, the total pitch variation is validated and the mean RPM value is also confirmed.
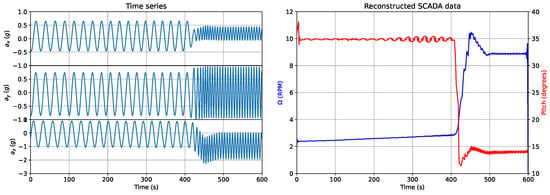
Figure 8.
Reconstructed SCADA data for a single setup.
Finally, a full month of data has been analysed and the estimates for the mean value of the rotor angular velocity and pitch value compared with the SCADA ones. The results are plotted in Figure 9. It should be noted that the purpose of the representation used in Figure 9 is not only to allow for a visual inspection of the results based on the typical pitch against angular velocity curves, as can be seen on the right panel, but also to highlight that the predictions and measured quantities are indeed in very good agreement for arbitrary conditions. For this purpose, the left panel exhibits the same pitch-rpm curves, but oriented in such a way that the main diagonal plots, the top left and bottom right corners, can be used to compared directly predicted and measured quantities of interest. In these plots, the curves plotted in black dashed line indicates a perfect fit, and, as can be seen, the predictions closely match the registered values in the SCADA system, implying that both the expressions and the methodology are validated.
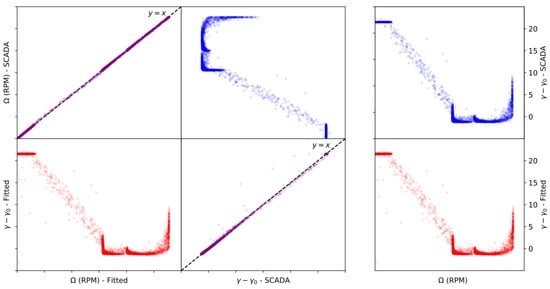
Figure 9.
Reconstructed SCADA full data. On the left, the comparison between estimated (red) and recorded (blue) values. On the right, the pitch curve reconstructed against the SCADA one. The rotor angular velocity values cannot be disclosed due to confidentiality constraints.
5. Conclusions
In this work it was shown that the blades accelerations measurements contain relevant information regarding both structural and operational conditions of the rotor. In particular, it was shown that differential measurements between consecutive time instants can be used to reproduce the SCADA system information, but with a much higher time resolution. With this, it may be possible to either eliminate the need for high resolution information on pitch angle and angular velocity or use it to monitor the SCADA system behaviour itself. Although the full reconstruction of these conditions is only possible if the geometrical angles of the rotor are known, it was also shown that, by carefully selecting setups with constant angular velocities, these can also be constrained by the accelerations measurements alone. In this case, it was shown that when any two orthogonal accelerations directions are considered, their values trace an ellipsis over time whose parameters are directly related to the geometrical characteristics of the rotor.
As a final note, it should be mentioned that the presented analyses can only be accomplished if the monitor layout includes accelerations measurements in the blades. This was only possible due to usage of the FEUP developed wireless nodes, that were once more shown to be a valid solution for the monitoring of this type of structures.
Author Contributions
Conceptualization, F.P. and F.M.; Methodology, F.P.; Validation, F.P. and F.M.; Formal analysis, F.P.; Investigation, F.M. and C.M.; Resources, F.M. and C.M.; Writing—Original draft, F.P.; Writing—Review & Editing, F.P., F.M. and C.M.; Supervision, F.M.; Project administration, F.M.; Funding acquisition, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by Foundation for Science and Technology (Fundação para a Ciência e Tecnologia, FCT) through the scholarship SFRH/BD/138980/2018, Base Funding IDB/04708/2020 of CONSTRUCT—Instituto de I&D em Estruturas e Construções and the project 2022.08120.PTDC (M4WIND), funded by national funds through the FCT/MCTES (PIDDAC).
Data Availability Statement
The authors do not have permission to share data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FEUP | Faculty of Engineering of the University of Porto |
| MEMS | Micro-electromechanical systems |
| SCADA | Supervisory control and data acquisition |
References
- Bezziccheri, M.; Castellini, P.; Evangelisti, P.; Santolini, C.; Paone, N. Measurement of mechanical loads in large wind turbines: Problems on calibration of strain gage bridges and analysis of uncertainty. Wind Energy 2017, 20, 1997–2010. [Google Scholar] [CrossRef]
- Moynihan, B.; Moaveni, B.; Liberatore, S.; Hines, E. Estimation of blade forces in wind turbines using blade root strain measurements with OpenFAST verification. Renew. Energy 2022, 184, 662–676. [Google Scholar] [CrossRef]
- Sheng, C.; Afjeh, A.; Li, X.; Zhao, Q.; Yousuf, Y. Comparative study of yaw and nacelle tilt control strategies for a two-bladed downwind wind turbine. Fluid Mech. Res. Int. J. 2018, 2, 85–97. [Google Scholar] [CrossRef][Green Version]
- Wang, Q.; Liao, K.; Ma, Q. The Influence of Tilt Angle on the Aerodynamic Performance of a Wind Turbine. Appl. Sci. 2020, 10, 5380. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S.; Lee, S. Influence of blade-tower interaction in upwind-type horizontal axis wind turbines on aerodynamics. J. Mech. Sci. Technol. 2011, 25, 1351. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zhang, J. Effects of Wind Rotor Tilt Angle on Aerodynamic Power of Wind Turbine under Typical Periodic Disturbances. In Proceedings of the Advances in Mechanism and Machine Science, Krakow, Poland, 15–18 July 2019; Uhl, T., Ed.; Springer: Cham, Switzerland, 2019; pp. 3459–3468. [Google Scholar]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595. [Google Scholar] [CrossRef]
- Straub, D.; Chatzi, E.; Bismut, E.; Courage, W.M.G.; Döhler, M.; Faber, M.H.; Köhler, J.; Lombaert, G.; Omenzetter, P.; Pozzi, M.; et al. Value of information: A roadmap to quantifying the benefit of structural health monitoring. In Proceedings of the 12th International Conference on Structural Safety and Reliability, Vienna, Austria, 6–10 August 2017. [Google Scholar]
- Kamariotis, A.; Chatzi, E.; Straub, D. Value of information from vibration-based structural health monitoring extracted via Bayesian model updating. Mech. Syst. Signal Process. 2022, 166, 108465. [Google Scholar] [CrossRef]
- Tautz-Weinert, J.; Watson, S.J. Using SCADA data for wind turbine condition monitoring—A review. IET Renew. Power Gener. 2017, 11, 382–394. [Google Scholar] [CrossRef]
- Papatheou, E.; Dervilis, N.; Maguire, E.; Worden, K. Wind turbine structural health monitoring: A short investigation based on SCADA data. In Proceedings of the EWSHM-7th European Workshop on Structural Health Monitoring, Nantes, France, 8–11 July 2014. [Google Scholar]
- Gong, X.; Qiao, W. Current-based eccentricity detection for direct-drive wind turbines via synchronous sampling. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 2972–2976. [Google Scholar] [CrossRef]
- Nath, S.; Wu, J.; Zhao, Y.; Qiao, W. Low Latency Bearing Fault Detection of Direct-Drive Wind Turbines Using Stator Current. IEEE Access 2020, 8, 44163–44174. [Google Scholar] [CrossRef]
- He, L.; Hao, L.; Qiao, W. Remote Monitoring and Diagnostics of Pitch-Bearing Defects in an MW-Scale Wind Turbine Using Pitch Symmetrical-Component Analysis. IEEE Trans. Ind. Appl. 2021, 57, 3252–3261. [Google Scholar] [CrossRef]
- Moutinho, C.; Cunha, A. New solutions of sensors and instrumentation for dynamic monitoring of Civil structures: ViBest/FEUP experience. In Proceedings of the 14th International Workshop on Advanced Smart Materials and Smart Structures Technology (ANCRiSST 2019), Rome, Italy, 18–21 July 2019. [Google Scholar]
- Moutinho, C.; Pereira, S.; Cunha, A. Continuous dynamic monitoring of human-induced vibrations at the Luiz I Bridge. J. Bridge Eng. 2020, 25, 5020006. [Google Scholar] [CrossRef]
- Zhang, G.; Moutinho, C.; Magalhães, F. Continuous dynamic monitoring of a large-span arch bridge with wireless nodes based on MEMS accelerometers. Struct. Control. Health Monit. 2022, 29, e2963. [Google Scholar] [CrossRef]
- Tcherniak, D.; Schwaab, M. On a method for finding position and orientation of accelerometers from their signals. Mech. Syst. Signal Process. 2020, 140, 106662. [Google Scholar] [CrossRef]
- Hoffmann, K. An introduction to stress analysis and transducer design using strain gauges. In Test and Measurement; HBM: Darmstadt, Germany, 2012; pp. 67–68. [Google Scholar]
- Pacheco, J.; Guimarães, S.; Moutinho, C.; Marques, M.; Matos, J.C.; Magalhães, F. New strategies for optimized structural monitoring of wind farms: Experimental campaign. Wind Energy Sci. 2020, 5, 983–996. [Google Scholar] [CrossRef]
- Pacheco, J. Development of New Methodologies for Structural Monitoring of Wind Farms. Ph.D. Thesis, Faculty of Engineering of University of Porto (FEUP), Porto, Portugal, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).