Abstract
The integration of renewable rnergy sources (RESs) into the power grid involves operational challenges due to the inherent RES energy-production variability. Imbalances between actual power generation and scheduled production can lead to grid instability and revenue loss for RES operators and aggregators. To address this risk, in this paper, we introduce a mutually beneficial bilateral trading scheme between a RES and a DR aggregator to internally offset real-time energy imbalances before resorting to the flexibility market. We consider that the DR aggregator manages the energy demand of users, characterized by uncertainty in their participation in DR events and thus the actual provision of flexibility, subject to their offered monetary incentives. Given that the RES aggregator faces penalties according to dual pricing for positive or negative imbalances, we develop an optimization framework to achieve the required flexibility while addressing the trade-off between maximizing the profit of the RES and DR aggregators and appropriately incentivizing the users. By using appropriate parameterization of the solution, the achievable revenue for the imbalance offsetting can be shared between the RES and the DR aggregators while keeping users satisfied. Our analysis highlights the interdependencies of the demand–production energy imbalance on user characteristics and the RES and DR aggregator profits. Based on our results, we show that a win–win outcome (for the RES and DR aggregators and the users) is possible for a wide range of cases, and we provide guidelines so that such bilateral agreements between RES and DR aggregators could emerge in practical settings.
Keywords:
balance responsible parties (BRPs); renewable energy sources (RESs); power grid; variability; operational challenges; demand response (DR); RES aggregators; DR aggregators; bilateral trading scheme; dual pricing mechanism; imbalances; flexibility; probabilistic incentives model; optimization framework; deviation offsetting 1. Introduction
The integration of renewable energy sources (RESs) into the existing power grid has gained significant traction. Renewable generation, such as solar and wind, provides a cleaner and more environmentally friendly alternative to conventional fossil fuel-based electricity production. However, the inherent intermittency and variability of these sources pose significant challenges to grid operators in maintaining a stable and reliable energy system. One of the key obstacles faced by RES aggregators is the management of imbalances caused by fluctuations in renewable energy generation. In order to address this issue and reduce revenue loss, a promising solution lies in the synergy between RES aggregators and demand response (DR) aggregators to offset any fluctuations in real-time generation by employing end-user demand-side flexibility (DSF) resources within the current structure of electricity markets.
Participation of DR aggregators in electricity markets has gained significant attention as a means to address imbalances that occurred from RES production and optimize their integration into the grid. In [1], the significance of the DR aggregators’ participation in electricity markets, as well as the importance of engaging end-users in DR implementation, are highlighted. Involving end-users manages intermittent RES energy production and alleviates load-supply balance. The involvement of end-users in DR events has already been discussed in [2], where price-based demand response motivates consumers to adjust their energy consumption based on market prices or tariffs (active participation in the electricity market).
The authors in [3] presented a novel approach for a market participant to handle its own production imbalances. Specifically, a wind producer is allowed to achieve energy balance by creating multiple DR agreements with DR aggregators as a joint asset in two stages: day-ahead market (DAM) clearing and regulated (balancing) market. In the first stage, the wind power producer submits its offers to the DAM, considering the volume of fixed DR contracts that have been negotiated with the DR aggregator. The second stage encompasses finding the final DR schedules and balancing settlements through an iterative profit-seeking approach until all periods of the day are cleared.
Apart from the imbalances in energy generation, there is also a field of interest regarding uncertainty in DR participation. Part of the available literature, e.g., [4], proposes a dynamic reallocation of the consumption schedule where uncertainties in real-time production are resolved via continuous refreshing of the load schedules in an environment of high PV penetration and load variability. Another proposed approach on the subject is the quantification of the possible variation in consumption, e.g., [5]. In [5], a framework is suggested for energy management that includes a DR aggregator coordinating the energy demand of end-users. The uncertainty in terms of forecasting error in RES production is approximated by constructing a data-driven risk-adjusted uncertainty set. Other methods prefer the adoption of robust optimization algorithms to account for this phenomenon. An optimization scheme with robustness capabilities is introduced in [6] to create a schedule for devices operated manually to minimize the effect of the uncertainty of DR approval by the user.
A robust method is presented in [7] for organizing the timing of smart appliances and electrical energy storage in households, with the goal of simultaneously decreasing electricity expenses and CO2 emissions. The suggested robust framework incorporates the uncertainty of user behavior, ensuring that the optimal schedule for appliances is less affected by unforeseen shifts in user preferences. Finally, in [8], a hybrid stochastic–robust optimization approach is proposed to account for the uncertainties of wholesale market prices and the participation rate of consumers.
In this paper, we investigate bilateral cooperation between RES and DR aggregators for mitigating imbalances in energy generation within an augmented common portfolio of RES units and end-user DSF resources so that both of them achieve higher profits in relation to their direct and independent participation in the balancing market. We consider DSF uncertainty by appropriately adapting the user model of [9], which includes the probability of user participation according to the provided incentives, a user selection process that considers their positive attitude towards the provision of flexibility, and a healthy incentivization policy promoting fair remuneration for their services, under a suitable optimization framework combining those features. We also consider dual-tariff penalties for positive or negative imbalances and develop an optimization framework to achieve the required flexibility to offset imbalances while addressing the trade-off between maximizing the profit of RES and DR aggregators and appropriately incentivizing the users. We numerically analyze our optimization framework and investigate the interdependencies of the demand–production energy imbalance with the user characteristics and the RES and DR aggregator profits. Our results indicate that mutually beneficial outcomes for the RES and DR aggregators and the users may emerge in a wide range of cases. Finally, we provide specific guidelines so that such bilateral agreements between RES and DR aggregators could emerge in real market settings.
The remainder of this paper is as follows: In Section 2, the bilateral trading scheme is explained in detail, including the dual pricing scheme that provides fertile ground for this proposal. In Section 3, the model for providing incentives is then described both for the users—consumption side—and the revenue from the market—generation side. Afterward, in Section 4, the optimization framework that realizes profit maximization for the stakeholders is exposed. In Section 5, a thorough analysis of the optimization results for a range of all the variables and parameters of the problem is conducted to investigate the dependencies among the three stakeholders. In Section 6, practical guidelines are provided to facilitate the efficient realization of such bilateral trading schemes that depend on user-side DR resources. Finally, in Section 7, we conclude our work.
2. Bilateral Trading Scheme
2.1. Cooperation of DR and RES Aggregators in Electricity Markets
Short-term electricity markets comprise a day-ahead market (DAM) and a balancing market (BM). A day-ahead market is a financial market where market participants (e.g., producers and retailers) sell and purchase electricity volumes at financially binding clearing prices (DAM clearing prices) for 24 h of the following day. On the contrary, the main purpose of the BM is the allocation of reserve capacity and the activation of upward/downward balancing energy in real-time (in the framework of the Real-Time Balancing Energy Market—RTBEM) provided by Balancing Service Providers (BSPs), such as thermal and hydro generating units, energy storage entities, etc., to fully address the positive/negative system imbalance (i.e., aggregate individual imbalances of energy producing and consuming stakeholders in the DAM) that may arise in real-time in order to maintain power system balance and ensure grid stability. Note that RTBEM emerges only in cases of system imbalance.
Non-dispatchable renewable energy sources (RESs) units (e.g., PV plants), due to their intermittent and stochastic nature, are one of the major sources of energy imbalances, which, in turn, require the provision of flexibility services from other eligible resources in real time. In this context, end-user demand-side flexibility (DSF) resources, which are typically represented by a demand response (DR) aggregator, can address and mitigate RES imbalances before the RES aggregator (i.e., the market entity that represents, in general, small-scale RES units in the wholesale electricity market) seeks to perform balancing in the relevant RTBEM. In practical terms, if the RES portfolio generates in real-time more than its declared DAM schedule, mainly due to inherent forecasting errors, then in the RTBEM, the end-user DSF resources will be asked to increase their consumption accordingly in order to collectively mitigate RES generation imbalances. Likewise, in cases of less generation than the DAM schedule, DSF will be asked to decrease their consumption [10].
2.2. Dual Pricing Scheme
In principle, RES and DR aggregators are considered to participate in a centralized wholesale electricity market where the “dual-pricing” scheme is adopted as regards the imbalance pricing, which is common in the European electricity markets [11]. Figure 1 illustrates the main characteristics of the “dual-pricing” scheme as regards the imbalanced pricing of market participants.
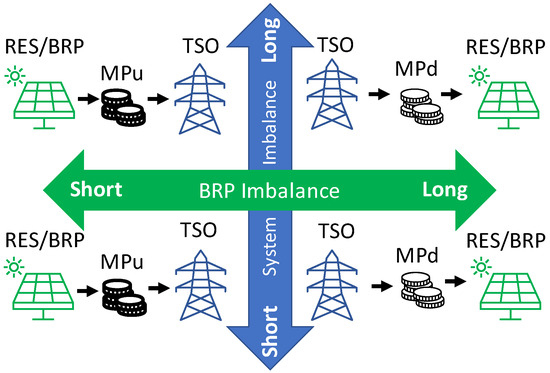
Figure 1.
Dual pricing scheme.
From a system point of view, the system imbalance shown in Figure 1 represents the algebraic sum of all balance responsible parties (BRPs) individual imbalances. A balance-responsible party, or BRP for short, is a company that can and may handle the balance between the energy quantity that the BRP has actually generated or consumed in real-time and the energy quantity that the BRP has contracted to generate or consume, respectively, in financial markets that take place prior to the actual delivery of electricity (e.g., in forward markets and/or day-ahead markets). In this framework, the system is considered “short” when the overall system imbalance is negative and, therefore, more energy needs to be produced (and/or less energy needs to be consumed) by the eligible BSPs with respect to their contracted market schedule (e.g., cleared DAM position) in order to restore the power system balance in real-time. On the contrary, the system is considered “long” when the overall system imbalance is positive and, therefore, less energy needs to be produced (and/or more energy needs to be consumed) by the eligible BSPs with respect to their contracted market schedule (e.g., cleared DAM position), in order to restore the power system balance in real-time. In this context, an individual BRP is considered “short” (resp. “long”), i.e., it has a negative (resp. positive) BRP imbalance when it produces less (or consumes more) (resp. produces more or consumes less) in real-time than its previously contracted market schedule (e.g., DAM schedule).
In principle, the imbalance of a single BRP (e.g., RES producer or DR aggregator) is mainly caused by its inherent forecasting errors and is independent of the sign of the overall system imbalance (positive/negative) since the latter is formulated by the collective individual imbalances of all BRPs and, therefore, cannot be correlated with the imbalance of a single BRP (e.g., RES Aggregator).
According to the dual-pricing pricing scheme, the remuneration/charge of a balance responsible party (BRP) is independent of the direction of the system imbalance and only depends on its own imbalance direction. Specifically, in case a BRP (e.g., RES aggregator) is short (i.e., it produces in real-time less than its DAM schedule), it is charged for its production deficit by the transmission system operator (TSO) at the marginal price of all accepted upward balancing offers () that have been provided by the BSPs in the balancing market, which is normally higher than the respective DAM clearing price (). On the contrary, in cases where a BRP is long (i.e., it produces in real-time more than its DAM schedule), for the excess generation, it is remunerated by the TSO at the marginal price of all accepted downward offers () that have been provided by the BSPs in the balancing market, which is normally lower than the respective DAM clearing price (). In this way, the BRP has no incentive to over-declare or under-declare its forecasted generation in the DAM. This, in turn, mitigates the possibility that gaming behaviors appear in the day-ahead and balancing market by all participants (BSPs and BRPs) [11].
2.3. Bilateral Agreement Scheme
In the above context, it is considered that RES and DR aggregators operate collectively under a common augmented portfolio of RES units and end-user DSF resources; moreover, DSF resources represented by a DR aggregator can be regularly called to bilaterally counterbalance the respective RES generation imbalances. For the financial clearing of the bilateral mitigation of the aforementioned RES generation imbalances, it is considered that a bilateral contract is concluded between the RES and DR aggregators. The detailed terms of this bilateral contract can be decided mutually by the involved parties (DR and RES aggregators) based on the following:
Let us assume that the bilateral contract price between RES and DR aggregators is equal to (in €/MWh), whereas is defined as the settlement price between the DR aggregator and the end-users. can be either lower or higher than , depending on the case (RES short or long, respectively; see explanation below). is added to ensure that the end-user will benefit from its contribution either in case of RES short or long imbalances (see Figure 2). Two distinct cases are identified, depending on the direction of RES imbalances (short or long), mathematically expressed as follows:
where is a common parameter for both market cases, and is a parameter that can be set arbitrarily and expresses the maximum DR aggregator desired net profit (e.g., α = 10%). In case the RES aggregator is short, the DR aggregator is remunerated by the RES aggregator at price . According to (1), is lower than , thus, the RES aggregator is charged less for its generation deficit than it would be charged if it participated independently in the RTBEM. On the other hand, DR aggregator remunerates its customers for their decreased load at , where is negative and, therefore, DR aggregator remunerates the end-user at a price lower than , thus retaining a profit equal to Premium for itself.
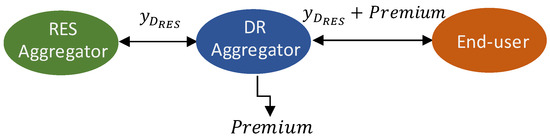
Figure 2.
DR and RES aggregators bilateral agreement scheme.
On the contrary, in cases where the RES aggregator is long, the RES aggregator is remunerated by the DR aggregator at , which is higher than , based on (2). , with now being positive, is the discounted price that is charged by the DR aggregator to the end-user for its increased consumption (i.e., end-user increases its consumption to counterbalance RES increased generation in real-time) and, therefore, the DR aggregator retains again a profit equal to for itself. However, the total price of that is charged to the end-user should be lower than the PDAM price (as enforced by the right part of (2)) in order to properly incentivize them for their engagement [10]. Note that the DR aggregator has notified in advance its end-users (with DSF resources) for potential periods of discounts in the electricity pricing and for potential periods where electricity-consumption curtailment is asked to them and they are offered appropriate incentives in return. The end-users, anticipating the above, are assumed to always increase their electricity consumption when they are offered a discounted electricity price, either storing electric energy for future use in their DSF resources (e.g., battery), or serving previously accumulated electricity consumption needs.
If, for the sake of comparison, we consider that no bilateral coordination scheme between RES and DR aggregators was applied, then the RES aggregator would have to go to the real-time balancing market (RTBEM) for the settlement of its inherent energy imbalances under the dual-pricing scheme, as is the current situation in the electricity market. In that case, the total net revenue of the RES aggregator would be calculated as the sum of the revenue obtained in the DAM plus the additional debit/credit for the settlement of its energy imbalance in the RTBEM, as expressed by
where is the declared production in DAM and is the DAM clearing price represents the energy imbalance of the RES aggregator, or, in other words, the deviation between its real-time production minus its DAM schedule. refers to the associated imbalance prices, which, for the purposes of this analysis, are considered to spread evenly (±20% hedge) around , i.e., and .
In case the RES aggregator is short (i.e.,), the RES aggregator is charged for its generation deficit at (which is normally higher than ). On the contrary, in cases where the RES aggregator is long (i.e.,), RES aggregator is remunerated for its generation surplus at (which is normally lower than ). Therefore, bilateral trading is obviously beneficial for the RES aggregator.
Also, consider that the DR aggregator may participate in RTBEM and benefit from offering flexibility services only when there is a system imbalance, which is, in general, independent from an individual energy imbalance that may arise for one RES aggregator. Moreover, the price per unit of energy flexibility provided in RTBEM would depend on the total energy flexibility demand and provision in this market. Therefore, it can be concluded that bilateral trading would represent an economically attractive opportunity for the DR aggregator to make instant and non-negligible profits, as opposed to expected and unknown ones.
Based on the aforementioned analysis, it can be concluded that all involved parties (i.e., RES aggregator, DR aggregator, and end-users) have a strong motivation to be engaged in such a bilateral agreement scheme for the mitigation of RES generation imbalances. (Recall that end users receive rewards for providing energy flexibility that renders their net benefit positive.) On the one hand, the RES aggregator is able to improve its financial position since it obtains more favorable prices for its imbalance settlement, irrespective of the direction of its own energy imbalances (negative/positive). On the other hand, the DR aggregator can take advantage of this coordinated operation and obtain some premium by engaging end-users to participate in DR programs to increase/decrease their load consumption. Finally, the application of the proposed framework will enable end-users to actively participate in such a DR scheme and reap significant monetary benefits. The optimization framework to estimate the trade-off between maximizing the profits of either the RES aggregator, the DR aggregator, or the users (while providing them with the appropriate incentives) lies among the main contributions of this work and is further analyzed in the following sections.
3. DR Incentives Modelling
The provision of incentives in this work is carried out according to the model proposed in [9] (with certain adaptations dictated by the dual pricing scheme) and more thoroughly explained in [12]. Our focus is on a provider/aggregator that aims to engage users in demand response (DR) and provides them with incentives. We employ a model that addresses the uncertainty regarding whether each targeted user will be able to achieve the desired flexibility. This model specifically relates to the selection of DR incentives to encourage users to abstain from using specific electrical devices. Participation in the DR event is realized by accepting the offered incentives and granting the provider control over the corresponding loads.
We make the assumption that a subset of users, denoted by indices 1 to , shall be aimed for DR, and a binary variable is employed to account for this targeting, either being equal to 1 if user is selected or 0 otherwise. When user is indeed selected for a particular DR event at a specific time slot, he is presented with incentives denoted as . These aim to achieve demand flexibility, which refers to the reduction in consumption within a specific time zone. The amount of demand flexibility is symbolized as , differs for each customer and relies on their individual load consumption profile.
The user here is presented with two options: either accepting the provided incentives and actively contributing to the desired demand flexibility, , or rejecting the incentives and maintaining their regular consumption schedule. If the DR incentives adequately compensate for the user’s discomfort [13], which arises from refraining from using specific loads, taking into account the potential savings in the energy bill, then participation in the DR event becomes the optimal decision for the user. In other words, if (representing the loss of net benefit due to DR), the user should participate. Consequently, we can define the minimum acceptable incentives for user as and assume that the probability of user participating in the DR event is a step function, increasing from 0 to 1 at .
To introduce uncertainty into our analysis and create a more comprehensive model, we consider the outcome of demand response (DR) as a Bernoulli trial, where success is determined by a probability function , which is affected by economic incentives. If the trial results in failure and the user does not participate in DR, he consequently misses out on any flexibility gains and does not receive the initially offered incentives . The opposite holds true in the case of success. The participation probability function should possess the following characteristics: (1) it is an increasing, continuous, and differentiable function of incentives , (2) in case of no incentives, the probability is equal to zero, and in case of infinite incentives, it is equal to 1, and (3) it rises sharply from low to high values around the minimum acceptable value. In other words, it should be a smooth approximation of the aforementioned step function. By employing such a function instead of a unit-step function, we can account for situations where users may accept (or reject) slightly lower (or higher) incentives than due to variations in their discomfort when not using the electrical device during the specific time slot. The sigmoid function satisfies all of the aforementioned properties. For a user with a minimum acceptable incentive level of , we can assume the following relationship:
This is a slightly adjusted form of the sigmoid function, where equals regardless of the value of , which determines the steepness of the function. A larger value of results in a steeper rise of the function. Figure 3 provides a visual representation of the function’s shape for different values of and .
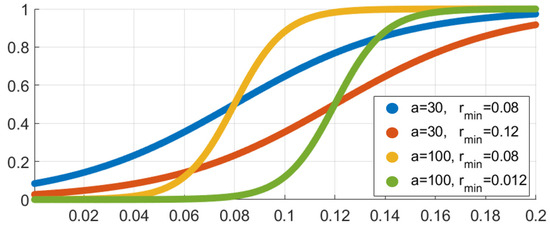
Figure 3.
Probability function for different values of and rmin.
In our case, end-user DSF resources are employed to mitigate RES imbalances before the RES aggregator seeks to perform balancing in the relevant markets. The end-user resources are represented by a DR aggregator who is responsible for informing the consumers about the upcoming DR event and the relevant adjustments they should perform on the flexible loads in their households. Following this strategy, the RES aggregator achieves a reduction in the penalty caused by its imbalance, the end-user receives monetary rewards for helping the system balance by activating or deactivating loads, and the DR aggregator receives a profit for his bilateral role.
4. Optimization Framework
The optimization problem of the DR aggregator is specified in this section. While similar to the approach presented in the third investigation of Section IV of [9], one of the main differences here is that the available budget for the DR aggregator is now based on the RES aggregator’s energy deviation . The impact of on the model’s results needs to be considered, and for this reason, in our optimization algorithm, a range of values shall be examined. The worse the prediction of the RES aggregator in the DAM, the more space it provides to the DR aggregator to fix the imbalance. Hence, more budget is available. From the perspective of the DR aggregator, the optimization target would be to maximize his profit by using the available budget. If we assume that our case is based on the system short—RES short scenario, the optimization expression under the bilateral trading scheme would be as follows:
where is the monetary compensation offered to the DR aggregator from the RES aggregator, and in this framework, its value ranges from . The requested flexibility is denoted as and is a binary variable that concerns targeting; it is equal to 1 if user is selected or 0 if user is not selected. Through the offered compensation value of the RES aggregator is able to decrease its revenue loss, which is caused by its deviation. The constraints ensure that the RES and DR profits are always positive. However, while the DR profit is clean, the RES profit corresponds to the decrease in its revenue loss. The constraint has been employed to achieve more robust targeting even though users might accept somewhat smaller incentives than [9]. Additionally, from another point of view, a fair optimization framework would dictate that targeted users are offered higher incentives than the minimum acceptable ones so that all three types of stakeholders are engaged in a win–win situation. Finally, the restriction about the total flexibility harnessing aims to achieve the collection of DR resources enough to fully offset the deviation.
5. Analysis
In this section, the optimization framework is investigated with regard to the incentives model to discover in practice what the correlation is between the DR budget that is created due to RES imbalances and the DR efficiency according to user characteristics. The optimization framework has been developed in MATLAB R2016a. The optimization will be executed for a range of values of the problem variables and user parameters (Table 1). The values and value ranges of the parameters have been chosen according to the following considerations: and can be regarded as indicative values of a real-life centralized wholesale electricity market. If their difference is small, the room for bilateral trading is also small, and vice versa. In any case, their exact values do not affect the essence of the results or the respective guidelines. The value range aims to consider all the different shapes that the probability function may take, from smooth to steep (see also Figure 3). The value range was reasonably selected to effectively illustrate the three stakeholders’ interdependencies: it spans from low values that lead to an inexpensive user incentivization cost to high values that cause a costly user incentivization expenditure. As far as the flexibility request is considered, its value does not influence the preceding analysis, and a simple value was chosen for easy readability. The results shall shed light on how the DR and RES aggregators and end-user profits are affected by the examined variables of and .

Table 1.
Problem, market, and user variables and parameters.
In the investigations that were conducted, we assumed that the users are symmetric, i.e., = , = , = , which implies . Assuming that the users are symmetric is by no means a limitation of the proposed optimization framework. In fact, a similar mathematical formulation for user targeting for energy flexibility provision has been considered in [9] with asymmetric users, which shows that the problem is mathematically tractable. The main objective of the assumption in the current paper regarding symmetric users was to numerically investigate how different user characteristics and different demand–production energy imbalances affect the RES and DR aggregator profits. In this case, the maximization problem becomes:
At the optimal point, due to symmetry, all targeted users will be offered the same and will be asked to provide the same. A range of deviation values is considered to investigate the relation between RES profit and deviation, and RES profit expresses the decrease in RES revenue loss. Deviation becomes negative when real-time production is less than the one declared on the DAM. The DR profit that can be seen in the following figures corresponds to the premium variable, as this is described in Section 2.
Figure 4a,b depicts the relationship of RES and DR aggregator profits with the deviation for different values of . It can be seen that the price for the offsetting of every kWh ( directly affects the aggregator profits. The higher the lower the RES profit and the higher the DR profit. For greater deviation values, the RES aggregator cannot sell the energy at a small price, and this gets more intense near the limit because the cost of user incentivization increases non-linearly. Near the limit, most or all of the users must be persuaded to participate, and this corresponds to high incentives per user in order to make their probability of participating high. The RES profit is analogous to the reduction of and for most of the index space, but this is not the case for the DR aggregator. His profit drops long before reaching the maximum deviation that he can support, and at the extreme values of , it gets near zero. This drop is dictated by the non-linear increase in the cost of incentivization when almost all users are required to participate. In any case, the profits of both aggregators always depend heavily on their deal, which is nicely illustrated in Figure 4c: according to the value the profit changes hands. However, it is also visible that the DR profit gets easily saturated for small values. Figure 4d highlights the fact that both aggregators have more room for benefit as the deviation increases. The previous statement considers it a fact that the deviation has occurred due to false predictions. The RES aggregator would rather have zero deviation.
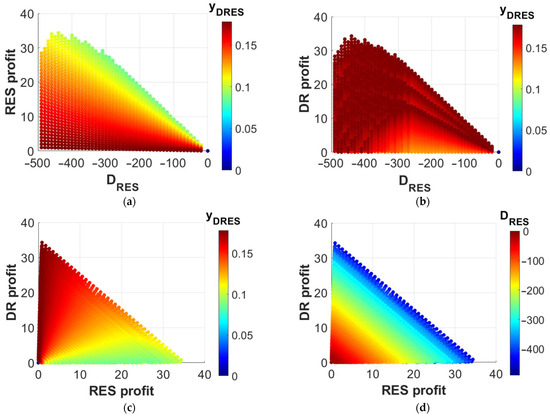
Figure 4.
(a) RES and (b) DR aggregator profit plotted against real-time deviation for various values of . RES and DR profits plotted against each other with respect to (c) , and (d) .
Figure 5 depicts the relationship between Total User Profit (TUP) and the aggregator profits for different values of and . TUP is calculated by the following equation:
and expresses the total rewards that are received by the end users who shall participate in the DR event. It can be seen that as the deviation increases, there is more room for profit for both the aggregators and the users (Figure 5a,c). An interesting result lies in Figure 5b, where the RES profit rises exponentially after a certain threshold, particularly in the lower values. The explanation lies in the fact that when the deviation is quite high, the RES aggregator has limited capability to decrease revenue loss. Hence, consumers will benefit from increased profits to the detriment of the RES profit. Moreover, the maximum TUP is reduced as becomes smaller. In Figure 5d, it is shown that the DR profit and the TUP go hand in hand in a win–win manner until a threshold is reached where the DR profit drops for a further increase in the TUP.
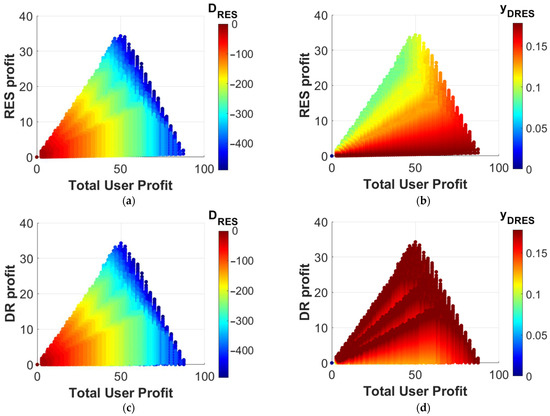
Figure 5.
Relationship of RES profit and DR profit with Total User Profit for various values of (a) real-time deviation and (b) bilateral trading agreed value . Again, DR profit plotted against (c) and (d) .
Figure 6a illustrates the analogy between the DR aggregator profit and the respective revenue. The DR aggregator profit saturates when all users have been selected and it may even decline in the presence of ample DR revenue. Figure 6b shows that unwilling users affect the profit of the DR aggregator negatively and begin to drastically affect his profit when all of them must be engaged. Figure 6c,d both include a y-axis dedicated to the RES aggregator loss, which corresponds to the loss of revenue when compared to the ideal case of zero deviation. It can be seen in Figure 6c that through bilateral trading, this loss can become smaller, and this capability gradually deteriorates as the deviation becomes greater. The loss is directly related to the selling price . Reduction of the RES loss includes an increase in the DR profit and the total profit of the users (Figure 6d), which illustrates the mutual profit of this scheme for all stakeholders.
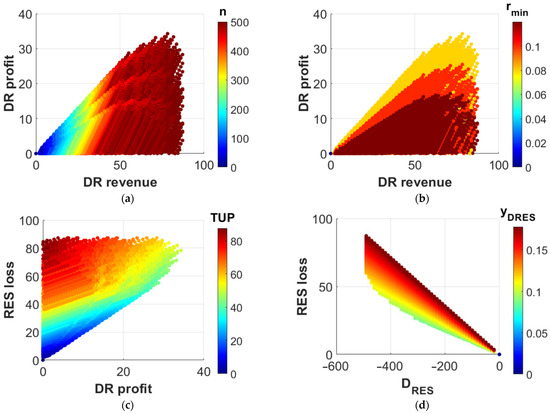
Figure 6.
Relationship of DR profit to DR revenue with regards to (a) the number of selected users and (b) the minimum acceptable incentives of the users . RES loss plotted against (c) DR Profit and Total User Profit and (d) and .
6. Guidelines
According to the preceding analysis, the proposed scheme of bilateral trading using DR resources has proven to be beneficial for all three types of stakeholders involved. However, dividing profits among the three stakeholders can be a complex exercise. Everyone will want to maximize their profit; if this is not conducted carefully, taking into consideration the proper incentivization of the other two entities, the program’s effectiveness might be jeopardized. For example, if the RES aggregator does not transfer enough resources to the DR aggregator, it might not be beneficial for him to engage at all. If the DR aggregator wishes to maximize his profit, the risk of not obtaining the required DR quantity can be greater. To enable the smooth and beneficial cooperation of the three stakeholders, useful guidelines are provided in this section regarding individual profit maximization and mutually beneficial sharing of profit.
The magnitude of the RES deviation that can be offset in the energy market is closely dependent on the user base size and parameters. If the available users are few or unresponsive to incentives, neutralizing a large deviation might be very costly or onerous. On the other hand, a high deviation can be easily taken care of if there are many users willing to contribute. As a result, the RES aggregator can follow a “riskier” policy in the DAM if he is aware that the DR resources are ample and vice versa. It is a strategic advantage for the RES to be able to identify this point in advance and act accordingly in the DAM.
Similarly for the DR aggregator: He should consider the availability of users because his profit might drop in the event that many users are needed, especially when they are unresponsive. When there is a high deviation and the user base is not large or adequately responsive, it is critical for the DR aggregator to negotiate high prices in order to realize the DR program and ensure its profit. Low prices for bilateral trading are often risky and not for the benefit of the DR aggregator. However, even if hefty values of DR revenue are available, this is not necessarily beneficial for the DR aggregator for the same reason.
Prudent definition of is an important part of the bilateral trading process. Very low values do not provide any profit for DR, and a fair starting point would be any value that is close to the DAM price. It should also be mentioned that both aggregators and users have more room for profit in the case of a large deviation.
There is a region in the problem where all three stakeholders achieve significant profits at the same time, as nicely shown in Figure 7. As a result, with proper coordination, all three stakeholders can benefit from a deviation. In the absence of coordination, any one of the three players can benefit disproportionally, thus drastically deteriorating the profits of one of the others or both of them. In other words, coordination is not only about the two aggregators but involves the users as well. Users who are not positively spaced towards this scheme and want to absorb as much profit as possible essentially ruin this opportunity.
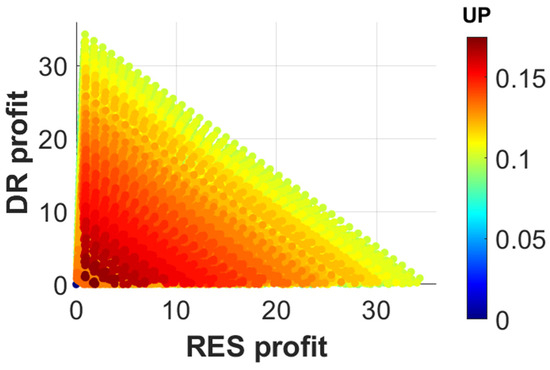
Figure 7.
Relationship of the profits of the three stakeholders: RES and DR aggregators and users.
7. Conclusions
In this work, a bilateral trading scheme between RES and DR aggregators was investigated under a dual-tariff penalty scheme for RES energy imbalances between real-time production and the day-ahead market declaration. Under a bilateral agreement between RES and DR aggregators, the DR aggregator internalizes the RES imbalance in its profit maximization strategy and, depending on the real-time scenario, aggregates the required flexibility by appropriately incentivizing its end-users. We considered uncertainty in the end-user participation in DR events subject to their offered rewards. We defined an optimization framework to analyze the trade-off between maximizing the profit of RES and DR aggregators and appropriately incentivizing the users. Depending on the size and sign of the RES energy imbalance, different profit sharing among RES/DR aggregators and different distributions of user rewards emerge. Through extensive numerical analysis, we found that the studied bilateral scheme can be mutually profitable for all stakeholders involved. Insights are also provided on the dependence of the trading strategies of RES and DR aggregators on user-base flexibility characteristics. Finally, guidelines have been proposed so that such bilateral agreements between RES and DR aggregators can be considered in everyday grid operations.
Author Contributions
Conceptualization, C.T.K., T.G.P., G.D.S., M.D.P., C.K.S. and A.P.; Methodology, C.T.K., T.G.P., G.D.S., M.D.P., C.K.S. and A.P.; Software, C.T.K.; Validation, C.T.K.; Formal analysis, C.T.K., T.G.P. and G.D.S.; Investigation, C.T.K., G.D.S. and N.N.; Writing—original draft, C.T.K., N.N., T.G.P., M.D.P., C.K.S. and A.P.; Writing—review & editing, T.G.P., C.T.K. and G.D.S.; Visualization, C.T.K. and N.N.; Supervision, T.G.P. and G.D.S.; Project administration, G.D.S.; Funding acquisition, G.D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been funded by the iFLEX project, which has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 957670.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to Dimitrios Chatzigiannis, Marion Paraschi, and Costas Baslis from Heron Energy S.A. for their valuable contribution to structuring the scheme of bilateral trading introduced in this paper.
Conflicts of Interest
Authors Malamatenia D. Patouni and Athanasios Papakonstantinou were employed by the company Heron Energy SA, Christos K. Simoglou was employed by the company Optimus Energy SA. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Carreiro, A.M.; Jorge, H.M.; Antunes, C.H. Energy management systems aggregators: A literature survey. Renew. Sustain. Energy Rev. 2017, 73, 1160–1172. [Google Scholar] [CrossRef]
- Algarvio, H.; Lopes, F. Bilateral Contracting and Price-Based Demand Response in Multi-Agent Electricity Markets: A Study on Time-of-Use Tariffs. Energies 2023, 16, 645. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Saha, T.K.; Eghbal, M. Wind Power Offering Strategy in Day-Ahead Markets: Employing Demand Response in a Two-Stage Plan. IEEE Trans. Power Syst. 2015, 30, 1888–1896. [Google Scholar] [CrossRef]
- Sharma, S.; Verma, A.; Panigrahi, B.K. Robustly Coordinated Distributed Voltage Control through Residential Demand Response Under Multiple Uncertainties. IEEE Trans. Ind. Appl. 2021, 57, 4042–4058. [Google Scholar] [CrossRef]
- Yuan, Z.-P.; Li, P.; Li, Z.-L.; Xia, J. Data-Driven Risk-Adjusted Robust Energy Management for Microgrids Integrating Demand Response Aggregator and Renewable Energies. IEEE Trans. Smart Grids 2023, 14, 365–377. [Google Scholar] [CrossRef]
- Du, Y.F.; Jiang, L.; Li, Y.; Wu, Q. A Robust Optimization Approach for Demand Side Scheduling Considering Uncertainty of Manually Operated Appliances. IEEE Trans. Smart Grids 2018, 9, 743–755. [Google Scholar] [CrossRef]
- Paridari, K.; Parisio, A.; Sandberg, H.; Robust, K.H.J. Scheduling of Smart Appliances in Active Apartments with User Behavior Uncertainty. IEEE Trans. Autom. Sci. Eng. 2016, 13, 247–259. [Google Scholar] [CrossRef]
- Vahid-Ghavidel, M.; Javadi, M.S.; Santos, S.F.; Gough, M.; Mohammadi-Ivatloo, B.; Shafie-Khah, M.; Catalao, J.P.S. Novel Hybrid Stochastic-Robust Optimal Trading Strategy for a Demand Response Aggregator in the Wholesale Electricity Market. IEEE Trans. Ind. Appl. 2021, 57, 5488–5498. [Google Scholar] [CrossRef]
- Krasopoulos, C.T.; Papaioannou, T.G.; Stamoulis, G.D. Flexibility Management for Residential Users Under Participation Uncertainty. In Proceedings of the 2022 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Singapore, 25–28 October 2022; pp. 405–411. [Google Scholar] [CrossRef]
- HORIZON 2020 iFLEX Project, D7.6 Small-Scale Pilot Deployment and Validation. 31 May 2023. Available online: https://www.iflex-project.eu/download/d7-6-small-scale-pilot-deployment-and-validation/ (accessed on 15 October 2023).
- Nordic Balancing Model, Analysing Different Alternatives for Single Pricing Model Implementation. 10 May 2019. Available online: https://nordicbalancingmodel.net/wp-content/uploads/2019/10/Single-pricing-model-timeline-report-clean-190910-For-publication.pdf (accessed on 15 October 2023).
- HORIZON 2020 iFLEX Project, D5.3 iFLEX Consumer Engagement and Incentive Mechanisms. 3 October 2022. Available online: https://www.iflex-project.eu/download/d5-3-iflex-consumer-engagement-and-incentive-mechanisms/ (accessed on 15 October 2023).
- Minou, M.; Stamoulis, G.D.; Thanos, G.; Chandan, V. Incentives and targeting policies for automated demand response contracts. In Proceedings of the 2015 IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015; pp. 557–562. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).