Abstract
Compressed-air energy storage and other energy storage technologies play crucial roles in the use of renewable energy sources. As a key component in energy storage technology, the throttle valve plays an important role in throttling and reducing the pressure. The proposed method incorporates a throttle valve without relative motion based on the auxetic tubular structure. The fundamental principle of the method is to exploit the elastic deformation characteristics of the auxetic tubular structure to achieve flow control. When the structure is subjected to tension or compression, its diameter changes, thereby altering the dimensions of the valve, and regulating the flow rate. To assess the efficacy of the proposed method, a geometrical analysis is conducted. A prototype of the flow control device, incorporating an auxetic tubular structure, is fabricated using 3D printing technology. Experimental tests substantiate the performance of the proposed flow control method, demonstrating excellent linearity and repeatability. The results of this study indicate the potential applications of this method in throttling, further highlighting the importance and feasibility of the utilization of elastic deformation in auxetic structures as a method to achieve predictable motion.
1. Introduction
The extensive use of traditional energy sources is one of the causes of current energy and environmental issues, leading to increased attention being given to renewable energy sources. The intermittency and instability of some renewable energy sources, such as solar, wind, and wave energy, have driven the development of energy storage technologies [1]. Compressed-air energy storage and wave energy converters are common energy storage technologies in which the throttle valve plays a significant role in throttling and reducing the pressure of the energy storage medium [2,3]. Throttle valves generally consist of a valve body that houses the opening or passage and a movable element, such as a disc or cone, which can be adjusted to vary the size of the orifice area [4]. Adjusting the position of the movable element allows for an effective increase or decrease in size, enabling precise control of the flow rate. The primary function of the throttle valve is to regulate the flow rate by adjusting its orifice area, typically measured in square units, such as square millimeters (mm2) or square inches (in2). The orifice area acts as a variable resistor, resulting in a decrease in pressure and an increase in velocity.
In addition to playing a significant role in energy storage technology, throttle valves also have important applications in other areas. Throttle valves are crucial in internal combustion engines, where they regulate the amount of air–fuel mixture entering the combustion chamber, thus controlling the engine’s power output [5,6]. They are also employed in various industrial applications, such as fluid pipelines and hydraulic systems, to regulate and control the flow of fluids [7,8,9].
Throttle valves also have some drawbacks and issues in practical engineering applications. Considerable energy loss can occur when the compressed air flows through the throttle valve used in the turbines in a large-scale compressed-air energy storage system [10]. In particular, cavitation caused by the transient reduction of the local pressure field [11], which leads to the generation of steam bubbles, can result in further noise and vibration and shorten the lifespan of the throttle valve [12]. Therefore, designing and optimizing throttle valves with longer service lifetimes has attracted the most attention [13,14,15,16]. Additionally, as mentioned above, throttle valves are typically assembled with multiple parts and components, and the variation in the orifice area is achieved through the relative movements of these parts and components. Those movements not only produce the necessary results for function but also bring about problems such as friction and wear [17,18]. These problems can significantly diminish the accuracy and efficiency of the throttle valve, thereby affecting the entire system.
Like throttle valves, many traditional mechanical systems consist of multiple components that rely on kinematic and other relationships to determine their relative motion and achieve specific functions or objectives. The design and operation of mechanical systems heavily rely on the determination of relative motion. Precise control and adjustment of the relative motion between components are crucial for achieving the desired functionality and performance. The mode and extent of relative motion vary depending on the specific mechanical system and application requirements. However, incorrect or unstable relative motion can lead to issues such as friction, wear, energy loss, and reduced efficiency. Despite careful consideration of the design and control of relative motion during the design and manufacturing process of mechanical systems in order to ensure system reliability and performance, friction and wear can still occur due to the inherent nature of relative motion.
This paper aims to investigate the utilization of elastic deformation in auxetic structures as a method to achieve predictable motion, starting with throttle valves. The objective is to simplify mechanical structures and address concerns related to wear and other associated issues.
The concept of auxetic materials and structures was first introduced in the 1980s by a British scientist, R. Lakes [19]. He observed that certain materials, when stretched or deformed, exhibited the counterintuitive behavior of expanding in the transverse direction rather than contracting, contraction being the typical response of most materials. This unique behavior led to the discovery of materials with a negative Poisson’s ratio, which are now commonly known as auxetic materials. The deformation is shown in Figure 1.
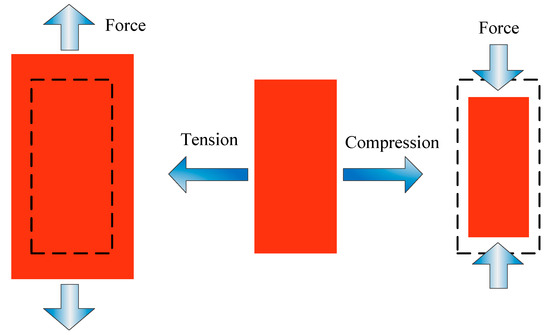
Figure 1.
Deformation of an auxetic material under tension and compression.
Compared to conventional materials, auxetic materials exhibit a counterintuitive behavior that imparts to them a range of advantageous effects. These include increased shear stiffness, enhanced plane-strain fracture toughness [20], improved resistance to indentation [21], and enhanced energy absorption performance [22,23].
Research studies [24,25,26] have demonstrated that when a tubular structure is constructed using auxetic materials (also known as auxetic tubular structure), it exhibits a similar radial expansion deformation when subjected to axial tension. This deformation is visualized in Figure 2, in which the auxetic tubular structure experiences radial tension, leading to an increase in diameter in the transverse direction, and a negative Poisson’s ratio would occur. This unique behavior of auxetic tubular structures has led to their application in many areas [27]. For example, in the field of energy absorption, square auxetic tubular structure [28] and combined auxetic tubular structure [29] have been developed and researched. Furthermore, researchers are also highly interested in the flexural performance and torsional deformation [30,31,32] of the auxetic tubular structure. These characteristics make the auxetic tubular structure potentially valuable in areas such as soft robotics technology, medical engineering, and future mechanical actuators.
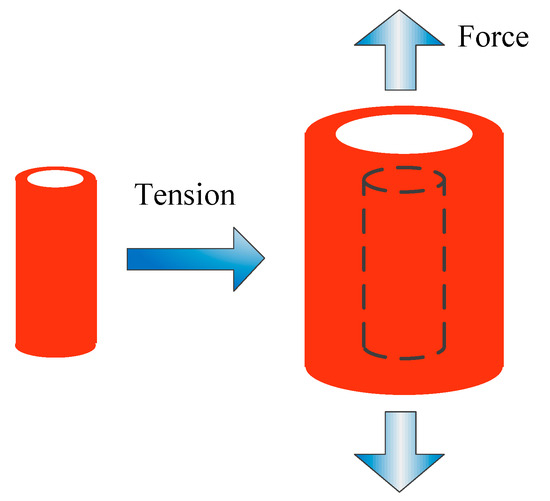
Figure 2.
Deformation of an auxetic tubular structure under tension.
This paper proposes a throttling valve that operates through elastic deformation, utilizing the characteristics of an auxetic tubular structure. Unlike traditional throttling valves that achieve throttling through relative motion, this valve can change the size of the orifice area by its own elastic deformation. To evaluate the valve’s performance in flow control, a prototype is designed and fabricated using 3D printing, and experimental tests are conducted to validate the approach.
2. Analytical and Numerical Models
In many cases, auxetic structures, such as those with internal honeycomb structures, lack air tightness and are unsuitable for throttle valves that require high sealing capabilities. Therefore, ensuring the sealing and leak-free performance of components that exhibit negative-Poisson’s-ratio effects has become a crucial concern for this study.
To address the issue of air tightness in honeycomb structures, a common approach is to encase the structure with an outer shell. However, this outer shell must be capable of exhibiting negative-Poisson’s-ratio deformation. Liu and Hu introduced a structure with a negative-Poisson’s-ratio effect [33], as depicted in Figure 3. The geometric configuration employed in this paper involves a three-dimensional structure composed of parallelogrammatic planes of uniform shapes and dimensions which induces the desired negative-Poisson’s-ratio effect.
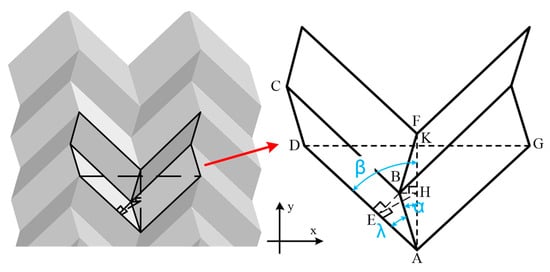
Figure 3.
Diagram of the geometrical structure of the auxetic structure.
To simplify the explanation, referring to Figure 3, we assume that ∠BAD = ∠BCD = λ, ∠BAF = α, and ∠DAF = β. Furthermore, we establish that two letters represent the length of the line segment starting from these two letters in Figure 3. For example, AB represents the length of line segment AB. In subsequent calculations and experiments, the values or ranges of each parameter of the cell structure will be based on the parameters provided in Table 1.

Table 1.
Parameters of the cell structure.
According to [33], the Poisson’s ratios of the three-dimensional structure in the x- and y-directions can be determined using the following equations:
where , and β0 represents the initial state of the β. Equations (1) and (2) demonstrate that the Poisson’s ratios υx and υy are determined exclusively by the values of β and β0.
According to Figure 3, it can be determined that the width of the cell, which is the length of line segment DG, can be obtained by
Figure 4 illustrates the relationship between the width and height of the cell structure (represented by line segments DG and AF, respectively) and the angle β. It is observed that as the angle β increases, the width of the cell structure also increases. Conversely, a decrease in angle β results in a decrease of DG. Similarly, AF also increases with the increase of β. The decrease in angle β is due to the compression applied to the structure. Therefore, according to Figure 4, it can be inferred that, as the structure undergoes compression, the width and height of the structure decrease simultaneously with the decrease in angle β. This clearly demonstrates that the structure possesses a negative Poisson’s ratio.
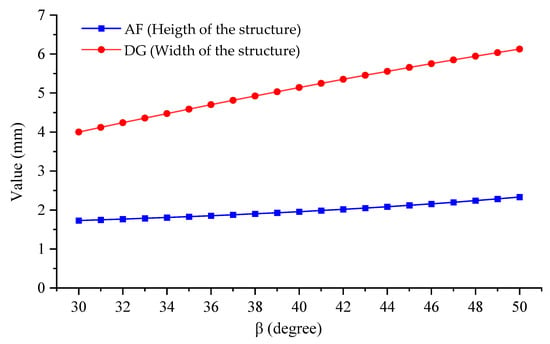
Figure 4.
Variations of cell structure width and height with β.
Figure 5 illustrates the internal mechanism, and the resulting auxetic effects, of the structure that has been transformed relative to the unit cell. It can be observed from the figure that the structure exhibits a contraction in the horizontal direction when compressed vertically, which demonstrates its auxetic properties.
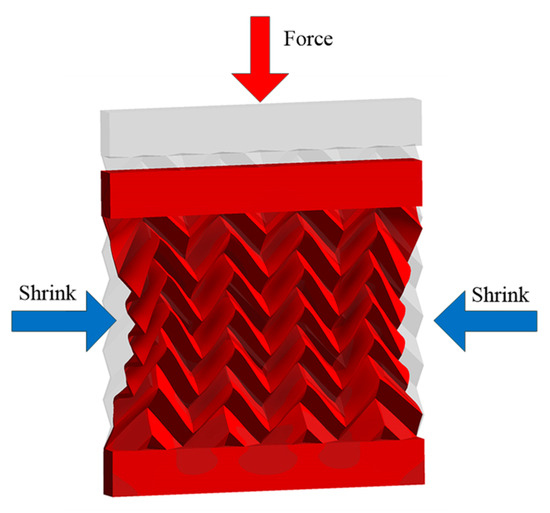
Figure 5.
Deformation of the 2D auxetic structure.
Plewa [26] designed an auxetic tubular structure by rolling up the planar structure of unit cells, following which the auxetic tubular structure is formed by transforming the 2D auxetic structure shown in Figure 5 into a tubular form. A similar radial contraction deformation could be expected when the auxetic tubular structure is subjected to axial compression. The deformation can be seen in Figure 6, where a reduction in diameter of the auxetic tubular structure is observed because there is a force applied along the axial direction.
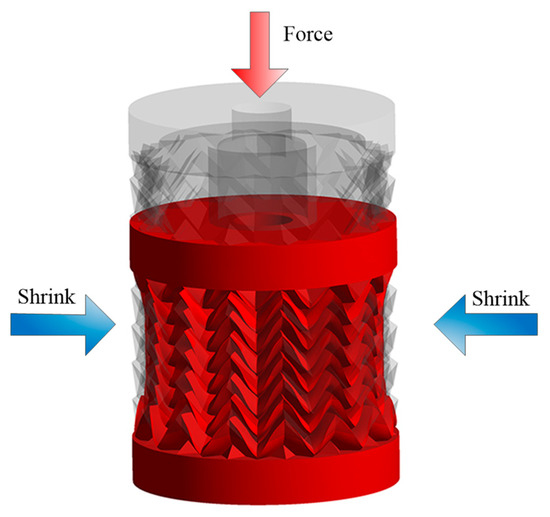
Figure 6.
Deformation of the auxetic tubular structure.
If the auxetic tubular structure consists of N unit cells in the circumferential direction, then its circumference is given by
According to Equation (5) and the basic formula of a circle, its radius can be obtained as
If the circumference of the auxetic tubular structure is used as the orifice of the throttle valve, the orifice area of the auxetic tubular structure can be determined when the fluid flows along the axial direction:
Combining Equations (4) and (8), the circumference can be expressed by:
The length of segment AF decreases when the structure is compressed, establishing a relationship between the size of AF and the compression displacement of the auxetic tubular structure. From Equation (9), when AF decreases, the orifice area also decreases. In other words, when the structure is compressed, the orifice area will decrease accordingly. For simplicity, Equation (7) is still used to describe the orifice area of the auxetic tubular structure.
Figure 7 depicts the variation of the orifice area with angle β for a given value. Observing the figure, it is clear that the orifice area exhibits a positive correlation with angle β, such that an increase in β leads to an increase in the orifice area. Conversely, when angle β decreases, the orifice area also decreases accordingly.
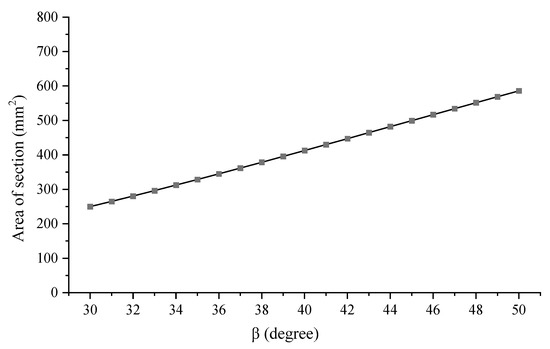
Figure 7.
Variations of orifice area width with β.
This positive correlation is very meaningful. When the angle β decreases, it implies that the axial length of the auxetic tubular structure also decreases. For the sake of convenience in explanation and analysis, we refer to the changes in length along the axial direction of the auxetic tubular structure when compressed as axial compression displacement. As shown in Figure 8, when the axial compression displacement is 0, there is no radial compression in the auxetic tubular structure. However, when compression displacement occurs, it indicates that the auxetic tubular structure is under compression, resulting in a decrease in angle β. Since orifice area and angle β are positively correlated, the orifice area also decreases. Consequently, the flow rate passing through the throttle valve would decrease. Therefore, there exists a direct relationship between the flow rate passing through the throttle valve and the compression displacement of the auxetic tubular structure.
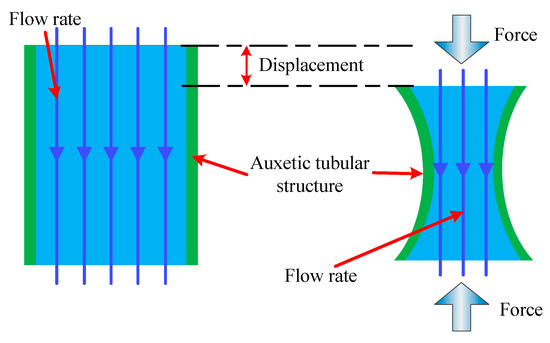
Figure 8.
Principle of the proposed flow-control method.
The relationship between the flow rate and the compression displacement is the basis of the proposed method. The principle of the method is to control the flow rate by controlling the compression of throttle valve based on the auxetic tubular structure. This method could avoid the problems caused by the relative motion between components of traditional throttle valves.
3. Experiment
3.1. Geometry of the Flow Control Device
In order to illustrate the principle and feasibility of the flow control method proposed in this paper, a flow control device has been designed (see Figure 9). The device consists of a throttle valve with an auxetic tube structure, along with a bolt-and-nut pair.
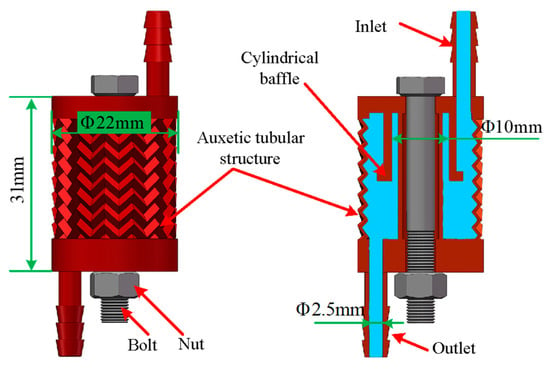
Figure 9.
Structural diagram of the flow control device.
The proposed throttle valve is manufactured using 3D printing technology. The device consists of a cylindrical outer shell made of an auxetic structure, with a cylindrical baffle positioned inside. The cylindrical baffle and the auxetic tubular shell are precisely matched to form a throttle port. Inlet and outlet connections are provided to link the device with the fluid circuit. The entire device has a cylindrical shape, and a bolt is inserted through its axis, which is then secured with a nut to enable the compression displacement control. By rotating the bolt, the compression of the cylindrical device is achieved through the interaction between the bolt and nut. As a result of the negative-Poisson’s-ratio structure of the shell, it undergoes radial contraction when compressed, leading to a reduction in the orifice area of the throttle port and enabling flow control.
As shown in Figure 3, the deformation of the auxetic tubular structure under compression depends on the geometric parameters of the structure. In this study, an auxetic cell is formed, with the parameters as shown in Table 1; in addition, the cell wall thickness is 0.4 mm, and the auxetic tube structure is 22 mm in diameter and 31 mm in height.
3.2. Preparation of the Flow Control Device
The flow control device was manufactured using a fused deposition modeling (FDM) 3D printer. FDM is an additive manufacturing process that builds parts layer-by-layer by depositing melted material in a predetermined path. The process utilizes thermoplastic polymers that come in filaments to form the final physical object. Compared to traditional manufacturing technologies, 3D printing offers advantages such as quicker prototyping, as well as reduced material waste and a reduced need for expensive tooling and assembly processes.
The physical properties of the material are listed in Table 2. Additionally, the 3D printing process achieves an accuracy of 0.01 mm per layer and takes approximately 8 h to complete production.

Table 2.
Properties of the 3D printing material.
The flow control device after the completion of printing is shown in Figure 10.

Figure 10.
Flow control device manufactured using 3D printer.
3.3. Experimental Set-Up
In the experiment, a simple constant-pressure device is used to maintain a constant pressure difference between the inlet and the outlet of the throttle valve. This device is illustrated in Figure 11.
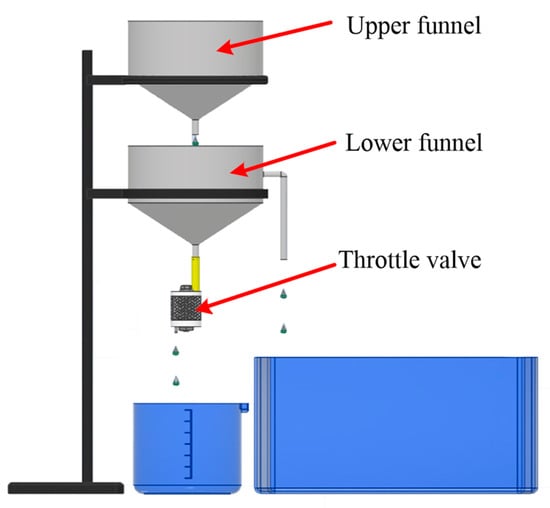
Figure 11.
Schematic diagram of the experimental set-up.
In the device, the upper funnel serves as the water source, supplying water that flows into the throttle valve through the lower funnel. The liquid level inside the lower funnel is determined by the outlet on its side. The upper end of the lower funnel receives water from the upper funnel and is connected to the inlet of the throttle valve through an outlet. When the flow rate of water from the upper funnel into the lower funnel exceeds the flow rate of water from the lower funnel into the throttle valve, the inlet pressure of the throttle valve, represented as p, will stabilize at a constant value:
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid’s level in the lower funnel.
In this way, the design of the constant pressure device ensures that the pressure difference between the inlet and outlet of the throttle valve remains stable. With a constant pressure at the inlet, the average flow-rate of water through the throttle valve can be calculated by measuring the time it takes for a fixed volume of water to pass through the throttle valve.
The test rig is constructed according to the schematic diagram shown in Figure 11 (Figure 12). The loading procedure of the experiments involves displacement-driven uniaxial compression, which means that the throttle valve is subjected to compression by applying a controlled displacement. In this case, a maximum displacement of 6 mm is set, and is divided into 12 increments to ensure accurate and controlled loading. The compression is achieved by using the combination of the bolt and the nut to compress the two ends of the throttle valve. This compression leads to deformation in the valve, which is then maintained at a constant value throughout the duration of the experiment. The flow rate and displacement under each compression state are recorded to analyze the relationship between the two parameters.

Figure 12.
Auxetic tubular throttle valve mounted on the test rig.
4. Results and Discussion
In Figure 13, the relationship between the compression displacement applied to the auxetic tubular structure and the flow rate of the throttle valve is illustrated, as obtained through the proposed flow-control methodology. To better comprehend the nature of the relationship, two lines of best fit (determined using the least-square method) have been plotted as solid line in Figure 13. The slope of the line of best fit serves as an indicator of the sensitivity of the proposed flow-control technique.
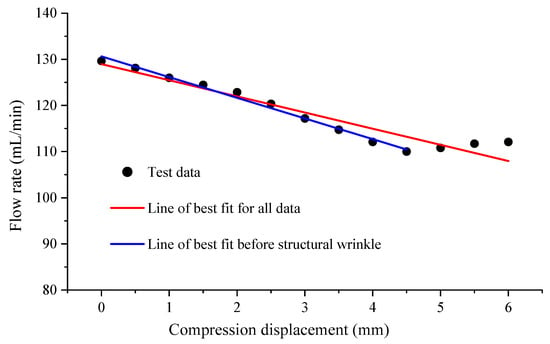
Figure 13.
Relationship between the flow rate and the compression displacement.
Figure 13 clearly demonstrates the linearity of the flow-rate control methodology based on the auxetic tubular structure within the compression displacement range of 0 to 4.5 mm. However, an interesting observation can be made at the point when the compression displacement exceeds 4.5 mm. Contrary to our expectations, the flow rate increases as the compression displacement increases.
Upon closer examination, we discovered that this unexpected behavior is attributed to the excessive deformation of the auxetic tubular structure during compression, leading to the formation of wrinkles in certain areas. This is illustrated in Figure 14, which depicts three distinct states of the auxetic tubular structure: no compression (0 mm), compression within the normal range (up to 4.5 mm), and excessive compression deformation with wrinkles (greater than 4.5 mm).

Figure 14.
Deformation of the auxetic tubular throttle valve at different compression displacements: (a) 0 mm, (b) 3 mm, and (c) 5 mm.
The two distinct lines of best fit shown in Figure 13 have a significant difference in slope. The blue solid line represents the compression displacement range of 0–4.5 mm, and the red solid one represents 0–6 mm. The slopes and nonlinear errors of two solid lines are calculated and shown in Table 3.

Table 3.
Slopes and nonlinear errors of the two lines of best fit.
Based on the analysis of Table 3 and Figure 13 and Figure 14, it can be concluded that the optimal displacement control range for the throttle valve obtained from the parameters listed in Table 1 using the proposed method is indeed 0–4.5 mm. This is because within this range, the deformation generated by the auxetic tubular structure is normal elastic deformation. It is important to note that exceeding this range may cause the auxetic tubular structure to experience excessive deformation and wrinkling, which may lead to a decrease in flow control performance and even render the structure unsuitable for continued use.
On the other hand, this also indicates the necessity of further research on the behavior and limitations of flow-rate control methods within different compression displacement ranges. Improvements or adjustments may be necessary to ensure consistent and reliable performance over a wider range of compressive displacements. However, it is recommended to use the method within the optimal displacement control range to ensure the best performance and longevity of the expansion-tube structure.
Although the linearity of the experimental results is not directly related to the sensitivity of the proposed method, it remains an important factor when calibration is needed. When the relationship between input and output of a system is nonlinear, the calibration becomes more complex and challenging. Despite the good linearity of the proposed method, the change in flow rate is inadequate. As shown in Figure 13, as the compression displacement increases from 0 to 4.5 mm, the flow only decreases by about 16%. This limited range of flow change clearly constrains the practical application of this method. Therefore, from an application perspective, further optimization of the structure used in this method is necessary to enable a larger flow change within an appropriate range of compression displacement. For example, the shape and size of the cylindrical baffle can be optimized, or the dimensions of the auxetic structure can be refined.
The consistency of flow control among different throttle valves with the same structural size is a crucial factor to consider for their application. To assess this issue, we conducted an experiment using three throttle valves which were manufactured using the same method and had identical structural sizes. The relationship between compression displacement and flow rate was then tested for each valve.
The results can be found in Figure 15, based on which we can determine that the three throttle valves exhibited good consistency in flow control. Especially when the compression displacement is within the range of 0–4.5 mm, a high degree of consistency can be observed. Despite their individual differences in manufacturing, the flow-rate response of each valve closely followed the expected values. However, when the compression displacement exceeds 4.5 mm, the flow rate of the three throttle valves become more dispersed due to factors such as wrinkling, resulting in a decrease in consistency.
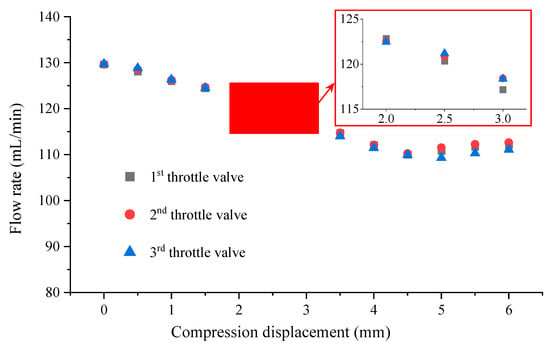
Figure 15.
Relationship between the compression displacement and flow rate for the three throttle valves.
The findings from this experiment provide confidence in the reliability and repeatability offered by throttle valves with the same structural size. It suggests that these valves can be used interchangeably in various applications without compromising their flow control capabilities. Of course, further research and testing are required to investigate this consistency under more varied conditions.
5. Conclusions
This paper introduces a novel approach to throttling, one which has been validated through the development of a simple test system. This approach can be widely applied in energy storage technology. The results of the experiments have confirmed a direct correlation between the displacement of the throttle valve and its flow rate and enabled us to draw the following conclusions:
- The proposed method exhibits good linearity, which means that the variation in flow rate can be predicted and controlled under different compression displacements. This linear relationship makes the method easier to calibrate and adjust in practical engineering applications.
- The proposed method demonstrates good repeatability, indicating that it can maintain its performance over long-term use, thereby enhancing its practicality and reliability.
- Although the current method has a limited range of flow-rate variation, optimization of the design of the auxetic tubular structure, such as by changing the shape and size of the cylindrical baffle or the dimensions of structures, can expand the controllable range of the flow rate. This enhancement would increase the method’s applicability and flexibility.
Moreover, this study not only provides valuable insights into the behavior of flow-rate control methods, but also investigates the utilization of elastic deformation in auxetic structures as a method used to achieve predictable motion. This method also has broad application value, including uses in hydraulic energy pumps and energy storage devices.
Author Contributions
Conceptualization, P.L. and Z.Z.; Methodology, H.T., Q.W. and Z.Z.; Validation, D.L. and H.T.; Formal analysis, Q.W. and P.L.; Writing—original draft preparation, P.L.; Writing—review and editing, H.T. and D.L.; Visualization, H.H. and Z.Z.; Supervision, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Xi’an Science and Technology Plan Project, grant number 2021JH-QCY7-0024, National Natural Science Foundation of China, grant number 51705394.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lund, H.; Salgi, G. The role of compressed air energy storage (CAES) in future sustainable energy systems. Energy Convers. Manag. 2009, 50, 1172–1179. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Li, R.; Li, C.; Hou, F.; Ben, Y. Thermodynamic analysis of cavern and throttle valve in large-scale compressed air energy storage system. Energy Convers. Manag. 2019, 183, 721–731. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Li, S.; He, T.; Liu, J. Experimental and simulative study on throttle valve function in the process of wave energy conversion. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, B.; Wang, Z.; Mu, X.; Sun, D. Multiphase throttling characteristic analysis and structure optimization design of throttling valve in managed pressure drilling. Energy 2023, 260, 125619. [Google Scholar] [CrossRef]
- Ren, R.; Su, T.; Ma, F.; Yang, W.; Zhao, X.; Xu, C. Research on the effect of the outlet throttle diameter deviation on the pressure relief rate of the injector control valve. Energies 2023, 16, 50. [Google Scholar] [CrossRef]
- Ren, R.; Su, T.; Ma, F.; Wu, X.; Xu, C.; Zhao, X. Study of the influence laws of the flow and cavitation characteristics in an injector control valve. Energy Sci. Eng. 2022, 10, 932–950. [Google Scholar] [CrossRef]
- Repin, S.; Vasileva, P.; Evtykov, S.; Maksimov, S.; Ruchkina, I.; Eremeev, A. Theoretical study of throttle valve system operation in the hydropneumatic shock absorber of the transport and technological machinery undercarriage. Transp. Res. Procedia 2021, 57, 562–572. [Google Scholar] [CrossRef]
- Sang, Y.; Wang, X.; Sun, W. Analysis of fluid flow through a bidirectional cone throttle valve using computational fluid dynamics. Aust. J. Mech. Eng. 2021, 19, 71–80. [Google Scholar] [CrossRef]
- Wan, H.-X.; Fang, J.; Huang, H. Numerical simulation on a throttle governing system with hydraulic butterfly valves in a marine environment. J. Mar. Sci. Appl. 2010, 9, 403–409. [Google Scholar] [CrossRef]
- Liu, J.-L.; Wang, J.-H. A comparative research of two adiabatic compressed air energy storage systems. Energy Convers. Manag. 2016, 108, 566–578. [Google Scholar] [CrossRef]
- Liu, H.; Cao, S.; Luo, X. Study on the effect of inlet fluctuation on cavitation in a cone flow channel. J. Fluids Eng. 2015, 137, 051301. [Google Scholar] [CrossRef]
- He, J.; Li, B.; Liu, X. Investigation of flow characteristics in the U-shaped throttle valve. Adv. Mech. Eng. 2019, 11, 168781401983049. [Google Scholar] [CrossRef]
- Zhang, J. Flow characteristics of a hydraulic cone-throttle valve during cavitation. Ind. Lubr. Tribol. 2019, 71, 1186–1193. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. Cavitation characteristics of shutoff valves in numerical modeling of transients in pipelines with column separation. J. Hydraul. Eng. 2015, 141, 04014077. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, T. Experimental study on the effect of pressure and flow rate on cavitation in a poppet throttle valve. Ind. Lubr. Tribol. 2020, 72, 629–636. [Google Scholar] [CrossRef]
- He, J.; Li, B.; Liu, X. Analysis of cavitation flow in conical throttle valve with different cone angle. J. Eng. 2019, 2019, 163–167. [Google Scholar] [CrossRef]
- Gandhi, Y.; Pawar, N.; Zoal, N.; Ramnathan, G. Investigation of valve tip end wear mechanism of a four-cylinder automotive engine under high-speed application. J. Fail. Anal. Prev. 2021, 21, 2098–2107. [Google Scholar] [CrossRef]
- Kesavan, D.; Done, V.; Sridhar, M.; Billig, R.; Nelias, D. High temperature fretting wear prediction of exhaust valve material. Tribol. Int. 2016, 100, 280–286. [Google Scholar] [CrossRef]
- Lakes, R. Foam Structures with a negative poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Shukla, S.; Behera, B. Auxetic fibrous structures and their composites: A review. Compos. Struct. 2022, 290, 115530. [Google Scholar] [CrossRef]
- Yang, C.; Vora, H.D.; Chang, Y. Behavior of auxetic structures under compression and impact forces. Smart Mater. Struct. 2018, 27, 025012. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Tensile and forming properties of auxetic warp-knitted spacer fabrics. Text. Res. J. 2017, 87, 1925–1937. [Google Scholar] [CrossRef]
- Ge, Z.; Hu, H. Innovative three-dimensional fabric structure with negative Poisson’s ratio for composite reinforcement. Text. Res. J. 2013, 83, 543–550. [Google Scholar] [CrossRef]
- Guo, M.-F.; Yang, H.; Ma, L. Design and characterization of 3D AuxHex lattice structures. Int. J. Mech. Sci. 2020, 181, 105700. [Google Scholar] [CrossRef]
- Ali, M.N.; Busfield, J.J.C.; Rehman, I.U. Auxetic oesophageal stents: Structure and mechanical properties. Int. J. Mech. Sci. 2014, 25, 527–553. [Google Scholar] [CrossRef]
- Plewa, J.; Płońska, M.; Feliksik, K. An experimental study of auxetic tubular structures. Materials 2022, 15, 5245. [Google Scholar] [CrossRef]
- Luo, C.; Han, C.Z.; Zhang, X.Y.; Zhang, X.G.; Ren, X.; Xie, Y.M. Design, manufacturing and applications of auxetic tubular structures: A review. Thin-Walled Struct. 2021, 163, 107682. [Google Scholar] [CrossRef]
- Han, D.; Ren, X.; Luo, C.; Zhang, Y.; Zhang, X.Y.; Zhang, X.G.; Jiang, W.; Hao, J.; Xie, Y.M. Experimental and computational investigations of novel 3D printed square tubular lattice metamaterials with negative Poisson’s ratio. Addit. Manuf. 2022, 55, 102789. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Ren, X.; Wang, X.Y.; Zhang, Y.; Xie, Y.M. A novel combined auxetic tubular structure with enhanced tunable stiffness. Compos. Part B Eng. 2021, 226, 109303. [Google Scholar] [CrossRef]
- Jiang, H.; Ziegler, H.; Zhang, Z.; Atre, S.; Chen, Y. Bending behavior of 3D printed mechanically robust tubular lattice metamaterials. Addit. Manuf. 2022, 55, 102565. [Google Scholar] [CrossRef]
- Farrell, D.T.; McGinn, C.; Bennett, G.J. Extension twist deformation response of an auxetic cylindrical structure inspired by deformed cell ligaments. Compos. Struct. 2020, 238, 111901. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, R.; Wang, L. Flexural behaviour of concrete-filled stainless steel SHS and RHS tubes. Eng. Struct. 2017, 134, 159–171. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, H.; Lam, J.K.C.; Liu, S. Negative Poisson’s ratio weft-knitted fabrics. Text. Res. J. 2010, 80, 856–863. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).