MPPT Strategy of Waterborne Bifacial Photovoltaic Power Generation System Based on Economic Model Predictive Control
Abstract
:1. Introduction
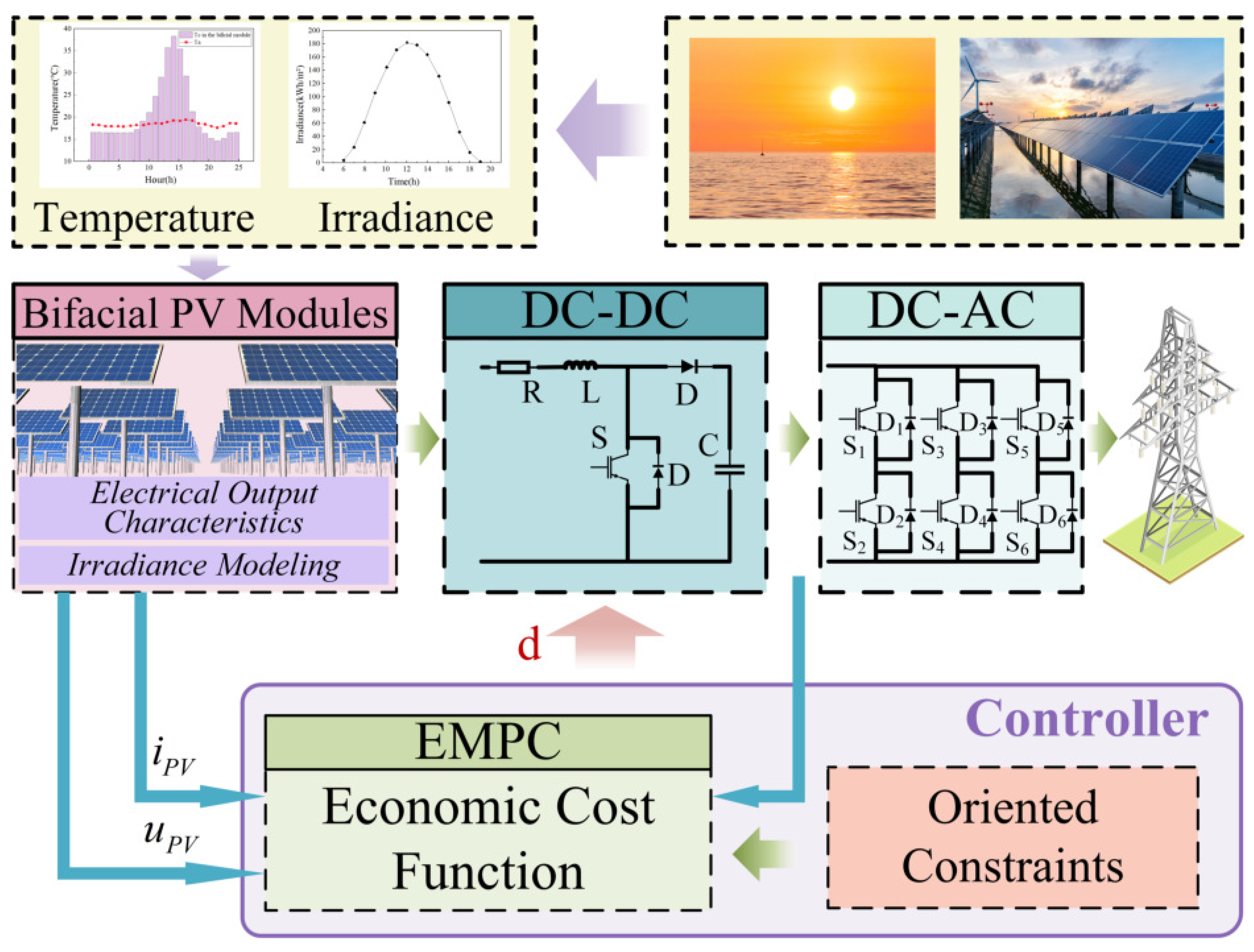
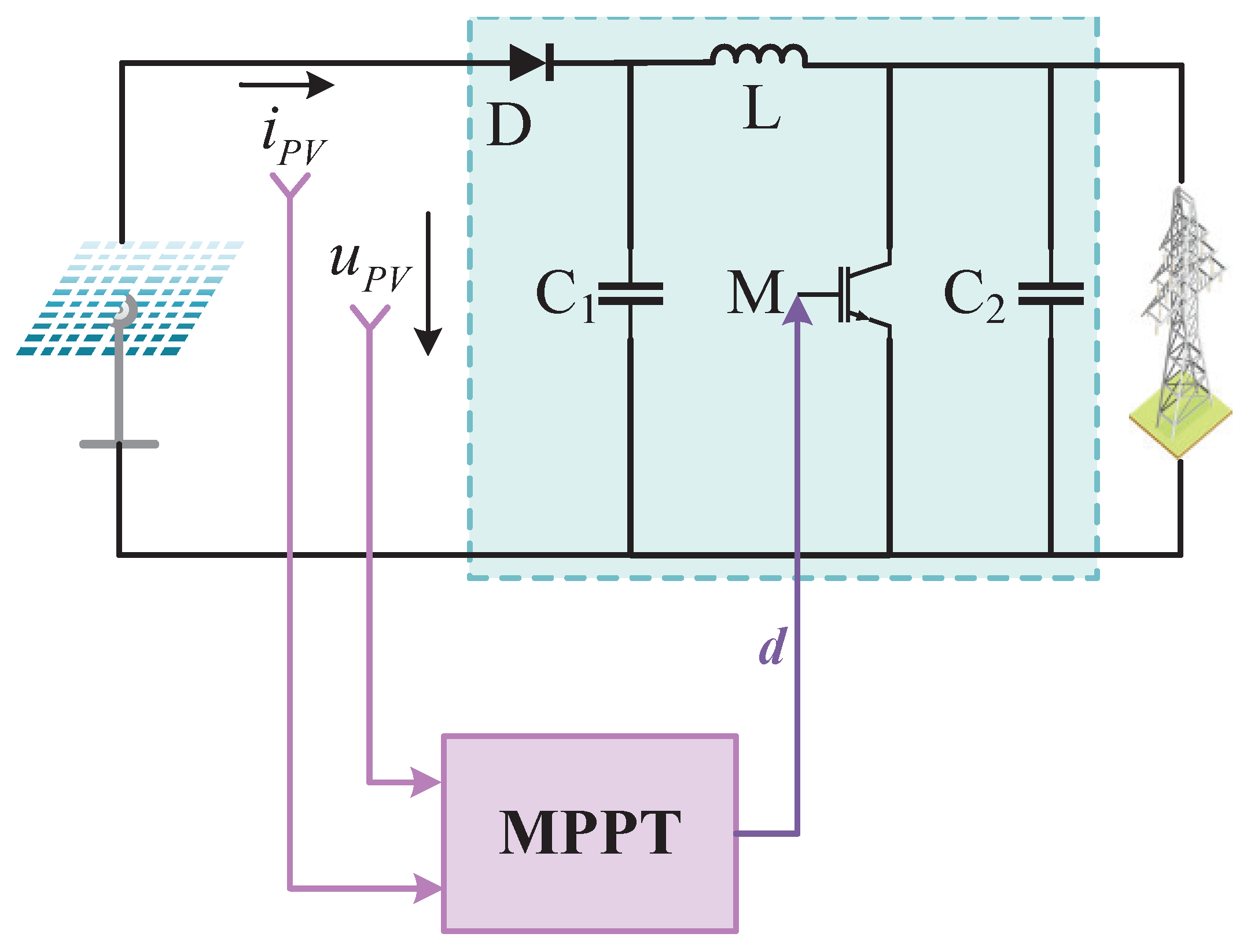
2. Modeling of Waterborne Bifacial PV Generation System
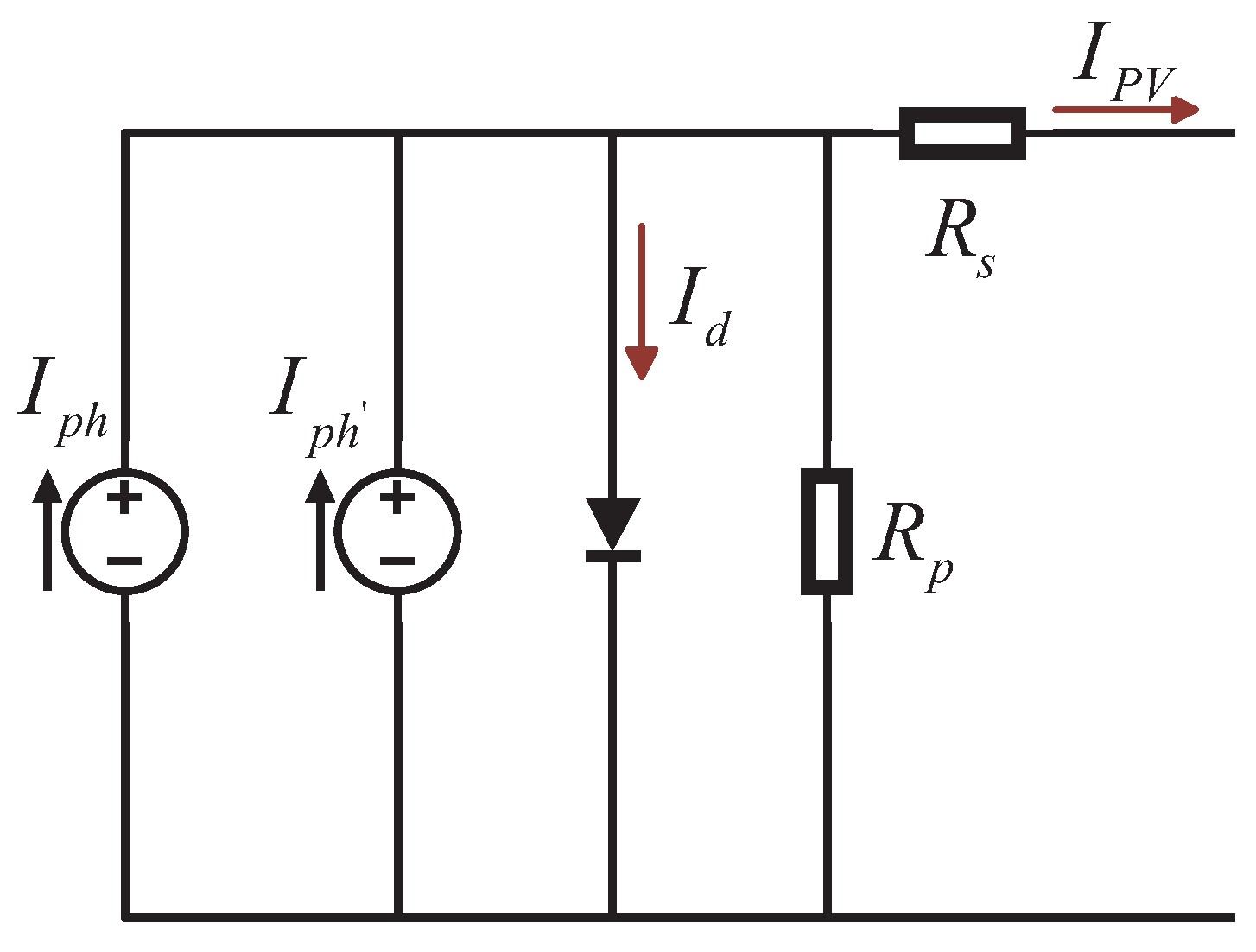
2.1. Mathematical Modeling of Waterborne Bifacial PV
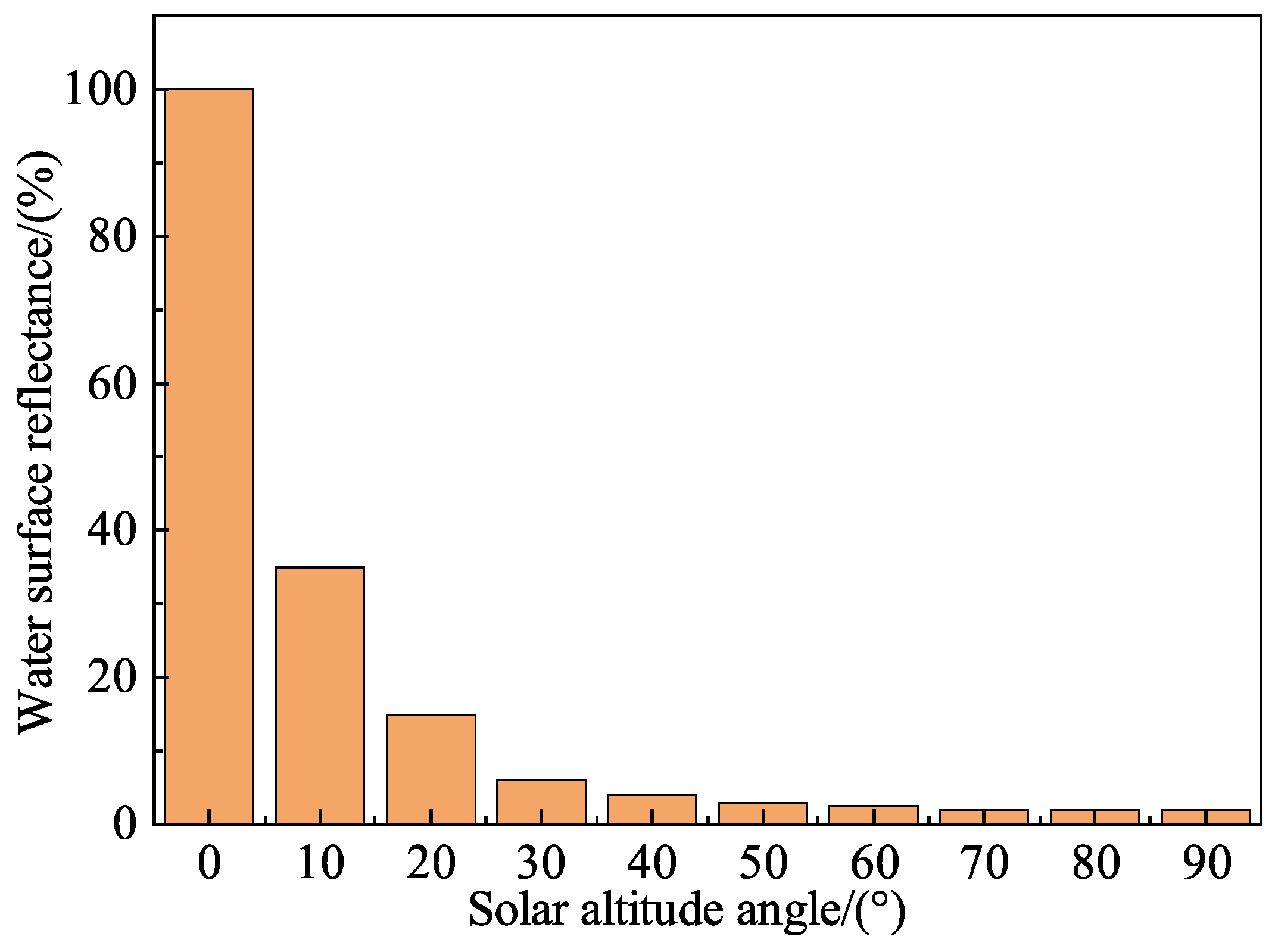
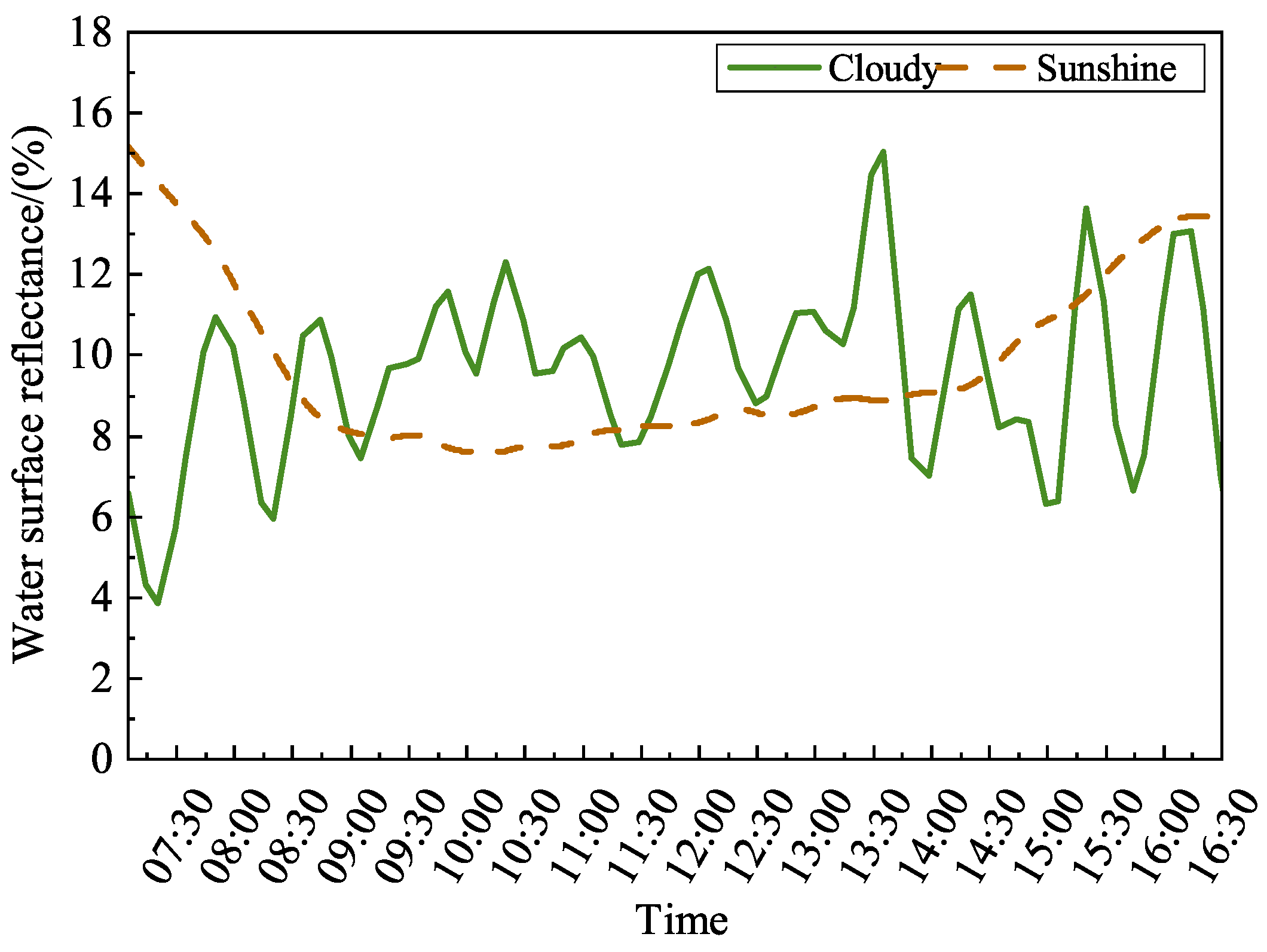
2.2. Water Surface Albedo
2.3. Irradiance Modeling of Waterborne Bifacial PV
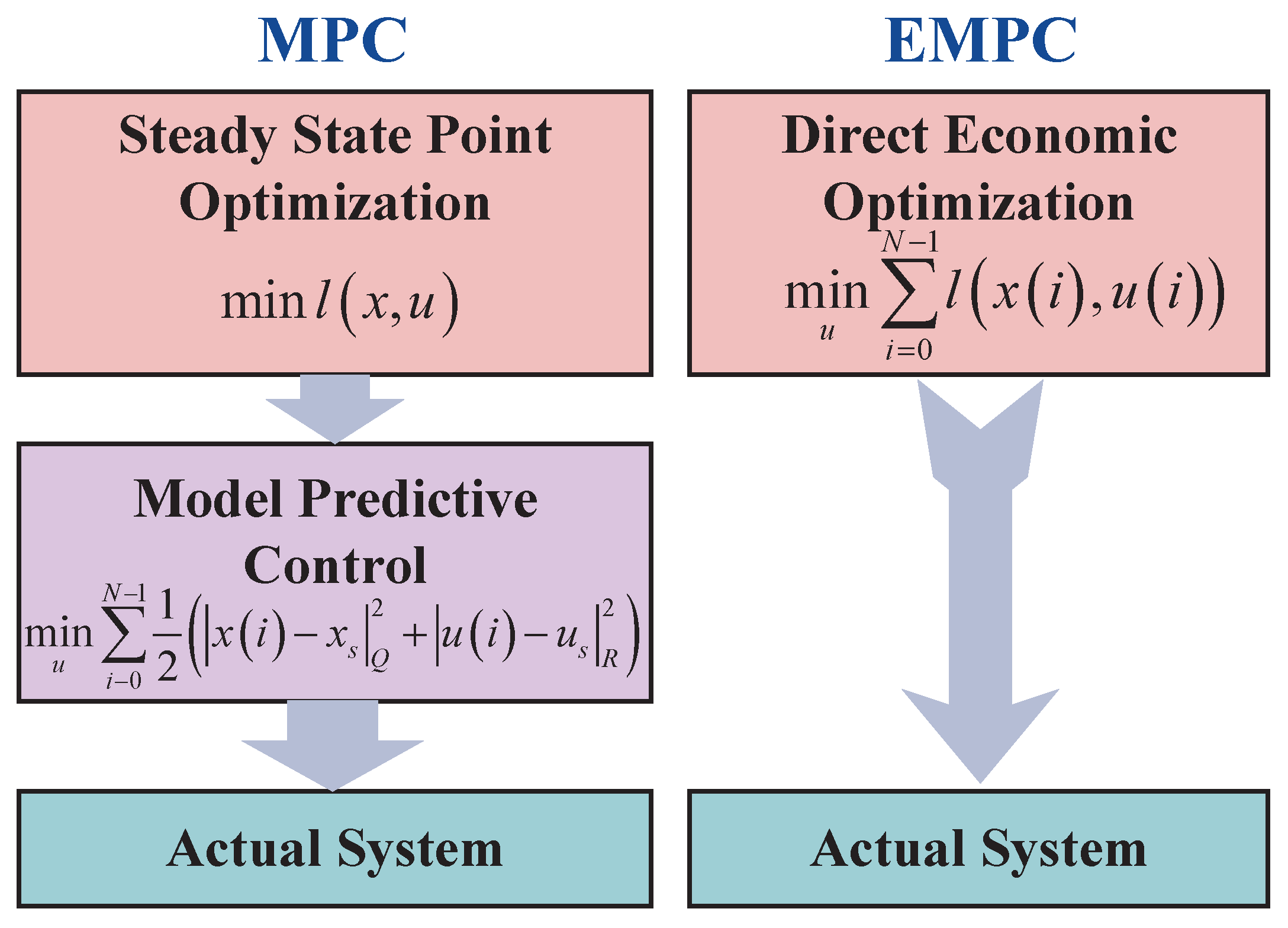
3. Designing of the Controller for EMPC
3.1. The Principles of EMPC
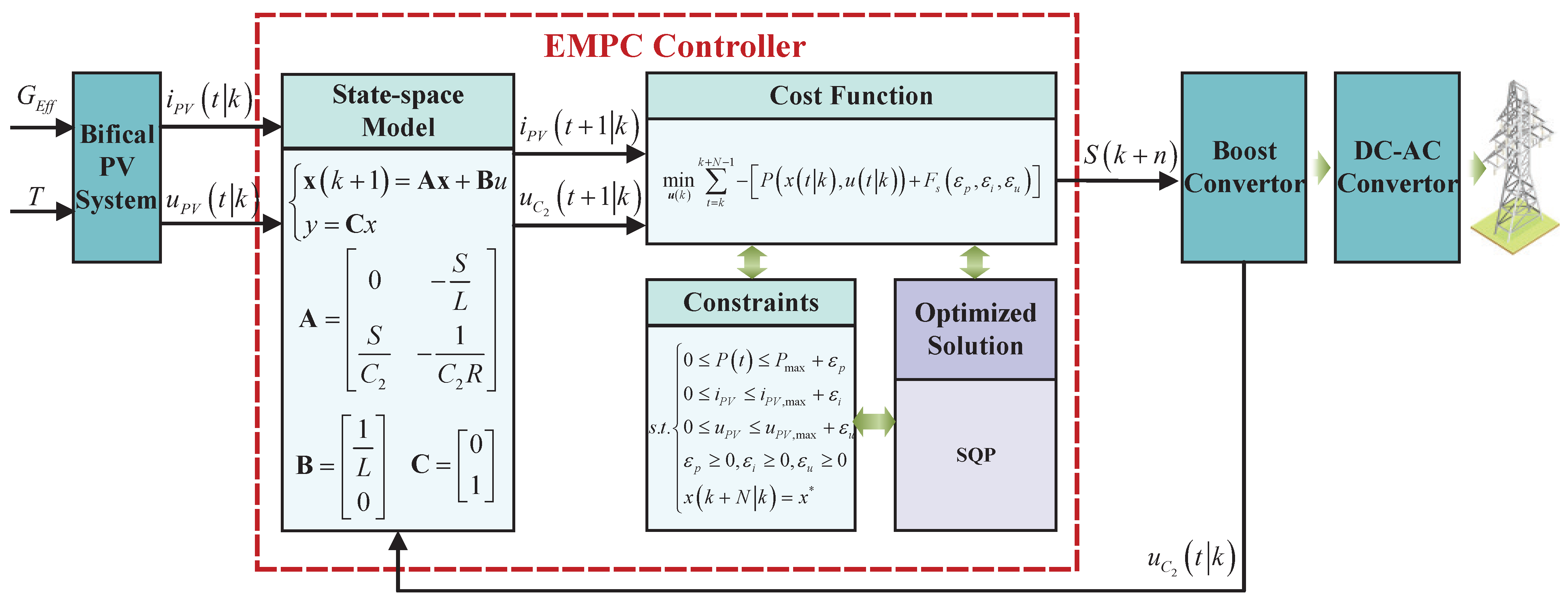
3.2. State-Space Modeling
3.3. Objective Functions and Constraints
3.4. The Design of Controller
3.5. Algorithmic Flow
4. Simulation Verification
4.1. Parameter Settings
4.2. Comparison of Mono−Facial PV and Bifacial PV Outputs under a Typical Day
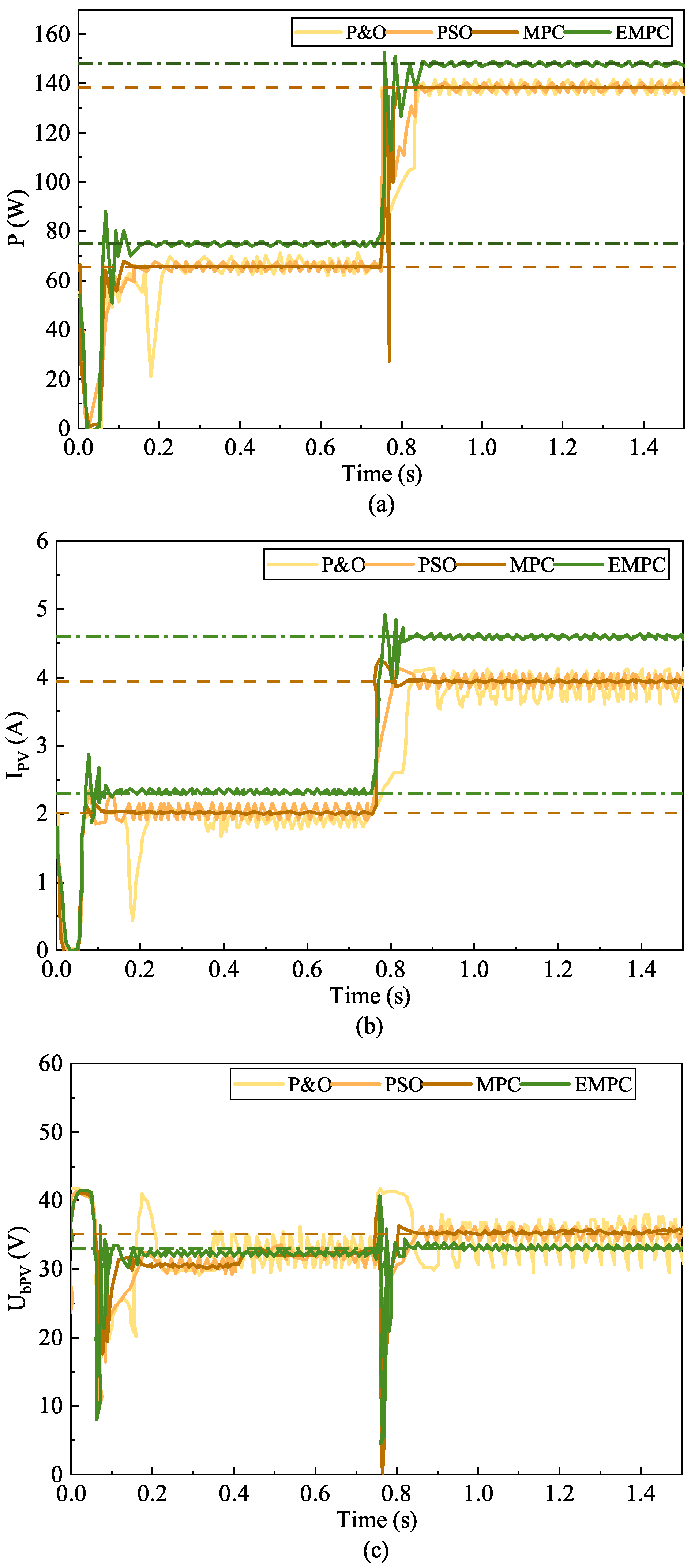
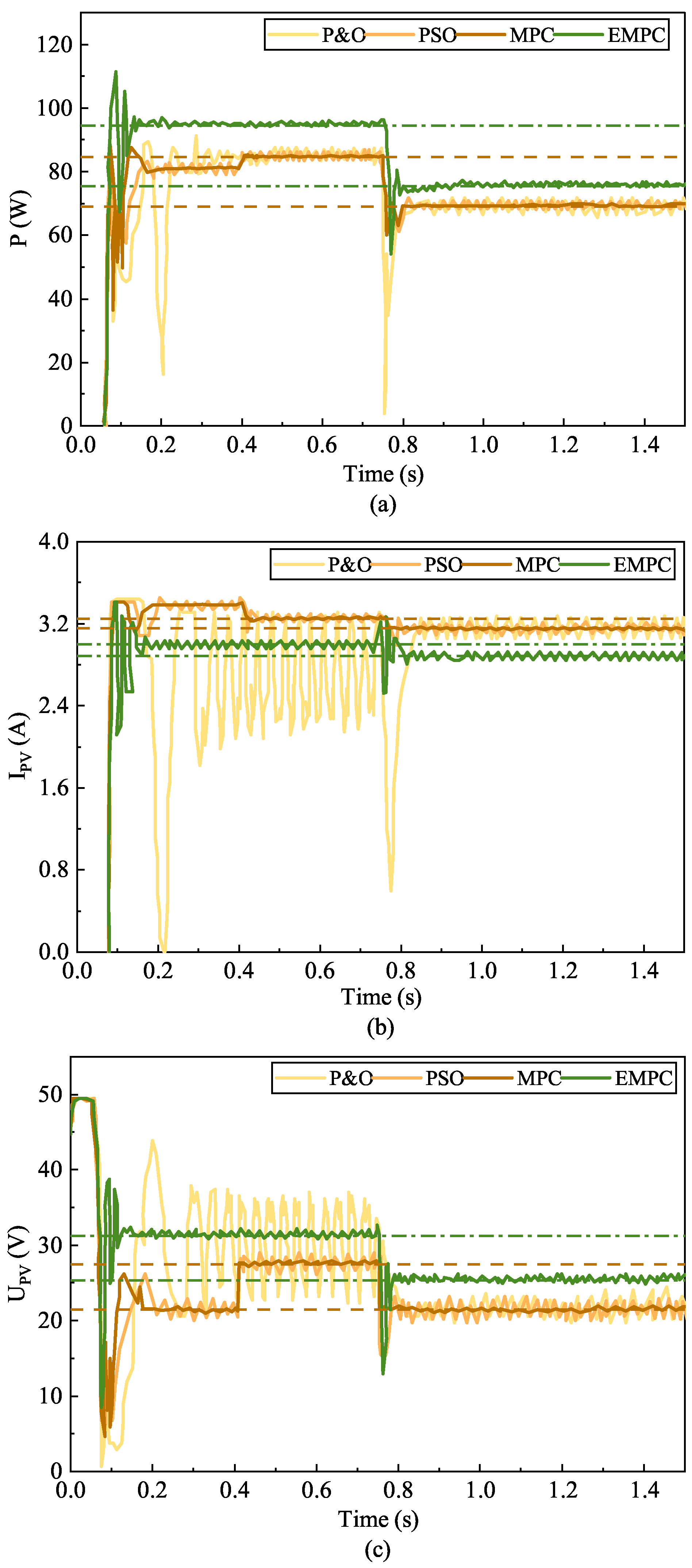
4.3. Comparison of MPPT Results under Irradiance Variation
4.4. Comparison of MPPT Results under Temperature Variation
4.5. Discussion and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PV | photovoltaic |
| MPPT | maximum power point tracking |
| EMPC | economic model predictive control |
| MPC | model predictive control |
| P&O | perturbation observation algorithm |
| INC | incremental conductance algorithm |
| PSO | particle swarm optimization |
References
- Poongavanam, P.; Chand, A.A.; Tai, V.B.; Gupta, Y.M.; Kuppusamy, M.; Dhanraj, J.A.; Velmurugan, K.; Rajagopal, R.; Ramachandran, T.; Prasad, K.A.; et al. Annual Thermal Management of the Photovoltaic Module to Enhance Electrical Power and Efficiency Using Heat Batteries. Energies 2023, 16, 4049. [Google Scholar] [CrossRef]
- Chaitanya, B.; Akhter, Z.M.; Ramachandran, T.; Al-Marzouqi, A.H.; Omar, F.K. Trends in Solar Powered Water Desalination Using Hydrogels: A Short Review. In Proceedings of the 2023 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 20–23 February 2023. [Google Scholar]
- Ramachandran, T.; Mourad, A.I.; Hamed, F. A Review on Solar Energy Utilization and Projects: Development in and around the UAE. Energies 2022, 15, 3754. [Google Scholar]
- Ali, A.; Almutairi, K.; Malik, M.Z.; Irshad, K.; Tirth, V.; Algarni, S.; Zahir, M.H.; Islam, S.; Shafiullah, M.; Shukla, N.K. Review of online and soft computing maximum power point tracking techniques under non-uniform solar irradiation conditions. Energies 2020, 13, 3256. [Google Scholar] [CrossRef]
- Ghenai, C.; Ahmad, F.F.; Rejeb, O.; Hamid, A.-K. Sensitivity analysis of design parameters and power gain correlations of bifacial solar PV system using response surface methodology. Sol. Energy 2021, 223, 44–53. [Google Scholar] [CrossRef]
- Wang, Z. Photovoltaic ‘Leader’ Program: A new attempt for policy support. Energy 2015, 8, 56–58. [Google Scholar] [CrossRef]
- Yan, Z. Research on Bifacial Photovoltaic Modeling and Fault Signal Transmission Strategy. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2022. [Google Scholar]
- Hasan, A.; Dincer, I. A new performance assessment methodology of bifacial photovoltaic solar panels for offshore applications. Energy Convers. Manag. 2020, 220, 112972. [Google Scholar] [CrossRef]
- Appelbaum, J. Bifacial photovoltaic panels field. Renew. Energy 2016, 85, 338–343. [Google Scholar] [CrossRef]
- Gu, W.; Ma, T.; Li, M.; Lu, S.; Zhang, Y. A coupled optical-electrical-thermal model of the bifacial photovoltaic module. Appl. Energy 2020, 258, 114075. [Google Scholar] [CrossRef]
- Tina, G.M.; Scavo, F.B.; Merlo, L.; Bizzarri, F. Comparative analysis of monofacial and bifacial photovoltaic modules for floating power plants. Appl. Energy 2021, 281, 116084. [Google Scholar] [CrossRef]
- Elmehdi, M.; Micheli, L.; Almonacid, F.M.; Fernández, E.F. Overview of the fundamentals and applications of bifacial photovoltaic technology: Agrivoltaics and aquavoltaics. Energies 2022, 15, 8777. [Google Scholar]
- Wang, S.; Wilkie, O.; Lam, J.; Steeman, R.; Zhang, W.; Khoo, K.S.; Siong, S.C.; Rostan, H. Bifacial photovoltaic systems energy yield modelling. Energy Procedia 2015, 77, 428–433. [Google Scholar] [CrossRef]
- Li, L.; Yang, T.; Yuan, Y.; Cai, Z. Maximum power point tracking algorithm for photovoltaic power generation system based on improved finite set model predictive control. Power Syst. Prot. Control 2021, 49, 28–37. [Google Scholar]
- Mazen, A.-S.; Mohamed Th, E.-M.; Mahmoud, E.-G. An efficient tracking of MPP in PV systems using a newly-formulated P&O-MPPT method under varying irradiation levels. J. Electr. Eng. Technol. 2021, 15, 501–513. [Google Scholar]
- Sheng, S.; Chen, Y. Maximum power point tracking strategy of variable step size incremental conductance method based on power prediction. Power Syst. Prot. Control 2017, 45, 42–48. [Google Scholar]
- Chen, J.; Zhang, W.; Li, X. Photovoltaic MPPT control based on improved conductance increment method. Smart Power 2021, 49, 47–55. [Google Scholar]
- Koad, R.B.; Zobaa, A.F.; El-Shahat, A. A novel MPPT algorithm based on particle swarm optimization for photovoltaic systems. IEEE Trans. Sustain. Energy 2016, 8, 468–476. [Google Scholar] [CrossRef]
- Li, H.; Yang, D.; Su, W.; Lü, J.; Yu, X. An overall distribution particle swarm optimization MPPT algorithm for photovoltaic system under partial shading. IEEE Trans. Ind. Electron. 2018, 66, 265–275. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Palani, S. Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions. Renew. Energy 2015, 75, 308–317. [Google Scholar] [CrossRef]
- Shi, P.; Du, Y.; Liu, S.; Cui, L. Analysis of photovoltaic maximum power point tracking strategy based on improved particle swarm optimization. Electron. Technol. 2023, 52, 78–80. [Google Scholar]
- Ali, M.; Shayan, E.; Padmanaban, S.; Mitolo, M.; Holm-Nielsen, J.B. Two fast metaheuristic-based MPPT techniques for partially shaded photovoltaic system. Int. J. Electr. Power Energy Syst. 2022, 137, 107567. [Google Scholar]
- Shang, L.; Li, F. Photovoltaic maximum power point tracking based on adaptive cuckoo search and disturbance observation. Power Syst. Prot. Control 2022, 50, 99–107. [Google Scholar]
- Wu, L.; Zhang, X.; Liu, Q.; Fan, C. MPPT control algorithm for photovoltaic power generation based on multi-universe optimization algorithm. J. Sol. Energy 2023, 44, 204–211. [Google Scholar]
- Wang, R.; Gao, H.; Zhang, X. Photovoltaic MPPT algorithm based on GA-GRU neural network. J. Sol. Energy 2023, 44, 212–219. [Google Scholar]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Shang, L.; Guo, H.; Zhu, W. An improved MPPT control strategy based on incremental conductance algorithm. Prot. Control. Mod. Power Syst. 2020, 5, 14. [Google Scholar] [CrossRef]
- Lashab, A.; Sera, D.; Guerrero, J.M. A dual-discrete model predictive control-based MPPT for PV systems. IEEE Trans. Power Electron. 2019, 34, 9686–9697. [Google Scholar] [CrossRef]
- Cui, J.; Liu, X.; Chai, T. Approximate scenario-based economic model predictive control with application to wind energy conversion system. IEEE Trans. Ind. Inform. 2022, 19, 5821–5829. [Google Scholar] [CrossRef]
- Sajadian, S.; Ahmadi, R.; Zargarzadeh, H. Extremum seeking-based model predictive MPPT for grid-tied Z-source inverter for photovoltaic systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 216–227. [Google Scholar] [CrossRef]
- Metry, M.; Shadmand, M.B.; Balog, R.S.; Abu-Rub, H. MPPT of photovoltaic systems using sensorless current-based model predictive control. IEEE Trans. Ind. Appl. 2016, 53, 1157–1167. [Google Scholar] [CrossRef]
- Wang, Q.; He, D.; Ping, H. Constrained nonlinear systems input to state stable economic model predictive control. Control Decis. 2022, 37, 1137–1144. [Google Scholar]
- Rodríguez, D.I.H.; Myrzik, J.M.A. Economic model predictive control for optimal operation of home microgrid with photovoltaic-combined heat and power storage systems. IFAC-Pap. OnLine 2017, 50, 10027–10032. [Google Scholar] [CrossRef]
- Köhler, P.N.; Müller, M.A.; Allgöwer, F. Approximate dissipativity of cost-Interconnected systems in distributed economic MPC. IEEE Trans. Autom. Control 2022, 68, 2170–2182. [Google Scholar] [CrossRef]
- Li, T.; Liu, H.; Wang, H.; Yao, Y. Hierarchical predictive control-based economic energy management for fuel cell hybrid construction vehicles. Energy 2020, 198, 117327. [Google Scholar] [CrossRef]
- Liu, X.; Cui, J. Fuzzy economic model predictive control for thermal power plant. IET Control Theory Appl. 2019, 13, 1113–1120. [Google Scholar] [CrossRef]
- Yang, Y.; Zou, Y.; Li, S. Economic model predictive control of enhanced operation performance for industrial hierarchical systems. IEEE Trans. Ind. Electron. 2021, 69, 6080–6089. [Google Scholar] [CrossRef]
- Jia, Y.; Meng, K.; Dong, L.; Liu, T.; Sun, C.; Dong, Z.Y. Economic model predictive control of a point absorber wave energy converter. IEEE Trans. Sustain. Energy 2020, 12, 578–586. [Google Scholar] [CrossRef]
- Albalawi, F.; Durand, H.; Christofides, P.D. Distributed economic model predictive control with Safeness-Index based constraints for nonlinear systems. Syst. Control Lett. 2017, 110, 21–28. [Google Scholar] [CrossRef]
- Kong, X.; Ma, L.; Liu, X.; Abdelbaky, M.A.; Wu, Q. Wind turbine control using nonlinear economic model predictive control over all operating regions. Energies 2020, 13, 184. [Google Scholar] [CrossRef]
- Angeli, D.; Casavola, A.; Tedesco, F. Theoretical advances on economic model predictive control with time-varying costs. Annu. Rev. Control 2016, 41, 218–224. [Google Scholar] [CrossRef]
- Worku, M.Y.; Hassan, M.; Hassan, M.; Shafiullah, M.; Elkadeem, M.R.; Hossain, M.I.; Abido, M.A. A comprehensive review of recent maximum power point tracking techniques for photovoltaic systems under partial shading. Sustainability 2023, 15, 11132. [Google Scholar] [CrossRef]
- Lu, W.; Tian, J. Water surface reflection characteristics and power generation of bifacial PV modules. IOP Conf. Ser. Earth Environ. Sci. 2020, 601, 012047. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, L.; Qin, Z.; Zhan, Z.; Wang, L.; Qin, Z.; Wu, M.; Xu, C.; Quan, P. Theoretical and experimental research on the factors affecting the power generation performance of bifacial photovoltaic modules. J. Sol. Energy 2022, 43, 171. [Google Scholar]
- Liao, D.; Huang, Z.; Fang, X. Study on irradiance model of bifacial PV modules. J. Sol. Energy 2021, 42, 471. [Google Scholar]



| Parameters | Value |
|---|---|
| Bifacial photovoltaics (PV) terminal capacitance | 100 |
| Bifacial PV end inductance | 20 |
| Boost circuit resistance | 20 |
| Boost circuit capacitance | 100 |
| Open-circuit voltage | 37.5 |
| Short-circuit current | 4.95 |
| Bifacial coefficient | 79.43 |
| Switching frequencies | 20 |
| Water surface albedo | 7 |
| Parameters | Reference Value | Perturbation Observation (P&O) | Particle Swarm Optimization (PSO) | Model Predictive Control (MPC) | Economic Model Predictive Control (EMPC) |
|---|---|---|---|---|---|
| 75.026 | 66.623 | 66.039 | 65.702 | 74.934 | |
| RMSE | 8.914 | 9.609 | 9.367 | 2.036 | |
| 31.563 | 32.258 | 33.482 | 33.447 | 32.253 | |
| RMSE | 0.755 | 2.395 | 2.022 | 0.141 | |
| 2.377 | 1.991 | 1.979 | 2.011 | 2.323 | |
| RMSE | 0.442 | 0.415 | 0.411 | 0.075 |
| Parameters | Reference Value | P&O | PSO | MPC | EMPC |
|---|---|---|---|---|---|
| 148.252 | 138.249 | 137.573 | 138.447 | 147.985 | |
| RMSE | 10.856 | 11.023 | 9.845 | 2.194 | |
| 31.732 | 35.350 | 34.804 | 35.801 | 32.18 | |
| RMSE | 3.629 | 3.375 | 4.140 | 0.469 | |
| 4.672 | 3.862 | 3.931 | 3.940 | 4.598 | |
| RMSE | 0.832 | 0.747 | 0.733 | 0.106 |
| Parameters | Reference Value | P&O | PSO | MPC | EMPC |
|---|---|---|---|---|---|
| 96.785 | 84.598 | 83.514 | 83.536 | 95.068 | |
| RMSE | 12.421 | 13.470 | 13.361 | 1.834 | |
| 31.754 | 30.223 | 25.364 | 24.925 | 31.497 | |
| RMSE | 4.877 | 7.087 | 7.509 | 0.521 | |
| 3.048 | 2.533 | 3.286 | 3.309 | 2.995 | |
| RMSE | 0.808 | 0.256 | 0.269 | 0.066 |
| Parameters | Reference Value | P&O | PSO | MPC | EMPC |
|---|---|---|---|---|---|
| 76.658 | 69.026 | 69.497 | 69.381 | 75.781 | |
| RMSE | 7.950 | 7.258 | 7.283 | 1.202 | |
| 25.717 | 21.707 | 21.426 | 21.487 | 25.551 | |
| RMSE | 4.296 | 4.448 | 4.239 | 0.430 | |
| 2.980 | 3.157 | 3.154 | 3.152 | 2.883 | |
| RMSE | 0.203 | 0.179 | 0.173 | 0.105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Li, J.; Qiu, J.; Guo, X.; An, B.; Zhang, Y.; Wang, W. MPPT Strategy of Waterborne Bifacial Photovoltaic Power Generation System Based on Economic Model Predictive Control. Energies 2024, 17, 152. https://doi.org/10.3390/en17010152
Tang M, Li J, Qiu J, Guo X, An B, Zhang Y, Wang W. MPPT Strategy of Waterborne Bifacial Photovoltaic Power Generation System Based on Economic Model Predictive Control. Energies. 2024; 17(1):152. https://doi.org/10.3390/en17010152
Chicago/Turabian StyleTang, Minan, Jinping Li, Jiandong Qiu, Xi Guo, Bo An, Yaqi Zhang, and Wenjuan Wang. 2024. "MPPT Strategy of Waterborne Bifacial Photovoltaic Power Generation System Based on Economic Model Predictive Control" Energies 17, no. 1: 152. https://doi.org/10.3390/en17010152
APA StyleTang, M., Li, J., Qiu, J., Guo, X., An, B., Zhang, Y., & Wang, W. (2024). MPPT Strategy of Waterborne Bifacial Photovoltaic Power Generation System Based on Economic Model Predictive Control. Energies, 17(1), 152. https://doi.org/10.3390/en17010152







