A Study and Optimization of the Unsteady Flow Characteristics in the Last Stage Impeller of a Small-Scale Multi-Stage Hydraulic Turbine
Abstract
:1. Introduction
2. Numerical Simulation and Validation
2.1. Two-Stage Hydraulic Turbine Model
2.2. Grid Independence Analysis
3. Calculation and Analysis Methods
3.1. Cavitation Model
3.2. Numerical Analysis Methods
3.3. Compressible Model
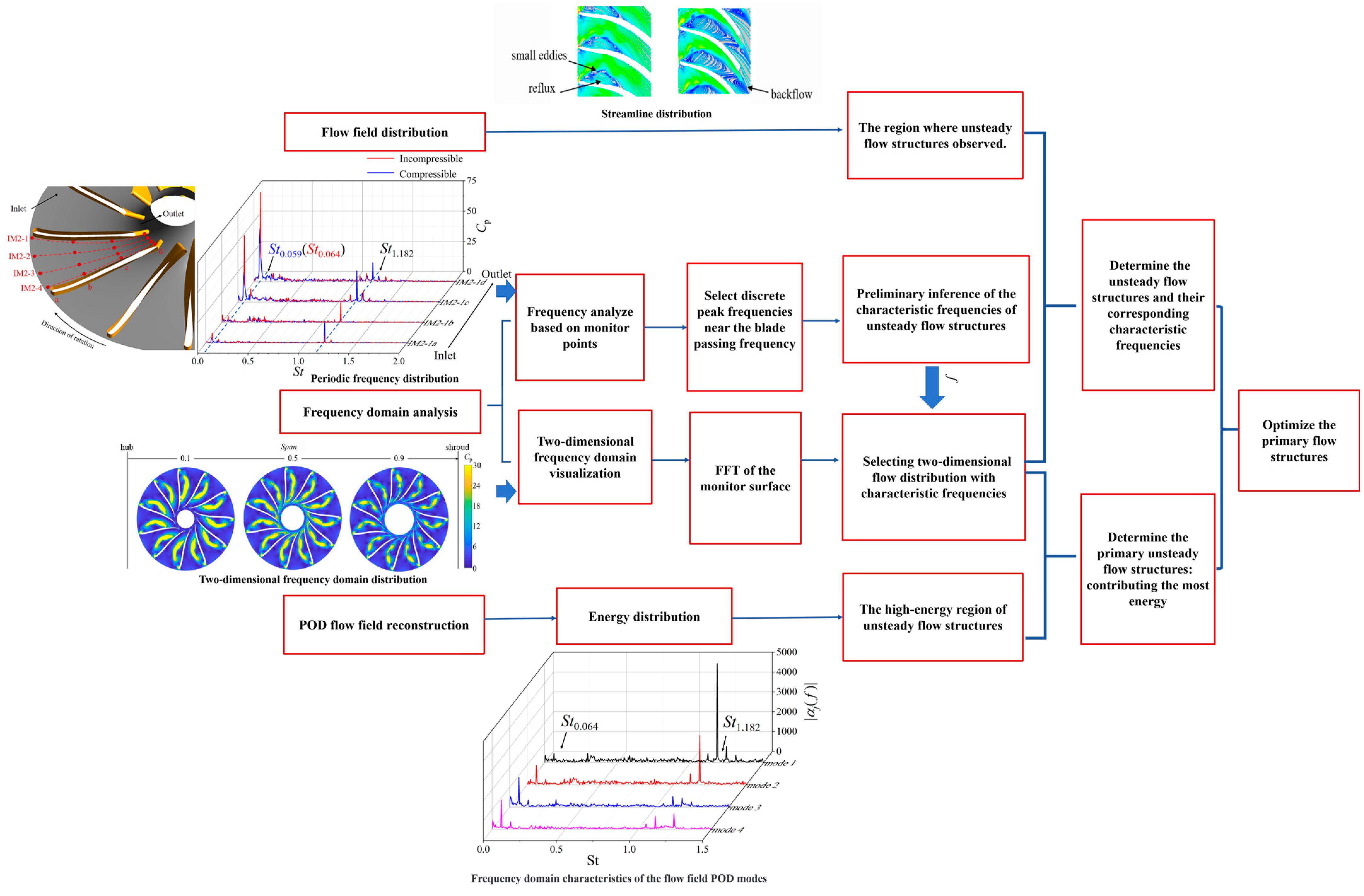
3.4. Flow Field Analysis Methods
4. Effect of Working Fluid Compressibility in the Last-Stage Impeller
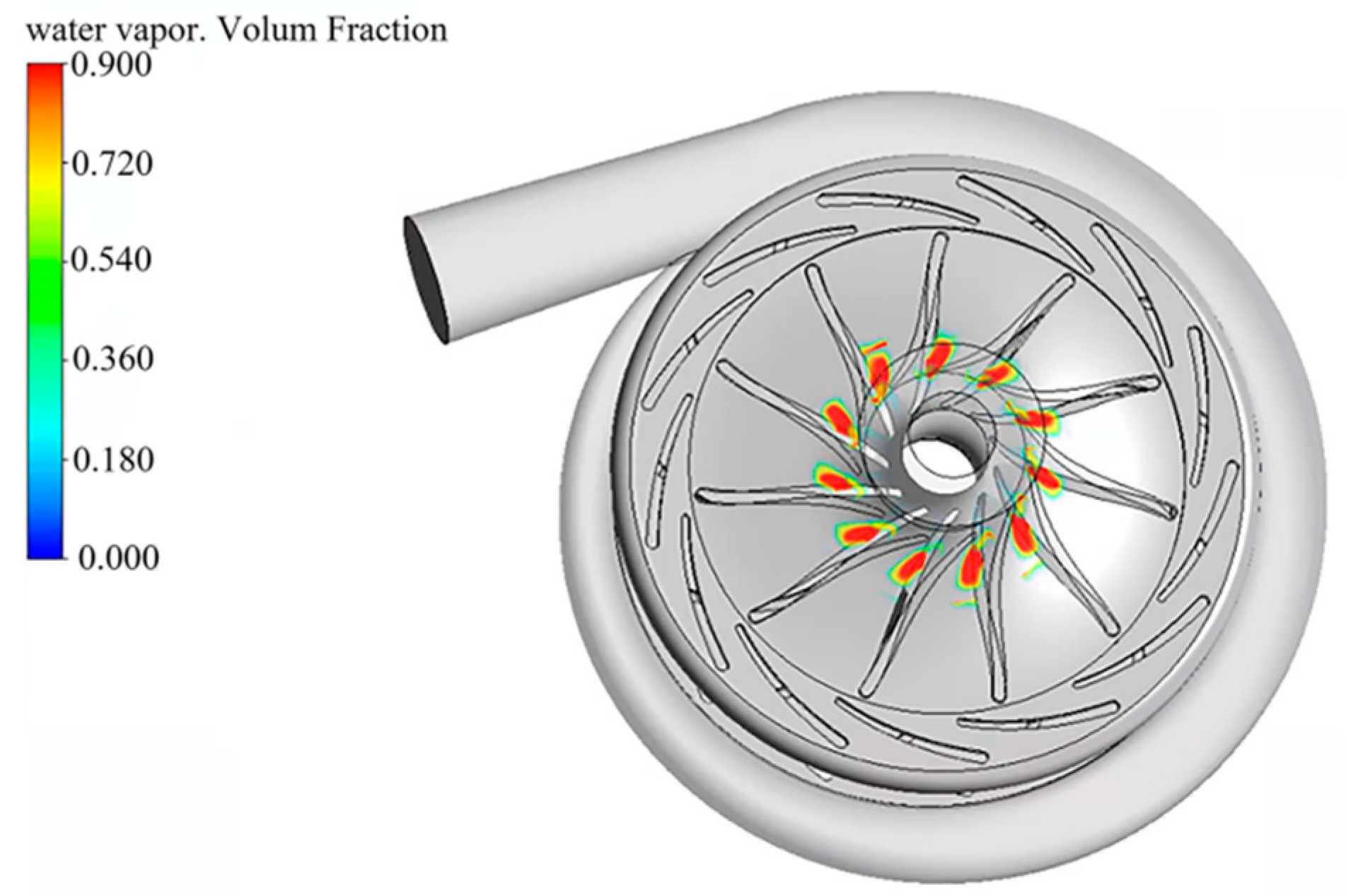
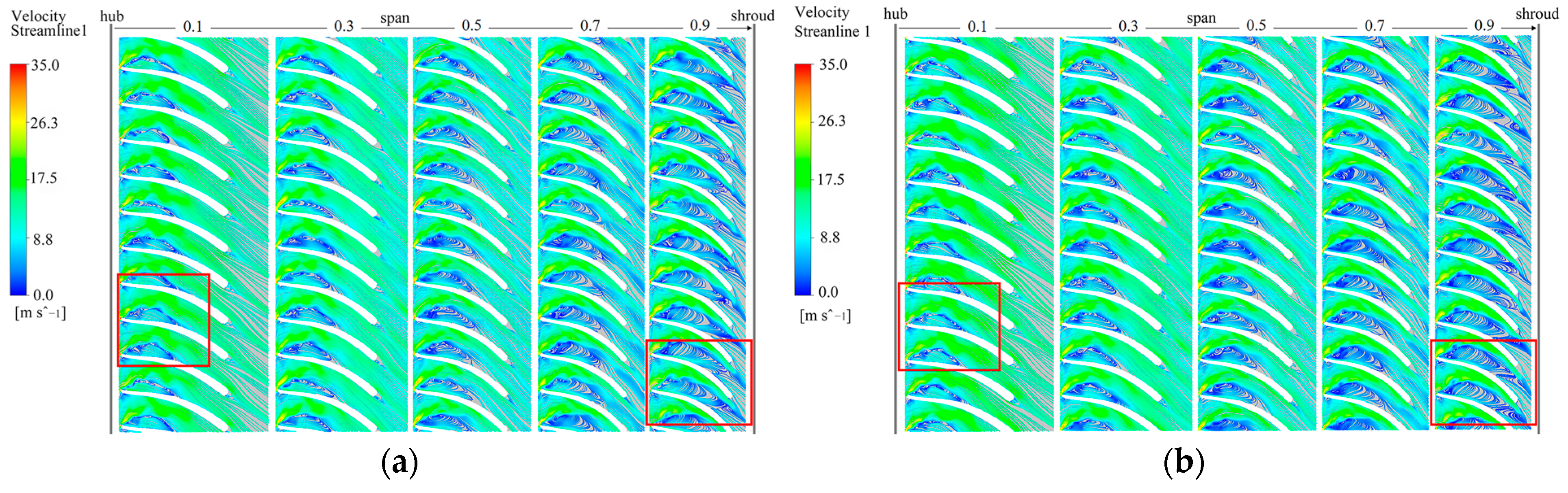
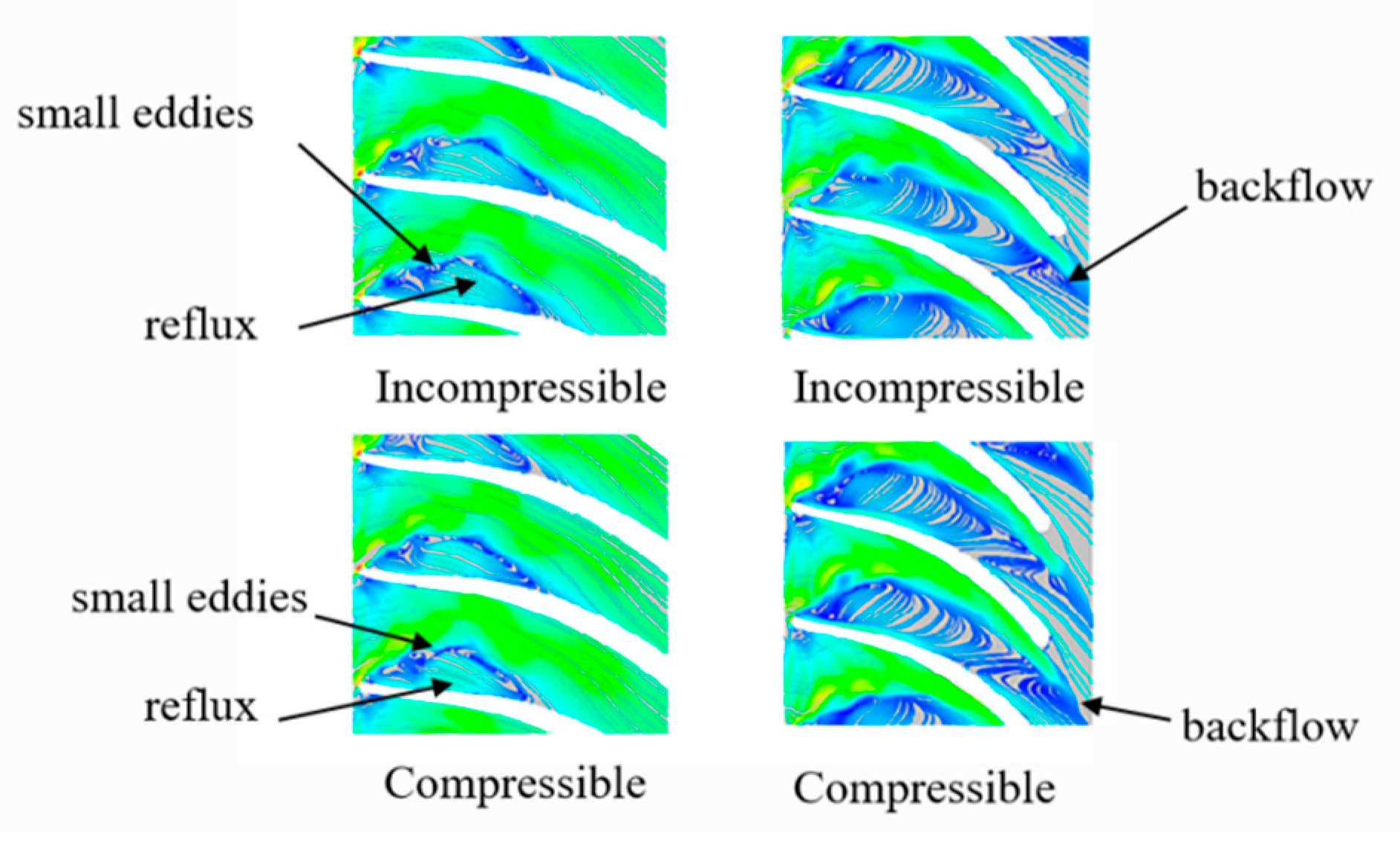
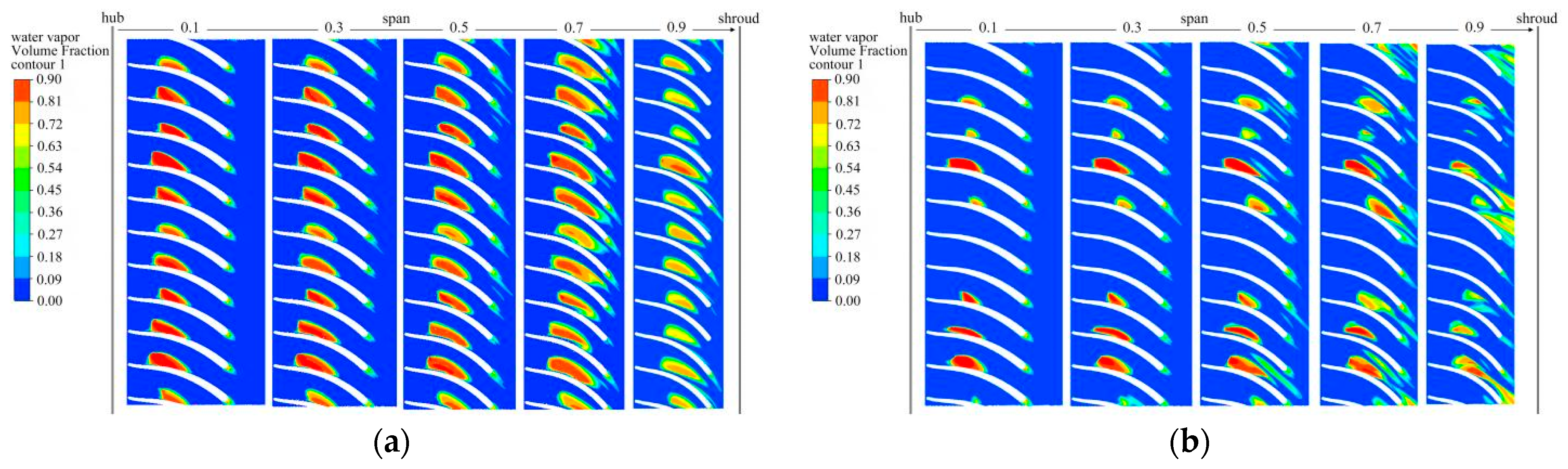
4.1. Flow Field Analysis of the Last-Stage Impeller
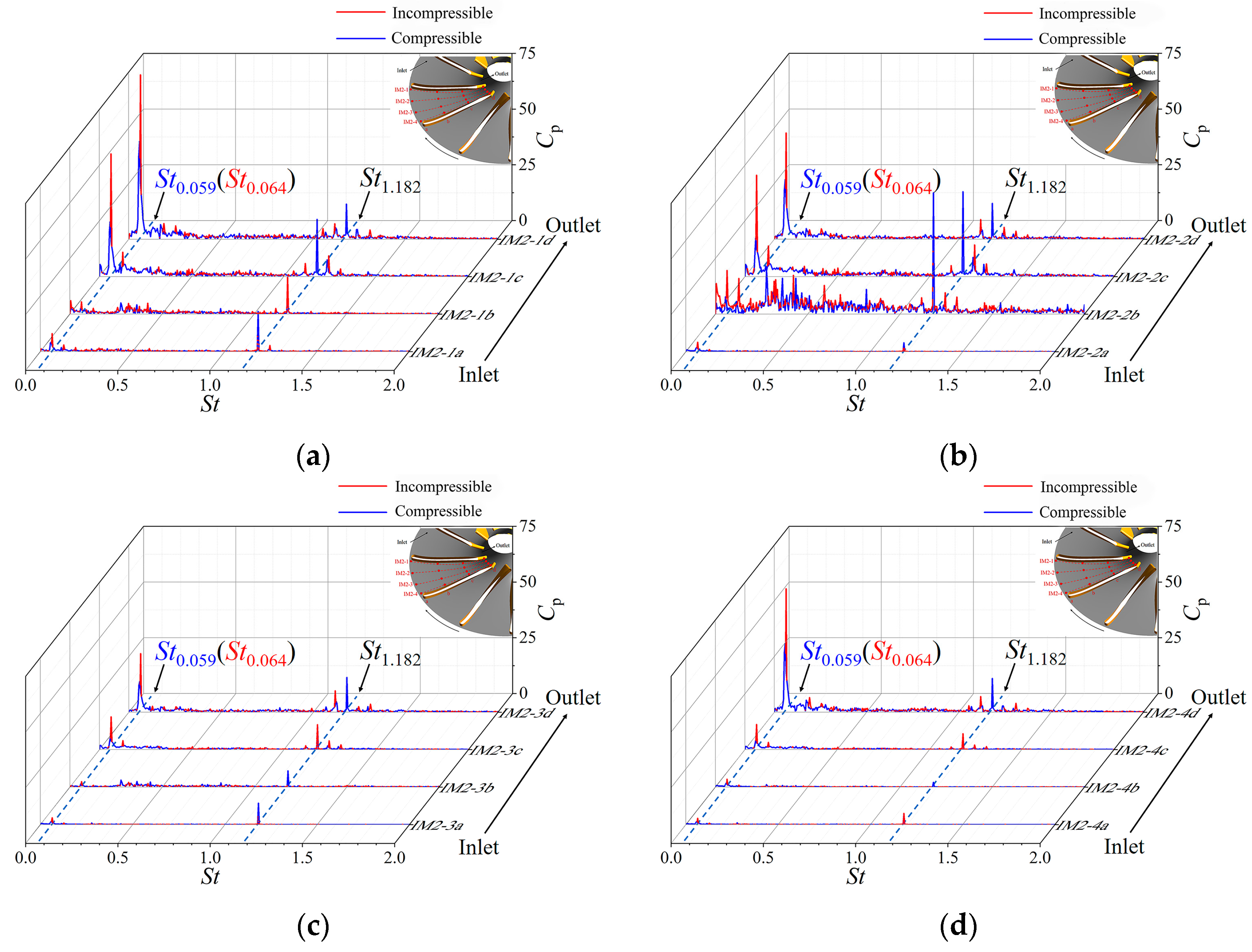
4.2. Pressure Spectrum Analysis of Secondary Impeller
4.3. Analysis of the Distribution of Unsteady Flow Structures in the Secondary Impeller
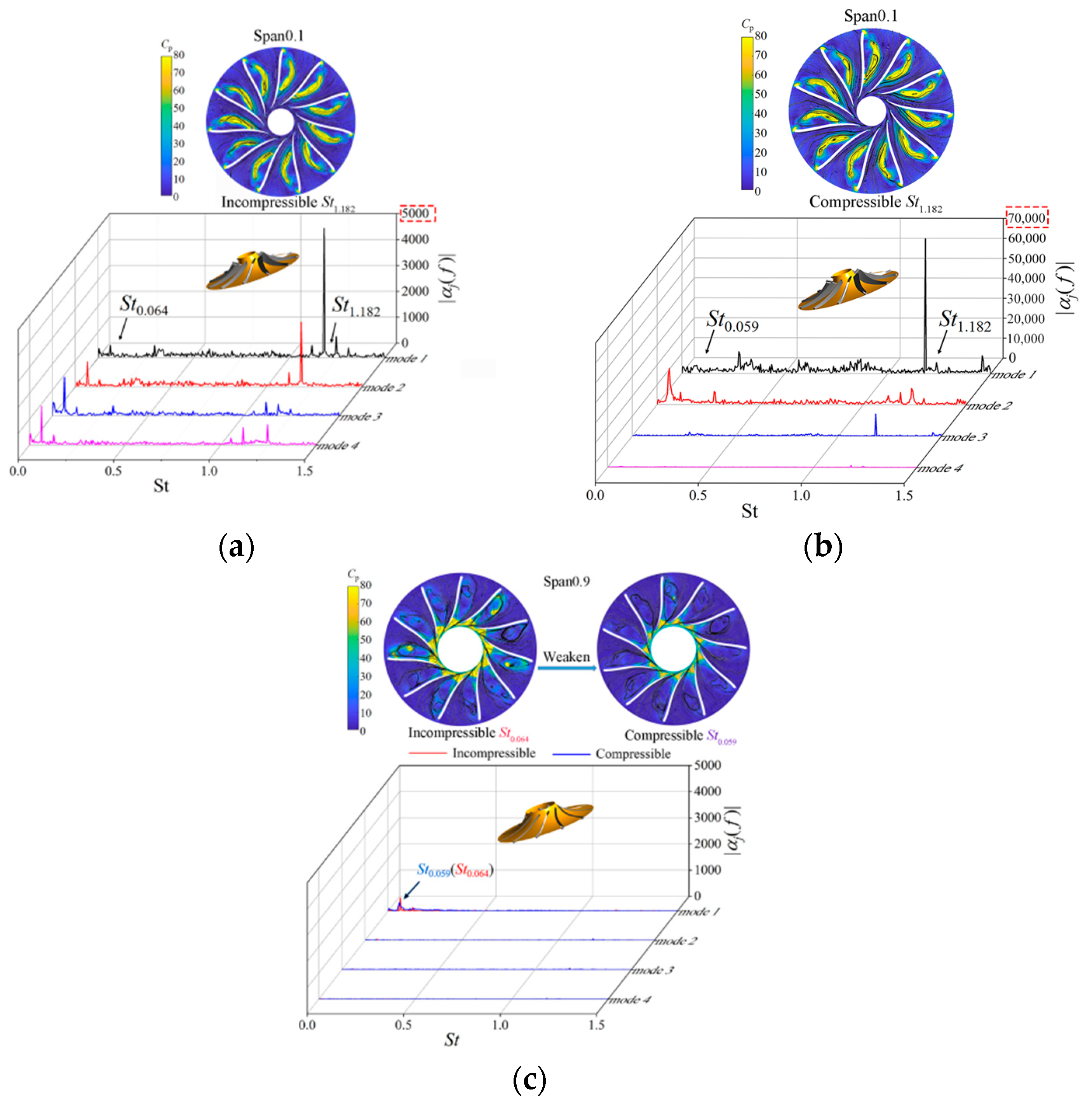
4.4. Analysis of Energy Distribution of Flow Field Based on POD
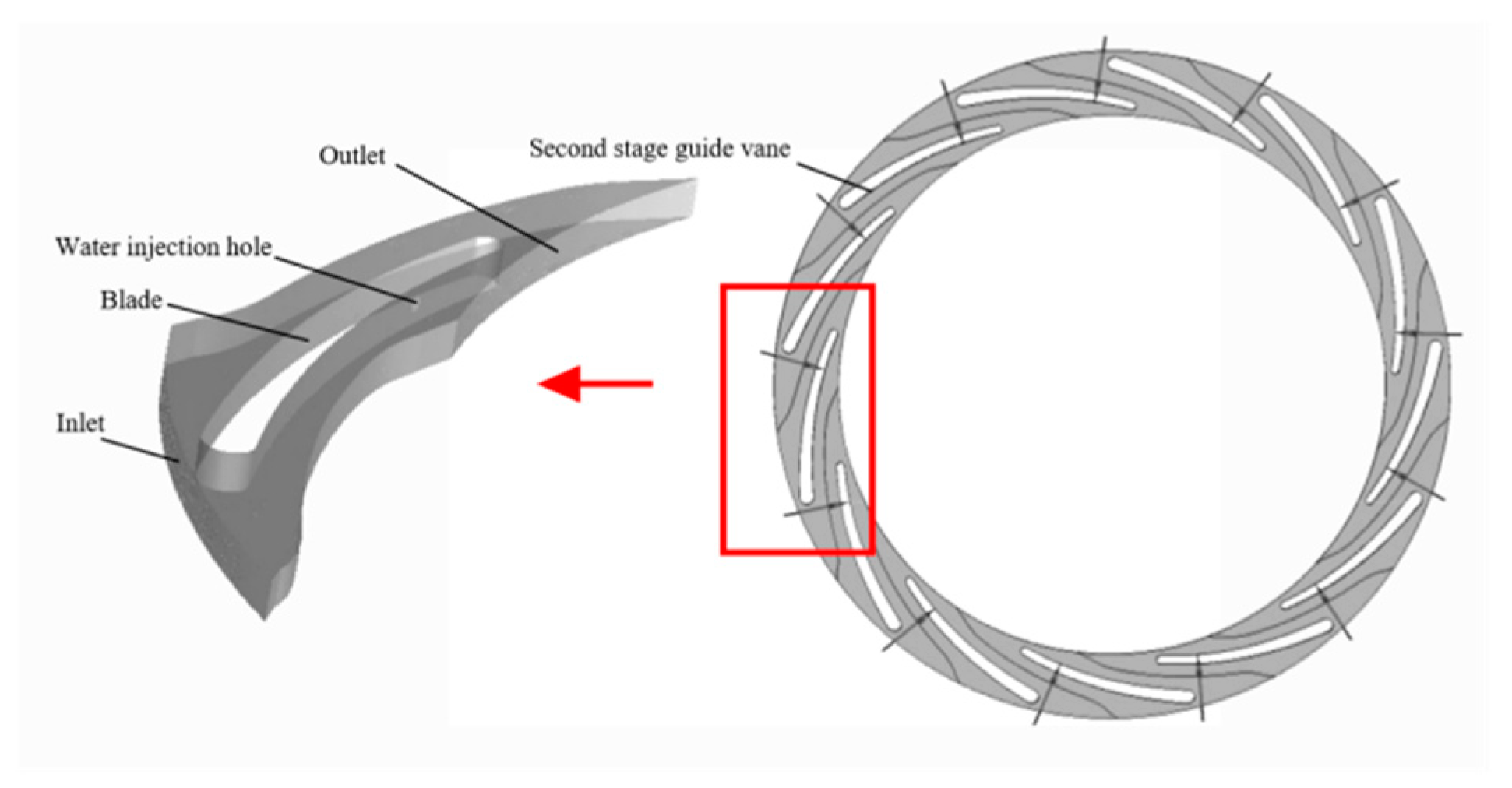
5. Optimization Scheme
6. Conclusions
- Based on the analysis of POD and two-dimensional frequency domain visualization and flow field distribution, it was found that the last stage impeller has two main flow structures, which were the areas with high risks of vaporization under this study condition. The corresponding characteristic frequencies were St0.064 and St1.182.
- The flow structure of St1.182 also had a high risk of forming an evaporation zone on the suction surface of the impeller near the hub. This flow structure was composed of a large reflux and some small eddies at the outer edge of the reflux. These small eddies were near the leading edge of the suction side of impeller blades and they were the largest energy contributor in the impeller. The impact of water compressibility on the internal flow structures was a significant factor that should not be ignored. The flow structures of St1.182 demonstrate amplified pressure fluctuations, while the other one exhibited reduced pressure fluctuations.
- The strategy of water injection in the upstream guide vane could mitigate the backflow arising from flow separation at the inlet leading edge of the secondary impeller to alleviate the vapor–liquid two-phase flow in this area. That means the analysis of space, frequency, and energy distribution had a good effect on the evaluation of unsteady flow structures in the flow field, which provided a direction for the establishment of the diagnosis and optimization framework of unsteady flow structures in rotating machinery.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Luo, H.; Wang, C. Progress and trends of global carbon neutrality pledges. Adv. Clim. Chang. Res. 2021, 17, 88–97. [Google Scholar]
- Peng, C.D. Contribute to the realization of the goal of “carbon peak and carbon neutrality” speed up the development of pumped storage power plants. Hydropower Pumped Storage 2021, 7, 4–6. [Google Scholar]
- Liu, X.; Pang, J.; Li, L.; Zhao, W.; Wang, Y.; Yan, D.; Zhou, L.; Wang, Z. Comparative Study on Numerical Calculation of Modal Characteristics of Pump-Turbine Shaft System. J. Mar. Sci. Eng. 2023, 11, 2068. [Google Scholar] [CrossRef]
- Nautiyal, H.; Varun; Kumar, A. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.; Wang, X.; Sun, Q.; Zhang, J. Overview of research on energy recovery hydraulic turbine. Fluid Mach. 2011, 39, 29–33. [Google Scholar]
- Varaksin, A.Y.; Ryzhkov, S.V. Vortex Flows with Particles and Droplets (A Review). Symmetry 2022, 14, 2016. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Liu, H.L.; Chen, J.; Lv, L.L.; Wang, X.L.; Zhang, G.X. Optimized Geometric Structure of a Rotational Hydrodynamic Cavitation Reactor. J. Appl. Fluid Mech. 2023, 16, 1218–1231. [Google Scholar]
- Yang, J.; Zhou, L.; Wang, Z. The numerical simulation of draft tube cavitation in Francis turbine at off-design conditions. Eng. Comput. 2016, 33, 139–155. [Google Scholar] [CrossRef]
- Escaler, X.; Ekanger, J.V.; Francke, H.H.; Kjeldsen, M.; Nielsen, T.K. Detection of Draft Tube Surge and Erosive Blade Cavitation in a Full-Scale Francis Turbine. J. Fluids Eng. 2015, 137, 1676–1685. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.; Wu, Y.; Jiao, L.; Wang, L.; Sun, Y. Numerical investigation of the hump characteristic of a pump–turbine based on an improved cavitation model. Comput. Fluids 2012, 68, 105–111. [Google Scholar] [CrossRef]
- Minakov, A.V.; Platonov, D.V.; Dekterev, A.A.; Sentyabov, A.V.; Zakharov, A.V. The analysis of unsteady flow structure and low frequency pressure pulsations in the high-head francis turbines. Int. J. Heat Fluid Flow 2015, 53, 183–194. [Google Scholar] [CrossRef]
- Xiao, Y.X.; Wang, Z.W.; Yan, Z.G.; Li, M.A.; Xiao, M.; Liu, D.Y. Numerical analysis of unsteady flow under high-head operating conditions in francis turbine. Eng. Comput. 2010, 27, 365–386. [Google Scholar]
- Liu, R.S.; Zhang, L.; Li, Y.M.; Wang, K. Analysis of Internal Flow Characteristics of Fuel Centrifugal Pump. Constr. Mach. Equip. 2023, 54, 88–96. [Google Scholar]
- Jafarzadeh Juposhti, H.; Maddahian, R.; Cervantes, M.J. Optimization of axial water injection to mitigate the Rotating Vortex Rope in a Francis turbine. Renew. Energy 2021, 175, 214–231. [Google Scholar] [CrossRef]
- Resiga, R.; Vu, T.; Muntean, S.; Ciocan, G.; Nennemann, B. Jet Control of the Draft Tube Vortex Rope in Francis Turbines at Partial Discharge. In Proceedings of the 23rd IAHR Symposium Conference, Gdansk, Poland, 12–14 September 2022; pp. 67–80. [Google Scholar]
- Muntean, S.; Resiga, R.; Bosioc, A. 3D Numerical Analysis of Unsteady Pressure Fluctuations in a Swirling Flow without and with Axial Water Jet Control. In Proceedings of the 14th International Conference on Fluid Flow Technologies (CMFF’09), Budapest, Hungary, 9–12 September 2009; Volume 2, pp. 510–518. [Google Scholar]
- Deniz, S.; von Burg, M.; Tiefenthaler, M. Investigation of the Flow Instabilities of a Low Specific Speed Pump Turbine Part 2: Flow Control with Fluid Injection. J. Fluids Eng. 2022, 144, 071210. [Google Scholar] [CrossRef]
- Deniz, S.; Del Rio, A.; von Burg, M.; Tiefenthaler, M. Investigation of the Flow Instabilities of a Low Specific Speed Pump Turbine Part 1: Experimental and Numerical Analysis. J. Fluids Eng. 2022, 144, 071209. [Google Scholar] [CrossRef]
- Lewis, B. Improving Unsteady Hydroturbine Performance during Off-Design Operation by Injecting Water from the Trailing Edge of the Wicket Gates; The Pennsylvania State University: State College, PA, USA, 2014. [Google Scholar]
- Khullar, S.; Singh, K.M.; Cervantes, M.J.; Gandhi, B.K. Numerical Analysis of Water Jet Injection in the Draft Tube of a Francis Turbine at Part Load Operations. J. Fluids Eng. 2022, 144, 111201. [Google Scholar] [CrossRef]
- Osman, F.K.; Zhang, J.; Lai, L.; Kwarteng, A.A. Effects of Turbulence Models on Flow Characteristics of a Vertical Fire Pump. J. Appl. Fluid Mech. 2022, 15, 1661–1674. [Google Scholar]
- Chen, J.; Zheng, Y.; Zhang, L.; Chen, X.; Liu, D.; Xiao, Z. Influence Analysis of Runner Inlet Diameter of Hydraulic Turbine in Turbine Mode with Ultra-Low Specific Speed. Energies 2023, 16, 7086. [Google Scholar] [CrossRef]
- Lai, H.; Wang, H.; Zhou, Z.; Zhu, R.; Long, Y. Research on Cavitation Performance of Bidirectional Integrated Pump Gate. Energies 2023, 16, 6784. [Google Scholar] [CrossRef]
- Song, Y.; Fan, H.; Huang, Z. Study on radial force characteristics of double-suction centrifugal pumps with different impeller arrangements under cavitation condition. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 421–431. [Google Scholar] [CrossRef]
- Fu, Y.; Xie, J.; Shen, Y.; Pace, G.; Valentini, D.; Pasini, A.; D’Agostino, L. Experimental and numerical study on cavitation performances of a turbopump with and without an inducer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 1098–1111. [Google Scholar] [CrossRef]
- Yuan, J.; Hou, J.; Fu, Y.; Hu, J.; Zhang, H.; Shen, C. A study on the unsteady characteristics of the backflow vortex cavitation in a centrifugal pump. Shock. Vib. 2018, 37, 24–30. [Google Scholar]
- Sun, H.; Yuan, S.; Luo, Y. Characterization of cavitation and seal damage during pump operation by vibration and motor current signal spectra. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 132–147. [Google Scholar] [CrossRef]
- Geng, L.; Escaler, X. Assessment of RANS turbulence models and Zwart cavitation model empirical coefficients for the simulation of unsteady cloud cavitation. Eng. Appl. Comput. Fluid Mech. 2020, 14, 151–167. [Google Scholar] [CrossRef]
- Kozubková, M.; Rautová, J.; Bojko, M. Mathematical Model of Cavitation and Modelling of Fluid Flow in Cone. Procedia Eng. 2012, 39, 9–18. [Google Scholar] [CrossRef]
- Li, D.Y.; Han, L.; Wang, H.J.; Gong, R.Z.; Wei, X.Z.; Qin, D.Q. Pressure fluctuation prediction in pump mode using large eddy simulation and unsteady Reynolds-averaged Navier-Stokes in a pump-turbine. Adv. Mech. Eng. 2016, 8, 965–974. [Google Scholar] [CrossRef]
- Yang, J.; Pavesi, G.; Liu, X.; Xie, T.; Liu, J. Unsteady Flow Characteristics Regarding Hump Instability in the First Stage of a Multistage Pump-Turbine in Pump Mode. Renew. Energy 2018, 127, 377–385. [Google Scholar] [CrossRef]
- He, J.; An, Q.; Jin, J.; Feng, S.; Zhang, K. Experimental Study and Simulation of Cavitation Shedding in Diesel Engine Nozzle using Proper Orthogonal Decomposition and Large Eddy Simulation. J. Therm. Sci. 2023, 32, 1487–1500. [Google Scholar] [CrossRef]
- Lin, D.; Su, X.; Yuan, X. The Development and Mechanisms of the High Pressure Turbine Vane Wake Vortex. J. Eng. Gas Turbines Power Trans. ASME 2018, 140, 092601. [Google Scholar] [CrossRef]
- Liao, Z.Y.; Yang, J.; Liu, X.H.; Hu, W.L.; Deng, X.R. Analysis of Unsteady Flow Structures in a Centrifugal Impeller Using Proper Orthogonal Decomposition. J. Appl. Fluid Mech. 2020, 14, 89–101. [Google Scholar]
- Yang, J.; Xie, T.; Liu, X.; Si, Q.; Liu, J. Study of Unforced Unsteadiness in Centrifugal Pump at Partial Flow Rates. J. Therm. Sci. 2019, 30, 88–99. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Liu, X.; Xie, T. Numerical Study of Pressure Pulsation of Centrifugal Pumps with the Compressible Mode. J. Therm. Sci. 2019, 28, 106–114. [Google Scholar] [CrossRef]
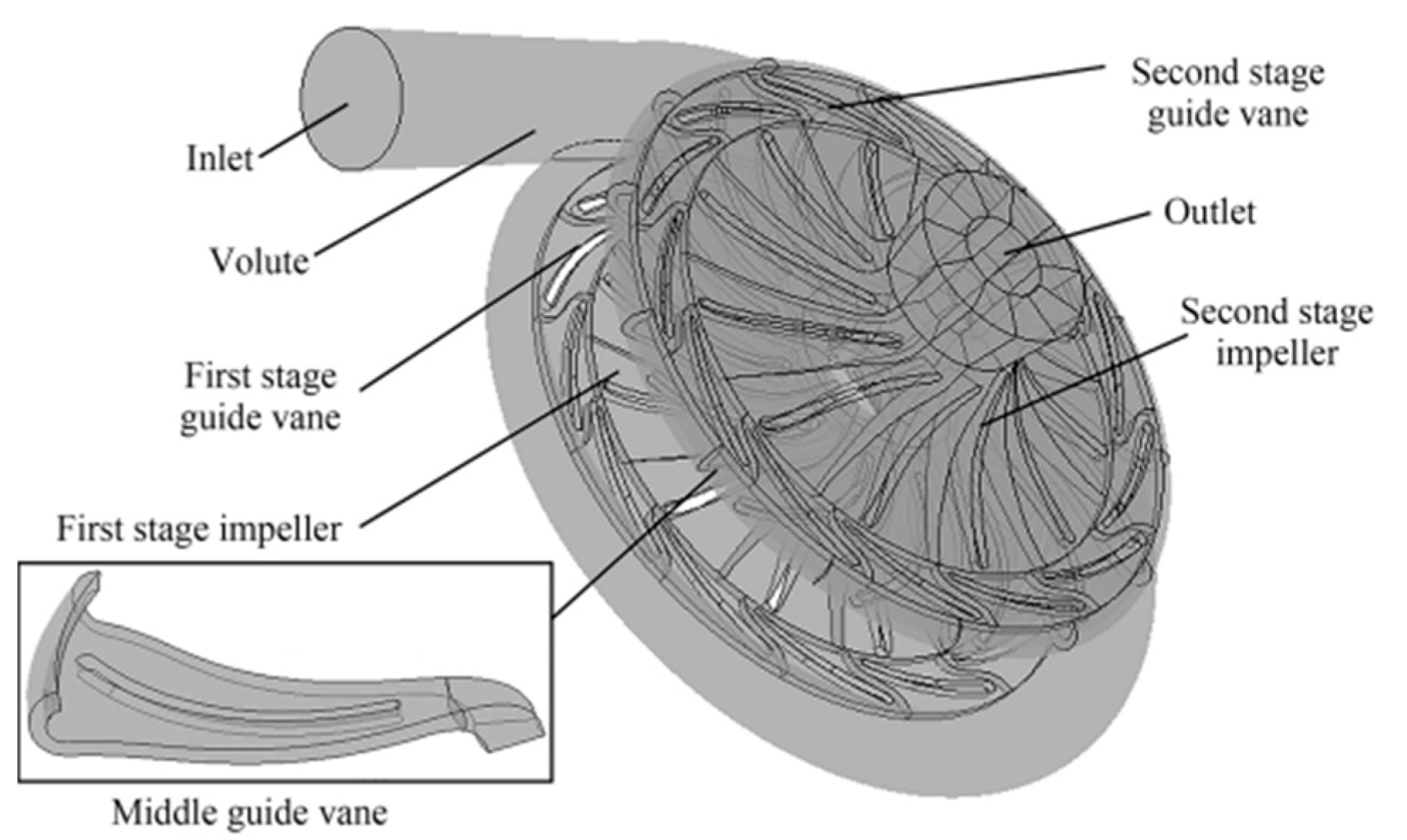
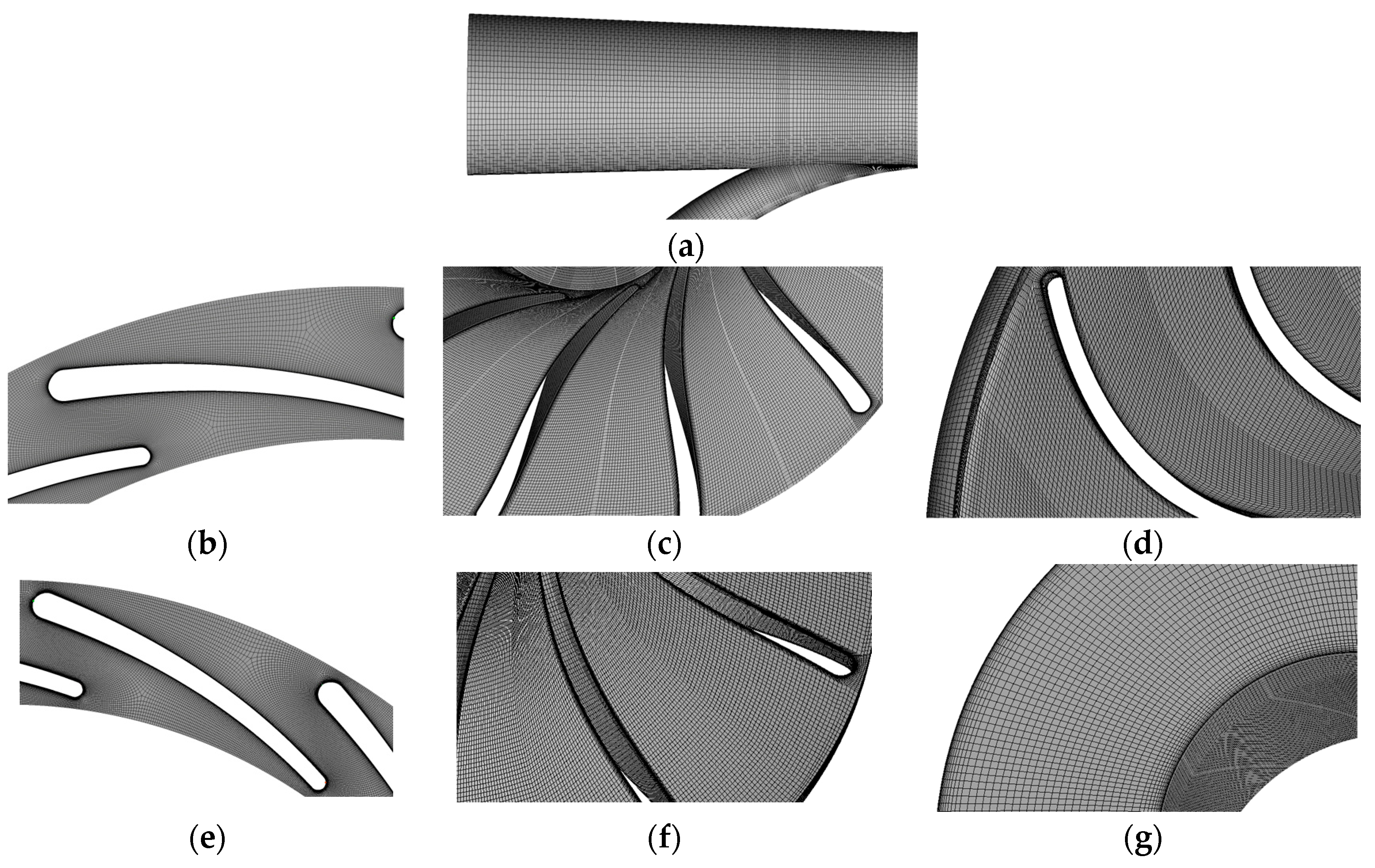
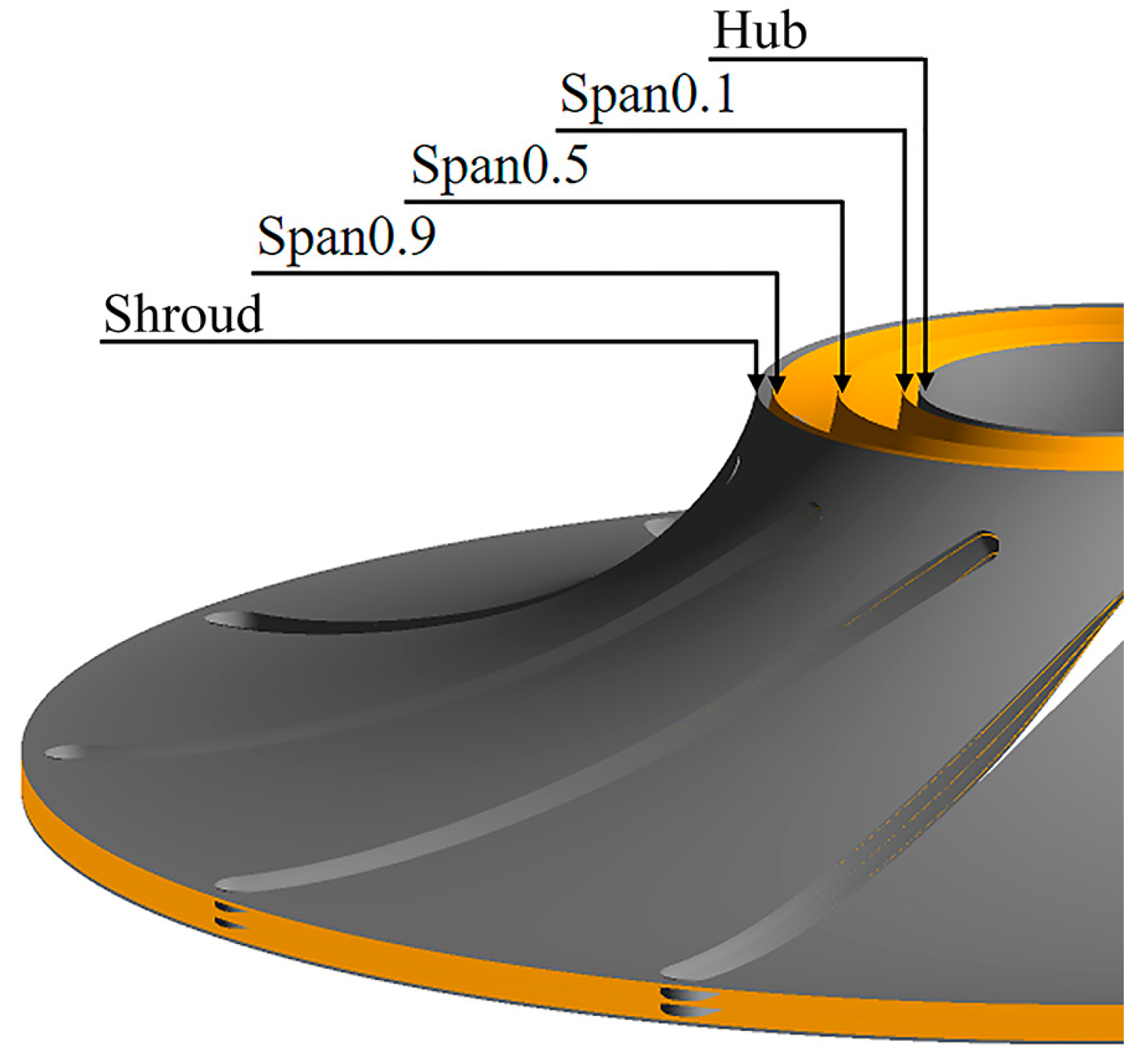
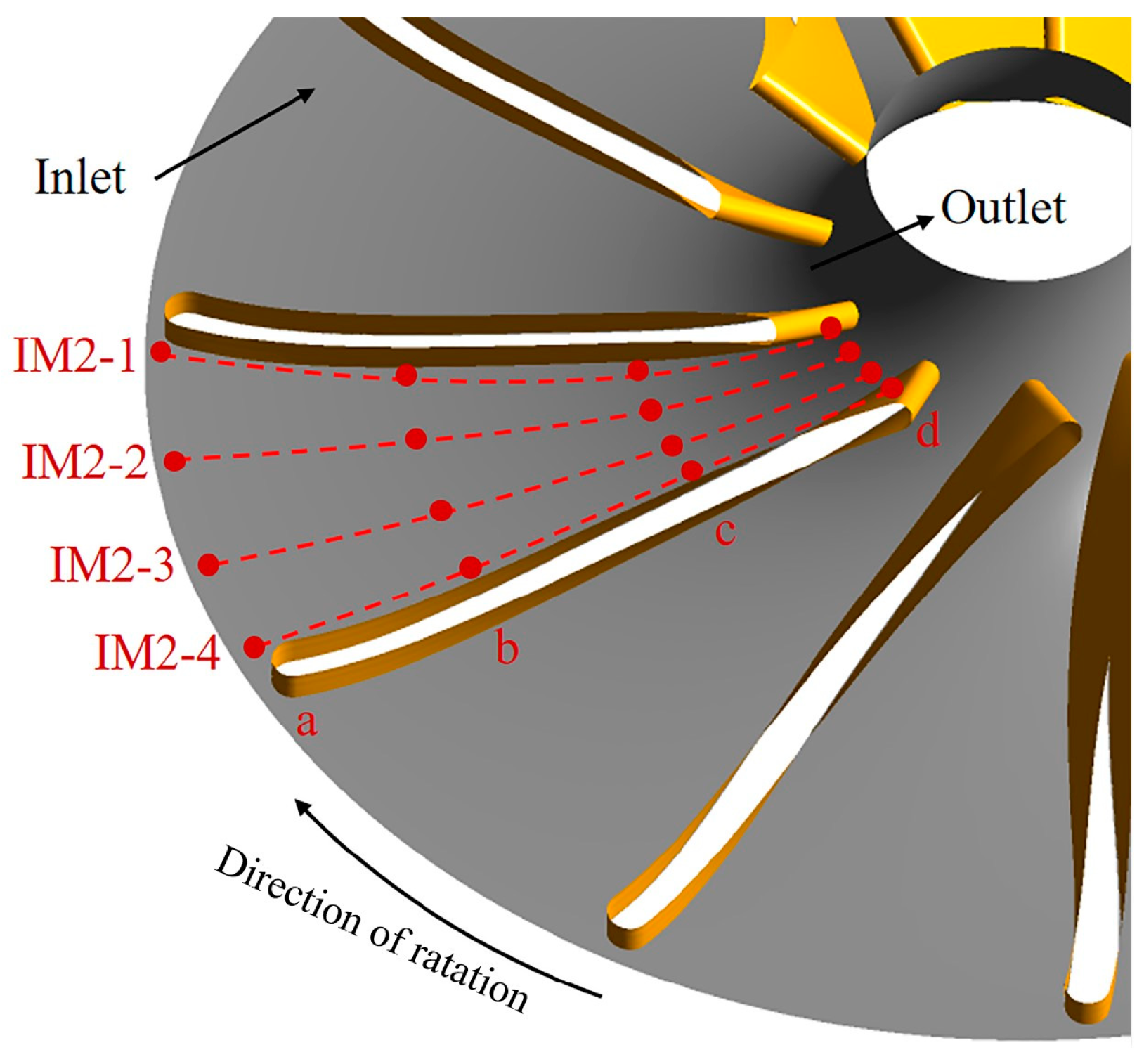
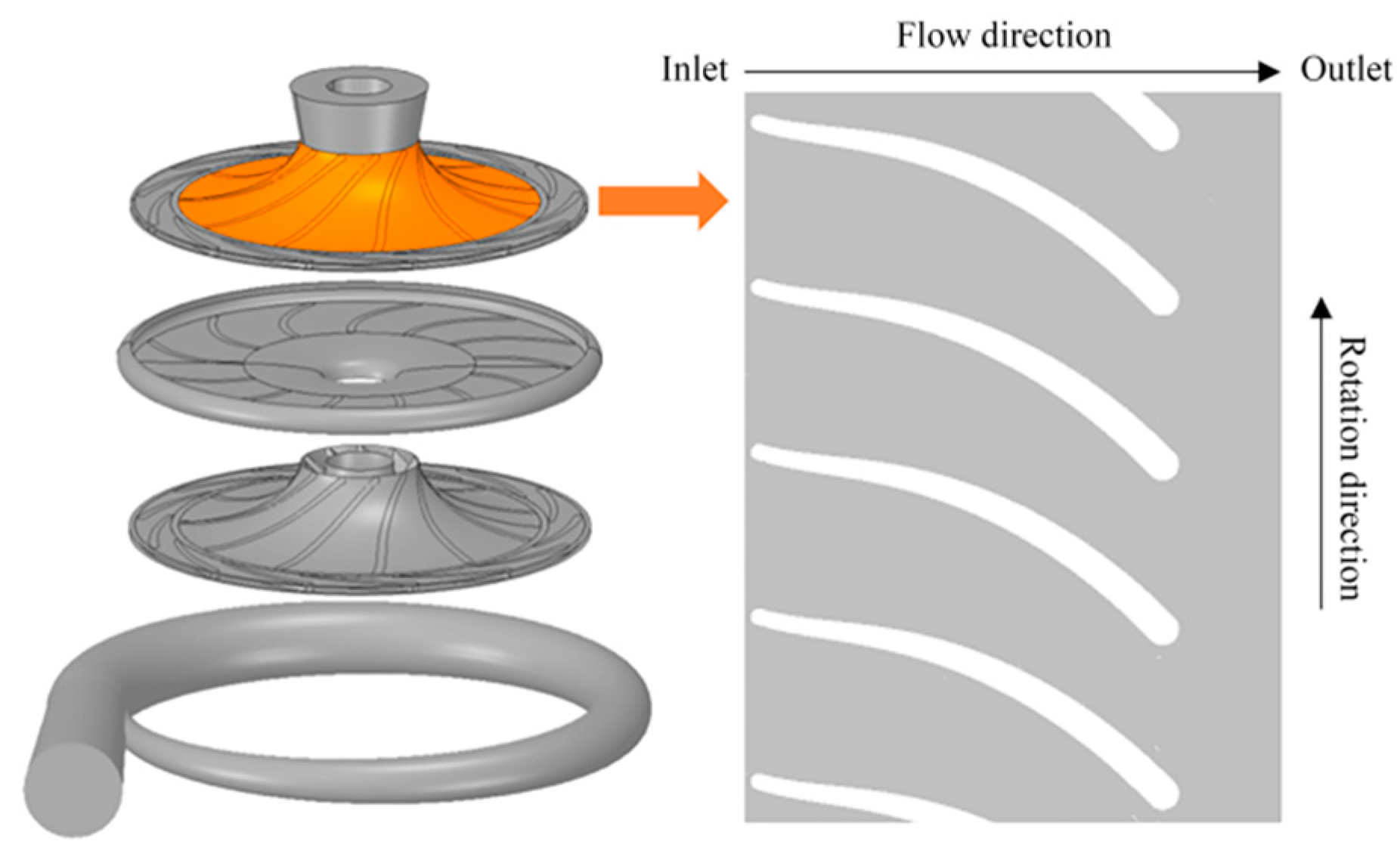





| Part | Parameters | Data |
|---|---|---|
| Impeller | Impeller outlet diameter D1/mm | 60.00 |
| Impeller inlet diameter D2/mm | 182.00 | |
| Impeller hub diameter Dh/mm | 32.50 | |
| Shroud blade wrap angle φf/(°) | 44.50 | |
| Hub blade wrap angle φr/(°) | 36.80 | |
| Shroud blade exit angle β1f/(°) | 35.00 | |
| Hub blade exit angle β1r/(°) | 51.00 | |
| Number of blades z | 11 | |
| Volute | Base circle diameter of volute D3/mm | 232.00 |
| Inlet tube length of volute L1/mm | 120.00 | |
| Inlet diameter of volute D4/mm | 50.00 |
| Flow-Passing Parts | Grid 1 | Grid 2 | Grid 3 | Grid 4 | |
|---|---|---|---|---|---|
| Volute | 0.37 × 106 | 0.47 × 106 | 0.70 × 106 | 1.11 × 106 | |
| First-stage guide vane | 0.34 × 106 | 0.46 × 106 | 0.83 × 106 | 1.21 × 106 | |
| First-stage impeller | 1.09 × 106 | 1.82 × 106 | 2.65 × 106 | 3.10 × 106 | |
| Middle guide vane | 0.73 × 106 | 1.10 × 106 | 1.75× 106 | 2.23 × 106 | |
| Second-stage guide vane | 0.54 × 106 | 0.80 × 106 | 1.04 × 106 | 1.50 × 106 | |
| Second-stage impeller | 1.34 × 106 | 2.09 × 106 | 2.90 × 106 | 3.31 × 106 | |
| Outlet chamber | 0.32 × 106 | 0.64 × 106 | 0.93 × 106 | 1.38 × 106 | |
| Total grid | 4.75 × 106 | 7.38 × 106 | 10.8 × 106 | 13.8 × 106 | |
| Result | η | 75.2% | 76.4% | 78.9% | 79.2% |
| H (m) | 272.57 | 272.50 | 293.92 | 296.37 | |
| (H-Hd)(Hd)−1 | 10.9% | 10.9% | 3.9% | 3.1% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Peng, T.; Xu, G.; Hu, W.; Zhong, H.; Liu, X. A Study and Optimization of the Unsteady Flow Characteristics in the Last Stage Impeller of a Small-Scale Multi-Stage Hydraulic Turbine. Energies 2024, 17, 107. https://doi.org/10.3390/en17010107
Yang J, Peng T, Xu G, Hu W, Zhong H, Liu X. A Study and Optimization of the Unsteady Flow Characteristics in the Last Stage Impeller of a Small-Scale Multi-Stage Hydraulic Turbine. Energies. 2024; 17(1):107. https://doi.org/10.3390/en17010107
Chicago/Turabian StyleYang, Jun, Tao Peng, Gang Xu, Wenli Hu, Huazhou Zhong, and Xiaohua Liu. 2024. "A Study and Optimization of the Unsteady Flow Characteristics in the Last Stage Impeller of a Small-Scale Multi-Stage Hydraulic Turbine" Energies 17, no. 1: 107. https://doi.org/10.3390/en17010107
APA StyleYang, J., Peng, T., Xu, G., Hu, W., Zhong, H., & Liu, X. (2024). A Study and Optimization of the Unsteady Flow Characteristics in the Last Stage Impeller of a Small-Scale Multi-Stage Hydraulic Turbine. Energies, 17(1), 107. https://doi.org/10.3390/en17010107







