A Parametric Physics-Informed Deep Learning Method for Probabilistic Design of Thermal Protection Systems
Abstract
1. Introduction
2. Methods
2.1. Thermal Protection System
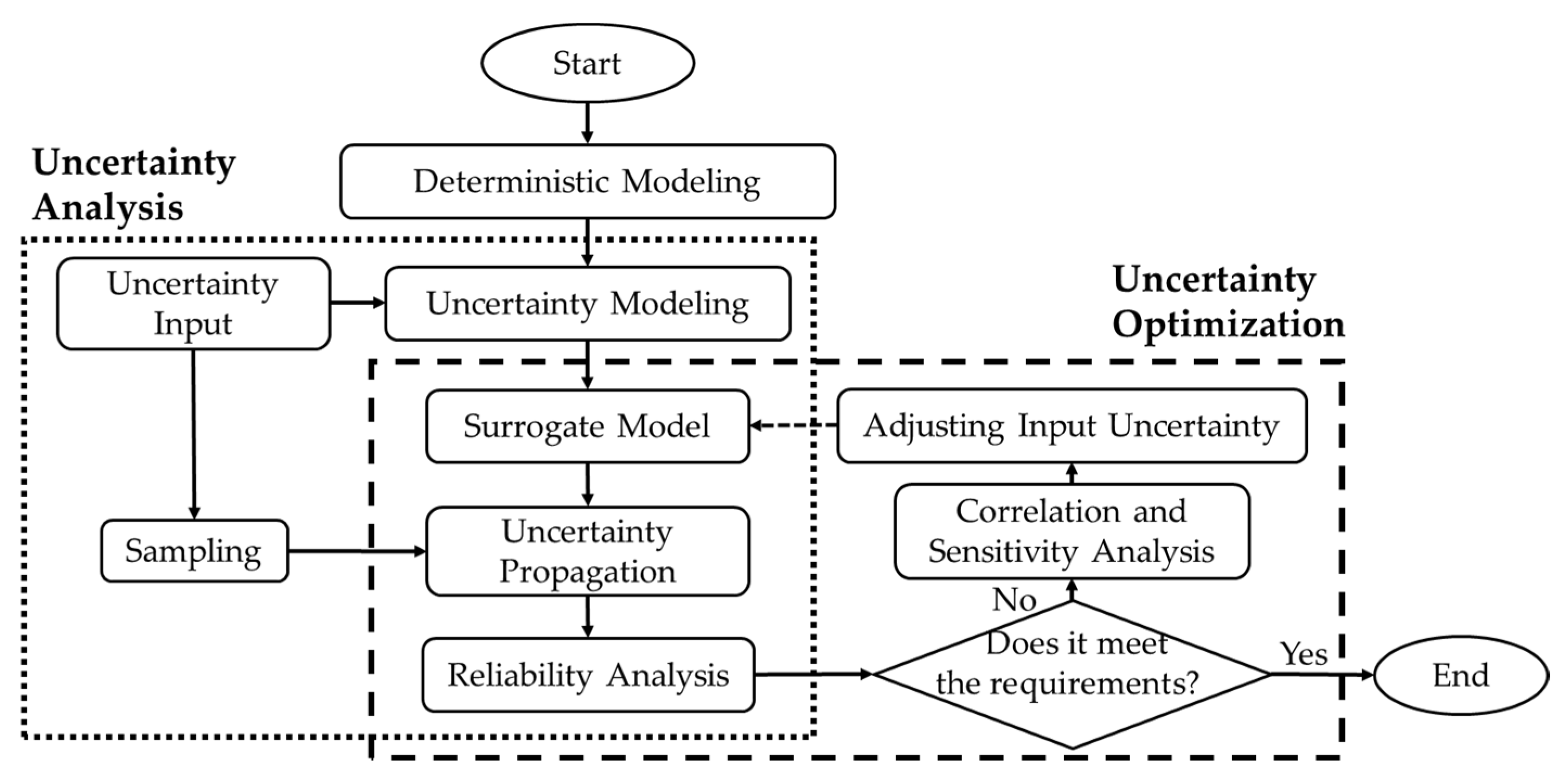
2.2. Uncertainty Design Process
- (1)
- Deterministic modeling: Firstly, traditional deterministic modeling is performed on the system. This involves mathematically abstracting and describing the TPS-related problems to simulate the real physical system, and analyzing each variable in the system as a deterministic constant.
- (2)
- Uncertainty input and uncertainty modeling: Based on this, the uncertain parameters that need to be considered are preliminarily determined according to the real environment and configuration requirements of the TPS, such as material properties, heat flux density, geometric shape, etc. These parameters are considered uncertain inputs, and each input’s probability distributions and range intervals are determined based on practical working experience and input into the model for uncertainty modeling.
- (3)
- Surrogate model: as the computational cost of high-precision models is significant, a surrogate model is constructed to approximate the original high-precision model.
- (4)
- Sampling and uncertainty propagation: Once the surrogate model is trained, it can quickly provide corresponding output results for a new input. Therefore, a large number of system response values can be obtained by drawing a large number of random samples for uncertain inputs and using surrogate models for fast calculations. This method is known as the Monte Carlo method. The Monte Carlo method can be used to propagate uncertainty in input variables through surrogate models.
- (5)
- Reliability analysis: based on this, the uncertainty of the system is analyzed, such as by quantitatively analyzing the distribution characteristics of system performance under uncertainty impact and calculating the reliability of the design scheme.
- (6)
- Correlation and sensitivity analysis and adjusting input uncertainty: The system is optimized based on the analysis results. If the reliability meets the requirements, the design process ends. Otherwise, the correlation and sensitivity analysis of the uncertain parameters in the previous inputs are performed. The parameters with low correlation can be removed from the uncertain inputs to reduce the complexity of surrogate model training. At the same time, the parameters with high sensitivity are adjusted and optimized, such as by reducing the uncertainty level of relevant parameters through process improvement methods.
- (7)
- Uncertainty optimization: finally, the adjusted model is trained again, and the above steps are repeated until the system meets the design requirements.
2.3. Surrogate Model
2.3.1. Response Surface Methodology
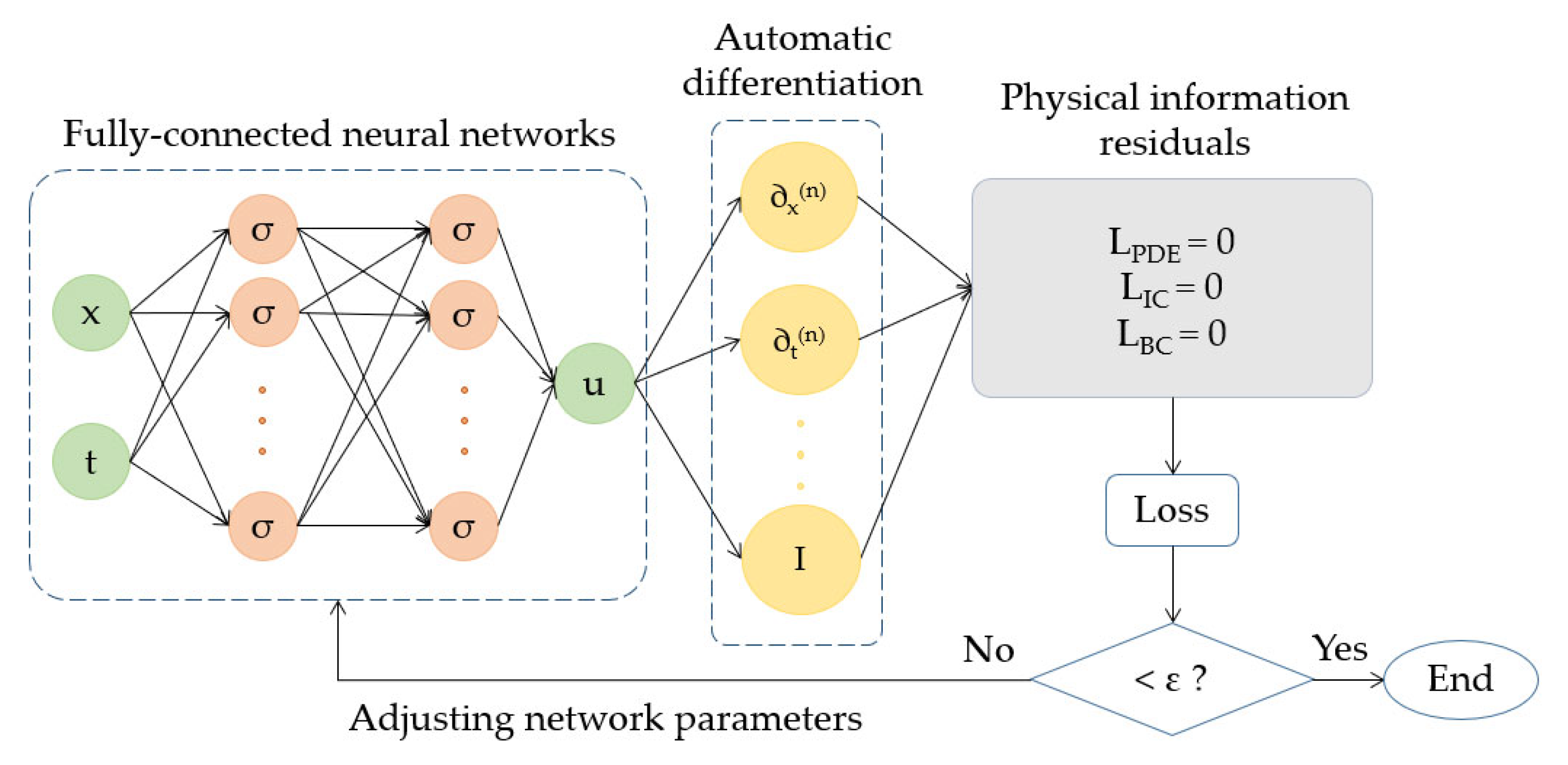
2.3.2. Physics-Informed Neural Networks
2.3.3. Parametric Physics-Informed Neural Networks
2.4. Reliability Analysis
2.5. Correlation and Sensitivity Analysis
3. Results
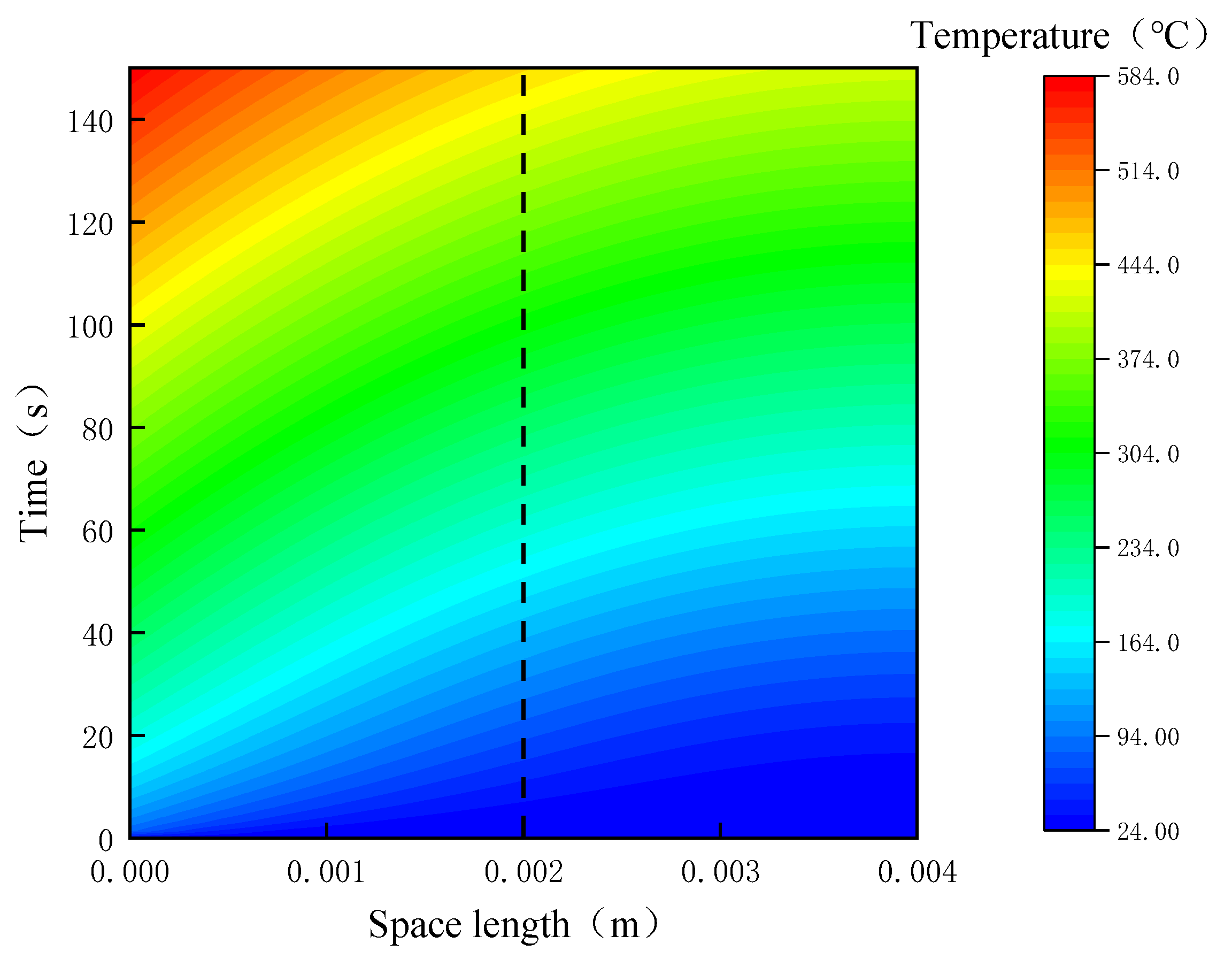
3.1. Deterministic PINN Surrogate Model
3.2. Uncertain PINN Surrogate Model
3.2.1. Parametric PINN Surrogate Model
3.2.2. Uncertainty Propagation
3.2.3. Reliability Analysis
3.2.4. Correlation and Sensitivity Analysis
3.3. PINN vs. Response Surface
3.3.1. Extrapolation Validation
3.3.2. Computational Efficiency
4. Conclusions
- In this study, the heat conduction equation of the TPS is used as an example, and the results show good agreement between the prediction results of the PINN surrogate model and those of numerical simulation, with a relative error of only 0.35 percent.
- In terms of uncertainty propagation, the parametric PINN and response surface surrogate models effectively predict the results. However, parametric PINN is superior in extrapolation due to the constraint of physical information.
- The PINN surrogate model is also more advantageous regarding computational efficiency, with a computation time of only 1/30 of that of the response surface surrogate model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nakamura, T.; Fujii, K. Probabilistic transient thermal analysis of an atmospheric reentry vehicle structure. Aerosp. Sci. Technol. 2006, 10, 346–354. [Google Scholar] [CrossRef]
- Katsikas, C.; Castle, G.; Higgins, J. Ablation Handbook Entry Materials Data and Design; Air Force Materials Laboratory, Research and Technology Division, Air Force: Arlington, VA, USA, 1966. [Google Scholar]
- Dong, Y.; Wang, E.; You, Y.; Yin, C.; Wu, Z. Thermal Protection System and Thermal Management for Combined-Cycle Engine: Review and Prospects. Energies 2019, 12, 240. [Google Scholar] [CrossRef]
- Howell, J.R. Monte Carlo treatment of data uncertainties in thermal analysis. J. Spacecr. Rocket. 1973, 10, 411–414. [Google Scholar] [CrossRef]
- Dec, J.; Mitcheltree, R. Probabilistic design of a Mars Sample Return Earth entry vehicle thermal protection system. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 910. [Google Scholar]
- Woo, M.-A.; Moon, Y.-H.; Song, W.-J.; Kang, B.-S.; Kim, J. Acquisition of Dynamic Material Properties in the Electrohydraulic Forming Process Using Artificial Neural Network. Materials 2019, 12, 3544. [Google Scholar] [CrossRef] [PubMed]
- Cunha, B.Z.; Zine, A.-M.; Ichchou, M.; Droz, C.; Foulard, S. On Machine-Learning-Driven Surrogates for Sound Transmission Loss Simulations. Appl. Sci. 2022, 12, 10727. [Google Scholar] [CrossRef]
- Sun, Y.; Elhanashi, A.; Ma, H.; Chiarelli, M.R. Heat Conduction Plate Layout Optimization Using Physics-Driven Convolutional Neural Networks. Appl. Sci. 2022, 12, 10986. [Google Scholar] [CrossRef]
- Lyathakula, K.R.; Yuan, F.-G. A probabilistic fatigue life prediction for adhesively bonded joints via ANNs-based hybrid model. Int. J. Fatigue 2021, 151, 106352. [Google Scholar] [CrossRef]
- Alqahtani, A.; He, X.; Yan, B.; Hoteit, H. Uncertainty Analysis of CO2 Storage in Deep Saline Aquifers Using Machine Learning and Bayesian Optimization. Energies 2023, 16, 1684. [Google Scholar] [CrossRef]
- Ravishankar, B.; Haftka, R.; Sankar, B. Uncertainty analysis of integrated thermal protection system with rigid insulation bars. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 19th AIAA/ASME/AHS Adaptive Structures Conference 13t, Denver, CO, USA, 4–7 April 2011; p. 1767. [Google Scholar]
- Tao, Z.; Guo, Z.; Song, L.; Li, J. Uncertainty quantification of aero-thermal performance of a blade endwall considering slot geometry deviation and mainstream fluctuation. J. Turbomach. 2021, 143, 111013. [Google Scholar] [CrossRef]
- Wang, C.; Matthies, H.G. Evidence theory-based reliability optimization design using polynomial chaos expansion. Comput. Methods Appl. Mech. Eng. 2018, 341, 640–657. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, S.; Hui, W.; Li, Y.; Xie, Z. Thermo-mechanical optimization of metallic thermal protection system under aerodynamic heating. Struct. Multidiscip. Optim. 2020, 61, 819–836. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks for heat transfer problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Yu, B. The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems. Commun. Math. Stat. 2018, 6, 1–12. [Google Scholar]
- Lu, L.; Jin, P.; Karniadakis, G.E. Deeponet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators. arXiv 2019, arXiv:1910.03193. [Google Scholar]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Chu, W.X.; Lien, Y.H.; Huang, K.R.; Wang, C.C. Energy saving of fans in air-cooled server via deep reinforcement learning algorithm. Energy Rep. 2021, 7, 3437–3448. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.-X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Gao, H.; Sun, L.; Wang, J.-X. PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. J. Comput. Phys. 2021, 428, 110079. [Google Scholar] [CrossRef]
- Marley, C.D.; Driscoll, J.F. Modeling an active and passive thermal protection system for a hypersonic vehicle. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0118. [Google Scholar]
- Holman, J.P. Heat Transfer; McGraw Hill Higher Education: New York, NY, USA, 2010. [Google Scholar]
- Wright, M.J. NASA Uncertainties Management in the TPS Design Process. In Proceedings of the 4TH AF/SNL/NASA Ablation Workshop, Albuquerque, NM, USA, 1–3 March 2011. [Google Scholar]
- Sun, J.; Zhang, G.; Vlahopoulos, N.; Hong, S.-B. Multi-disciplinary design optimization under uncertainty for thermal protection system applications. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; p. 7002. [Google Scholar]
- Vlahopoulos, N.; He, J. Designing the Thermal Protection System of an Apollo Type Vehicle under Uncertainty; 0148-7191; SAE Technical Paper: Warrendale, PA, USA, 2009. [Google Scholar]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]
- Hornik, K.; Stinchcombe, M.; White, H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Netw. 1990, 3, 551–560. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Marchine Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Paté-Cornell, M.-E.; Fischbeck, P.S. Risk management for the tiles of the space shuttle. Interfaces 1994, 24, 64–86. [Google Scholar] [CrossRef]
- Tortorelli, D.A.; Michaleris, P. Design sensitivity analysis: Overview and review. Inverse Probl. Eng. 1994, 1, 71–105. [Google Scholar] [CrossRef]
- Brune, A.J.; West, T.K.; Hosder, S. Uncertainty quantification of planetary entry technologies. Prog. Aeosp. Sci. 2019, 111, 17. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]












| Input Parameter | Symbol | Value | Unit |
|---|---|---|---|
| thermal conductivity | k | 0.12 | W·m−1·K−1 |
| density | ρ | 560 | kg·m−3 |
| specific heat capacity | c | 1510 | J·kg−1·°C−1 |
| Input Parameter | Symbol | Unit | Mean | Standard Deviation | Upper Bound | Lower Bound |
|---|---|---|---|---|---|---|
| thermal conductivity | k | W·m−1·K−1 | 0.12 | 0.003 | 0.13 | 0.10 |
| density | ρ | kg·m−3 | 560 | 14 | 602 | 518 |
| specific heat capacity | c | J·kg−1·°C −1 | 1510 | 38 | 1624 | 1396 |
| Thermal Conductivity | Density | Specific Heat Capacity | Finite Element Method | Response Surface Surrogate Model | Parametric PINN Surrogate Model |
|---|---|---|---|---|---|
| 0.119370 | 539.645 | 1528.84 | 421.728 | 421.912 | 424.996 |
| 0.116521 | 558.481 | 1513.49 | 409.513 | 409.433 | 412.654 |
| 0.120067 | 563.618 | 1515.11 | 406.717 | 406.515 | 409.758 |
| 0.122154 | 584.524 | 1546.61 | 383.424 | 383.177 | 386.121 |
| 0.117357 | 542.746 | 1523.59 | 419.727 | 419.806 | 422.894 |
| Method | Mean | Standard Deviation |
|---|---|---|
| parametric PINN | 414.94 | 15.94 |
| response surface | 411.51 | 15.67 |
| Method | Thermal Conductivity | Density | Specific Heat Capacity |
|---|---|---|---|
| parametric PINN | 0.101 | −0.697 | −0.709 |
| response surface | 0.077 | −0.694 | −0.695 |
| Thermal Conductivity | Density | Specific Heat Capacity | |
|---|---|---|---|
| temperature | 0.0672 | 0.4702 | 0.4626 |
| Method | Time |
|---|---|
| parametric PINN | 18.48 min |
| response surface | 597.24 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Xu, N.; Zhang, K.; Wang, L.; Lu, G. A Parametric Physics-Informed Deep Learning Method for Probabilistic Design of Thermal Protection Systems. Energies 2023, 16, 3820. https://doi.org/10.3390/en16093820
Zhang R, Xu N, Zhang K, Wang L, Lu G. A Parametric Physics-Informed Deep Learning Method for Probabilistic Design of Thermal Protection Systems. Energies. 2023; 16(9):3820. https://doi.org/10.3390/en16093820
Chicago/Turabian StyleZhang, Runlin, Nuo Xu, Kai Zhang, Lei Wang, and Gui Lu. 2023. "A Parametric Physics-Informed Deep Learning Method for Probabilistic Design of Thermal Protection Systems" Energies 16, no. 9: 3820. https://doi.org/10.3390/en16093820
APA StyleZhang, R., Xu, N., Zhang, K., Wang, L., & Lu, G. (2023). A Parametric Physics-Informed Deep Learning Method for Probabilistic Design of Thermal Protection Systems. Energies, 16(9), 3820. https://doi.org/10.3390/en16093820





