Generation of Synthetic CPTs with Access to Limited Geotechnical Data for Offshore Sites
Abstract
1. Introduction
2. Study Area and Data Sets
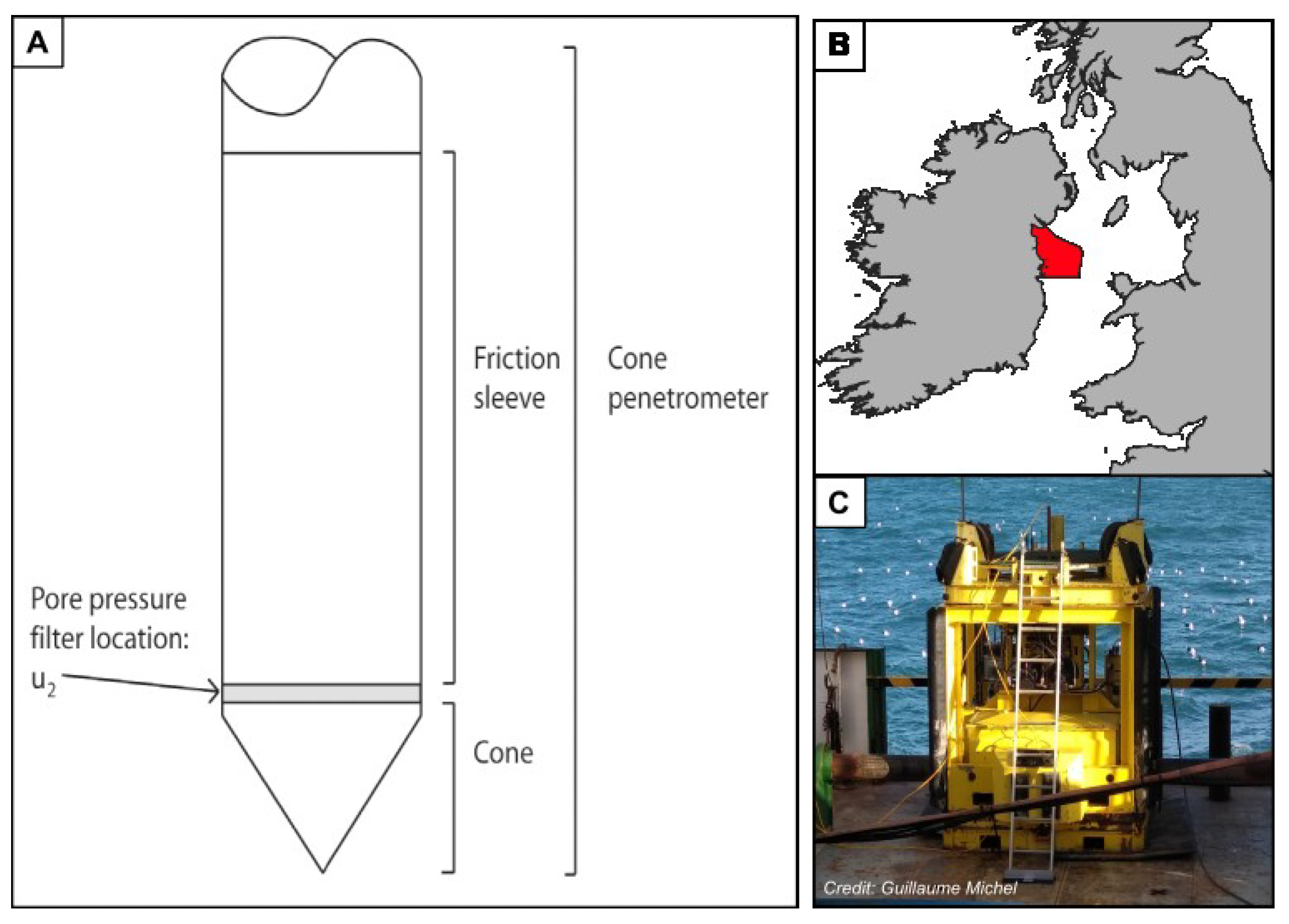
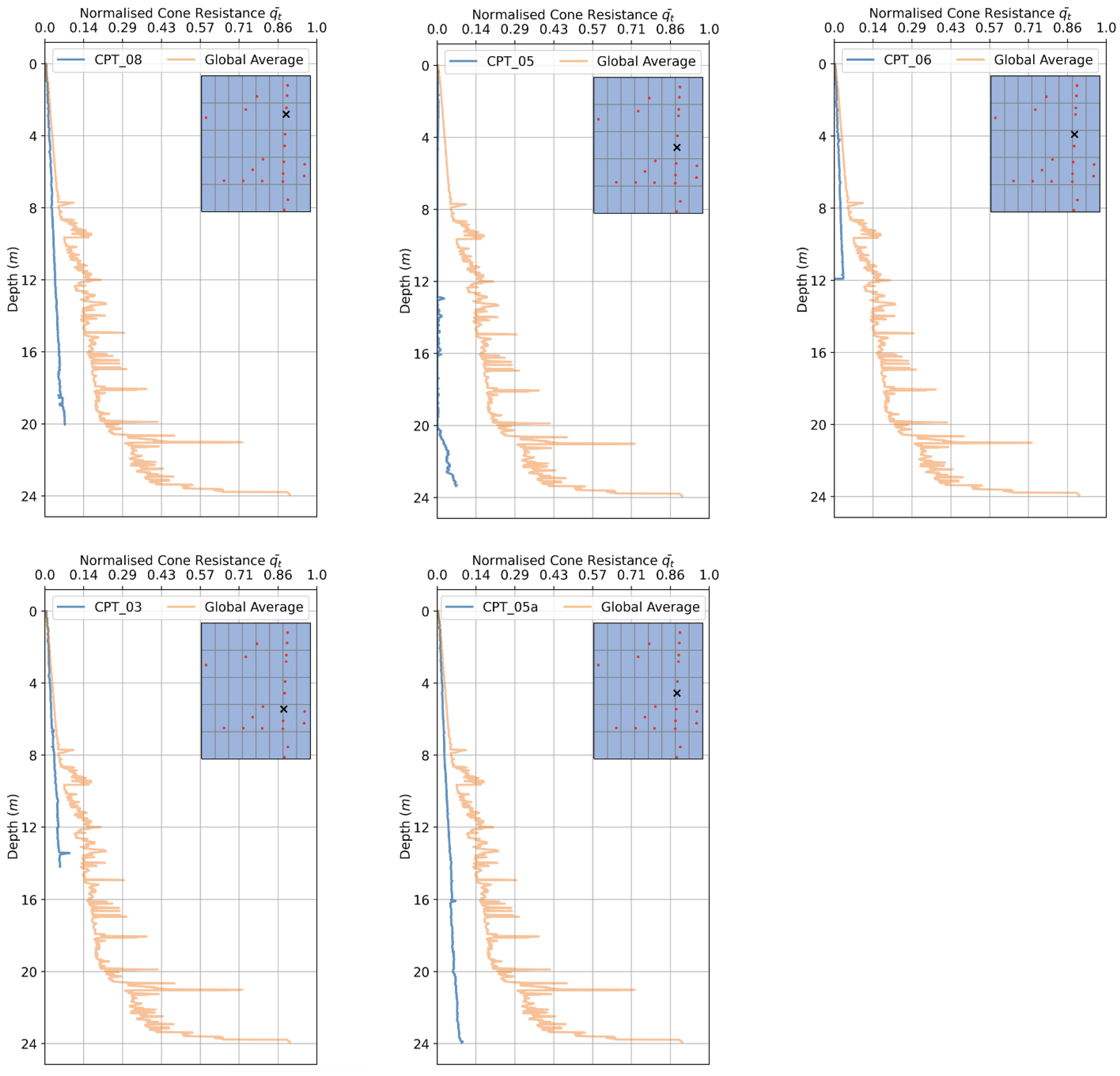
2.1. Cone Penetration Testing (CPT)
2.2. Site Description
3. Methodology
3.1. Inputs
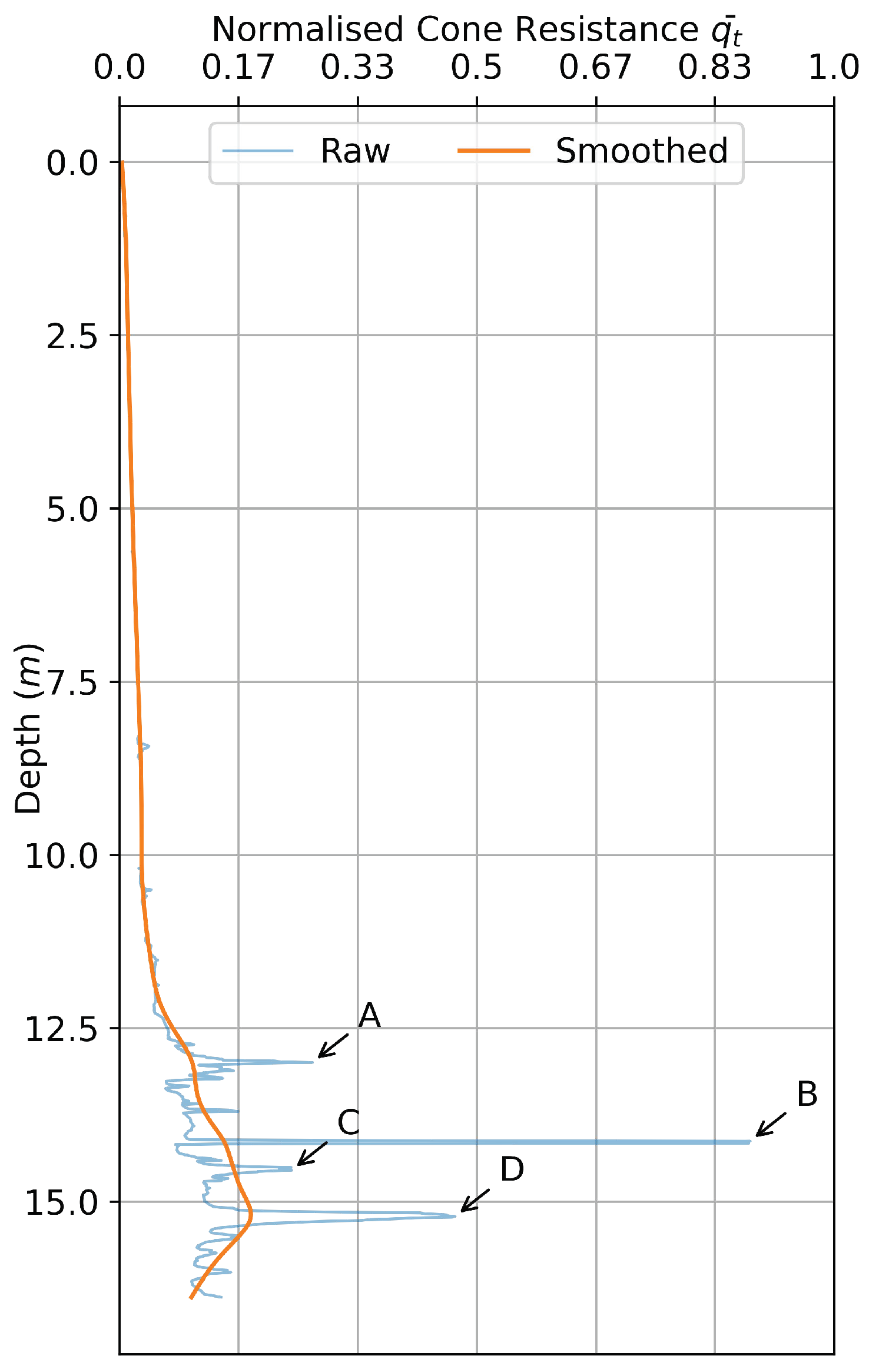
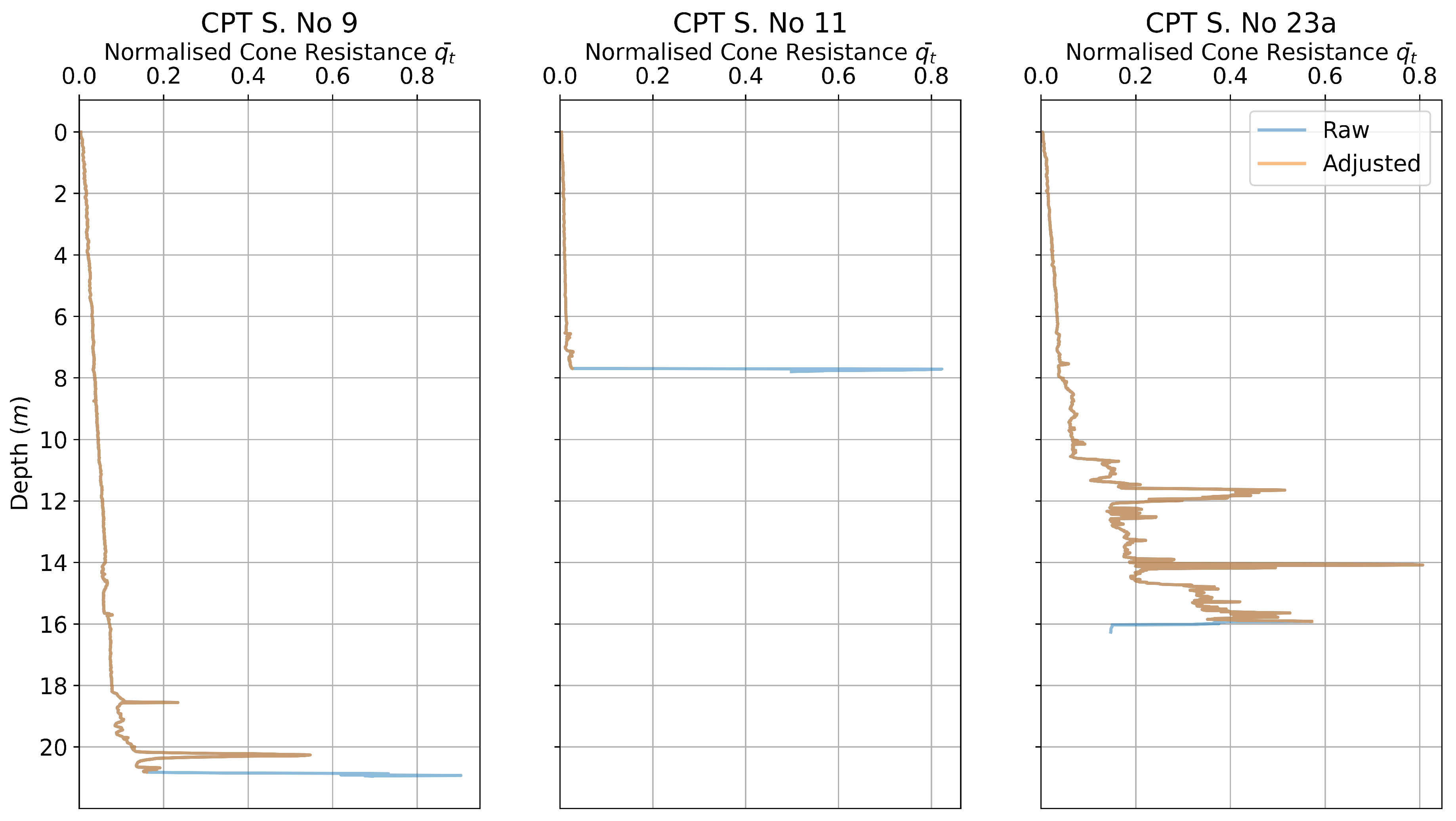
3.2. Averaging CPT Readings
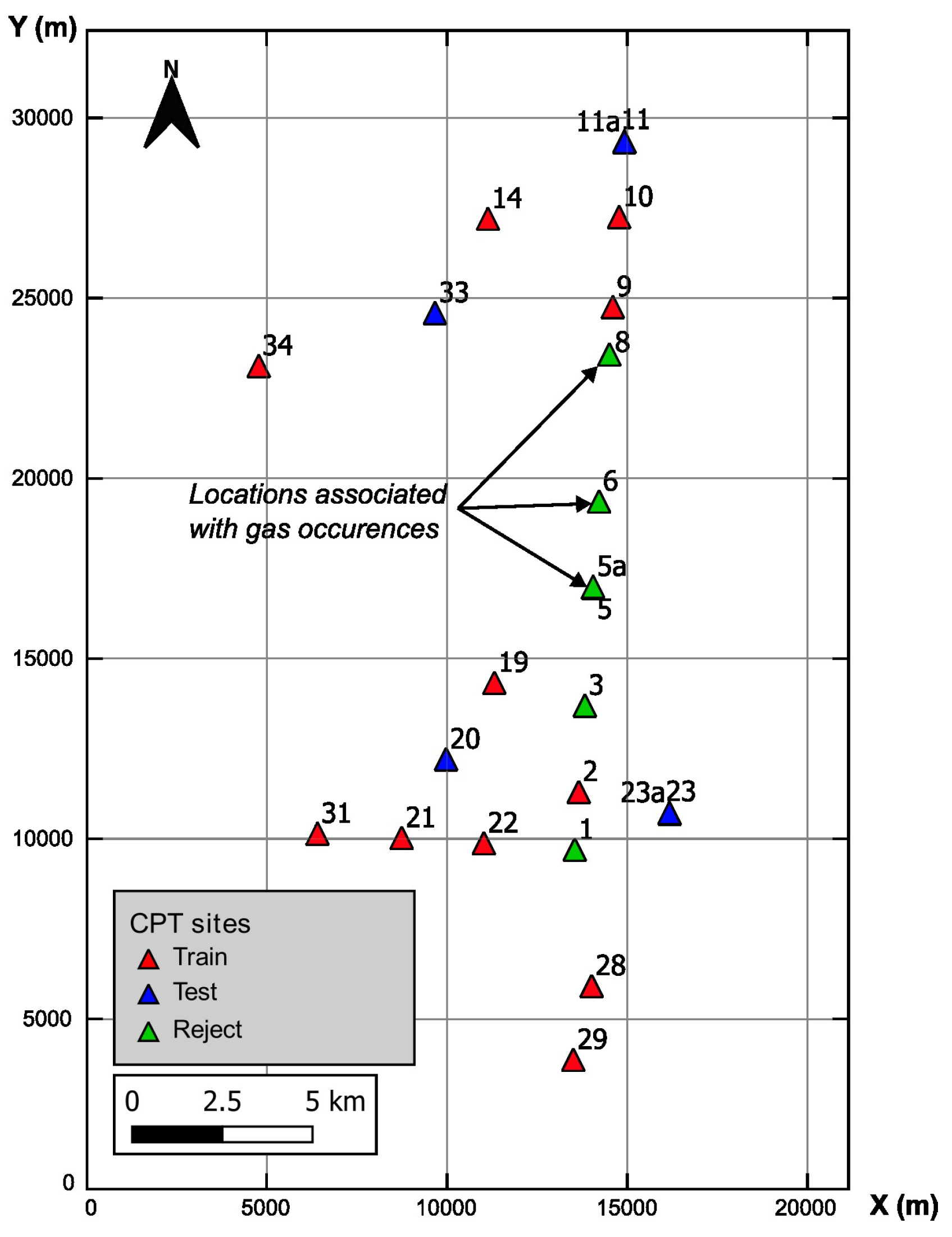
3.3. Excluding CPT Data for Shallow Gas Affected Locations
3.4. Outputs
3.5. Data Normalisation
- Z-Score normalisation: Z-score normalisation [47] is carried out via calculating the mean and standard deviation of the data, and then adjusting every point using them. The mathematical formula to complete this is given in Equation (2). If a value of the feature is exactly equal to the mean, the new normalised value will come out to be zero. If it is below the mean, it obtains a negative value, and if it is above the mean, it obtains a positive value;
- Min-max scalar normalisation: This is one of the simplest ways to normalise the data. For a given range of data, the minimum value takes the value of 0 and the highest value takes the value of 1. Every other value is then transformed into a floating point number between these two bounding integers. Mathematically [48], this is achieved via the Equation (3).
3.6. Machine Learning
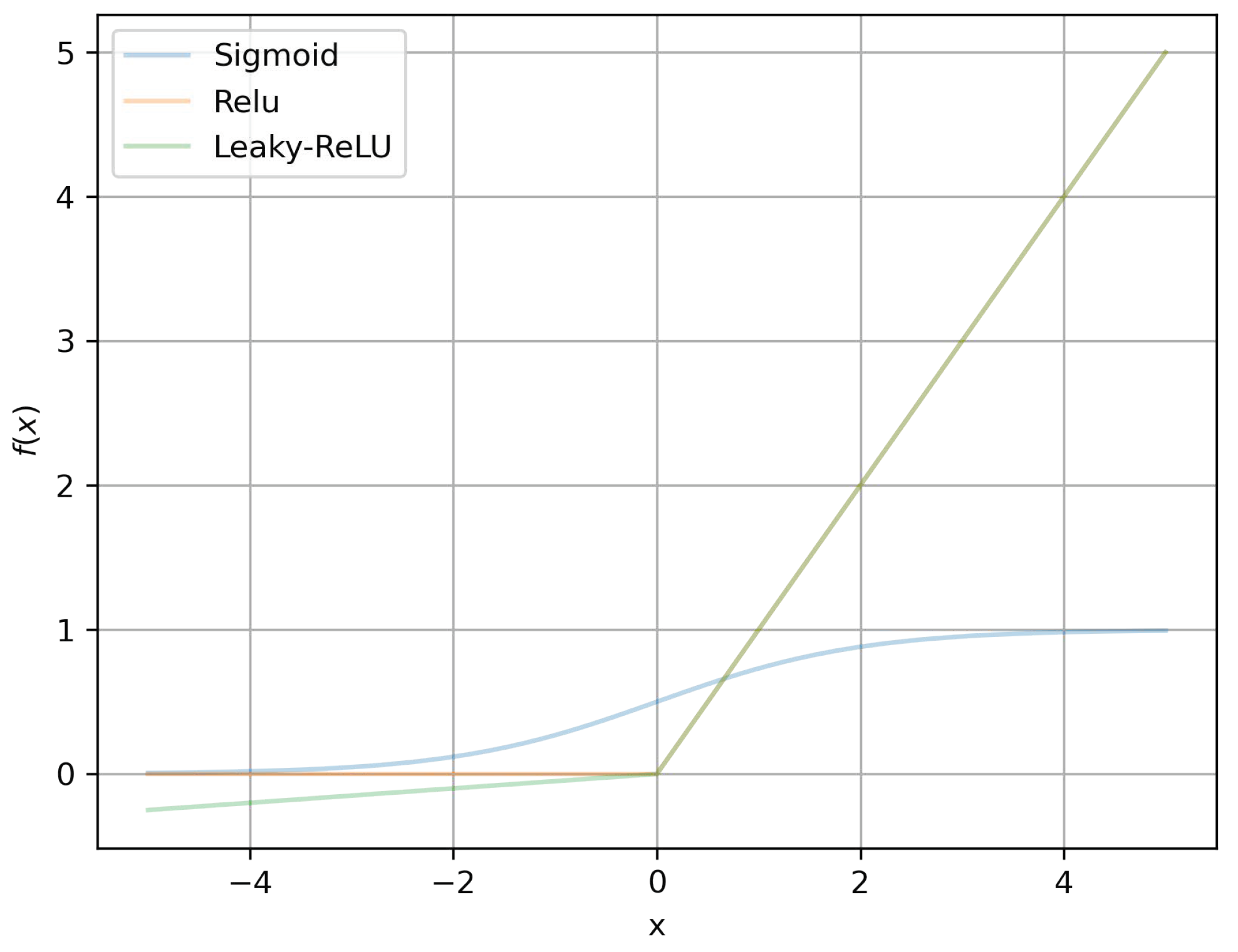
- Vanishing gradients: This is a problem encountered while training ANNs with gradient-based learning methods and back propagation. During each iteration of the learning process, the NN’s weights at each neuron are updated proportionally to the partial derivative of the error function, with respect to the current weight. In the worst case scenario, the gradients become vanishingly small, bringing the training process to a virtual halt, i.e., the value of the weight does not change because the partial derivative is infinitesimally small. This holds for non-linear activation functions, such as sigmoid or hyperbolic tangent, as shown in Figure 6 towards the edges of the function, where the derivative is close to zero but not zero. Their gradients are within the range of 0 and 1, and because back propagation computes gradients via the chain rule, multiplying these very small gradients for an n layered system, the gradients would drop exponentially with n, and the first couple of layers would train very slowly [54];
- Sparsity: Sparse matrices are matrices in which most of the elements are zero. Since negative input values generate a zero output, the resulting matrix is a simpler matrix with true zero values, instead of vanishingly small non-zero values. This prevents some neurons from activating in a particular layer. This has several advantages in itself. Deactivating several neurons in every layer makes the learning process faster. This in turn, causes the network’s predictive accuracy to improve by preventing over fitting [55].
- Weights and/or bias initialisation: Each synapse-connection between two neurons in successive layers has a weight associated with it. This weight multiplies itself with the input from the previous layer, if there is any, and calculates the result of the activation function. This is then fed as the input to the next layer. If a network has neurons in the layer, and neurons in the layer, then will be of dimension , where is a matrix holding the weights that control the function mapping from layer j to . Weights can be initialised, either as zero or randomly. Zero initialisation can cause the NN to enter into a state of symmetry, and prevent efficient learning. Every subsequent iteration will then be the same for the network since the derivative, with respect to the loss function, will be the same. Random initialisation is preferred. However, there is a chance that random initialisation might assign weights that may be too small or too high, that would then give rise to vanishing or exploding gradients. While vanishing gradients can be accounted for by using a ReLU-type activation function, it can still suffer from exploding gradients. Biases however, need not to be randomly initialised and can be set to zero;
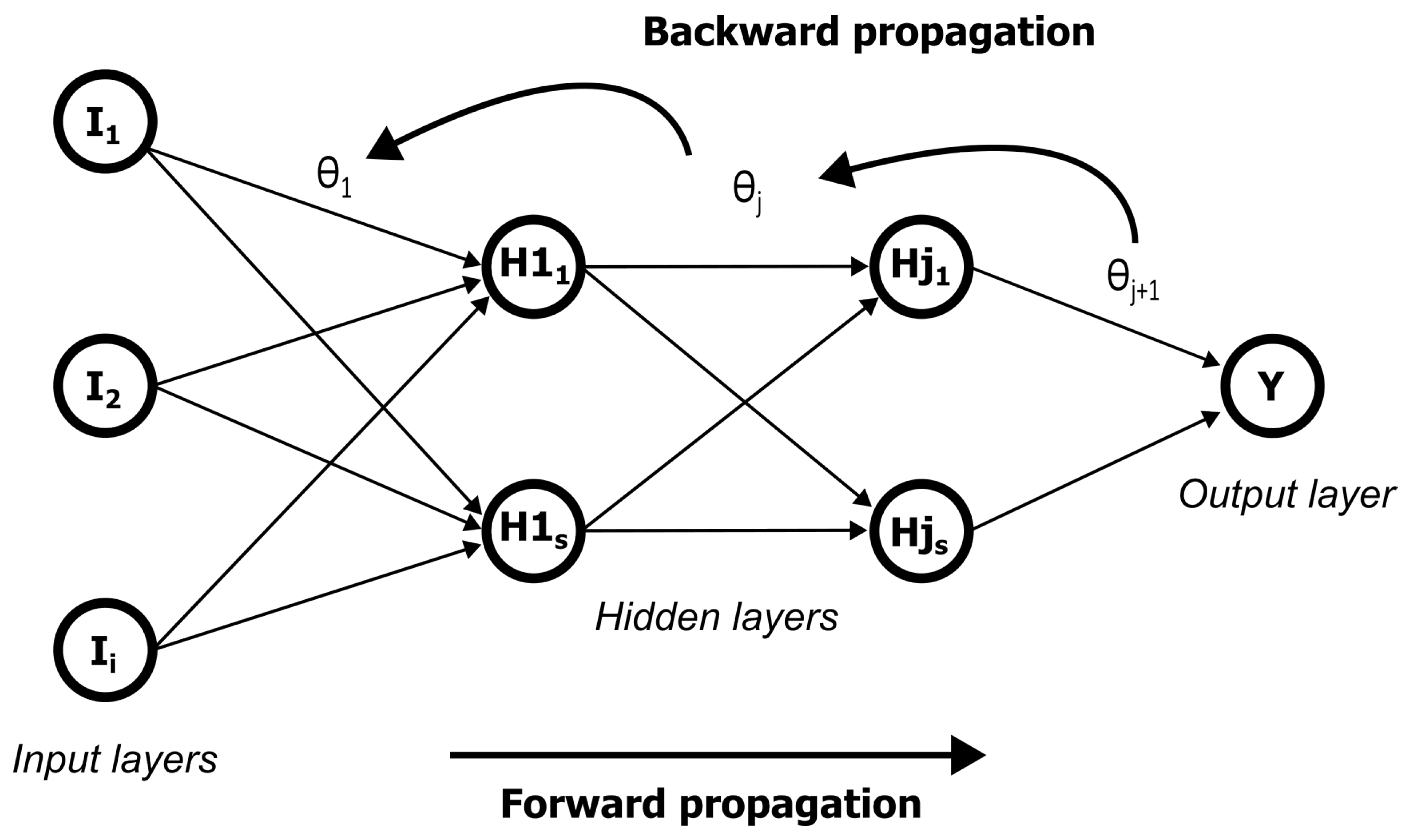
- Forward propagation: This step is shown in the solid lines that move from left to right in Figure 7. Forward propagation can be further broken down into two sub-steps. The first is the pre-activation. Pre-activation is the weighted sum of inputs, i.e., linear transformation of inputs using weights calculated either from the random initialisation in the first pass or the adjusted weights after the back propagation step. Based on this aggregated sum, and after routing this sum through the activation function, the neuron makes a decision on whether this information is passed on to the next layer or not. The second constituent step of the forward propagation is the activation. The weighted sum of inputs are passed on to the activation function from the pre-activation step. The two equations below give the forward propagation step using the following two equations:z here signifies the pre-activation step that is calculated using the linear weighted sum of inputs. is the weights for the specific layer in question. g is the activation function, the leaky-ReLU;
- Cost/Error function: A penalty term to assist the network in training the weights, so as to minimize the overall network cost in making a prediction. In supervised learning, the actual output for a set of input features is known. Therefore, by comparing the output with the input, and calculating the overall error within the network, the weights can be adjusted in the forward propagation step to improve accuracy. The cost function used here is the mean square error given by the following equation:Notice how the equation makes use of the term instead of —the output of every hidden layer is indeed , barring the output layer. Since this is a regression problem, the final set of neurons in the output layer does not route the pre-activation sum through the activation function. Therefore, the comparison of the network output is made through the actual result y;
- Backward propagation to adjust the weights and/or biases: Back propagation is the right to left pass shown in the dashed grey lines in Figure 7. In essence, it makes use of the cost function to adjust the weights. Properly tuning the weights and biases allow for reduced errors. To reduce the errors, a method called gradient descent is used. Gradient descent is a numerical method to calculate the differential increase or decrease in the cost function with respect to the weight. It computes the gradient of the loss function for each weight using the chain rule.is the weight that is being adjusted. The second term is the penalty term obtained from the cost differential that provides the direction and magnitude for the penalty. is the learning rate that, for the purpose of this study needs not be adjusted, since the optimiser used for the network is the ADAM optimiser [56].
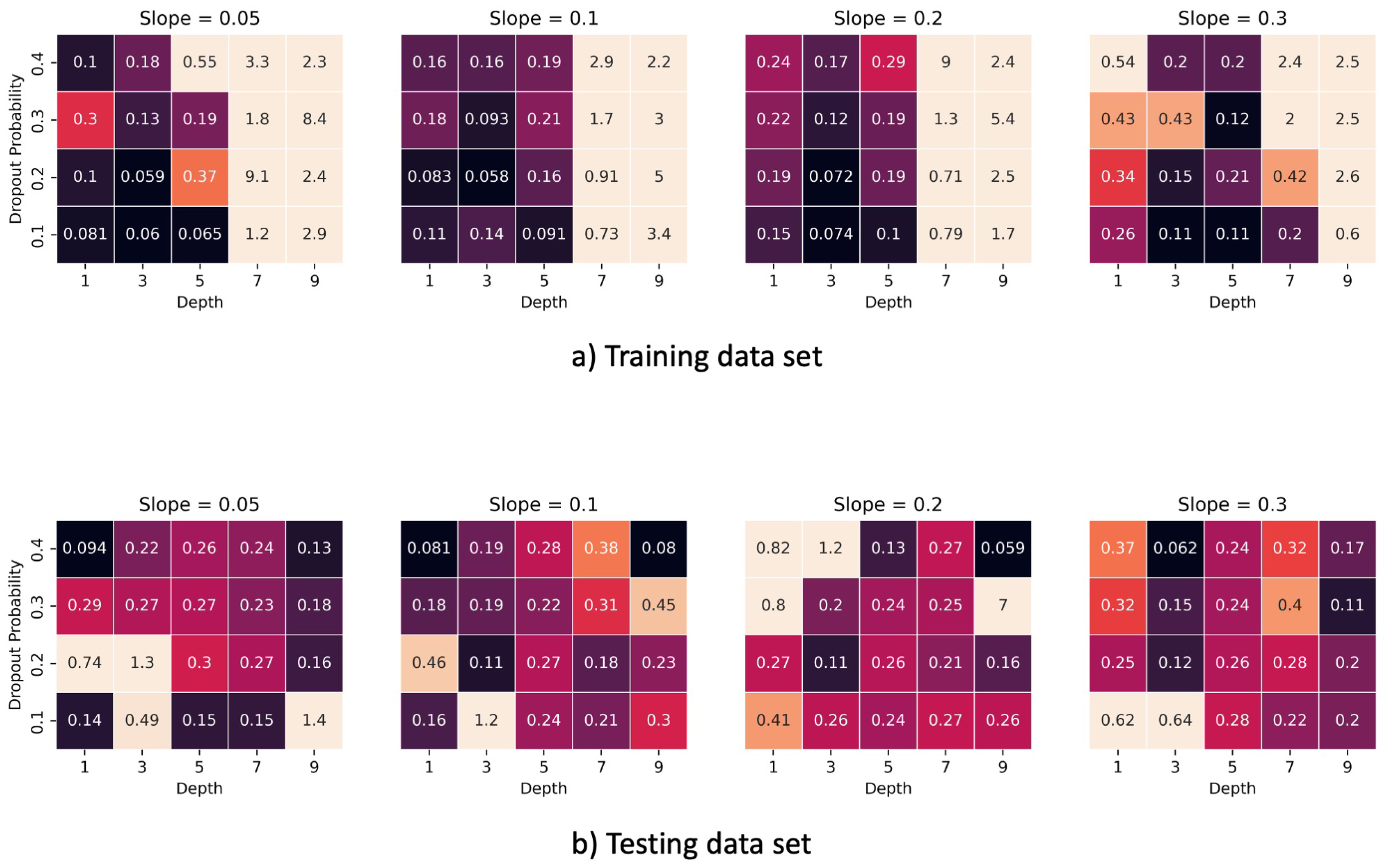
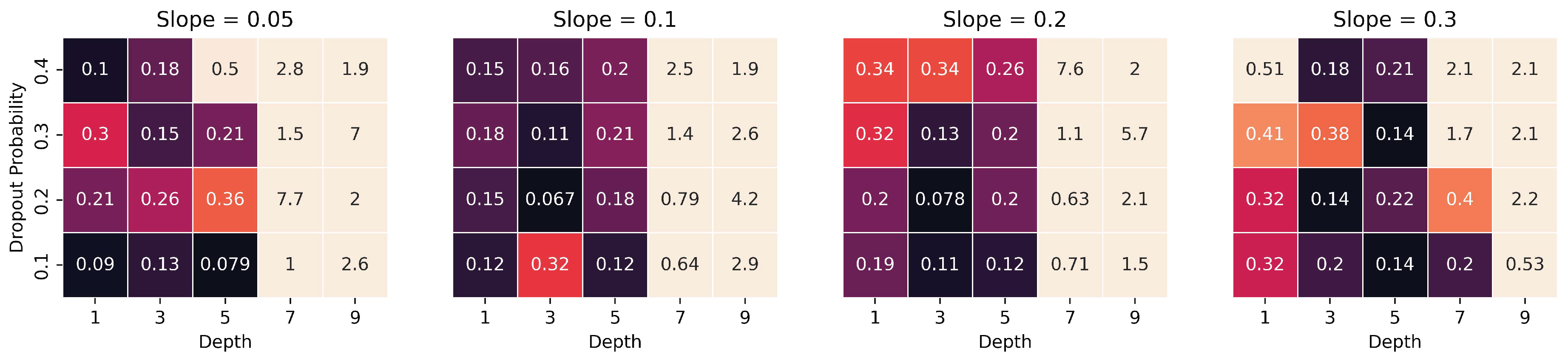
3.7. Hyperparameter Tuning
4. Results
4.1. Training Neural Network
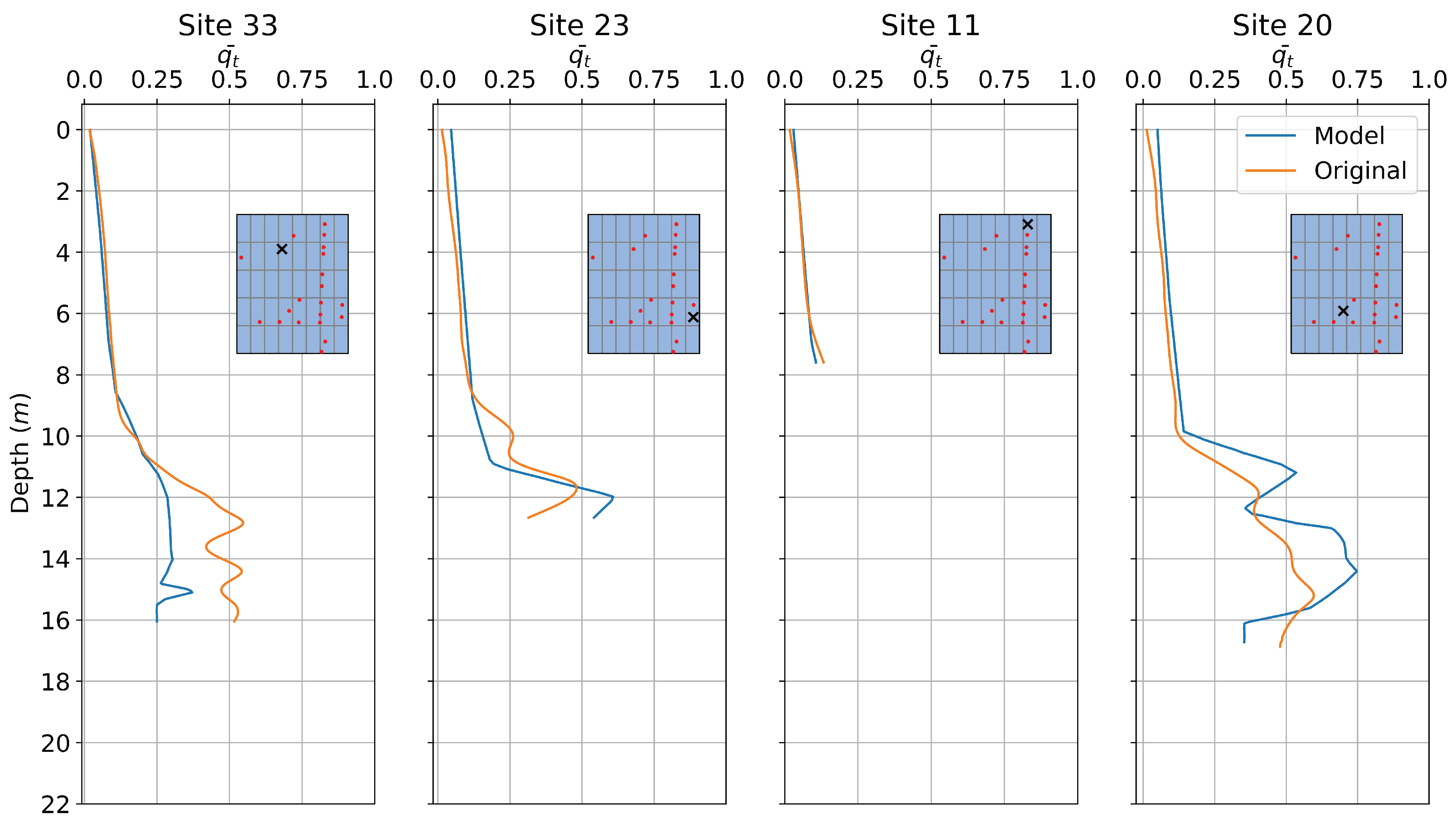
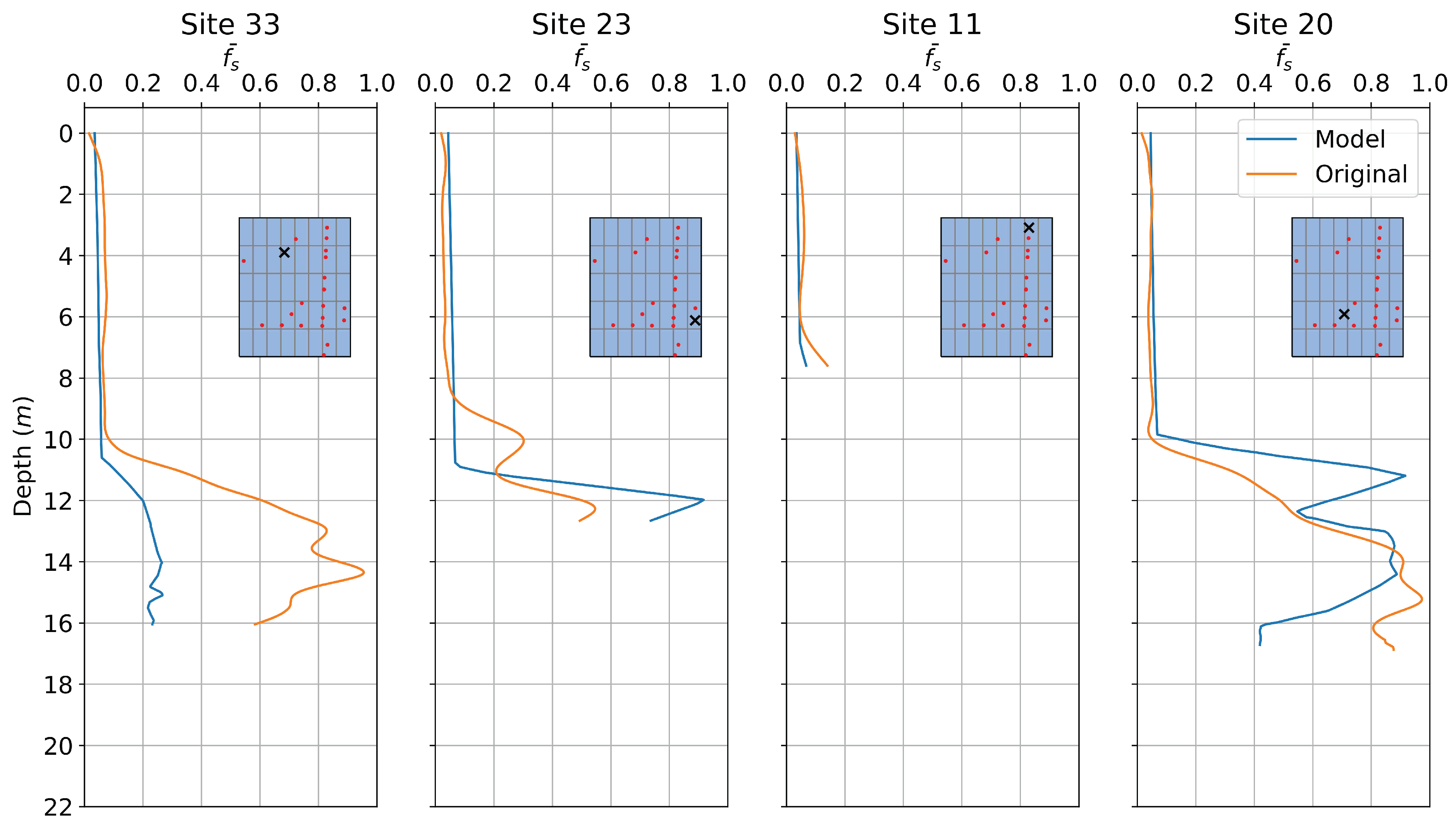
4.2. Model Performances
Prediction Using NN
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| S. No | Serial Number |
| NN | Neural Network |
| ANN | Artificial Neural Network |
| CNN | Convolution Neural Network |
| ReLU | Rectified Linear Unit |
| CPT | Cone Penetration Tests |
| Syn-CPT | Synthetic Cone Penetration Testing |
| RMSE | Root Mean Square Error |
| MSE | Mean Square Error |
References
- European Commission.Boosting Offshore Renewable Energy for a Climate Neutral Europe. Available online: https://ec.europa.eu/commission/presscorner/detail/en/ip_20_2096 (accessed on 20 March 2023).
- Barrett, M.; Farrell, N.; Roantree, B. Energy Poverty and Deprivation in Ireland; ESRI Research Series 144; The Economic and Social Research Institute: Dublin, Ireland, 2022. [Google Scholar]
- Forsberg, C.; Lunne, T.; Vanneste, M.; James, L.; Tjelta, T.; Barwise, A.; Duffy, C. Stothetic CPTS from Intelligent Ground Models Based on the Integration of Geology, Geotectoics and Geophysics as a Tool for Conceptual Foundation Design and Soil Investigation Planning. In Proceedings of the Offshore Site Investigation Geotechnics 8th International Conference Proceeding, London, UK, 12–14 September 2017; Society for Underwater Technology: London, UK, 2017; Volume 1254, pp. 1254–1259. [Google Scholar]
- Lunne, T.; Powell, J.J.; Robertson, P.K. Cone Penetration Testing in Geotechnical Practice; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Arshid, M.U.; Kamal, M.A. Regional Geotechnical Mapping Employing Kriging on Electronic Geodatabase. Appl. Sci. 2020, 10, 7625. [Google Scholar] [CrossRef]
- Robertson, P.K.; Cabal, K.L. Guide to Cone Penetration Testing for Geotechnical Engineering; Gregg Drilling & Testing, Inc.: Martinez, CA, USA, 2015. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press on Demand: Oxford, UK, 1997. [Google Scholar]
- Sauvin, G.; Vanneste, M.; Vardy, M.E.; Klinkvort, R.T.; Forsberg, C.F. Machine Learning and Quantitative Ground Models for Improving Offshore Wind Site Characterization. In Proceedings of the OTC Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar]
- Carpentier, S.; Peuchen, J.; Paap, B.; Boullenger, B.; Meijninger, B.; Vandeweijer, V.; Kesteren, W.V.; Erp, F.V. Generating synthetic CPTs from marine seismic reflection data using a neural network approach. In Proceedings of the Second EAGE Workshop on Machine Learning, Onine, 8–10 March 2021; Volume 2021, pp. 1–3. [Google Scholar]
- Phoon, K.K.; Zhang, W. Future of machine learning in geotechnics. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 17, 7–22. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Rauter, S.; Tschuchnigg, F. CPT Data Interpretation Employing Different Machine Learning Techniques. Geosciences 2021, 11, 265. [Google Scholar] [CrossRef]
- Erdogan Erten, G.; Yavuz, M.; Deutsch, C.V. Combination of Machine Learning and Kriging for Spatial Estimation of Geological Attributes. Nat. Resour. Res. 2022, 31, 191–213. [Google Scholar] [CrossRef]
- Vardy, M.E.; Vanneste, M.; Henstock, T.J.; Clare, M.A.; Forsberg, C.F.; Provenzano, G. State-of-the-art remote characterization of shallow marine sediments: The road to a fully integrated solution. Surf. Geophys. 2017, 15, 387–402. [Google Scholar] [CrossRef]
- Michel, G. Photograph of Geomil Manta-200 CPT during CE22002 Survey; Geomil Equipment: Westbaan, The Netherlands, 2022. [Google Scholar]
- Coughlan, M.; Wheeler, A.; Dorschel, B.; Long, M.; Doherty, P.; Mörz, T. Stratigraphic model of the Quaternary sediments of the Western Irish Sea Mud Belt from core, geotechnical and acoustic data. Geo-Mar. Lett. 2019, 39, 223–237. [Google Scholar] [CrossRef]
- Belderson, R.H. Holocene sedimentation in the western half of the Irish Sea. Mar. Geol. 1964, 2, 147–163. [Google Scholar] [CrossRef]
- Jackson, D.I.; Jackson, A.A.; Evans, D.; Wingfield, R.T.R.; Barnes, R.P.; Arthur, M.J. The Geology of the Irish Sea; British Geological Survey: Keyworth, UK, 1995; p. 133. [Google Scholar]
- McCabe, A.M. Glacial Geology and Geomorphology: The Landscapes of Ireland; Dunedin Academic Press: Edinburgh, Scotland, 2008. [Google Scholar]
- Chiverrell, R.C.; Thrasher, I.M.; Thomas, G.S.; Lang, A.; Scourse, J.D.; van Landeghem, K.J.; McCarroll, D.; Clark, C.D.; Cofaigh, C.Ó.; Evans, D.J.; et al. Bayesian modelling the retreat of the Irish Sea Ice Stream. J. Quat. Sci. 2013, 28, 200–209. [Google Scholar] [CrossRef]
- Dickson, C.; Whatley, R. The biostratigraphy of a Holocene borehole from the Irish Sea. In Proceedings of the 2nd European Ostracodologists Meeting, London, UK, 23–27 July 1993; British Micropalaeontological Society: London, UK, 1993; pp. 145–148. [Google Scholar]
- Michel, G.; Coughlan, M.; Arosio, R.; Emery, A.R.; Wheeler, A.J. Stratigraphic and palaeo-geomorphological evidence for the glacial-deglacial history of the last British-Irish Ice Sheet in the north-western Irish Sea. Quat. Sci. Rev. 2023, 300, 107909. [Google Scholar] [CrossRef]
- Coughlan, M.; Long, M.; Doherty, P. Geological and geotechnical constraints in the Irish Sea for offshore renewable energy. J. Maps 2020, 16, 420–431. [Google Scholar] [CrossRef]
- Bishop, J.M. Artificial intelligence is stupid and causal reasoning will not fix it. Front. Psychol. 2021, 11, 513474. [Google Scholar] [CrossRef]
- Buckley, T.; Ghosh, B.; Pakrashi, V. A Feature Extraction & Selection Benchmark for Structural Health Monitoring. Struct. Health Monit. 2022, 22, 2082–2127. [Google Scholar]
- Eslami, A.; Moshfeghi, S.; MolaAbasi, H.; Eslami, M.M. 6—CPT in foundation engineering; scale effect and bearing capacity. In Piezocone and Cone Penetration Test (CPTu and CPT) Applications in Foundation Engineering; Eslami, A., Moshfeghi, S., MolaAbasi, H., Eslami, M.M., Eds.; Butterworth-Heinemann: Oxford, UK, 2020; pp. 145–181. [Google Scholar]
- Rogers, D.; PE, R. Fundamentals of Cone Penetrometer Test (CPT) Soundings; Missouri University of Science and Technology: Rolla, MO, USA, 2020. [Google Scholar]
- Alshibli, K.; Okeil, A.; Alramahi, B.; Zhang, Z. Reliability Analysis of CPT Measurements for Calculating Undrained Shear Strength. Geotech. Test. J. 2011, 34, 721–729. [Google Scholar]
- Kordos, M.; Rusiecki, A. Improving MLP Neural Network Performance by Noise Reduction. In Theory and Practice of Natural Computing; Dediu, A.H., Martín-Vide, C., Truthe, B., Vega-Rodríguez, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 133–144. [Google Scholar]
- Penrod, C.; Wagner, T. Another Look at the Edited Nearest Neighbor Rule; Technical report; Texas University at Austin Department of Electrical Engineering: Austin, TX, USA, 1976. [Google Scholar]
- Yu, L.; Jin, Q.; Lavery, J.E.; Fang, S.C. Univariate Cubic L1 Interpolating Splines: Spline Functional, Window Size and Analysis-based Algorithm. Algorithms 2010, 3, 311–328. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Kernel smoothing methods. In The Elements of Statistical Learning; Springer: Berlin, Germany, 2009; pp. 191–218. [Google Scholar]
- Rose, P. Considerations in the normalisation of the fundamental frequency of linguistic tone. Speech Commun. 1987, 6, 343–352. [Google Scholar] [CrossRef]
- De Boor, C.; De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978; Volume 27. [Google Scholar]
- Öz Yilmaz. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data; Society of Exploration Geophysicists: Houston, TX, USA, 2001; p. 2092. [Google Scholar]
- Kim, Y.J.; Cheong, S.; Chun, J.H.; Cukur, D.; Kim, S.P.; Kim, J.K.; Kim, B.Y. Identification of shallow gas by seismic data and AVO processing: Example from the southwestern continental shelf of the Ulleung Basin, East Sea, Korea. Mar. Pet. Geol. 2020, 117, 104346. [Google Scholar] [CrossRef]
- Davis, A. Shallow gas: An overview. Cont. Shelf Res. 1992, 12, 1077–1079. [Google Scholar] [CrossRef]
- Sultan, N.; Voisset, M.; Marsset, T.; Vernant, A.M.; Cauquil, E.; Colliat, J.L.; Curinier, V. Detection of free gas and gas hydrate based on 3D seismic data and cone penetration testing: An example from the Nigerian Continental Slope. Mar. Geol. 2007, 240, 235–255. [Google Scholar] [CrossRef]
- Steiner, A.; Kopf, A.J.; Henry, P.; Stegmann, S.; Apprioual, R.; Pelleau, P. Cone penetration testing to assess slope stability in the 1979 Nice landslide area (Ligurian Margin, SE France). Mar. Geol. 2015, 369, 162–181. [Google Scholar] [CrossRef]
- Luan, S.; Gu, Z.; Freidovich, L.B.; Jiang, L.; Zhao, Q. Out-of-Distribution Detection for Deep Neural Networks With Isolation Forest and Local Outlier Factor. IEEE Access 2021, 9, 132980–132989. [Google Scholar] [CrossRef]
- Geron, A. Handson Machine Learning with Scikitlearn; Keras & TensorFlow o’Reiley Media Inc.: Sebatopol, CA, USA, 2019. [Google Scholar]
- Momeny, M.; Neshat, A.A.; Hussain, M.A.; Kia, S.; Marhamati, M.; Jahanbakhshi, A.; Hamarneh, G. Learning-to-augment strategy using noisy and denoised data: Improving generalizability of deep CNN for the detection of COVID-19 in X-ray images. Comput. Biol. Med. 2021, 136, 104704. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, M.M.; Schuller, B.W. Normalise for Fairness: A Simple Normalisation Technique for Fairness in Regression Machine Learning Problems. arXiv 2022, arXiv:2202.00993. [Google Scholar]
- Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2020, 358, 112623. [Google Scholar] [CrossRef]
- Wu, H.; Köhler, J.; Noé, F. Stochastic normalizing flows. Adv. Neural Inf. Process. Syst. 2020, 33, 5933–5944. [Google Scholar]
- Schober, P.; Mascha, E.J.; Vetter, T.R. Statistics from a (agreement) to Z (z score): A guide to interpreting common measures of association, agreement, diagnostic accuracy, effect size, heterogeneity, and reliability in medical research. Anesth. Analg. 2021, 133, 1633–1641. [Google Scholar] [CrossRef]
- Eliazar, I.; Metzler, R.; Reuveni, S. Universal max-min and min-max statistics. arXiv 2018, arXiv:1808.08423v1. [Google Scholar]
- Wang, S.C. Artificial neural network. In Interdisciplinary Computing in Java Programming; Springer: Berlin, Germany, 2003; pp. 81–100. [Google Scholar]
- Salman, S.; Liu, X. Overfitting mechanism and avoidance in deep neural networks. arXiv 2019, arXiv:1901.06566. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM 2021, 64, 107–115. [Google Scholar] [CrossRef]
- Hestness, J.; Ardalani, N.; Diamos, G. Beyond human-level accuracy: Computational challenges in deep learning. In Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming, Washington, DC, USA, 16–20 February 2019; pp. 1–14. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Tan, H.H.; Lim, K.H. Vanishing Gradient Mitigation with Deep Learning Neural Network Optimization. In Proceedings of the 2019 7th International Conference on Smart Computing & Communications (ICSCC), Miri, Malaysia, 28–30 June 2019; pp. 1–4. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of Machine Learning Research, Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; Gordon, G., Dunson, D., Dudík, M., Eds.; PMLR: Fort Lauderdale, FL, USA, 2011; Volume 15, pp. 315–323. [Google Scholar]
- Bae, K.; Ryu, H.; Shin, H. Does Adam optimizer keep close to the optimal point? arXiv 2019, arXiv:1911.00289. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Poli, A.A.; Cirillo, M.C. On the use of the normalized mean square error in evaluating dispersion model performance. Atmos. Environ. Part A Gen. Top. 1993, 27, 2427–2434. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Seifert, A. In Situ Detection and Characterisation of Fluid Mud and Soft Cohesive Sediments by Dynamic Piezocone Penetrometer Testing. Ph.D. Thesis, Universität Bremen, Bremen, Germany, 2011. [Google Scholar]
| Symbol | Definition | Formula |
|---|---|---|
| Total force experienced by the cone | - | |
| Total force experienced by the cone | - | |
| Cone resistance ratio of the total forcing acting on the cone to the projected area of the one | ||
| Total force experienced by the friction sleeve | - | |
| Surface area of the friction sleeve | - | |
| Sleeve resistance ratio of the total force acting on the sleeve to the surface area of the sleeve | ||
| Pore pressure | - | |
| Corrected cone resistance ratio of the total force acting on the cone to the projected area of the sleeve with the correction of the pore pressure effects | ) | |
| Normalised sleeve friction by dividing the local value with the local maximum | ||
| Normalised corrected cone resistance by dividing the local value with the local maximum |
| Activation Function | |||
|---|---|---|---|
| Property | Sigmoid | ReLU | Leaky-ReLU |
| Range | 0–1 | 0–∞ | ∞–∞ |
| Vanishing Gradients | Yes | No | No |
| Nature | Non Linear | Linear | Linear |
| Zero Centred | No | No | No |
| Dying ReLU | - | Yes | No |
| Computational Expense | High | Low | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoukat, G.; Michel, G.; Coughlan, M.; Malekjafarian, A.; Thusyanthan, I.; Desmond, C.; Pakrashi, V. Generation of Synthetic CPTs with Access to Limited Geotechnical Data for Offshore Sites. Energies 2023, 16, 3817. https://doi.org/10.3390/en16093817
Shoukat G, Michel G, Coughlan M, Malekjafarian A, Thusyanthan I, Desmond C, Pakrashi V. Generation of Synthetic CPTs with Access to Limited Geotechnical Data for Offshore Sites. Energies. 2023; 16(9):3817. https://doi.org/10.3390/en16093817
Chicago/Turabian StyleShoukat, Gohar, Guillaume Michel, Mark Coughlan, Abdollah Malekjafarian, Indrasenan Thusyanthan, Cian Desmond, and Vikram Pakrashi. 2023. "Generation of Synthetic CPTs with Access to Limited Geotechnical Data for Offshore Sites" Energies 16, no. 9: 3817. https://doi.org/10.3390/en16093817
APA StyleShoukat, G., Michel, G., Coughlan, M., Malekjafarian, A., Thusyanthan, I., Desmond, C., & Pakrashi, V. (2023). Generation of Synthetic CPTs with Access to Limited Geotechnical Data for Offshore Sites. Energies, 16(9), 3817. https://doi.org/10.3390/en16093817








