State-of-Health Prediction of Lithium-Ion Batteries Based on Diffusion Model with Transfer Learning
Abstract
1. Introduction
- The fast-charging mode, consisting of multiple stages matching the maximum charging rate under limited conditions, is widely popularized in real-life EV application. The statistical features are extracted from the voltage profile of each stage as the model latent variables. The results prove that the selected features can distinctly characterize the battery degradation trend in the multi-stage charging process.
- Based on diffusion model, the prediction model is established with time series information tackled via BiLSTM, a versatile multivariate probabilistic time series forecasting method that leverages estimating its gradient to learn and sample from the data distribution at each time step, autoregressively. The transfer learning method is applied on different batteries, enabling the generalizability of proposed approach.
- The proposed method is verified on two LIBs datasets with different electrochemical properties and charging conditions, and the verification results reveal the higher accuracy compared with other methods, accomplishing an obvious performance improvement in generalizability and robustness.
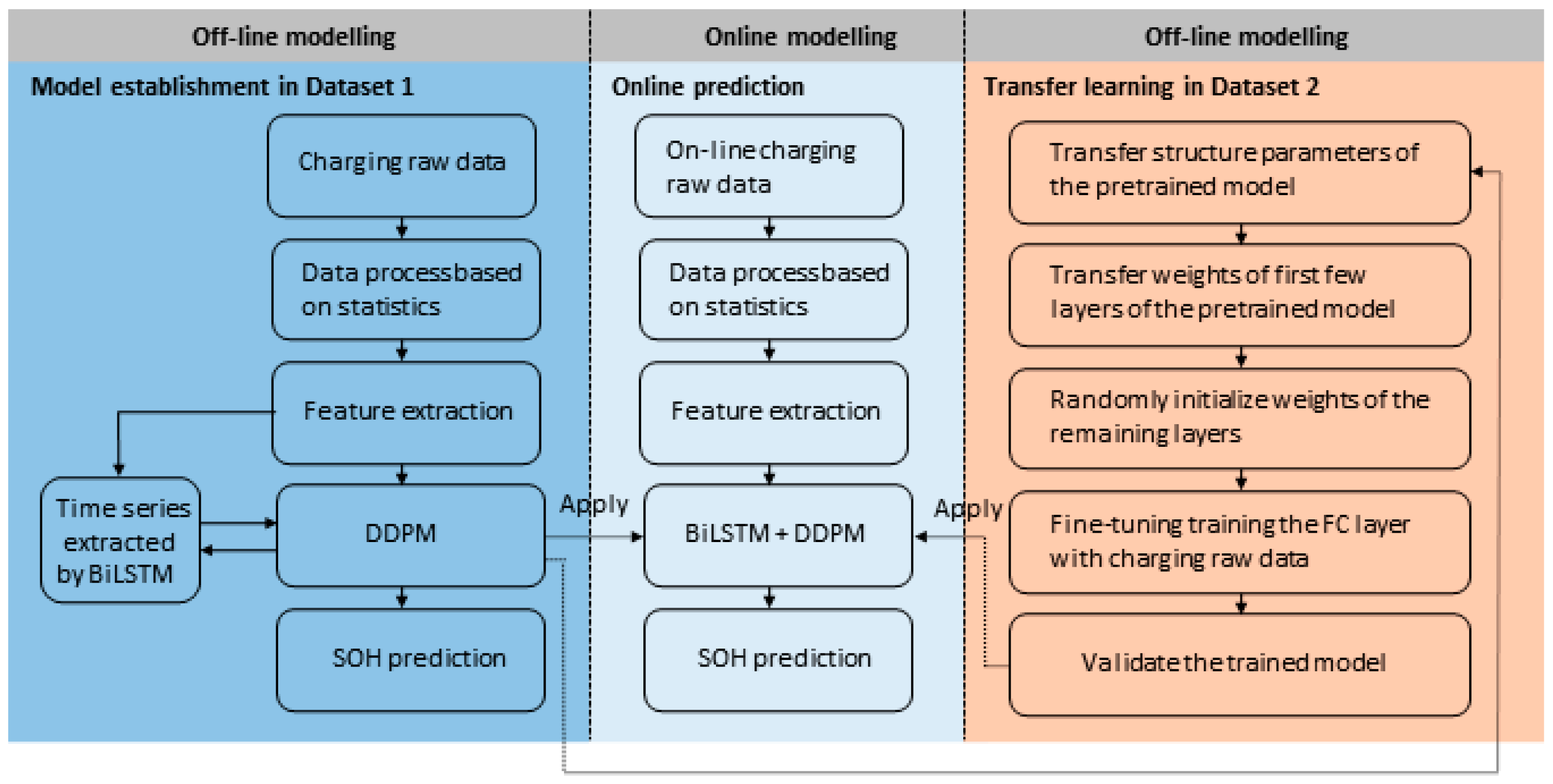
2. Methodology
2.1. Diffusion Model Applied to SOH Prediction
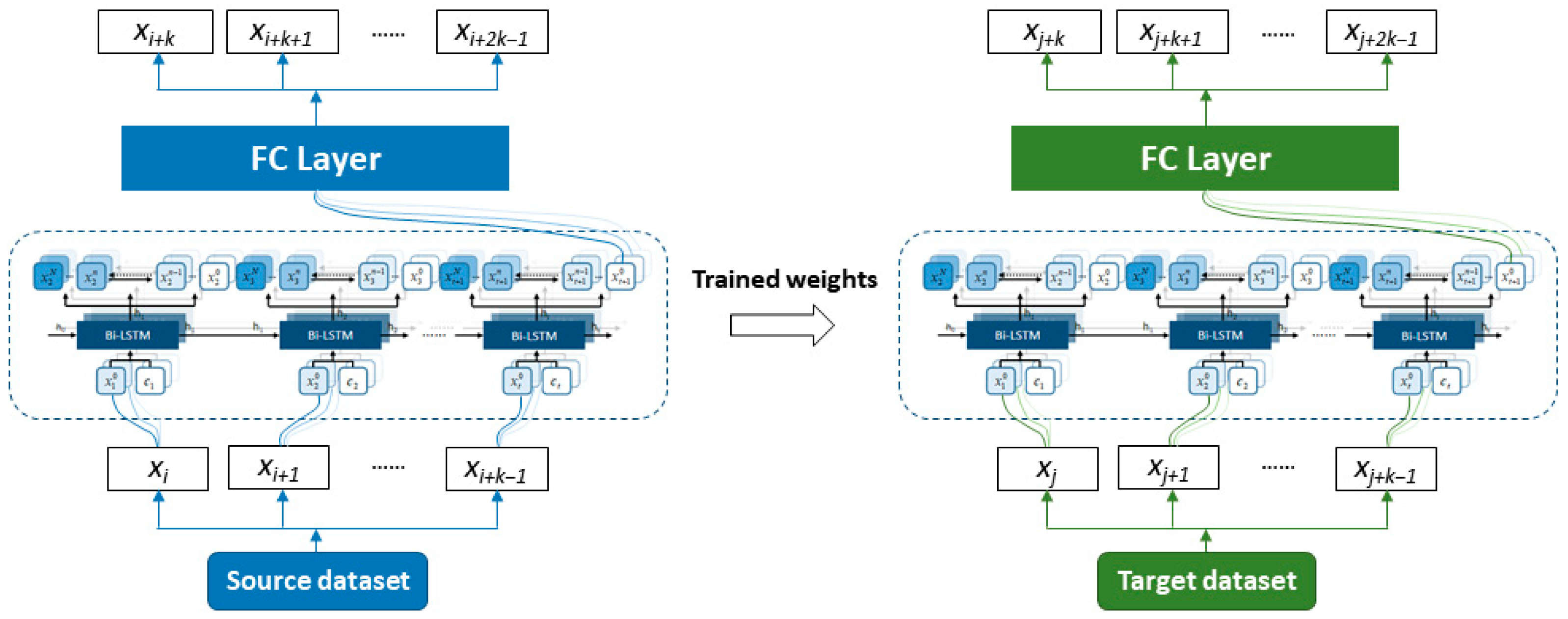
2.2. Transfer Learning
3. Experiment Validation
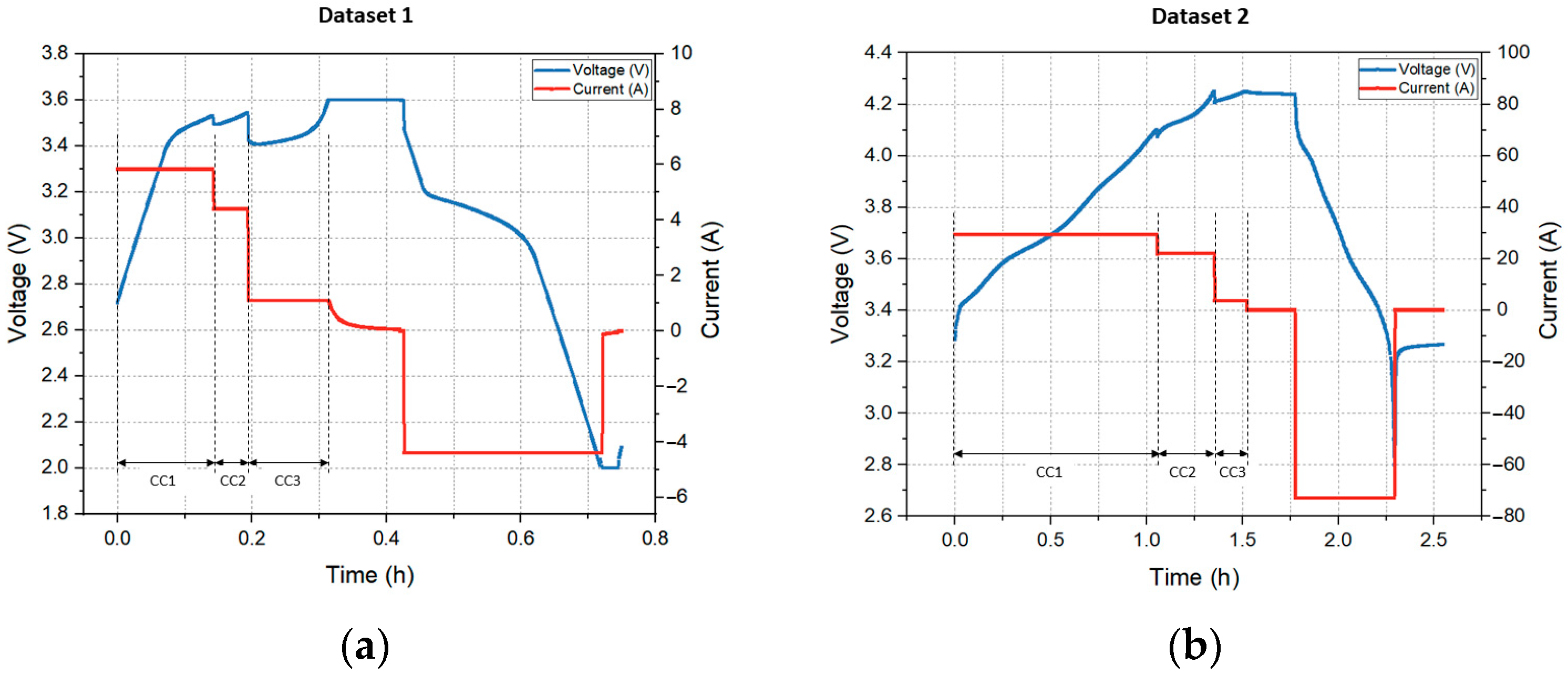
3.1. Experimental Dataset
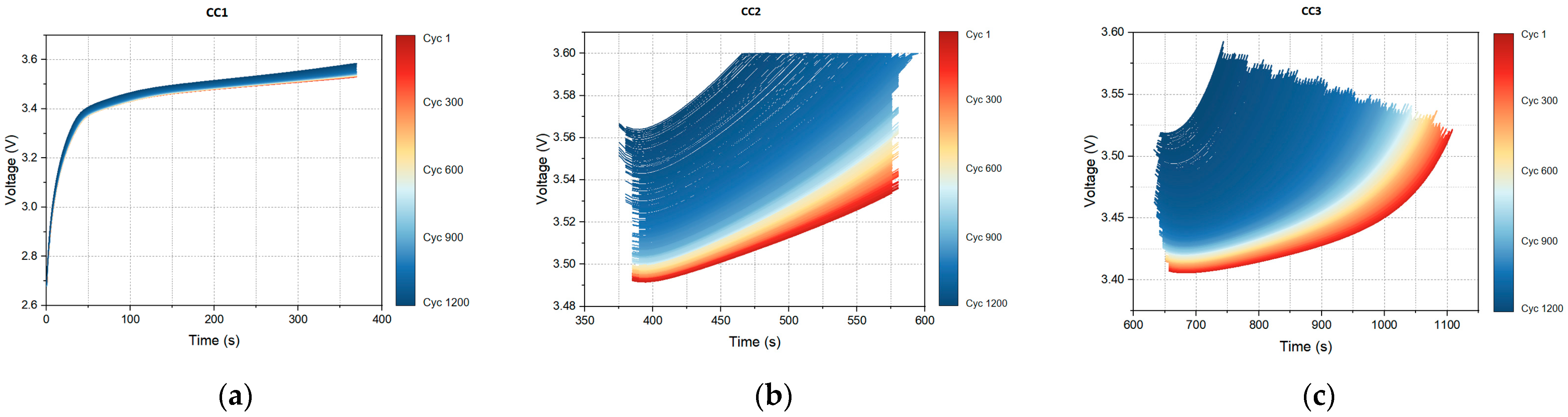
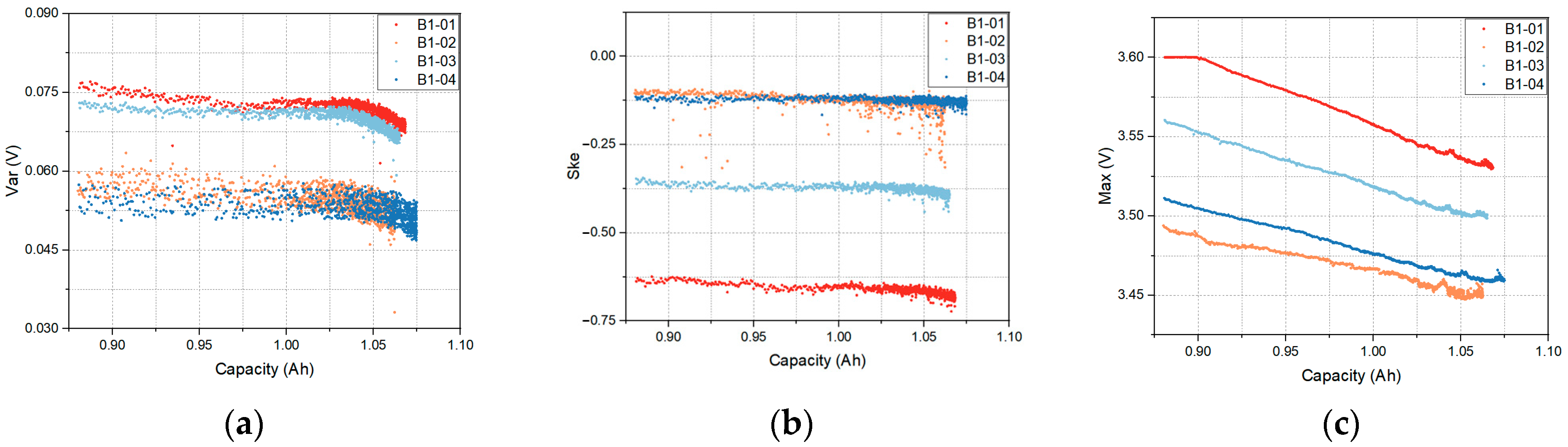
3.2. Feature Extraction
3.3. Implementation Details
4. Results and Discussion
4.1. Evaluation Criteria
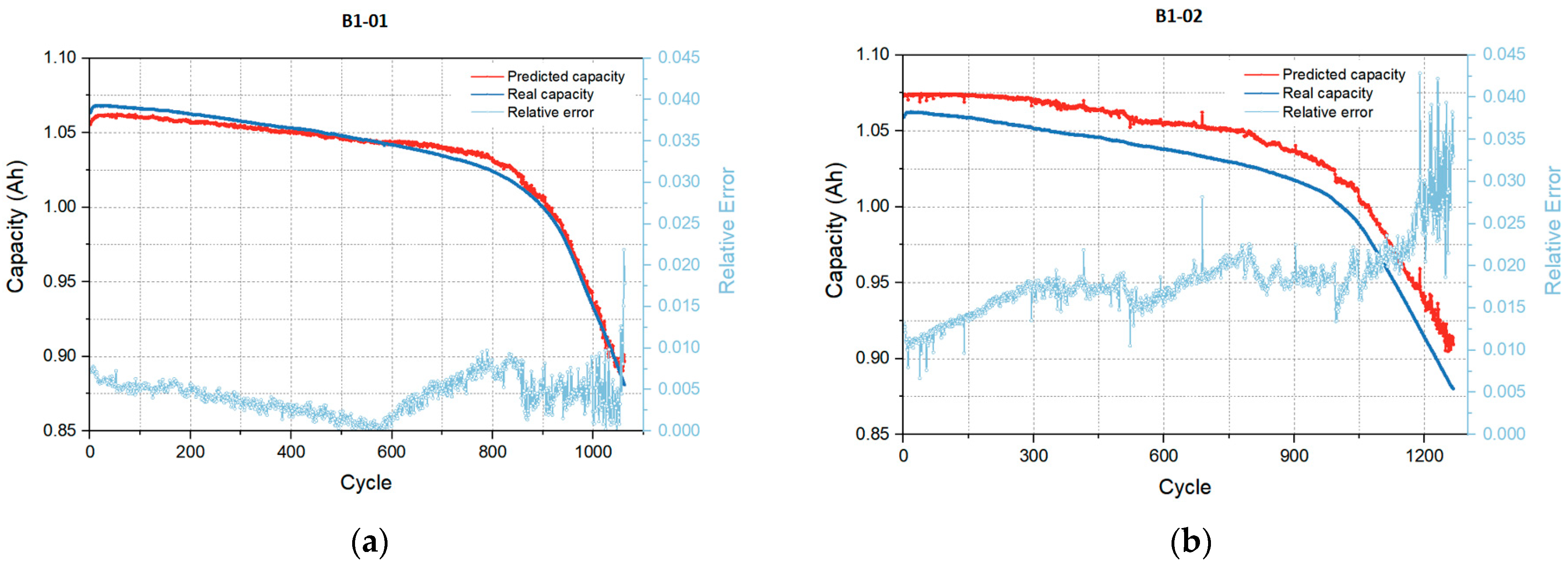
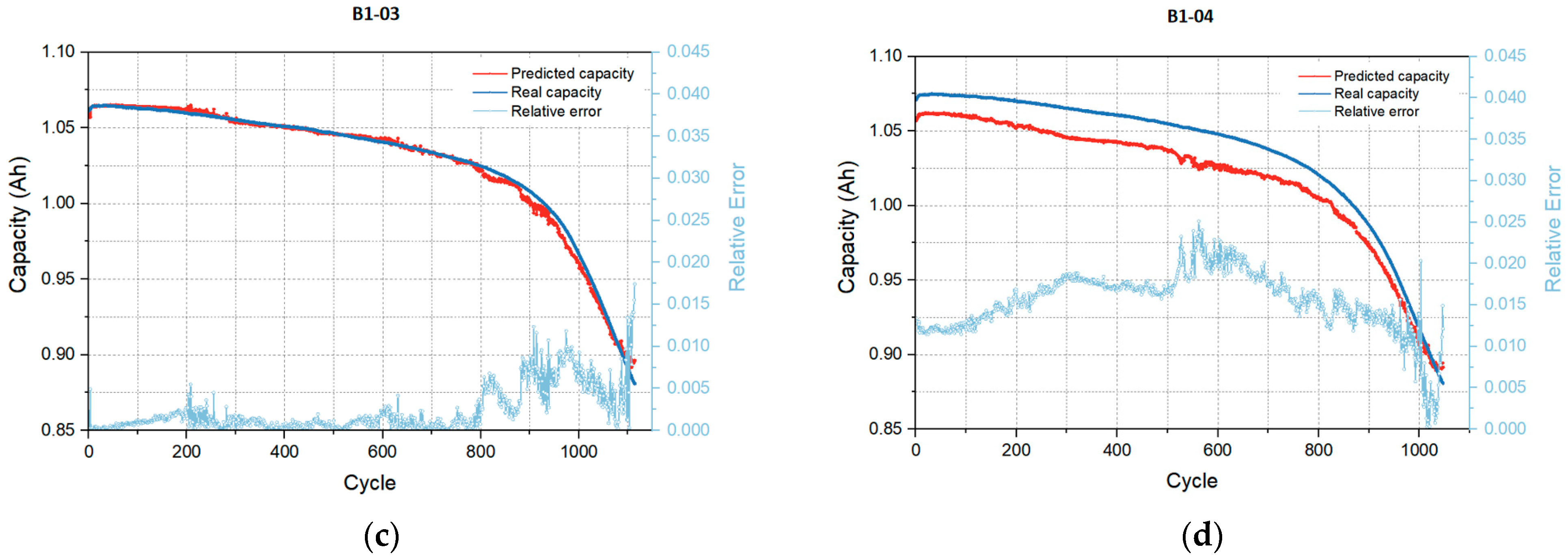
4.2. Performance on Source Dataset
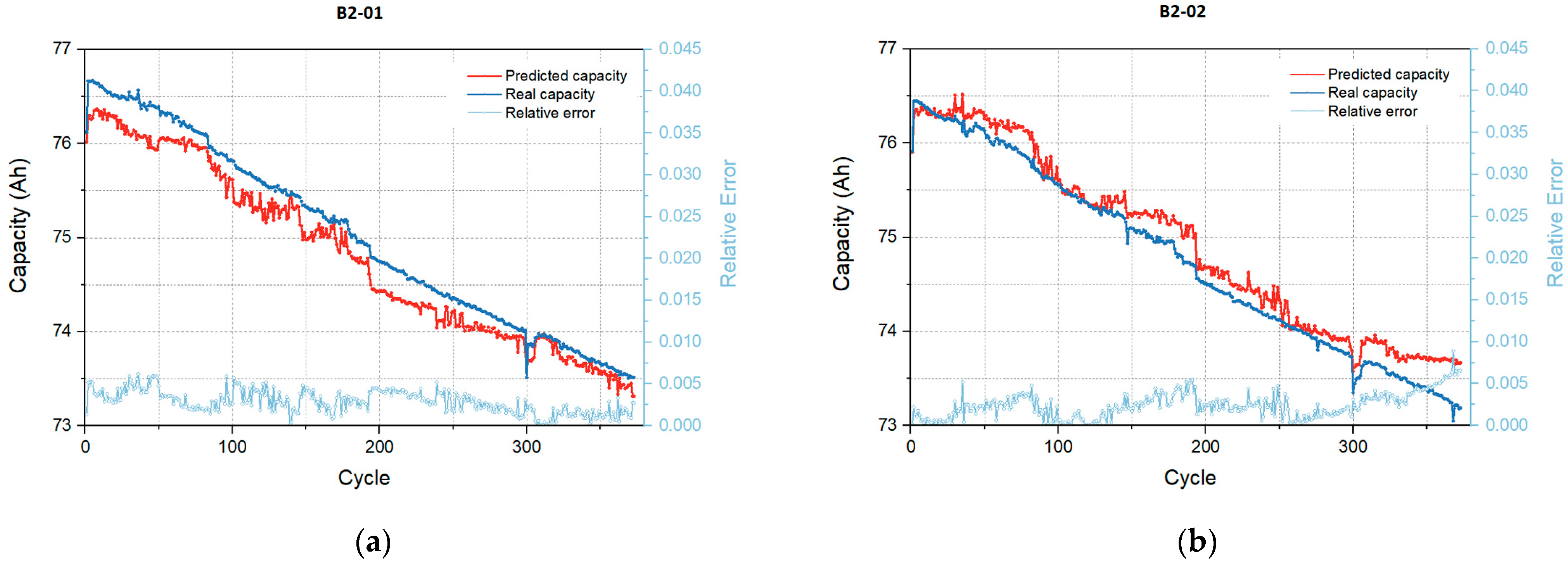
4.3. Performance on Target Dataset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lai, X.K.; Chen, Q.; Tang, X.; Zhou, Y.; Gao, F.; Guo, Y.; Bhagat, R.; Zheng, Y. Critical review of life cycle assessment of lithium-ion batteries for electric vehicles: A lifespan perspective. eTransportation 2022, 12, 100169. [Google Scholar] [CrossRef]
- Tian, H.; Qin, P.; Li, K.; Zhao, Z. A review of the state of health for lithium-ion batteries: Research status and suggestions. J. Clean. Prod. 2020, 261, 120813. [Google Scholar] [CrossRef]
- Lai, X.K.; Deng, C.; Li, J.; Zhu, Z.; Han, X.; Zheng, Y. Rapid Sorting and Regrouping of Retired Lithium-Ion Battery Modules for Echelon Utilization Based on Partial Charging Curves. IEEE Trans. Veh. Technol. 2021, 70, 1246–1254. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Cai, J.; Hu, X. Battery health estimation with degradation pattern recognition and transfer learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Li, W.; Cao, D.; Jöst, D.; Ringbeck, F.; Kuipers, M.; Frie, F.; Sauer, D.U. Parameter sensitivity analysis of electrochemical model-based battery management systems for lithium-ion batteries. Appl. Energy 2020, 269, 115104. [Google Scholar] [CrossRef]
- Randall, A.V.; Perkins, R.D.; Zhang, X.; Plett, G.L. Controls oriented reduced order modeling of solid-electrolyte interphase layer growth. J. Power Sources 2012, 209, 282–288. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Xu, L.; Che, Y.; Hu, L. General Discharge Voltage Information Enabled Health Evaluation for Lithium-Ion Batteries. IEEE ASME Trans. Mechatron. 2021, 26, 1295–1306. [Google Scholar] [CrossRef]
- Zheng, Y.; Qin, C.; Lai, X.K.; Han, X.; Xie, Y. A novel capacity estimation method for lithium-ion batteries using fusion estimation of charging curve sections and discrete Arrhenius aging model. Appl. Energy 2019, 251, 113327. [Google Scholar] [CrossRef]
- Song, Z.; Wu, X.; Li, X.; Hou, J.; Hofmann, H.F.; Sun, J. The Sequential Algorithm for Combined State of Charge and State of Health Estimation of Lithium Ion Battery based on Active Current Injection. arXiv 2019, arXiv:1901.06000. [Google Scholar] [CrossRef]
- Sung, W.; Lee, J. Implementation of SOH Estimator in Automotive BMSs Using Recursive Least-Squares. Electronics 2019, 8, 1237. [Google Scholar] [CrossRef]
- Song, Y.; Liu, D.; Peng, Y. FPGA-based Implementation of Lithium-ion Battery SOH Estimator Using Particle Filter. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25 May–25 June 2020. [Google Scholar]
- Lin, H.; Liang, T.P.; Chen, S. Estimation of Battery State of Health Using Probabilistic Neural Network. IEEE Trans. Ind. Inform. 2013, 9, 679–685. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L.; Cai, Y.; Deng, H.; Sun, L.J. Online available capacity prediction and state of charge estimation based on advanced data-driven algorithms for lithium iron phosphate battery. Energy 2016, 112, 469–480. [Google Scholar] [CrossRef]
- Klass, V.L.; Behm, M.; Lindbergh, G. A support vector machine-based state-of-health estimation method for lithium-ion batteries under electric vehicle operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, Z.; Qiao, D.; Lai, X.K.; Li, Y.; Wang, S. Life Prediction under Charging Process of Lithium-Ion Batteries Based on AutoML. Energies 2022, 15, 4594. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yan, J. Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Sohn, S.; Byun, H.; Lee, J.H. CNN-based Online Diagnosis of Knee-point in Li-ion Battery Capacity Fade Curve. IFAC-PapersOnLine 2022, 55, 181–185. [Google Scholar] [CrossRef]
- Harada, Y.; Lin, L.; Fukui, M. An RNN Approach for Lithium-ion Battery Internal Impedance Estimation. In Proceedings of the 2020 IEEE Region 10 Conference (Tencon), Osaka, Japan, 16–19 November 2020. [Google Scholar]
- Singh, M.; Bansal, S.; Vandana; Panigrahi, B.K.; Garg, A.R. A Genetic Algorithm and RNN-LSTM Model for Remaining Battery Capacity Prediction. ASME. J. Comput. Inf. Sci. Eng. 2022, 22, 041009. [Google Scholar] [CrossRef]
- Rouhi Ardeshiri, R.; Ma, C. Multivariate gated recurrent unit for battery remaining useful life prediction: A deep learning approach. Int. J. Energy Res. 2021, 45, 16633–16648. [Google Scholar] [CrossRef]
- Chen, D.; Hong, W.; Zhou, X. Transformer network for remaining useful life prediction of lithium-ion batteries. IEEE Access 2022, 10, 19621–19628. [Google Scholar] [CrossRef]
- Gozalo-Brizuela, R.; Garrido-Merchán, E. ChatGPT is not all you need. A State of the Art Review of large Generative AI models. arXiv 2023, arXiv:2301.04655. [Google Scholar]
- Cao, H.; Tan, C.; Gao, Z.; Chen, G.; Heng, P.; Li, S. A Survey on Generative Diffusion Model. arXiv 2022, arXiv:2209.02646. [Google Scholar]
- Yang, L.; Zhang, Z.; Hong, S.; Xu, R.; Zhao, Y.; Shao, Y.; Zhang, W.; Yang, M.; Cui, B. Diffusion Models: A Comprehensive Survey of Methods and Applications. arXiv 2022, arXiv:2209.00796. [Google Scholar]
- Bond-Taylor, S.; Leach, A.; Long, Y.; Willcocks, C.G. Deep Generative Modelling: A Comparative Review of VAEs, GANs, Normalizing Flows, Energy-Based and Autoregressive Models. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7327–7347. [Google Scholar] [CrossRef]
- Challu, C.; Jiang, P.; Wu, Y.N.; Callot, L. Deep Generative model with Hierarchical Latent Factors for Time Series Anomaly Detection. In Proceedings of the 2022 International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 30 March–1 April 2022. [Google Scholar]
- Tashiro, Y.; Song, J.; Song, Y.; Ermon, S. CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation. In Proceedings of the 2021 Neural Information Processing Systems, Virtual, 6–14 December 2021. [Google Scholar]
- Wu, Y.; Ni, J.; Cheng, W.; Zong, B.; Song, D.; Chen, Z.; Liu, Y.; Zhang, X.; Chen, H.; Davidson, S.B. Dynamic Gaussian Mixture based Deep Generative Model for Robust Forecasting on Sparse Multivariate Time Series. arXiv 2021, arXiv:2103.02164. [Google Scholar] [CrossRef]
- Kim, S.; Yun, Y.C.; Choi, J.I. Impedance-based capacity estimation for lithium-ion batteries using generative adversarial network. Appl. Energy 2022, 308, 118317. [Google Scholar] [CrossRef]
- He, H.; Zhang, J.; Wang, Y.; Huang, S.; Wang, C.; Zhang, Y.; Guo, D.; He, G.; Ouyang, M. Detecting Electric Vehicle Battery Failure via Dynamic-VAE. arXiv 2022, arXiv:2201.12358. [Google Scholar]
- Ardeshiri, R.R.; Razavi-Far, R.; Li, T.; Wang, X.; Ma, C.; Liu, M. Gated recurrent unit least-squares generative adversarial network for battery cycle life prediction. Measurement 2022, 196, 111046. [Google Scholar] [CrossRef]
- Oussidi, A.; Elhassouny, A. Deep generative models: Survey. In Proceedings of the 2018 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 2–4 April 2018. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. arXiv 2020, arXiv:2006.11239. [Google Scholar]
- Rasul, K.; Seward, C.; Schuster, I.; Vollgraf, R. Autoregressive Denoising Diffusion Models for Multivariate Probabilistic Time Series Forecasting. In Proceedings of the 2021 International Conference on Machine Learning, Virtual, 18–24 July 2021. [Google Scholar]
- Abedi, S.; Yoon, S.W.; Kwon, S. Battery energy storage control using a reinforcement learning approach with cyclic time-dependent Markov process. Int. J. Electr. Power Energy Syst. 2022, 134, 107368. [Google Scholar] [CrossRef]
- Sun, H.; Sun, J.; Zhao, K.; Wang, L.; Wang, K. Data-Driven ICA-Bi-LSTM-Combined Lithium Battery SOH Estimation. Math. Probl. Eng. 2022, 2022, 8. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.Y.; Kim, K.J.; Choi, J.I. Forecasting state-of-health of lithium-ion batteries using variational long short-term memory with transfer learning. J. Energy Storage 2021, 41, 102893. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Huang, Y.; Bhushan Gopaluni, R.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Mereacre, L.; Dai, H.; Liu, X.; et al. Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation. Nat. Commun. 2022, 13, 2262. [Google Scholar] [CrossRef]
- LI, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. arXiv 2019, arXiv:1907.00235. [Google Scholar]



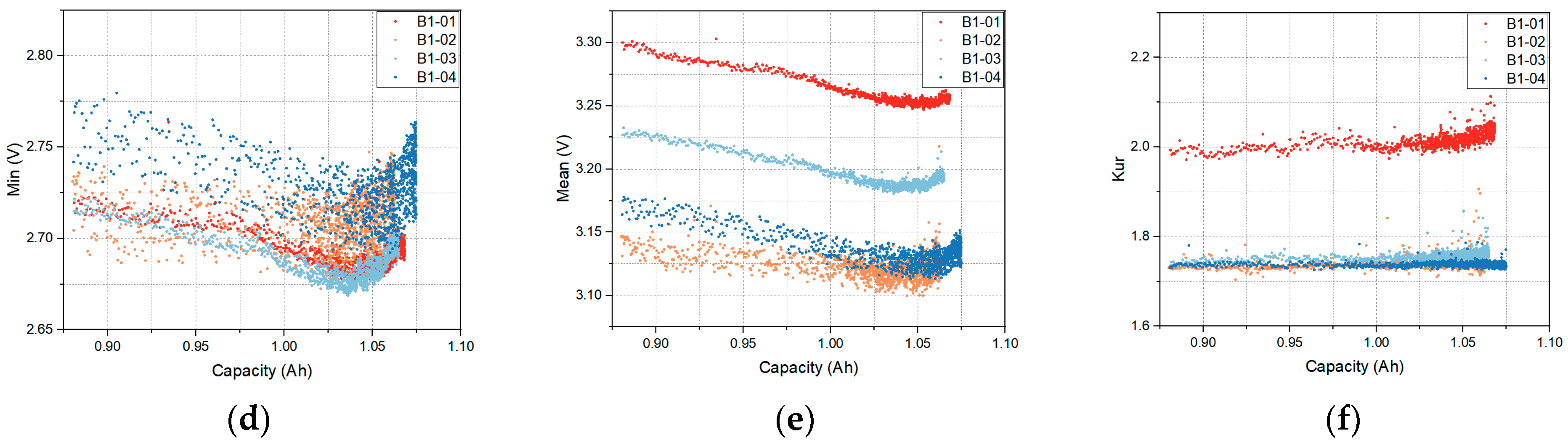
| Spec. | Dataset 1 | Dataset 2 |
|---|---|---|
| Rated capacity (Ah) | 1.1 | 73 |
| Number of cells | 4 | 2 |
| Charging current (A) | 2.64-1.43-1.1 | 29.2-21.9-3.65 |
| Discharging current (A) | 4.4 | 73 |
| Max cut-off voltage (V) | 3.6 | 4.3 |
| Min cut-off voltage (V) | 2.0 | 2.7 |
| Number of cycles (Bn mm denotes the battery code) | B1-01:1062 B1-02:1266 B1-03:1114 B1-04:1047 | B2-01:373 B2-02:373 |
| Index | B1-01 | B1-02 | B1-03 | B1-04 |
|---|---|---|---|---|
| RMSE | 0.0049 | 0.0187 | 0.0034 | 0.0166 |
| MAE | 0.0044 | 0.0183 | 0.0022 | 0.0164 |
| MAPE | 0.43% | 1.81% | 0.23% | 1.55% |
| Index | RNN | LSTM | GRU | Transformer | CNN-Transformer | Proposed Approach |
|---|---|---|---|---|---|---|
| RMSE | 0.0253 | 0.0167 | 0.0121 | 0.0364 | 0.0227 | 0.0109 |
| MAE | 0.0271 | 0.0134 | 0.0115 | 0.0278 | 0.0218 | 0.0103 |
| MAPE | 2.94% | 1.32% | 1.07% | 3.03% | 2.11% | 1.01% |
| Case | Index | B2-01 | B2-02 |
|---|---|---|---|
| With transfer learning | RMSE | 0.0031 | 0.0028 |
| MAE | 0.0027 | 0.0023 | |
| MAPE | 0.28% | 0.24% | |
| Without transfer learning | RMSE | 0.0411 | 0.0437 |
| MAE | 0.0387 | 0.0388 | |
| MAPE | 4.03% | 4.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Zhang, Z.; Zhu, S.; Li, Y. State-of-Health Prediction of Lithium-Ion Batteries Based on Diffusion Model with Transfer Learning. Energies 2023, 16, 3815. https://doi.org/10.3390/en16093815
Luo C, Zhang Z, Zhu S, Li Y. State-of-Health Prediction of Lithium-Ion Batteries Based on Diffusion Model with Transfer Learning. Energies. 2023; 16(9):3815. https://doi.org/10.3390/en16093815
Chicago/Turabian StyleLuo, Chenqiang, Zhendong Zhang, Shunliang Zhu, and Yongying Li. 2023. "State-of-Health Prediction of Lithium-Ion Batteries Based on Diffusion Model with Transfer Learning" Energies 16, no. 9: 3815. https://doi.org/10.3390/en16093815
APA StyleLuo, C., Zhang, Z., Zhu, S., & Li, Y. (2023). State-of-Health Prediction of Lithium-Ion Batteries Based on Diffusion Model with Transfer Learning. Energies, 16(9), 3815. https://doi.org/10.3390/en16093815





