Optimal Neutral Grounding in Bipolar DC Networks with Asymmetric Loading: A Recursive Mixed-Integer Quadratic Formulation
Abstract
1. Introduction
1.1. General Context
- i.
- Reduced energy losses due to resistive effects in cables operated with DC are lower than those in cables operated with AC due to the skin effect [7]. Additionally, these energy losses are also reduced because, in DC networks, no reactance effects are considered. This implies that the voltage droops in the lines are lower, resulting in reduced current magnitudes for these branches. This reduction is directly linked to the power loss level [8].
- ii.
- DC networks are easily controllable, as the only variable of interest is the voltage supplied at the substation bus, which is a real and constant variable. The main advantage is that no frequency issues are considered since this variable does not exist in DC technology [9].
- iii.
- DC technology is the natural choice for operating batteries, photovoltaic (PV) sources, fuel cells, supercapacitors, and superconductor energy storage systems. This implies that integrating these devices in DC grids requires fewer power conversion stages, which can reduce the expected investment costs and increase the reliability of the entire grid by reducing the number of cascade devices (i.e., DC to AC conversion stages) [10,11].
1.2. Motivation
1.3. Literature Review
1.4. Contributions and Scope
- i.
- A mixed-integer convex model is proposed to represent the optimal selection of nodes to be solidly grounded in order to minimize the total grid power losses.
- ii.
- The convex approximation model uses the first Taylor term to linearize the nonlinear relation between powers and voltages in the constant power demands.
- iii.
- A recursive solution methodology is presented to reduce/eliminate the error introduced by the linearization approach. This methodology is based on Taylor’s series expansion, which updates the voltages in all of the network poles at each iteration until the desired convergence error is reached.
- iv.
- Numerical results in three test systems demonstrate the performance and effect of the model in reducing the grid power losses.
1.5. Document Structure
2. Optimal Neutral Grounding Model
2.1. Objective Function
2.2. Set of Constraints
2.2.1. Current Balance Equation
2.2.2. Current Demand Formulation
2.2.3. Operating Limits
2.2.4. Grounding of the Neutral Wire
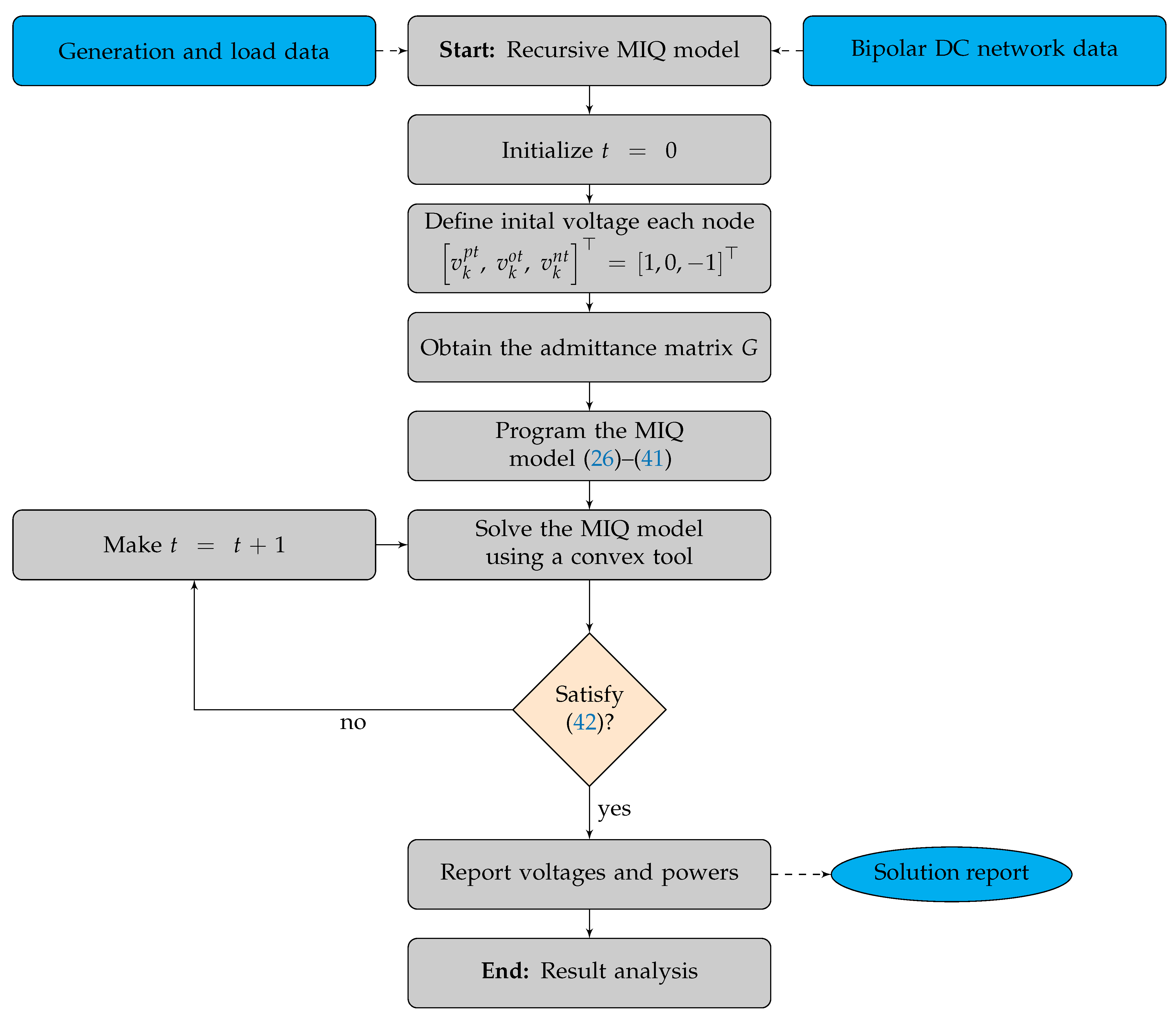
3. Recursive Quadratic Approximation for the Optimal Neutral Grounding
3.1. Objective Function Analysis
3.2. Linear Approximation Applied to Constant Power Loads
3.3. Recursive Mixed-Integer Quadratic Algorithm
4. Test Feeders
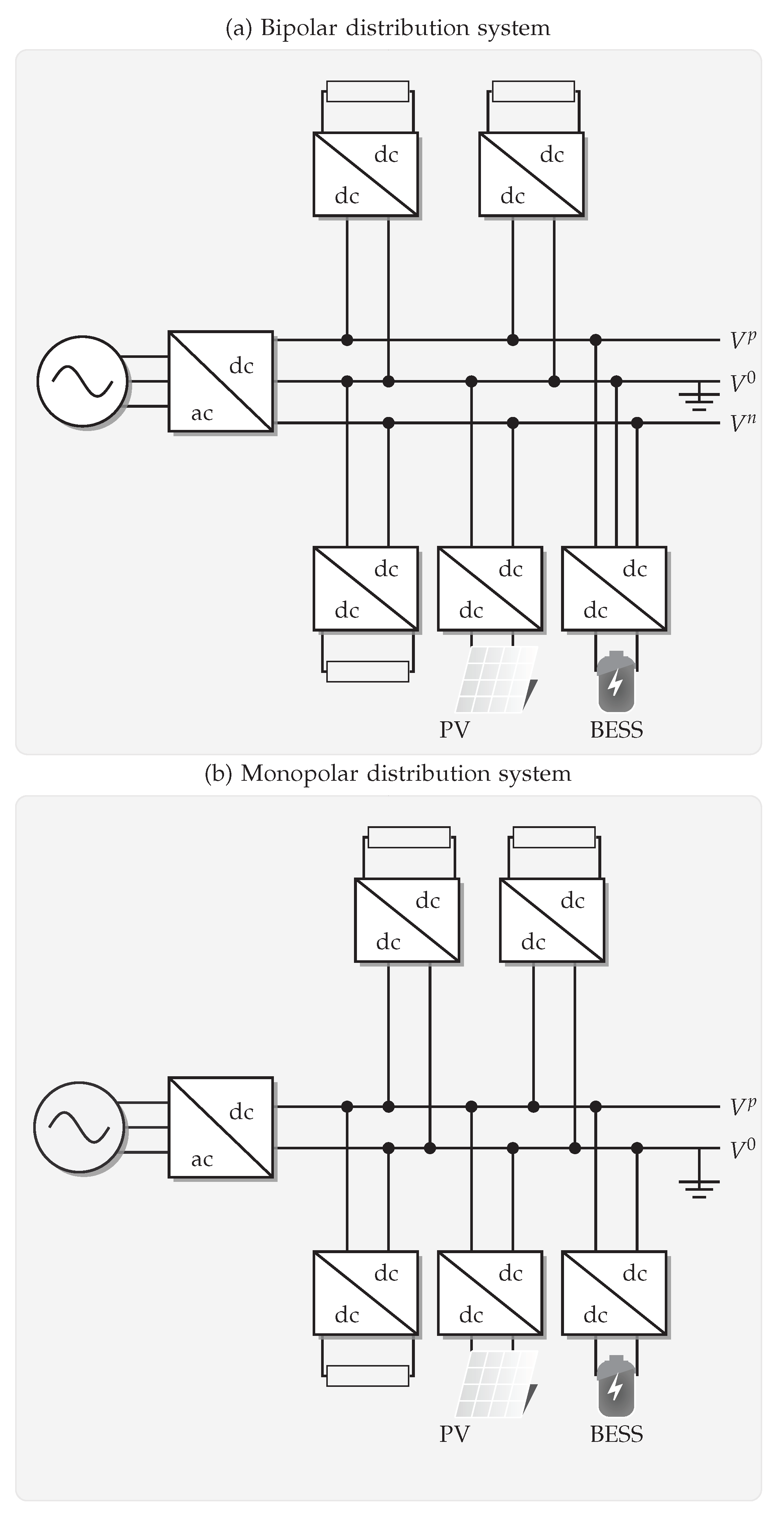
4.1. Bipolar DC 21-Bus System
4.2. Bipolar DC 33-Bus System
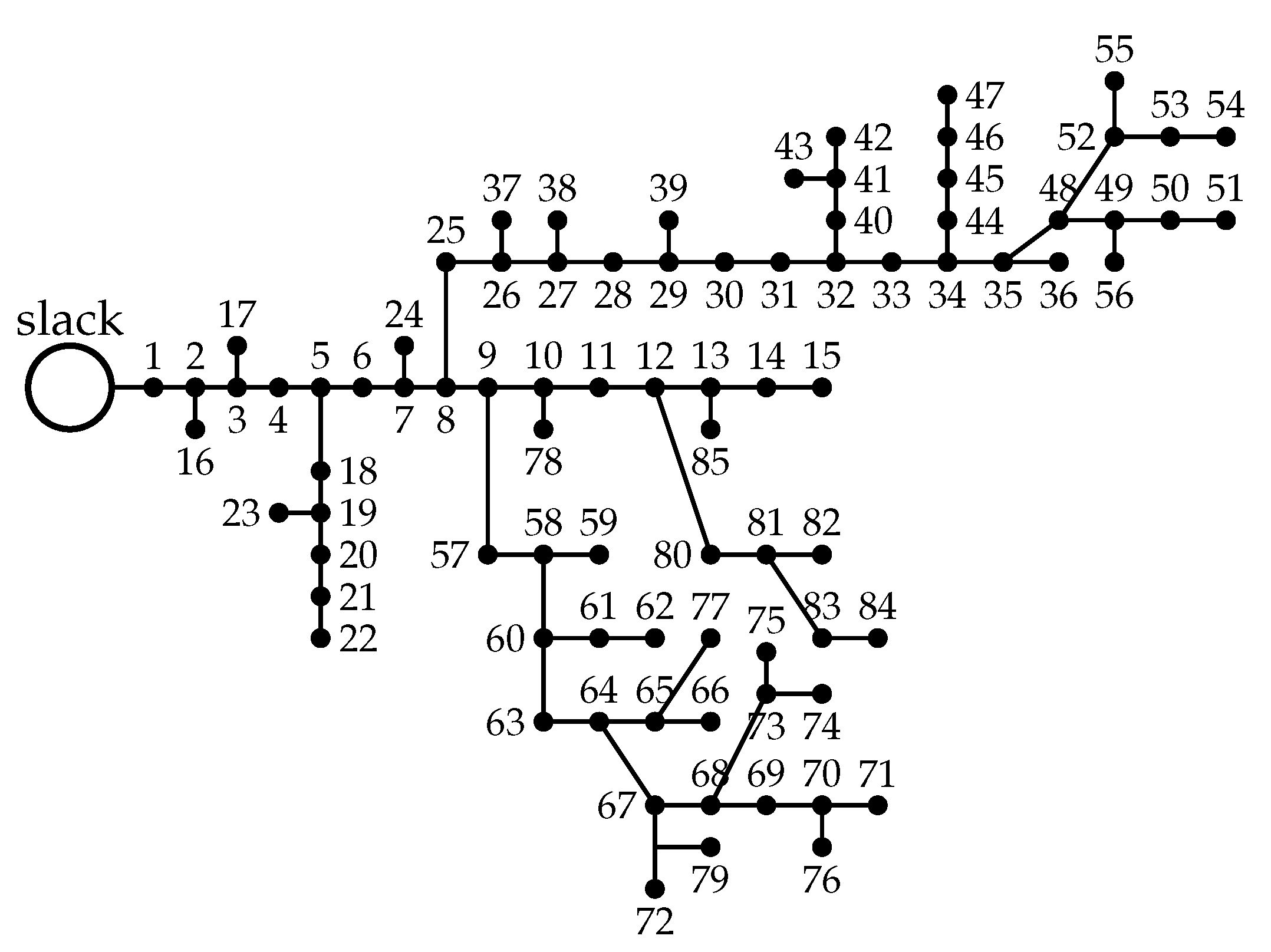
4.3. Bipolar DC 85-Bus System
5. Computational Results
- C1:
- The proposed recursive MIQ model and the non-convex MINLP model were assessed while only considering the grounding of the three neutral wires.
- C2:
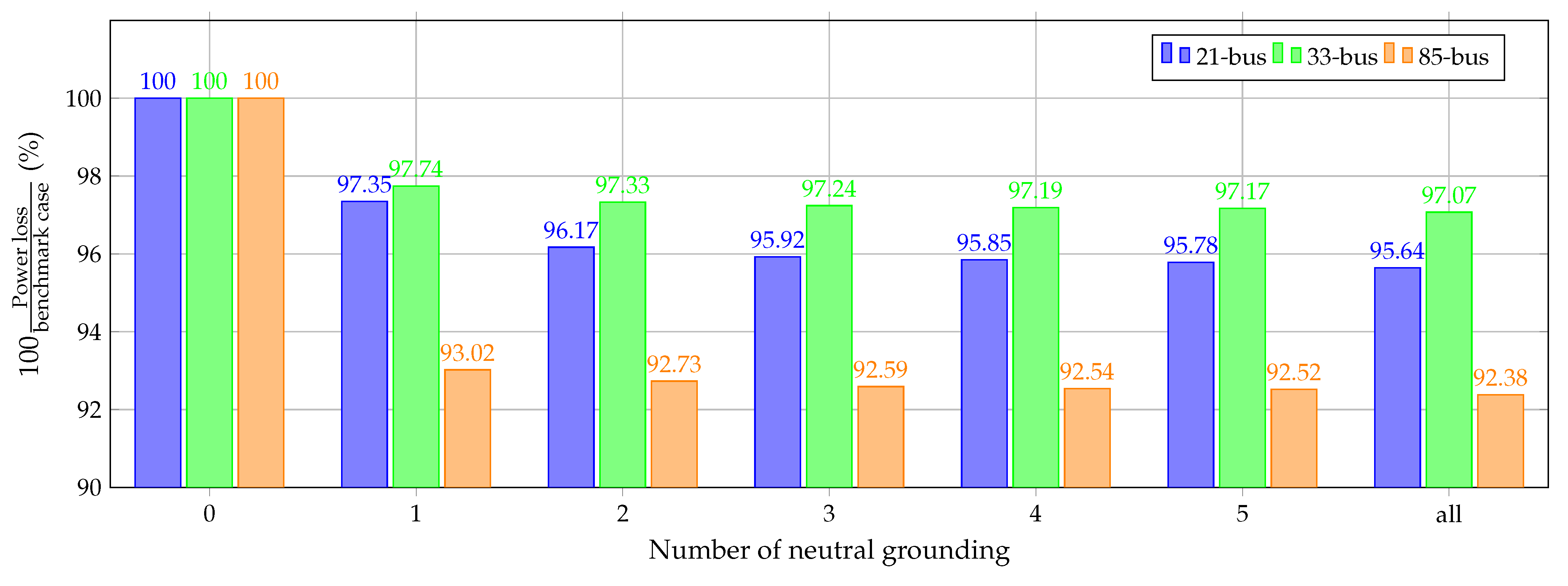
- The impact on the total power losses caused by varying the number of neutral wires grounded from 0 to 5 was analyzed.
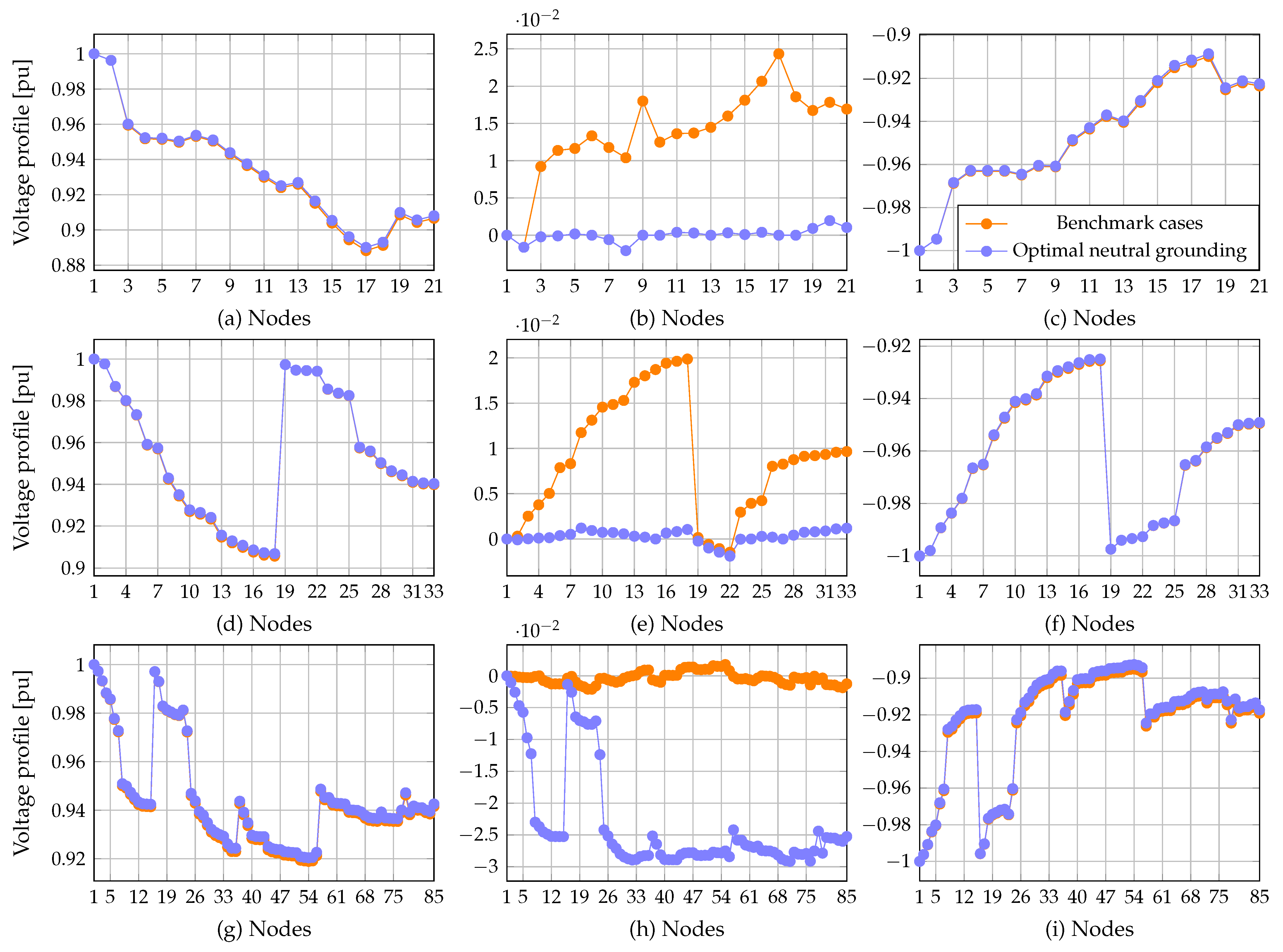
5.1. Analysis of Case 1 (C1)
- The proposed recursive MIQ model reached the best solution in the analyzed networks, with objective function values of 91.5346 kW, 335.0946 kW, and 453.3122 kW for the bipolar DC 21-, 33-, and 85-node systems, respectively. These results were also obtained by the non-convex MINLP model. In addition, the results show power loss reductions of 4.07%, 2.75%, and 7.40% (compared to the benchmark cases) for the bipolar DC 21-, 33-, and 85-node test feeders.
- For the bipolar DC 21-bus system, it can be observed that the CBC solver found the same result as the recursive MIQ model. In comparison, the other solvers (BONMIN and GUROBI) achieved the worst solutions; they became stuck in local optima. These results reduced the power losses by 3.40% and 3.88%.
- For the bipolar DC 33-bus system, it can be noted that no GAMS solver could find the same solution as the proposed model; they all reached different local optima, reducing the power losses by 2.46%, 2.47%, and 2.25% for the CBC, BONMIN, and GUROBI solvers, respectively.
- For the bipolar DC 85-bus system, no GAMS solver could reach the same solution as the proposed model, and the solutions differ. This indicates that the GAMS solvers found local optima, reducing the grid power losses by 6.94%, 6.94%, and 6.17%, that is, the CBC, BONMIN, and GUROBI solvers, respectively.
- No GAMS solver outperformed the others, since the CBC solver found a better solution in the bipolar DC 21- and 85-node systems, while the BONMIN solver reached a better solution for the 33-bus system.
5.2. Analysis of Case 2 (C2)
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lakshmi, S.; Ganguly, S. Transition of Power Distribution System Planning from Passive to Active Networks: A State-of-the-Art Review and a New Proposal. In Sustainable Energy Technology and Policies; Springer: Singapore, 2017; pp. 87–117. [Google Scholar] [CrossRef]
- Liu, G.; Huang, R.; Pu, T.; Yang, Z. Design of energy management system for Active Distribution Network. In Proceedings of the 2014 China International Conference on Electricity Distribution (CICED), Shenzhen, China, 23–26 September 2014. [Google Scholar] [CrossRef]
- Li, Z.; Su, S.; Zhao, Y.; Jin, X.; Chen, H.; Li, Y.; Zhang, R. Energy management strategy of active distribution network with integrated distributed wind power and smart buildings. IET Renew. Power Gener. 2020, 14, 2255–2267. [Google Scholar] [CrossRef]
- Zhou, D.; Chen, S.; Wang, H.; Guan, M.; Zhou, L.; Wu, J.; Hu, Y. Autonomous Cooperative Control for Hybrid AC/DC Microgrids Considering Multi-Energy Complementarity. Front. Energy Res. 2021, 9, 692026. [Google Scholar] [CrossRef]
- Siraj, K.; Khan, H.A. DC distribution for residential power networks—A framework to analyze the impact of voltage levels on energy efficiency. Energy Rep. 2020, 6, 944–951. [Google Scholar] [CrossRef]
- Jing, G.; Zhang, A.; Zhang, H. Review on DC Distribution Network Protection Technology with Distributed Power Supply. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018. [Google Scholar] [CrossRef]
- Liu, Z.; Li, M. Research on Energy Efficiency of DC Distribution System. AASRI Procedia 2014, 7, 68–74. [Google Scholar] [CrossRef]
- Garces, A. Uniqueness of the power flow solutions in low voltage direct current grids. Electr. Power Syst. Res. 2017, 151, 149–153. [Google Scholar] [CrossRef]
- Garces, A. On the Convergence of Newton’s Method in Power Flow Studies for DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5770–5777. [Google Scholar] [CrossRef]
- Justo, J.J.; Mwasilu, F.; Lee, J.; Jung, J.W. AC-microgrids versus DC-microgrids with distributed energy resources: A review. Renew. Sustain. Energy Rev. 2013, 24, 387–405. [Google Scholar] [CrossRef]
- Razmi, D.; Babayomi, O.; Davari, A.; Rahimi, T.; Miao, Y.; Zhang, Z. Review of Model Predictive Control of Distributed Energy Resources in Microgrids. Symmetry 2022, 14, 1735. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, M.; Zhang, J.; Cai, X.; Dai, N. Topology and operation mechanism of monopolar-to-bipolar DC-DC converter interface for DC grid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar] [CrossRef]
- Najafi, P.; Viki, A.H.; Shahparasti, M. An integrated interlinking converter with DC-link voltage balancing capability for bipolar hybrid microgrid. Electr. Eng. 2019, 101, 895–909. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W. Optimal Pole-Swapping in Bipolar DC Networks with Multiple CPLs Using an MIQP Model. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Liao, J.; Zhou, N.; Wang, Q.; Chi, Y. Load-Switching Strategy for Voltage Balancing of Bipolar DC Distribution Networks Based on Optimal Automatic Commutation Algorithm. IEEE Trans. Smart Grid 2021, 12, 2966–2979. [Google Scholar] [CrossRef]
- Chew, B.S.H.; Xu, Y.; Wu, Q. Voltage Balancing for Bipolar DC Distribution Grids: A Power Flow Based Binary Integer Multi-Objective Optimization Approach. IEEE Trans. Power Syst. 2019, 34, 28–39. [Google Scholar] [CrossRef]
- Montoya, O.D.; Medina-Quesada, Á.; Hernández, J.C. Optimal Pole-Swapping in Bipolar DC Networks Using Discrete Metaheuristic Optimizers. Electronics 2022, 11, 2034. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S.; Jeon, J.H. Generic power flow algorithm for bipolar DC microgrids based on Newton–Raphson method. Int. J. Electr. Power Energy Syst. 2022, 142, 108357. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Optimal Power Flow Solution for Bipolar DC Networks Using a Recursive Quadratic Approximation. Energies 2023, 16, 589. [Google Scholar] [CrossRef]
- Garces, A.; Montoya, O.D.; Gil-Gonzalez, W. Power Flow in Bipolar DC Distribution Networks Considering Current Limits. IEEE Trans. Power Syst. 2022, 37, 4098–4101. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garcés, A. A successive approximations method for power flow analysis in bipolar DC networks with asymmetric constant power terminals. Electr. Power Syst. Res. 2022, 211, 108264. [Google Scholar] [CrossRef]
- Mackay, L.; Dimou, A.; Guarnotta, R.; Morales-Espania, G.; Ramirez-Elizondo, L.; Bauer, P. Optimal power flow in bipolar DC distribution grids with asymmetric loading. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016. [Google Scholar] [CrossRef]
- Mackay, L.; Guarnotta, R.; Dimou, A.; Morales-Espana, G.; Ramirez-Elizondo, L.; Bauer, P. Optimal Power Flow for Unbalanced Bipolar DC Distribution Grids. IEEE Access 2018, 6, 5199–5207. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Hernández, J.C. A Recursive Conic Approximation for Solving the Optimal Power Flow Problem in Bipolar Direct Current Grids. Energies 2023, 16, 1729. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S.; Jeon, J.H. Optimal power flow for bipolar DC microgrids. Int. J. Electr. Power Energy Syst. 2022, 142, 108375. [Google Scholar] [CrossRef]
- Barbu, V.; Precupanu, T. Convexity and Optimization in Banach Spaces; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Berkovitz, L.D. Convexity and Optimization in Rn, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar]
- Montoya, O.D.; Molina-Cabrera, A.; Gil-González, W. A mixed-integer convex approximation for optimal load redistribution in bipolar DC networks with multiple constant power terminals. Results Eng. 2022, 16, 100689. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Optimal Scheduling of Photovoltaic Generators in Asymmetric Bipolar DC Grids Using a Robust Recursive Quadratic Convex Approximation. Machines 2023, 11, 177. [Google Scholar] [CrossRef]
- Sepúlveda-García, S.; Montoya, O.D.; Garcés, A. Power Flow Solution in Bipolar DC Networks Considering a Neutral Wire and Unbalanced Loads: A Hyperbolic Approximation. Algorithms 2022, 15, 341. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. 2014. Available online: http://cvxr.com/cvx (accessed on 28 March 2023).
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Beaverton, OR, USA, 2023. [Google Scholar]
- Soroudi, A. Power System Optimization Modeling in GAMS; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]

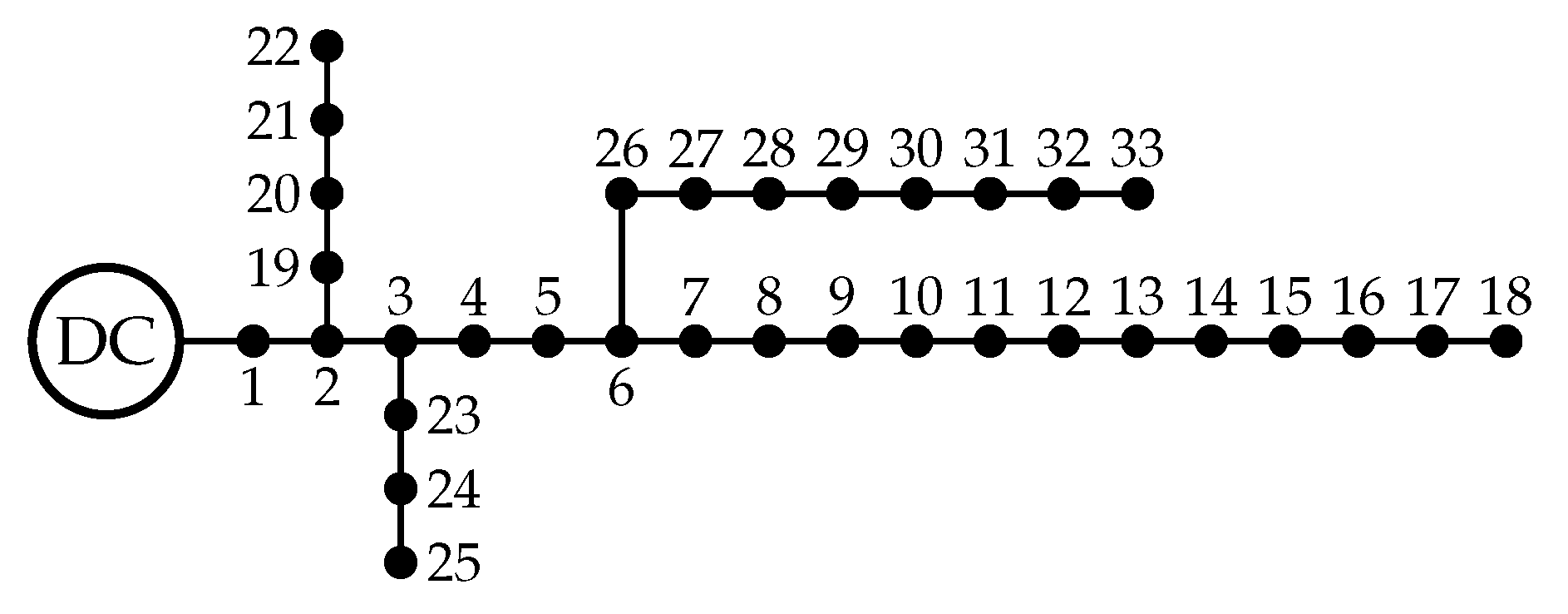
| Node j | Node k | () | |||
|---|---|---|---|---|---|
| 1 | 2 | 0.053 | 70 | 100 | 0 |
| 1 | 3 | 0.054 | 0 | 0 | 0 |
| 3 | 4 | 0.054 | 36 | 40 | 120 |
| 4 | 5 | 0.063 | 4 | 0 | 0 |
| 4 | 6 | 0.051 | 36 | 0 | 0 |
| 3 | 7 | 0.037 | 0 | 0 | 0 |
| 7 | 8 | 0.079 | 32 | 50 | 0 |
| 7 | 9 | 0.072 | 80 | 0 | 100 |
| 3 | 10 | 0.053 | 0 | 10 | 0 |
| 10 | 11 | 0.038 | 45 | 30 | 0 |
| 11 | 12 | 0.079 | 68 | 70 | 0 |
| 11 | 13 | 0.078 | 10 | 0 | 75 |
| 10 | 14 | 0.083 | 0 | 0 | 0 |
| 14 | 15 | 0.065 | 22 | 30 | 0 |
| 15 | 16 | 0.064 | 23 | 10 | 0 |
| 16 | 17 | 0.074 | 43 | 0 | 60 |
| 16 | 18 | 0.081 | 34 | 60 | 0 |
| 14 | 19 | 0.078 | 9 | 15 | 0 |
| 19 | 20 | 0.084 | 21 | 10 | 50 |
| 19 | 21 | 0.082 | 21 | 20 | 0 |
| Node j | Node k | () | |||
|---|---|---|---|---|---|
| 1 | 2 | 0.0922 | 100 | 150 | 0 |
| 2 | 3 | 0.4930 | 90 | 75 | 0 |
| 3 | 4 | 0.3660 | 120 | 100 | 0 |
| 4 | 5 | 0.3811 | 60 | 90 | 0 |
| 5 | 6 | 0.8190 | 60 | 0 | 200 |
| 6 | 7 | 0.1872 | 100 | 50 | 150 |
| 7 | 8 | 1.7114 | 100 | 0 | 0 |
| 8 | 9 | 1.0300 | 60 | 70 | 100 |
| 9 | 10 | 1.0400 | 60 | 80 | 25 |
| 10 | 11 | 0.1966 | 45 | 0 | 0 |
| 11 | 12 | 0.3744 | 60 | 90 | 0 |
| 12 | 13 | 1.4680 | 60 | 60 | 100 |
| 13 | 14 | 0.5416 | 120 | 100 | 200 |
| 14 | 15 | 0.5910 | 60 | 30 | 50 |
| 15 | 16 | 0.7463 | 110 | 0 | 350 |
| 16 | 17 | 1.2890 | 60 | 90 | 0 |
| 17 | 18 | 0.7320 | 90 | 45 | 0 |
| 2 | 19 | 0.1640 | 90 | 150 | 0 |
| 19 | 20 | 1.5042 | 150 | 50 | 115 |
| 20 | 21 | 0.4095 | 0 | 90 | 0 |
| 21 | 22 | 0.7089 | 0 | 90 | 145 |
| 3 | 23 | 0.4512 | 90 | 110 | 35 |
| 23 | 24 | 0.8980 | 120 | 0 | 40 |
| 24 | 25 | 0.8960 | 150 | 100 | 100 |
| 6 | 26 | 0.2030 | 60 | 80 | 0 |
| 26 | 27 | 0.2842 | 60 | 0 | 225 |
| 27 | 28 | 1.0590 | 0 | 0 | 130 |
| 28 | 29 | 0.8042 | 120 | 75 | 65 |
| 29 | 30 | 0.5075 | 100 | 100 | 0 |
| 30 | 31 | 0.9744 | 50 | 150 | 125 |
| 31 | 32 | 0.3105 | 175 | 100 | 75 |
| 32 | 33 | 0.3410 | 95 | 60 | 120 |
| Node j | Node k | () | Node j | Node k | () | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.108 | 0 | 0 | 10.075 | 34 | 44 | 1.002 | 17.64 | 17.995 | 0 |
| 2 | 3 | 0.163 | 50 | 0 | 40.35 | 44 | 45 | 0.911 | 50 | 17.64 | 17.995 |
| 3 | 4 | 0.217 | 28 | 28.565 | 0 | 45 | 46 | 0.911 | 25 | 17.64 | 17.995 |
| 4 | 5 | 0.108 | 100 | 50 | 0 | 46 | 47 | 0.546 | 7 | 7.14 | 10 |
| 5 | 6 | 0.435 | 17.64 | 17.995 | 25.18 | 35 | 48 | 0.637 | 0 | 10 | 0 |
| 6 | 7 | 0.272 | 0 | 8.625 | 0 | 48 | 49 | 0.182 | 0 | 0 | 25 |
| 7 | 8 | 1.197 | 17.64 | 17.995 | 30.29 | 49 | 50 | 0.364 | 18.14 | 0 | 18.505 |
| 8 | 9 | 0.108 | 17.8 | 350 | 40.46 | 50 | 51 | 0.455 | 28 | 28.565 | 0 |
| 9 | 10 | 0.598 | 0 | 100 | 0 | 48 | 52 | 1.366 | 30 | 0 | 15 |
| 10 | 11 | 0.544 | 28 | 28.565 | 0 | 52 | 53 | 0.455 | 17.64 | 35 | 17.995 |
| 11 | 12 | 0.544 | 0 | 40 | 45 | 53 | 54 | 0.546 | 28 | 30 | 28.565 |
| 12 | 13 | 0.598 | 45 | 40 | 22.5 | 52 | 55 | 0.546 | 38 | 0 | 48.565 |
| 13 | 14 | 0.272 | 17.64 | 17.995 | 35.13 | 49 | 56 | 0.546 | 7 | 40 | 32.14 |
| 14 | 15 | 0.326 | 17.64 | 17.995 | 20.175 | 9 | 57 | 0.273 | 48 | 35.065 | 10 |
| 2 | 16 | 0.728 | 17.64 | 67.5 | 33.49 | 57 | 58 | 0.819 | 0 | 50 | 0 |
| 3 | 17 | 0.455 | 56.1 | 57.15 | 50.25 | 58 | 59 | 0.182 | 18 | 28.565 | 25 |
| 5 | 18 | 0.820 | 28 | 28.565 | 200 | 58 | 60 | 0.546 | 28 | 43.565 | 0 |
| 18 | 19 | 0.637 | 28 | 28.565 | 10 | 60 | 61 | 0.728 | 18 | 28.565 | 30 |
| 19 | 20 | 0.455 | 17.64 | 17.995 | 150 | 61 | 62 | 1.002 | 12.5 | 29.065 | 0 |
| 20 | 21 | 0.819 | 17.64 | 70 | 152.5 | 60 | 63 | 0.182 | 7 | 7.14 | 5 |
| 21 | 22 | 1.548 | 17.64 | 17.995 | 30 | 63 | 64 | 0.728 | 0 | 0 | 50 |
| 19 | 23 | 0.182 | 28 | 75 | 28.565 | 64 | 65 | 0.182 | 12.5 | 25 | 37.5 |
| 7 | 24 | 0.910 | 0 | 17.64 | 17.995 | 65 | 66 | 0.182 | 40 | 48.565 | 33 |
| 8 | 25 | 0.455 | 17.64 | 17.995 | 50 | 64 | 67 | 0.455 | 0 | 0 | 0 |
| 25 | 26 | 0.364 | 0 | 28 | 28.565 | 67 | 68 | 0.910 | 0 | 0 | 0 |
| 26 | 27 | 0.546 | 110 | 75 | 175 | 68 | 69 | 1.092 | 13 | 18.565 | 25 |
| 27 | 28 | 0.273 | 28 | 125 | 28.565 | 69 | 70 | 0.455 | 0 | 20 | 0 |
| 28 | 29 | 0.546 | 0 | 50 | 75 | 70 | 71 | 0.546 | 17.64 | 38.275 | 17.995 |
| 29 | 30 | 0.546 | 17.64 | 0 | 17.995 | 67 | 72 | 0.182 | 28 | 13.565 | 0 |
| 30 | 31 | 0.273 | 17.64 | 17.995 | 0 | 68 | 73 | 1.184 | 30 | 0 | 0 |
| 31 | 32 | 0.182 | 0 | 175 | 0 | 73 | 74 | 0.273 | 28 | 50 | 28.565 |
| 32 | 33 | 0.182 | 7 | 7.14 | 12.5 | 73 | 75 | 1.002 | 17.64 | 6.23 | 17.995 |
| 33 | 34 | 0.819 | 0 | 0 | 0 | 70 | 76 | 0.546 | 38 | 48.565 | 0 |
| 34 | 35 | 0.637 | 0 | 0 | 50 | 65 | 77 | 0.091 | 7 | 17.14 | 25 |
| 35 | 36 | 0.182 | 17.64 | 0 | 17.995 | 10 | 78 | 0.637 | 28 | 6 | 28.565 |
| 26 | 37 | 0.364 | 28 | 30 | 28.565 | 67 | 79 | 0.546 | 17.64 | 42.995 | 0 |
| 27 | 38 | 1.002 | 28 | 28.565 | 25 | 12 | 80 | 0.728 | 28 | 28.565 | 30 |
| 29 | 39 | 0.546 | 0 | 28 | 28.565 | 80 | 81 | 0.364 | 45 | 0 | 75 |
| 32 | 40 | 0.455 | 17.64 | 0 | 17.995 | 81 | 82 | 0.091 | 28 | 53.75 | 0 |
| 40 | 41 | 1.002 | 10 | 0 | 0 | 81 | 83 | 1.092 | 12.64 | 32.995 | 62.5 |
| 41 | 42 | 0.273 | 17.64 | 25 | 17.995 | 83 | 84 | 1.002 | 62 | 72.2 | 0 |
| 41 | 43 | 0.455 | 17.64 | 17.995 | 0 | 13 | 85 | 0.819 | 10 | 10 | 10 |
| 21-Bus Bipolar DC Grid | 33-Bus Bipolar DC Grid | 85-Bus Bipolar DC Grid | ||||
|---|---|---|---|---|---|---|
| Method | Location (Bus) | (kW) | Location (Bus) | (kW) | Location (Bus) | (kW) |
| Ben. case | 95.4237 | 344.4797 | 489.5759 | |||
| CBC | 91.5346 | 336.0032 | 455.5865 | |||
| BONMIN | 92.1718 | 335.9671 | 455.5984 | |||
| GUROBI | 91.7213 | 336.7072 | 459.3622 | |||
| MIQ | 91.5346 | 334.9963 | 453.3122 | |||
| Number of Nodes for Grounding | Grounded Nodes | ||
|---|---|---|---|
| 21-Test System | 33-Test System | 85-Test System | |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil-González, W.; Montoya, O.D.; Hernández, J.C. Optimal Neutral Grounding in Bipolar DC Networks with Asymmetric Loading: A Recursive Mixed-Integer Quadratic Formulation. Energies 2023, 16, 3755. https://doi.org/10.3390/en16093755
Gil-González W, Montoya OD, Hernández JC. Optimal Neutral Grounding in Bipolar DC Networks with Asymmetric Loading: A Recursive Mixed-Integer Quadratic Formulation. Energies. 2023; 16(9):3755. https://doi.org/10.3390/en16093755
Chicago/Turabian StyleGil-González, Walter, Oscar Danilo Montoya, and Jesús C. Hernández. 2023. "Optimal Neutral Grounding in Bipolar DC Networks with Asymmetric Loading: A Recursive Mixed-Integer Quadratic Formulation" Energies 16, no. 9: 3755. https://doi.org/10.3390/en16093755
APA StyleGil-González, W., Montoya, O. D., & Hernández, J. C. (2023). Optimal Neutral Grounding in Bipolar DC Networks with Asymmetric Loading: A Recursive Mixed-Integer Quadratic Formulation. Energies, 16(9), 3755. https://doi.org/10.3390/en16093755