Steady-State Load Flow Model of DFIG Wind Turbine Based on Generator Power Loss Calculation

Rudy Gianto; Purwoharjono; Fitri Imansyah; Rudi Kurnianto; Danial

doi:10.3390/en16093640

,

and

Department of Electrical Engineering, Tanjungpura University, Pontianak 78124, Indonesia

^*

Author to whom correspondence should be addressed.

Energies2023, 16(9), 3640;https://doi.org/10.3390/en16093640

This article belongs to the Special Issue Advances in Power System Analysis and Control

Version Notes

Order Reprints

Abstract

Penetration of wind power plants (WPPs) in the electric power system will complicate the system load flow analysis. Consequently, the traditional load flow algorithm can no longer be used to find the solution to the load flow problem of such a system. This paper proposes a doubly fed induction generator (DFIG)-based WPP model for a load flow analysis of the electric power system. The proposed model is derived based on the power formulations of the WPP—namely, DFIG power, DFIG power loss, and WPP power output formulas. The model can be applied to various DFIG power factor operating modes. In the present paper, applications of the proposed methods in two representative electric power systems (i.e., IEEE 14-bus and 30-bus systems) have been investigated. The investigation results verify the proposed method’s capability to solve the load flow problem of the system embedded with DFIG-based variable-speed WPPs.

Keywords:

DFIG steady-state model; wind farm; load flow; power system

1. Introduction

Information about the steady-state performances of an electric power system is usually obtained from load flow analysis. Quantities such as system voltages, generator powers, line power flows, and line losses are generally available as the output of the analysis. Based on the load flow results, an assessment or evaluation of the power system performance can then be carried out. If some values of the electrical quantities are outside the limits, corrective action needs to be taken to bring the quantities back to their allowable limits.

It has been well acknowledged that penetration of WPPs in the electric power system will complicate the system load flow analysis. Consequently, the traditional load flow algorithm can no longer be used to find the solution to the load flow problem of such a system. Several techniques for solving the load flow problem of power systems embedded with WPPs have been proposed, and some of the current methods are reported in [1,2,3,4,5,6,7,8,9,10,11,12,13]. In [1,2,3], three-node models of fixed-speed WPPs were proposed. By using these models, conventional load flow programs can be employed in the analysis. In [4], the models for representing asynchronous generator-based fixed-speed WPPs have been proposed. The models in [4] were developed based on the formulas that calculate the electric powers exchanged between the WPPs and the power grid. A fixed-speed WPP model for distribution load flow analysis has been proposed in [5]. In [5], the WPP model was formulated in the form of WPP output power.

In [6,7], three-phase models of DFIG-based variable-speed WPPs have been proposed. In [6], the model was derived in the form of DFIG output power and expressed in terms of bus voltage and wind speed. In [7], the DFIG model was formed using the sequence components theory. A technique to integrate DFIG-based WPPs in load flow analysis was discussed in [8]. The equivalent circuit of the induction generator has been used in the proposed approach [8]. In [9], a load flow model of the DFIG under power control has been proposed. Limitations of the DFIG and the power system were simultaneously solved to achieve the desired output. The DFIG model in [10] was based on an induction generator equivalent circuit and also took into consideration the voltage-dependent reactive power limits associated with the DFIG. References [11,12,13] proposed various models of DFIGs for load flow analysis. Derivation of the models has been carried out based on the WPP power formulas. However, in [11], the DFIG power factor was assumed to be unity. In [12], a DFIG steady-state model in voltage control mode of operation was proposed. In the method, DFIG voltage can be regulated by allowing the power factor to change. A simple load flow model of the DFIG was proposed in [13]. The model can be used for DFIGs operating in power factor control mode. Three DFIG power factor operation modes (i.e., unity, lagging, and leading) were considered in [13].

This paper presents a model of a DFIG-based variable-speed WPP for a load flow analysis of an electric power system. The proposed model is derived based on the power formulations of the WPP—namely, DFIG power, DFIG power loss, and WPP power output formulas. The model proposed in this paper also serves as an alternative to the model discussed in [13]. It, therefore, retains the important features as follows: (i) the model can be applied to all three power factor (PF) modes of operation—namely, UPF (unity PF), LePF (leading PF), and LaPF (lagging PF), and (ii) both DFIG conditions (i.e., sub-synchronous and super-synchronous) can be modeled using the same equations. Moreover, as the model in this paper is derived based on induction generator power losses calculation, the generator power losses are readily available as the output of the proposed method.

More results are also included in the present paper to verify the method further. In addition to the IEEE 14-bus power network, a more complex electric power network (i.e., IEEE 30-bus system) is also used and investigated in the case study. Based on the investigation results, verification of the proposed method is obtained. The rest of the paper is organized as follows. Section 2 briefly discusses the basic configuration and equivalent circuit of the DFIG. The proposed model is also presented in this section. The application of the method in finding the solution to the power system load flow is given in Section 3. Section 4 points out some important conclusions of the present work.

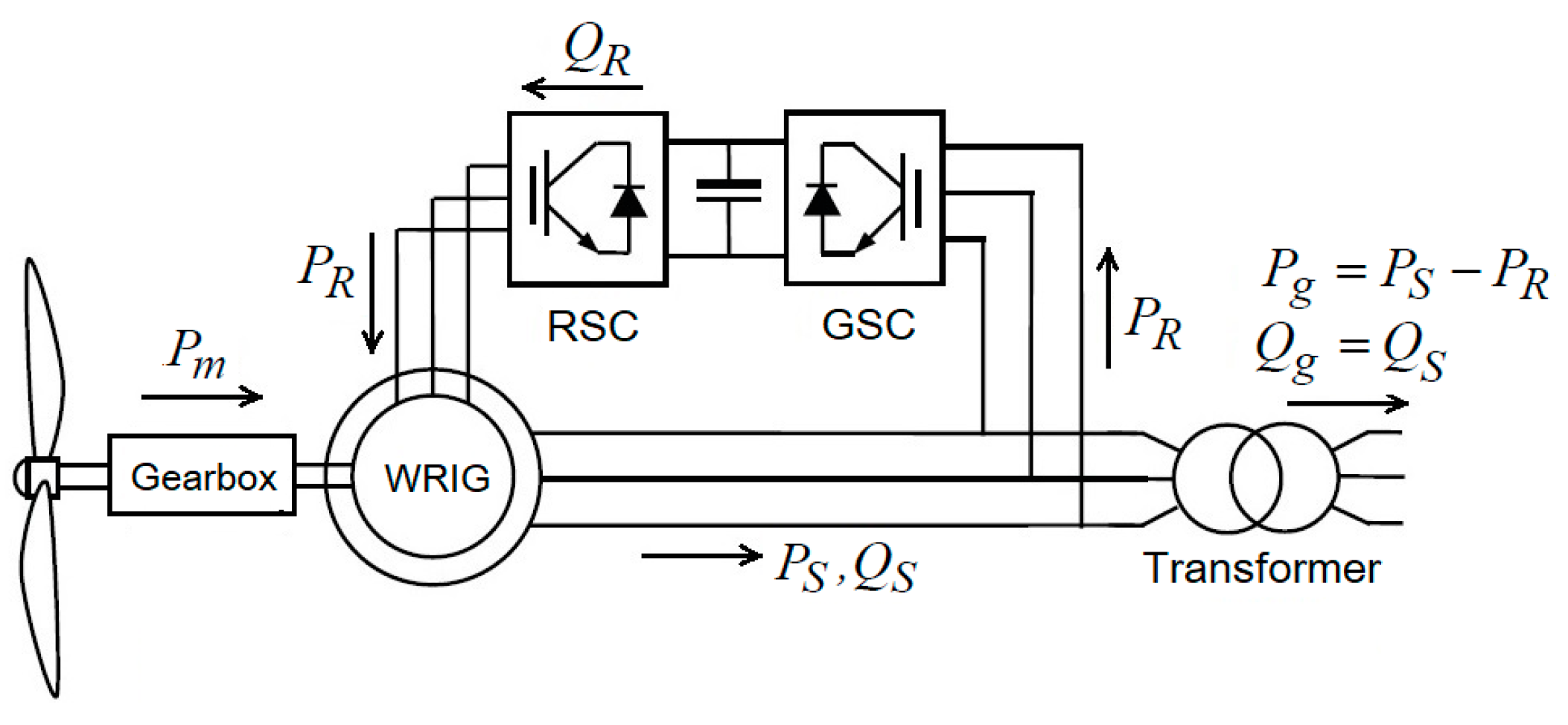
2. DFIG-Based Wind Turbine

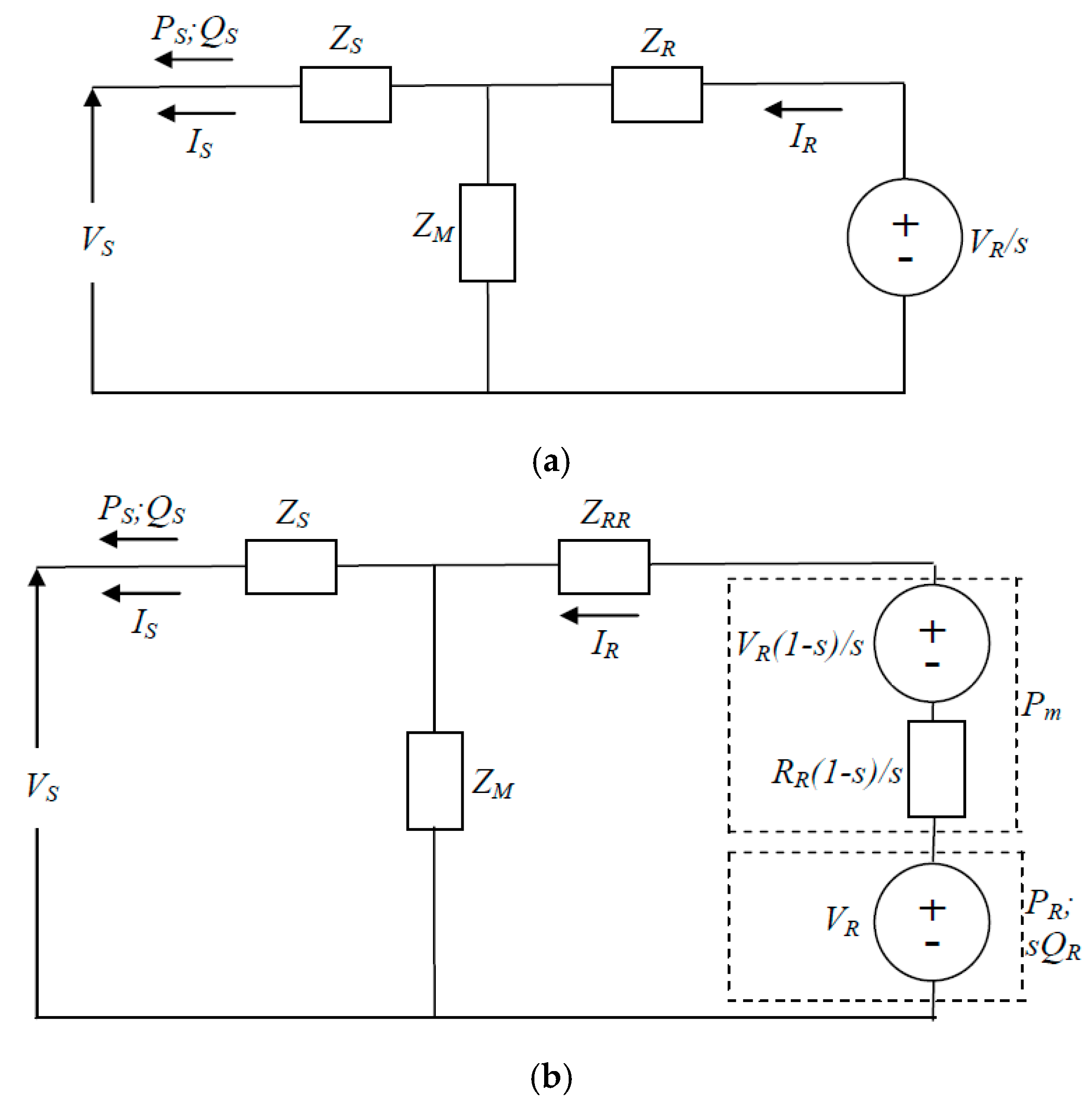
2.1. DFIG Configuration and Equivalent Circuit

The basic configuration of the DFIG is presented in Figure 1 [11,12,13,14,15,16,17,18]. It can be seen from Figure 1 that the main components of the DFIG system include the wind turbine, gearbox, WRIG (wound rotor induction generator), and power electronic converter (PEC). The PEC, which consists of the RSC (rotor side converter), DC link, and GSC (grid side converter), has the function of regulating WRIG rotor reactive power. In Figure 1, P_m is turbine power, P_S and Q_S are WRIG stator powers, P_g and Q_g are DFIG output powers, and P_R and Q_R are WRIG rotor powers.

Figure 1. DFIG configuration.

Figure 2 shows steady-state equivalent circuits of the DFIG [11,12,13,14,15,16,17,18]. In Figure 2, V_S and I_S are stator voltage and current, V_R and I_R are rotor voltage and current, and s is WRIG slip. The impedances (i.e., Z_S, Z_R, Z_RR, and Z_M) in Figure 2 are determined based on the induction generator resistance, reactance, and slip as follows:

Z_{S} = R_{S} + j X_{S}

(1a)

Z_{R} = \frac{R_{R}}{s} + j X_{R}

(1b)

Z_{R R} = R_{R} + j X_{R}

(1c)

Z_{M} = \frac{j R_{c} X_{m}}{R_{c} + j X_{m}}

(1d)

where R_S and X_S are stator resistance and reactance, R_R and X_R are rotor resistance and reactance, and R_c and X_m are core circuit resistance and reactance of WRIG.

Figure 2. DFIG equivalent circuits. (a) Original; (b) Modified.

DFIG-based wind turbines can be operated in power factor control mode. In the power factor control mode of operation, the DFIG is set to regulate the power factor. Three power factors (i.e., leading, lagging, and unity) are usually adopted in the DFIG operation. The DFIG can deliver reactive power to the power system or grid in LePF operation. In this mode of operation, the DFIG can be employed to support the system’s reactive power demand and improve the voltage profile. On the other hand, in LaPF operation, the DFIG absorbs reactive power from the grid. This reactive power (together with the reactive power produced by the DFIG rotor) is used for induction generator magnetization. In UPF operation, no reactive power is delivered or absorbed to or from the grid. All reactive power needed for magnetization comes from the DFIG rotor.

2.2. DFIG Power and WRIG Loss Formulas

By looking at Figure 1, the WPP active and reactive power outputs are:

P_{g} = P_{S} - P_{R}

(2)

and

Q_{g} = Q_{S} = P_{g} \tan ϕ

(3)

where ϕ is the DFIG power factor angle.

Furthermore, based on Figure 2, the complex power in the WRIG stator and rotor circuits are:

P_{S} + j Q_{S} = V_{S} I_{S}^{*}

(4)

and

P_{R} + j s Q_{R} = V_{R} I_{R}^{*}

(5)

On using (4) and (5) in (2), the WPP active power output becomes:

P_{g} = Re (V_{S} I_{S}^{*}) - Re (V_{R} I_{R}^{*})

(6)

In addition to the above power formulas, power loss in the WRIG will also be used in deriving the proposed DFIG steady-state load flow model. Based on Figure 2b, WRIG power loss is:

S_{l o s s} = I_{S} I_{S}^{*} Z_{S} + I_{R} I_{R}^{*} Z_{R R} + (I_{R} - I_{S}) (I_{R}^{*} - I_{S}^{*}) Z_{M}

(7)

Rearranging (7), WRIG power loss can be formulated as:

S_{l o s s} = I_{S} I_{S}^{*} (Z_{S} + Z_{M}) + I_{R} I_{R}^{*} (Z_{R R} + Z_{M}) - (I_{R} I_{S}^{*} + I_{S} I_{R}^{*}) Z_{M}

(8)

2.3. DFIG Steady-State Load Flow Model

Power loss in the DFIG system is the difference between power input and power output of the DFIG. Since the active and reactive power inputs are P_m and Q_R, and the active and reactive power outputs are P_g and Q_g, then the following relationships are valid:

Re (S_{l o s s}) = P_{m} - P_{g}

(9)

and

Im (S_{l o s s}) = Q_{R} - Q_{g} = Q_{R} - P_{g} \tan ϕ

(10)

It is to be noted that power losses in the DFIG power electronic converter are very small compared to those in the WRIG. Therefore, in (9) and (10), they have been neglected. Equations (3) and (6) can be combined to obtain a more compact formulation as follows:

P_{g} (1 + j t a n ϕ) = V_{S} I_{S}^{*} - R e (V_{R} I_{R}^{*})

(11)

where (4) has also been used in forming the combination. In the same way, combining (9) and (10) results in:

S_{l o s s} = P_{m} - P_{g} + j (Q_{R} - P_{g} \tan ϕ)

(12)

Based on (11) and (12), the steady-state model of a WPP that uses a DFIG as its primary energy converter can be formulated as:

P_{g} (1 + j t a n ϕ) - V_{S} I_{S}^{*} + R e (V_{R} I_{R}^{*}) = 0

(13a)

P_{m} - P_{g} + j (Q_{R} - P_{g} t a n ϕ) - S_{l o s s} = 0

(13b)

In the load flow study of a system embedded with DFIG-based WPPs, (13) is used in conjunction with the following power system nodal equation [13]:

S_{G i} - S_{L i} - V_{i} \sum_{j = 1}^{n} Y_{i j}^{*} V_{j}^{*} = 0

(14)

In (14), S_G and S_L are power generation and power demand, V is nodal voltage, Y is nodal admittance matrix, and n is the total number of power system nodes. Table 1 gives the equations to be solved and quantities to be calculated in the load flow analysis. It is to be noted that V_S = |V_S|∟δ_S in (13) is also the voltage at the WPP bus (i.e., V = |V|∟δ). Furthermore, the stator and rotor currents in (8) and (13) can be expressed in terms of stator and rotor voltages as follows [11]:

I_{S} = E V_{R} - F V_{S}

(15a)

I_{R} = G V_{R} - H V_{S}

(15b)

where

E = \frac{1}{s (Z_{S} + Z_{R} + Z_{R} Z_{S} / Z_{M})}

(16a)

F = \frac{1 + Z_{R} / Z_{M}}{Z_{S} + Z_{R} + Z_{R} Z_{S} / Z_{M}}

(16b)

G = \frac{1 + Z_{S} / Z_{M}}{s (Z_{S} + Z_{R} + Z_{R} Z_{S} / Z_{M})}

(16c)

H = \frac{1}{Z_{S} + Z_{R} + Z_{R} Z_{S} / Z_{M}}

(16d)

Table 1. Equation and quantity.

3. Case Study

3.1. WPP Data

The WPP used in the study is assumed to consist of 100 identical wind turbine generator (WTG) units. Data of the WTG and generator slip and turbine power values used in the case study can be found in [13]. To simplify the calculation in load flow analysis, the WPP is aggregated into a single machine equivalent. Parameters of the WPP single machine equivalent can also be found in [13].

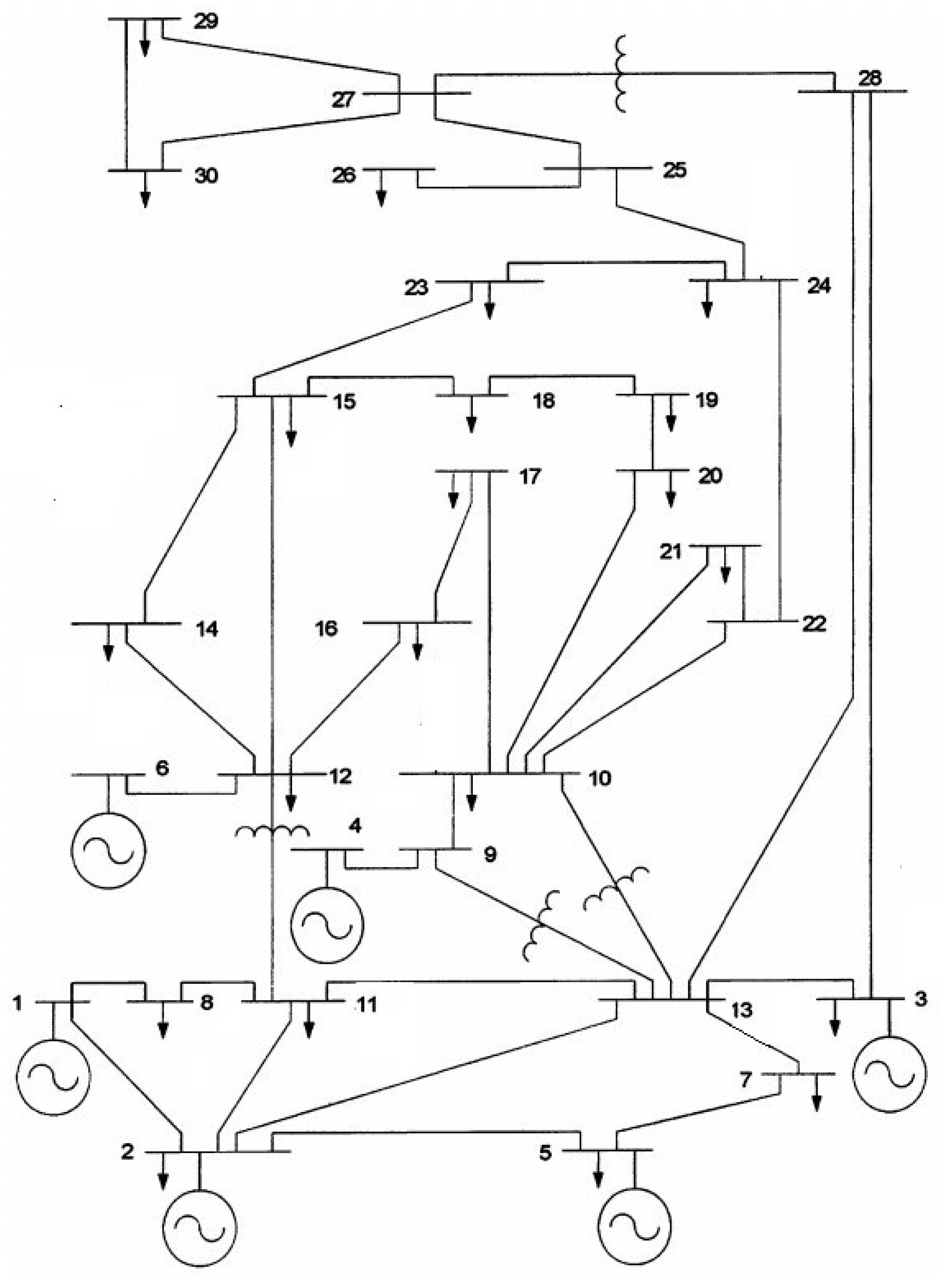
3.2. Test Systems

Two representative power systems (i.e., IEEE 14-bus and 30-bus systems) adapted from [19] will be used to test the method proposed in Section 2. Single-line diagrams of the systems are displayed in Figure 3 and Figure 4. For the IEEE 14-bus, the line and load data can be found in [13]. On the other hand, details of the line and load data for the 30-bus system are given in Table 2 and Table 3. The total three-phase loads for both test systems and locations of the WPP (i.e., WPP point of connection) are summarized in Table 4. In both systems, the WPP is connected to the power system via a step-up transformer. The transformer impedance is assumed to be j0.05 pu. It is to be noted that the base for all data in pu is 100 MVA.

Figure 3. IEEE 14-bus system.

Figure 4. IEEE 30-bus system.

Table 2. Line data of IEEE 30-bus system (in pu).

Table 3. Bus data of IEEE 30-bus system (in pu).

Table 4. Total system three-phase load and WPP location.

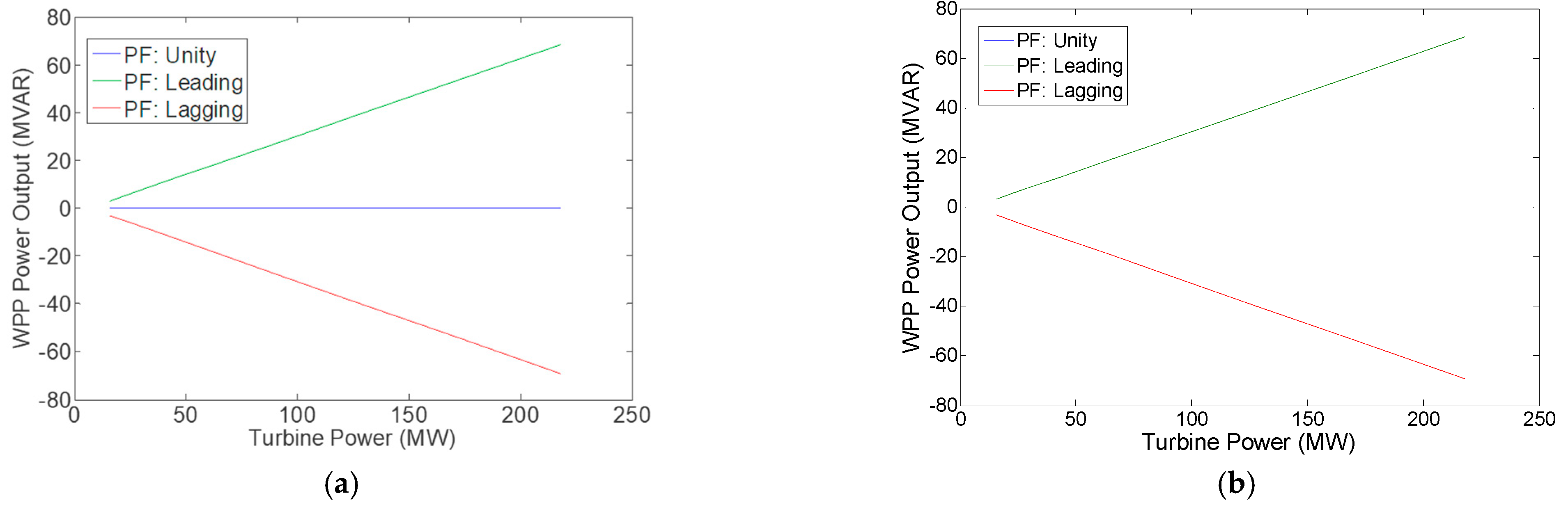
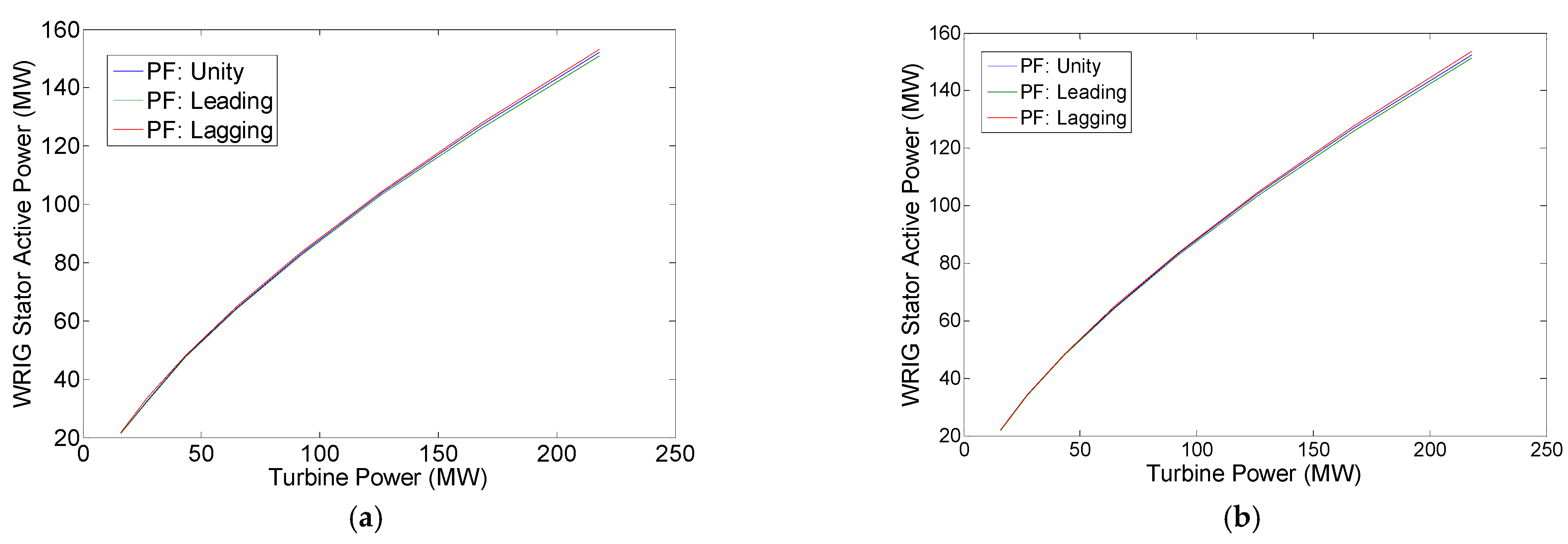
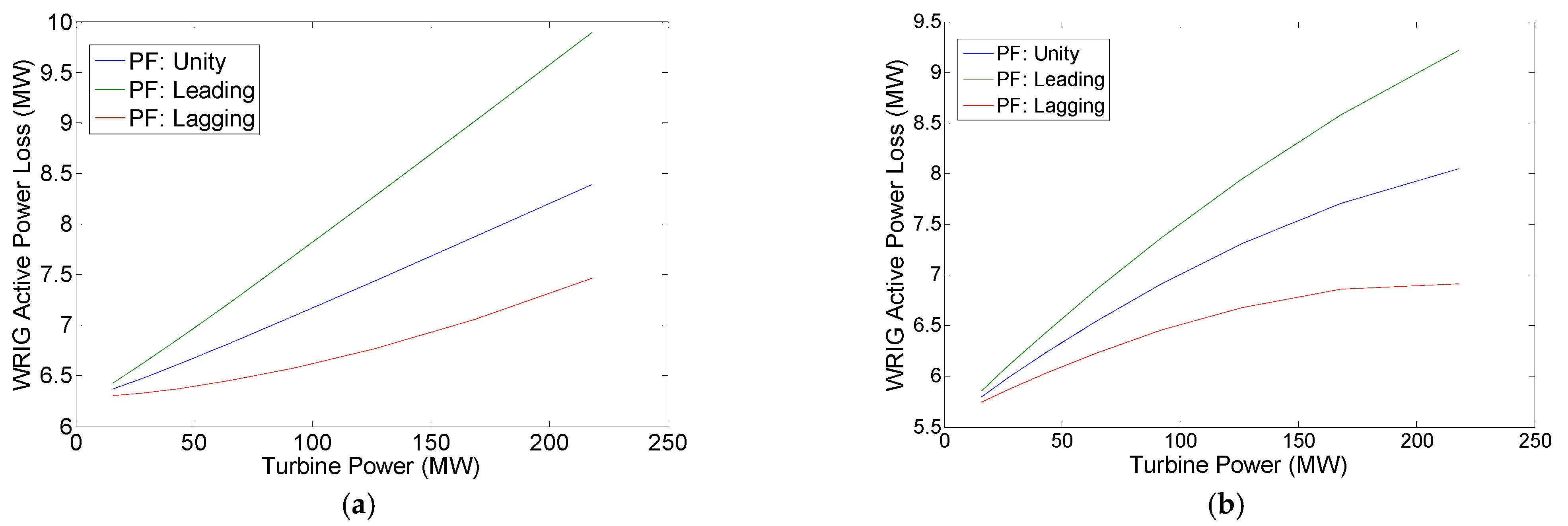
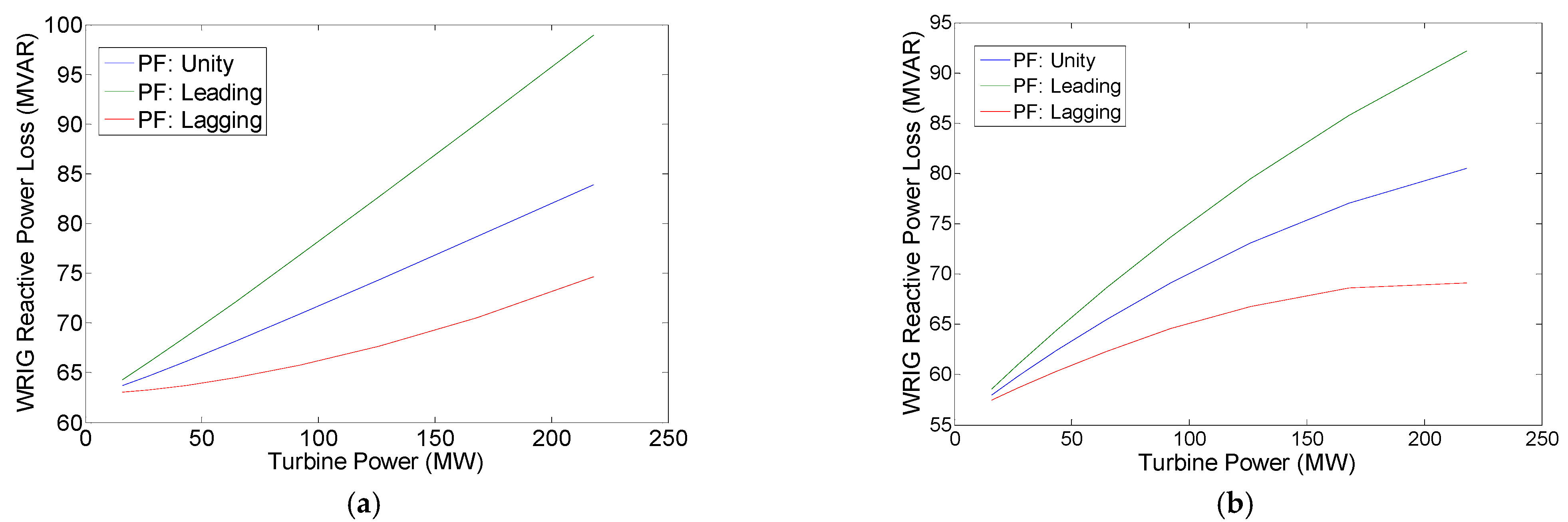
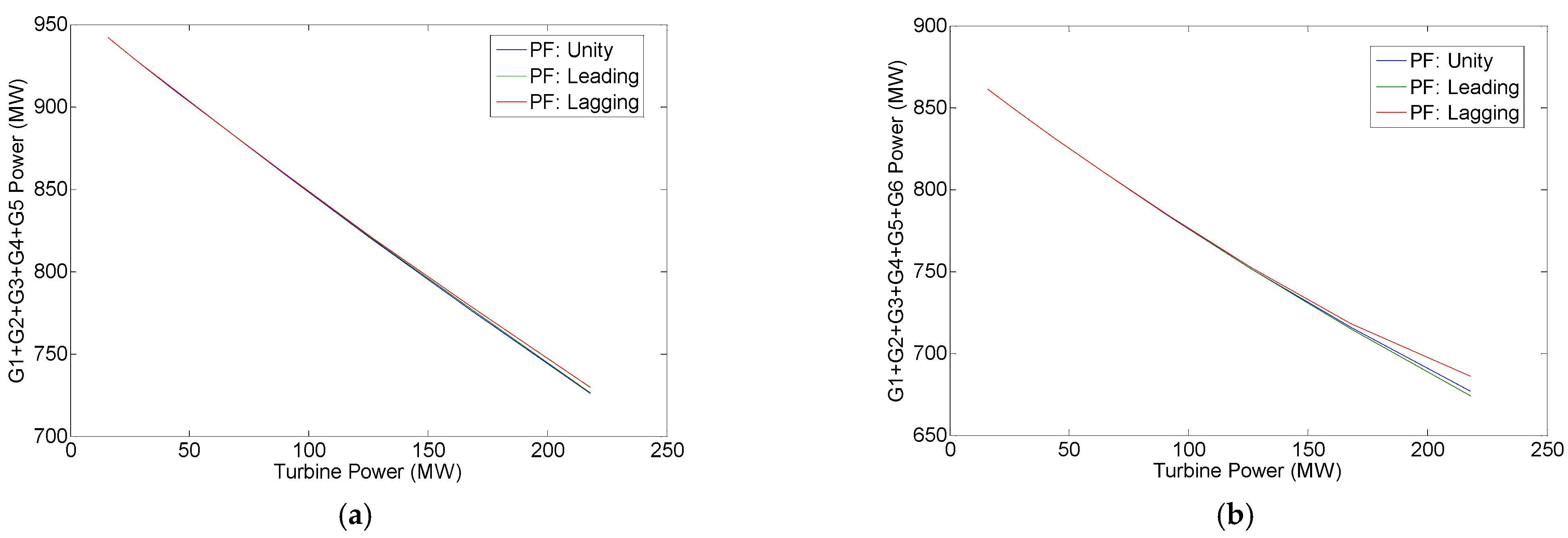
3.3. Results and Discussion

By using the slip and turbine power values described in Section 3.1, load flow studies for the systems in Figure 3 and Figure 4 were then conducted. The results of these studies are presented in Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16. Some of the results are also given in graphical form (see Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10) to make the observation easier. Three DFIG power factor (PF) modes of operation (i.e., LePF, LaPF, and UPF) have been considered and investigated in the studies. It is to be noted that the results in Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 are in exact agreement with the results in [13], which confirms the validity of the proposed model.

Table 5. DFIG power flows and losses of 14-bus system (PF = 1.0).

Table 6. WPP voltages, G1 to G5 powers and losses of 14-bus system (PF = 1.0).

Table 7. DFIG power flows and losses of 14-bus system (PF = 0.95 leading).

Table 8. WPP voltages, G1 to G5 powers and losses of 14-bus system (PF = 0.95 leading).

Table 9. DFIG power flows and losses of 14-bus system (PF = 0.95 lagging).

Table 10. WPP voltages, G1 to G5 powers and losses of 14-bus system (PF = 0.95 lagging).

Table 11. DFIG power flows and losses of 30-bus system (PF = 1.0).

Table 12. WPP voltages, G1 to G6 powers and losses of 30-bus system (PF = 1.0).

Table 13. DFIG power flows and losses of 30-bus system (PF = 0.95 leading).

Table 14. WPP voltages, G1 to G6 powers and losses of 30-bus system (PF = 0.95 leading).

Table 15. DFIG power flows and losses of 30-bus system (PF = 0.95 lagging).

Table 16. WPP voltages, G1 to G6 powers and losses of 30-bus system (PF = 0.95 lagging).

Figure 5. WPP active power. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 6. WPP reactive power. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 7. WRIG stator active power. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 8. WRIG active power loss. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 9. WRIG reactive power loss. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 10. Total active power output of conventional generators. (a) IEEE 14-bus; (b) IEEE 30-bus.

The results in Table 5 and Table 11 show that, in the UPF operating mode, the WPP reactive power output is always zero (no reactive power is delivered or absorbed by the WPP). In this mode of operation, the rotor’s reactive power is used for induction generator magnetization. In LePF operating mode (see Table 7 and Table 13), the WPP reactive power output is always positive (i.e., the WPP delivers reactive power to the power system or grid). In this operation mode, most of the reactive power produced by the rotor is used for magnetization, while the rest of the reactive power is used to support the system’s reactive power demand.

On the other hand, in LaPF operating mode (see Table 9 and Table 15), the WPP reactive power output is always negative (i.e., the WPP absorbs reactive power from the grid). In this mode of operation, the reactive power for generator magnetization comes from the DFIG rotor and power grid. It should also be noted that the WPP will always deliver active power to the grid in the above three modes of operation. Figure 5 and Figure 6 show the variations of WPP active power and WPP reactive power, respectively. The values of WRIG stator active power for the three power factor operating modes are given in Table 5, Table 7, Table 9, Table 11, Table 13 and Table 15. These WRIG stator active power variations are also presented in graphical form (see Figure 7). It can be seen that the values of the WRIG stator active power are almost not affected by the DFIG power factor.

The load flow analysis also provides the values of the rotor’s active powers (see Table 5, Table 7, Table 9, Table 11, Table 13 and Table 15). In DFIG sub-synchronous operations, the rotor’s active power is always positive (power is absorbed). On the other hand, in DFIG super-synchronous operations, the rotor’s active power is always negative (power is delivered). These rotor active powers are also almost not affected by the DFIG power factor. These results verify the validity of the proposed model to represent the DFIG in both sub-synchronous and super-synchronous conditions.

Table 5, Table 7, Table 9, Table 11, Table 13 and Table 15 show the values of WRIG power loss for the three power factor operating modes. These WRIG power losses are calculated using (8) and are readily available as the output of the proposed algorithm. It can be seen that the WRIG power loss increases when the turbine mechanical power (i.e., DFIG power output) goes up (see also Figure 8 and Figure 9). This result is expected since more current is flowing in the WRIG circuit as the DFIG power output is raised. Table 6, Table 8, Table 10, Table 12, Table 14 and Table 16 show that the conventional power plant output can be reduced as the turbine and WPP output powers are increased (see also Figure 10). It can also be observed from the load flow results that for each case of turbine power, the WPP output plus conventional power plant output is always equal to the total system load plus line losses. These results further verify the validity of the proposed method.

4. Conclusions

In this paper, a model of a DFIG-based WPP for a load flow analysis of electric power systems has been proposed. The proposed model is derived based on the power formulations of the WPP—namely, DFIG power, DFIG power loss, and WPP power output formulas. The model can be applied to various DFIG power factor operating modes, i.e., UPF, LePF, and LaPF. Both DFIG conditions (i.e., sub-synchronous and super-synchronous) can be modeled using the same equations. As the model in this paper is derived based on induction generator power losses calculation, the generator power losses are readily available as the output of the proposed method. Results of the case studies are also given in the present paper. In the case study, applications of the proposed methods on representative electric power systems have been investigated. Based on the investigation results, verification of the proposed method has been obtained. For future work, the DFIG model proposed in the present paper can be used as a reference to develop other variable-speed WPPs (SCIG-based variable-speed WPPs and PMSG-based WPPs).

Author Contributions

Conceptualization, R.G. and P.; methodology, R.G. and P.; software, R.G.; validation, R.G., P., and F.I.; formal analysis, R.K.; investigation, D.; resources, F.I.; data curation, R.K.; writing—original draft preparation, R.G.; writing—review and editing, P.; visualization, D.; supervision, F.I.; project administration, R.K.; funding acquisition, D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Kemendikbud-Ristek Republik Indonesia.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Haque, M.H. Evaluation of power flow solutions with fixed speed wind turbine generating systems. Energy Convers. Manag. 2014, 79, 511–518. [Google Scholar] [CrossRef]
Haque, M.H. Incorporation of fixed speed wind turbine generators in load flow analysis of distribution systems. Int. J. Renew. Energy Technol. 2015, 6, 317–324. [Google Scholar] [CrossRef]
Wang, J.; Huang, C.; Zobaa, A.F. Multiple-node models of asynchronous wind turbines in wind farms for load flow analysis. Electr. Power Compon. Syst. 2015, 44, 135–141. [Google Scholar] [CrossRef]
Feijoo, A.; Villanueva, D. A PQ model for asynchronous machines based on rotor voltage calculation. IEEE Trans. Energy Convers. 2016, 31, 813–814, Correction in IEEE Trans. Energy Convers. 2016, 31, 1228. [Google Scholar] [CrossRef]
Ozturk, O.; Balci, M.E.; Hocaoglu, M.H. A new wind turbine generating system model for balanced and unbalanced distribution systems load flow analysis. Appl. Sci. 2018, 8, 502. [Google Scholar]
Dadhania, A.; Venkatesh, B.; Nassif, A.B.; Sood, V.K. Modeling of doubly fed induction generators for distribution system power flow analysis. Electr. Power Energy Syst. 2013, 53, 576–583. [Google Scholar] [CrossRef]
Ju, Y.; Ge, F.; Wu, W.; Lin, Y.; Wang, J. Three-phase steady-state model of DFIG considering various rotor speeds. IEEE Access 2016, 4, 9479–9948. [Google Scholar] [CrossRef]
Kumar, V.S.S.; Thukaram, D. Accurate modeling of doubly fed induction based wind farms in load flow analysis. Electr. Power Syst. Res. 2018, 15, 363–371. [Google Scholar]
Li, S. Power flow modeling to doubly-fed induction generators (DFIGs) under power regulation. IEEE Trans. Power Syst. 2013, 28, 3292–3301. [Google Scholar] [CrossRef]
Anirudh, C.V.S.; Seshadri, S.K.V. Enhanced modeling of doubly fed induction generator in load flow analysis of distribution systems. IET Renew. Power Gener. 2021, 15, 980–989. [Google Scholar]
Gianto, R. Steady state model of DFIG-based wind power plant for load flow analysis. IET Renew. Power Gener. 2021, 15, 1724–1735. [Google Scholar] [CrossRef]
Gianto, R. Constant voltage model of DFIG-based variable speed wind turbine for load flow analysis. Energies 2021, 14, 8549. [Google Scholar] [CrossRef]
Gianto, R. Constant power factor model of DFIG-based wind turbine for steady state load flow analysis. Energies 2022, 15, 6077. [Google Scholar] [CrossRef]
Anaya-Lara, O.; Jenkins, N.; Ekanayake, J.B.; Cartwright, P.; Hughes, M. Wind Energy Generation: Modelling and Control; John Wiley & Sons, Ltd.: Chichester, UK, 2009. [Google Scholar]
Akhmatov, V. Induction Generators for Wind Power; Multi-Science Publishing Co., Ltd.: Brentwood, UK, 2007. [Google Scholar]
Boldea, I. Variable Speed Generators; Taylor & Francis Group LLC.: Roca Baton, FL, USA, 2005. [Google Scholar]
Fox, B.; Flynn, B.; Bryans, L.; Jenkins, J. Wind Power Integration: Connection and System Operational Aspects; The Institution of Engineering and Technology: Stevenage Herts, UK, 2007. [Google Scholar]
Patel, M.R. Wind and Solar Power Systems; CRC Press LLC.: Boca Raton, FL, USA, 1999. [Google Scholar]
Pai, M.A. Computer Techniques in Power System Analysis; Tata McGraw-Hill Publishing Co., Ltd.: New Delhi, India, 1984. [Google Scholar]

Figure 1. DFIG configuration.

Figure 2. DFIG equivalent circuits. (a) Original; (b) Modified.

Figure 3. IEEE 14-bus system.

Figure 4. IEEE 30-bus system.

Figure 5. WPP active power. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 6. WPP reactive power. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 7. WRIG stator active power. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 8. WRIG active power loss. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 9. WRIG reactive power loss. (a) IEEE 14-bus; (b) IEEE 30-bus.

Figure 10. Total active power output of conventional generators. (a) IEEE 14-bus; (b) IEEE 30-bus.

Table 1. Equation and quantity.

Bus	Equation(s)	Knowns	Unknowns
Slack	(14)	\|V\| and δ = 0°	P_G and Q_G
PV	(14)	P_G and \|V\|	δ and Q_G
PQ	(14)	P_G = Q_G = 0	\|V\| and δ
WPP	(13) and (14)	ϕ, s, and P_m	\|V\| = \|V_S\|, δ = δ_S, P_G = P_g, Q_R, Re(V_R) and Im(V_R)

Table 2. Line data of IEEE 30-bus system (in pu).

Line	Sending Bus	Receiving Bus	Series Impedance
1	1	2	0.0192 + j0.0575
2	1	8	0.0452 + j0.1852
3	2	11	0.0570 + j0.1737
4	8	11	0.0132 + j0.0379
5	2	5	0.0472 + j0.1983
6	2	13	0.0581 + j0.1763
7	11	13	0.0119 + j0.0414
8	5	7	0.0460 + j0.1160
9	7	13	0.0267 + j0.0820
10	3	13	0.0120 + j0.0420
11	9	13	j0.2080
12	10	13	j0.5560
13	4	9	j0.2080
14	9	10	j0.1100
15	11	12	j0.2560
16	6	12	j0.1400
17	12	14	0.1231 + j0.2559
18	12	15	0.0662 + j0.1304
19	12	16	0.0945 + j0.1987
20	14	15	0.2210 + j0.1997
21	16	17	0.0824 + j0.1932
22	15	18	0.1073 + j0.2185
23	18	19	0.0639 + j0.1292
24	19	20	0.0340 + j0.0680
25	10	20	0.0936 + j0.2090
26	10	17	0.0324 + j0.0845
27	10	21	0.0348 + j0.0749
28	10	22	0.0727 + j0.1499
29	21	22	0.0116 + j0.0236
30	15	23	0.1000 + j0.2020
31	22	24	0.1150 + j0.1790
32	23	24	0.1320 + j0.2700
33	24	25	0.1885 + j0.3292
34	25	26	0.2544 + j0.3800
35	25	27	0.1093 + j0.2087
36	27	28	j0.3960
37	27	29	0.2198 + j0.4153
38	27	30	0.3202 + j0.6027
39	29	30	0.2399 + j0.4533
40	3	28	0.0636 + j0.2000
41	13	28	0.0169 + j0.0599

Table 3. Bus data of IEEE 30-bus system (in pu).

Bus	\|V\|	δ	Generation	Load	Note
1	1.0500	0	-	0	Slack
2	1.0338	-	0.5756 + j-	0.217 + j0.127	PV
3	1.0230	-	0.3500 + j-	0.300 + j0.300	PV
4	1.0913	-	0.1793 + j-	0	PV
5	1.0058	-	0.2456 + j-	0.942 + j0.190	PV
6	1.0883	-	0.1691 + j-	0	PV
7	-	-	0	0.228 + j0.109	PQ
8	-	-	0	0.024 + j0.012	PQ
9	-	-	0	0	PQ
10	-	-	0	0.058 + j0.020	PQ
11	-	-	0	0.076 + j0.016	PQ
12	-	-	0	0.112 + j0.075	PQ
13	-	-	0	0	PQ
14	-	-	0	0.062 + j0.016	PQ
15	-	-	0	0.082 + j0.025	PQ
16	-	-	0	0.035 + j0.018	PQ
17	-	-	0	0.090 + j0.058	PQ
18	-	-	0	0.032 + j0.009	PQ
19	-	-	0	0.095 + j0.034	PQ
20	-	-	0	0.022 + j0.007	PQ
21	-	-	0	0.175 + j0.112	PQ
22	-	-	0	0	PQ
23	-	-	0	0.032 + j0.016	PQ
24	-	-	0	0.087 + j0.067	PQ
25	-	-	0	0	PQ
26	-	-	0	0.035 + j0.023	PQ
27	-	-	0	0	PQ
28	-	-	0	0	PQ
29	-	-	0	0.024 + j0.009	PQ
30	-	-	0	0.106 + j0.019	PQ

Note: notation ‘-’ denotes quantities to be calculated.

Table 4. Total system three-phase load and WPP location.

System	Total Load (MW; MVAr)	WPP Location
IEEE 14-bus	897; 243.9	Bus 14
IEEE 30-bus	850.2; 378.6	Bus 30

Table 5. DFIG power flows and losses of 14-bus system (PF = 1.0).

ΣP_m (MW)	P_g (MW)	P_S (MW)	P_R (MW)	P_LOSS (MW)	Q_LOSS (MVAR)
15.78	9.4127	21.4955	12.0828	6.3673	63.6728
27.27	20.8045	32.8212	12.0167	6.4655	64.6551
43.30	36.6883	47.9329	11.2446	6.6117	66.1171
64.63	57.8139	64.4185	6.6046	6.8161	68.1608
92.02	84.9318	83.0831	−1.8487	7.0882	70.8821
126.23	118.7934	103.9265	−14.8669	7.4366	74.3658
168.01	160.1414	126.9522	−33.1892	7.8686	78.6861
218.12	209.7292	152.1444	−57.5848	8.3908	83.9077

Table 6. WPP voltages, G1 to G5 powers and losses of 14-bus system (PF = 1.0).

ΣP_m (pu)	Voltage (pu)	G1 to G5 Outputs		Line Losses
ΣP_m (pu)	Voltage (pu)	MW	MVAR	MW	MVAR
15.78	1.0160	941.7797	479.5449	54.1924	235.6449
27.27	1.0196	928.6547	470.9905	52.4592	227.0905
43.30	1.0243	910.5415	459.8925	50.2298	215.9925
64.63	1.0301	886.7778	446.5797	47.5917	202.6797
92.02	1.0368	856.8002	431.8180	44.7320	187.9180
126.23	1.0440	820.1648	416.8994	41.9582	172.9994
168.01	1.0512	776.5829	403.7411	39.7243	159.8411
218.12	1.0575	725.9341	395.0049	38.6634	151.1049

Table 7. DFIG power flows and losses of 14-bus system (PF = 0.95 leading).

ΣP_m (MW)	P_g (MW)	P_S (MW)	Q_g = Q_S (MVAR)	P_R (MW)	P_LOSS (MW)	Q_LOSS (MVAR)
15.78	9.3484	21.4447	3.0727	12.0962	6.4316	64.3156
27.27	20.6617	32.5085	6.7912	11.8469	6.6083	66.0830
43.30	36.4350	47.7337	11.9756	11.2987	6.8650	68.6499
64.63	57.4122	64.1035	18.8705	6.6913	7.2178	72.1783
92.02	84.3374	82.6185	27.7203	−1.7189	7.6826	76.8265
126.23	117.9556	103.2733	38.7701	−14.6823	8.2744	82.7441
168.01	159.0028	126.0661	52.2617	−32.9368	9.0072	90.0716
218.12	208.2259	150.9748	68.4405	−57.2511	9.8941	98.9412

Table 8. WPP voltages, G1 to G5 powers and losses of 14-bus system (PF = 0.95 leading).

ΣP_m (pu)	Voltage (pu)	G1 to G5 Outputs		Line Losses
ΣP_m (pu)	Voltage (pu)	MW	MVAR	MW	MVAR
15.78	1.0192	941.7856	476.2581	54.1341	235.4308
27.27	1.0265	928.6796	463.7667	52.3413	226.6579
43.30	1.0364	910.6097	447.2361	50.0447	215.3117
64.63	1.0489	886.9239	426.7644	47.3361	201.7349
92.02	1.0641	857.0613	402.8550	44.3987	186.6753
126.23	1.0818	820.5608	376.4609	41.5164	171.3310
168.01	1.1016	777.0774	349.0208	39.0802	157.3825
218.12	1.1232	726.3667	322.4684	37.5925	147.0090

Table 9. DFIG power flows and losses of 14-bus system (PF = 0.95 lagging).

ΣP_m (MW)	P_g (MW)	P_S (MW)	Q_g = Q_S (MVAR)	P_R (MW)	P_LOSS (MW)	Q_LOSS (MVAR)
15.78	9.4768	21.5466	−3.1149	12.0698	6.3032	63.0324
27.27	20.9437	33.7330	−6.8838	12.7893	6.3263	63.2634
43.30	36.9277	48.1273	−12.1376	11.1996	6.3723	63.7228
64.63	58.1782	64.7191	−19.1222	6.5409	6.4518	64.5183
92.02	85.4413	83.5136	−28.0832	−1.9278	6.5787	65.7866
126.23	119.4594	104.5087	−39.2644	−14.9507	6.7706	67.7056
168.01	160.9575	127.7034	−52.9042	−33.2541	7.0525	70.5249
218.12	210.6572	153.0724	−69.2397	−57.5848	7.4628	74.6282

Table 10. WPP voltages, G1 to G5 powers and losses of 14-bus system (PF = 0.95 lagging).

ΣP_m (pu)	Voltage (pu)	G1 to G5 Outputs		Line Losses
ΣP_m (pu)	Voltage (pu)	MW	MVAR	MW	MVAR
15.78	1.0128	941.7820	482.9034	54.2587	235.8885
27.27	1.0125	928.6695	478.4409	52.6131	227.6571
43.30	1.0118	910.5955	473.1122	50.5232	217.0747
64.63	1.0103	886.9325	467.6194	48.1106	204.5972
92.02	1.0074	857.1856	463.2116	45.6270	191.2284
126.23	1.0025	821.0420	461.8678	43.5014	178.7034
168.01	0.9940	778.4596	466.5709	42.4171	169.7667
218.12	0.9801	729.7969	479.8147	41.4541	168.6751

Table 11. DFIG power flows and losses of 30-bus system (PF = 1.0).

ΣP_m (MW)	P_g (MW)	P_S (MW)	P_R (MW)	P_LOSS (MW)	Q_LOSS (MVAR)
15.78	9.9799	22.0540	12.0741	5.8001	58.0014
27.27	21.2845	34.0960	12.8115	5.9855	59.8548
43.30	37.0649	48.3081	11.2432	6.2351	62.3509
64.63	58.0831	64.6896	6.6065	6.5469	65.4688
92.02	85.1089	83.2642	−1.8447	6.9111	69.1115
126.23	118.9212	104.0600	−14.8612	7.3088	73.0881
168.01	160.3025	127.1258	−33.1767	7.7075	77.0748
218.12	210.0714	152.5323	−57.5391	8.0486	80.4863

Table 12. WPP voltages, G1 to G6 powers and losses of 30-bus system (PF = 1.0).

ΣP_m (pu)	Voltage (pu)	G1 to G6 Outputs		Line Losses
ΣP_m (pu)	Voltage (pu)	MW	MVAR	MW	MVAR
15.78	0.9689	861.1725	475.9636	20.9524	97.3636
27.27	0.9797	848.7626	471.3917	19.8471	92.7917
43.30	0.9928	831.8933	466.5188	18.7582	87.9188
64.63	1.0073	810.1809	462.5414	18.0640	83.9414
92.02	1.0215	783.4382	461.3343	18.3471	82.7343
126.23	1.0326	751.7550	465.7200	20.4762	87.1200
168.01	1.0360	715.7093	480.1532	25.8118	101.5532
218.12	1.0222	677.0272	513.0331	36.8985	134.4331

Table 13. DFIG power flows and losses of 30-bus system (PF = 0.95 leading).

ΣP_m (MW)	P_g (MW)	P_S (MW)	Q_g = Q_S (MVAR)	P_R (MW)	P_LOSS (MW)	Q_LOSS (MVAR)
15.78	9.9246	22.0052	3.2621	12.0806	5.8554	58.5541
27.27	21.1675	33.9925	6.9574	12.8251	6.1025	61.0254
43.30	36.8627	48.1287	12.1162	11.2660	6.4373	64.3730
64.63	57.7687	64.4091	18.9877	6.6404	6.8613	68.6132
92.02	84.6505	82.8519	27.8233	−1.7987	7.3695	73.6945
126.23	118.2810	103.4768	38.8771	−14.8043	7.9490	79.4896
168.01	159.4321	126.3169	52.4028	−33.1153	8.5779	85.7788
218.12	208.9003	151.4039	68.6622	−57.4965	9.2197	92.1968

Table 14. WPP voltages, G1 to G6 powers and losses of 30-bus system (PF = 0.95 leading).

ΣP_m (pu)	Voltage (pu)	G1 to G6 Outputs		Line Losses
ΣP_m (pu)	Voltage (pu)	MW	MVAR	MW	MVAR
15.78	0.9726	861.1997	472.5582	20.9243	97.2203
27.27	0.9875	848.8277	464.1540	19.7952	92.5114
43.30	1.0062	832.0124	453.9357	18.6751	87.4519
64.63	1.0280	810.3520	442.7732	17.9207	83.1609
92.02	1.0516	783.6027	432.0805	18.0533	81.3038
126.23	1.0752	751.7148	423.9357	19.7959	84.2128
168.01	1.0958	714.9279	421.3683	24.1601	95.1711
218.12	1.1089	673.9794	429.1207	32.6797	119.1829

Table 15. DFIG power flows and losses of 30-bus system (PF = 0.95 lagging).

ΣP_m (MW)	P_g (MW)	P_S (MW)	Q_g = Q_S (MVAR)	P_R (MW)	P_LOSS (MW)	Q_LOSS (MVAR)
15.78	10.0357	22.1034	−3.2986	12.0677	5.7443	57.4434
27.27	21.4024	34.2009	−7.0346	12.7985	5.8676	58.6761
43.30	37.2678	48.4901	−12.2493	11.2223	6.0322	60.3225
64.63	58.3968	64.9744	−19.1941	6.5776	6.2332	62.3317
92.02	85.5627	83.6837	−28.1231	−1.8790	6.4573	64.5730
126.23	119.5492	104.6569	−39.2939	−14.8924	6.6808	66.8076
168.01	161.1478	127.9682	−52.9667	−33.1795	6.8622	68.6223
218.12	211.2058	153.7980	−69.4200	−57.4078	6.9142	69.1418

Table 16. WPP voltages, G1 to G6 powers and losses of 30-bus system (PF = 0.95 lagging).

ΣP_m (pu)	Voltage (pu)	G1 to G6 Outputs		Line Losses
ΣP_m (pu)	Voltage (pu)	MW	MVAR	MW	MVAR
15.78	0.9651	861.1494	480.0511	20.9850	97.5225
27.27	0.9716	848.7158	478.7718	19.9182	93.1372
43.30	0.9789	831.8295	479.4241	18.8972	88.5748
64.63	0.9854	810.1472	482.9774	18.3440	85.1833
92.02	0.9889	783.5856	491.9249	18.9483	85.2018
126.23	0.9849	752.4921	510.2345	21.8414	92.3406
168.01	0.9647	718.1868	545.1564	29.1345	113.5897
218.12	0.8987	685.9859	617.6366	46.9917	169.6166

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Steady-State Load Flow Model of DFIG Wind Turbine Based on Generator Power Loss Calculation

Abstract

1. Introduction

2. DFIG-Based Wind Turbine

2.1. DFIG Configuration and Equivalent Circuit

2.2. DFIG Power and WRIG Loss Formulas

2.3. DFIG Steady-State Load Flow Model

3. Case Study

3.1. WPP Data

3.2. Test Systems

3.3. Results and Discussion

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics