3D Transient CFD Simulation of an In-Vessel Loss-of-Coolant Accident in the EU DEMO WCLL Breeding Blanket
Abstract
1. Introduction
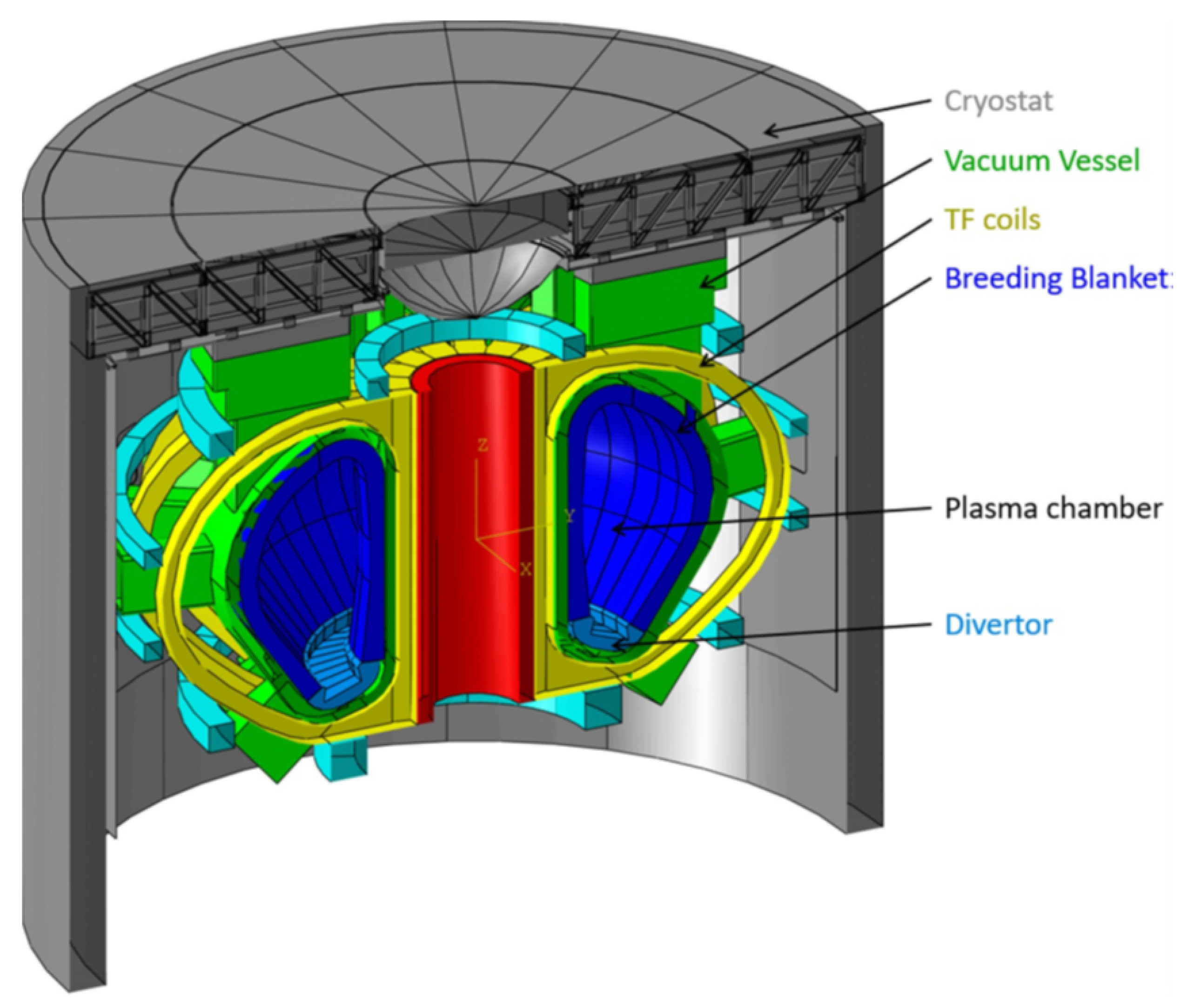
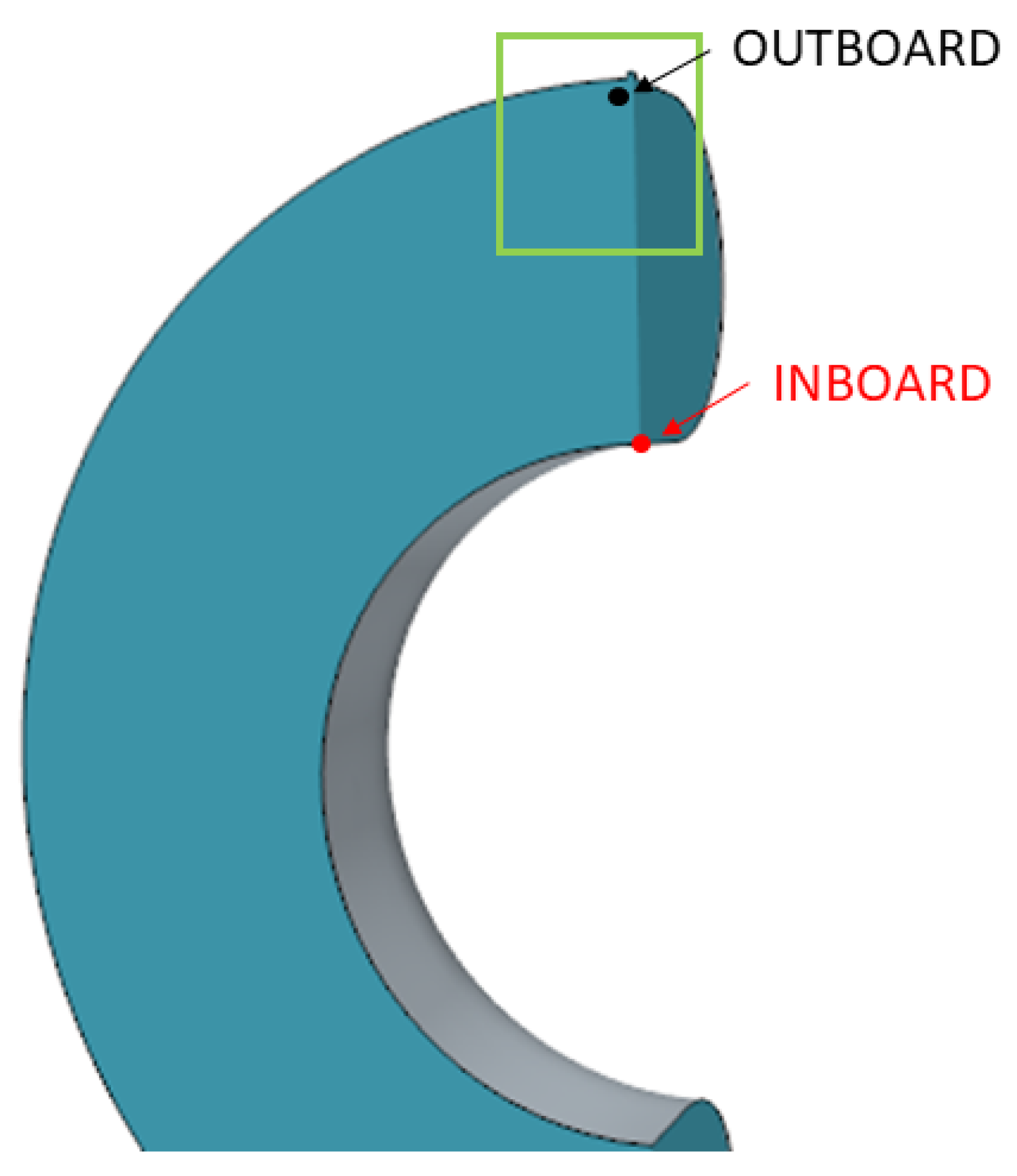
2. Scenario and Geometry Description
3. Simulation Setup
3.1. Boundary and Initial Conditions
3.1.1. Boundary Conditions
3.1.2. Initial Conditions
- : molecular mean free path;
- L: characteristic length (in this case, the distance between the inlet and the wall in front of it);
- : Boltzmann constant;
- T: temperature of the system;
- : particle diameter;
- p: pressure of the system.
3.2. Model and Solvers
3.2.1. Model
3.2.2. Solvers
- Implicit Unsteady.
- Time step adaptivity based on Courant number:Due to the strong difference between upstream and downstream conditions, the start-up of the transient is the most critical time interval; therefore, a very small time step, such as 1 × 10−10 s, must be used during this period. However, such a small time step is not needed throughout the whole simulation. This model allows one to automatically define the most suitable time step during the transient, basing the tuning on the Courant number , where v is the local speed, is the time step, and is the local grid size. In particular, if both the mean and maximum in the domain are below 0.5 and 5, respectively, the time step is increased by a factor of 1.1; otherwise, it is halved. After the start-up phase, the average time step is ∼2 μs before the impact of the reflected wave (see Section 4.1 below), and ∼4 μs after.
- Segregated flow and segregated energy:For both these solvers, the discretisation scheme is left with the default second-order upwind. However, the adopted cycle employed in the algebraic multi-grid solver is an F-type cycle, which, in supersonic conditions, performs better than the default one (V-type). In addition, it represents a good compromise between the W-type and the V-type from the computational point of view [18].
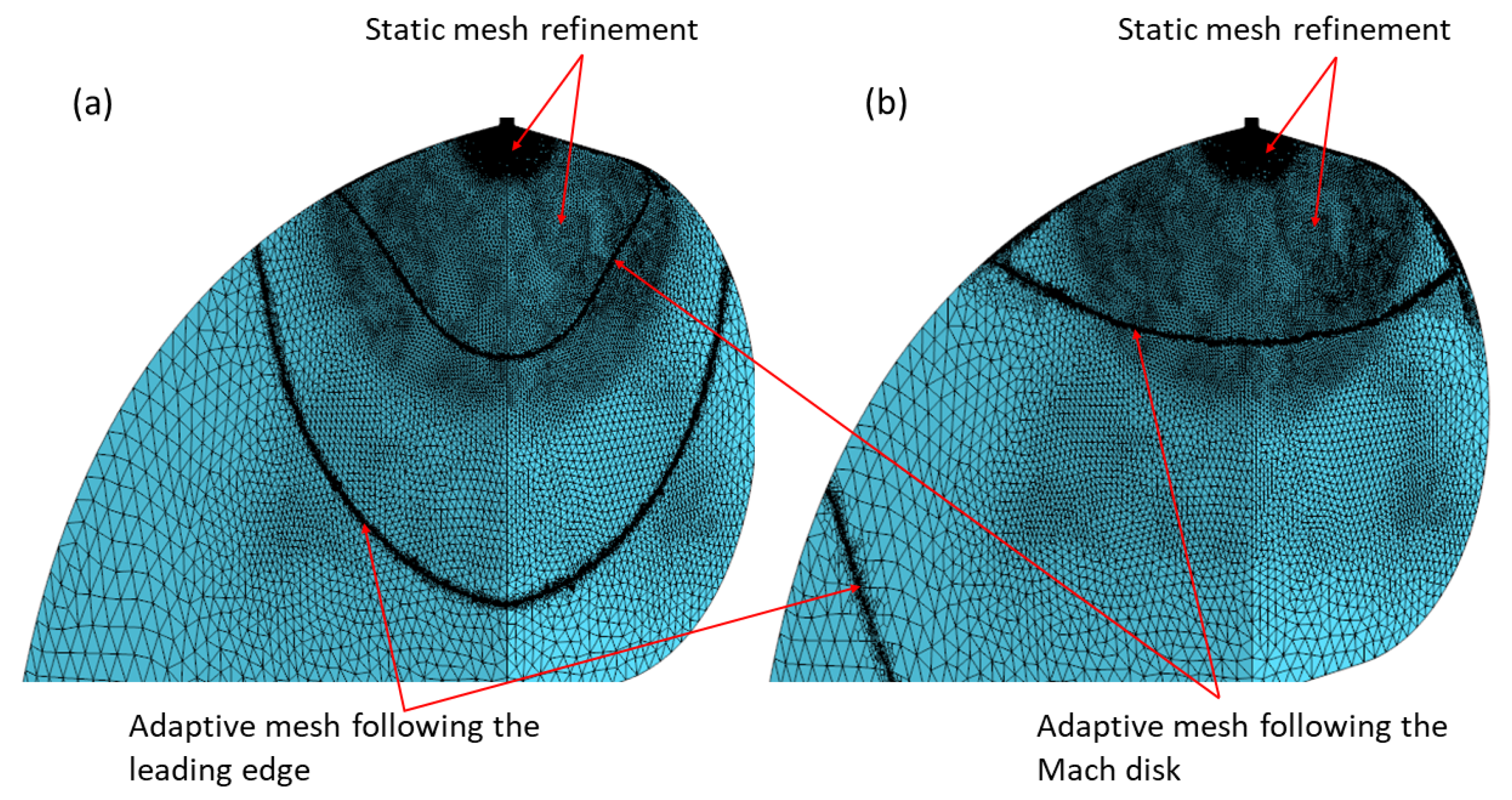
3.3. Mesh Adaptivity Strategy
- The user selects two values of the AMR function that define a range (in this case, ).
- The solver behaviour is then specified by choosing between three different actions: “Refine”, “Keep” or “Coarsen”.
- For each cell, the function is evaluated, and the action is chosen according to the local value:
4. Results
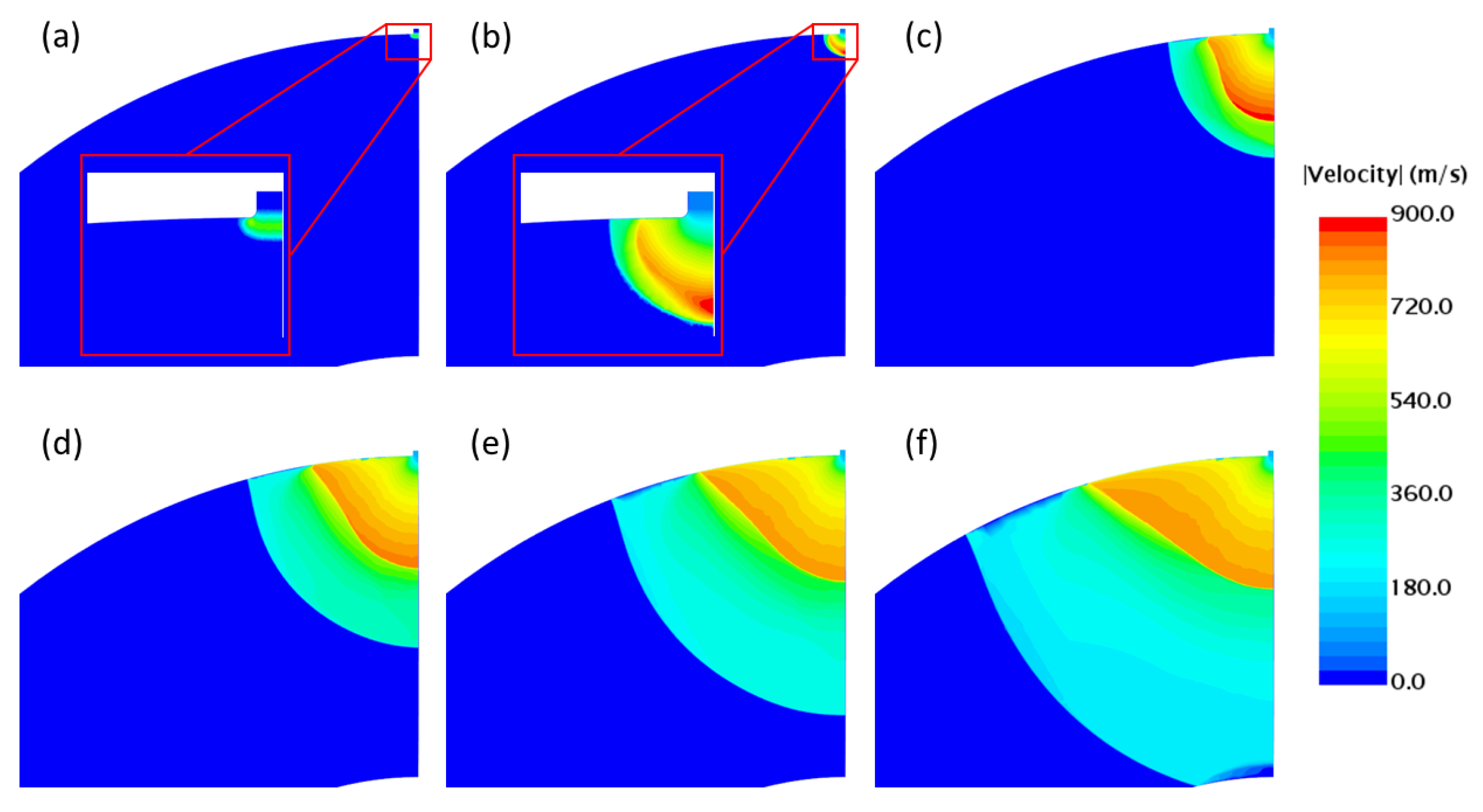
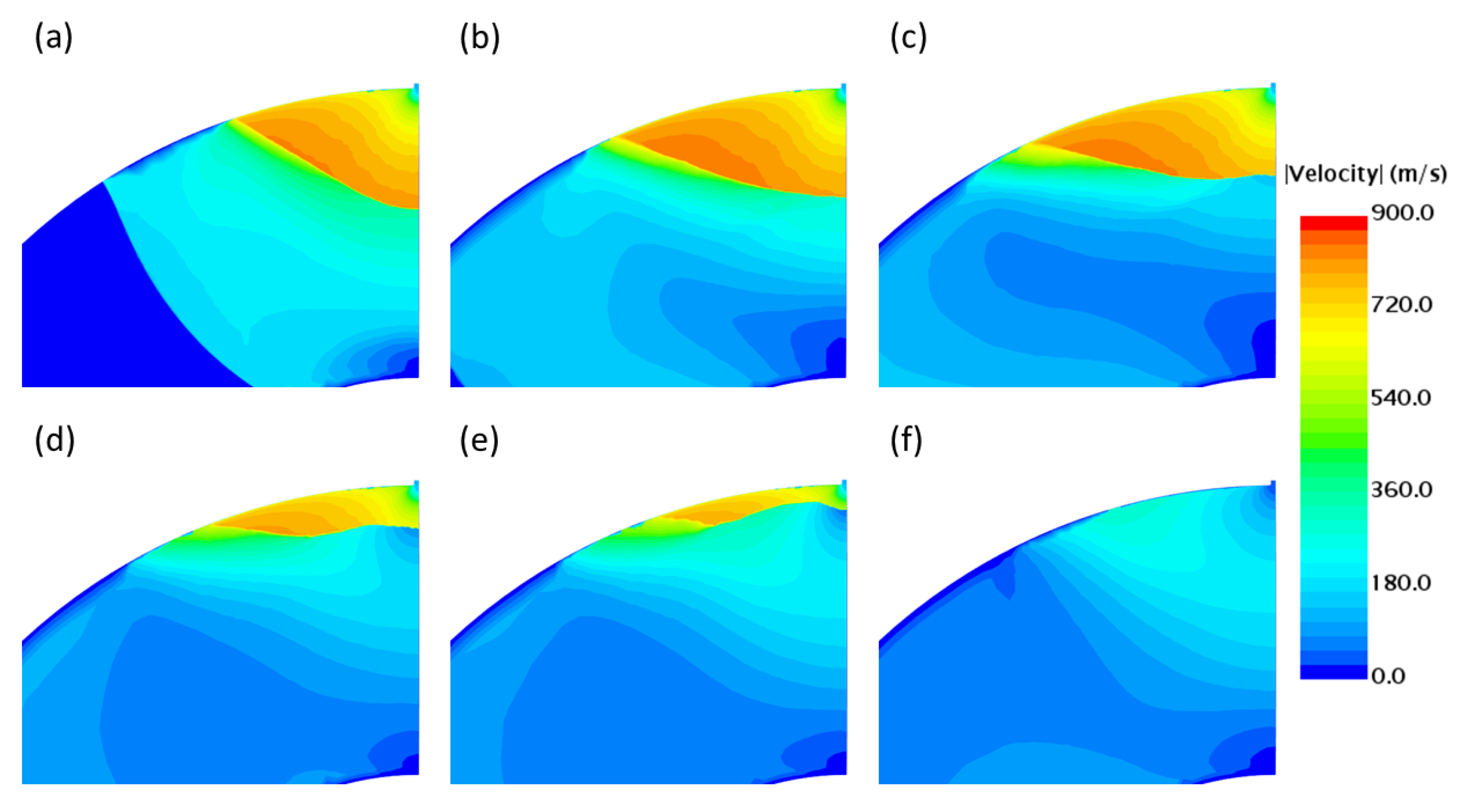
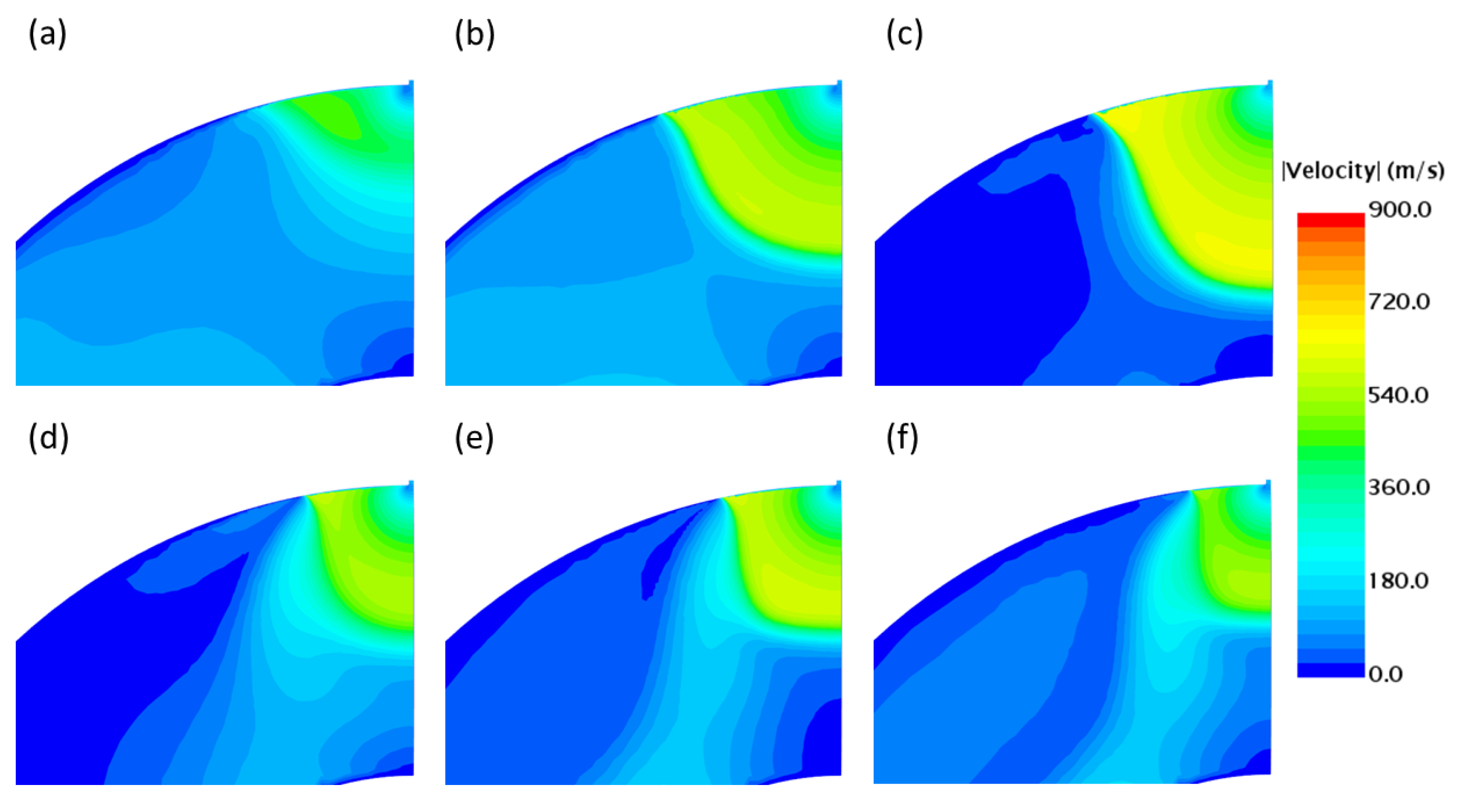
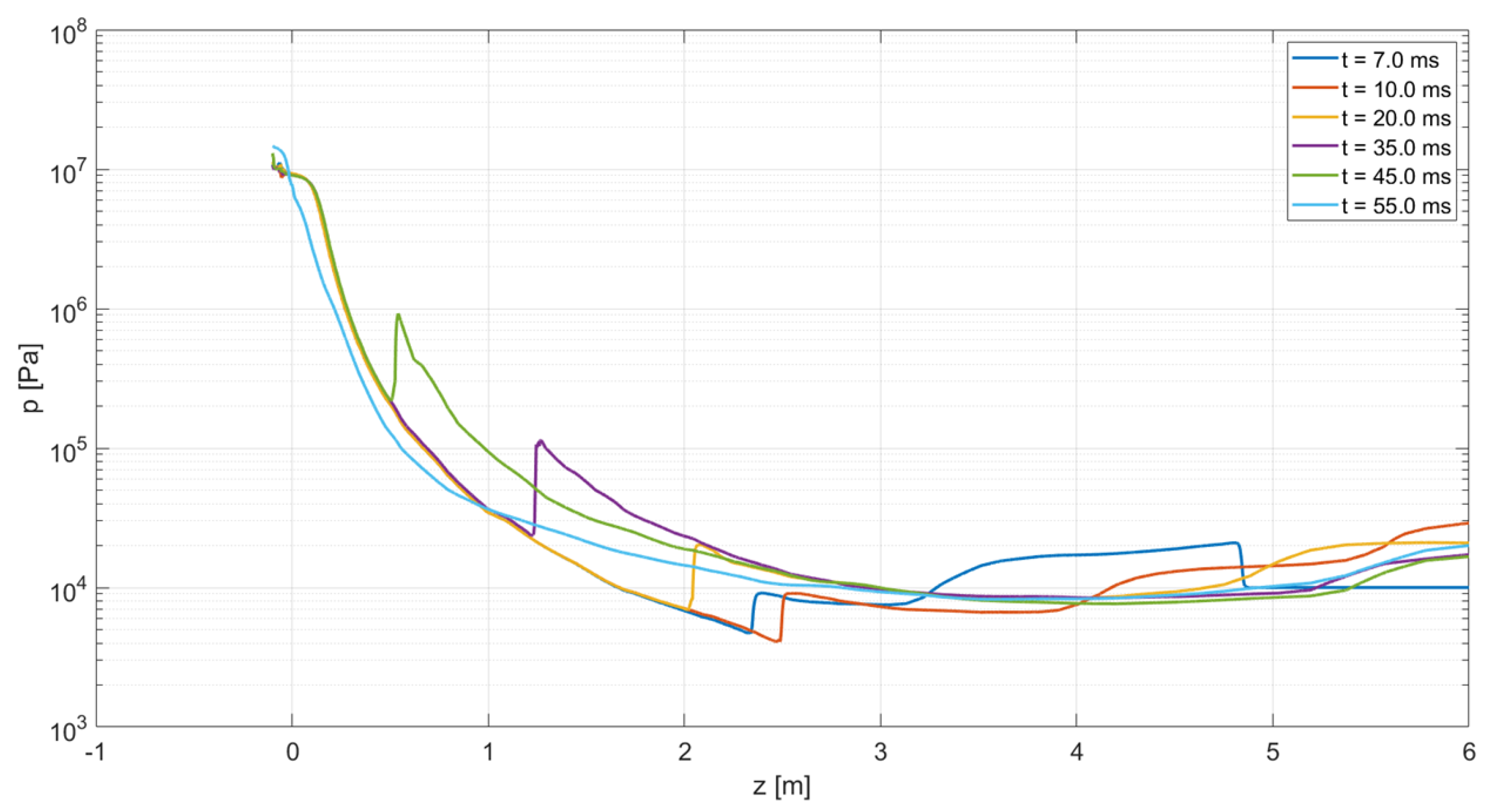
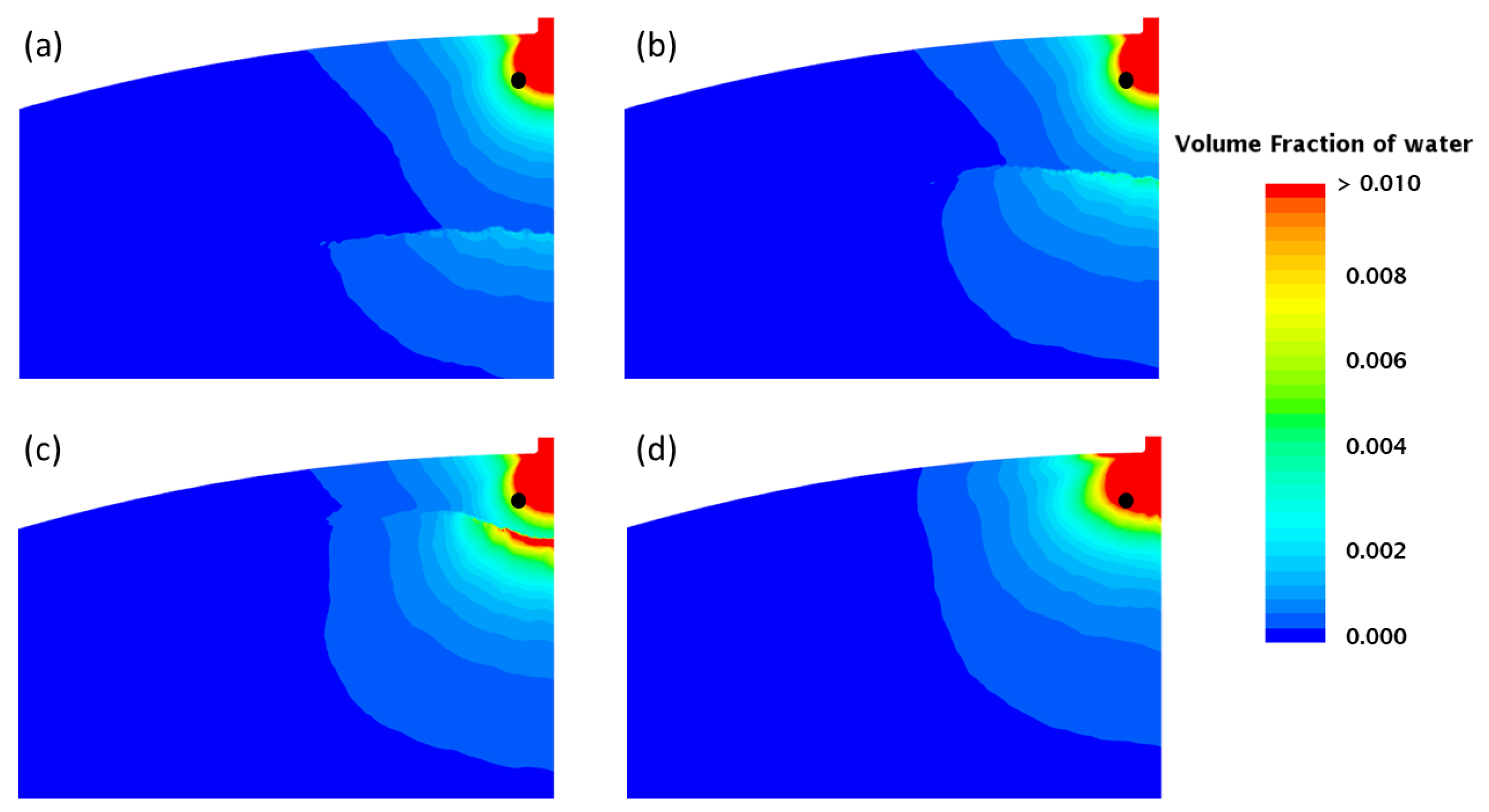
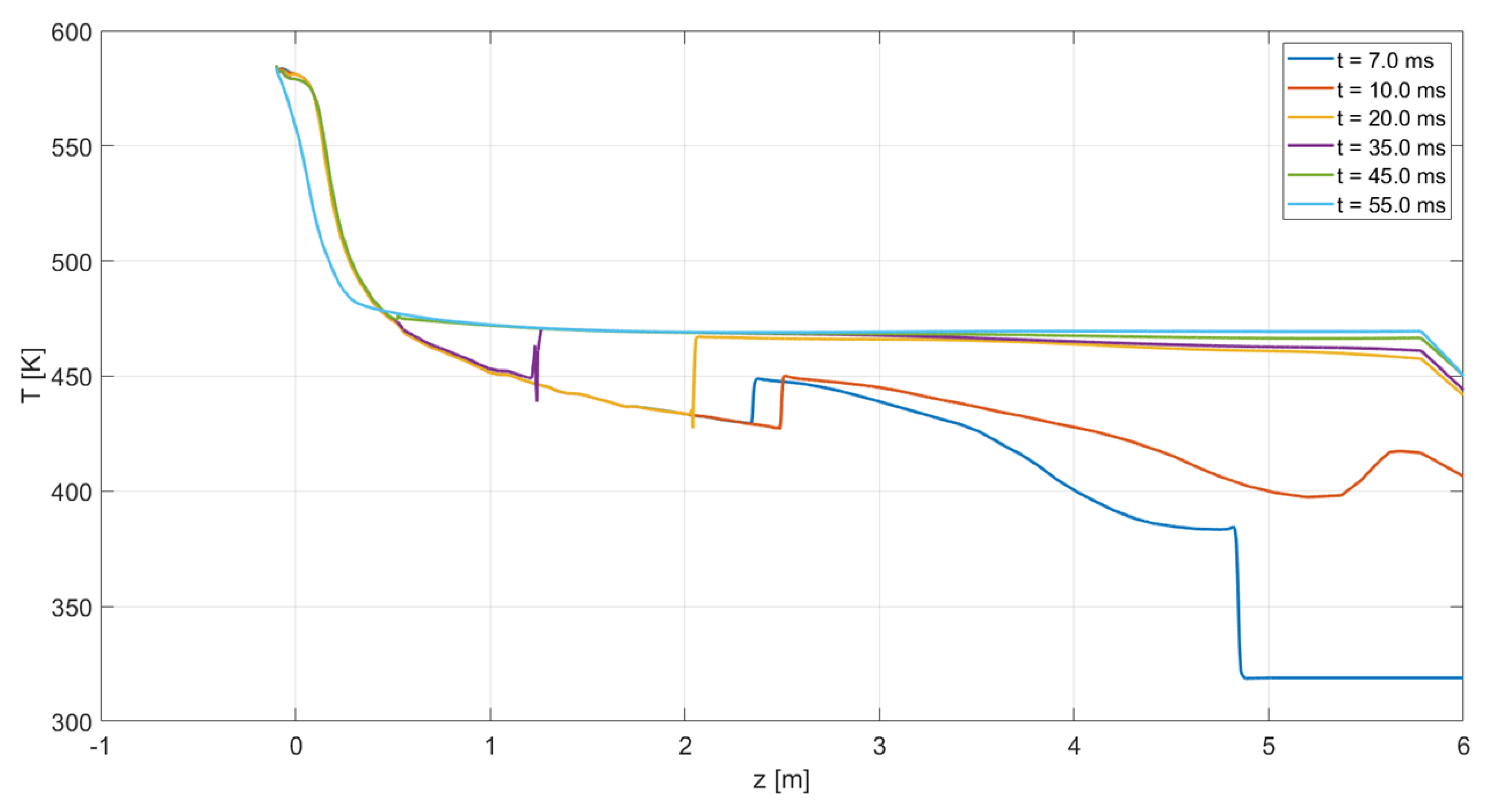
4.1. Flow Field
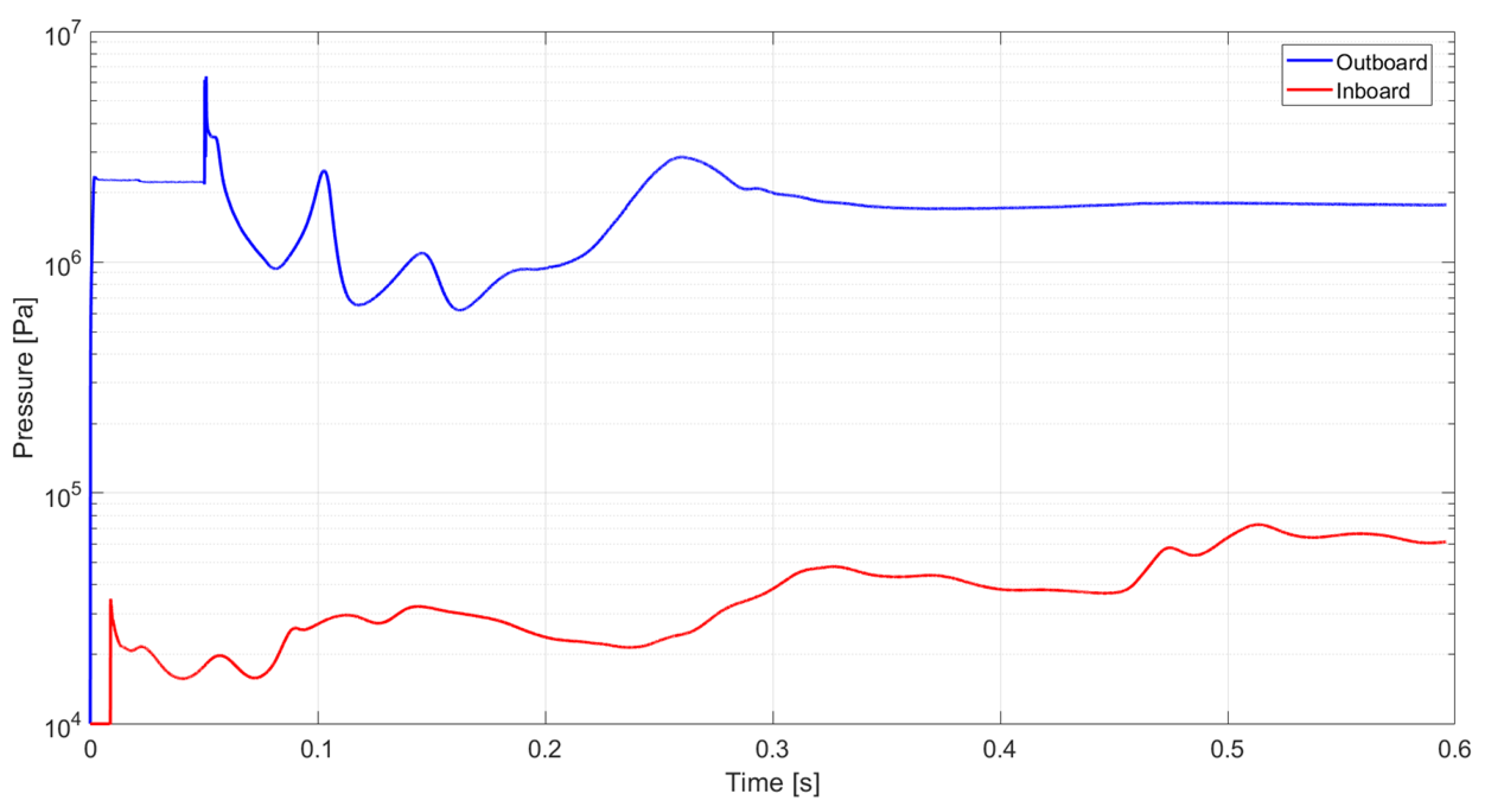
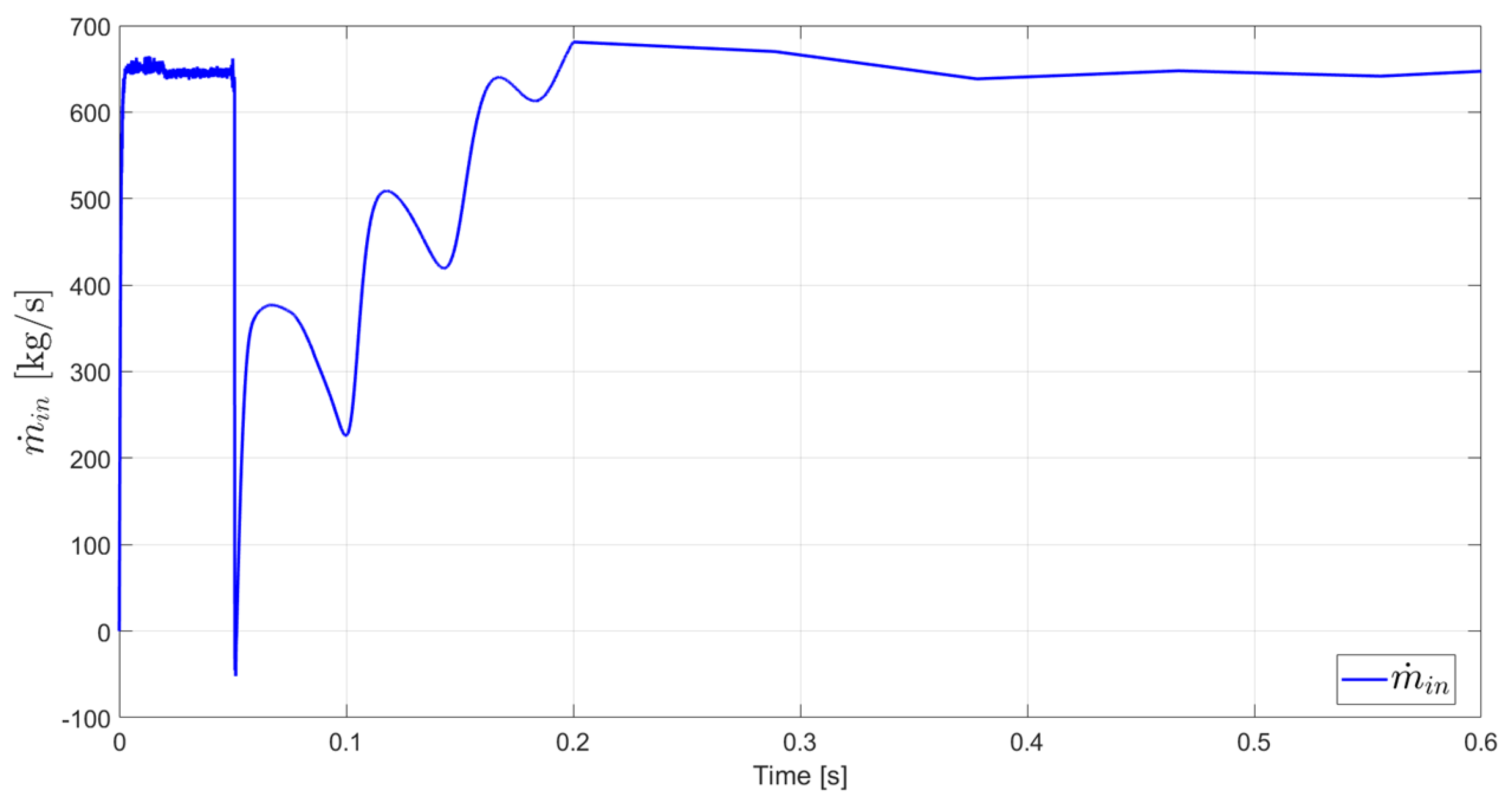
4.2. Pressure Evolution and Phase Change
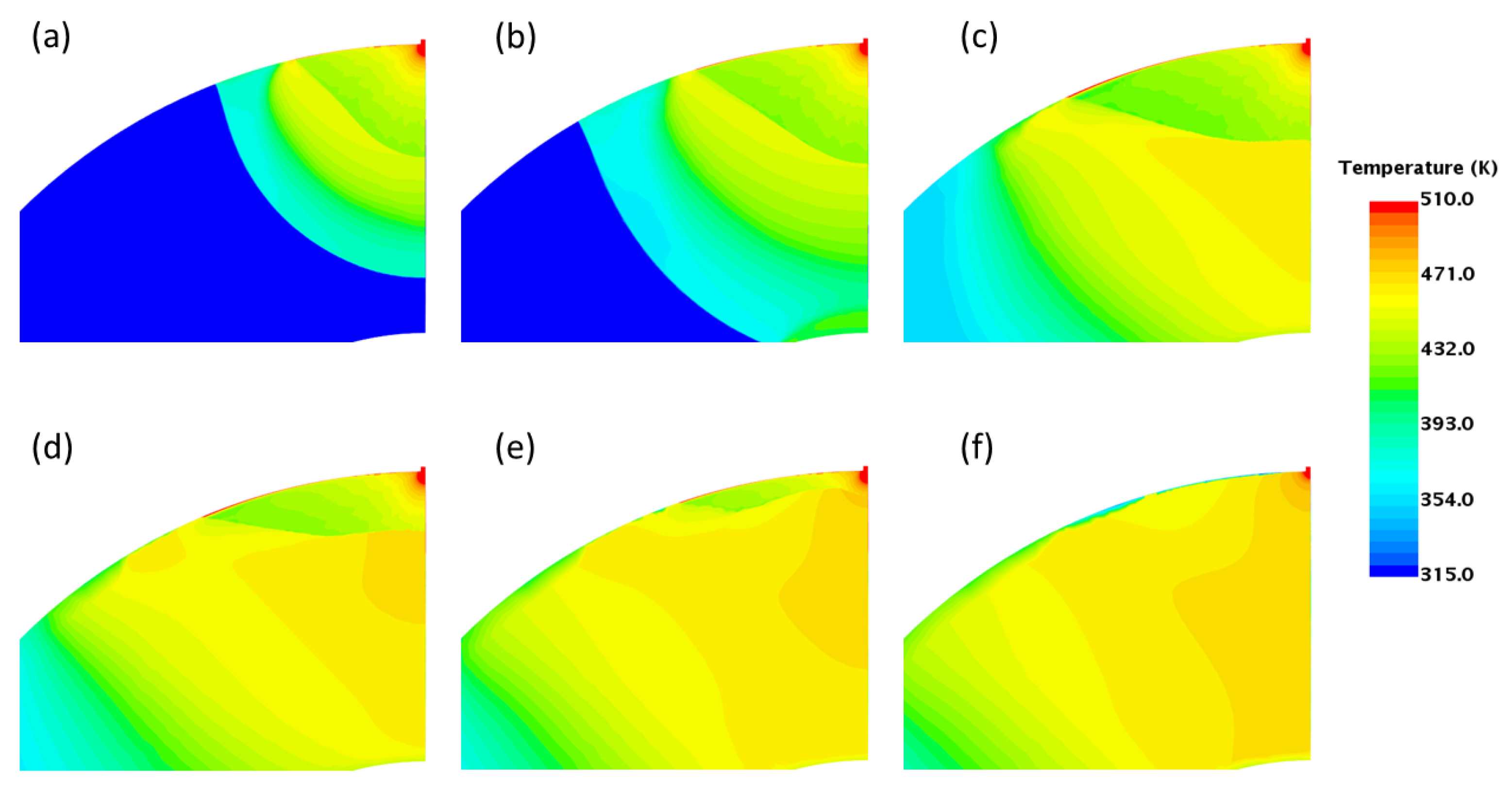
4.3. Temperature Field
5. Comparison with the Helium-Cooled BB Case
6. Conclusions and Perspective
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Model Development and Validation

Appendix A.1. Setup
- Inlet: stagnation inlet with fixed supersonic pressure, total pressure and total temperature.
- Outlet: pressure outlet with fixed pressure and temperature.
- Bottom boundary: symmetry plane.
- Walls: no slip condition.
| pin [MPa] | Tin [K] | |
|---|---|---|
| Water | 5.0 | 519.1 |
| Vapour | 0.1 | 372.8 |
Appendix A.2. Model
- (a)
- 2D
- (b)
- Implicit unsteady
- (c)
- Turbulent (realisable two-layer)
- (d)
- Multiphase
- (e)
- Volume of Fluid (VOF)
- (f)
- Segregated flow
- (g)
- Segregated multiphase temperature
Appendix A.3. Results

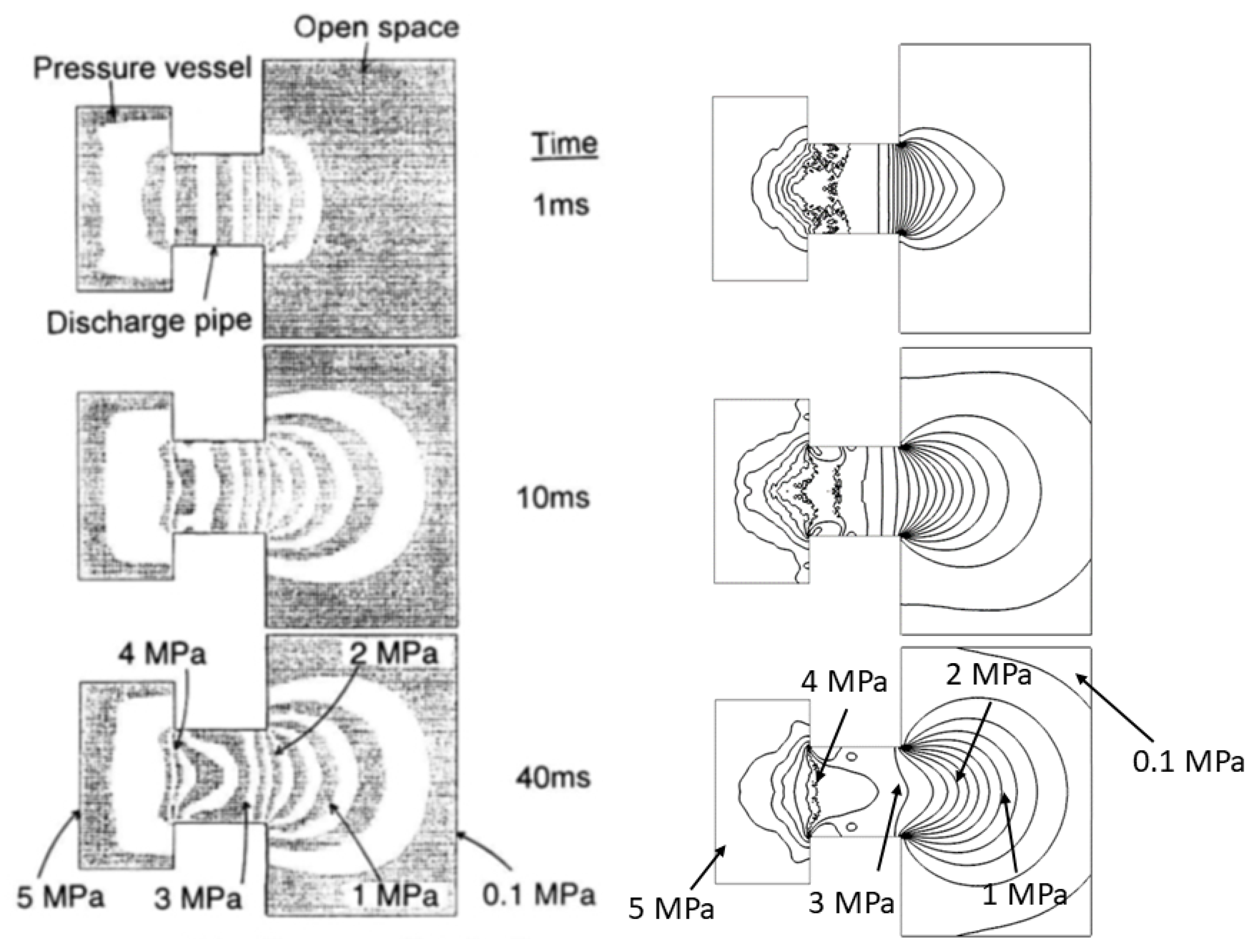
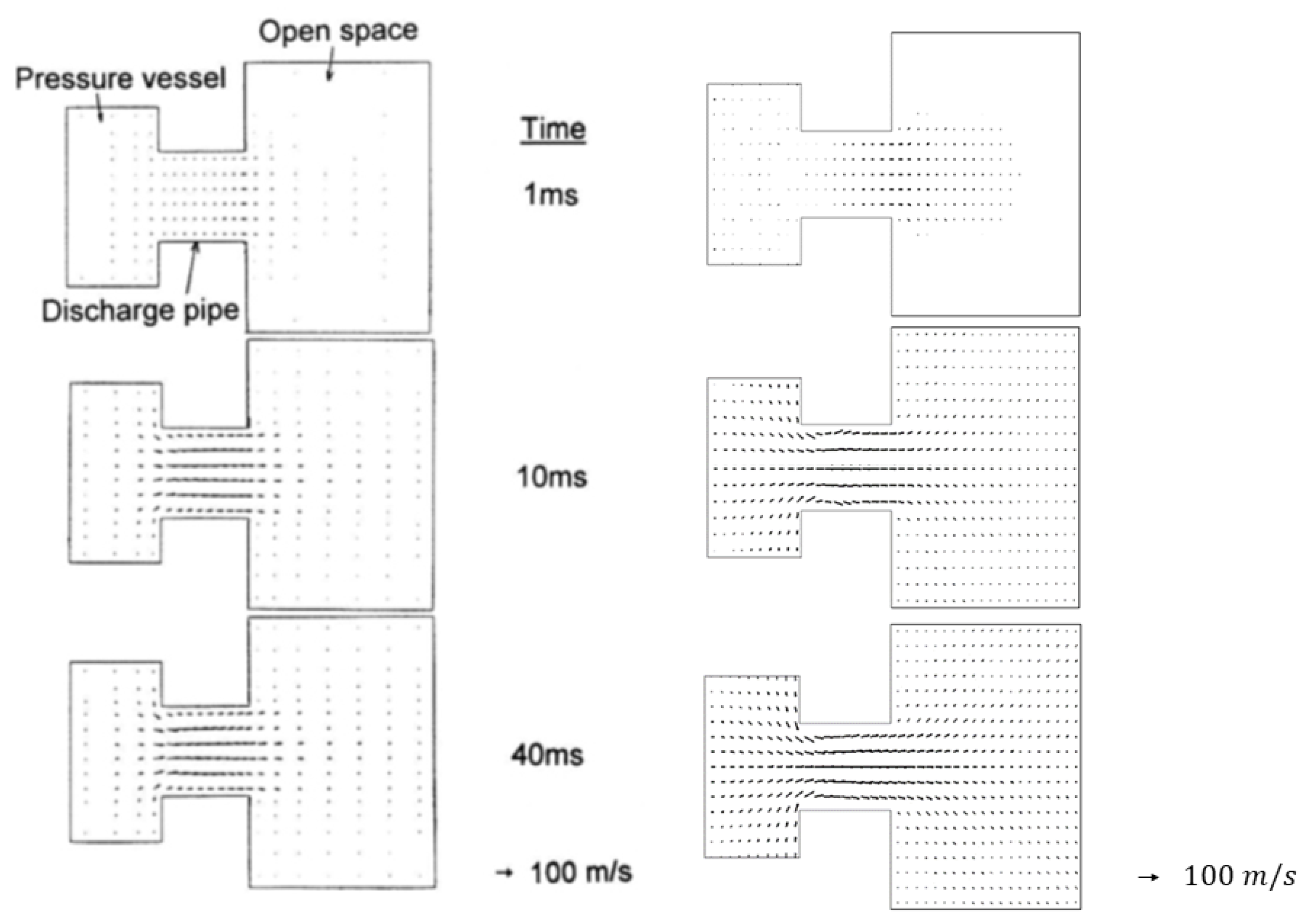
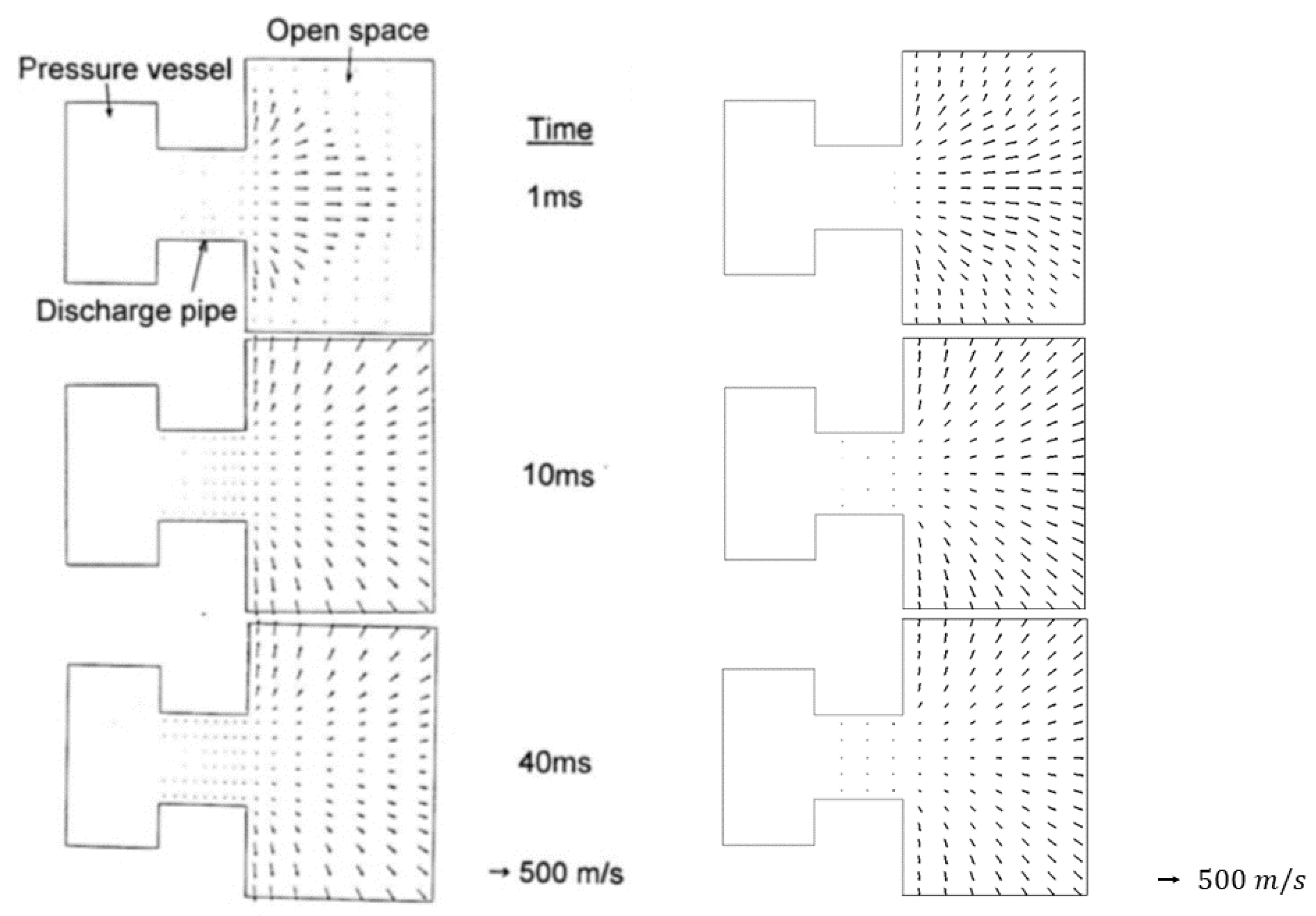
References
- Donné, A.J.H.; Morris, W.; Litaudon, X.; Hidalgo, C.; McDonald, D.; Zohm, H.; Diegele, E.; Möslang, A.; Nordlund, K.; Federici, G.; et al. European Reasearch Roadmap to the Realisation of Fusion Energy; EUROfusion Consortium: Garching, Germany, 2018; ISBN 978-3-00-061152-0. [Google Scholar]
- Federici, G.; Baylard, C.; Beaumont, A.; Holden, J. The plan forward for EU DEMO. Fusion Eng. Des. 2021, 173, 112960. [Google Scholar] [CrossRef]
- Federici, G.; Holden, J.; Baylard, C.; Beaumont, A. The EU DEMO staged design approach in the Pre-Concept Design Phase. Fusion Eng. Des. 2021, 173, 112959. [Google Scholar] [CrossRef]
- Caruso, G.; Ciattaglia, S.; Colling, B.; Di Pace, L.; Dongiovanni, D.L.; D’Onorio, M.; Garcia, M.; Jin, X.Z.; Johnston, J.; Leichtle, D.; et al. DEMO—The main achievements of the Pre–Concept phase of the safety and environmental work package and the development of the GSSR. Fusion Eng. Des. 2022, 176, 113025. [Google Scholar] [CrossRef]
- Froio, A.; Moscato, I. Effect of different system parameters on the design of the EU DEMO Vacuum Vessel Pressure Suppression System. Fusion Eng. Des. 2023, 190, 113543. [Google Scholar] [CrossRef]
- Spagnuolo, G.A.; Arredondo, R.; Boccaccini, L.V.; Chiovaro, P.; Ciattaglia, S.; Cismondi, F.; Coleman, M.; Cristescu, I.; D’Amico, S.; Day, C.; et al. Integrated design of breeding blanket and ancillary systems related to the use of helium or water as a coolant and impact on the overall plant design. Fusion Eng. Des. 2021, 173, 112933. [Google Scholar] [CrossRef]
- Ahn, M.Y.; Cho, S.; Kim, D.H.; Lee, E.S.; Kim, H.S.; Suh, J.S.; Yun, S.; Cho, N.Z. Preliminary safety analysis of Korea Helium Cooled Solid Breeder Test Blanket Module. Fusion Eng. Des. 2008, 83, 1753–1758. [Google Scholar] [CrossRef]
- D’Onorio, M.; D’Amico, S.; Froio, A.; Porfiri, M.T.; Spagnuolo, G.A.; Caruso, G. Benchmark analysis of in-vacuum vessel LOCA scenarios for code-to-code comparison. Fusion Eng. Des. 2021, 173, 112938. [Google Scholar] [CrossRef]
- Nakamura, M.; Tobita, K.; Someya, Y.; Utoh, H.; Sakamoto, Y.; Gulden, W. Thermohydraulic responses of a water-cooled tokamak fusion DEMO to loss-of-coolant accidents. Nucl. Fusion 2015, 55, 123008. [Google Scholar] [CrossRef]
- D’Onorio, M.; Giannetti, F.; Porfiri, M.T.; Caruso, G. Preliminary safety analysis of an in-vessel LOCA for the EU-DEMO WCLL blanket concept. Fusion Eng. Des. 2020, 155, 111560. [Google Scholar] [CrossRef]
- Porfiri, M.; Meloni, P. Post-test calculations with ISAS-ITER system for ICE experiments. In Proceedings of the 19th IEEE/IPSS Symposium on Fusion Engineering, 19th SOFE (Cat. No.02CH37231), Atlantic City, NJ, USA, 25 January 2002; pp. 48–51. [Google Scholar] [CrossRef]
- Caruso, G.; Bartels, H.; Iseli, M.; Meyder, R.; Nordlinder, S.; Pasler, V.; Porfiri, M. Simulation of cryogenic He spills as basis for planning of experimental campaign in the EVITA facility. Nucl. Fusion 2005, 46, 51. [Google Scholar] [CrossRef]
- Froio, A.; Bertinetti, A.; Ciattaglia, S.; Cismondi, F.; Savoldi, L.; Zanino, R. Modelling an in-vessel loss of coolant accident in the EU DEMO WCLL breeding blanket with the GETTHEM code. Fusion Eng. Des. 2018, 136, 1226–1230. [Google Scholar] [CrossRef]
- Froio, A.; Barucca, L.; Ciattaglia, S.; Cismondi, F.; Savoldi, L.; Zanino, R. Analysis of the effects of primary heat transfer system isolation valves in case of in-vessel loss-of-coolant accidents in the EU DEMO. Fusion Eng. Des. 2020, 159, 111926. [Google Scholar] [CrossRef]
- Zappatore, A.; Froio, A.; Spagnuolo, G.A.; Zanino, R. 3D transient CFD simulation of an in-vessel loss-of-coolant accident in the EU DEMO fusion reactor. Nucl. Fusion 2020, 60, 126001. [Google Scholar] [CrossRef]
- Arena, P.; Del Nevo, A.; Moro, F.; Noce, S.; Mozzillo, R.; Imbriani, V.; Giannetti, F.; Edemetti, F.; Froio, A.; Savoldi, L.; et al. The DEMO Water-Cooled Lead-Lithium Breeding Blanket: Design Status at the End of the Pre-Conceptual Design Phase. Appl. Sci. 2021, 11, 11592. [Google Scholar] [CrossRef]
- Gliss, C. DEMO Reference Configuration Model; EFDA_D_2MUNPL; EUROfusion Consortium: Garching, Germany, 2017. [Google Scholar]
- Siemens Digital Industries Software. Simcenter STAR-CCM+ User Guide v. 2021.2; Siemens: Munich, Germany, 2021. [Google Scholar]
- Jin, X.Z. BB LOCA analysis for the reference design of the EU DEMO HCPB blanket concept. Fusion Eng. Des. 2018, 136, 958–963. [Google Scholar] [CrossRef]
- Froio, A.; Bertinetti, A.; Savoldi, L.; Zanino, R.; Cismondi, F.; Ciattaglia, S. Benchmark of the GETTHEM Vacuum Vessel Pressure Suppression System (VVPSS) model for a helium-cooled EU DEMO blanket. In Proceedings of the 27th European Safety and Reliability Conference on Safety and Reliability—Theory and Applications, Portorož, Slovenia, 18–22 June 2017; pp. 59–66. [Google Scholar] [CrossRef]
- De Lorenzo, M.; Lafon, P.; Di Matteo, M.; Pelanti, M.; Seynhaeve, J.M.; Bartosiewicz, Y. Homogeneous two-phase flow models and accurate steam-water table look-up method for fast transient simulations. Int. J. Multiph. Flow 2017, 95, 199–219. [Google Scholar] [CrossRef]
- Shapiro, A.H. The Dynamics and Thermodynamics of Compressible Fluid Flow; Wiley: New York, NY, USA, 1953; Volume 1. [Google Scholar]
- Anderson, J.D. Modern Compressible Flow with Historical Perspective, 3rd ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Franquet, E.; Perrier, V.; Gibout, S.; Bruel, P. Free underexpanded jets in a quiescent medium: A review. Prog. Aerosp. Sci. 2015, 77, 25–53. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A Review of Water Hammer Theory and Practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Griffith, P. Screening Reactor Steam/Water Piping Systems for Water Hammer; Technical Report; OSTI: Washington, DC, USA, 1997. [CrossRef]
- Barna, I.F.; Imre, A.R.; Baranyai, G.; Ézsöl, G. Experimental and theoretical study of steam condensation induced water hammer phenomena. Nucl. Eng. Des. 2010, 240, 146–150. [Google Scholar] [CrossRef]
- Datta, P.; Chakravarty, A.; Ghosh, K.; Mukhopadhyay, A.; Sen, S.; Dutta, A.; Goyal, P.; Thangamani, I. Modeling and analysis of condensation induced water hammer. Numer. Heat Transf. Part A Appl. 2018, 74, 975–1000. [Google Scholar] [CrossRef]
- Boccaccini, L.; Arbeiter, F.; Arena, P.; Aubert, J.; Bühler, L.; Cristescu, I.; Nevo, A.D.; Eboli, M.; Forest, L.; Harrington, C.; et al. Status of maturation of critical technologies and systems design: Breeding blanket. Fusion Eng. Des. 2022, 179, 113116. [Google Scholar] [CrossRef]
- Hernández, F.A.; Pereslavtsev, P.; Zhou, G.; Kang, Q.; D’Amico, S.; Neuberger, H.; Boccaccini, L.V.; Kiss, B.; Nádasi, G.; Maqueda, L.; et al. Consolidated design of the HCPB Breeding Blanket for the pre-Conceptual Design Phase of the EU DEMO and harmonization with the ITER HCPB TBM program. Fusion Eng. Des. 2020, 157, 111614. [Google Scholar] [CrossRef]
- Minato, A.; Takamori, K.; Suzuki, A. Numerical Study of Two-Dimensional Structure in Critical Steam-Water Two-Phase Flow. J. Nucl. Sci. Technol. 1995, 32, 464–475. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sprò, M.; Froio, A.; Zappatore, A. 3D Transient CFD Simulation of an In-Vessel Loss-of-Coolant Accident in the EU DEMO WCLL Breeding Blanket. Energies 2023, 16, 3637. https://doi.org/10.3390/en16093637
Sprò M, Froio A, Zappatore A. 3D Transient CFD Simulation of an In-Vessel Loss-of-Coolant Accident in the EU DEMO WCLL Breeding Blanket. Energies. 2023; 16(9):3637. https://doi.org/10.3390/en16093637
Chicago/Turabian StyleSprò, Mauro, Antonio Froio, and Andrea Zappatore. 2023. "3D Transient CFD Simulation of an In-Vessel Loss-of-Coolant Accident in the EU DEMO WCLL Breeding Blanket" Energies 16, no. 9: 3637. https://doi.org/10.3390/en16093637
APA StyleSprò, M., Froio, A., & Zappatore, A. (2023). 3D Transient CFD Simulation of an In-Vessel Loss-of-Coolant Accident in the EU DEMO WCLL Breeding Blanket. Energies, 16(9), 3637. https://doi.org/10.3390/en16093637






