Numerical Investigation of Compression and Expansion Process of Twin-Screw Machine Using R-134a
Abstract
1. Introduction
2. Geometric Modeling and Meshing
3. Simulation Settings
3.1. Governing Equations and Boundary Conditions
3.2. Meshing of the Fluid Domains
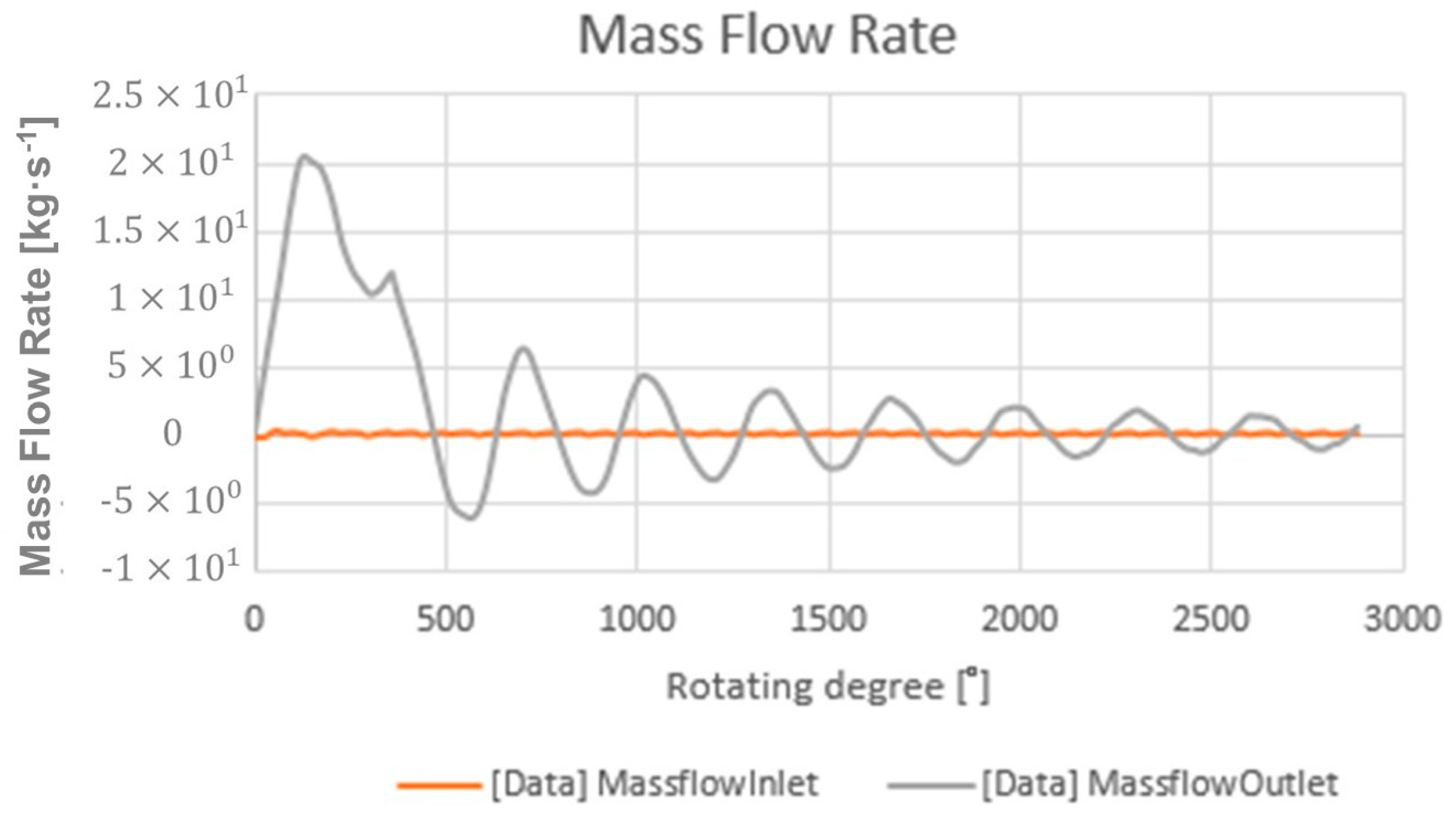
3.3. Grid Independence Verification
4. Simulation Results
4.1. Twin-Screw Compressor
4.2. Twin-Screw Expander
5. Conclusions
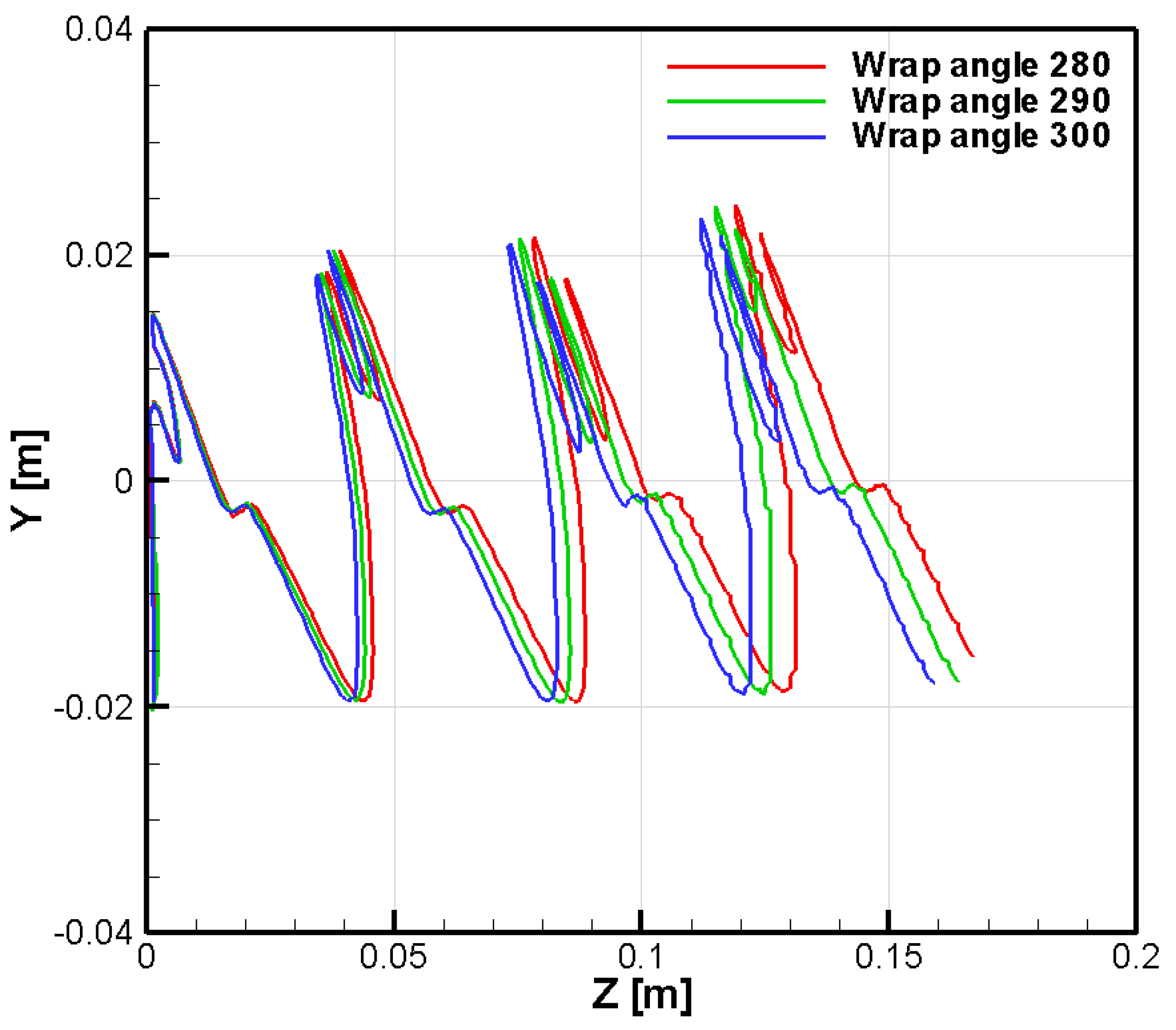
- The wrap angle influenced the distribution of the sealing lines and altered the leakage flow, which affected the delivery rate and volumetric efficiency by up to 2%.
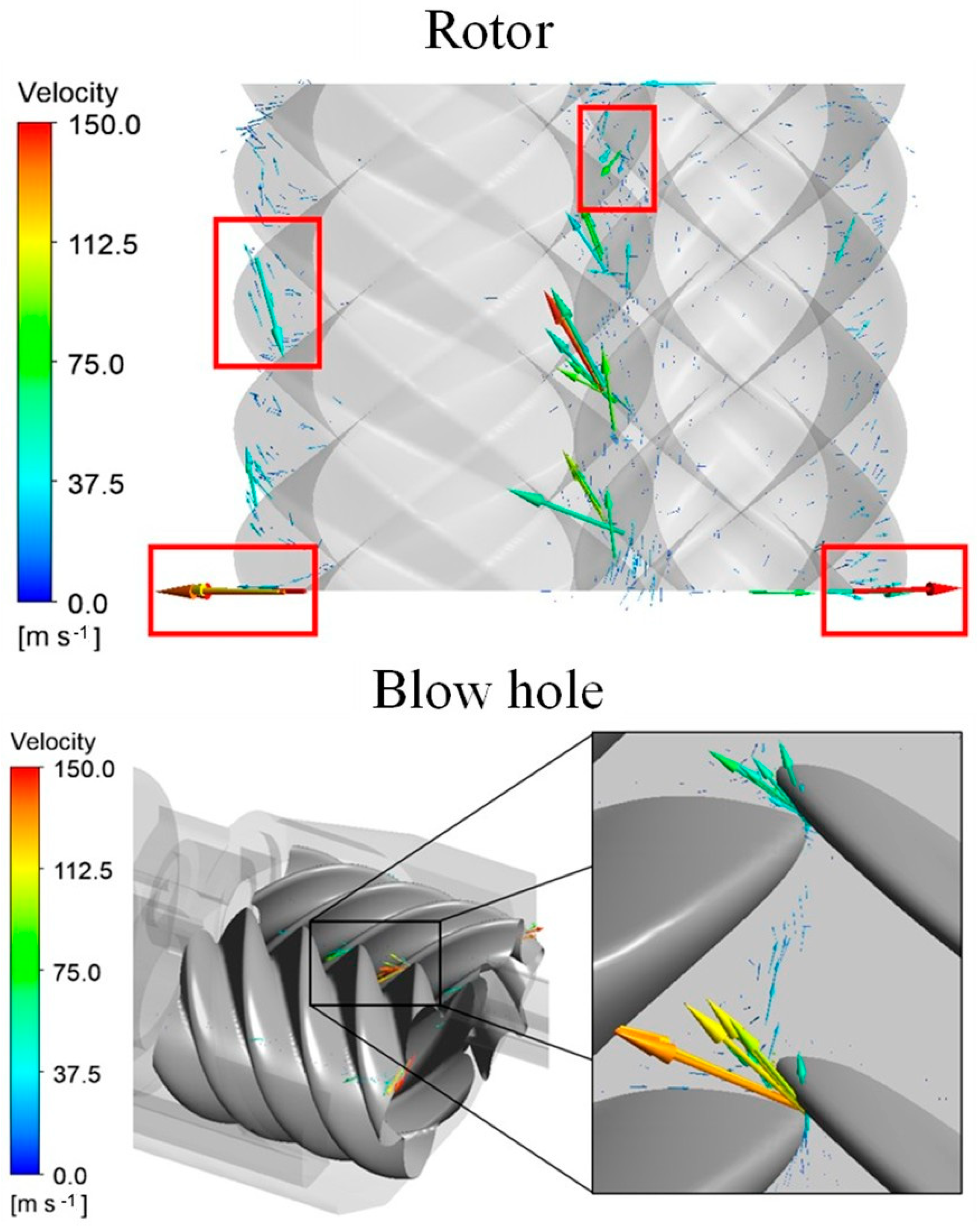
- The leakage flow could be determined from the predicted flow distribution, and the highest velocity was above 100 m·s−1 during the compression process as a result of the small gap clearance.
- The isentropic efficiency was not sensitive to the change in the wrap angle, and the difference was within 1%.
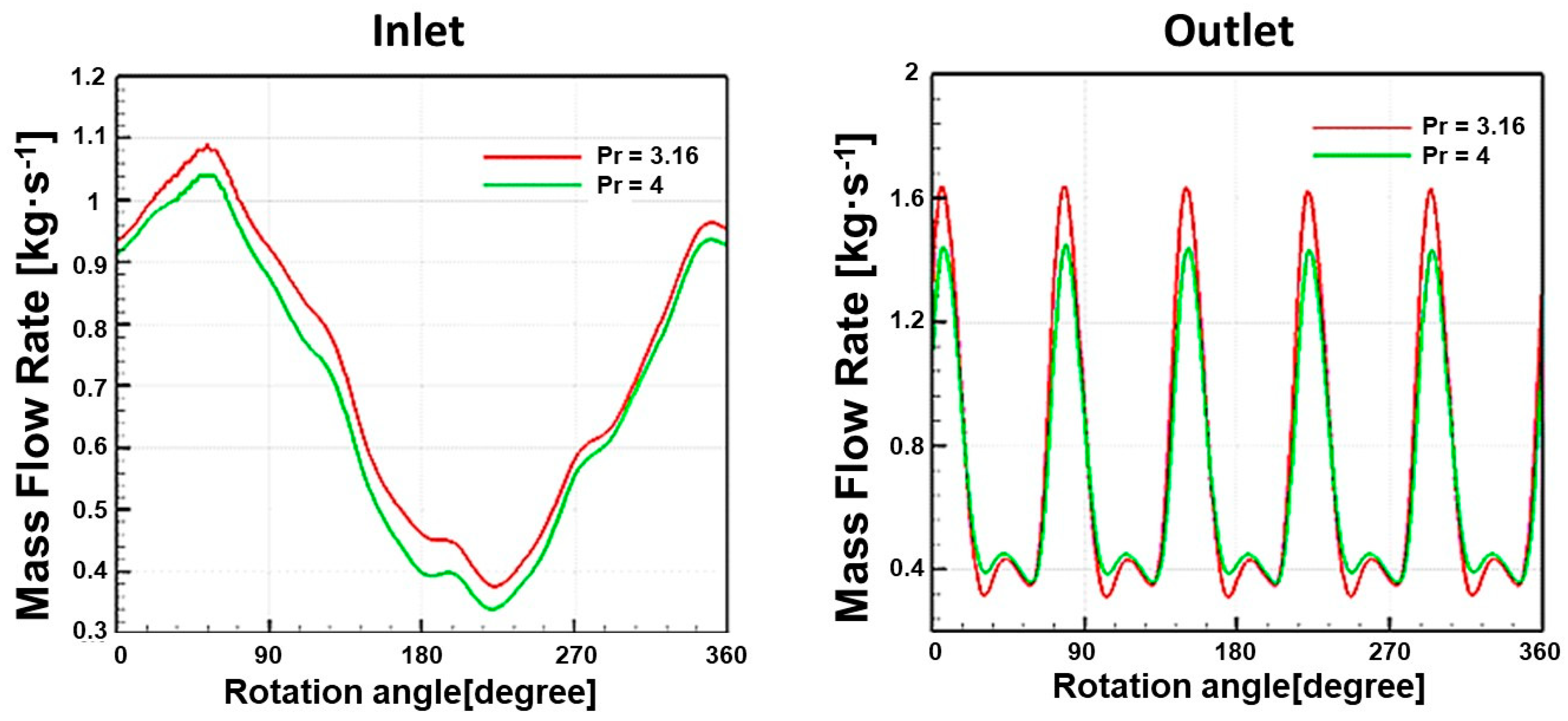
- An increase in the pressure ratio led to a decrease in the mass flow rate and volumetric efficiency because of the higher leakage flow rate. However, its influence on the isentropic efficiency was also unnoticeable.
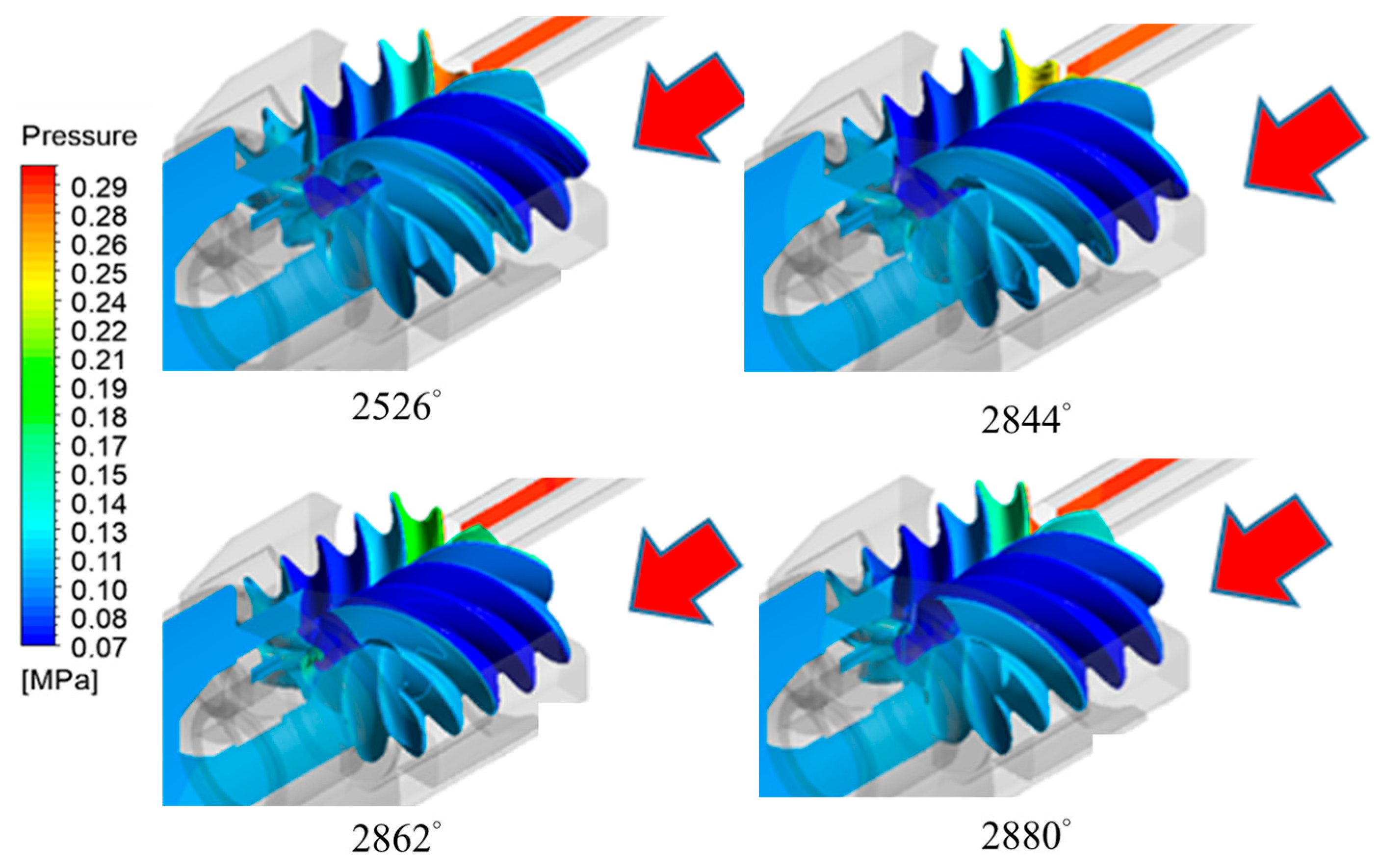
- This screw expander was operated in underexpanded conditions, and the pressure contours demonstrated a minimum pressure level below the outlet pressure. Higher volumetric and isentropic efficiencies could be achieved if the expander was operated at a ratio that was close to the built-in expansion ratio.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Specific heat capacity | |
| K | Thermal conductivity |
| P | Pressure |
| R | Gas constant |
| Internal heat source and the viscous dissipation term | |
| T | Temperature |
| u, v, w | Velocity |
| μ | Viscosity |
| ρ | Density |
| τ | Component of the viscous stress |
References
- Stošić, N.; Hanjalić, K. Contribution towards modelling of two-stage reciprocating compressors. Int. J. Mech. Sci. 1977, 19, 439–445. [Google Scholar] [CrossRef]
- Stošic, N.; Milutinović, L.; Hanjalić, K.; Kovačević, A. Investigation of the influence of oil injection upon the screw compressor working process. Int. J. Refrig. 1992, 15, 206–220. [Google Scholar] [CrossRef]
- Stošić, N.; Smith, I.K.; Kovačević, A.; Aldis, C.A. The design of a twin-screw compressor based on a new rotor profile. J. Eng. Des. 1997, 8, 389–399. [Google Scholar] [CrossRef]
- You, C.; Tang, Y.; Fleming, J.S. Optimum rotor geometrical parameters in refrigeration helical twin screw compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 23–26 July 1996; p. 1074. [Google Scholar]
- Fleming, J.S.; Tang, Y.; Cook, G. The twin helical screw compressor Part 1: Development, applications and competitive position. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1998, 212, 355–367. [Google Scholar] [CrossRef]
- Lee, W.S.; Ma, R.H.; Chen, S.L.; Wu, W.F.; Hsia, H.W. Numerical simulation and performance analysis of twin screws air compressors. Int. J. Rotating Mach. 2001, 7, 132087. [Google Scholar] [CrossRef]
- Rane, S.; Kovacevic, A.; Stosic, N.; Kethidi, M. Deforming grid generation and CFD analysis of variable geometry screw compressors. Comput. Fluids 2014, 99, 124–141. [Google Scholar] [CrossRef]
- Utri, M.; Brümmer, A. Improvement of the efficiency of twin-screw refrigeration compressors by means of dual lead rotors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 11–14 July 2016; p. 2474. [Google Scholar]
- Kovačević, A.; Stošić, N.; Smith, I.K. Grid aspects of screw compressor flow calculations. In Proceedings of the 2000 International Mechanical Engineering Congress & Exposition, Orlando, FL, USA, 5–10 November 2000. [Google Scholar]
- Kovacevic, A.; Stosic, N.; Smith, I.K. Screw Compressors: Three Dimensional Computational Fluid Dynamics and Solid Fluid Interaction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Pascu, M.; Kovacevic, A.; Udo, N. Performance optimization of Screw Compressors based on numerical investigation of the flow behaviour in the discharge chamber. In Proceedings of the International Compressor Conference, West Lafayette, IN, USA, 16–19 July 2012; p. 2051. [Google Scholar]
- Kovacevic, A.; Stosic, N. CFD analysis of oil flooded twin screw compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 11–14 July 2016; p. 2392. [Google Scholar]
- Wu, H.; Lin, K.; Huang, H.; Xiong, B.; Zhang, B.; Xing, Z. Research on effects of vapor injection on twin-screw compressor performance. Int. J. Refrig. 2020, 118, 483–490. [Google Scholar] [CrossRef]
- Wu, X.; Xing, Z.; He, Z.; Wang, X.; Chen, W. Effects of lubricating oil on the performance of a semi-hermetic twin screw refrigeration compressor. Appl. Therm. Eng. 2017, 112, 340–351. [Google Scholar] [CrossRef]
- Wu, H.; Huang, H.; Zhang, B.; Xiong, B.; Lin, K. CFD Simulation and Experimental Study of Working Process of Screw Refrigeration Compressor with R134a. Energies 2019, 12, 2054. [Google Scholar] [CrossRef]
- Wang, W.; Wu, Y.T.; Ma, C.F.; Liu, L.D.; Yu, J. Preliminary experimental study of single screw expander prototype. Appl. Therm. Eng. 2011, 31, 3684–3688. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wu, Y.T.; Xia, G.D.; Ma, C.F.; Ji, W.N.; Liu, S.W.; Yang, K.; Yang, F.B. Development and experimental study on organic Rankine cycle system with single-screw expander for waste heat recovery from exhaust of diesel engine. Energy 2014, 77, 499–508. [Google Scholar] [CrossRef]
- Papes, I.; Degroote, J.; Vierendeels, J. New insights in twin screw expander performance for small scale ORC systems from 3D CFD analysis. Appl. Therm. Eng. 2015, 91, 535–546. [Google Scholar] [CrossRef]
- Andres, R.; Hesse, J.; Babic, H.; Salecker, U.; Spille-kohoff, A.; Nikolov, A.; Bruemmer, A. CFD Simulation of a twin screw expander including leakage flows. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 11–14 July 2016; p. 2497. [Google Scholar]
- Rane, S.; Kovačević, A.; Stošić, N.; Smith, I. Analysis of real gas equation of state for CFD modelling of twin screw expanders with R245fa, R290, R1336mzz (Z) and R1233zd (E). Int. J. Refrig. 2021, 121, 313–326. [Google Scholar] [CrossRef]
- Ansys, C.F.X. 10.0 User’s Manual; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Yang, S.; Ouyang, H.; Wu, Y.; Wang, L.; Mei, L.; Wang, H. CFD simulation for the internal pressure characteristics of an oil-injected twin-screw refrigeration compressor. Int. J. Refrig. 2021, 126, 143–154. [Google Scholar] [CrossRef]
- Rane, S.; Kovacevic, A.; Stosic, N.; Kethidi, M. Grid deformation strategies for CFD analysis of screw compressors. Int. J. Refrig. 2013, 36, 1883–1893. [Google Scholar] [CrossRef]
- Rane, S.; Kovacevic, A.; Stosic, N.; Kethidi, M. CFD grid generation and analysis of screw compressor with variable geometry rotors. In Proceedings of the Institution of Mechanical Engineers-8th International Conference on Compressors and Their Systems, London, UK, 9–10 September 2013; pp. 601–612. [Google Scholar]
- Kovacevic, A.; Rane, S.; Stosic, N. Computational fluid dynamics in rotary positive displacement screw machines. In Proceedings of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, JI, USA, 10–15 April 2016. [Google Scholar]
- Papes, I.; Degroote, J.; Vierendeels, J. 3D CFD analysis of a twin screw expander for small scale ORC systems. In Proceedings of the 11th World Congress on Computational Mechanics, Barcelona, Spain, 20–25 July 2014; pp. 7207–7217. [Google Scholar]
- Stosic, N. On heat transfer in screw compressors. Int. J. Heat Fluid Flow 2015, 51, 285–297. [Google Scholar] [CrossRef]
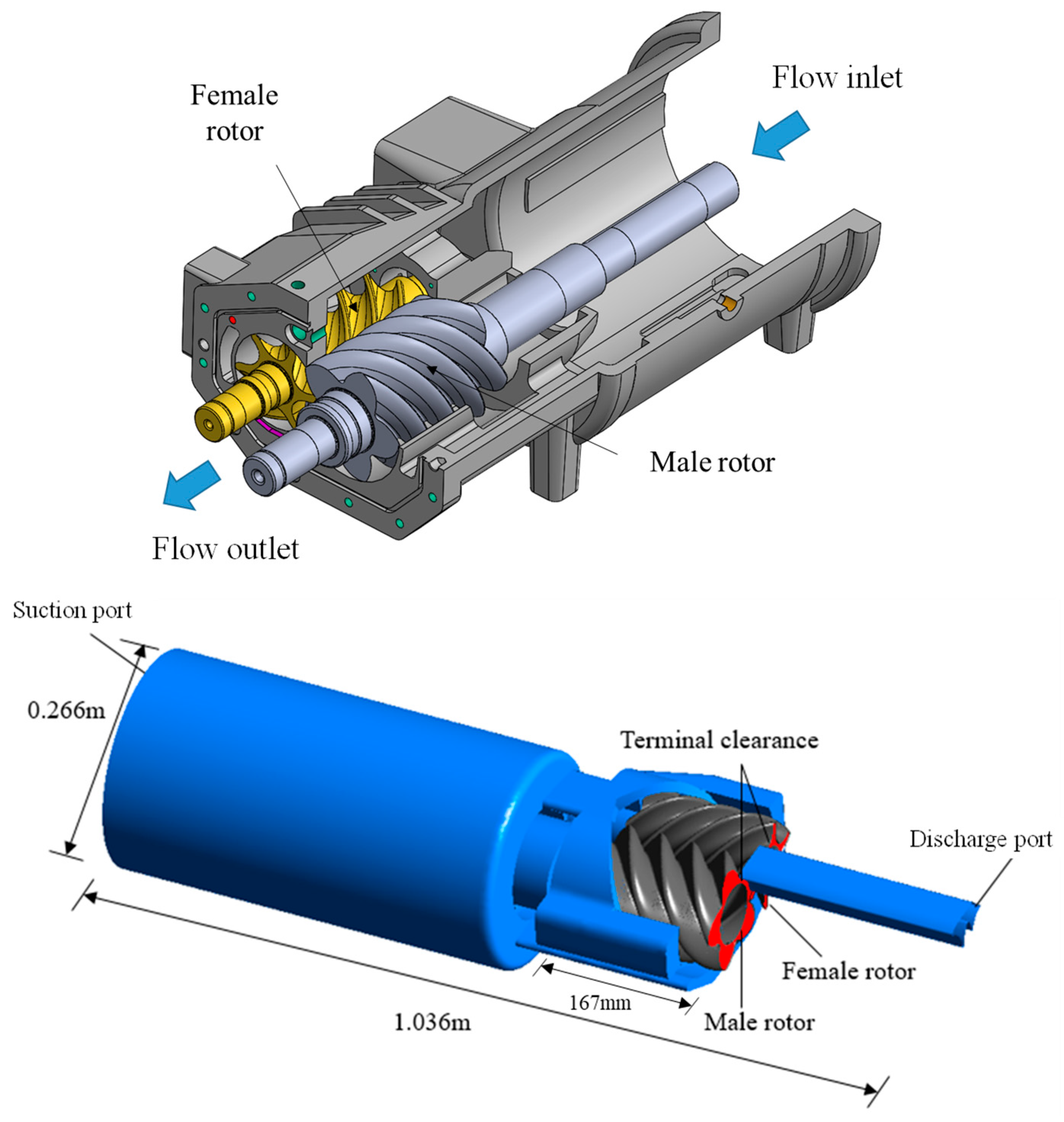
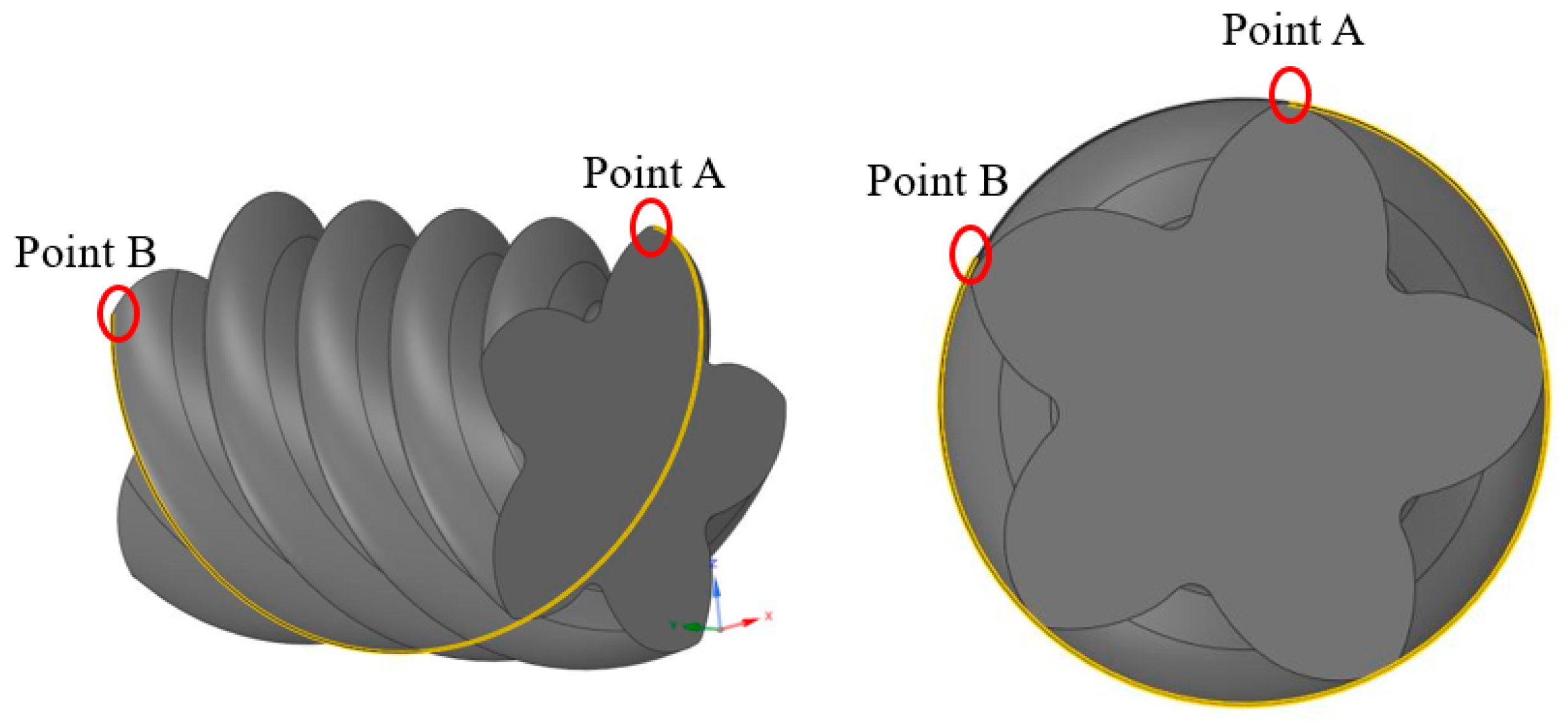
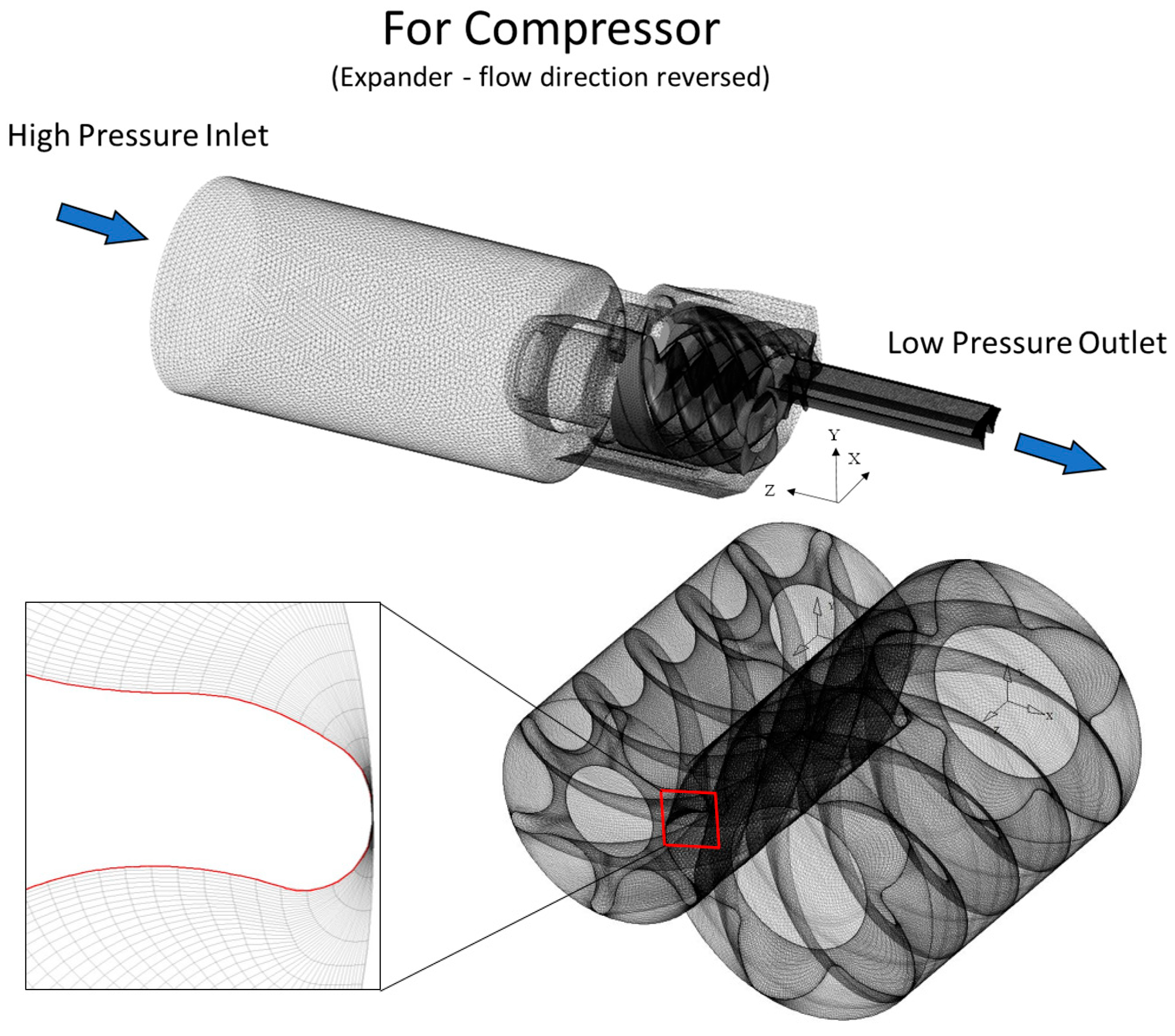
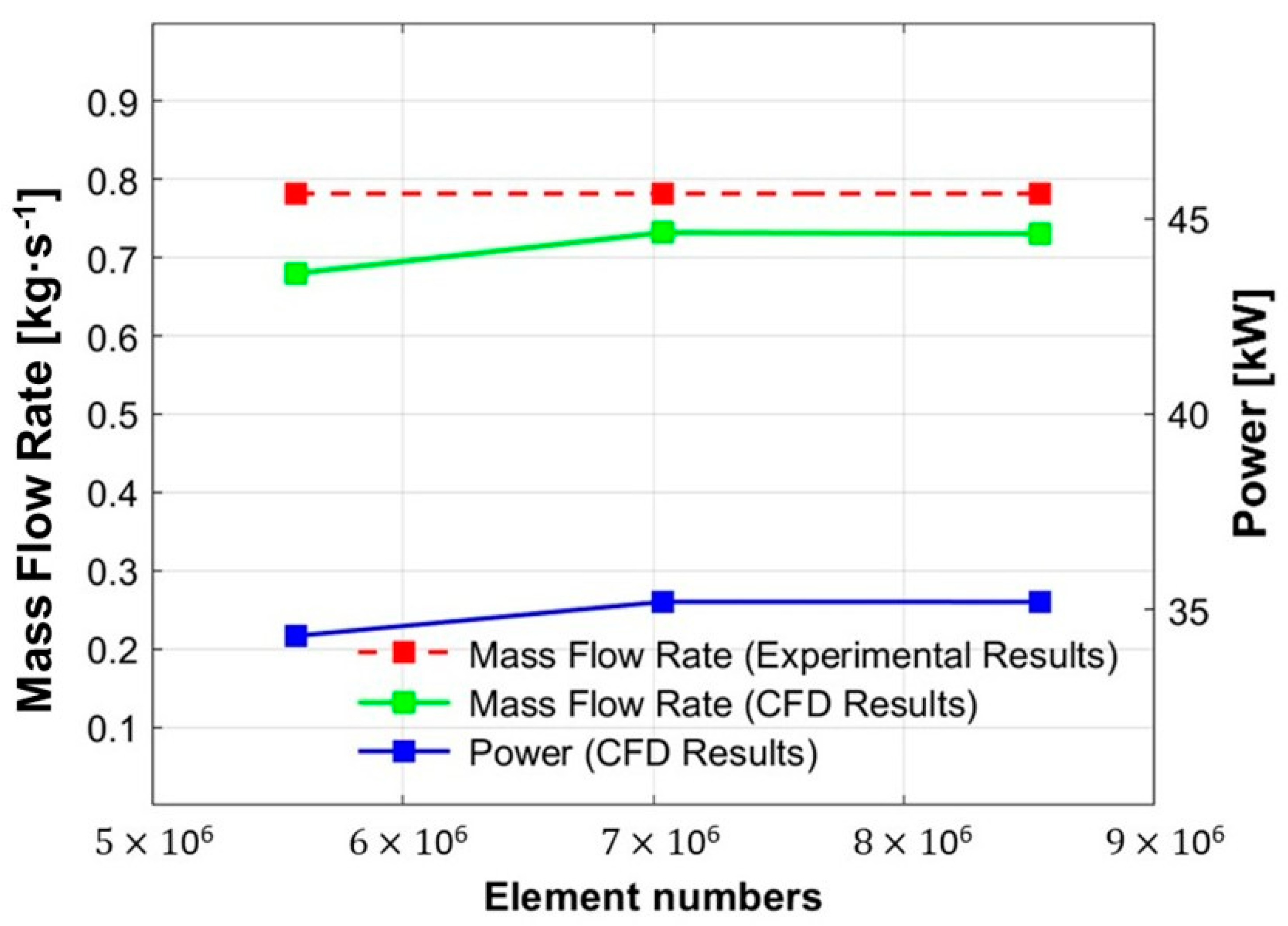






| Parameters | Value |
|---|---|
| Lobe combination | 5/6 |
| Rotor length (mm) | 167 |
| Inlet angle (°) | 280.52 |
| Outlet angle (°) | 60.48 |
| Male rotor head diameter (mm) | 138.54 |
| Female rotor head diameter (mm) | 109.86 |
| Center distance (mm) | 98 |
| Wrap angle (male rotor) (°) | 280, 290, 300 |
| Parameters | Value | |
|---|---|---|
| Compressor (R134a) | Wrap angle (degree) | 280, 290, 300 |
| Inlet pressure (bar) | 2.55 | |
| Inlet temperature (K) | 288.47 | |
| Discharge pressure (bar) | 8.05, 10.24 | |
| Discharge temperature (K) | 328.98, 337.45 | |
| Rotational speed (rpm) | 3600 | |
| Expander (R134a) | Inlet pressure (bar) | 3 |
| Inlet temperature (K) | 350.15 | |
| Discharge pressure (bar) | 1 | |
| Discharge temperature (K) | 311.03 | |
| Rotational speed (rpm) | 3600 |
| Wrap Angle | Flow Rate (kg·s−1) | Power (kW) | Volumetric Efficiency (%) | Isentropic Efficiency (%) |
|---|---|---|---|---|
| 280° | 0.742 | 35.6 | 74.5 | 54.6 |
| 290° | 0.732 | 35.2 | 73.85 | 54.5 |
| 300° | 0.719 | 34.83 | 72.9 | 54.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsao, C.-C.; Lin, W.-K.; Lai, K.-Y.; Yavuzkurt, S.; Liu, Y.-H. Numerical Investigation of Compression and Expansion Process of Twin-Screw Machine Using R-134a. Energies 2023, 16, 3599. https://doi.org/10.3390/en16083599
Tsao C-C, Lin W-K, Lai K-Y, Yavuzkurt S, Liu Y-H. Numerical Investigation of Compression and Expansion Process of Twin-Screw Machine Using R-134a. Energies. 2023; 16(8):3599. https://doi.org/10.3390/en16083599
Chicago/Turabian StyleTsao, Chia-Cheng, Wen-Kai Lin, Kai-Yuan Lai, Savas Yavuzkurt, and Yao-Hsien Liu. 2023. "Numerical Investigation of Compression and Expansion Process of Twin-Screw Machine Using R-134a" Energies 16, no. 8: 3599. https://doi.org/10.3390/en16083599
APA StyleTsao, C.-C., Lin, W.-K., Lai, K.-Y., Yavuzkurt, S., & Liu, Y.-H. (2023). Numerical Investigation of Compression and Expansion Process of Twin-Screw Machine Using R-134a. Energies, 16(8), 3599. https://doi.org/10.3390/en16083599






