Treatment of Oil Production Data under Fines Migration and Productivity Decline
Abstract
1. Introduction
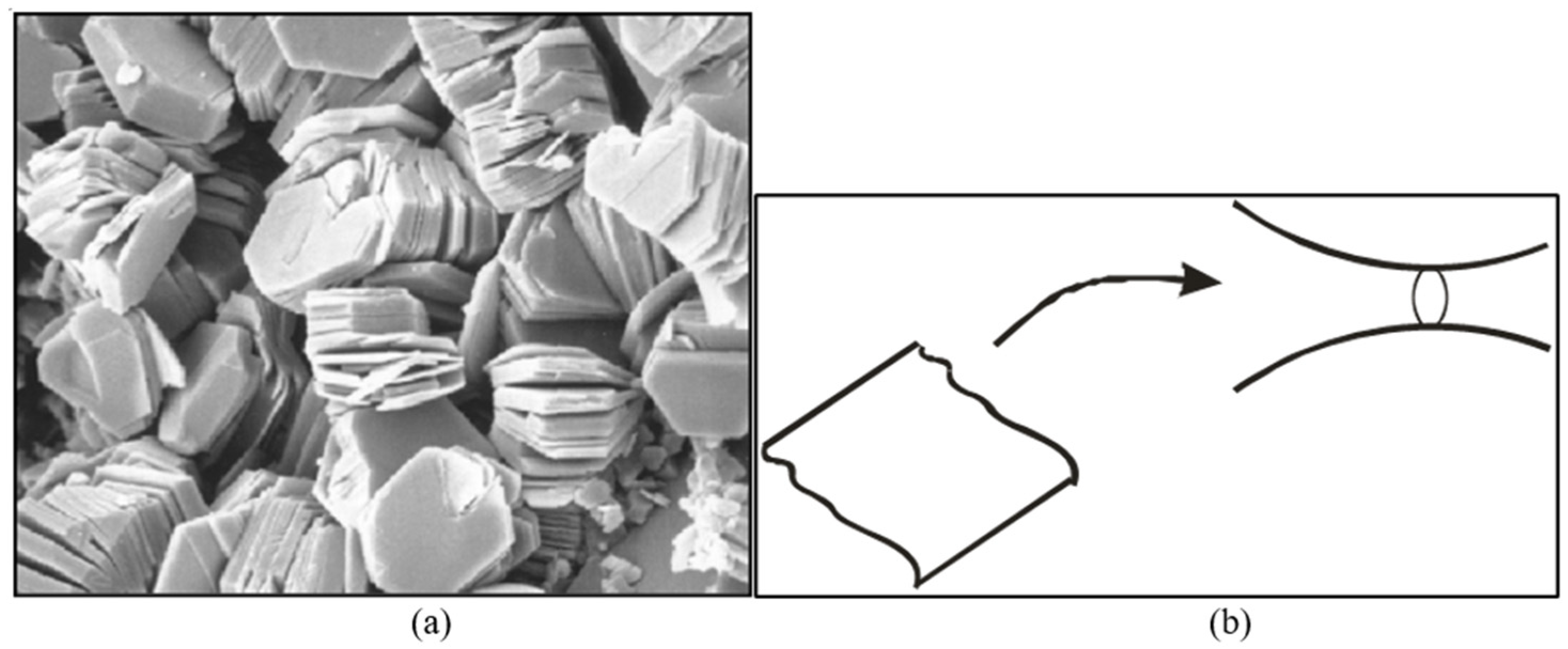
2. Fines Detachment at the Presence of Connate Water
2.1. Formulation of Maximum Retention Function
2.2. Sensitivity Analysis
3. Mathematical Model for Well Inflow Performance under Fines Migration
3.1. Assumptions of the Model
- The incompressibility of the particle suspension and of retained particles;
- The validity of Darcy’s law for the flow of oil in the presence of connate water;
- A universal relationship relating the decline in permeability to the concentration of retained particles;
- A linear expression for the kinetics of suspended particle capture, analogous to the active mass law of pores and particles;
- Amagat’s law of volume additivity during particle suspension and capture, leading to the flux conservation during particle suspension and retention;
- Instant particle detachment;
- The flow rate is non-increasing with time, following the decrease in rock permeability due to fines migration;
- The well is not hydraulically fractured.
3.2. Governing Equations for Axi-Symmetric Flow of Suspension-Colloidal Fluid
3.3. Initial and Boundary Conditions
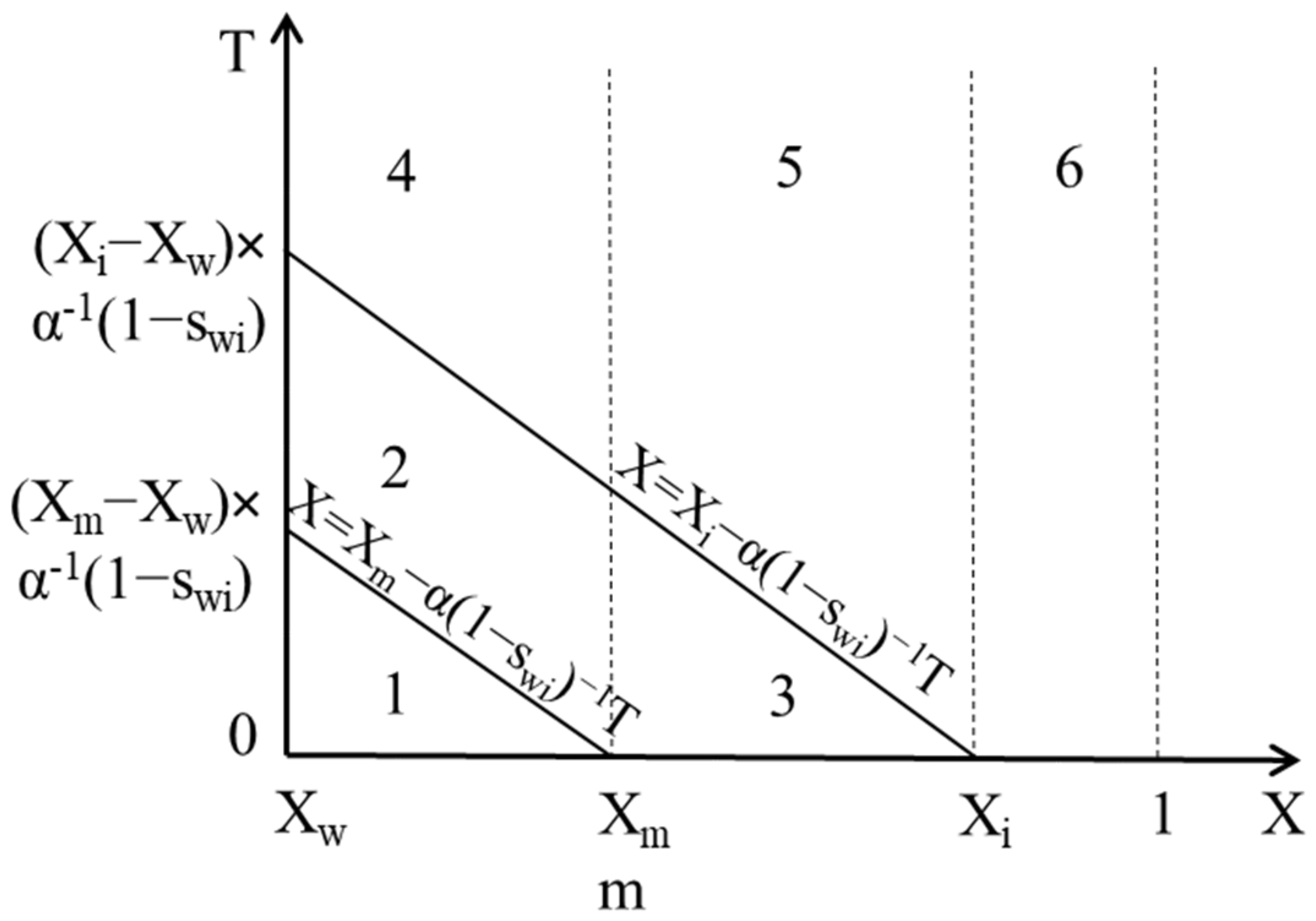
4. Analytical Model for Well Inflow Performance under Fines Migration
4.1. The Case of Linear Suspension Function F(C) = C
4.2. Calculation of Well Index, Impedance and Skin Factor
5. Analysis of Productivity Decline
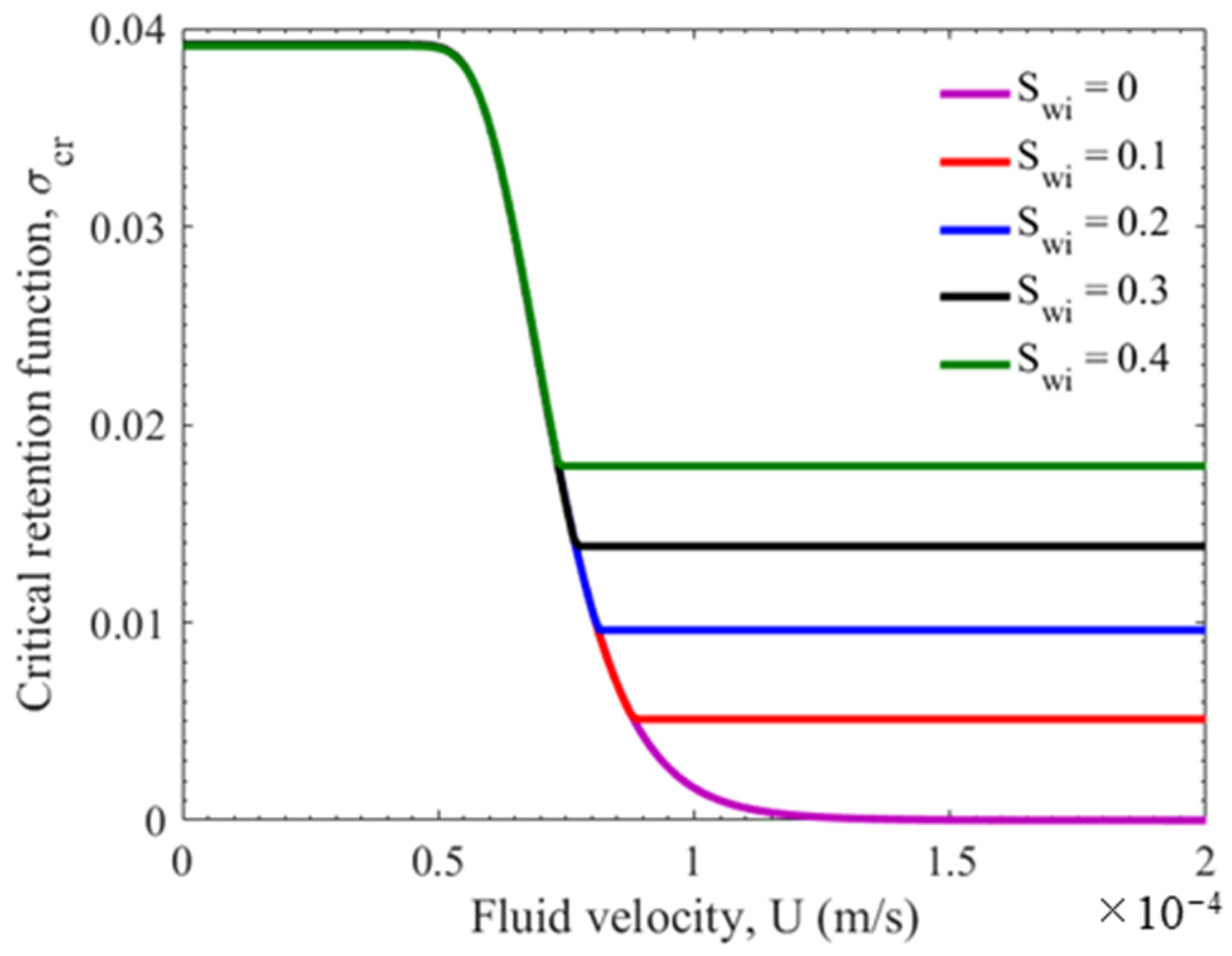
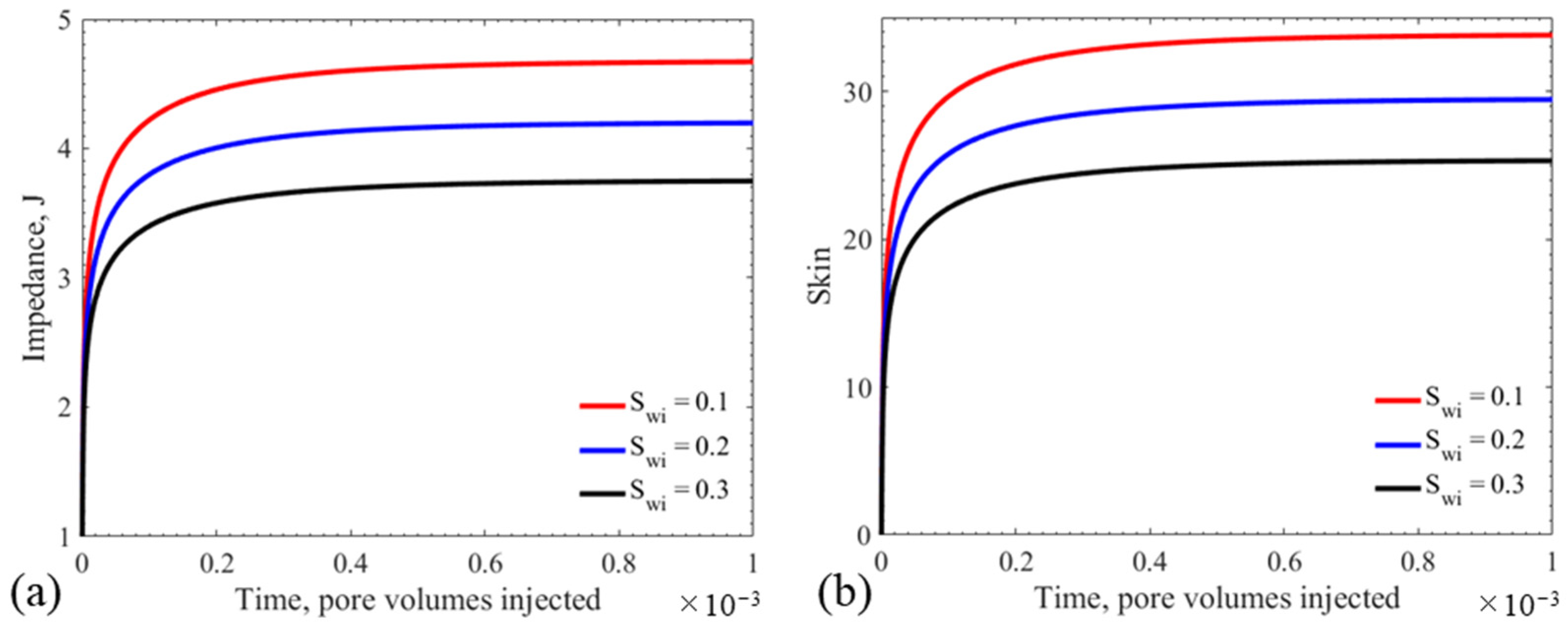
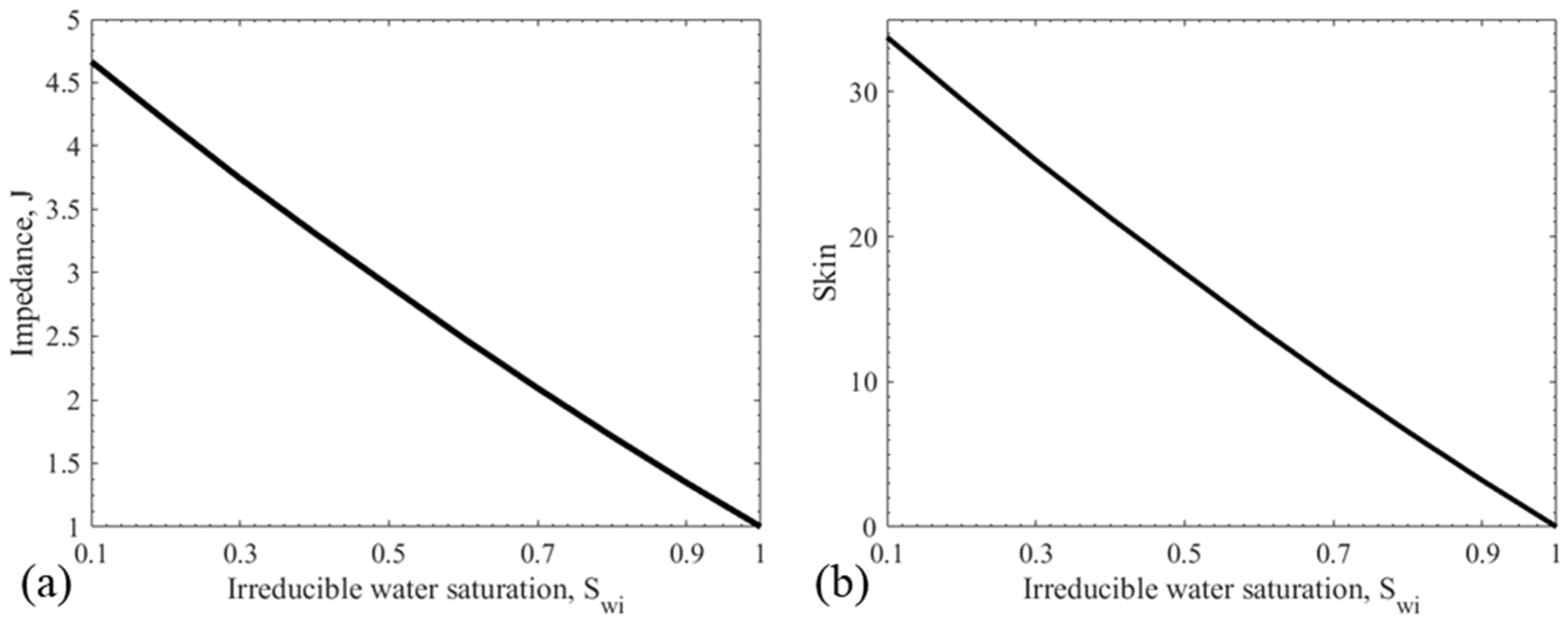
5.1. Effects of Connate Water on Well Productivity
5.2. Simplified Maximum Retention Function
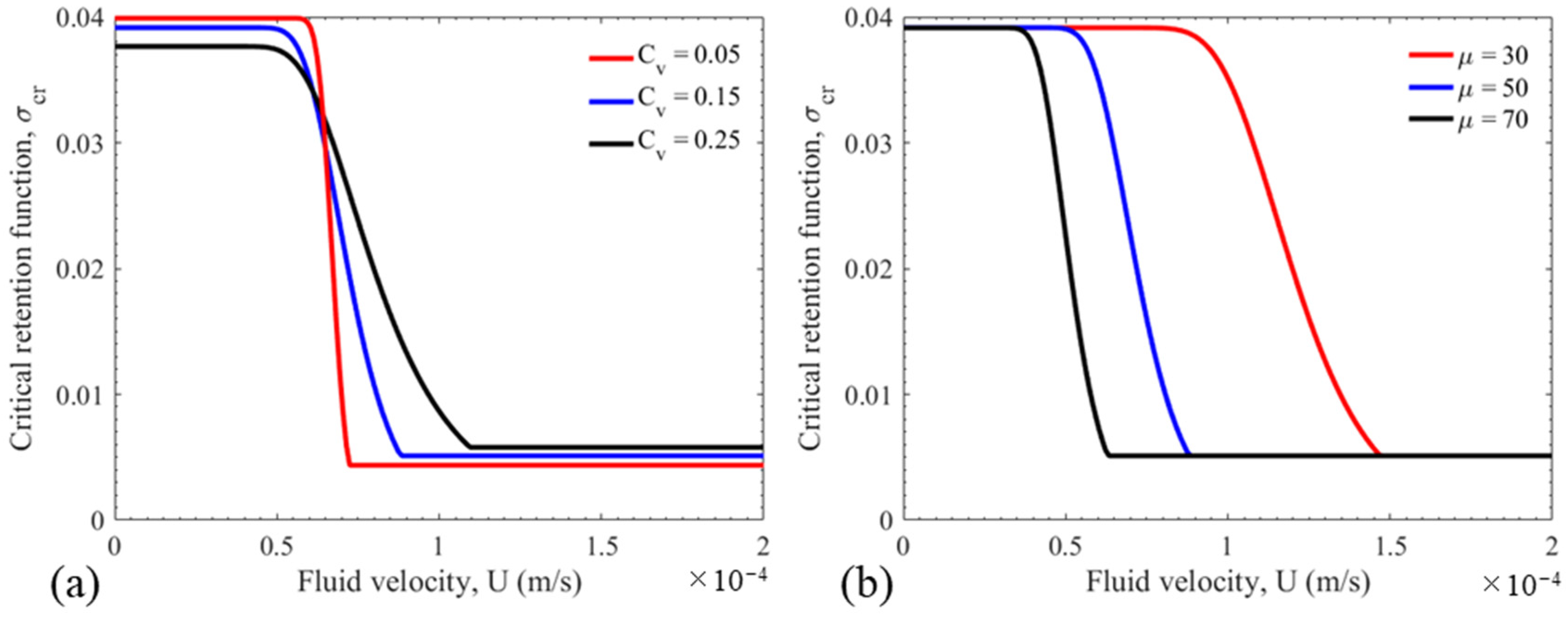
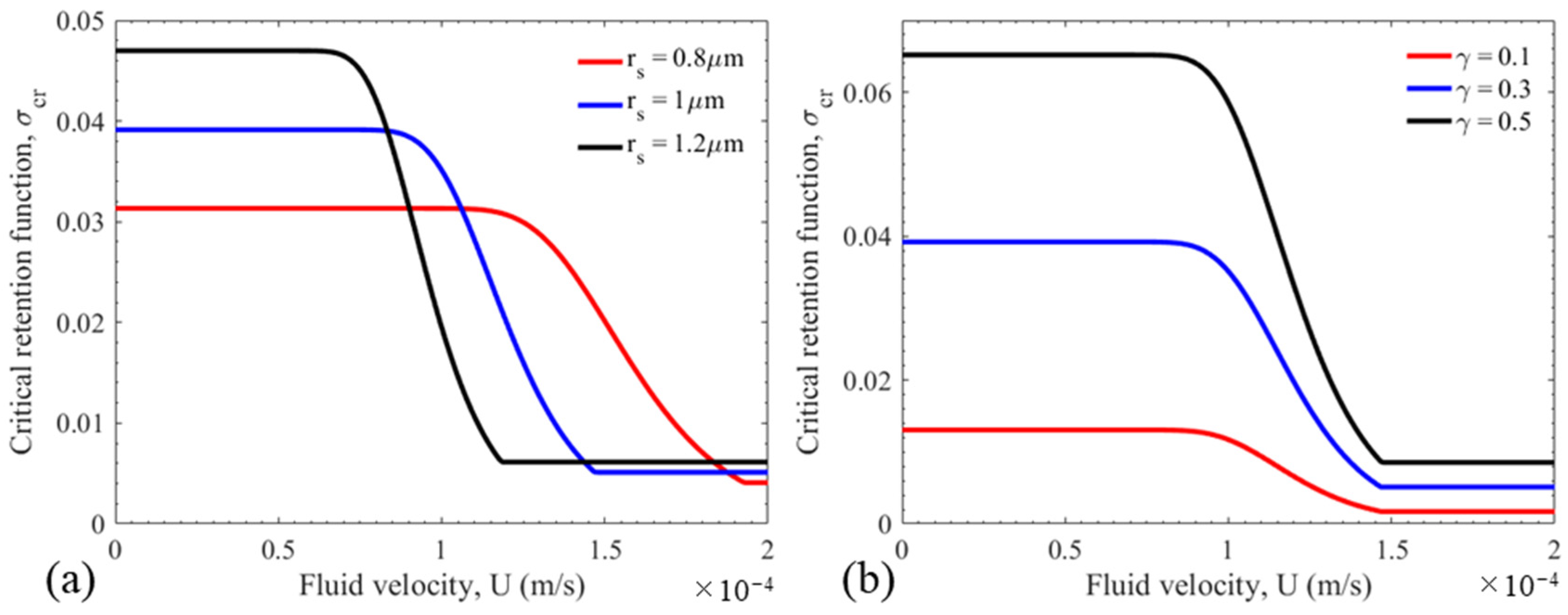
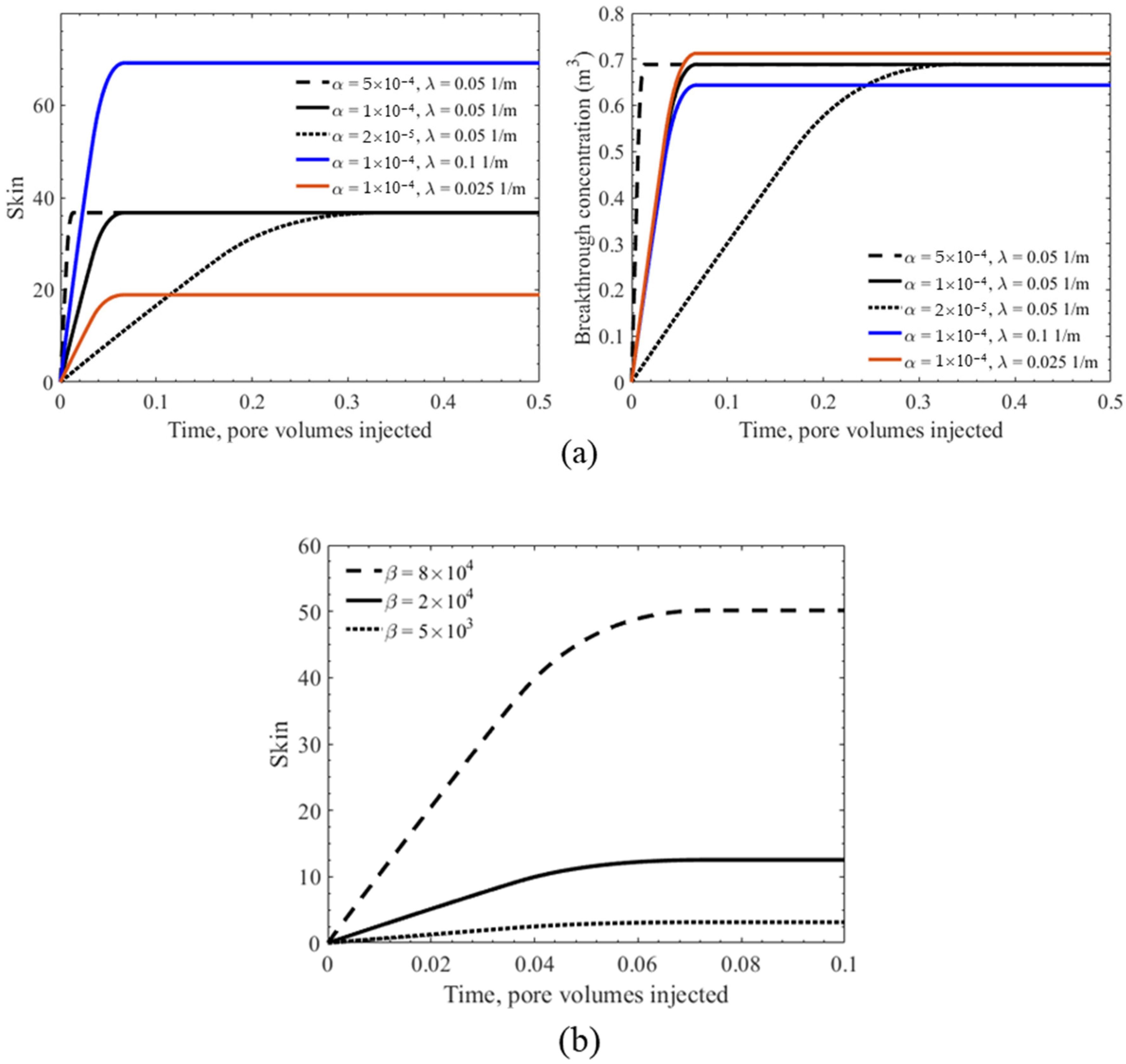
5.3. Sensitivity Study
6. Treatment of Well Productivity Data
| Parameters | Typical Values | Unit | References |
|---|---|---|---|
| σaI | 5 × 10−3 | - | Russell et al., 2017 [42] |
| λ | 1 × 10−2 | 1/m | Marquez et al., 2014 [43] |
| Um | 1 × 10−4 | m/s | You et al., 2019 [24] |
| α | 1 × 10−4–1 × 10−3 | - | Yang et al., 2016 [35] |
| Case # | References |
|---|---|
| 1 | Marquez et al., 2014 [43] |
| 2 | Marquez et al., 2014 [43] |
| 3 | Kamps et al., 2010 [4] |
| 4 | Reinoso et al., 2016 [44] |
| 5 | Deskin et al., 1991 [45] |
| 6 | Ziauddin et al., 2002 [46] |
| 7 | Davidson et al., 1997 [47] |
| 8 | Marquez et al., 2014 [43] |
| 9 | Saldungaray et al., 2001 [5] |
| 10 | Marquez et al., 2014 [43] |
| Case # | σaI | Um (m/s) | Ui (m/s) | λ (1/m) | α | β | R2 |
|---|---|---|---|---|---|---|---|
| 1 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 2.3 × 10−2 | 1.4 × 10−3 | 7.56 × 103 | 0.912 |
| 2 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 5 × 10−2 | 1.3 × 10−3 | 1.87 × 103 | 0.928 |
| 3 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 2 × 10−3 | 9.16 × 10−5 | 2.80 × 105 | 0.966 |
| 4 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 2.2 × 10−2 | 7.6 × 10−2 | 1.83 × 103 | 0.862 |
| 5 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 1.2 × 10−2 | 1.7 × 10−3 | 3.3 × 103 | 0.963 |
| 6 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 1 × 10−2 | 7 × 10−5 | 7.57 × 104 | 0.864 |
| 7 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 1 × 10−2 | 7 × 10−5 | 8.78 × 104 | 0.984 |
| 8 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 1 × 10−2 | 1 × 10−3 | 7.83 × 103 | 0.949 |
| 9 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 1 × 10−2 | 1 × 10−4 | 1.48 × 104 | 0.967 |
| 10 | 5 × 10−3 | 1 × 10−4 | 7 × 10−5 | 1.1 × 10−2 | 3 × 10−4 | 3.55 × 104 | 0.917 |
| Case # | re (m) | rw (m) | rm (m) | ri (m) | rd (m) | Jstab | Sstab | Tstab (PV) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1000 | 0.1 | 5.39 | 7.71 | 0.80 | 6.57 | 50.62 | 0.040 |
| 2 | 1000 | 0.1 | 5.39 | 7.71 | 0.82 | 3.72 | 25.17 | 0.043 |
| 3 | 1000 | 0.1 | 1.84 | 2.63 | 0.58 | 2.69 | 15.6 | 0.072 |
| 4 | 1000 | 0.1 | 4.48 | 6.40 | 0.76 | 1.41 | 3.74 | 0.041 |
| 5 | 1000 | 0.1 | 8.89 | 12.71 | 0.86 | 4.29 | 30.37 | 0.09 |
| 6 | 1000 | 0.1 | 1.84 | 2.63 | 0.58 | 3.61 | 24.09 | 0.094 |
| 7 | 1000 | 0.1 | 1.84 | 2.63 | 0.58 | 4.01 | 27.81 | 0.33 |
| 8 | 1000 | 0.1 | 34.69 | 49.56 | 0.97 | 90.26 | 822.1 | 2.26 |
| 9 | 1000 | 0.1 | 3.91 | 5.59 | 0.74 | 3.38 | 22 | 0.31 |
| 10 | 1000 | 0.1 | 1.84 | 2.63 | 0.58 | 2.34 | 12.38 | 0.023 |
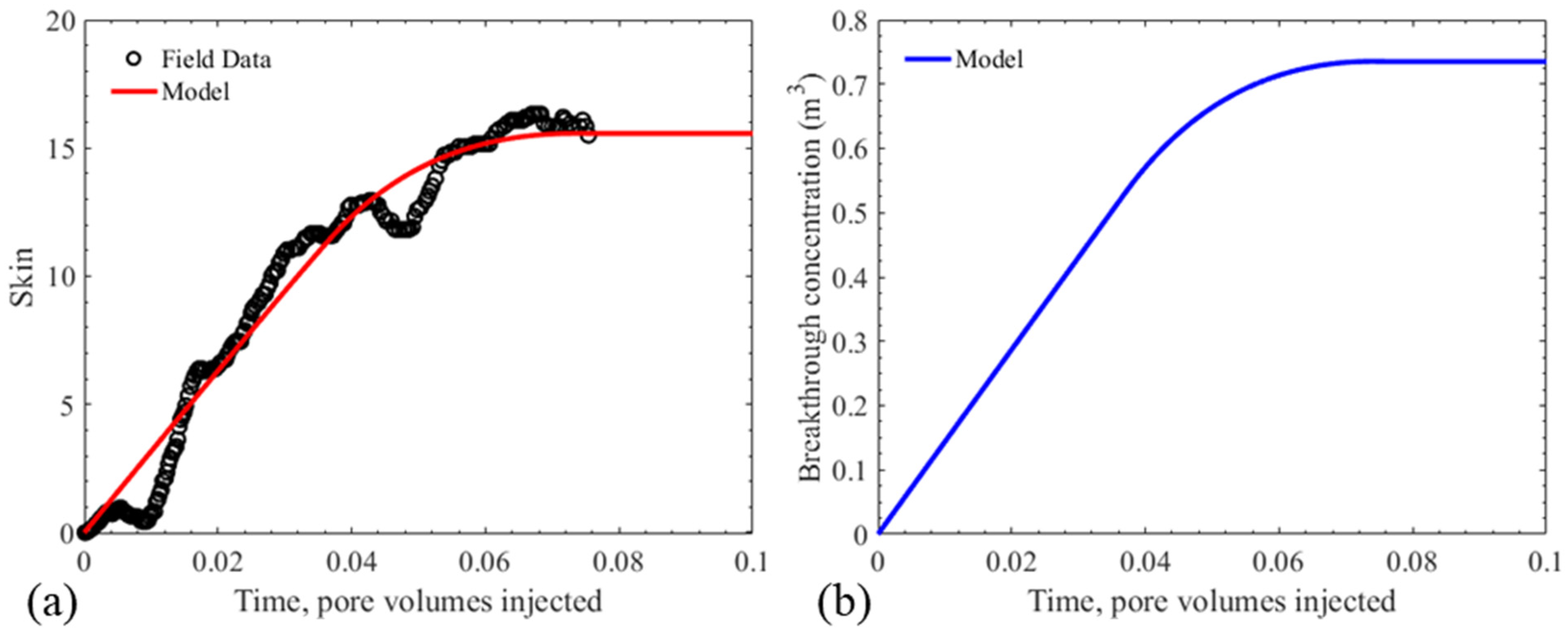
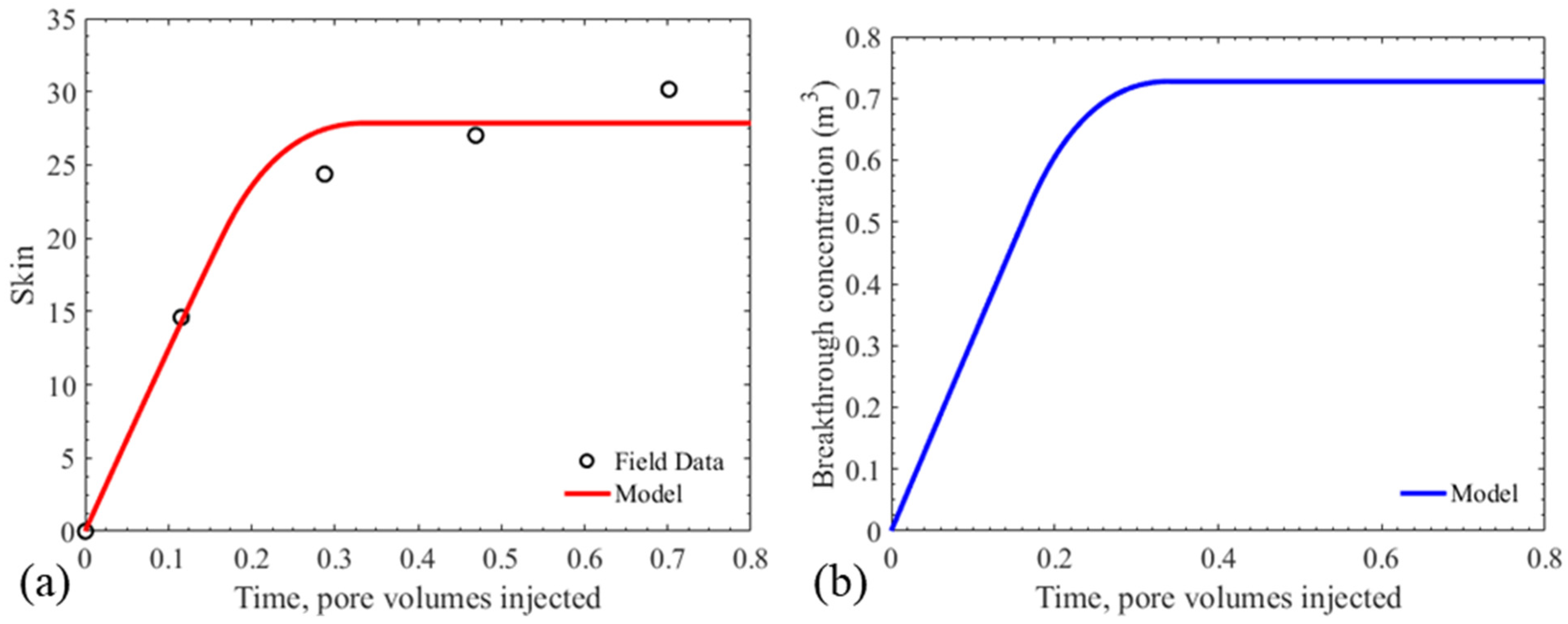
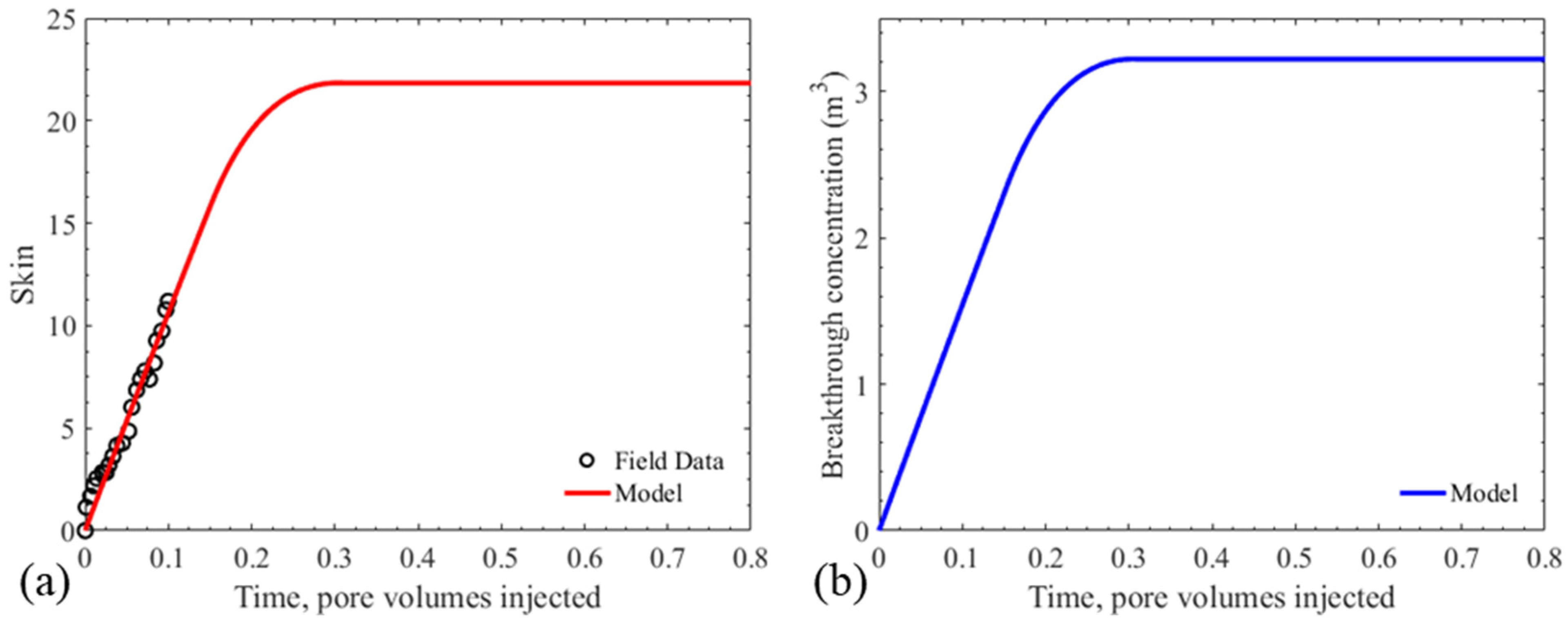
7. Discussion
7.1. Unique Determination of the Six Model Coefficients
- At the beginning of production and the initial stage of well exploitation, skin S(T) grows linearly with time from its initial value of zero. Therefore, only one parameter can be determined from the skin curve S(T). The other five parameters must be chosen from values commonly reported in the literature;
- When the skin curve shows a tendency towards stabilisation, three parameters can be determined from the skin vs. time, and the other three parameters must be chosen from values commonly reported in the literature.
7.2. Incorporating More Complex Reservoir Physics
8. Summary and Conclusions
- A new form of the critical retention function is derived based on a pore space comprised of a size-distributed bundle of capillaries. The new formulation allows for including the effects of connate water on fines detachment during oil production;
- Connate water saturation can significantly decrease maximum retention function by preventing fines detachment from the pores filled by the immobile water;
- The new equations show that skin growth is more severe in reservoirs with low connate water saturation, where more particles can be detached by the mobile oil phase;
- The axi-symmetric flow of oil towards a well with the mobilisation, transport, and straining of fine particles under the presence of connate water allows for an analytical solution. In the case of a large concentration of suspended particles, where the retention rate is proportional to the suspension function, F(C), the expressions for the suspended and strained particle concentrations are implicit. For the two cases where the function F(C) is quadratic or for the case where the suspended concentration is sufficiently small to assume F(C) = C, the expressions are explicit;
- The analytical model allows the quantification of the growth of well impedance and skin during fines mobilization;
- Analysis of 10 field production wells shows good agreement between the data and the analytical model. The formation damage parameters obtained from tuning are within commonly reported intervals;
- The final model contains six parameters which describe the extent of fines migration. Depending on whether the skin history curve covers the initial productivity decline or if it contains the progression towards productivity stabilisation, the curve can be used to determine 1–3 parameters. Thus the full determination of the system requires laboratory coreflooding. An alternative approach is to assume typical values of a subset of the parameters from published research in similar rocks;
- Following tuning, the analytical model provides accurate estimates of the well skin growth until stabilization, including the final skin value, as well as the size of the formation damage zone around the well. This information allows field operators to make informed decisions on well design and well-stimulation procedures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin letters | |
| c | Suspended particles concentration |
| C | Dimensionless suspended particles concentration |
| Cv | Coefficient of variation of the pore size distribution |
| J | Impedance |
| k | Permeability, [L]2, m2 |
| Mrp | Mean pore size, [L], m |
| p | Pressure, [M][T] −2[L]−1, Pa |
| P | Dimensionless pressure |
| q | Flow rate per unit of the reservoir thickness, [L]2[T]−1, m2s−1 |
| r | Radial coordinate, [L], m |
| re | Drainage radius, [L], m |
| ri | Radius of the zone where particles are detached, [L], m |
| rm | Radius of the zone where all attached particles are detached, [L], m |
| s | Saturation |
| S | Skin factor |
| Sa | Dimensionless concentration of attached particles |
| Ss | Dimensionless concentration of strained particles |
| t | Time, [T], s |
| T | Dimensionless time, PVI |
| U | Darcy’s velocity, [L][T]−1, m.s−1 |
| Ui | Darcy’s velocity corresponding to r = ri, [L][T]−1, m.s−1 |
| Um | Darcy’s velocity corresponding to r = rm, [L][T]−1, m.s−1 |
| X | Dimensionless radial coordinate |
| Xi | Dimensionless radius of the zone where particles are detached |
| Xm | Dimensionless radius of the zone where all attached particles are detached |
| X0 | Intersection of characteristic line with x axis |
| Greek letters | |
| α | Drift delay factor |
| β | Formation damage coefficient |
| ε | Accuracy |
| γ | Salinity |
| λ | Filtration coefficient, [L]−1, m−1 |
| Λ | Dimensionless filtration coefficient |
| µ | Dynamic viscosity, [M][L]−1[T]−1, kg.m−1s−1 |
| σa | Concentration of attached particles |
| σaI | Initial attached particles concentration |
| σa0 | Concentration of attached particles for U = 0 m/s |
| σs | Concentration of strained particles |
| ϕ | Porosity |
| ω | Drag coefficient |
| Super/subscripts | |
| cr | Critical, retention concentration |
| d | Damage, for radius |
| w | Well, for pressure and radius |
| wi | Water initial (for end point) |
Appendix A. Exact Solution for Linear Suspension Function F(C) = C
Appendix B. Derivation of Critical Retention Function with Connate Water
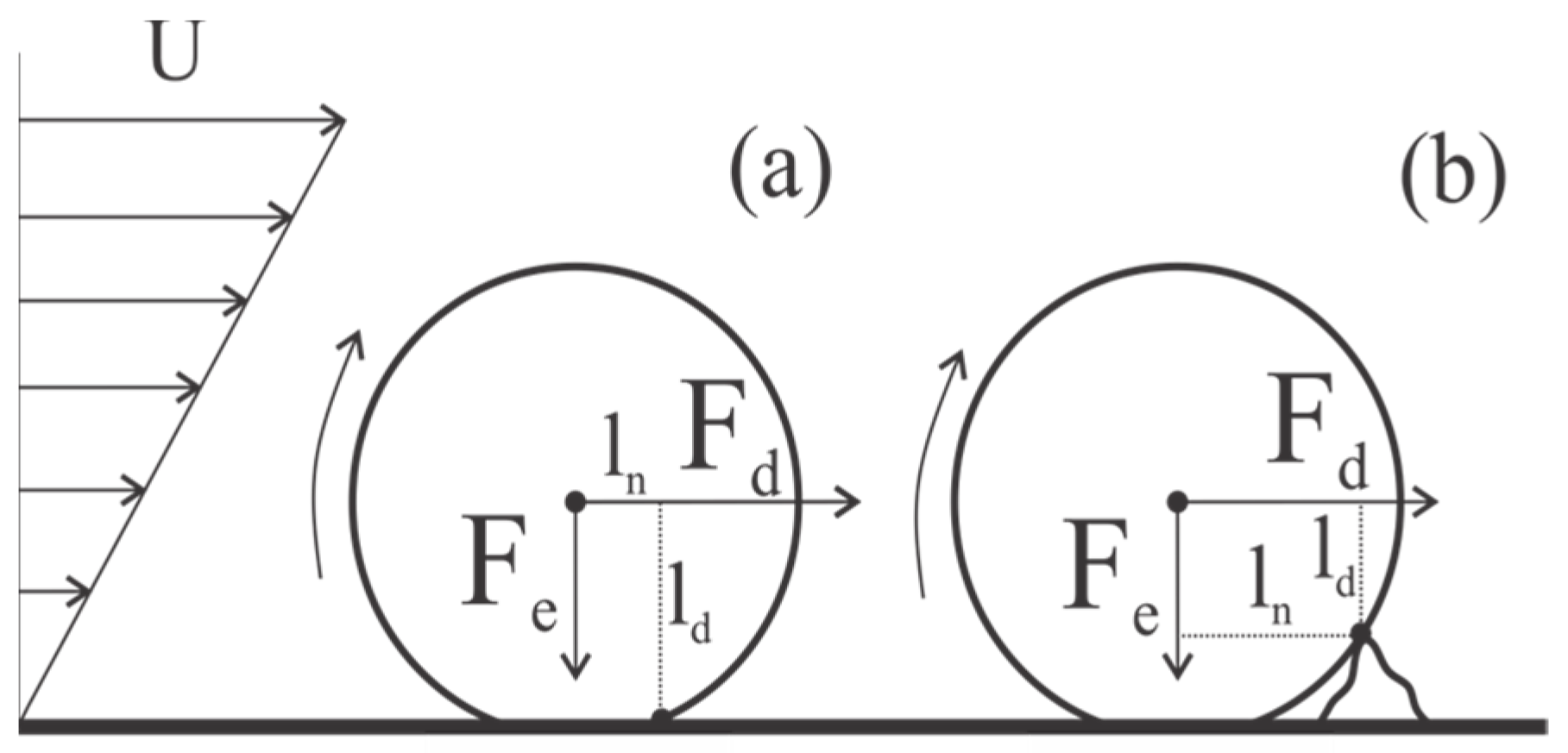
Appendix C. Evaluation of the Torque Balance with Distributed Pore Radii
References
- Akhmetgareev, V.; Khisamov, R. 40 Years of Low-Salinity Waterflooding in Pervomaiskoye Field, Russia: Incremental Oil. Proceedings of SPE European Formation Damage Conference and Exhibition, Budapest, Hungary, 3–5 June 2015. [Google Scholar]
- Barkman, J.; Abrams, A.; Darley, H.; Hill, H. An Oil-Coating Process To Stabilize Clays in Fresh Waterflooding Operations (includes associated paper 6405). J. Pet. Technol. 1975, 27, 1053–1059. [Google Scholar] [CrossRef]
- Olayiwola, S.O.; Dejam, M. Synergistic interaction of nanoparticles with low salinity water and surfactant during alternating injection into sandstone reservoirs to improve oil recovery and reduce formation damage. J. Mol. Liq. 2020, 317, 114228. [Google Scholar] [CrossRef]
- Kamps, E.J.; Chando, J.M.; Ellis, R.C. Improving Well Productivity through Openhole Frac-Pack Completion Design. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Saldungaray, P.M.; Caretta, F.; Sofyan, M. Formation Fines Stabilization Using Surface Adsorption Polimerization: Field Application of an Emerging Technology. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 17–19 April 2001. [Google Scholar]
- Salimi, S.; Ghalambor, A. Experimental Study of Formation Damage during Underbalanced-Drilling in Naturally Fractured Formations. Energies 2011, 4, 1728–1747. [Google Scholar] [CrossRef]
- Prommer, H.; Descourvieres, C.; Handyside, M.; Johnston, K.; Harris, B.; Li, Q.; Fang, H.; Costello, P.; Seibert, S.; Martin, M. Final Report—Aquifer Storage and Recovery of Potable Water in the Leederville Aquifer; CSIRO: Perth, Australia, 2013. [Google Scholar] [CrossRef]
- Nguyen, M.C.; Dejam, M.; Fazelalavi, M.; Zhang, Y.; Gay, G.W.; Bowen, D.W.; Spangler, L.H.; Zaluski, W.; Stauffer, P.H. Skin factor and potential formation damage from chemical and mechanical processes in a naturally fractured carbonate aquifer with implications to CO2 sequestration. Int. J. Greenh. Gas Control. 2021, 108, 103326. [Google Scholar] [CrossRef]
- Guo, Z.; Kang, N.; Le-Hussain, F. An NMR-assisted laboratory investigation of coal fines migration in fracture proppants during single-phase water production. Fuel 2023, 343, 127926. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Modeling dense-colloid and virus cotransport in three-dimensional porous media. J. Contam. Hydrol. 2015, 181, 102–113. [Google Scholar] [CrossRef]
- Kretzschmar, R.; Borkovec, M.; Grolimund, D.; Elimelech, M. Mobile subsurface colloids and their role in contaminant transport. Adv. Agron. 1999, 66, 121–193. [Google Scholar] [CrossRef]
- Shapiro, A.A. Two-phase immiscible flows in porous media: The Mesocopic Maxwell–Stefan approach. Transp. Porous Media 2015, 107, 335–363. [Google Scholar] [CrossRef]
- Shapiro, A.A. Mechanics of the separating surface for a two-phase co-current flow in a porous medium. Transp. Porous Media 2016, 112, 489–517. [Google Scholar] [CrossRef]
- Sarkar, A.K.; Sharma, M.M. Fines migration in two-phase flow. J. Pet. Technol. 1990, 42, 646–652. [Google Scholar] [CrossRef]
- Kalantariasl, A.; Farajzadeh, R.; You, Z.; Bedrikovetsky, P. Nonuniform external filter cake in long injection wells. Ind. Eng. Chem. Res. 2015, 54, 3051–3061. [Google Scholar] [CrossRef]
- Han, X.; Zhong, L.; Liu, Y.; Fang, T.; Chen, C. Experimental study and pore network modeling of formation damage induced by fines migration in unconsolidated sandstone reservoirs. J. Energy Resour. Technol. 2020, 142, 113006. [Google Scholar] [CrossRef]
- El-Monier, I.A.; Nasr-El-Din, H.A. An Al/Zr-based clay stabilizer for high pH applications. J. Energy Resour. Technol. 2013, 135, 022903. [Google Scholar] [CrossRef]
- Zhang, D.; Kang, Y.; You, L.; Li, J. Investigation of formation damage induced during drill-in process of ultradeep fractured tight sandstone gas reservoirs. J. Energy Resour. Technol. 2019, 141, 072901. [Google Scholar] [CrossRef]
- Schembre, J.; Kovscek, A. Mechanism of formation damage at elevated temperature. J. Energy Resour. Technol. 2005, 127, 171–180. [Google Scholar] [CrossRef]
- Mays, D.C.; Hunt, J.R. Hydrodynamic aspects of particle clogging in porous media. Environ. Sci. Technol. 2005, 39, 577–584. [Google Scholar] [CrossRef]
- Ting, H.Z.; Yang, Y.; Tian, Z.F.; Carageorgos, T.; Bedrikovetsky, P. Image interpretation for kaolinite detachment from solid substrate: Type curves, stochastic model. Colloids Surf. A Physicochem. Eng. Asp. 2022, 650, 129451. [Google Scholar] [CrossRef]
- Bedrikovetsky, P.; Siqueira, F.D.; Furtado, C.A.; Souza, A.L.S. Modified Particle Detachment Model for Colloidal Transport in Porous Media. Transp. Porous Media 2011, 86, 383–413. [Google Scholar] [CrossRef]
- Chequer, L.; Carageorgos, T.; Naby, M.; Hussaini, M.; Lee, W.; Bedrikovetsky, P. Colloidal detachment from solid surfaces: Phase diagrams to determine the detachment regime. Chem. Eng. Sci. 2021, 229, 116146. [Google Scholar] [CrossRef]
- You, Z.; Badalyan, A.; Yang, Y.; Bedrikovetsky, P.; Hand, M. Fines migration in geothermal reservoirs: Laboratory and mathematical modelling. Geothermics 2019, 77, 344–367. [Google Scholar] [CrossRef]
- Miri, R.; Salimi, M.; Lange, C.F.; Nouri, A. Permeability decline by fines migration near sand control screens in steam assisted gravity drainage: A numerical assessment. Fuel 2023, 334, 126578. [Google Scholar] [CrossRef]
- Chequer, L.; Bedrikovetsky, P.; Badalyan, A.; Gitis, V. Water level and mobilisation of colloids in porous media. Adv. Water Resour. 2020, 143, 103670. [Google Scholar] [CrossRef]
- Vasheghani Farahani, M.; Foroughi, S.; Norouzi, S.; Jamshidi, S. Mechanistic Study of Fines Migration in Porous Media Using Lattice Boltzmann Method Coupled With Rigid Body Physics Engine. J. Energy Resour. Technol. 2019, 141, 123001. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, B.; Santamarina, J.C. Particle migration and clogging in porous media: A convergent flow microfluidics study. J. Geophys. Res. Solid Earth 2019, 124, 9495–9504. [Google Scholar] [CrossRef]
- Bedrikovetsky, P.; Osipov, Y.; Kuzmina, L.; Malgaresi, G. Exact upscaling for transport of size-distributed colloids. Water Resour. Res. 2019, 55, 1011–1039. [Google Scholar] [CrossRef]
- Muneer, R.; Pourafshary, P.; Hashmet, M.R. An integrated modeling approach to predict critical flow rate for fines migration initiation in sandstone reservoirs and water-bearing formations. J. Mol. Liq. 2023, 376, 121462. [Google Scholar] [CrossRef]
- Bradford, S.A.; Torkzaban, S.; Shapiro, A. A theoretical analysis of colloid attachment and straining in chemically heterogeneous porous media. Langmuir ACS J. Surf. Colloids 2013, 29, 6944–6952. [Google Scholar] [CrossRef]
- Polubarinova-Koch, P.I. Theory of ground water movement. In Theory of Ground Water Movement; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Panfilov, M. Macroscale Models of Flow through Highly Heterogeneous Porous Media; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000; Volume 16. [Google Scholar]
- Streltsova, T.D. Well Testing in Heterogeneous Formations; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Yang, Y.; Siqueira, F.D.; Vaz, A.S.; You, Z.; Bedrikovetsky, P. Slow migration of detached fine particles over rock surface in porous media. J. Nat. Gas Sci. Eng. 2016, 34, 1159–1173. [Google Scholar] [CrossRef]
- Zamani, A.; Maini, B. Flow of dispersed particles through porous media—Deep bed filtration. J. Petrol. Sci. Eng. 2009, 69, 71–88. [Google Scholar] [CrossRef]
- Pang, S.; Sharma, M. A model for predicting injectivity decline in water-injection wells. SPE Form. Eval. 1997, 12, 194–201. [Google Scholar] [CrossRef]
- Mojarad, R.S.; Settari, A. Coupled numerical modelling of reservoir flow with formation plugging. J. Can. Pet. Technol. 2007, 46. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Mathematics for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Polyanin, A.; Zaitsev, V. Handbook of Nonlinear Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Russell, T.; Wong, K.; Zeinijahromi, A.; Bedrikovetsky, P. Effects of delayed particle detachment on injectivity decline due to fines migration. J. Hydrol. 2018, 564, 1099–1109. [Google Scholar] [CrossRef]
- Russell, T.; Pham, D.; Neishaboor, M.T.; Badalyan, A.; Behr, A.; Genolet, L.; Kowollik, P.; Zeinijahromi, A.; Bedrikovetsky, P. Effects of kaolinite in rocks on fines migration. J. Nat. Gas Sci. Eng. 2017, 45, 243–255. [Google Scholar] [CrossRef]
- Marquez, M.; Williams, W.; Knobles, M.M.; Bedrikovetsky, P.; You, Z. Fines Migration in Fractured Wells: Integrating Modeling with Field and Laboratory Data. SPE Prod. Oper. 2014, 29, 309–322. [Google Scholar] [CrossRef]
- Reinoso, W.; Torres, F.; Aldana, M.; Campo, P.; Alvarez, E.; Tovar, E. Removing Formation Damage From Fines Migration in the Putumayo Basin in Colombia: Challenges, Results, Lessons Learned, and New Opportunities after More than 100 Sandstone Acidizing Treatments. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control, Lafayette, LA, USA, 24–26 February 2016. [Google Scholar]
- Deskin, R.; Tinker, G.; Crawford, G. Using a pulse test to determine pore volume compressibility in a Gulf of Mexico unconsolidated reservoir. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, Texas, 6–9 October 1991. [Google Scholar]
- Ziauddin, M.; Kotlar, H.; Vikane, O.; Frenier, W.; Poitrenaud, H. The Use of a Virtual Chemistry Laboratory for the Design of Matrix Stimulation Treatments in the Heidrun Field. In Proceedings of the European Petroleum Conference, Aberdeen, UK, 29–31 October 2002. [Google Scholar]
- Davidson, B.; Franco, V.; Gonzalez, S.; Robinson, B. Stimulation Program In High Permeability Oil Sands-Case Study. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Rio de Janeiro, Brazil, 30 August–3 September 1997. [Google Scholar]
- Iglauer, S.; Al-Yaseri, A.; Al Mukainah, H.; Lebedev, M.; Barifcani, A. Impact of fines and rock wettability on reservoir formation damage. Geophys. Prospect. 2016, 64, 860–874. [Google Scholar]
- Iglauer, S.; Rahman, T.; Sarmadivaleh, M.; Al-Hinai, A.; Fernø, M.A.; Lebedev, M. Influence of wettability on residual gas trapping and enhanced oil recovery in three-phase flow: A pore-scale analysis by use of microcomputed tomography. SPE J. 2016, 21, 1916–1929. [Google Scholar] [CrossRef]
- Iglauer, S. CO2–water–rock wettability: Variability, influencing factors, and implications for CO2 geostorage. Acc. Chem. Res. 2017, 50, 1134–1142. [Google Scholar] [CrossRef]
- Mahani, H.; Keya, A.L.; Berg, S.; Bartels, W.B.; Nasralla, R.; Rossen, W.R. Insights into the Mechanism of Wettability Alteration by Low-Salinity Flooding (LSF) in Carbonates. Energy Fuels 2015, 29, 1352–1367. [Google Scholar] [CrossRef]
- Tokunaga, T.K. Hydraulic properties of adsorbed water films in unsaturated porous media. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Guo, H.; van Winden, J.; Bruining, J. Cation exchange in the presence of oil in porous media. ACS Earth Space Chem. 2017, 1, 101–112. [Google Scholar] [CrossRef]
- Yuan, B.; Moghanloo, R.G. Analytical model of well injectivity improvement using nanofluid preflush. Fuel 2017, 202, 380–394. [Google Scholar] [CrossRef]
- Yuan, B.; Moghanloo, R.G. Analytical modeling nanoparticles-fines reactive transport in porous media saturated with mobile immiscible fluids. AIChE J. 2019, 65, e16702. [Google Scholar] [CrossRef]
- Mahani, H.; Keya, A.L.; Berg, S.; Nasralla, R. The effect of salinity, rock type and ph on the electrokinetics of carbonate-brine interface and surface complexation modeling. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 14–16 September 2015. [Google Scholar]
- Mahani, H.; Keya, A.L.; Berg, S.; Nasralla, R. Electrokinetics of carbonate/brine interface in low-salinity waterflooding: Effect of brine salinity, composition, rock type, and pH on?-potential and a surface-complexation model. SPE J. 2017, 22, 53–68. [Google Scholar] [CrossRef]
- Maya, G.; Carreño Otero, A.L.; Monares Bueno, F.L.; Romero Bohórquez, A.R.; Cortés, F.B.; Franco, C.A.; Manrique, E. Rock–Oil–Brine Dominant Mechanisms in Smart Water Flooding. Energies 2023, 16, 2043. [Google Scholar] [CrossRef]
- Golmohammadi, M.; Mahani, H.; Ayatollahi, S. Toward low-salinity waterflooding predictive capability development in carbonates for fast screening of oil-brine-rock candidates. Geoenergy Sci. Eng. 2023, 221, 111258. [Google Scholar] [CrossRef]
- Shapiro, A.A. Elliptic equation for random walks. Application to transport in microporous media. Phys. A Stat. Mech. Its Appl. 2007, 375, 81–96. [Google Scholar] [CrossRef]
- Shapiro, A.; Wesselingh, J. Gas transport in tight porous media: Gas kinetic approach. Chem. Eng. J. 2008, 142, 14–22. [Google Scholar] [CrossRef]
- Erfani, H.; Joekar-Niasar, V.; Farajzadeh, R. Impact of microheterogeneity on upscaling reactive transport in geothermal energy. ACS Earth Space Chem. 2019, 3, 2045–2057. [Google Scholar] [CrossRef]
- Meulenbroek, B.; Farajzadeh, R.; Bruining, H. Process-based upscaling of reactive flow in geological formations. Int. J. Heat Mass Transf. 2020, 157, 119969. [Google Scholar] [CrossRef]
- Goldman, A.J.; Cox, R.G.; Brenner, H. Slow viscous motion of a sphere parallel to a plane wall—II Couette flow. Chem. Eng. Sci. 1967, 22, 653–660. [Google Scholar] [CrossRef]


| Parameters | Value | Unit |
|---|---|---|
| rs | 1 × 10−6 | m |
| ld | 2 × 10−6 | m |
| ϕ | 0.25 | - |
| μ = μo/μw | 50 | - |
| γ(rp) | 0.3 | - |
| Mrp(m) | 5 × 10−6 | m |
| Cv | 0.15 | - |
| ω | 1.7 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loi, G.; Nguyen, C.; Chequer, L.; Russell, T.; Zeinijahromi, A.; Bedrikovetsky, P. Treatment of Oil Production Data under Fines Migration and Productivity Decline. Energies 2023, 16, 3523. https://doi.org/10.3390/en16083523
Loi G, Nguyen C, Chequer L, Russell T, Zeinijahromi A, Bedrikovetsky P. Treatment of Oil Production Data under Fines Migration and Productivity Decline. Energies. 2023; 16(8):3523. https://doi.org/10.3390/en16083523
Chicago/Turabian StyleLoi, Grace, Cuong Nguyen, Larissa Chequer, Thomas Russell, Abbas Zeinijahromi, and Pavel Bedrikovetsky. 2023. "Treatment of Oil Production Data under Fines Migration and Productivity Decline" Energies 16, no. 8: 3523. https://doi.org/10.3390/en16083523
APA StyleLoi, G., Nguyen, C., Chequer, L., Russell, T., Zeinijahromi, A., & Bedrikovetsky, P. (2023). Treatment of Oil Production Data under Fines Migration and Productivity Decline. Energies, 16(8), 3523. https://doi.org/10.3390/en16083523






