Research on Solidity of Horizontal-Axis Tidal Current Turbine
Abstract
:1. Introduction
2. Key Parameters of Blade Design
2.1. Solidity of blade
2.2. Number of Blades
2.3. Blade Diameter
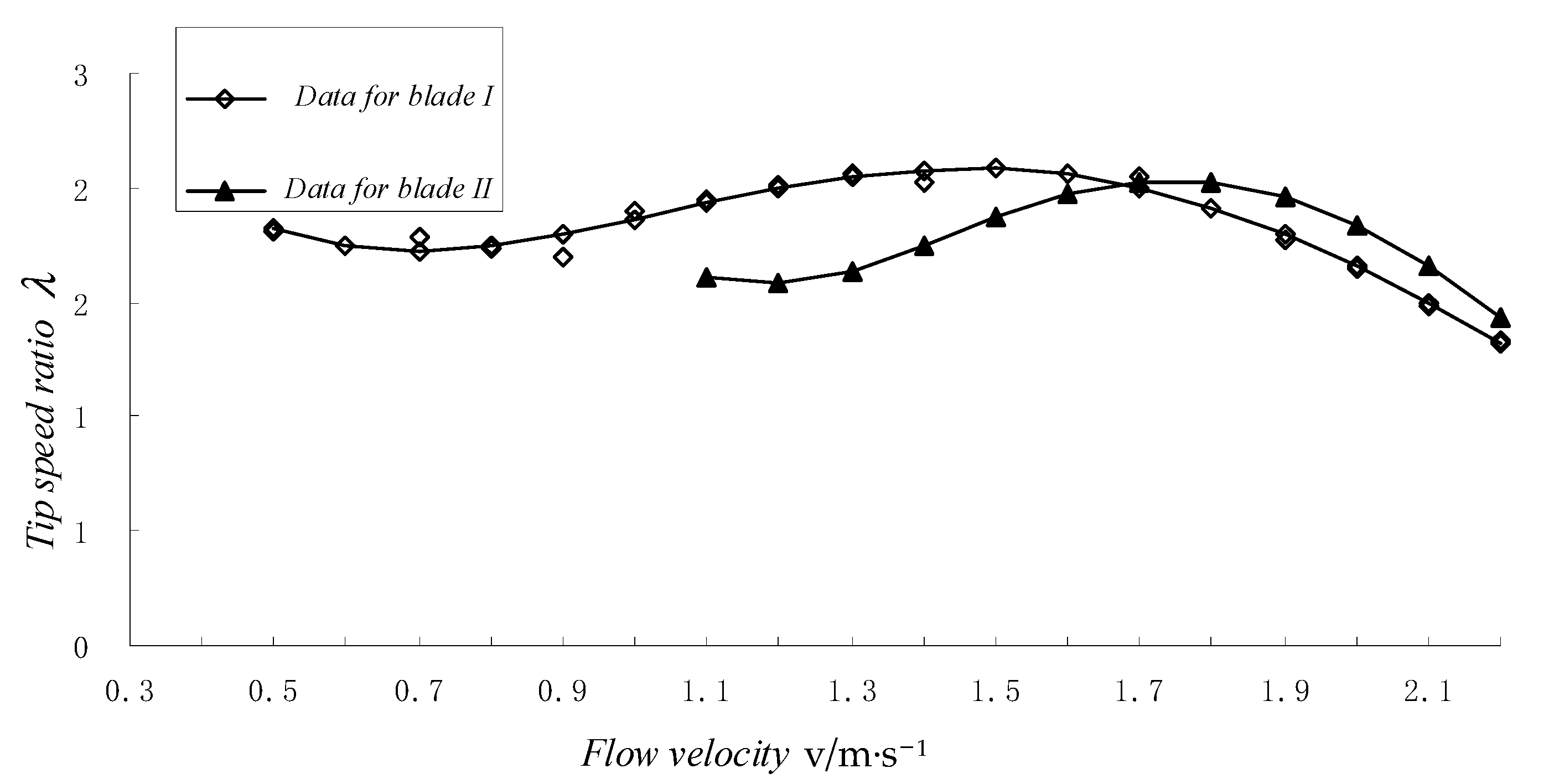
2.4. Tip Speed Ratio
2.5. Airfoil
- (1)
- Chord: As shown in Figure 4a, the line between the frontmost point A of the airfoil and the rearmost point B of the airfoil is called the chord. The upper cambered surface of the chord is represented by in the figure, and the lower cambered surface is represented by in the figure. The value of the chord length is the length of the chord . It is the datum length of the airfoil.
- (2)
- Leading edge radius and leading edge angle: The leading edge refers to the frontmost point of the chord; the radius of the incircle at the leading edge of the airfoil is called the leading edge radius of the airfoil; and the angle between the tangent lines above and below the leading edge point is the leading edge angle.
- (3)
- Thickness and thickness distribution: As shown in Figure 4b, the X-axis passes through the chord, and the Y-axis passes through the frontmost end of the airfoil. The airfoil is divided into the upper and lower airfoils. The diameter of the tangential circle between the upper and lower airfoils is called the airfoil thickness represented by in the figure. The change rule of the thickness with is called thickness distribution and is expressed as .
3. Design and Manufacture of the Tidal Current Energy Capture Device for the Experiment
3.1. Overall Design Parameters of Blades
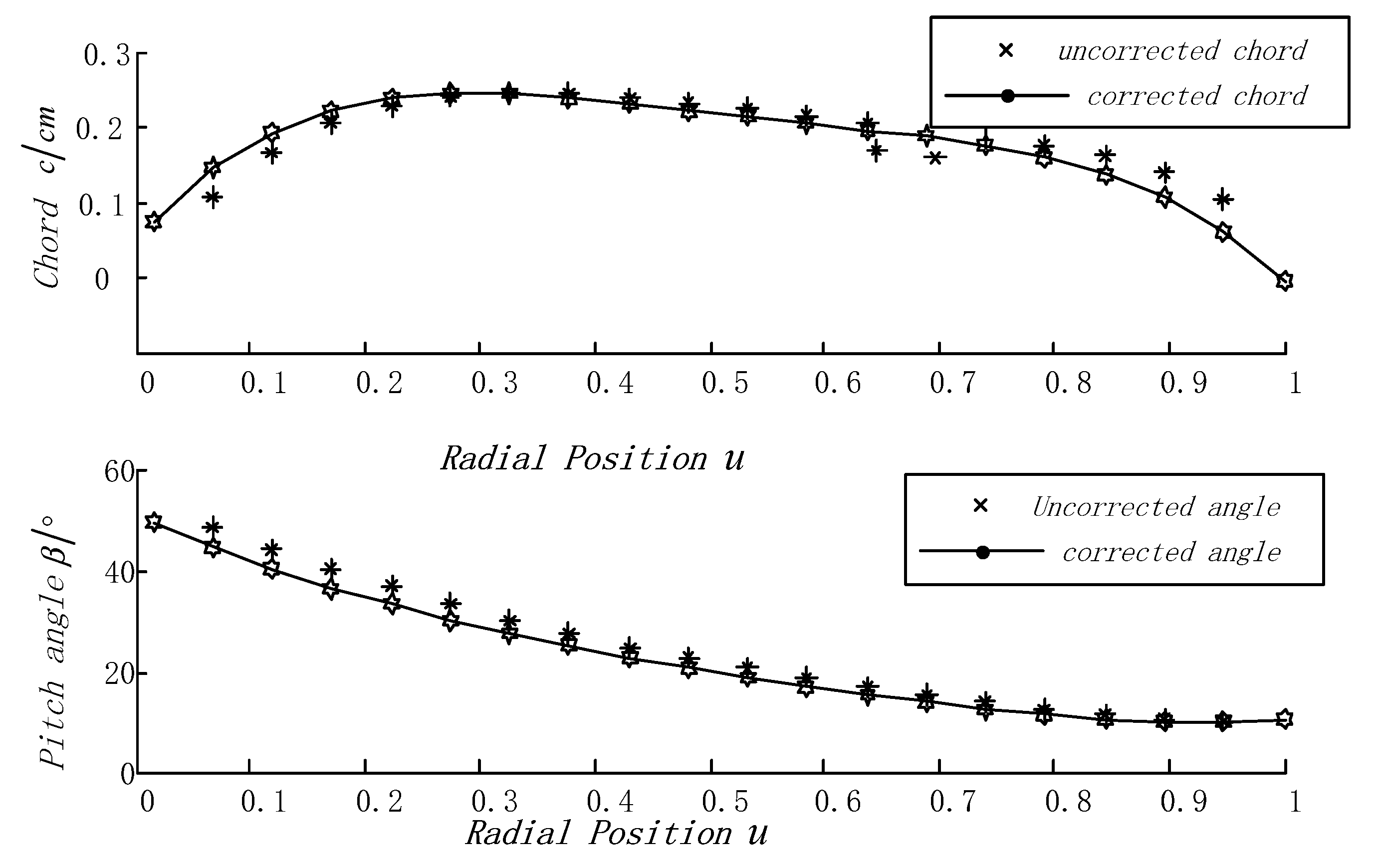
3.2. Blade Design Steps
- (1)
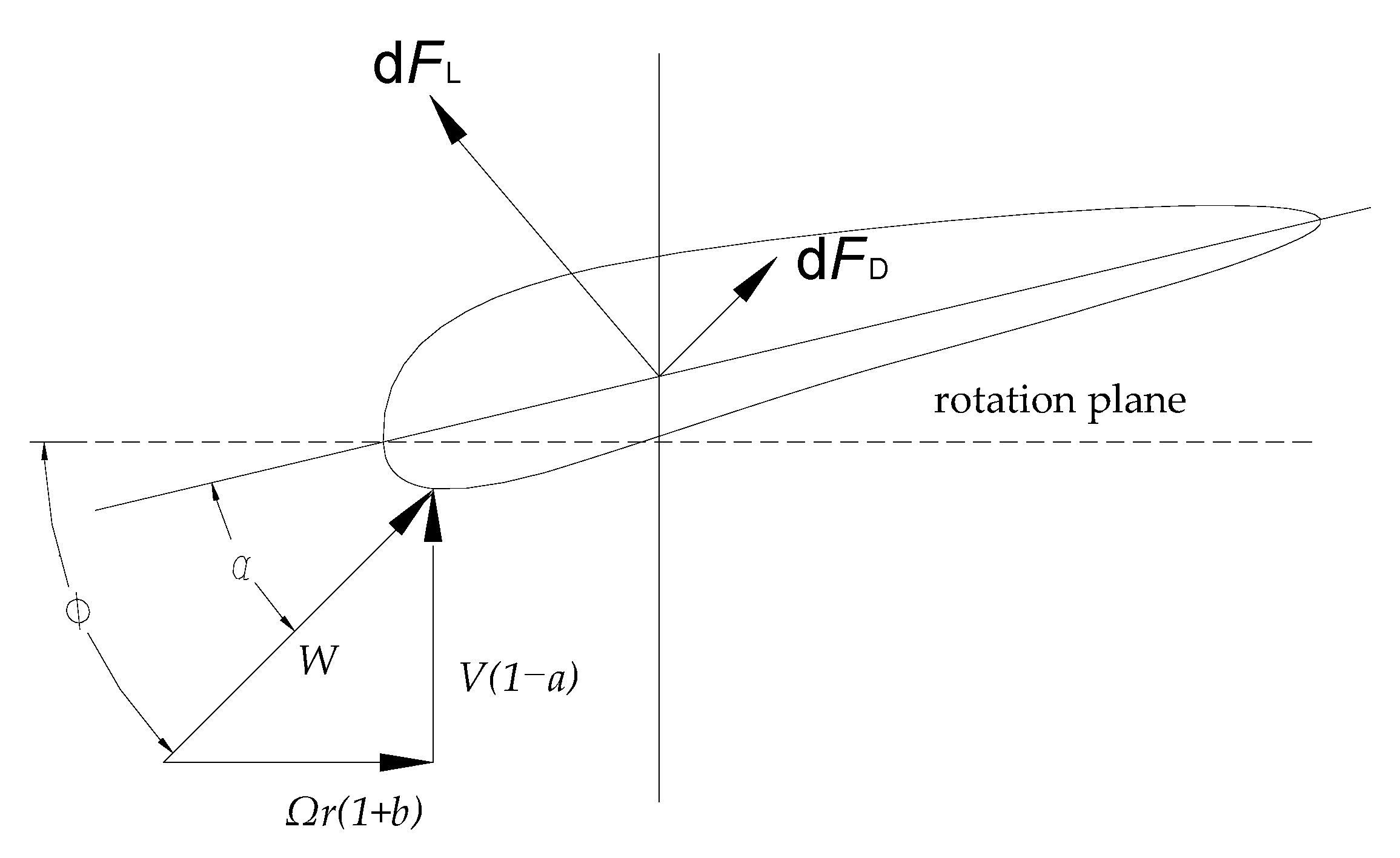
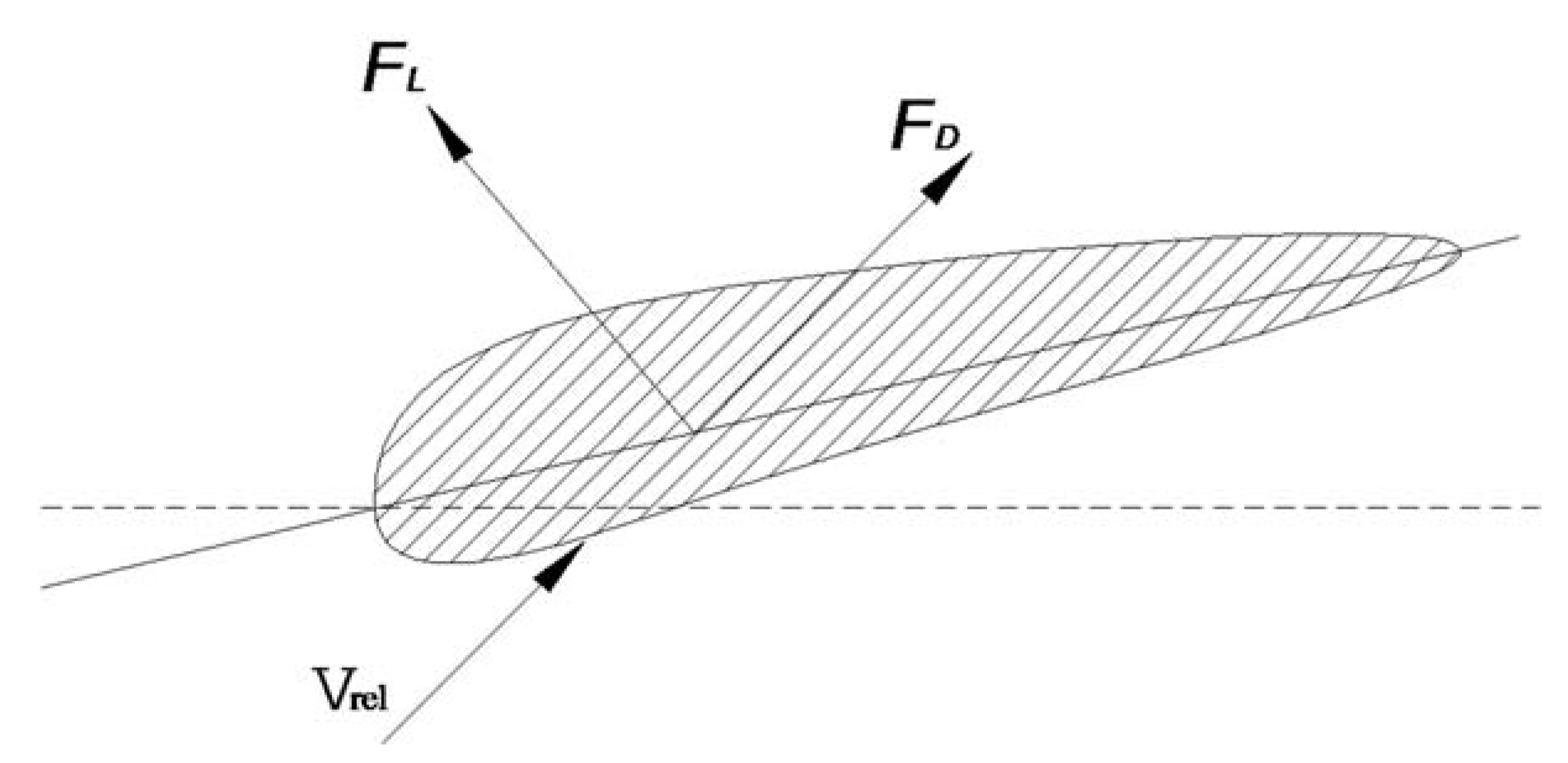
- After dividing the blades equally, the peripheral speed ratio of each section is calculated. The peripheral speed ratio corresponding to the radius of the th section is as follows [11]:
- (2)
- The axial inducer , the tangential inducer and the tip loss coefficient are calculated for each section . This is also the process of solving the following conditional extreme value problem. The most important performance index of the blade is the energy capture coefficient. In order to obtain the maximum capture coefficient, the value of each blade element should be maximized. Therefore, the maximum value is taken as the objective function of optimization to obtain each parameter [12].The values can be solved by the nonlinearly constrained optimization function in the optimization toolbox.
- (3)
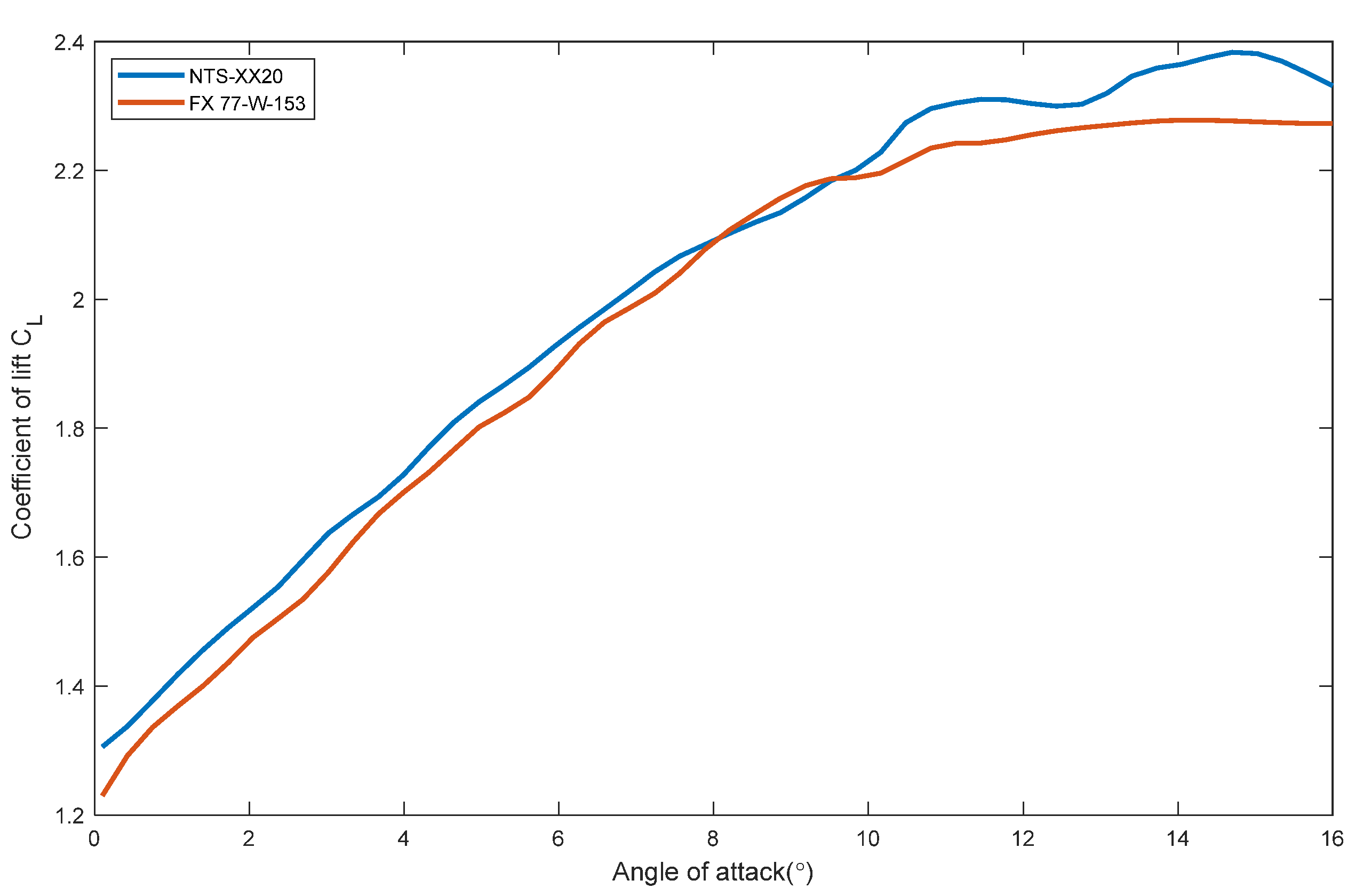
- The airfoil type is selected using the Profili software. The curves of the optimum lift–drag ratio with the Reynolds number at different angles of attack can be calculated and analyzed by the software Profili 2.2. It can be calculated that the Reynolds number from the blade root to the blade tip is different. The lift coefficient and drag coefficient corresponding to these angles of attack can be determined by finding the angles of attack based on different lift–drag ratios according to the Reynolds number. However, since turbines have different powers, different radii and different distributions in each section, the angles of the attack required and the corresponding dynamic coefficient and drag coefficient also change greatly. For convenient design calculation, the relation between the angle of attack and lift coefficient of the airfoil can be determined using the software or a numerical calculation method [13] as follows:
3.3. Processing and Production of Blade Model
3.4. Solid Modeling of Blade
3.5. Material Selection and Processing of Blade
- (1)
- Blades should be light, or they will increase the burden on other components such as hubs, controllers and generators, resulting in such defects as control delay and poor system coordination.
- (2)
- On the basis of blade design, the blade structure should be designed considering the influence of the actual operating environment factors of the unit, ensuring sufficient strength and stiffness of blades. This ensures that no damage occurs to blades in the provided service environment throughout their service life.
- (3)
- In terms of blade strength, static and fatigue strengths are usually analyzed and verified. The stability of pressurized parts should be verified to ensure that no deformation such as expansion, wrinkling and warping occurs in materials. The strength analysis is mainly based on the loads on blades. Inertial loads, gravity, motion loads and other loads are mainly calculated.
4. Analysis of Blade Test Data
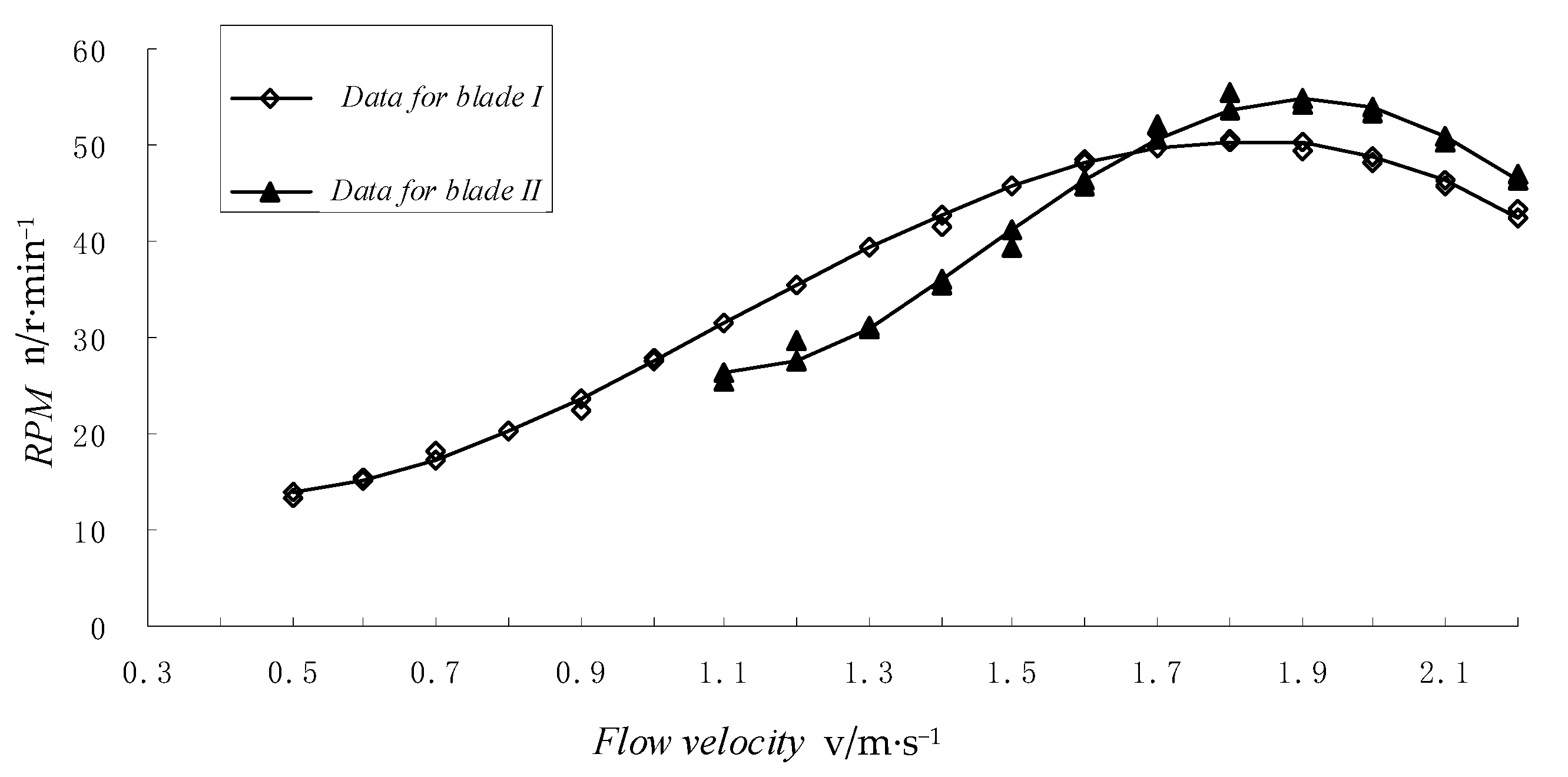
4.1. Start Flow Velocity Comparison Experiment
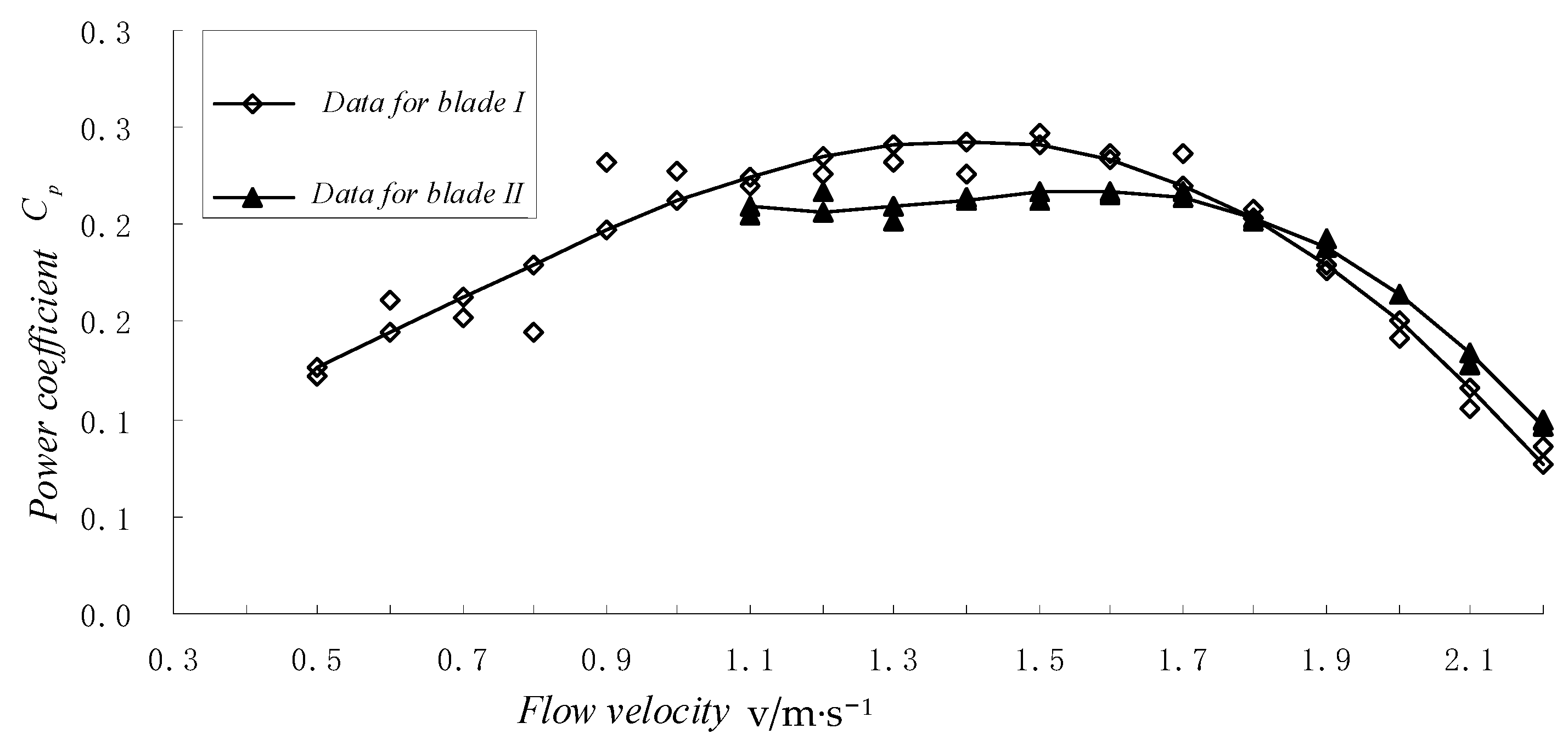
4.2. Generation Power Comparison Experiment
4.3. Blade Thrust Experiment
5. Experimental Conclusions
- 1.
- The design flow velocity has a great impact on the solidity of turbine. When the pitch angle is unchanged, increasing the blade solidity can effectively improve the self-starting performance of the blade. Nevertheless, since the blade speed and solidity are inversely proportional, the two should be taken into consideration when selecting the appropriate design flow velocity.
- 2.
- A comparison of power generation experiments shows that at low flow rates, Blade I generates more power than Blade II, and as the flow velocity increases, Blade II generates more power than Blade I. Therefore, choosing the appropriate blade allows the turbine to capture the most power over a varying range of flow rates.
- 3.
- The test comparison in the thrust experiment showed that throughout the range of flow velocity, the thrust on Blade I is greater than that on Blade II. This is also due to the high blade solidity and is inevitable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Colby, J.A.; Corren, D.R.; Pe, M.A.A.; Hernandez, A.A. Advancement of a Tidal Energy Converter Mount Through Integrated Design Process and Risk Management. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar]
- Ma, S.; Li, W.; Liu, H.; Lin, Y. Research on the Energy Capture Device of Horizontal Axis Tidal Current Energy Conversion Systems. J. Mech. Eng. 2010, 46, 150–156. [Google Scholar] [CrossRef]
- Li, G.; Zhu, W. A Review on Up-to-Date Gearbox Technologies and Maintenance of Tidal Current Energy Converters. Energies 2022, 15, 9236. [Google Scholar] [CrossRef]
- Seo, J.; Yi, J.H.; Park, J.S.; Lee, K.S. Review of tidal characteristics of Uldolmok Strait and optimal design of blade shape for horizontal axis tidal current turbines. Renew. Sustain. Energy Rev. 2019, 113, 109273. [Google Scholar] [CrossRef]
- Goundar, J.N.; Ahmed, M.R. Design of a horizontal axis tidal current turbine. Appl. Energy 2013, 111, 161–174. [Google Scholar] [CrossRef]
- Mahmuddin, F. Rotor blade performance analysis with blade element momentum theory. Energy Procedia 2017, 105, 1123–1129. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.; Lin, Y.; Li, W.; Gu, Y. Design and test of a 600-kW horizontal-axis tidal current turbine. Energy 2019, 182, 177–186. [Google Scholar] [CrossRef]
- Borg, M.G.; Xiao, Q.; Allsop, S.; Incecik, A.; Peyrard, C. A numerical performance analysis of a ducted, high-solidity tidal turbine. Renew. Energy 2020, 159, 663–682. [Google Scholar] [CrossRef]
- Sagharichi, A.; Zamani, M.; Ghasemi, A. Effect of solidity on the performance of variable-pitch vertical axis wind turbine. Energy 2018, 161, 753–775. [Google Scholar] [CrossRef]
- Faizan, M.; Badshah, S.; Badshah, M.; Haider, B.A. Performance and wake analysis of horizontal axis tidal current turbine using Improved Delayed Detached Eddy Simulation. Renew. Energy 2022, 184, 740–752. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Xie, Y.; Xu, G.; Liu, K.; Zheng, Y. The effects of surge motion on hydrodynamics characteristics of horizontal-axis tidal current turbine under free surface condition. Renew. Energy 2021, 170, 773–784. [Google Scholar] [CrossRef]
- Kim, S.J.; Singh, P.M.; Hyun, B.S.; Lee, Y.H.; Choi, Y.D. A study on the floating bridge type horizontal axis tidal current turbine for energy independent islands in Korea. Renew. Energy 2017, 112, 35–43. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Xie, Y.; Xu, G.; Liu, K.; Zheng, Y. Hydrodynamic analysis of horizontal axis tidal current turbine under the wave-current condition. J. Mar. Sci. Eng. 2020, 8, 562. [Google Scholar] [CrossRef]
- Ledoux, J.; Riffo, S.; Salomon, J. Analysis of the blade element momentum theory. SIAM J. Appl. Math. 2021, 81, 2596–2621. [Google Scholar] [CrossRef]
- Dehouck, V.; Lateb, M.; Sacheau, J.; Fellouah, H. Application of the blade element momentum theory to design horizontal axis wind turbine blades. J. Sol. Energy Eng. 2018, 140, 014501. [Google Scholar] [CrossRef]
- Borg, M.G.; Xiao, Q.; Allsop, S.; Incecik, A.; Peyrard, C. A numerical structural analysis of ducted, high-solidity, fibre-composite tidal turbine rotor configurations in real flow conditions. Ocean Eng. 2021, 233, 109087. [Google Scholar] [CrossRef]








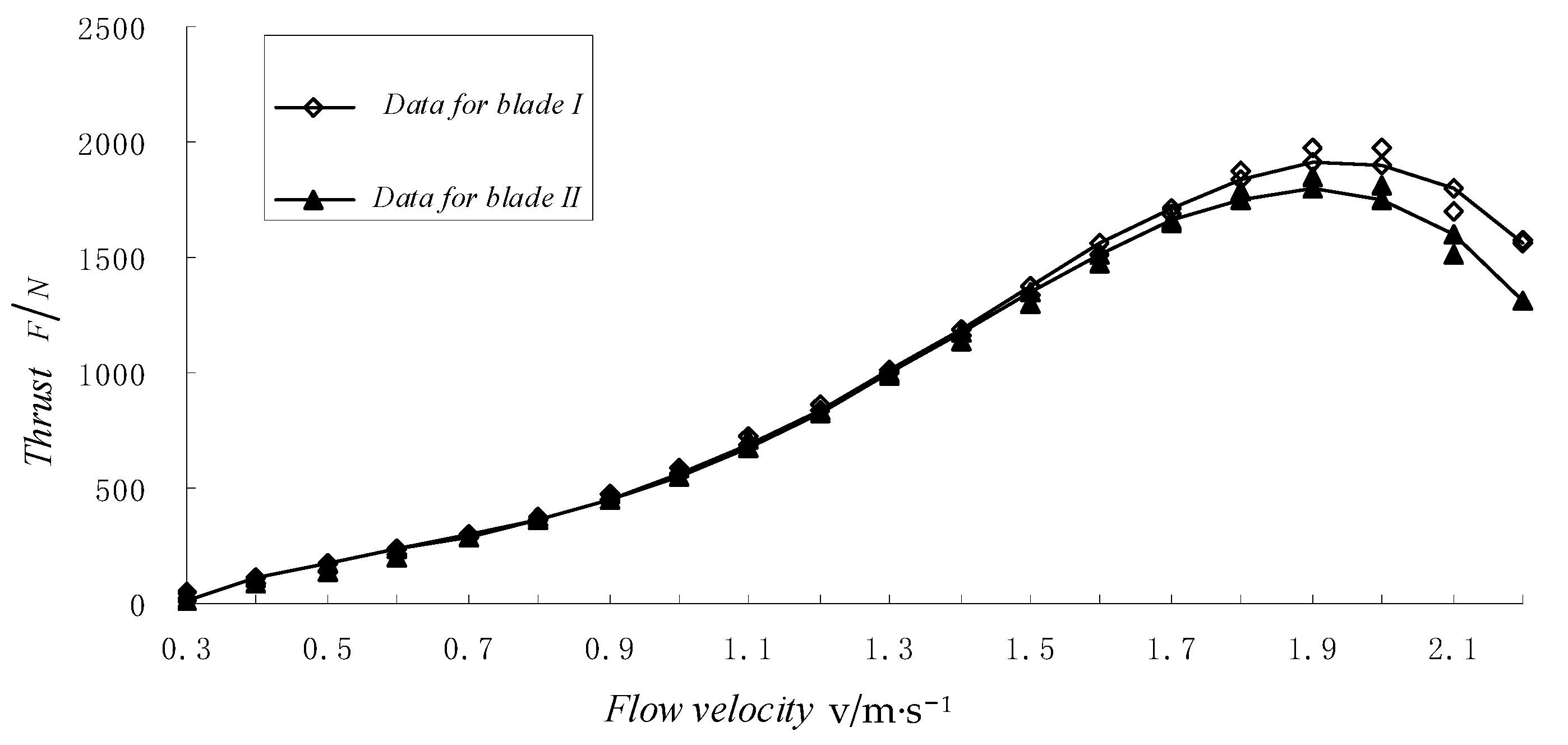
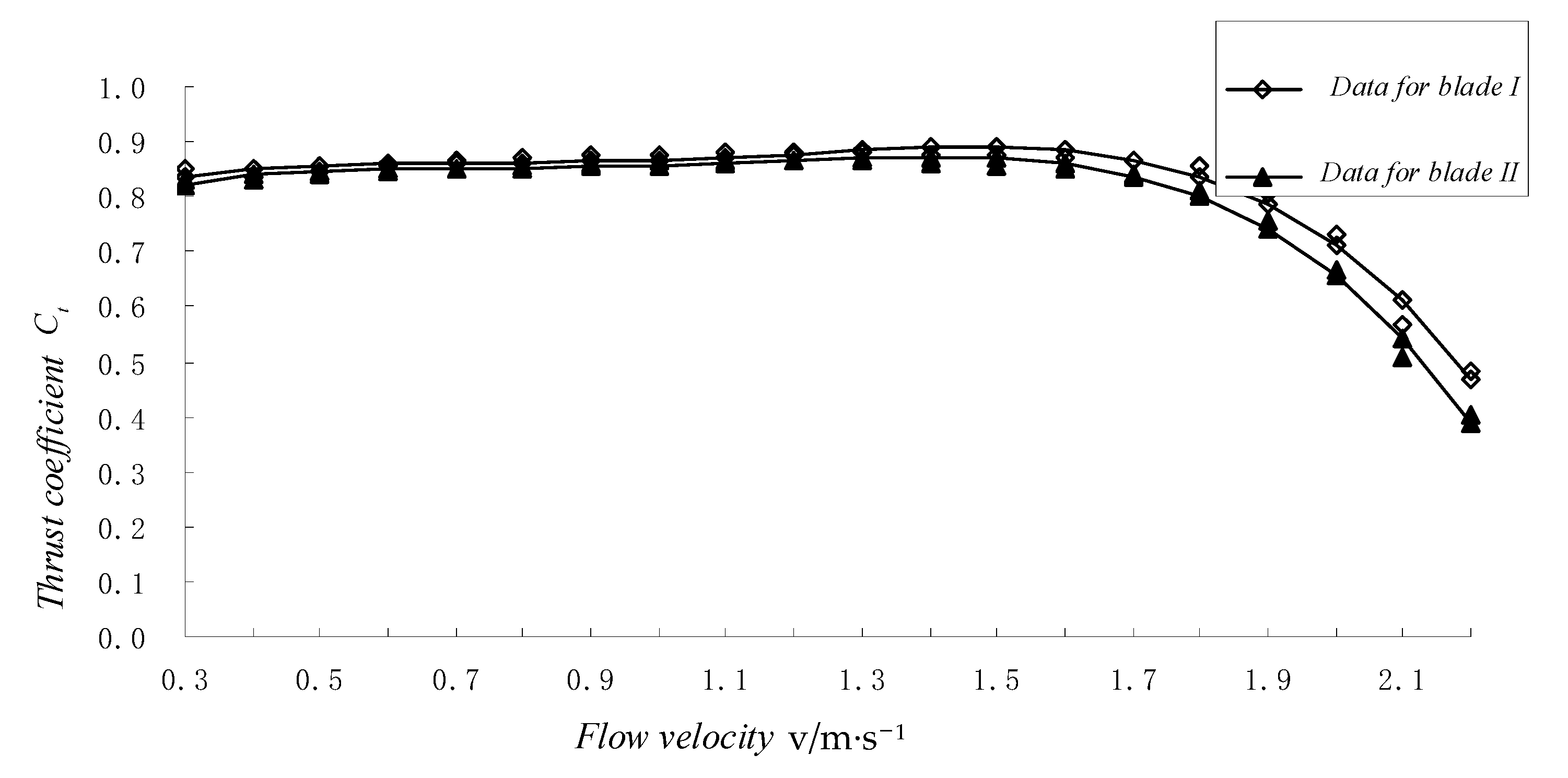
| Tip Speed Ratio | Number of Blades |
|---|---|
| 1 | 8~24 |
| 2 | 6~12 |
| 3 | 3~8 |
| 4 | 3~5 |
| 5~8 | 2~4 |
| 9~15 | 2~3 |
| Parameter | Blade I | Blade II |
|---|---|---|
| Design flow velocity, | 1.50 | 2.20 |
| Number of blades, | 3 | 3 |
| Blade diameter, | 1.30 | 1.30 |
| Design speed, | 48 | 48 |
| Hub diameter, /m | 0.1 | 0.1 |
| Tip speed ratio, | 2.17 | 1.48 |
| Blade airfoil | FX 77-W-153 | FX 77-W-153 |
| NO. | Position of Blade Element (m) | Axial Induction (a) of Blade I | Tangential Induction (b) of Blade I | Axial Induction (a) of Blade II | Tangential Induction (b) of Blade II | Thickness (%) |
|---|---|---|---|---|---|---|
| 1 | 0.01 | 0.3356 | 1.0325 | 0.3221 | 2.6811 | 30 |
| 2 | 0.0437 | 0.3487 | 1.0468 | 0.2695 | 2.5475 | 28 |
| 3 | 0.0774 | 0.3210 | 0.6727 | 0.2806 | 1.2897 | 26 |
| 4 | 0.1111 | 0.3121 | 0.4813 | 0.2901 | 0.8085 | 24 |
| 5 | 0.1447 | 0.3109 | 0.3665 | 0.2979 | 0.5603 | 20 |
| 6 | 0.1784 | 0.3133 | 0.2905 | 0.3044 | 0.4125 | 20 |
| 7 | 0.2121 | 0.3171 | 0.2368 | 0.3101 | 0.3167 | 19 |
| 8 | 0.2458 | 0.3215 | 0.1972 | 0.3155 | 0.251 | 19 |
| 9 | 0.2795 | 0.3263 | 0.1671 | 0.3206 | 0.2041 | 19 |
| 10 | 0.3132 | 0.3314 | 0.1437 | 0.3259 | 0.1695 | 19 |
| 11 | 0.3468 | 0.3371 | 0.1254 | 0.3316 | 0.1434 | 18 |
| 12 | 0.3805 | 0.3435 | 0.1108 | 0.3379 | 0.1235 | 18 |
| 13 | 0.4142 | 0.3511 | 0.0993 | 0.3453 | 0.108 | 18 |
| 14 | 0.4479 | 0.3603 | 0.0902 | 0.3542 | 0.096 | 17 |
| 15 | 0.4816 | 0.3717 | 0.0831 | 0.3653 | 0.0868 | 17 |
| 16 | 0.5153 | 0.3800 | 0.0690 | 0.3797 | 0.08 | 17 |
| 17 | 0.5489 | 0.3800 | 0.0620 | 0.3809 | 0.0643 | 17 |
| 18 | 0.5826 | 0.3787 | 0.0471 | 0.3799 | 0.0571 | 16 |
| 19 | 0.6163 | 0.3708 | 0.0554 | 0.3688 | 0.0482 | 16 |
| 20 | 0.65 | 0.3303 | 0.0285 | 0.3572 | 0.0359 | 16 |
| X | Upper X | Lower Y |
|---|---|---|
| 0 | 0 | 0 |
| 0.1082 | 0.5978 | −0.46917 |
| 0.43291 | 1.381 | −1.12723 |
| 0.97189 | 2.16847 | −1.49776 |
| 1.72335 | 3.12598 | −1.83573 |
| 2.68312 | 4.08078 | −2.03599 |
| 3.84929 | 5.10965 | −2.27645 |
| 5.21459 | 6.0881 | −2.43568 |
| 6.77518 | 7.1001 | −2.62006 |
| 8.52277 | 8.02742 | −2.73455 |
| 10.44949 | 8.94786 | −2.86996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, H.; Chen, J.; Jiang, C.; Bao, L. Research on Solidity of Horizontal-Axis Tidal Current Turbine. Energies 2023, 16, 3467. https://doi.org/10.3390/en16083467
Wang X, Li H, Chen J, Jiang C, Bao L. Research on Solidity of Horizontal-Axis Tidal Current Turbine. Energies. 2023; 16(8):3467. https://doi.org/10.3390/en16083467
Chicago/Turabian StyleWang, Xiancheng, Hao Li, Junhua Chen, Chuhua Jiang, and Lingjie Bao. 2023. "Research on Solidity of Horizontal-Axis Tidal Current Turbine" Energies 16, no. 8: 3467. https://doi.org/10.3390/en16083467
APA StyleWang, X., Li, H., Chen, J., Jiang, C., & Bao, L. (2023). Research on Solidity of Horizontal-Axis Tidal Current Turbine. Energies, 16(8), 3467. https://doi.org/10.3390/en16083467






