Unidimensional and 3D Analyses of a Radial Inflow Turbine for an Organic Rankine Cycle under Design and Off-Design Conditions
Abstract
1. Introduction
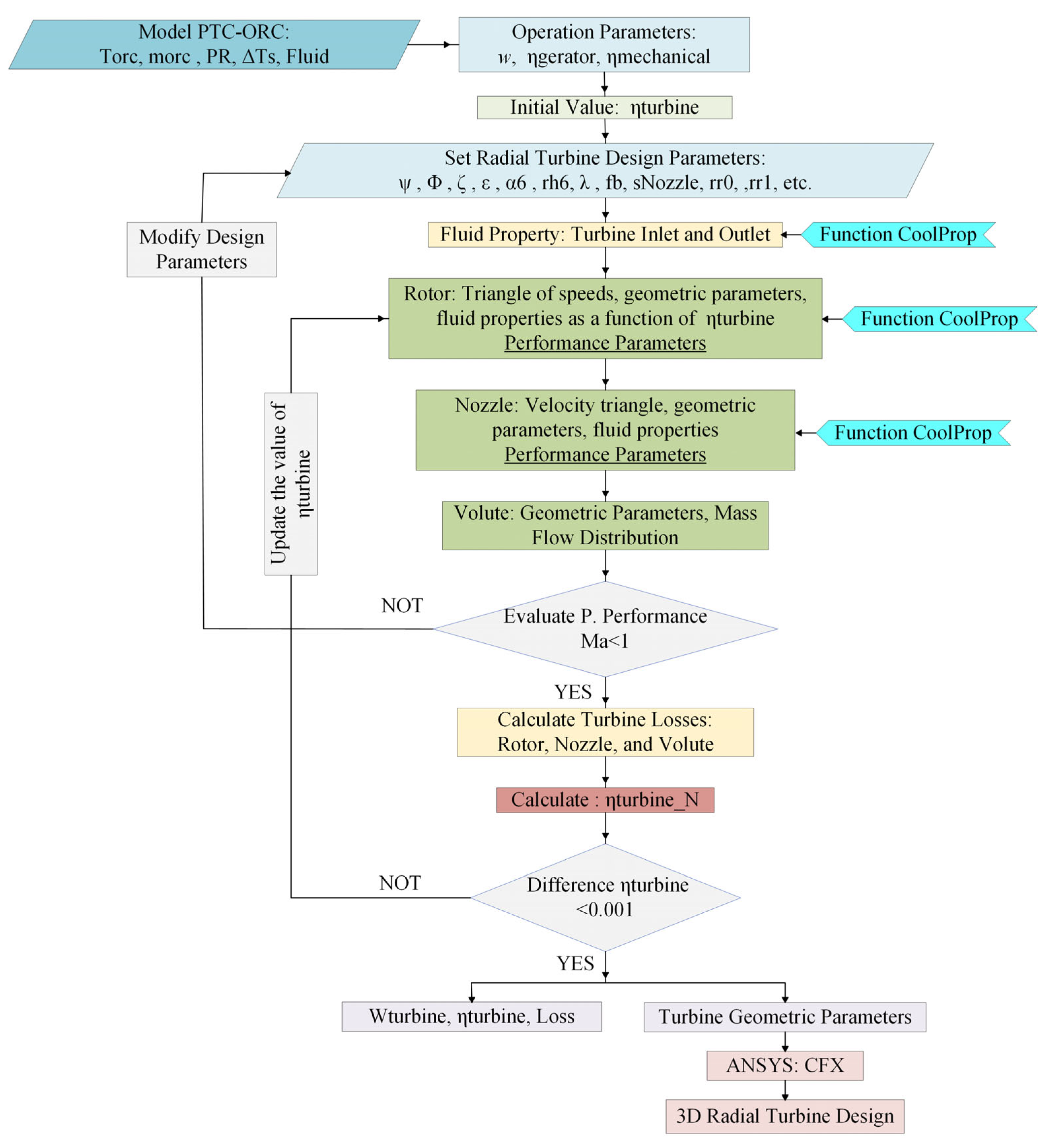
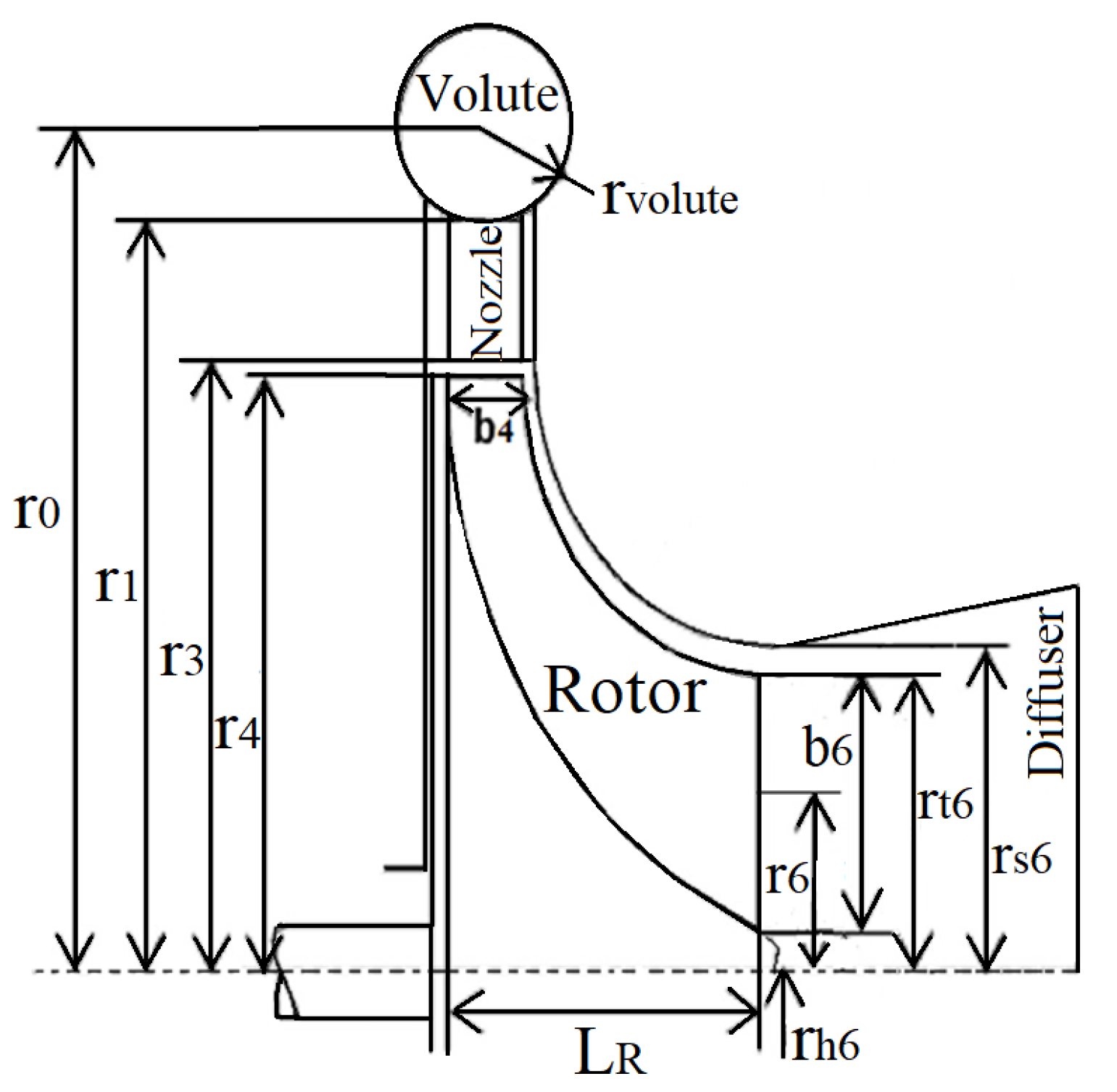
2. One-Dimensional Model of the Radial Turbine
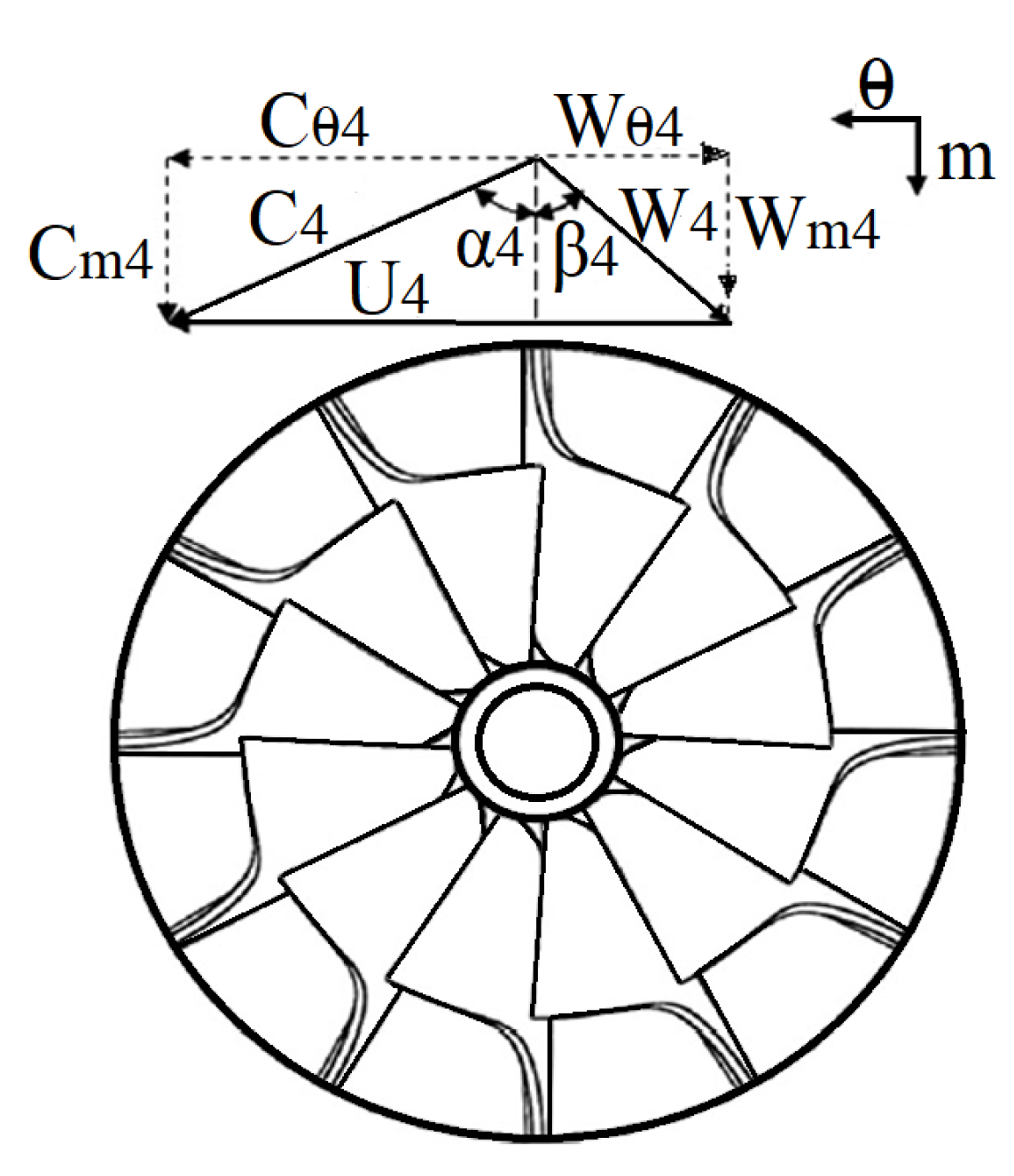
3. Rotor Model
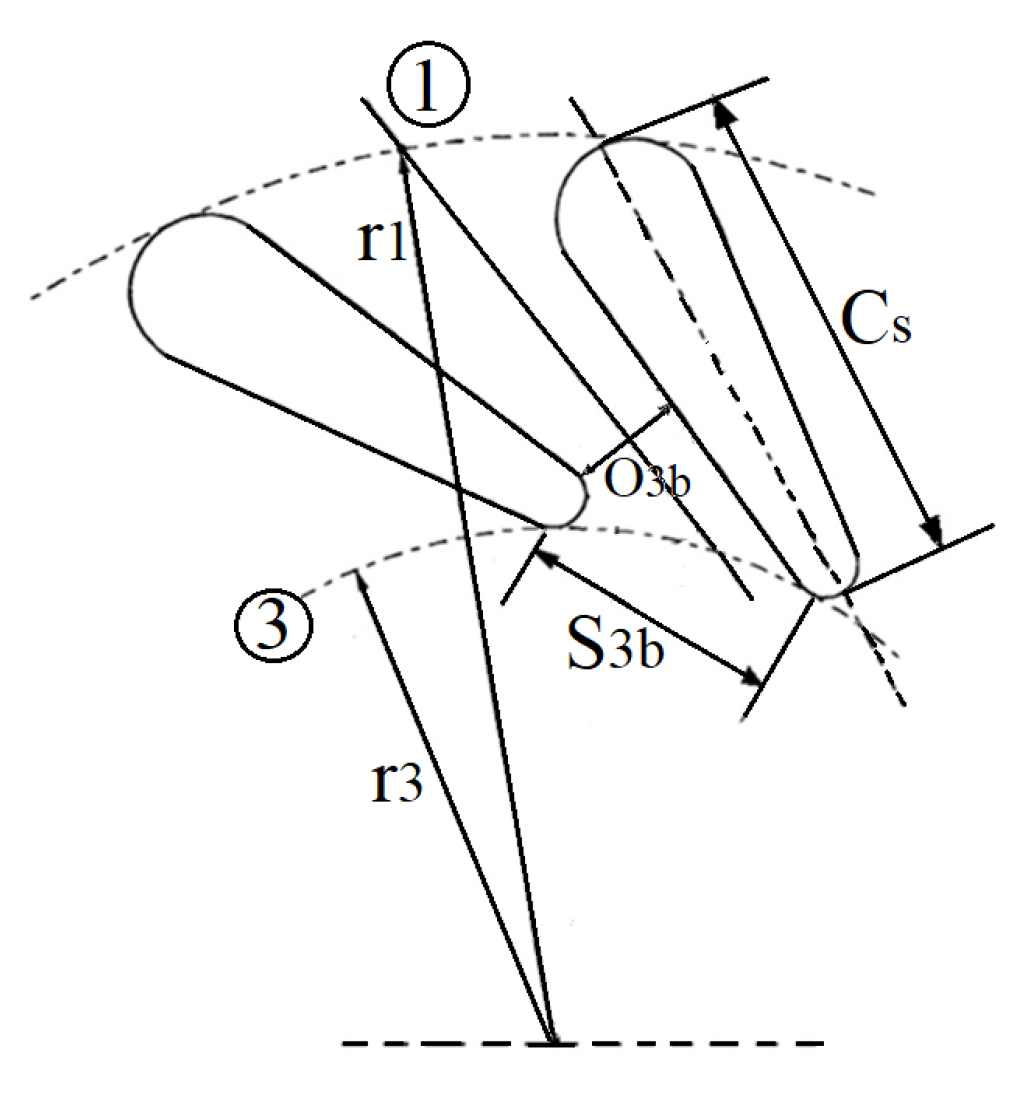
4. Nozzle Model
5. Volute Model
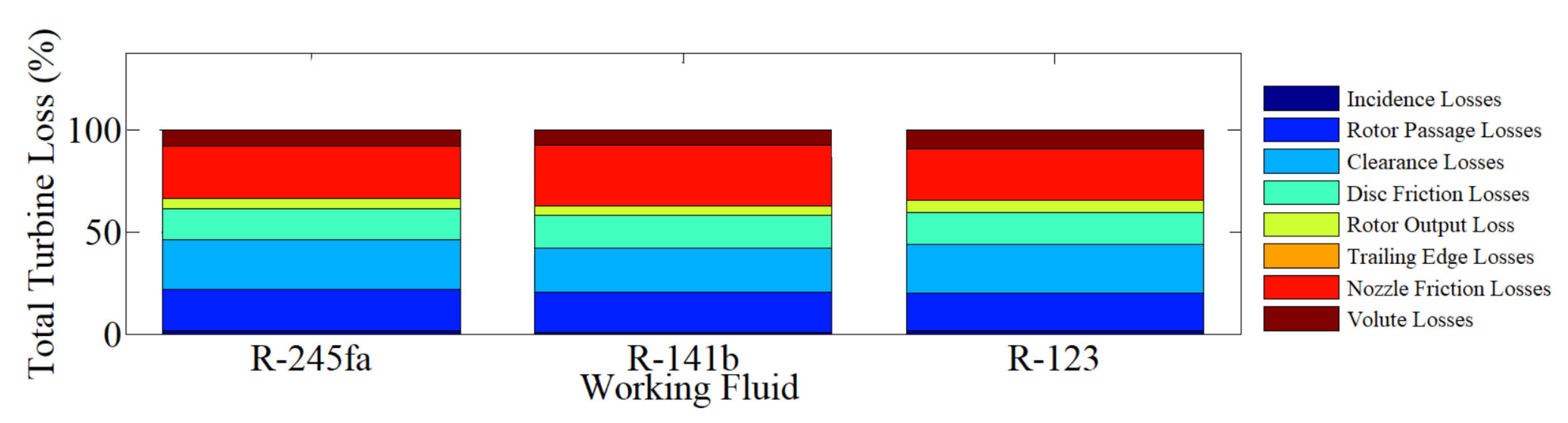
6. Radial Turbine Losses
6.1. Rotor Losses
6.1.1. Friction Losses
6.1.2. Outlet Losses
6.1.3. Aerodynamic Load Losses
6.1.4. Trailing Edge Loss
6.2. Nozzle Losses
6.3. Volute Losses
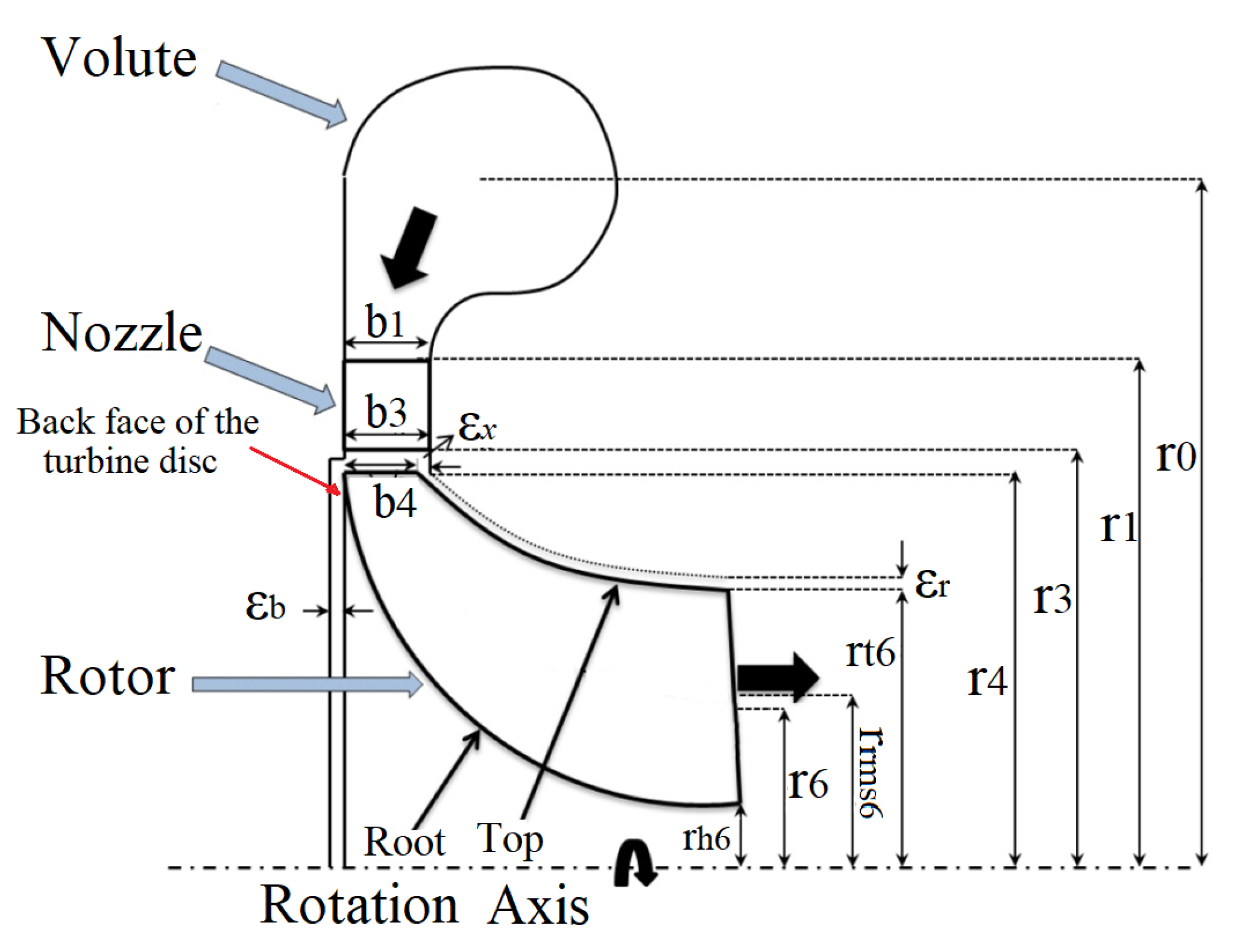
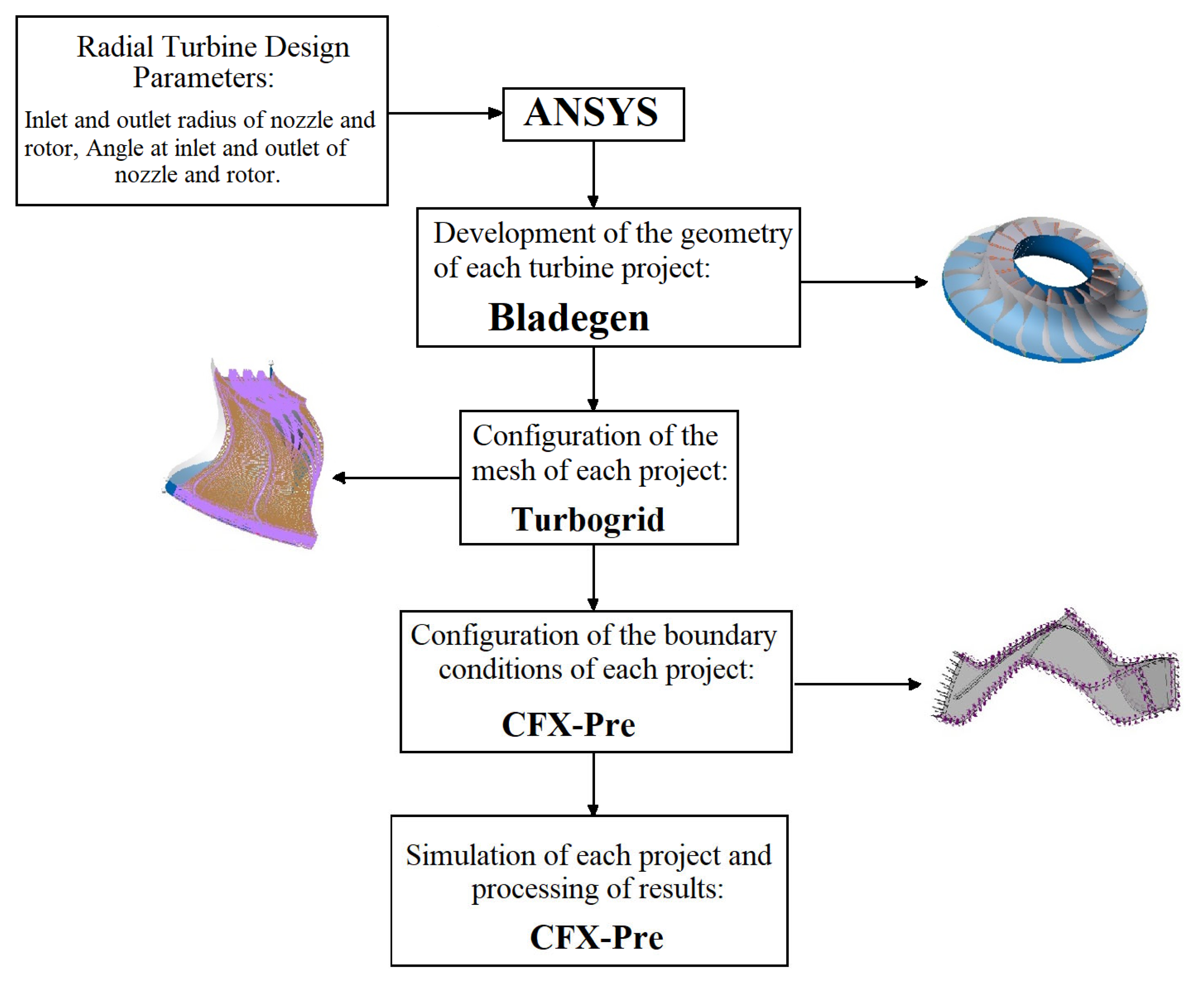
7. 3D Radial Turbine Design
8. Validation of One-Dimensional Mathematical Models of the Radial Turbine
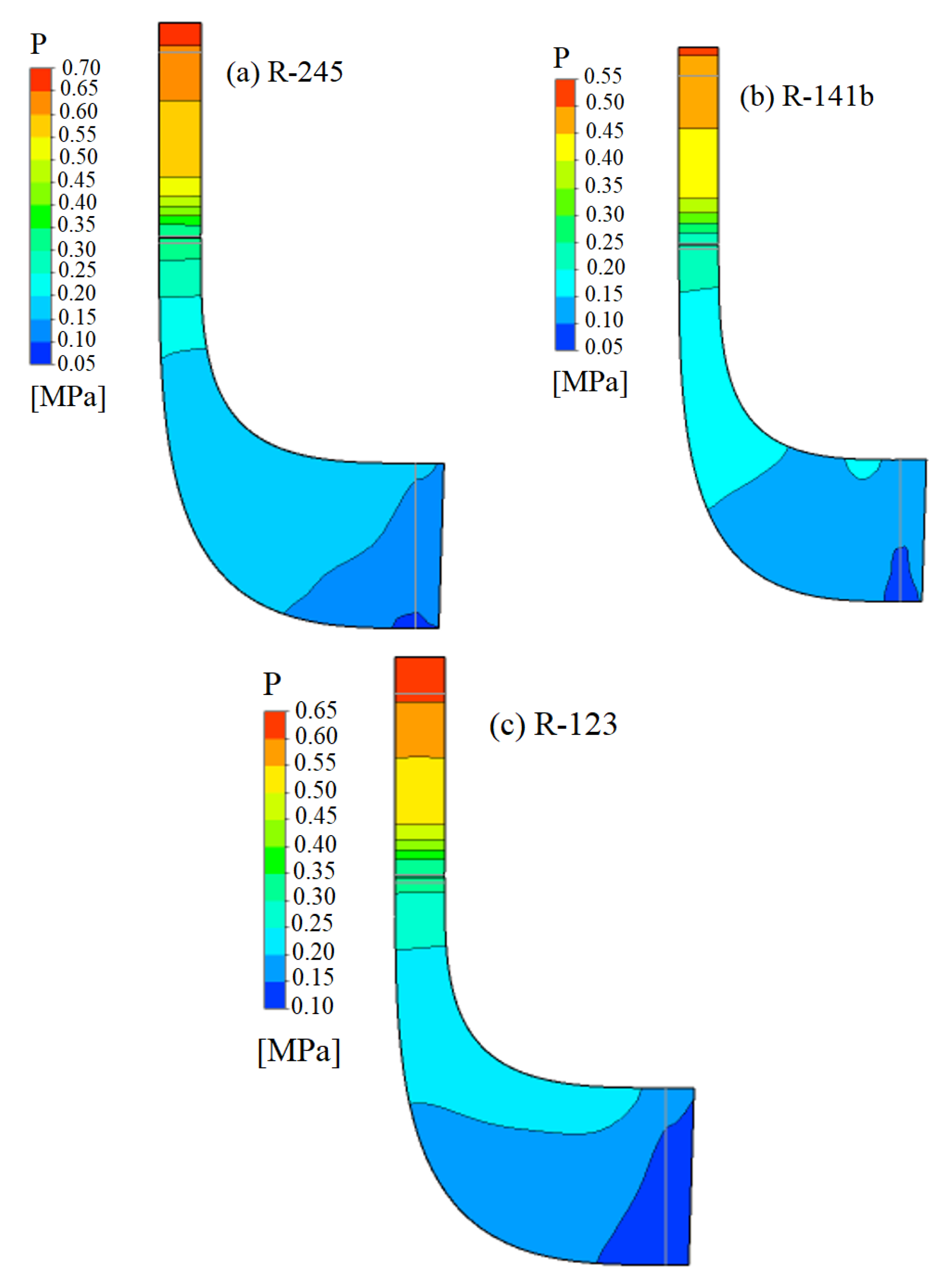
9. Radial Turbine Design Results
10. Efficiency Characteristics of the Radial Turbine Nozzle-Rotor Set
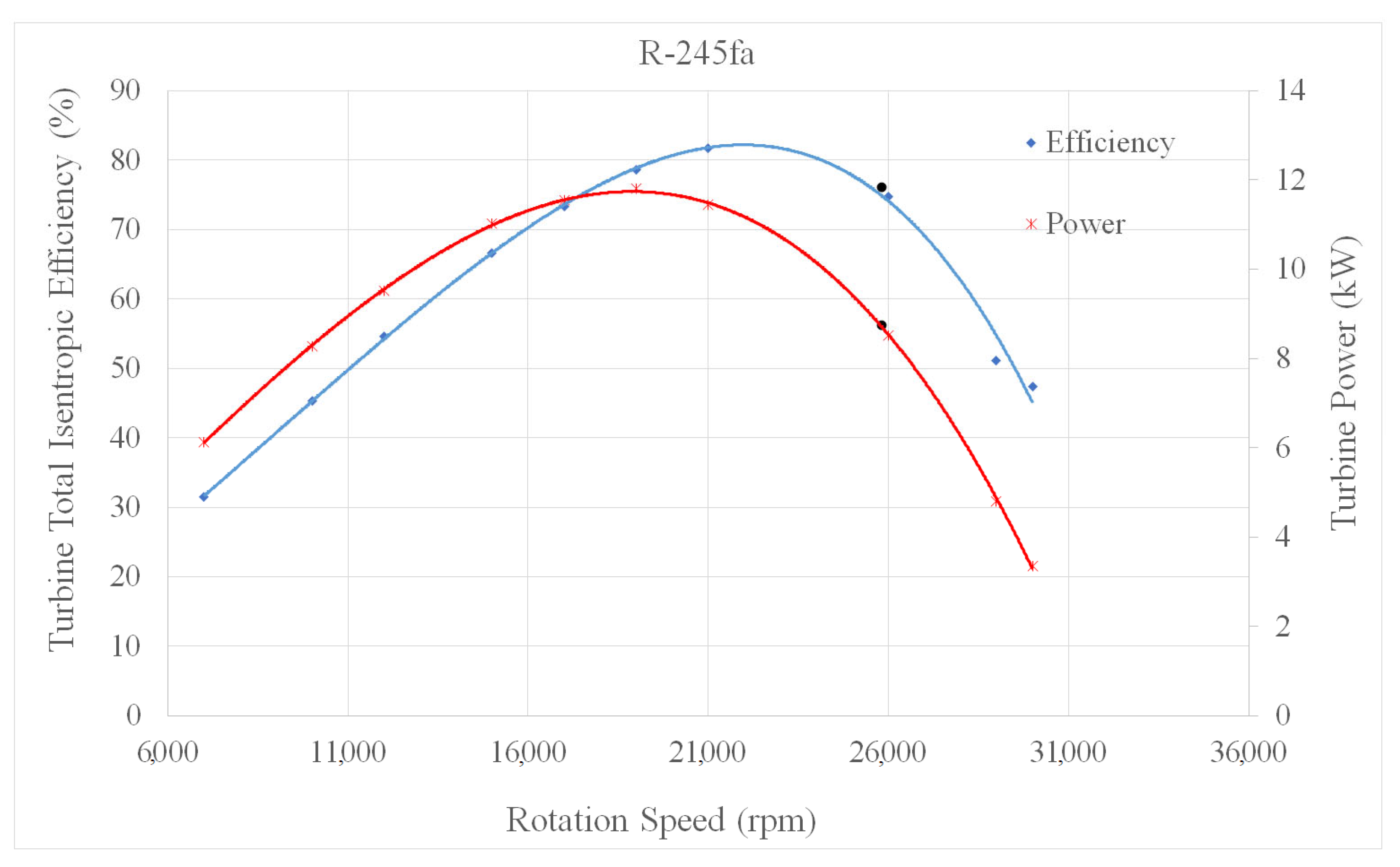
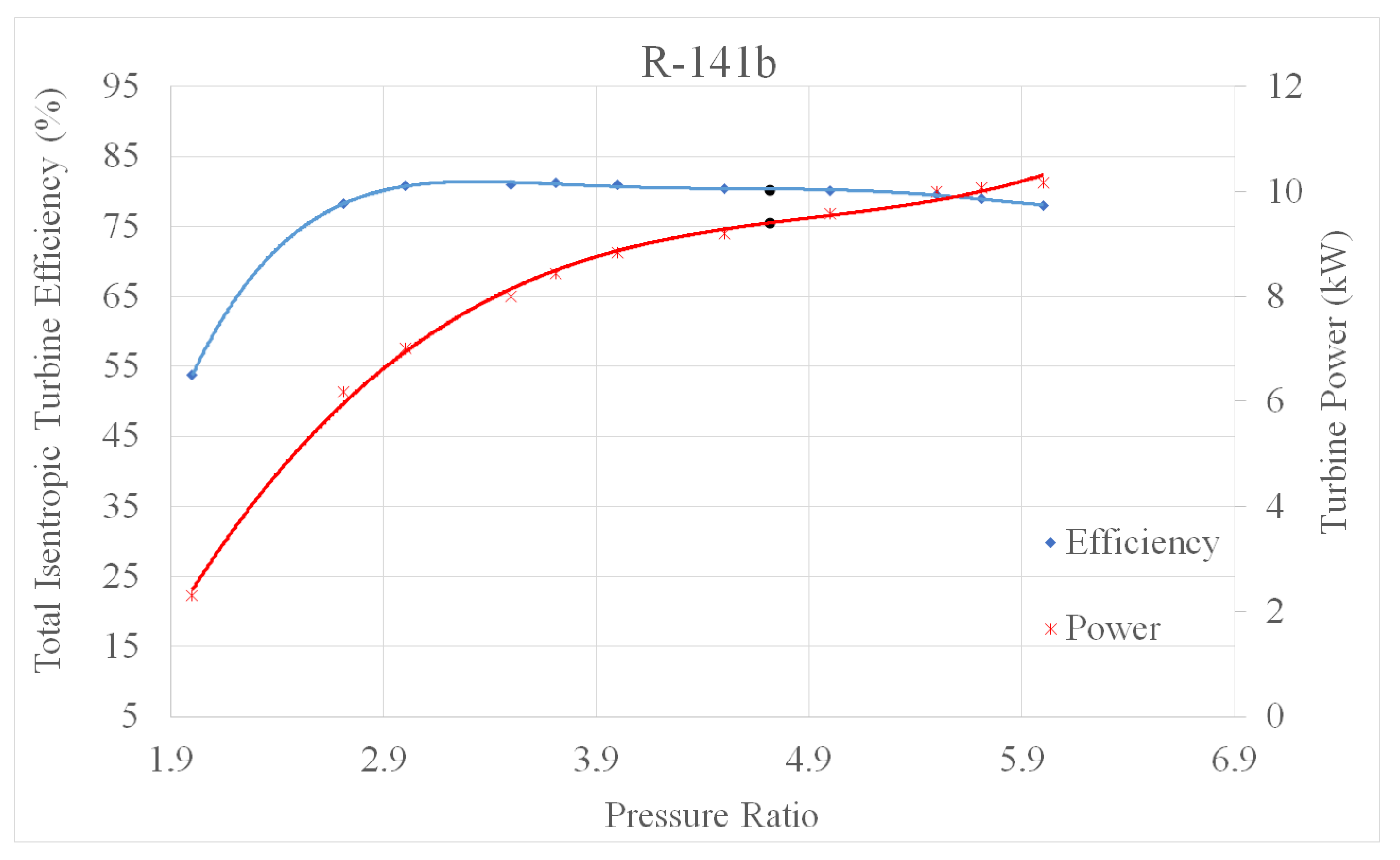
11. Characteristic Curves of Radial Turbines
12. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Area (m2) | |
| b | Normal, interaction coefficient, base, nozzle blade |
| C | Specific heat (kJ/kg·K), Absolute velocity |
| Nozzle Chord | |
| d | Diffuse |
| Diameter (m) | |
| eva | Evaporator |
| Friction factor, fluid | |
| Ft | Correction factor |
| hub | |
| Pressure loss coefficient | |
| L | Length (m) |
| m | Meridional plane |
| Mass flow (kg/s) | |
| p | Constant pressure, loss, projection |
| R | Rotor blade |
| r | Radius (m) |
| rms | Root mean square radius |
| Temperature (K) | |
| s | shroud, storage, dry section |
| Nozzle design parameter | |
| U | Circumferential rotation speed (m/s) |
| v | Volute, Volume (m3) |
| W | Relative velocity (m/s) |
| Nozzle blades number | |
| Rotation speed (rad/s) | |
| Greek symbols | |
| Absolute flow angle (°) | |
| β | Relative flow angle (°) |
| Rotor radius ratio | |
| Tangential plane | |
| γfi | Interception factor |
| ξ | Meridional speed ratio |
| Loading coefficient | |
| Φ | Flow coefficient |
| Subscribed | |
| 0 | Total, Volute input |
| 1 | Receiver side one, Nozzle inlet |
| 2 | Receiver side two |
| 3 | Nozzle outlet |
| 4 | Rotor inlet |
| 6 | Rotor outlet |
| in | Inlet |
| Isentropic | |
| Outlet | |
| orc | Organic Rankine Cycle |
| PTC | Parabolic Trough Collectors |
| wf | Working fluid |
| Surroundings | |
References
- Wang, H.; Wang, G.; Qi, J.; Schandl, H.; Li, Y.; Feng, C.; Yang, X.; Wang, Y.; Wang, X.; Liang, S. Scarcity-weighted fossil fuel footprint of China at the provincial level. Appl. Energy 2020, 258, 114081. [Google Scholar] [CrossRef]
- Curtin, J.; McInerney, C.; Gallachóir, B.Ó.; Hickey, C.; Deane, P.; Deeney, P. Quantifying stranding risk for fossil fuel assets and implications for renewable energy investment: A review of the literature. Renew. Sustain. Energy Rev. 2019, 116, 109402. [Google Scholar] [CrossRef]
- Gaete-Morales, C.; Gallego-Schmid, A.; Stamford, L.; Azapagic, A. Life cycle environmental impacts of electricity from fossil fuels in Chile over a ten-year period. J. Clean. Prod. 2019, 232, 1499–1512. [Google Scholar] [CrossRef]
- Carrillo Caballero, G. Estudo E Modelagem Dos Componentes de Um Sistema Dish Stirling Visando à Otimização Da Potência E a Eficiência Do Sistema. Dissertação de Mestrado, Universidade Federal de Itajubá, Itajubá, Brazil, 2013. [Google Scholar]
- Woodland, B.J.; Ziviani, D.; Braun, J.E.; Groll, E.A. Considerations on alternative organic Rankine Cycle congurations for low-grade waste heat recovery. Energy 2020, 193, 116810. [Google Scholar] [CrossRef]
- Abrosimov, K.A.; Baccioli, A.; Bischi, A. Techno-economic analysis of combined inverted Brayton—Organic Rankine cycle for high-temperature waste heat recovery. Energy Convers. Manag. 2020, 207, 112336. [Google Scholar] [CrossRef]
- Liu, X.; Nguyen, M.Q.; Chu, J.; Lan, T.; He, M. A novel waste heat recovery system combing steam Rankine cycle and organic Rankine cycle for marine engine. J. Clean. Prod. 2020, 265, 121502. [Google Scholar] [CrossRef]
- Xu, B.; Rathod, D.; Yebi, A.; Filipi, Z. A comparative analysis of real-time power optimization for organic Rankine cycle waste heat recovery systems. Appl. Therm. Eng. 2020, 164, 114442. [Google Scholar] [CrossRef]
- Elakhdar, M.; Landoulsi, H.; Tashtoush, B.; Nehdi, E.; Kairouani, L. A combined thermal system of ejector refrigeration and Organic Rankine cycles for power generation using a solar parabolic trough. Energy Convers. Manag. 2019, 199, 111947. [Google Scholar] [CrossRef]
- Arteconi, A.; Del Zotto, L.; Tascioni, R.; Cioccolanti, L. Modelling system integration of a micro solar organic Rankine Cycle plant into a residential building. Appl. Energy 2019, 251, 113408. [Google Scholar] [CrossRef]
- Khanmohammadi, S.; Saadat-Targhi, M.; Ahmed, F.W.; Afrand, M. Potential of thermoelectric waste heat recovery in a combined geothermal, fuel cell and organic Rankine flash cycle (thermodynamic and economic evaluation). Int. J. Hydrogen Energy 2020, 45, 6934–6948. [Google Scholar] [CrossRef]
- Han, J.; Wang, X.; Xu, J.; Yi, N.; Talesh, S.S.A. Thermodynamic analysis and optimization of an innovative geothermal-based organic Rankine cycle using zeotropic mixtures for power and hydrogen production. Int. J. Hydrogen Energy 2020, 45, 8282–8299. [Google Scholar] [CrossRef]
- Simpson, M.C.; Chatzopoulou, M.A.; Oyewunmi, O.A.; Le Brun, N.; Sapin, P.; Markides, C.N. Technoeconomic analysis of internal combustion engine—Organic Rankine cycle systems for combined heat and power in energy-intensive buildings. Appl. Energy 2019, 253, 113462. [Google Scholar] [CrossRef]
- Shi, L.; Shu, G.; Tian, H.; Deng, S. A review of modified Organic Rankine cycles (ORCs) for internal combustion engine waste heat recovery (ICE-WHR). Renew. Sustain. Energy Rev. 2018, 92, 95–110. [Google Scholar] [CrossRef]
- Kim, D.K.; Choi, H.W.; Kim, M.S. Design of a rotary expander as an expansion device integrated into organic Rankine cycle (ORC) to recover low-grade waste heat. Appl. Therm. Eng. 2019, 163, 114326. [Google Scholar] [CrossRef]
- Liao, G.; Jiaqiang, E.; Zhang, F.; Chen, J.; Leng, E. Advanced exergy analysis for organic Rankine Cycle-based layout to recover waste heat of flue gas. Appl. Energy 2020, 266, 114891. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Wang, W.-H.; Pan, S.-Y.; Ho, C.-C.; Hou, C.-J.; Chiang, P.-C. Environmental impacts and benefits of organic Rankine cycle power generation technology and wood pellet fuel exemplified by electric arc furnace steel industry. Appl. Energy 2016, 183, 369–379. [Google Scholar] [CrossRef]
- Yang, H.; Xu, C.; Yang, B.; Yu, X.; Zhang, Y.; Mu, Y. Performance analysis of an organic Rankine Cycle system using evaporative condenser for sewage heat recovery in the petrochemical industry. Energy Convers. Manag. 2020, 205, 112402. [Google Scholar] [CrossRef]
- de Campos, G.B.; Bringhenti, C.; Traverso, A.; Tomita, J.T. Thermoeconomic optimization of organic Rankine bottoming cycles for micro gas turbines. Appl. Therm. Eng. 2020, 164, 114477. [Google Scholar] [CrossRef]
- Zhai, L.; Xu, G.; Wen, J.; Quan, Y.; Fu, J.; Wu, H.; Li, T. An improved modeling for low-grade organic Rankine cycle coupled with optimization design of radial-inflow turbine. Energy Convers. Manag. 2017, 153, 60–70. [Google Scholar] [CrossRef]
- Li, Y.-R.; Du, M.-T.; Wu, C.-M.; Wu, S.-Y.; Liu, C. Potential of organic Rankine cycle using zeotropic mixtures as working fluids for waste heat recovery. Energy 2014, 77, 509–519. [Google Scholar] [CrossRef]
- Rayegan, R.; Tao, Y.X. A procedure to select working fluids for solar Organic Rankine Cycles (ORCs). Renew. Energy 2011, 36, 659–670. [Google Scholar] [CrossRef]
- Li, Y.; Ren, X.-d. Investigation of the organic Rankine cycle (ORC) system and the radial-inflow turbine design. Appl. Therm. Eng. 2016, 96, 547–554. [Google Scholar] [CrossRef]
- Kang, S.H. Design and preliminary tests of ORC (organic Rankine cycle) with two-stage radial turbine. Energy 2016, 96, 142–154. [Google Scholar] [CrossRef]
- Al Jubori, A.M.; Al-Dadah, R.; Mahmoud, S. An innovative small-scale two-stage axial turbine for low-temperature organic Rankine cycle. Energy Convers. Manag. 2017, 144, 18–33. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Xia, X.; Zhao, B.; He, N.; Peng, D. Preliminary design and numerical analysis of a radial inflow turbine in organic Rankine cycle using zeotropic mixtures. Appl. Therm. Eng. 2019, 162, 114266. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Sauret, E.; Rowlands, A.S. Candidate radial-inflow turbines and high-density working fluids for geothermal power systems. Energy 2011, 36, 4460–4467. [Google Scholar] [CrossRef]
- Atkinson, M.J. The Design of Efficient Radial Turbines for Low Power Applications. Ph.D. Thesis, University of Sussex, Falmer, UK, 1998. [Google Scholar]
- Salih, U.M. Numerical Simulation, Design and Optimization of Radial Inflow Turbine for Energy Recovery Usage of Automobile. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2015. [Google Scholar]
- Miranda, R. Projeto de Turbinas Radiais Operadas Com Fluidos Orgânicos Para Baixas Potências. Ph.D. Thesis, Universidade Federal de Itajubá, Itajubá, Brazil, 2015. [Google Scholar]
- Song, J.; Gu, C.-W.; Ren, X. Influence of the radial-inflow turbine efficiency prediction on the design and analysis of the Organic Rankine Cycle (ORC) system. Energy Convers. Manag. 2016, 123, 308–316. [Google Scholar] [CrossRef]
- Song, Y.; Sun, X.; Huang, D. Preliminary design and performance analysis of a centrifugal turbine for Organic Rankine Cycle (ORC) applications. Energy 2017, 140, 1239–1251. [Google Scholar] [CrossRef]
- Da Lio, L.; Manente, G.; Lazzaretto, A. A mean-line model to predict the design efficiency of radial inflow turbines in organic Rankine cycle (ORC) systems. Appl. Energy 2017, 205, 187–209. [Google Scholar] [CrossRef]
- Zheng, Y.; Hu, D.; Cao, Y.; Dai, Y. Preliminary design and off-design performance analysis of an organic Rankine Cycle radial-inflow turbine based on mathematic method and CFD method. Appl. Therm. Eng. 2017, 112, 25–37. [Google Scholar] [CrossRef]
- Han, Z.; Jia, X.; Li, P. Preliminary design of radial inflow turbine and working fluid selection based on particle swarm optimization. Energy Convers. Manag. 2019, 199, 111933. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Gao, X.; Ling, X. Thermodynamic analysis and optimization of organic Rankine cycles based on radial-inflow turbine design. Appl. Therm. Eng. 2021, 184, 116277. [Google Scholar] [CrossRef]
- Carrillo Caballero, G.; Escorcia, Y.C.; Mendoza Castellanos, L.S.; Galindo Noguera, A.L.; Venturini, O.J.; Silva Lora, E.E.; Gutiérrez Velásquez, E.I.; Alviz Meza, A. Thermal Analysis of a Parabolic Trough Collectors System Coupled to an Organic Rankine Cycle and a Two-Tank Thermal Storage System: Case Study of Itajubá-MG Brazil. Energies 2022, 15, 8261. [Google Scholar] [CrossRef]
- Carrillo Caballero, G. Modelagem Do Comportamento Integrado de Um Sistema de Coletor Cilíndrico Parabólico Operando com Ciclo Rankine Orgânico E Armazenamento Térmico de Dois Tanques. Ph.D. Thesis, Universidade Federal de Itajubá, Itajubá, Brazil, 2018. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library coolprop. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Moustapha, H.; Zelesky, M.F.; Baines, N.C.; Japikse, D. Axial and Radial Turbines; Concepts NREC: White River Junction, VT, USA, 2003. [Google Scholar]
- Aungier, R.H. Turbine Aerodynamics: Axial-Flow and Radial-Inflow Trubine Design and Analysis; ASME Press: New York, NY, USA, 2006. [Google Scholar]
- Japikse, D.; Baines, N. Introduction to Turbomachinery; Concepts ETI: Oxfordshire, UK, 1997. [Google Scholar]
- Dixon, S. Fluid Mechanics and Thermodynamics of Turbomachinery; Elsevier: Oxford, UK, 1998; pp. 1–27. [Google Scholar]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N. Modelling and optimization of organic Rankine cycle based on a small-scale radial inflow turbine. Energy Convers. Manag. 2015, 91, 186–198. [Google Scholar] [CrossRef]
- Benson, R.S. A review of methods for assessing loss coefficients in radial gas turbines. Int. J. Mech. Sci. 1970, 12, 905–932. [Google Scholar] [CrossRef]
- Glassman, A.J. Turbine Design and Application; Technical Report; Scientific and Technical Information Office, National Aeronautics and and Space Administration: Washington, DC, USA, 1990; Volume 1. [Google Scholar]
- Balje, O.E. Turbomachines: A Guide to Design Selection and Theory; John Wiley & Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Ventura, C.A.M.; Jacobs, P.A.; Rowlands, A.S.; Petrie-Repar, P.; Sauret, E. Preliminary design and performance estimation of radial inflow turbines: An automated approach. J. Fluids Eng. 2012, 134, 031102. [Google Scholar] [CrossRef]
- Al Jubori, A.; Al-Dadah, R.K.; Mahmoud, S.; Bahr Ennil, A.S.; Rahbar, K. Three dimensional optimization of small-scale axial turbine for low temperature heat source driven organic Rankine cycle. Energy Convers. Manag. 2017, 133, 411–426. [Google Scholar] [CrossRef]
- Watanabe, I.; Ariga, I.; Mashimo, T. Effect of dimensional parameters of impellers on performance characteristics of a radial-inflow turbine. J. Eng. Power 1971, 93, 81–102. [Google Scholar] [CrossRef]
- Paltrinieri, A. A Mean-Line Model to Predict the Design Performance of Radial Inflow Turbines in Organic Rankine Cycles. Master’s Thesis, Università Degli Studi Di Padova, Technische Universität Berlin, Berlin, Germany, 2014. [Google Scholar]
- Baloni, B.D.; Channiwala, S.A.; Mayavanshi, V.K. Pressure recovery and loss coefficient variations in the two different centrifugal blower volute designs. Appl. Energy 2012, 90, 335–343. [Google Scholar] [CrossRef]
- Suhrmann, J.F.; Peitsch, D.; Gugau, M.; Heuer, T.; Tomm, U. Validation and development of loss models for small size radial turbines. Turbo Expo Power Land Sea Air 2010, 44021, 1937–1949. [Google Scholar]
- Churchill, S.W. Friction factor equation spans all fluid flow regimes. Chem. Eng. J. 1977, 84, 91–92. [Google Scholar]
- Wasserbauer, C.A.; Glassman, A.J. FORTRAN Program for Predicting the Off-Design Performance of Radial Inflow Turbines; NASA Technical Note TN D-8063; NASA: Cleveland, OH, USA, 1975. [Google Scholar]
- Rudinger, G. Chamber dimension effects on induced flow and frictional resistance of enclosed rotating disks. J. Basic Eng. 1960, 82, 230. [Google Scholar] [CrossRef]
- Erbas, M.; Sofuoglu, M.A.; Biyikoglu, A.; Uslan, I. Design and optimization of a low temperature organic rankine cycle and turbine. In ASME 2013 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2013; pp. 1–7. [Google Scholar]
- Glassman, A.J. Computer Program for Design Analysis of Radial-Inflow Turbines; Technical Report; NASA: Washington, DC, USA, 1976. [Google Scholar]
- Abas, N.; Kalair, A.R.; Khan, N.; Haider, A.; Saleem, Z.; Saleem, M.S. Natural and synthetic refrigerants, global warming: A review. Renew. Sustain. Energy Rev. 2018, 90, 557–569. [Google Scholar] [CrossRef]
- Long, R.; Bao, Y.J.; Huang, X.M.; Liu, W. Exergy analysis and working fluid selection of organic Rankine cycle for low grade waste heat recovery. Energy 2014, 73, 475–483. [Google Scholar] [CrossRef]
- Lim, T.-W.; Choi, Y.-S.; Hwang, D.-H. Optimal working fluids and economic estimation for both double stage organic Rankine cycle and added double stage organic Rankine cycle used for waste heat recovery from liquefied natural gas fueled ships. Energy Convers. Manag. 2021, 242, 114323. [Google Scholar] [CrossRef]
- Wei, Z. Meanline Analisis of Radial Inflow Turbines. Master’s Thesis, Carleton University, Ottawa, ON, Canada, 2014. [Google Scholar]
- Sauret, E.; Gu, Y. 3D CFD simulations of a candidate R143A radial-inflow turbine for geothermal power applications. In Proceedings of the ASME Power 2014, 32158; American Society of Mechanical Engineers: Baltimore, MD, USA, 2014. [Google Scholar]
- Al Jubori, A.; Daabo, A.; Al-Dadah, R.K.; Mahmoud, S.; Ennil, A.B. Development of micro-scale axial and radial turbines for low-temperature heat source driven organic Rankine cycle. Energy Convers. Manag. 2016, 130, 141–155. [Google Scholar] [CrossRef]

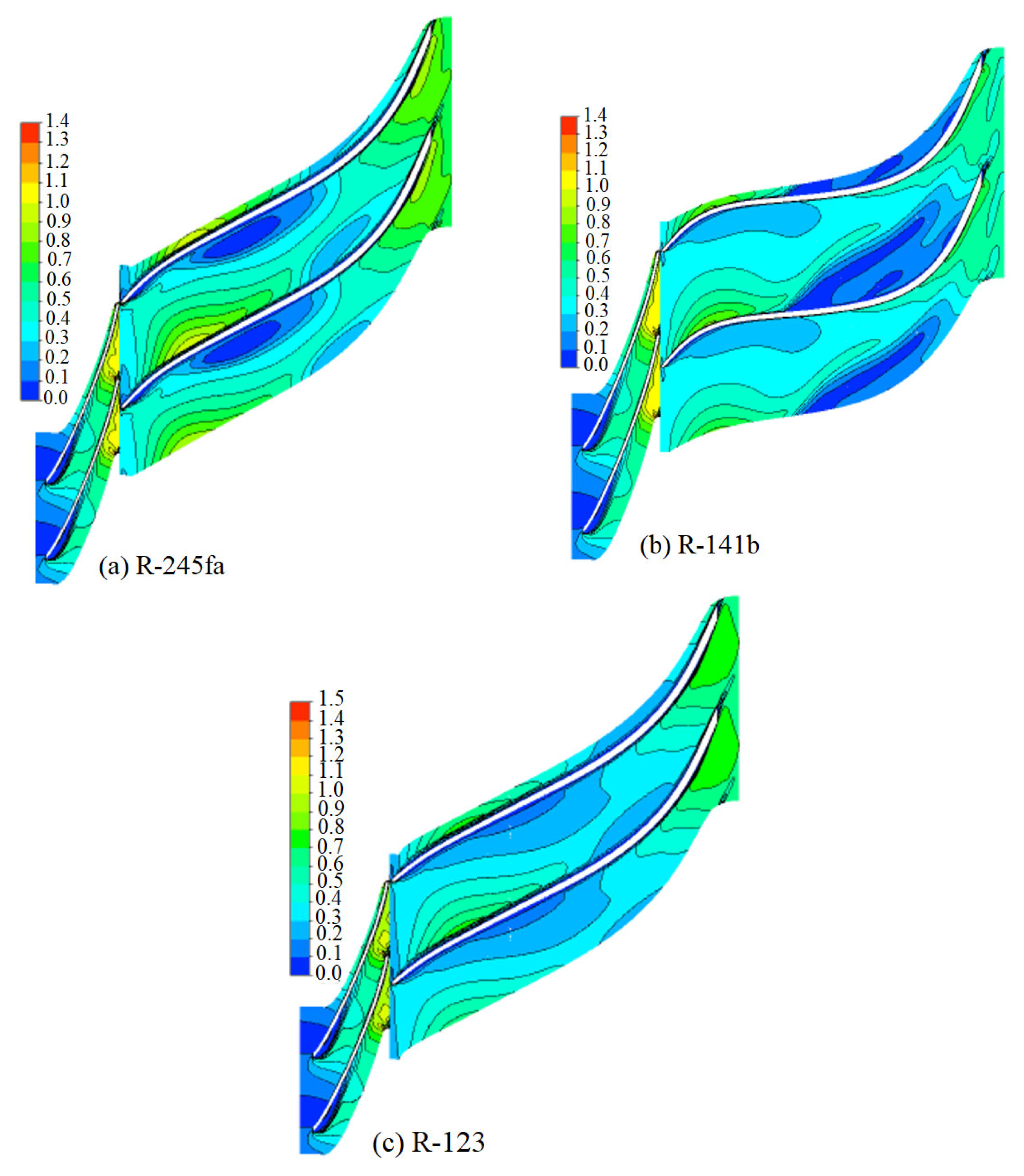
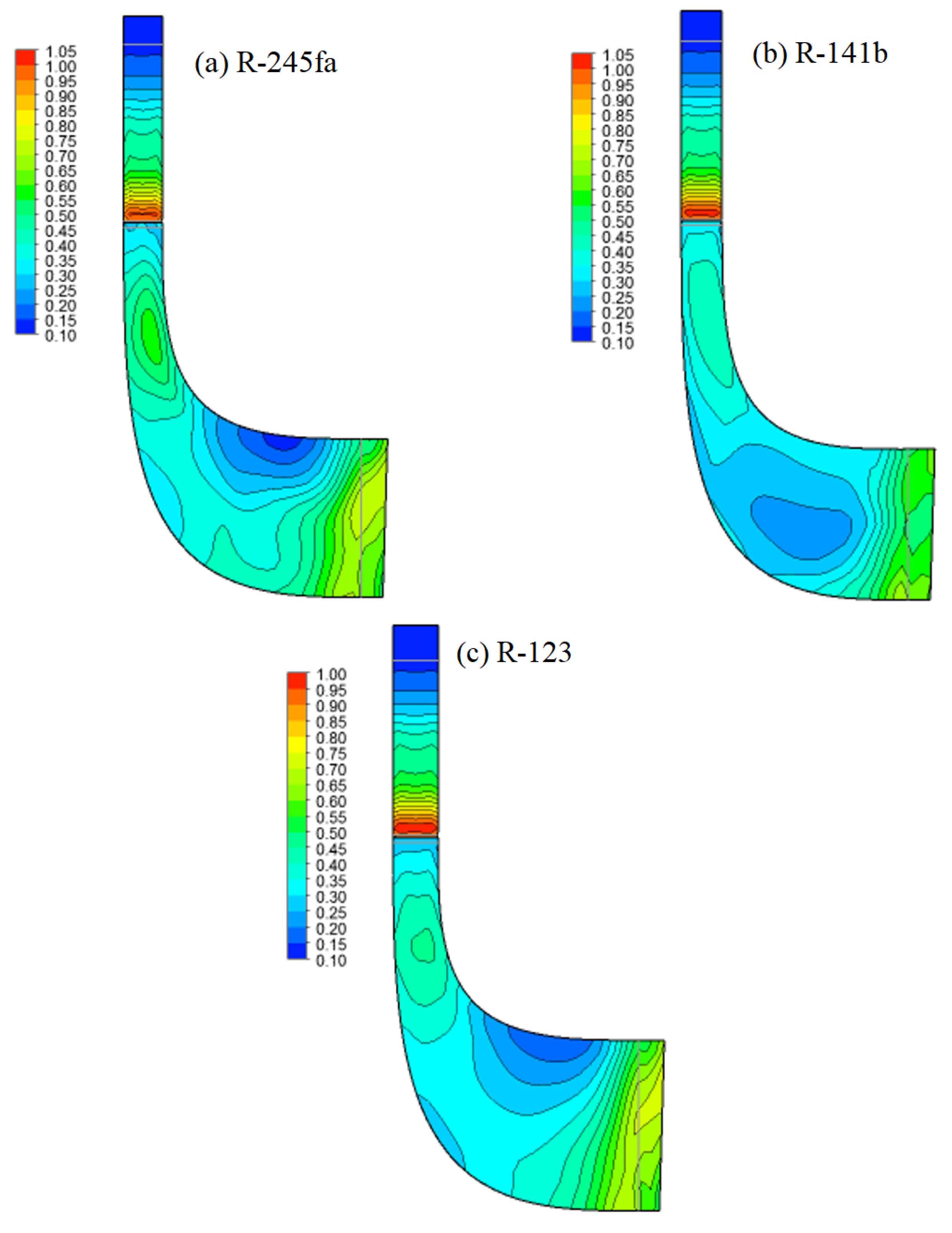


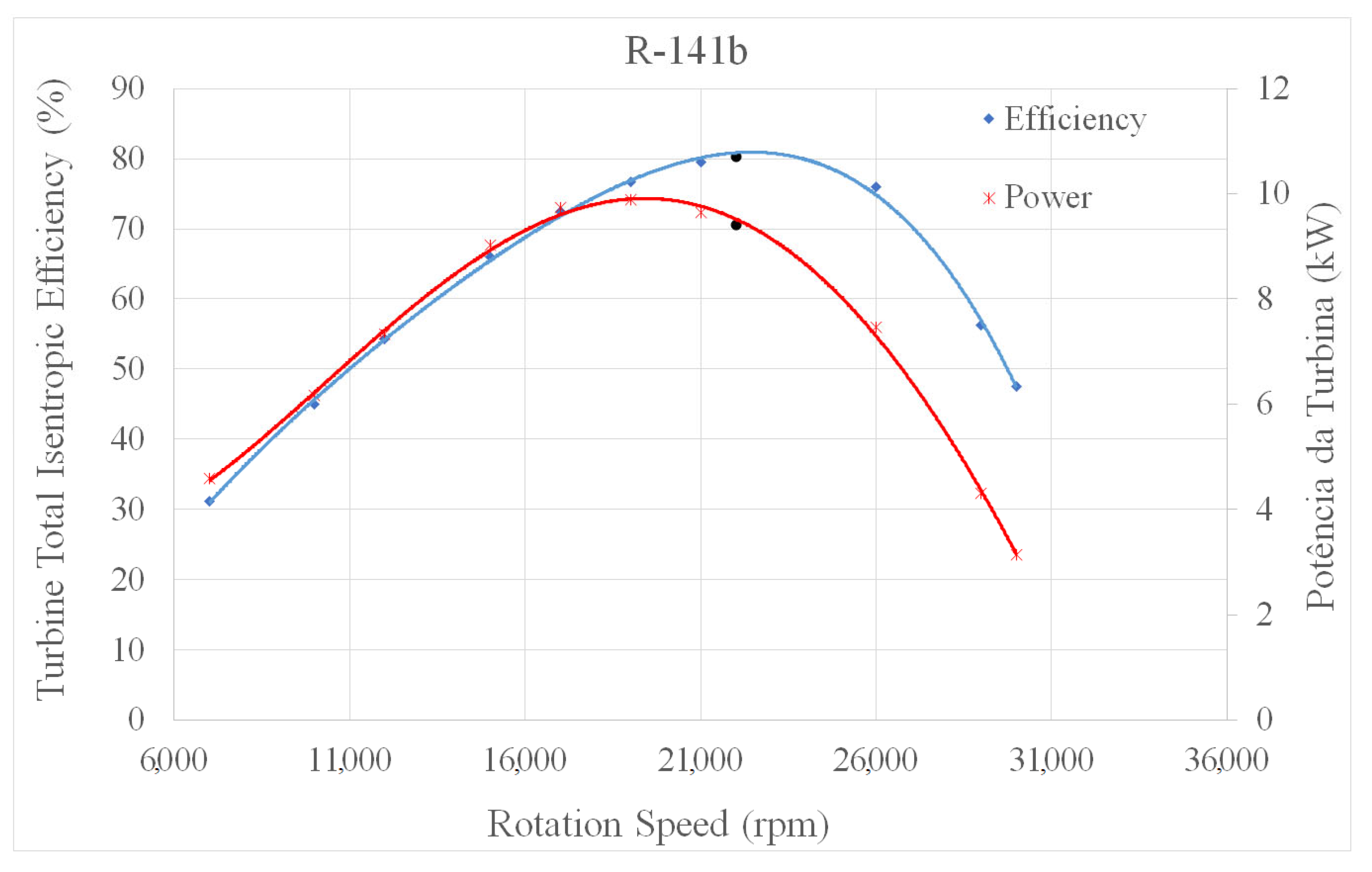
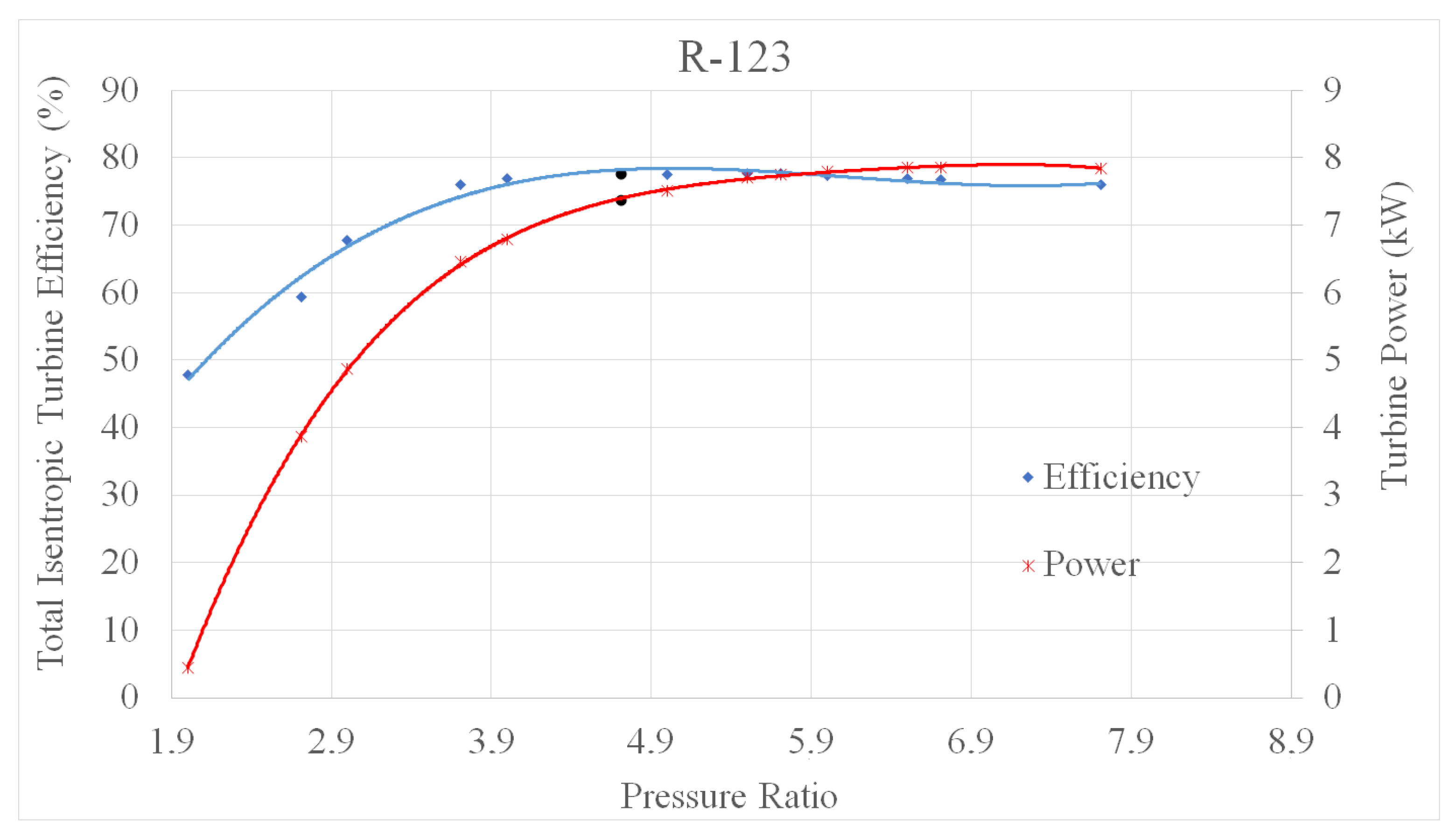
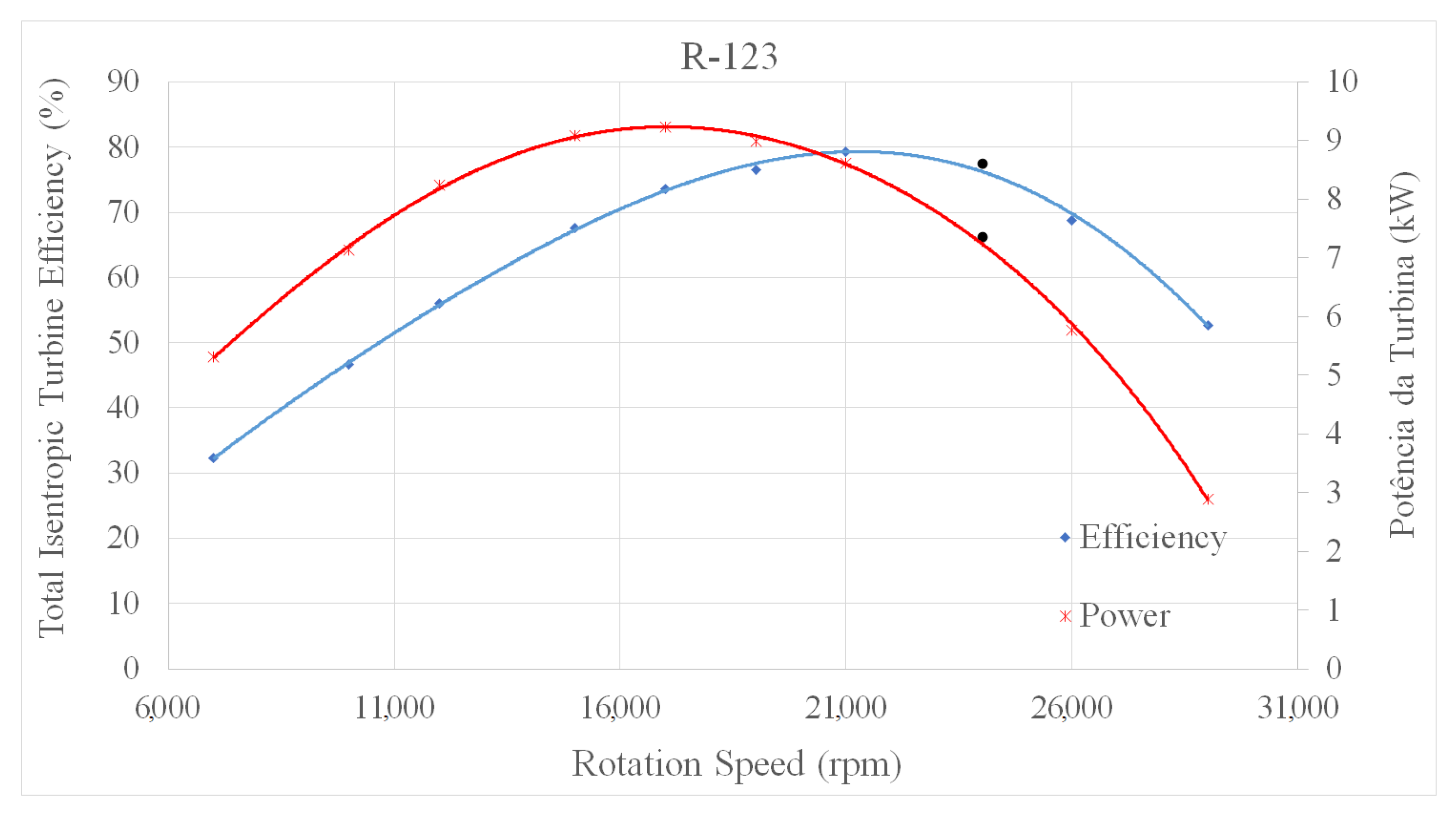
| Radial Turbine Parameters | |
|---|---|
| Fluid | R-245fa |
| Flow coefficient (ϕ) | 0.215 |
| Pressure coefficient (ψ) | 0.918 |
| Inlet total pressure (kPa) | 1000 |
| Condenser working temperature (K) | 303.15 |
| Rotation (rpm) | 9000 |
| Mass flow rate (kg/s) | 10.92 |
| Parameter | Paltrinieri [52] | NEST Model | Difference (%) |
|---|---|---|---|
| Rotor | |||
| Inlet radius, r4 (m) | 0.1796 | 0.1709 | 4.8 |
| Inlet blade height, b4 (m) | 0.0114 | 0.0106 | 7.0 |
| Inlet absolute flow angle, α4 (°) | 76.8186 | 76.8186 | 0 |
| Inlet relative flow angle, β4 (°) | −43.4682 | −42.5484 | 2.1 |
| Inlet static temperature, T4 (K) | 354.62 | 353.7832 | 0.24 |
| Inlet static pressure, p4 (kPa) | 585.37 | 590.7688 | 0.92 |
| Inlet absolute Mach number, Ma4 | 1.0369 | 1.0479 | 1.06 |
| Inlet relative Mach number, Ma4′ | 0.3258 | 0.2788 | 14.4 |
| Outlet hub radius, r6h (m) | 0.0539 | 0.053 | 1.7 |
| Outlet shroud radius, r6s (m) | 0.1169 | 0.1182 | 1.1 |
| Outlet blade height, b6 (m) | 0.063 | 0.0653 | 3.7 |
| Outlet absolute flow angle, α6 (°) | −0.4018 | −0.4018 | 0 |
| Outlet relative flow angle, β6_rms | −64.0532 | −65.0962 | 1.6 |
| Outlet static temperature, T6 (K) | 325.74 | 323.8017 | 0.59 |
| Outlet static pressure, p6 (kPa) | 171.81 | 175.12 | 1.92 |
| Outlet absolute Mach number, Ma6 | 0.2582 | 0.2434 | 5.7 |
| Outlet relative Mach number, Ma6´ | 0.59 | 0.6277 | 4.7 |
| Number of blades, ZR (−) | * | 18 | |
| Nozzle | |||
| Inlet radius, r1 (m) | 0.2335 | 0.2222 | 4.8 |
| Inlet blade height, b1 (m) | 0.0114 | 0.0106 | 7.0 |
| Inlet static temperature, T1 (K) | 369.75 | 369.89 | 0.04 |
| Inlet static pressure, p1 (kPa) | 995.88 | 999.9 | 0.4 |
| Inlet absolute Mach number, Ma1 | 0.095 | 0.1100 | 15.7 |
| Outlet radius, r2 (m) | 0.1811 | 0.1734 | 4.3 |
| Outlet blade height, b2 (m) | 0.0114 | 0.0106 | 4.38 |
| Outlet absolute flow angle, α2 (°) | 76.8186 | 76.8186 | 4.14 |
| Inlet static temperature, T2 (K) | 354.62 | 353.7832 | 0.174 |
| Outlet static pressure, p2 (kPa) | 585.37 | 590.7688 | 0.107 |
| Outlet absolute Mach number, Ma2 | 1.0369 | 1.0479 | 1.06 |
| Number of blades, ZB (−) | 25 | 25 | 0 |
| Total to static efficiency, ηts (%) | 74.1 | 71.85 | 3.0 |
| Net Power, P (kW) | 267 | 260.5 | 2.4 |
| Parameter/Fluid | R-245fa | R-141b | R-123b |
|---|---|---|---|
| Turbine nozzle inlet total temperature (°C) | 79.9 | 94.3 | 96.6 |
| Mass flow rate of the working fluid (kg/s) | 0.61 | 0.45 | 0.62 |
| Flow coefficient (ϕ) | 0.215 | 0.215 | 0.215 |
| Load coefficient (ψ) | 0.918 | 0.918 | 0.918 |
| Pressure ratio | 5.71 | 4.71 | 4.71 |
| Rotation speed, ω (rpm) | 25,800 | 22,000 | 24,000 |
| Parameter | R-245fa | R-141b | R-123 |
|---|---|---|---|
| Rotor | |||
| Inlet radius, r4 (m) | 0.0568 | 0.0592 | 0.0531 |
| Inlet blade height, b4 (m) | 0.0036 | 0.0039 | 0.0041 |
| Inlet absolute flow angle, α4 (°) | 76.8186 | 76.8186 | 76.8186 |
| Inlet relative flow angle, β4 (°) | −45.718 | −46.0327 | −40.3337 |
| Inlet static temperature, T4 (°C) | 66.5 | 80.3 | 81.5 |
| Inlet static pressure, p4 (kPa) | 394.8306 | 325.7557 | 371.049 |
| Inlet absolute Mach number, Ma4 | 0.9591 | 0.8798 | 0.9586 |
| Inlet relative Mach number, Ma4′ | 0.2618 | 0.2392 | 0.2541 |
| Outlet hub radius, r6h (m) | 0.0222 | 0.0231 | 0.0207 |
| Outlet shroud radius, r6s (m) | 0.037 | 0.0376 | 0.0357 |
| Outlet blade height, b6 (m) | 0.0148 | 0.0145 | 0.015 |
| Outlet absolute flow angle, α6 (°) | 0 | 0 | 0 |
| Outlet relative flow angle, β6_rms (°) | −66.8922 | −66.6462 | −67.2171 |
| Outlet relative flow angle, β6_h (°) | −61.1328 | −61.1328 | −61.1328 |
| Outlet relative flow angle, β6_t (°) | −71.7233 | −71.3152 | −72.2554 |
| Outlet static temperature, T6 (°C) | 37.5 | 47.4 | 53.5 |
| Outlet static pressure, p6 (kPa) | 116.4663 | 107.3252 | 131.6736 |
| Outlet absolute Mach number, Ma6 | 0.2357 | 0.2219 | 0.2299 |
| Outlet relative Mach number, Ma6′ | 0.5967 | 0.5617 | 0.5819 |
| Number of blades, ZR (−) | 18 | 18 | 18 |
| Nozzle | |||
| Inlet radius, r1 (m) | 0.0739 | 0.0769 | 0.0691 |
| Inlet blade height, b1 (m) | 0.0036 | 0.0039 | 0.0041 |
| Inlet static temperature, T1 (°C) | 79.9 | 94.4 | 96.7 |
| Inlet static pressure, p1 (kPa) | 659.1412 | 505.5017 | 620.1825 |
| Inlet absolute Mach number, Ma1 | 0.1955 | 0.1796 | 0.1891 |
| Inlet absolute flow angle, α1 (°) | 49.1958 | 49.3194 | 49.4424 |
| Outlet radius, r2 (m) | 0.0575 | 0.0599 | 0.0539 |
| Outlet blade height, b2 (m) | 0.0026 | 0.0039 | 0.0041 |
| Outlet absolute flow angle, α2 (°) | 76.8186 | 76.8186 | 76.8186 |
| Outlet static temperature, T2 (°C) | 66.5 | 80.3 | 81.5 |
| Outlet static pressure, p2 (kPa) | 394.8306 | 325.7557 | 371.049 |
| Outlet absolute Mach number, Ma2 | 0.9591 | 0.8798 | 0.9586 |
| Blade thickness (mm) | 0.59171 | 0.58982 | 0.57152 |
| Number of blades, ZB (−) | 25 | 25 | 25 |
| Working Fluid | Number of Elements | (%) | (kW) | ||
|---|---|---|---|---|---|
| R-245fa | 413,845 | 76.12 | 8.76 | - | - |
| 629,391 | 76.73 | 8.71 | 0.8 | 0.57 | |
| R-141b | 510,330 | 80.30 | 9.41 | - | - |
| 782,506 | 80.47 | 9.37 | 0.21 | 0.42 | |
| R-123 | 418,276 | 77.60 | 7.37 | - | - |
| 627,414 | 78.20 | 7.40 | 0.77 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrillo Caballero, G.; Cardenas Escorcia, Y.; Venturini, O.J.; Silva Lora, E.E.; Alviz Meza, A.; Mendoza Castellanos, L.S. Unidimensional and 3D Analyses of a Radial Inflow Turbine for an Organic Rankine Cycle under Design and Off-Design Conditions. Energies 2023, 16, 3383. https://doi.org/10.3390/en16083383
Carrillo Caballero G, Cardenas Escorcia Y, Venturini OJ, Silva Lora EE, Alviz Meza A, Mendoza Castellanos LS. Unidimensional and 3D Analyses of a Radial Inflow Turbine for an Organic Rankine Cycle under Design and Off-Design Conditions. Energies. 2023; 16(8):3383. https://doi.org/10.3390/en16083383
Chicago/Turabian StyleCarrillo Caballero, Gaylord, Yulineth Cardenas Escorcia, Osvaldo José Venturini, Electo Eduardo Silva Lora, Anibal Alviz Meza, and Luis Sebastián Mendoza Castellanos. 2023. "Unidimensional and 3D Analyses of a Radial Inflow Turbine for an Organic Rankine Cycle under Design and Off-Design Conditions" Energies 16, no. 8: 3383. https://doi.org/10.3390/en16083383
APA StyleCarrillo Caballero, G., Cardenas Escorcia, Y., Venturini, O. J., Silva Lora, E. E., Alviz Meza, A., & Mendoza Castellanos, L. S. (2023). Unidimensional and 3D Analyses of a Radial Inflow Turbine for an Organic Rankine Cycle under Design and Off-Design Conditions. Energies, 16(8), 3383. https://doi.org/10.3390/en16083383







