Comprehensive Thermodynamic Analysis of He–Xe in Microchannels with Different Structures
Abstract
1. Introduction
2. Numerical Model
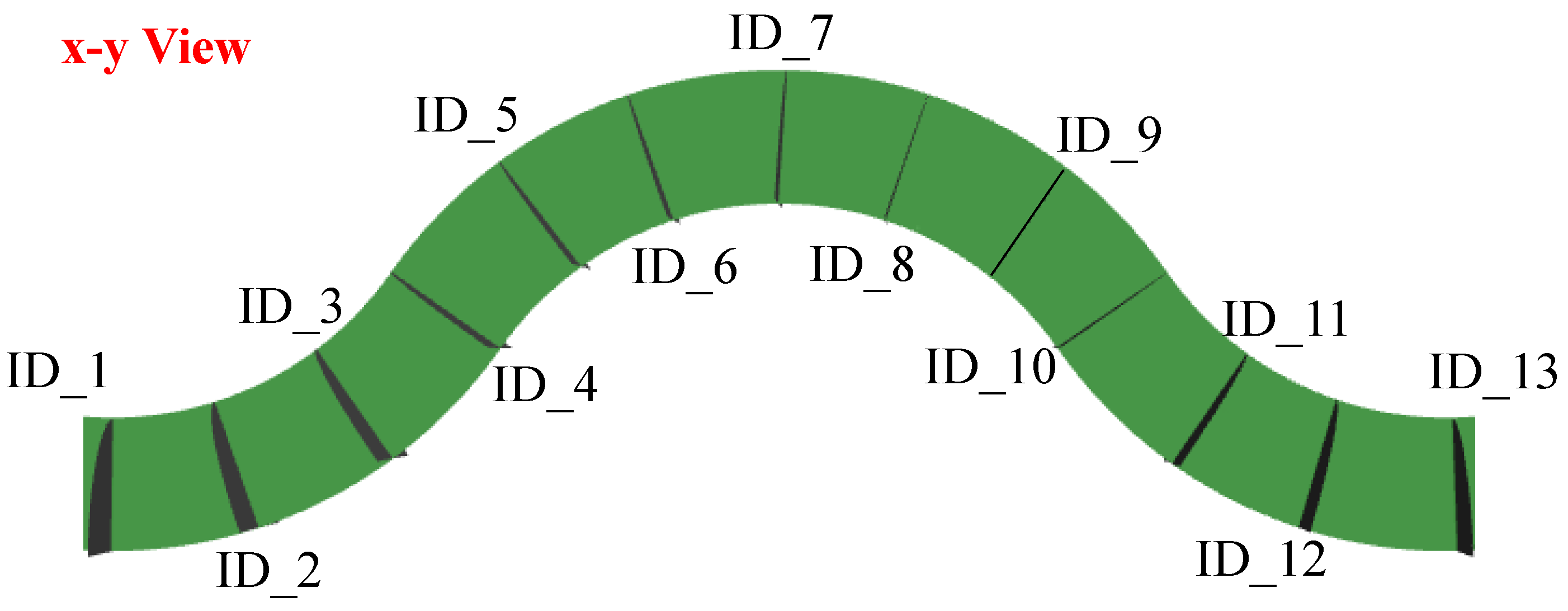
2.1. Geometry and Boundary Conditions
2.2. Grid Independence and Experimental Verification
3. Results and Discussion
3.1. Analysis of Factors Determining He–Xe Heat Transfer in Channel
3.1.1. Theoretical Analysis
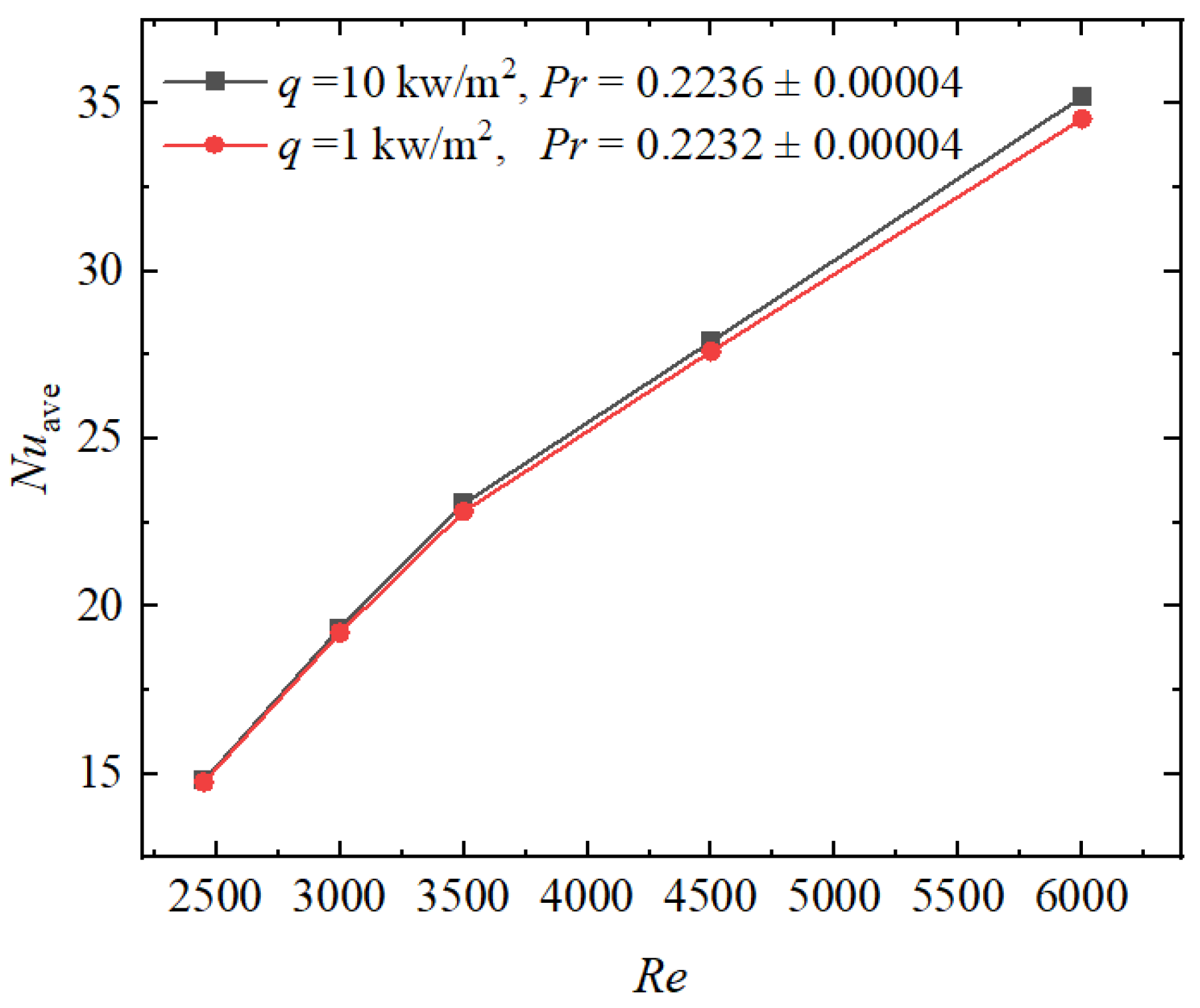
3.1.2. Numerical Verification
3.2. Configuration Comparison
3.2.1. Influence of the He–Xe Property
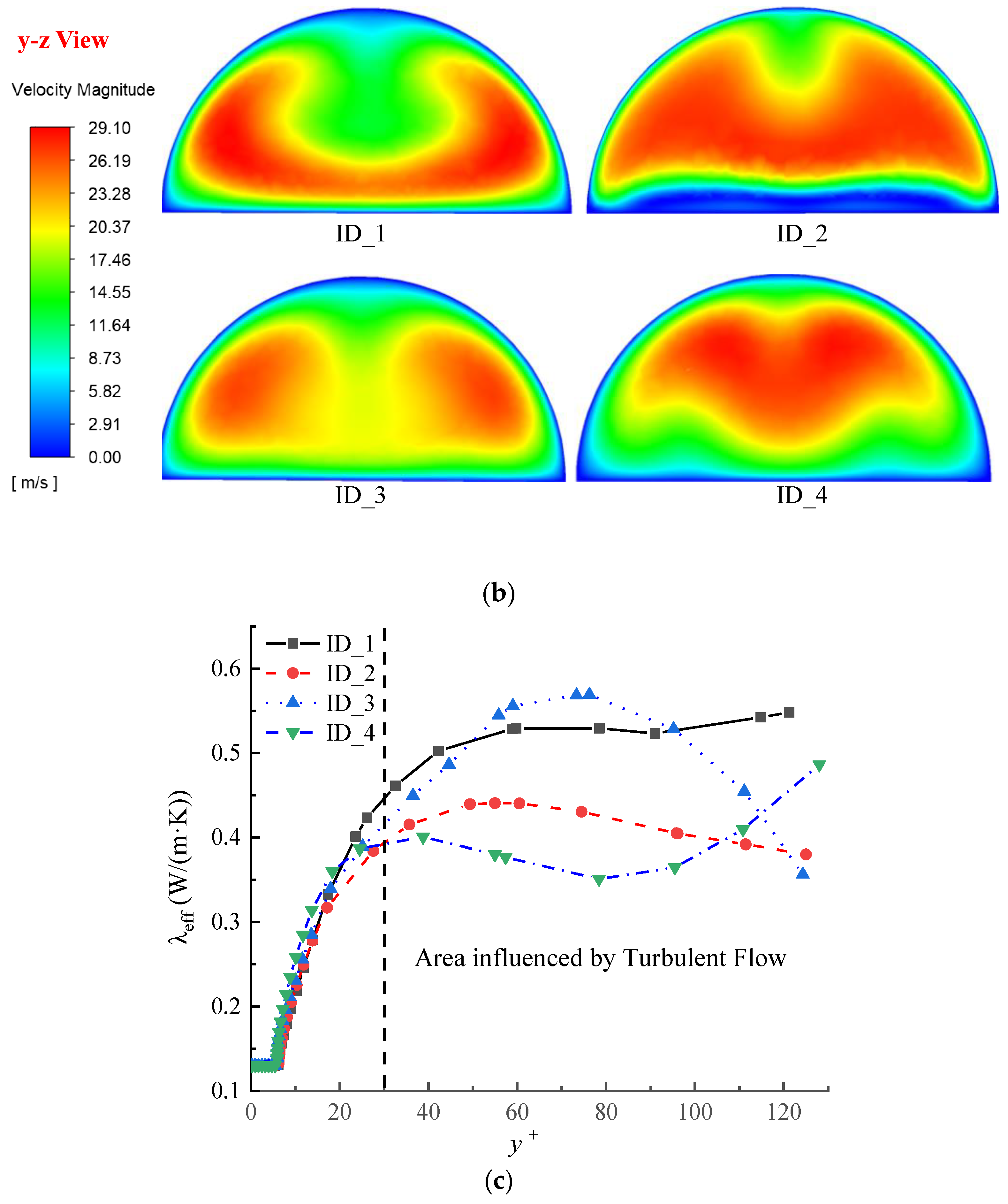
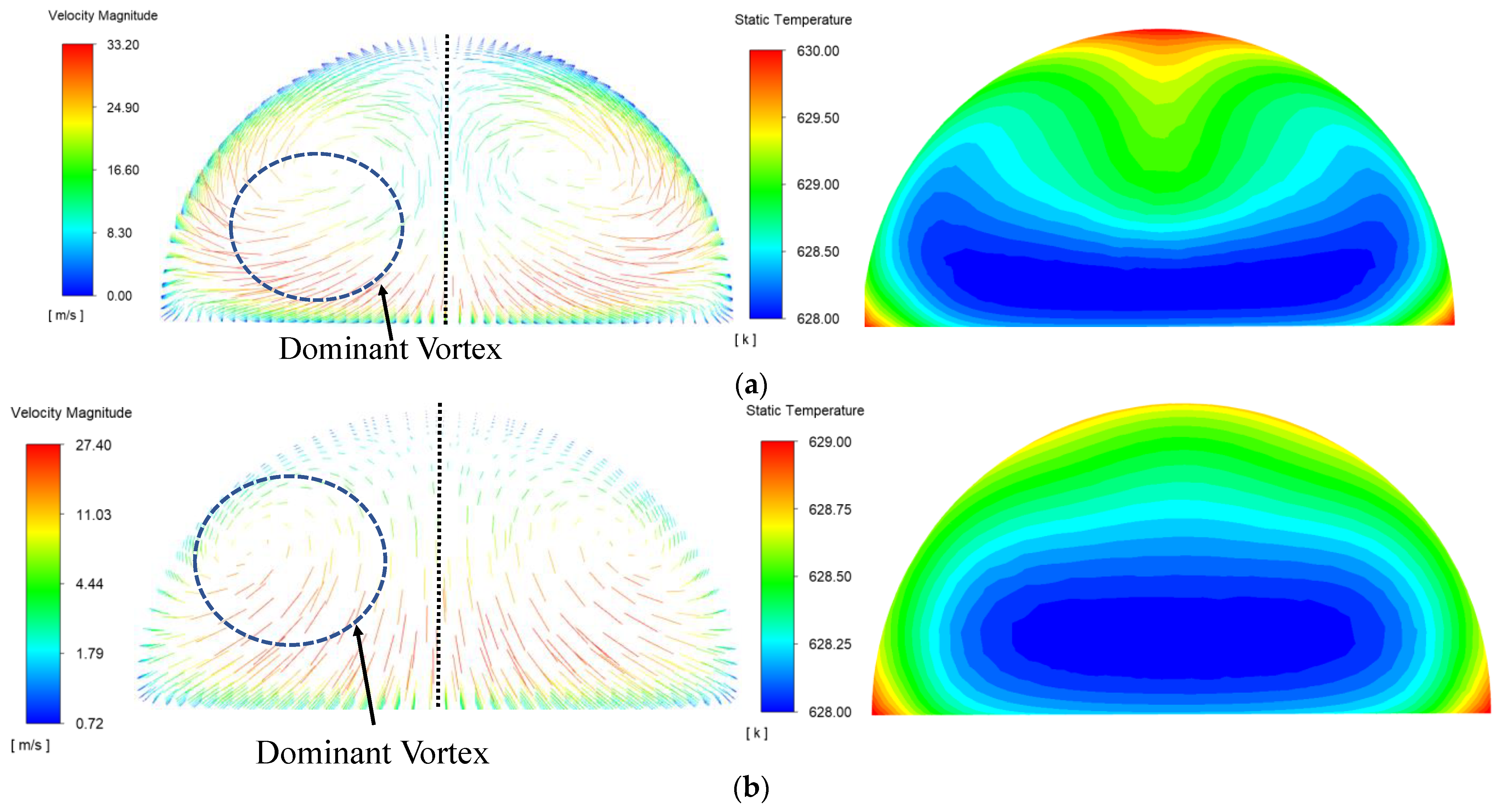
3.2.2. Flow Heat Transfer Analysis in Different Configurations
- (1)
- Comparison of flow heat transfer in passage section
- (2)
- Comparison of flow pattern along the passage
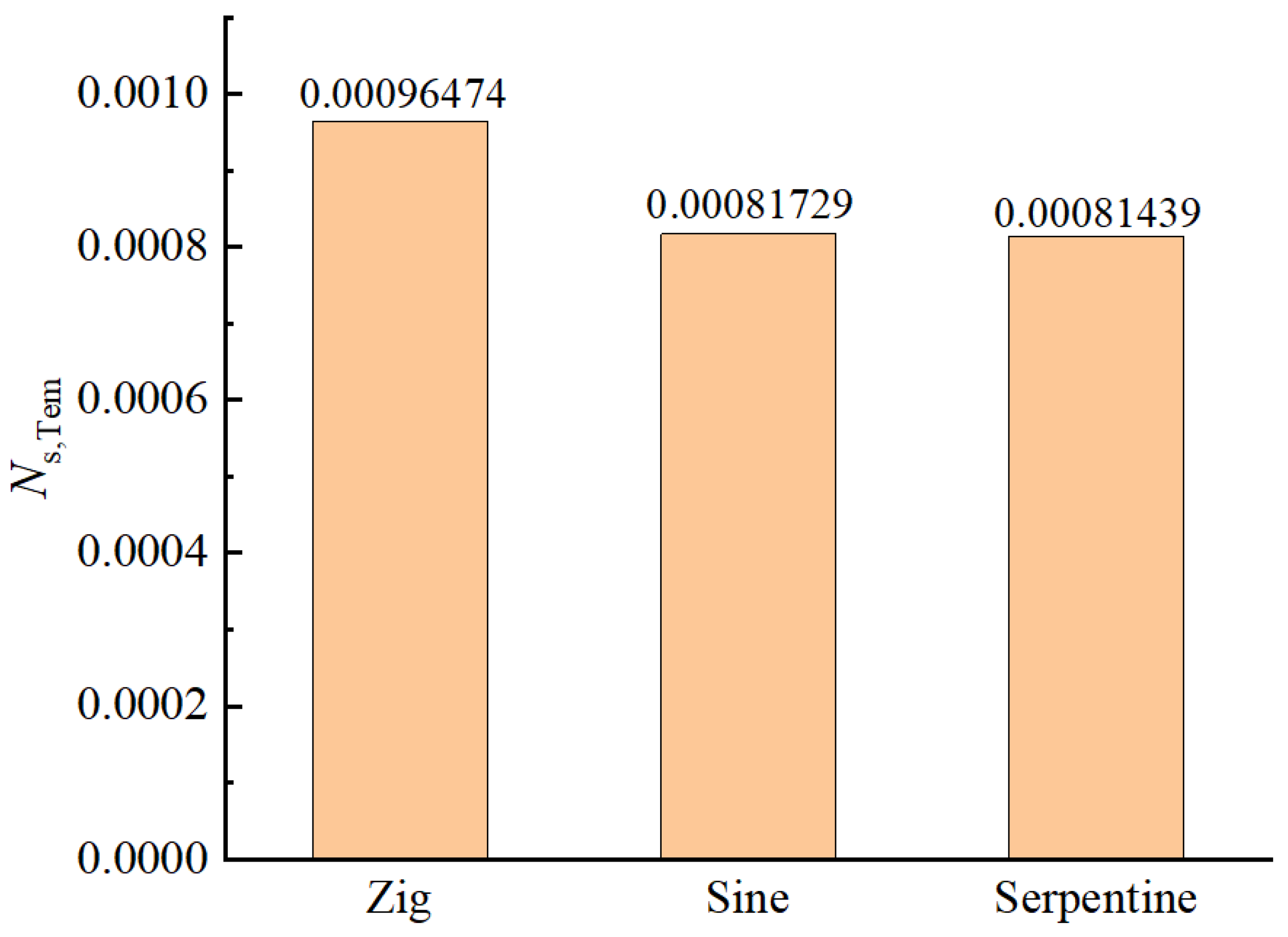
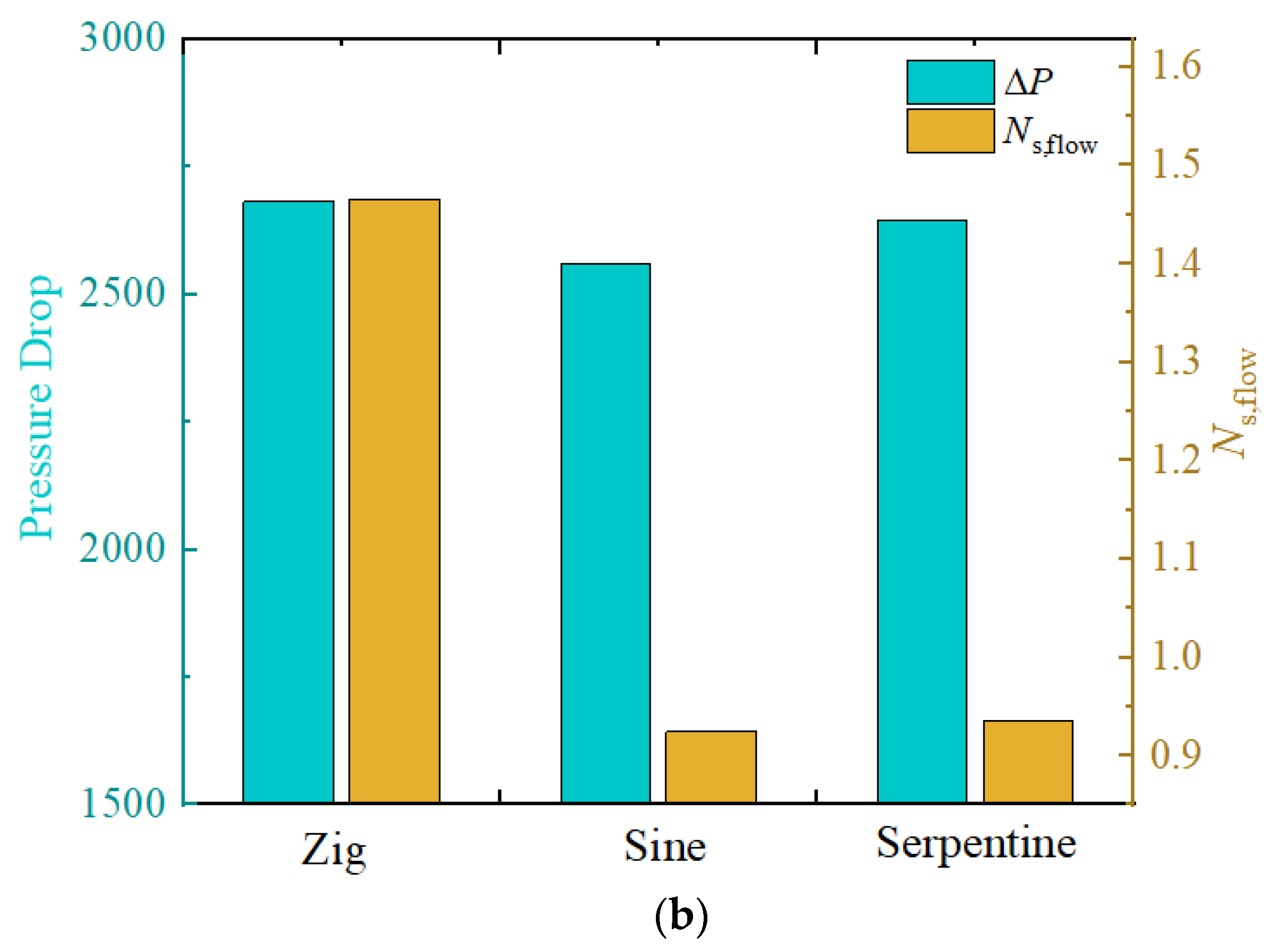
3.2.3. Configuration Selection
3.3. Influence of Shape Factor on Thermodynamic Performance in Serpentine Channel
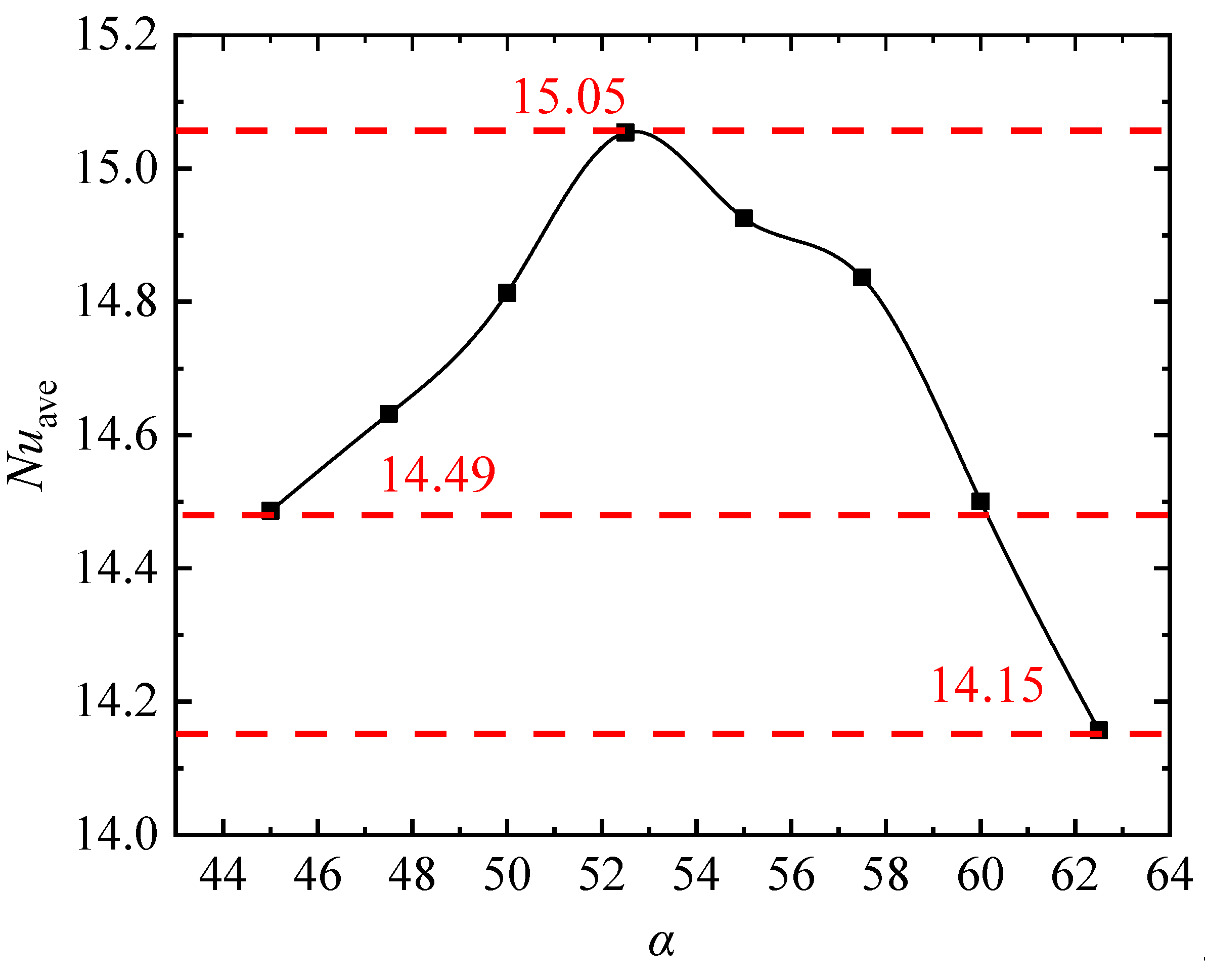
3.3.1. Influence of A on the First Law of Thermodynamics
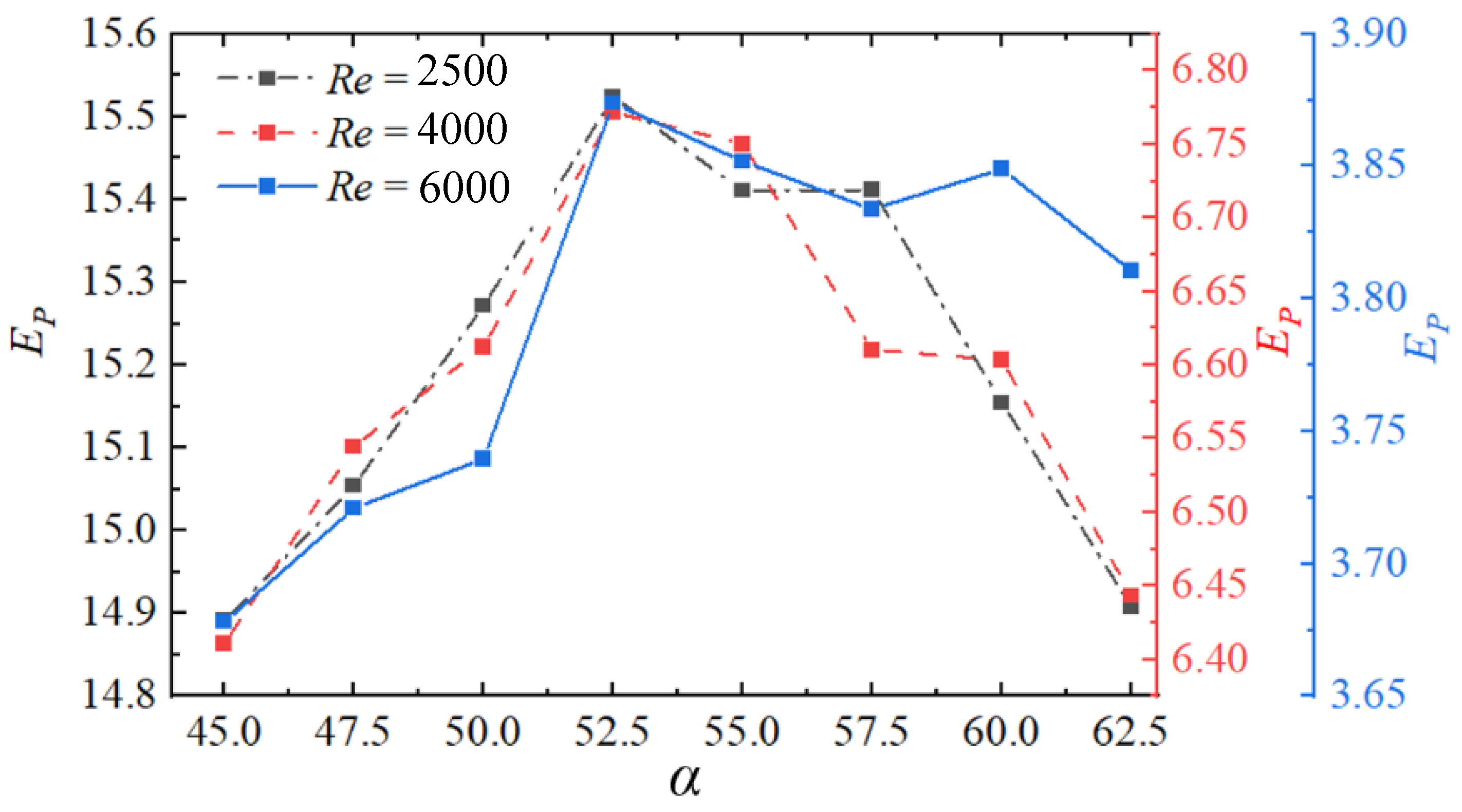
3.3.2. Influence of A on the Second Law of Thermodynamics
4. Conclusions
- (1)
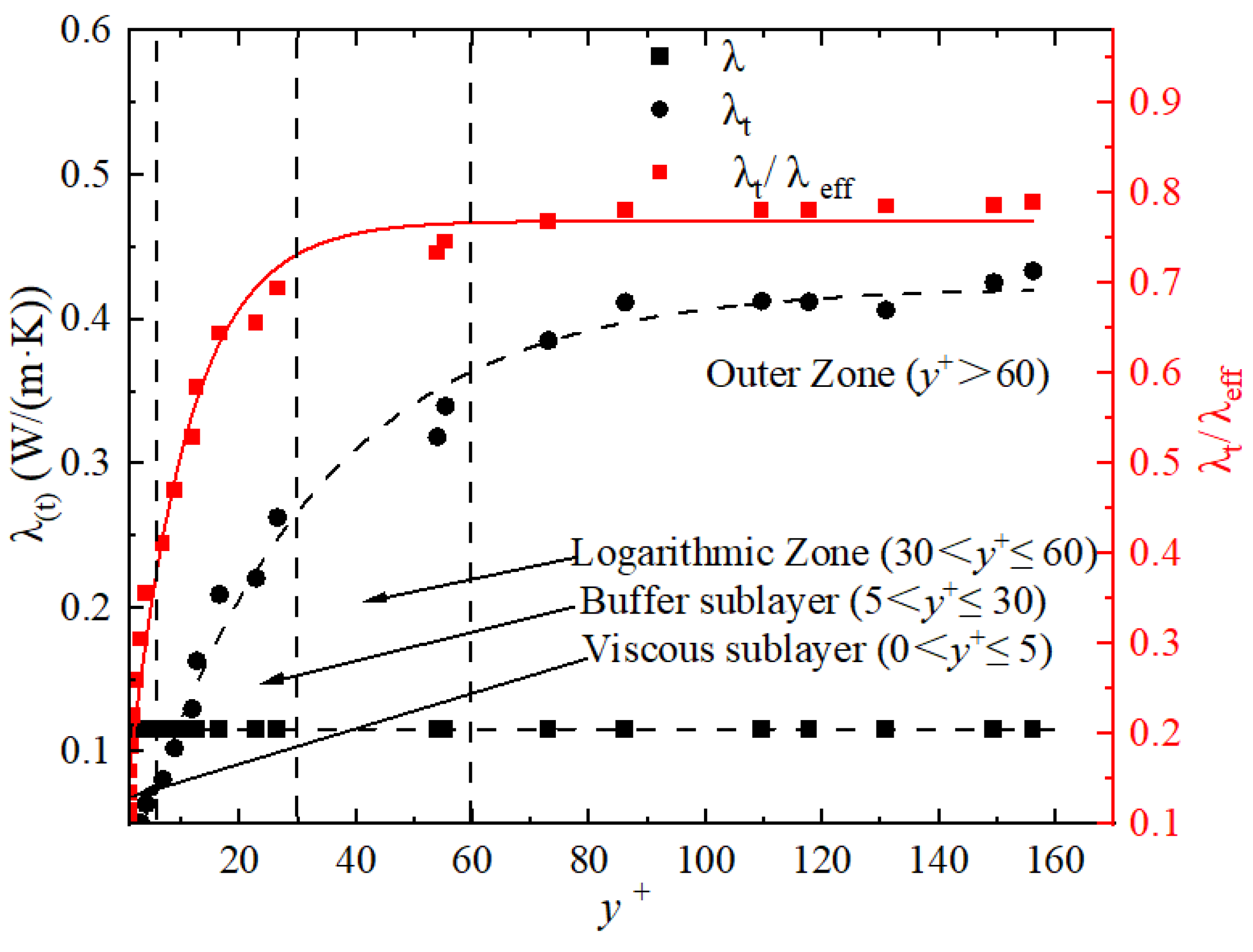
- It is found by analyzing the effective thermal diffusivity distribution of He–Xe that the temperature distribution of He–Xe at the bottom of the flow domain (y+ < 30) under different flow conditions is the same. The effective thermal diffusivity distribution of He–Xe is determined by the flow pattern in and logarithmic zone and beyond (y+ > 30). Additionally, it is found that the influence of Pr on Nu is stronger than that of Re under different heat fluxes. This indicates that increasing the working temperature of He–Xe fluid is an effective way to enhance heat transfer capacity under the same Re number and channel characteristics.
- (2)
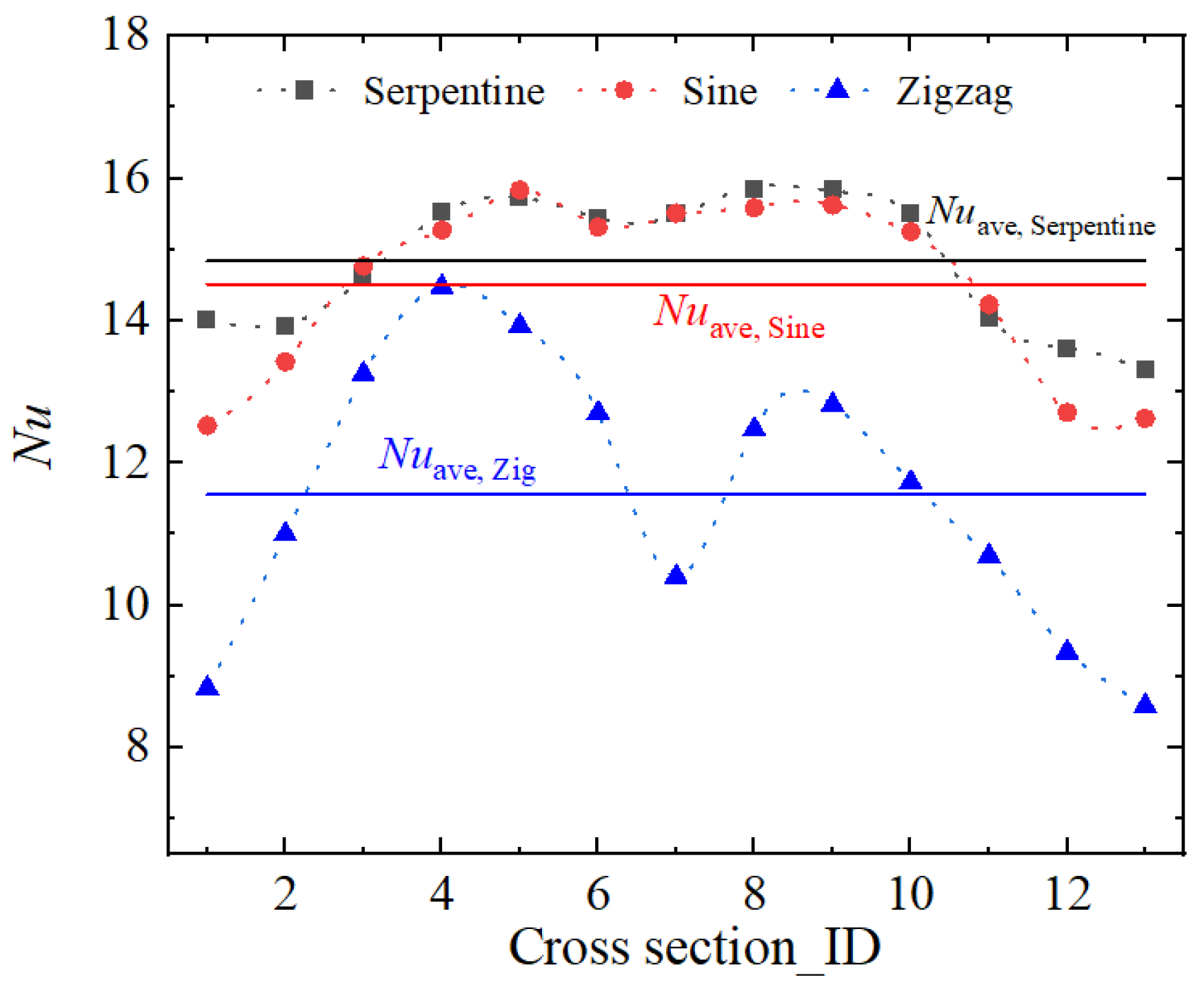
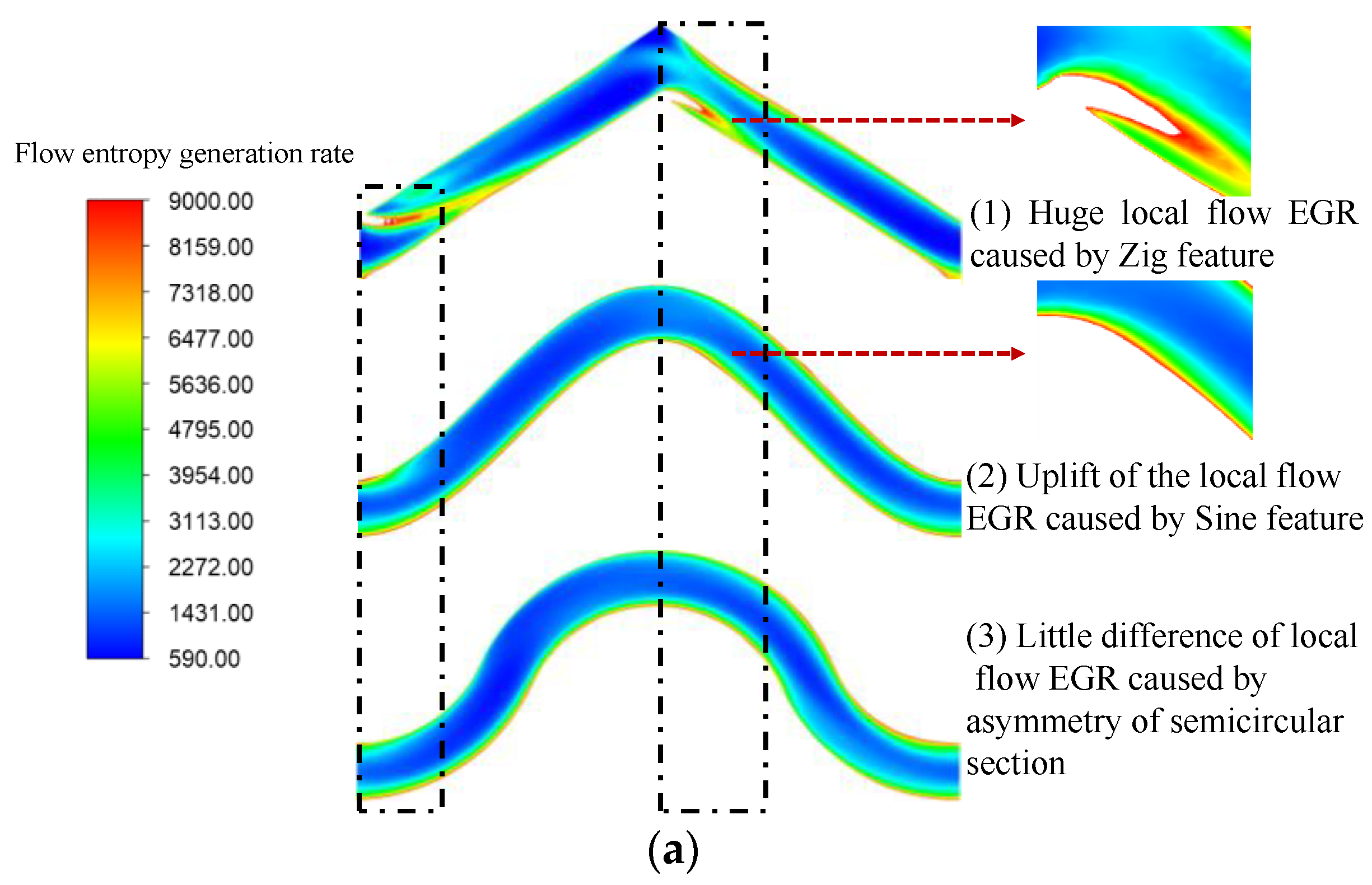
- By analyzing the flow characteristics of helium–xenon inside the Zig tube, it is found that the dead flow zone and low-velocity zone inside the Zig channel will significantly affect the energy loss where local flow entropy generation reached 1.05 × 106. The maximum flow entropy generation of Sine and Serpentine pipelines with a smooth transition is only around 9000. The average Nu of one period of the Zig channel is 11.5, while that of the Sine and Serpentine channels is 14.5 and 14.84, respectively. In general, the helium–xenon flow field in the Sine channel and Serpentine channel are better than that in the Zig channel from both the first law of thermodynamics and the second law of thermodynamics.
- (3)
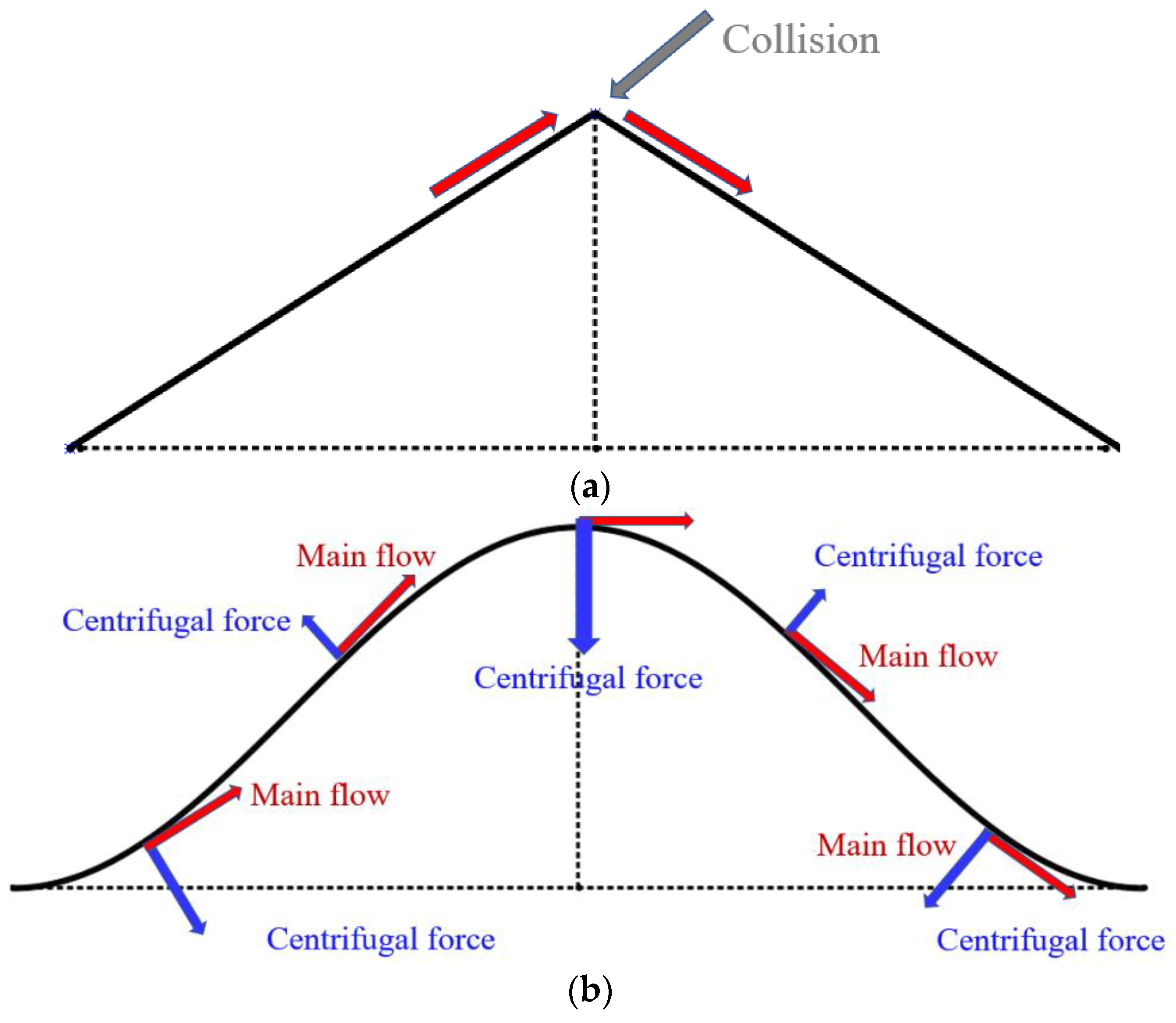
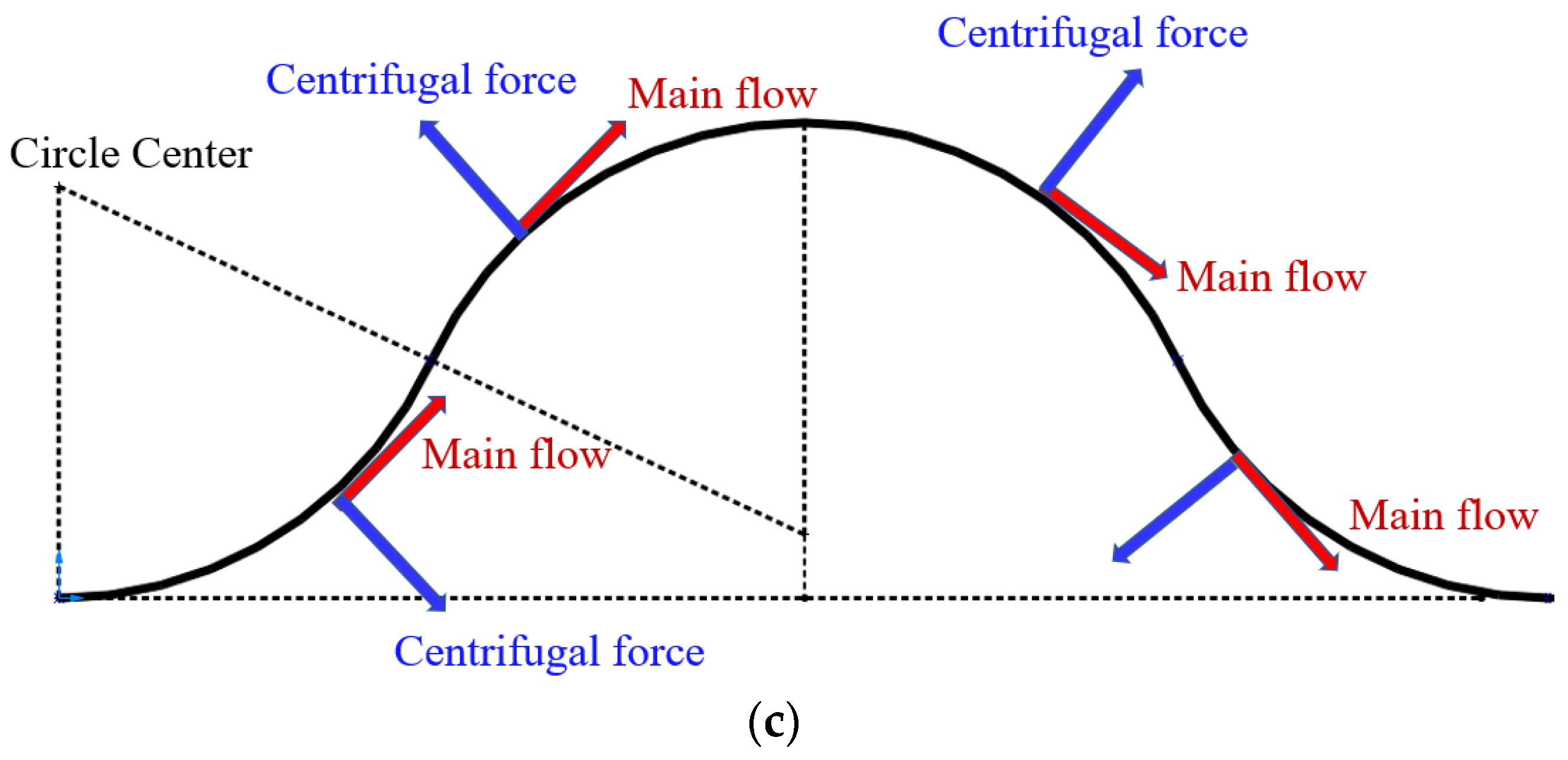
- The centrifugal force on the He–Xe flow in the Sine channel is a function of the X-axis location, while the centrifugal force on the He–Xe flow in the Serpentine channel keeps constant. Therefore, the heat transfer capacity of the He–Xe flow in the Serpentine channel is slightly stronger than that in the Sine channel under the continuous influence of centrifugal force. Meanwhile, the irreversibility of the He–Xe flow in the Serpentine channel is also slightly higher than that in the Sine channel. In this paper, Nu/Ns is adopted as an index to evaluate the thermal economic performance of the He–Xe flow in the Serpentine channel. It is found that the He–Xe flow in the Serpentine channel is featured with a better thermal economic performance.
- (4)
- The Serpentine channel with a shape factor of is characterized by the best thermodynamic performance considering the first and second laws of thermodynamics. The PCHE with the Serpentine channel as the unit channel may have a better industrial performance with high heat flux and low velocity, considering the increase of the heat transfer cost with the increase of Re.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Shape factor | V | Volume (m3) |
| a | Thermal diffusivity (m2/s) | U | Velocity vector (m/s) |
| c | Length of half a period (mm) | u | The component of velocity in the x direction (m/s) |
| cp | Specific heat capacity [kJ/(kg·K)] | v | The component of velocity in the y direction (m/s) |
| Hydraulic diameter (mm) | w | The component of velocity in the z direction (m/s) | |
| Thermal economic performance | y+ | Dimensionless distance to the wall | |
| H | The height of one single period (m) | x | Cartesian coordinates x-axis (m) |
| Convective heat transfer coefficient [W/(m2·K)] | y | Cartesian coordinates y-axis (m) | |
| Average convective heat transfer coefficient of one single period [W/(m2·K)] | z | Cartesian coordinates z-axis (m) | |
| Local convective heat transfer coefficient [W/(m2·K)] | Greek symbols | ||
| Influence factor of Pr | α | Angle of the arc (°) | |
| Influence factor of Re | β | Angle of the arc (°) | |
| Influence factor of A | Friction coefficient | ||
| k | Turbulent kinetic energy (m2/s2) | Thermal conductivity [W/(m·K)] | |
| K | Radius of curvature (m) | Turbulent thermal diffusivity [W/(m·K)] | |
| Hesselgreaves number | Effective thermal diffusivity | ||
| Hesselgreaves number caused by heat transfer | Density (kg/m3) | ||
| Hesselgreaves number caused by the flow | Viscosity (Pa·s) | ||
| Nu | Nusselt number | Turbulent viscosity (Pa·s) | |
| Average Nusselt number of one single period | Turbulent dissipation rate | ||
| Local Nusselt number | ν | Kinematic viscosity | |
| P | Pressure (Pa) | Thickness of the Viscous layer | |
| Pr | Prandtl number | Thickness of the Buffer layer | |
| Prt | Turbulent Prandtl number | Thickness of the Logarithmic layer | |
| Heat transfer rate (W) | Subscript | ||
| q | Heat flux (W/m2) | Bulk | |
| r | The radius of arc (m) | Wall | |
| Re | Reynolds number | Local | |
| Rein | Reynolds number of velocity inlet | Viscous layer | |
| Source Term | Buffer layer | ||
| Volumetric entropy generation rate [W/(m3·K)] | Logarithmic layer | ||
| Temperature (K) | Turbulent | ||
| Temperature of heat wall (K) | Effective | ||
| Temperature of flow bulk (K) | Inlet pattern | ||
References
- El-Genk, M.S.; Schriener, T.M. Long operation life reactor for lunar surface power. Nucl. Eng. Des. 2011, 241, 2339–2352. [Google Scholar] [CrossRef]
- National Research Council. NASA Space Technology Roadmaps and Priorities: Restoring NASA’s Technological Edge and Paving the Way for a New Era in Space; National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
- NASA. Technology Roadmaps TA3: Space Power and Energy Storage; NASA: Washington, DC, USA, 2015.
- Liu, H.; Chi, Z.; Zang, S. Optimization of a closed Brayton cycle for space power systems. Appl. Therm. Eng. 2020, 179, 115611. [Google Scholar] [CrossRef]
- Romano, L.F.R.; Ribeiro, G.B. Optimization of a heat pipe-radiator assembly coupled to a recuperated closed Brayton cycle for compact space power plants. Appl. Therm. Eng. 2021, 196, 117355. [Google Scholar] [CrossRef]
- Wu, P.; Ma, Y.; Gao, C.; Liu, W.; Shan, J.; Huang, Y.; Wang, J.; Zhang, D.; Ran, X. A review of research and development of supercritical carbon dioxide Brayton cycle technology in nuclear engineering applications. Nucl. Eng. Des. 2020, 368, 110767. [Google Scholar] [CrossRef]
- MacDonald, P.E.; Baxter, A.M.; Bayless, P.D.; Bolin, J.M.; Gougar, H.D.; Moore, R.L.; Ougouag, A.M.; Richards, M.B.; Sant, R.L.; Sterbentz, J.W.; et al. The Next Generation Nuclear Plant-Insights Gained from the INEEL Point Design Studies; Idaho National Lab (INL): Idaho Falls, ID, USA, 2004.
- El-Genk, M.S.; Tournier, J.M. On the use of noble gases and binary mixtures as reactor coolants and CBC working fluids. Energy Convers. Manag. 2008, 49, 1882–1891. [Google Scholar] [CrossRef]
- Schleicher, R.; Raffray, A.R.; Wong, C.P. An assessment of the Brayton cycle for high performance power plants. Fusion Sci. Technol. 2001, 39 Pt 2, 823–827. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Tournier, J.M. Noble gas binary mixtures for gas-cooled reactor power plants. Nucl. Eng. Des. 2008, 238, 1353–1372. [Google Scholar] [CrossRef]
- Tournier, J.M.P.; El-Genk, M.S. Properties of noble gases and binary mixtures for closed Brayton Cycle applications. Energy Convers. Manag. 2008, 49, 469–492. [Google Scholar] [CrossRef]
- Xu, C.; Kong, F.; Yu, D.; Yu, J.; Khan, M.S. Influence of non-ideal gas characteristics on working fluid properties and thermal cycle of space nuclear power generation system. Energy 2021, 222, 119881. [Google Scholar] [CrossRef]
- El-Genk, M.; Tournier, J.M. Selection of noble gas binary mixtures for Brayton space nuclear power systems. In Proceedings of the 4th International Energy Conversion Engineering Conference and Exhibit (IECEC), San Diego, CA, USA, 26–29 June 2006; p. 4168. [Google Scholar]
- Wang, Z. Study on Bretton Cycle Characteristics of Helium-Xenon Mixed Working Fluid Based on Space Nuclear Power System; Harbin Institute of Technology: Harbin, China, 2021. [Google Scholar]
- Yang, X.; Shi, L. Thermodynamic Analysis of closed Brayton Cycle in space nuclear reactor Power Supply. J. Tsinghua Univ. Nat. Sci. 2008, 58, 821–826. [Google Scholar]
- Hu, W.; Deng, J.; Liu, X.; Li, Z.; Xue, B. Preliminary study on Key parameters of small helium-xenon cooled reactor. Nucl. Technol. 2021, 44, 85–90. [Google Scholar]
- Lee, Y.; Lee, J.I. Structural assessment of intermediate printed circuit heat exchanger for sodium-cooled fast reactor with supercritical CO2 cycle. Ann. Nucl. Energy 2014, 73, 84–95. [Google Scholar] [CrossRef]
- Kim, I.H. Experimental and Numerical Investigations of Thermal-Hydraulic Characteristics for the Design of a Printed Circuit Heat Exchanger (PCHE) in HTGRs. Ph.D. Thesis, Korea Advanced Institute of Science and Technology, Daejeon, Republic of Korea, 2012. Available online: http://hdl.handle.net/10203/182224 (accessed on 12 March 2023).
- Peng, Y.; Li, Z.; Li, S.; Cao, B.; Wu, X.; Zhao, X. The experimental study of the heat transfer performance of a zigzag-serpentine microchannel heat sink. Int. J. Therm. Sci. 2021, 163, 106831. [Google Scholar] [CrossRef]
- Kim, S.G.; Lee, Y.; Ahn, Y.; Lee, J.I. CFD aided approach to design printed circuit heat exchangers for supercritical CO2 Brayton cycle application. Ann. Nucl. Energy. 2016, 92, 175–185. [Google Scholar] [CrossRef]
- Taylor, M.F.; Bauer, K.E.; McEligot, D.M. Internal forced convection to low-Prandtl-number gas mixtures. Int. J. Heat Mass Transf. 1988, 31, 13–25. [Google Scholar]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transf. 1985, 12, 3–22. [Google Scholar]
- Pickett, P.E.; Taylor, M.F.; McEaligot, D.M. Heated turbulent flow of helium—Argon mixtures in tubes. Int. J. Heat Mass Transf. 1979, 22, 705–719. [Google Scholar] [CrossRef]
- Kays, W.M.; Crawford, M.E.; Weigand, B. Convective Heat and Mass Transfer; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Qin, H.; Wang, C.; Tian, W.; Qiu, S.; Su, G. Experimental investigation on flow and heat transfer characteristics of He-Xe gas mixture. Int. J. Heat Mass Transf. 2022, 192, 122942. [Google Scholar] [CrossRef]
- Vitovsky, O.V. Experimental study of heat transfer during the flow of a gas coolant in a heated quasi-triangular channel. Int. J. Heat Mass Transf. 2022, 190, 122771. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Vitovsky, O.V. Study of heat transfer of a helium–xenon mixture in heated channels with different cross-sectional shapes. J. Appl. Mech. Tech. Phys. 2017, 58, 664–669. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Elistratov, S.L.; Vitovsky, O.V.; Slesareva, E.Y. Experimental investigation of heat transfer in helium-xenon mixtures in triangle channels. J. Eng. Thermophys. 2015, 24, 139–142. [Google Scholar] [CrossRef]
- Qin, H.; Fang, Y.; Wang, C.; Tian, W.; Qiu, S.; Su, G.; Deng, J. Numerical investigation on heat transfer characteristics of helium-xenon gas mixture. Int. J. Energy Res. 2021, 45, 11745–11758. [Google Scholar] [CrossRef]
- Zhou, B.; Ji, Y.; Sun, J.; Sun, Y. Modified turbulent Prandtl number model for helium–xenon gas mixture with low Prandtl number. Nucl. Eng. Des. 2020, 366, 110738. [Google Scholar] [CrossRef]
- Vitovsky, O.V.; Makarov, M.S.; Nakoryakov, V.E.; Naumkin, V.S. Heat transfer in a small diameter tube at high Reynolds numbers. Int. J. Heat Mass Transf. 2017, 109, 997–1003. [Google Scholar] [CrossRef]
- Bejan, A. The concept of irreversibility in heat exchanger design: Counterflow heat exchangers for gas-to-gas applications. J. Heat Transfer. 1977, 99, 374–380. [Google Scholar] [CrossRef]
- Hesselgreaves, J.E. Rationalisation of second law analysis of heat exchangers. Int. J. Heat Mass Transf. 2000, 43, 4189–4204. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, H.-C.; Tong, J.-F.; Wang, X.-W.; Wang, H.; Zhang, Y.-N. Entropy assessment on direct contact condensation of subsonic steam jets in a water tank through numerical investigation. Entropy 2016, 18, 21. [Google Scholar] [CrossRef]
- Fluent Inc. Fluent User’s Guide; Fluent Inc.: New York, NY, USA, 2019. [Google Scholar]
- Dragunov, Y.G.; Smetannikov, V.P.; Gabaraev, B.A.; Belyakov, M.S.; Kobzev, P.V. On the choice of correlations for calculating the heat transfer coefficient in binary gas mixtures. J. Eng. Thermophys. 2013, 22, 30–42. [Google Scholar] [CrossRef]
- Sleicher, C.A.; Rouse, M.W. A convenient correlation for heat transfer to constant and variable property fluids in turbulent pipe flow. Int. J. Heat Mass Transf. 1975, 18, 677–683. [Google Scholar] [CrossRef]
- Jischa, M.; Rieke, H.B. About the prediction of turbulent Prandtl and Schmidt numbers from modeled transport equations. Int. J. Heat Mass Transf. 1979, 22, 1547–1555. [Google Scholar] [CrossRef]
- Azer, N.Z.; Chao, B.T. A mechanism of turbulent heat transfer in liquid metals. Int. J. Heat Mass Transf. 1960, 1, 121–138. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef]
- McEligot, D.M.; Taylor, M.F. The turbulent Prandtl number in the near-wall region for low-Prandtl-number gas mixtures. Int. J. Heat Mass Transf. 1996, 39, 1287–1295. [Google Scholar] [CrossRef]
- Schlichting, H.; Kestin, J. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Sun, Z.; Zhang, H.; Wang, Q.; Sun, W. Entropy Generation Analysis of the Flow Boiling in Microgravity Field. Entropy 2022, 24, 569. [Google Scholar] [CrossRef] [PubMed]
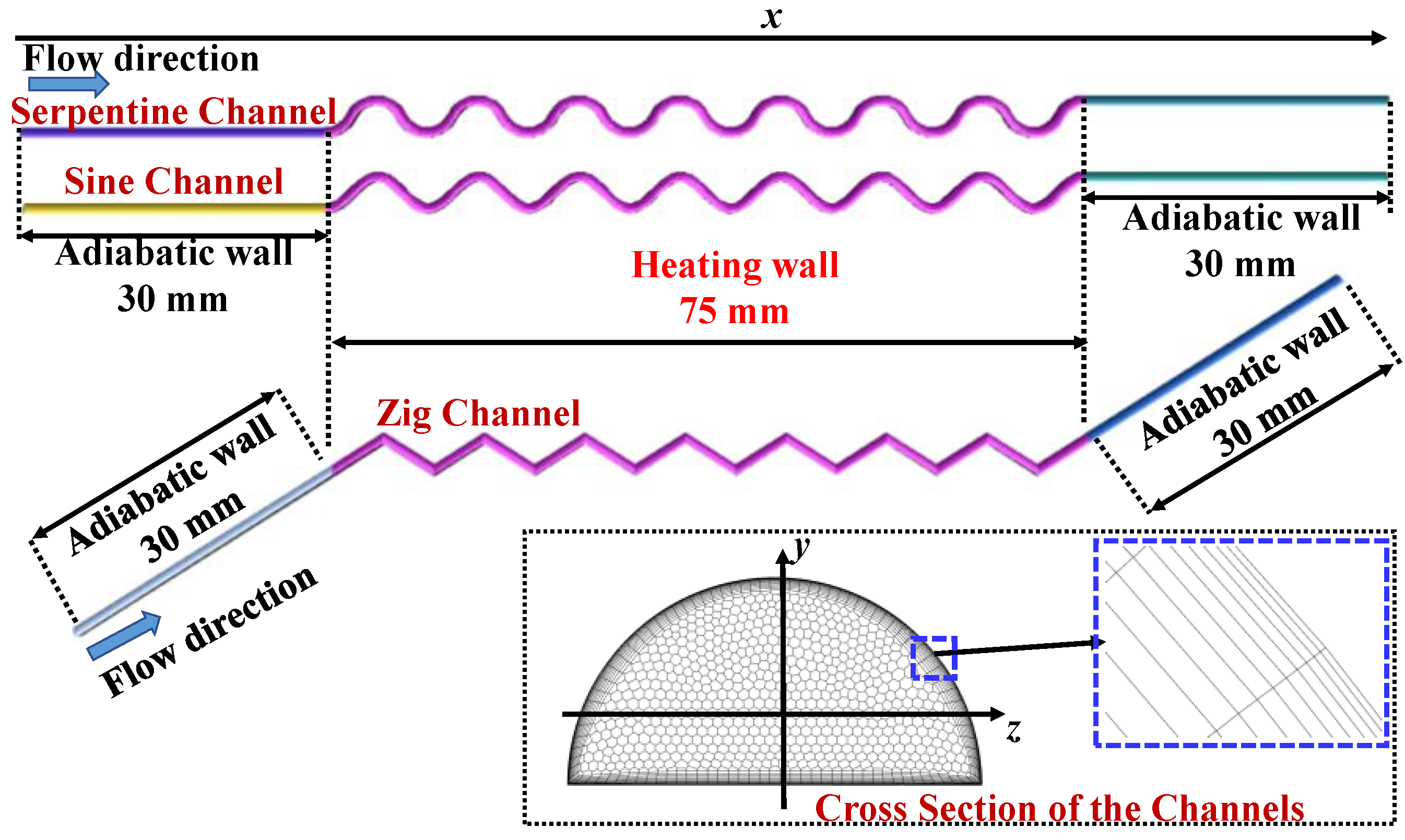


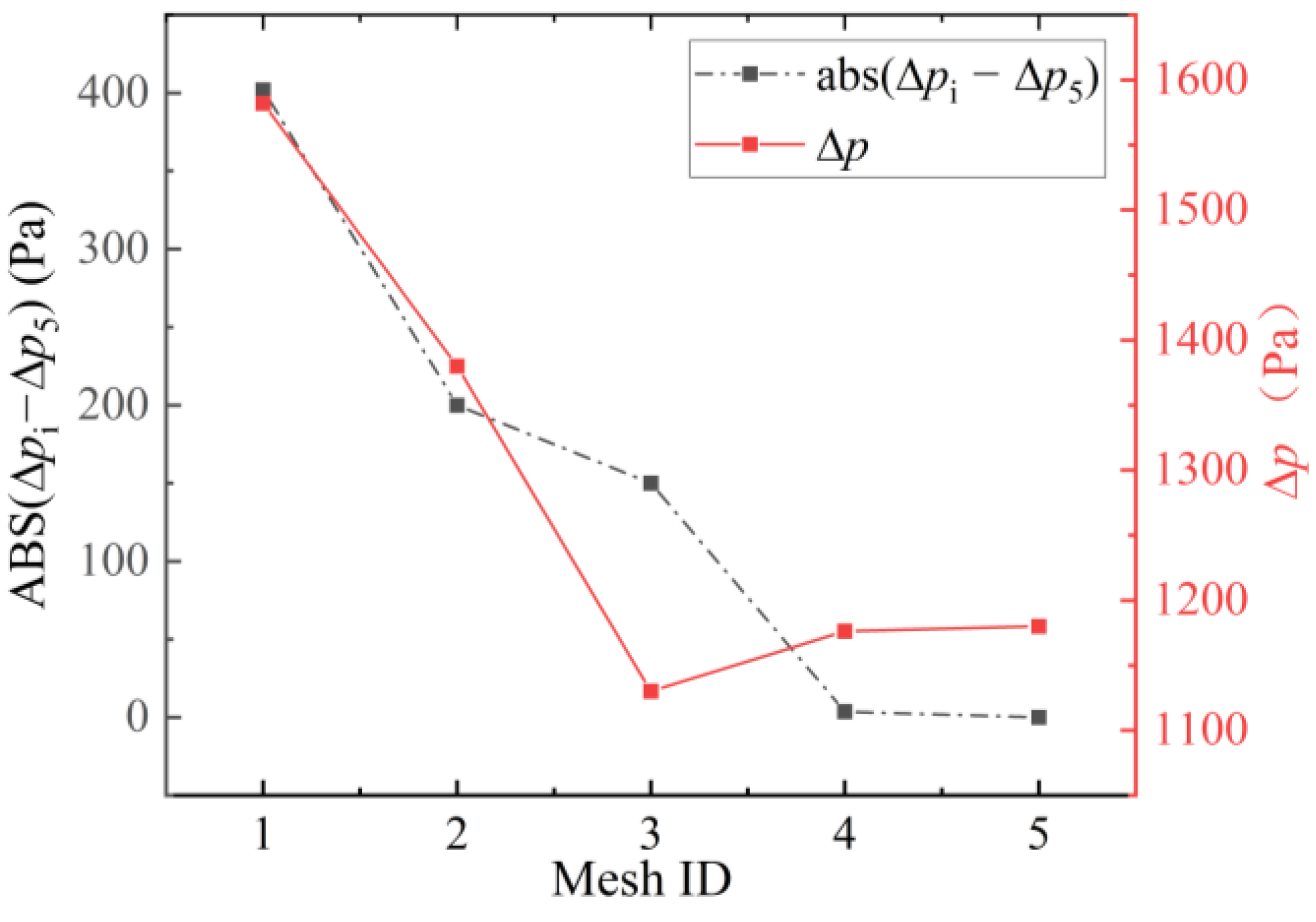




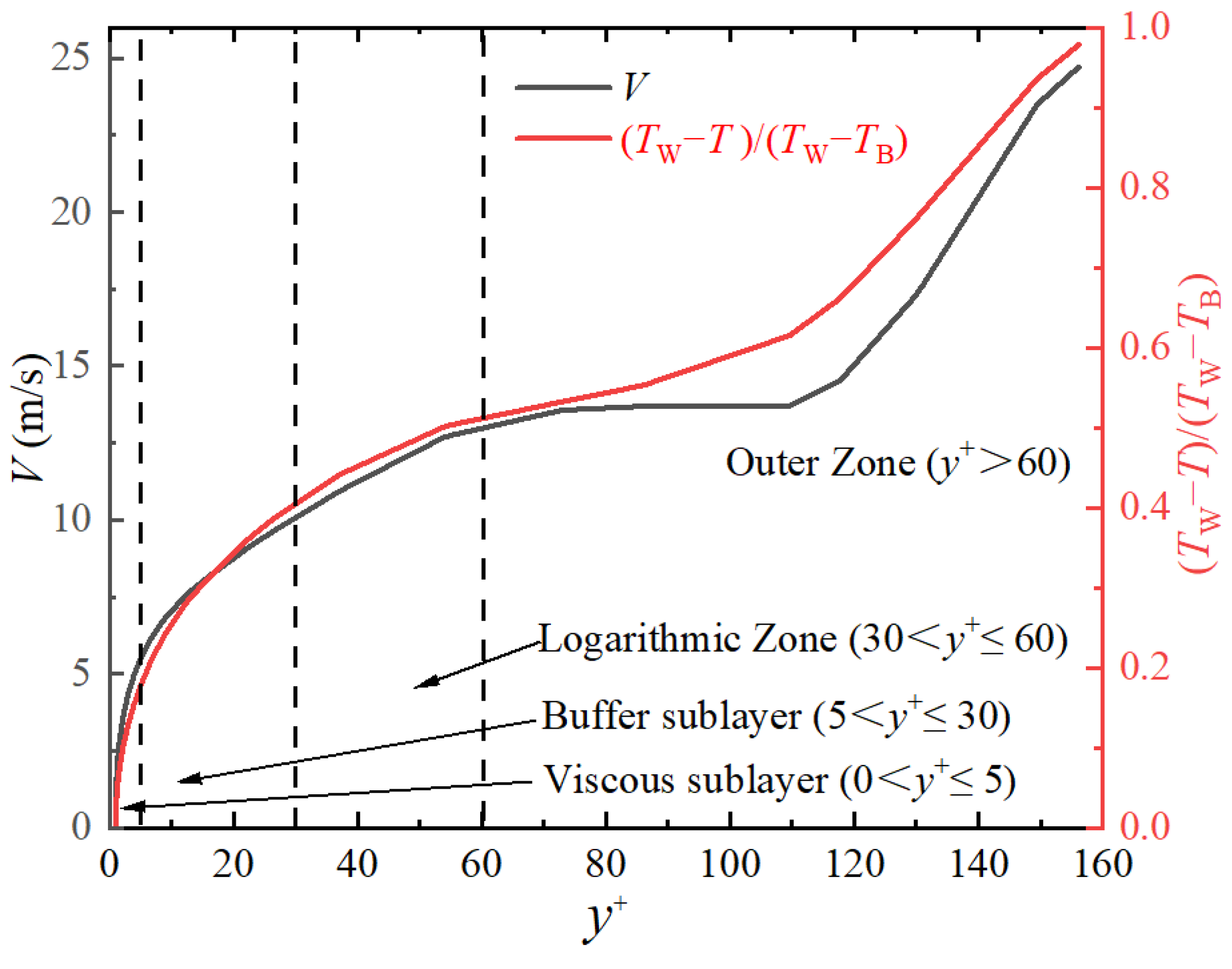

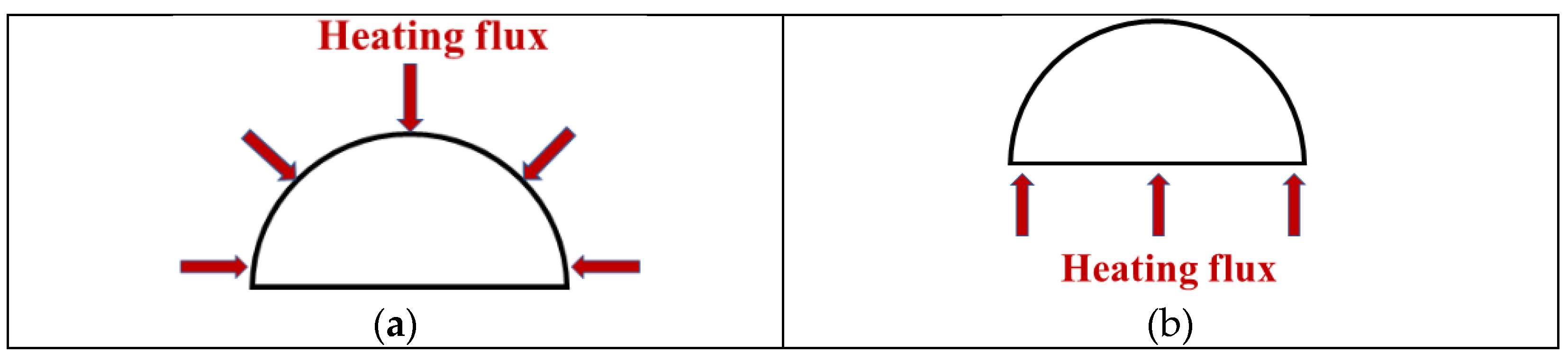











| Case | Structure | (K) | q (kW/m2) | Shape Factor (A) | (×10−3) |
|---|---|---|---|---|---|
| 1 | Sine | 624.5 | 1 | 2.5 | |
| 2 | Zigzag | 624.5 | 1 | 2.5 | |
| 3 | Serpentine | 624.5 | 1 | 2.5/3/3.5/4.5/6 | |
| 4 | Serpentine | 624.5 | 5/10/15/20 | ||
| 5 | Serpentine | 624.5 | 10 | 2.5/3/3.5/4.8 | |
| 6 | Serpentine | 624.5 | 1 | 2.5/4/6 | |
| 7 | Serpentine | 624.5 | 1 | 2.5/4/6 | |
| 8 | Serpentine | 624.5 | 1 | 2.5/4/6 | |
| 9 | Serpentine | 624.5 | 1 | 2.5/4/6 | |
| 10 | Serpentine | 624.5 | 1 | 2.5/4/6 | |
| 11 | Serpentine | 624.5 | 1 | 2.5/4/6 | |
| 12 | Serpentine | 624.5 | 1 | 2.5/4/6 |
| Mesh | Sizemax of the Cell (mm) | Ratio (y1/y0) | y+max |
|---|---|---|---|
| Mesh 1 | 0.12 | 1.2 | 10.8 |
| Mesh 2 | 0.1 | 1.2 | 5.2 |
| Mesh 3 | 0.085 | 1.2 | 2.4 |
| Mesh 4 | 0.08 | 1.2 | 1.03 |
| Mesh 5 | 0.075 | 1.2 | 0.75 |
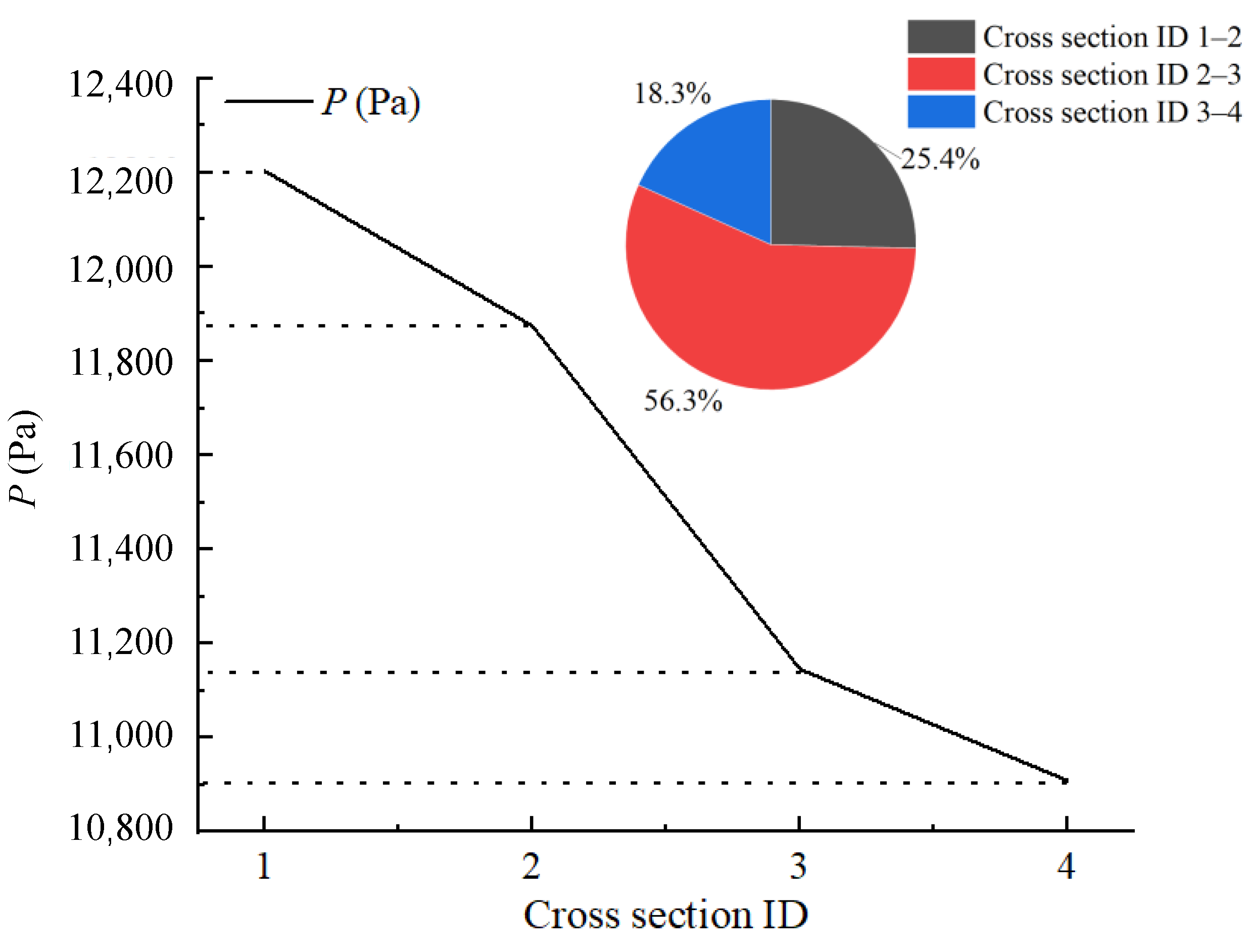
| Interval | Cross-section IDs 1–2 | Cross-section IDs 1–3 | Cross-section IDs 3–4 |
| Pressure Drop (Pa) | 328.687 | 729.047 | 236.347 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Zhang, H.; Sun, Q.; Zhang, C. Comprehensive Thermodynamic Analysis of He–Xe in Microchannels with Different Structures. Energies 2023, 16, 3322. https://doi.org/10.3390/en16083322
Sun Z, Zhang H, Sun Q, Zhang C. Comprehensive Thermodynamic Analysis of He–Xe in Microchannels with Different Structures. Energies. 2023; 16(8):3322. https://doi.org/10.3390/en16083322
Chicago/Turabian StyleSun, Zijian, Haochun Zhang, Qiqi Sun, and Cheng Zhang. 2023. "Comprehensive Thermodynamic Analysis of He–Xe in Microchannels with Different Structures" Energies 16, no. 8: 3322. https://doi.org/10.3390/en16083322
APA StyleSun, Z., Zhang, H., Sun, Q., & Zhang, C. (2023). Comprehensive Thermodynamic Analysis of He–Xe in Microchannels with Different Structures. Energies, 16(8), 3322. https://doi.org/10.3390/en16083322







