Analytical Modeling of Magnetic Air-Gap Field Distribution Due to Armature Reaction

Abstract

The following paper presents an analytical study of the air-gap magnetic field distribution produced by the armature reaction of a linear machine. Based on the method of images, the magnetic field generated by a current carrying conductor inside the air-gap between two smooth infinitely permeable iron surfaces is modeled as a complex 2D function. The conductor model then becomes a current sheet model and horizontally oriented current sheets are used to model the magnetic field produced by the armature reaction for smooth ferromagnetic surfaces. Focus will be given to the study of the slot opening function in front of energized slots in comparison to the not energized ones of the classical theory pointing out some remarkable differences. Later, the model is extended to slotted geometries using a complex slotting function adapted for energized slots. At last, the Maxwell tensor expressed in complex formulation will be integrated to obtain the force components acting on the machine tooth tips, quantities that will be compared with FEM simulations in order to validate the proposed analytical model.

1. Introduction

The knowledge of the magnetic field distribution generated by the armature reaction inside the air-gap of the electrical machines can be of interest to determine demagnetization limits in permanent magnet machines but also integral quantities such as self, mutual inductances and forces. For what concern the forces, especially in fractional winding machines, they can be the cause of vibration and acoustic noise; thus, being able to estimate them is an important matter in particular during the early stage of a project.

The analytical methods present in the literature to estimate the armature reaction are several. There are the methods that make use of a winding function [1] to describe the spatial distribution of the stator magnetomotive force (m.m.f.) [2,3,4,5]. The subdomain methods, which model the flux density field by dividing the entire domain into subdomains, solving the Maxwell’s equations in the domains using the separation of variables [6,7,8] and the methods based on the solution of the analytical 2D Laplacian quasi-Poissonian field equations generalized in [9]. Initially developed by [10] for slotless machine, it was later extended to slotted geometries in [11] by the use of a relative permeance function for the flux density normal component. The relative permeance function when multiplied by the slotless flux density gives the flux density inside the air-gap of slotted geometries. Later, a complex relative permeance function was introduced [12], made by a normal and tangential component, useful to obtain the Maxwell stress tensor components and to calculate forces. The procedure to retrieve this complex permeance function makes use of the conformal mapping, requiring the solution of a nonlinear complex equation. An easier way to obtain the relative complex permeance function on the middle air-gap line has been implemented in [13], a formulation that has been generalized as a compact formulation for any complex point z inside the air-gap domain in [14].

The presented paper introduces an alternative method based on Lord Kelvin’s methods of images and duality between the electric and magnetic field [15].

In Section 2.1 and Section 2.2, the flux density air-gap expression produced by a powered conductor has been extended to a current sheet segment, indefinitely long in the direction perpendicular to the drawing plane, energized by a linear current density. A horizontal current sheet has been used to model the field produced in front of an energized slot.

In Section 2.3 a sequence of current sheets positioned along the machine periphery has been used to model the winding armature reaction also introducing the variable time. Then, in Section 3.1, using FEM simulations the flux density in front of an energized slot has been investigated and compared with the flux density in front of a not energized slot, proving that the relative permeance function originally obtained in [12] overestimates the armature reaction field and it is more appropriate the use of a reduction coefficient. Hence, in Section 3.2, the complex slotting function has been modified by a reduction coefficient $k_r$ and multiplied to the smooth flux density to give the slotted flux density profile, comparing the obtained results with FEM simulations.

In Section 4.1, the Maxwell stress in complex formulation retrieved from [14] is used to calculate the forces acting on each tooth-tip of the slotted machine due to the armature reaction field. Finally, in Section 4.2, the time required for the proposed method has been investigated and compared with FEM calculations.

The advantages of the proposed method are simplicity of implementation and fast response, bringing accurate results for the field components of the slotted machine but also for the calculation of the Maxwell stress tensor and forces. On the other side, the weak point of the proposed method is the absence of saturation.

2. Magnetic Field between Smooth Ferromagnetic Surfaces

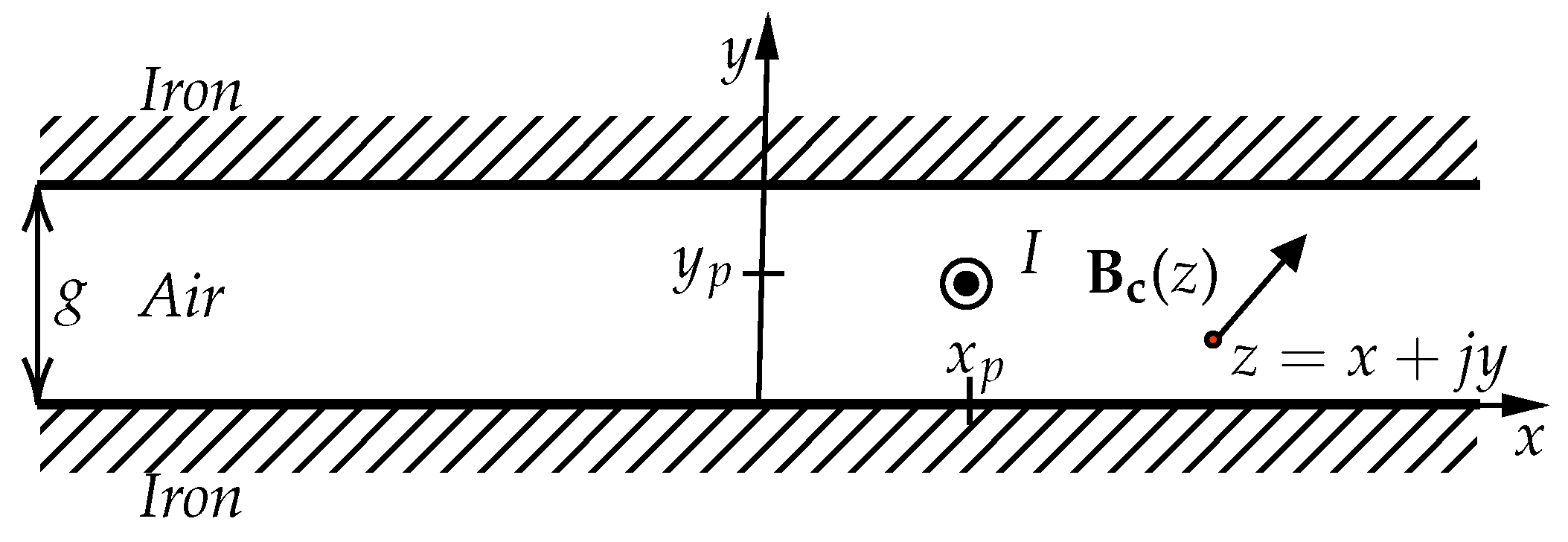
2.1. Linear Conductor with Infinitesimal Section

The magnetic field distribution produced by an indefinite current carrying conductor, cutting the paper plane perpendicularly and placed into the air-gap between two smooth ideal ferromagnetic surfaces, can be modeled analytically in Cartesian coordinates using the method of images described in [15]. The aforementioned method makes use of the following assumptions and limitations:

• Stator and moving surfaces are supposed to be smooth and separated by an air-gap of uniform width.
• Magnetic field is just 2D and lies in the paper plane.
• The machine is supposed to be so long into the paper plane direction, so that end effects are negligible.
• If surface mounted permanent magnet exists between the two parallel iron surfaces, the analysis of the field caused just by currents is performed, by assuming zero remanence and relative recoil permeability equal to the vacuum permeability.
• Iron permeability is assumed to be infinite so the method of superimposition can be used.
• The iron parts are perfectly laminated; thus, no eddy current can be induced in the iron by the varying magnetic field.
• The conductors placed inside the air-gap extend indefinitely perpendicular to the paper plane.
• Skin effect due to alternating currents flowing in the conductors is neglected.

By representing the magnetic field vector quantities as complex numbers made by a real and imaginary parts, representative, respectively, of the tangential and normal vector components, let us focus on Figure 1, where a conductor powered by a current I, flowing perpendicularly outwards from the paper plane $xy$, is positioned into the air-gap complex plane at a generic point p of coordinates $z_p$ between two smooth infinitely permeable iron surfaces. To be able to calculate the field strength vector at a certain point z between two smooth iron surfaces, the aforementioned configuration can be exchanged with an equivalent one in which the iron parts are removed and substituted with two infinite series of images. The conductors from the first and second series of images are placed at positions $z_p+j2ng$ and ${\overline{z}}_p+j2ng$, with $n\in Z$ ranging from minus and plus infinity. By using the theorem of superimposition the field strength inside the air-gap can be expressed as the sum of two mathematical series representative of the two image series [16]:

$${\mathbf{B}}_{\mathbf{c}}\left(z\right)={\mu }_o\frac{jI}{4g}·\left[coth\frac{\pi (\overline{z}-{\overline{z}}_p)}{2g}+coth\frac{\pi (\overline{z}-z_p)}{2g}\right]$$

(1)

where I is the current flowing inside the conductor, g the air-gap length, $z_p$ and ${\overline{z}}_p$ the position of the conductor in complex coordinates and its conjugate.

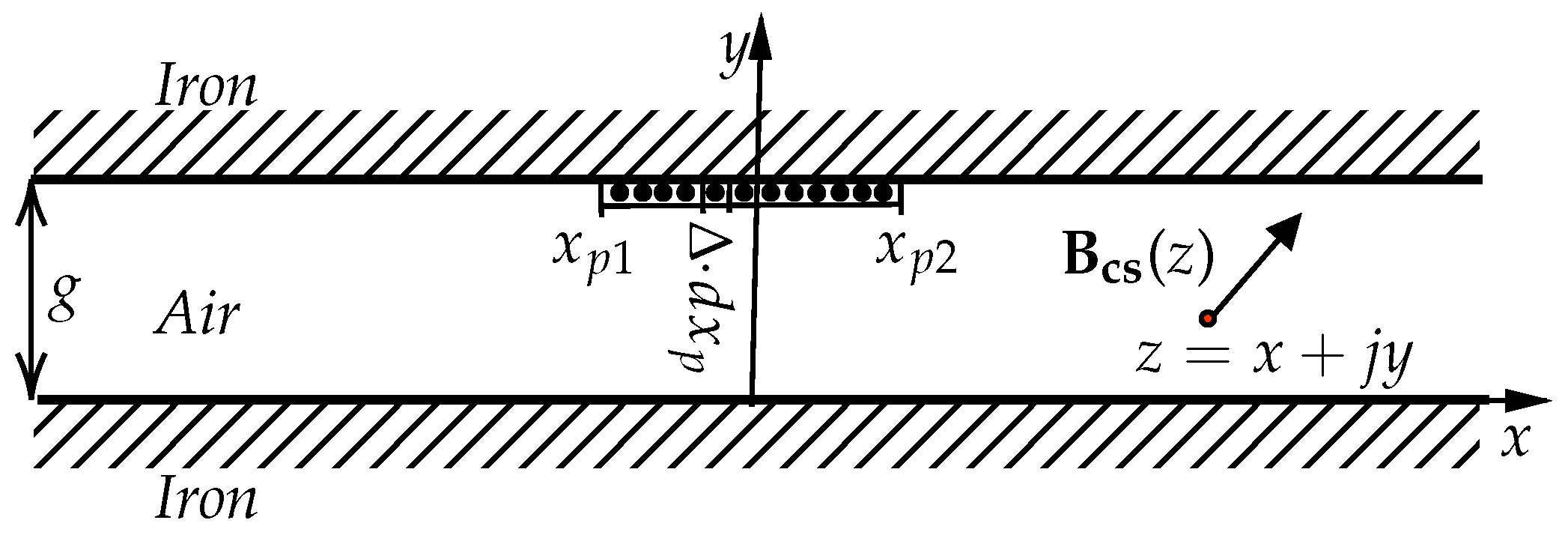
2.2. Horizontal Current Sheet Model

In this subsection, the model of the magnetic field produced by a conductor set between two smooth ideal iron surfaces previously introduced will be extended to current sheets so as to model the magnetic field produced by the windings distribution of an electrical machine.

In Figure 2, a current sheet indefinitely extended into the paper plane and horizontally oriented inside the air-gap of two smooth iron surfaces is considered and distributed along the points p with coordinates $z_p=x_p+j{y}_p$. This distribution has extreme points $z_{p1}=x_{p1}+j{y}_p$ and $z_{p2}=x_{p2}+j{y}_p$. Let us assume that the current sheet is powered by a constant current density of $\Delta =I/b_{cs}$, flowing outwards from the paper plane, where I is the total current and $b_{cs}$ is the current sheet finite length.

By taking into consideration an infinitesimal current sheet element $\Delta ·d{x}_p$ it is possible to express the infinitesimal flux density air-gap complex vector as:

$$d{\mathbf{B}}_{\mathbf{cs}}\left(z\right)={\mu }_o\frac{j\Delta ·d{x}_p}{4g}·\left[coth\frac{\pi (\overline{z}-x_p+j{y}_p)}{2g}+coth\frac{\pi (\overline{z}-x_p-j{y}_p)}{2g}\right].$$

(2)

Then, by integrating (2) between $x_{p1}$ and $x_{p2}$, with $y_p=g$ (current sheet in contact with the upper iron surface), the air-gap flux density vector, produced by a current sheet of length $b_{cs}$, with $z_{p1}=x_{p1}+jg$ and $z_{p2}=x_{p2}+jg$ its ends points and powered by a current density $\Delta$ flowing outwards from the paper plane is retrieved:

$$\begin{array}{c}\hfill {\mathbf{B}}_{\mathbf{cs}}\left(z\right)={\mu }_o\frac{j\Delta }{2\pi }·\{ln\left[sinh\frac{\pi (\overline{z}-x_{p1}+jg)}{2g}/sinh\frac{\pi (\overline{z}-x_{p2}+jg)}{2g}\right]+\\ \hfill ln\left[sinh\frac{\pi (\overline{z}-x_{p1}-jg)}{2g}/sinh\frac{\pi (\overline{z}-x_{p2}-jg)}{2g}\right]\}.\end{array}$$

(3)

Therefore, positioning the current sheet end points at $z_{p1}=-b_{cs}/2+jg$ and $z_{p2}=b_{cs}/2+jg$, the magnetic field distribution inside the air-gap between two smooth ferromagnetic iron surfaces can be expressed as follows:

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\mathbf{cso}}\left(z\right)=\frac{j{\mu }_o\Delta }{2\pi }·\{ln& \left[\frac{sinh\frac{\pi (\overline{z}+z_{p2})}{2g}}{sinh\frac{\pi (\overline{z}-{\overline{z}}_{p2})}{2g}}\right]+ln\left[\frac{sinh\frac{\pi (\overline{z}+{\overline{z}}_{p2})}{2g}}{sinh\frac{\pi (\overline{z}-z_{p2})}{2g}}\right]\}\hfill \\ \hfill & z_{p2}=b_{cs}/2+jg.\hfill \end{array}$$

(4)

Inside which the real part $B_{cs{o}_x}(z)=\mathfrak{Re}\left\{{\mathbf{B}}_{\mathbf{cso}}\left(z\right)\right\}$ and imaginary part $B_{cs{o}_y}(z)=\mathfrak{Im}\left\{{\mathbf{B}}_{\mathbf{cso}}\left(z\right)\right\}$ represent, respectively, the tangential and normal components of the vector flux density function of a generic complex point z.

The flux density distribution produced by the expression of the current sheet stated in (4), positioned between two smooth ideal iron surfaces indefinitely extended along x, is now compared with FEM simulations, where the current sheet inside the simulation environment is modeled with a rectangle of width equal to the current sheet length and very thin transversal size ($b_{cs}/h_{cs}=60$). Figure 3a,b show the analytical and FEM normal and tangential flux density distribution components on the exploration line at $y_{e_1}=g-\delta /2$, over a peripheral extension which is four times the current sheet length ($z=x+j{y}_{e_1}$, $-4b_{cs}\le x\le 4b_{cs}$).

Simulations are FEM magneto static executed using infinitely permeable iron, the normal and tangential distributions are expressed in p.u. with respect to $B_i={\mu }_o·U/g$, which is the ideal flux density flat profile reference value, with U the air-gap magnetic voltage drop and g the air-gap length. For the considered case of study $U=I/2$ and $B_i={\mu }_o·I/2g$ where I is the total current flowing outwards from the horizontal current sheet.

2.3. Magnetic Field due to a Sequence of Horizontal Current Sheets

Inside the electrical machine research area, the use of linear current density distributions and current sheets positioned on the slot opening of slotted geometries is a notorious method to model the magnetic field produced by the machine windings distribution [17,18,19,20]. In the following subsection, the field produced by windings distribution inside the machine air-gap will be modeled throughout horizontal current sheets using the formulation of the current sheet previously obtained.

The machine considered for the following study is the SPM linear machine shown in Figure 4a whose main data are listed in

Table 1. Machine main data.

Parameters
number of teeth, $N_{th}$; number of PMs, $N_m$	9; 8
number of turns per coil, $N_{tc}$	20
pole pitch, ${\tau }_m$  (mm); p.u. ratio, ${\alpha }_m$	113.39; 0.9
PM height, $h_m$ (mm); mechanical air-gap, $\delta$ (mm);	10; 1.5
slot height, $h_s$ (mm); width, $b_s$ (mm)	20.5; 44.3
slot opening height, $h_{so}$ (mm); width, $b_{so}$ (mm)	2; 6
tooth tip height, $h_{ps}$ (mm); width, $b_{ps}$ (mm)	12; 94.79
active length, ℓ (mm)	61.25

. The study here reported aims to analyze the armature reaction only, the PMs here are passive ($B_r=0$) and being the relative recoil permeability set to one their occupied area is basically air.

Let us consider the slotted machine of Figure 5a where Ⓐ is filled with iron and Ⓑ with air. Before the analysis of the slotted configuration, whose slots are filled with phase windings, it is useful to consider a simple slotless configuration (Ⓐ and Ⓑ both filled with iron); in which, horizontal current sheets of length equal to the slot opening width $b_{so}$ are positioned at $z_p=x_{n_s}+jg$ with $x_{n_s}$ ($n_s=1,2,\dots ,10$) the x coordinate of the slot opening center referred to the initial slotted geometry of Figure 5a.

The air-gap field produced in front of a $n_s$ slot of the machine can be modeled by the use of a current sheet horizontally oriented, whose current density equals ${\Delta }_{n_s}=M_{s_{n_s}}/b_{so}$ with $M_{s_{n_s}}$ the total slot m.m.f. produced by its active sides and $b_{so}$ the slot opening width, respectively. So, for example the slot $n_s=4$, inside which there are the phase windings A and B, produces a total m.m.f. at a generic time t equal to: $M_{s_4}\left(t\right)=N_{tc}·(i_b\left(t\right)-i_a\left(t\right))/a$, with $N_{tc}$ the number of turns per coil, a the parallel branches and $i_a\left(t\right)$, $i_b\left(t\right)$ the instantaneous current values of the two phases (active side m.m.f. of positive sign when directed out of the paper).

Let us examine Figure 5: In Figure 5a the flux lines are produced by the rectangular active sides within a slotted geometry; in Figure 5b a current sheet of length $b_{so}$ is positioned at $z_p=jg$ between slotless surfaces and centered with respect to the slot opening symmetry axis. It appears evident that, inside the air-gap region the flux lines of the two configuration are very much similar each other: of course this is just a qualitative way to motivate the previous assumption that will be later proved in a more rigorous manner. Interestingly, it could be shown that regardless the values of current flowing inside the two rectangular active sides, positioned into the slot, the flux density produced inside the air-gap domain and so the flux lines, only depends on the total m.m.f. generated by the two rectangular active sides and not by their individual instantaneous values. On the basis of the above considerations, the flux density generated at a certain time t by a generic current sheet, belonging to the slotless machine periphery, can be expressed as follows:

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\mathbf{CS}}(z,n_s,t)=\frac{j{\mu }_o{M}_{s_{n_s}}\left(t\right)}{2\pi b_{so}}·\{ln& \left[\frac{sinh\frac{\pi (\overline{z}+z_{p2}-x_{n_s})}{2g}}{sinh\frac{\pi (\overline{z}-{\overline{z}}_{p2}-x_{n_s})}{2g}}\right]+ln\left[\frac{sinh\frac{\pi (\overline{z}+{\overline{z}}_{p2}-x_{n_s})}{2g}}{sinh\frac{\pi (\overline{z}-z_{p2}-x_{n_s})}{2g}}\right]\}\hfill \\ \hfill & z_{p2}=b_{so}/2+jg\hfill \end{array}$$

(5)

where $x_{n_s}$ gives the x coordinate of the current sheet representative of the $n_s$ slot with $M_{s_{n_s}}\left(t\right)$ its current source which is the total m.m.f. produced by the slot $n_s$ of the slotted geometry shown in Figure 4a. Due to the hypothesis of magnetic linearity starting from (5), the flux density due to the current sheets along the slotless machine periphery can be now stated as:

$$\mathbf{B}(z,t)=\sum _{n_s=1}^{N_{th}+1}{\mathbf{B}}_{\mathbf{CS}}(z,n_s,t).$$

(6)

This expression is representative of the armature reaction of the machine case of study, keeping in mind that in (5), the m.m.f value of $n_s=1$ and $n_s=10$ refer to half slot and that it is appropriate to replicate at least once the distribution obtained by (6) on the left and on the right to model periodicity and avoid distortion of the flux density at the machine borders. Figure 6a and Figure 7a show the flux density distribution components from (6) on the exploration line $y_{e_1}=g-\delta /2$, in comparison with a magneto-static FEM simulation of the slotted machine of Figure 4a, powered by a three phase circuit $i_a\left(t\right)=I_{pk}·cos(2\pi t/T+\pi /2)$, $i_b\left(t\right)=i_a(t-T/3)$ and $i_c\left(t\right)=i_a(t+T/3)$ at t = T/15 ($T=16.67$ ms).

Looking at the pattern of those two distributions compared with magneto static FEM simulations proves that the assumptions previously made are reasonable to model the armature reaction of the considered machine, although it is noticeable that there are some mismatches to be attributed to the absence of the slot openings in the model.

3. Magnetic Field in Case of Slotted Ferromagnetic Surfaces

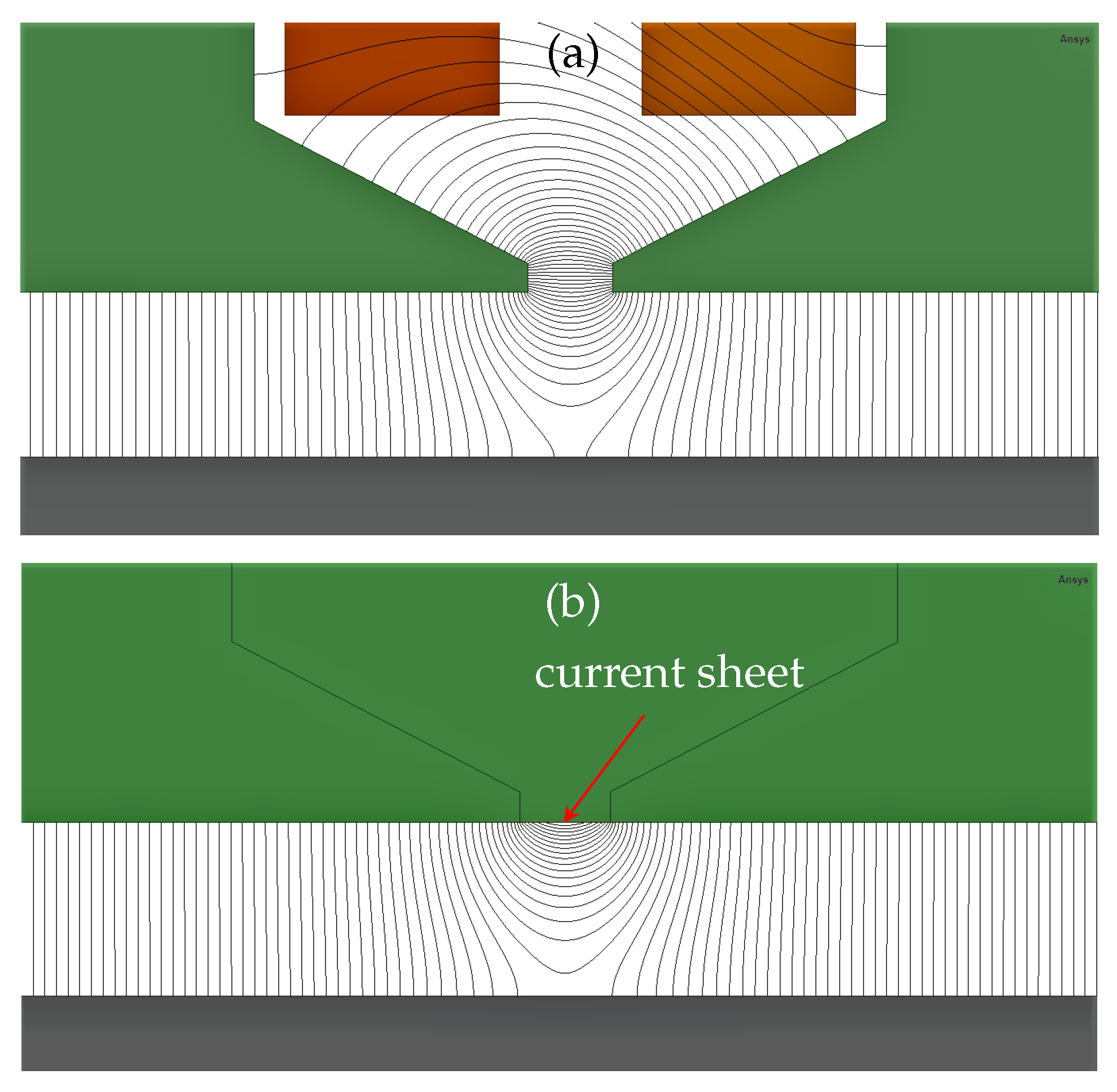
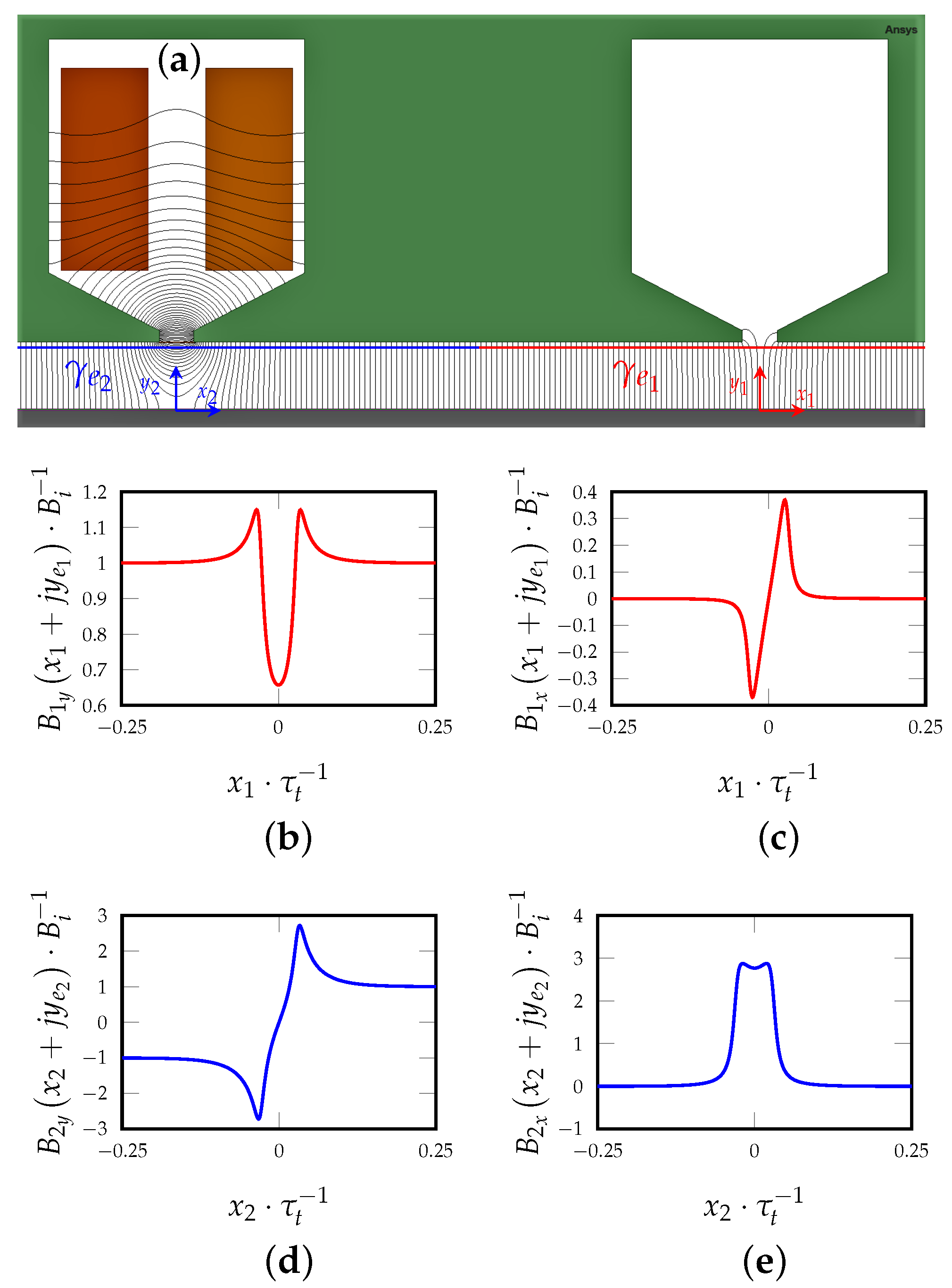
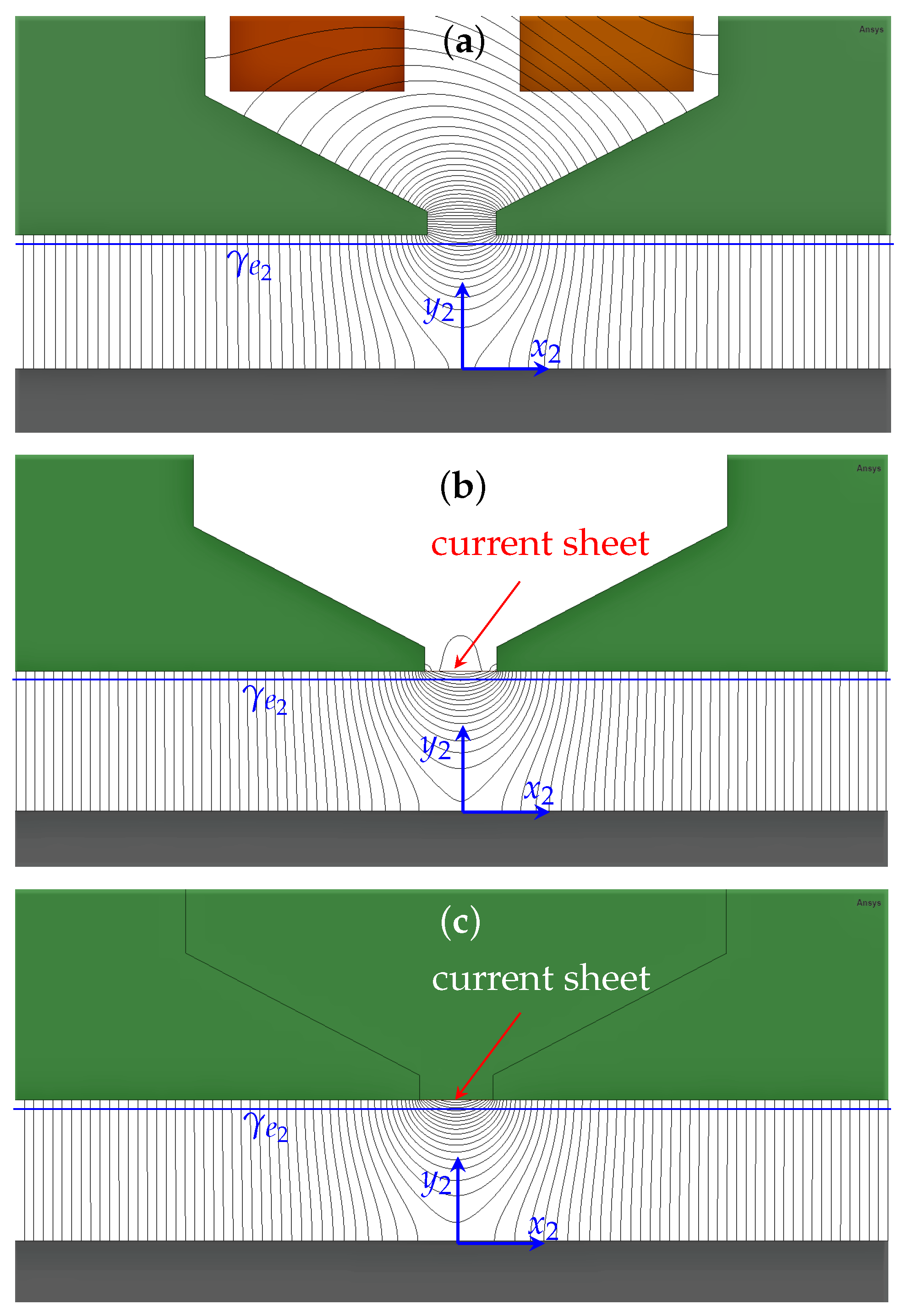
3.1. Energized Slot Opening Model

The following sections will introduce the slot opening and its influence on the magnetic field distribution inside the air-gap of the machine. In [14], the slot opening effect was investigated with particular focus on the flux lines produced in front of the not energized empty slot in order to obtain the expression of the complex slotting function to account for the slotting effect.

Here, instead, the focus will be placed on the flux lines produced inside the air-gap in front of the energized slot in comparison with the not energized one, pointing out some remarkable differences. To this purpose, it can be useful to look at Figure 8a, that reveals the flux lines generated inside a linear ferromagnetic slotted structure by two rectangular energized active sides, situated in a slot whose total m.m.f. value is constant and equal to $M_s$. Figure 8b–e instead, show the normal and tangential p.u. flux density distributions on the exploration segments ${\gamma }_{e_1}$ and ${\gamma }_{e_2}$.

There is no doubt that:

• The flux lines in the region inside the air-gap in front of those slots are quiet different and so their flux density distributions;
• It comes natural to think if there might be a sort of correlation between those two functions and for a while, let us put the attention on the air-gap area just in front of the energized slot considering three different case of studies:
  • The slotted geometry of Figure 9a.
  • The horizontal current sheet slotted model of Figure 9b.
  • The horizontal current sheet slotless model of Figure 9c.

At first sight, the flux lines inside the air-gap region for those three cases appear to be very similar and this is true only inside the air-gap region because inside the slot regions of Figure 9a,b the flux patterns are completely different. Proof of the aforementioned similitude inside the air-gap region is given in Figure 10a,b, where the normal and tangential flux density distributions on the exploration segment ${\gamma }_{e_2}$ for the three case of study are shown. The case of studies 1 and 2 are perfectly superimposed, while 3 differs from them due to the absence of the slot opening.

The usual procedure present in the literature in order to account for the slot opening effect is to retrieve the complex permeability function in front of the not energized slot and then multiply it to the slotless flux density distribution. This approach is carried out both for the no load and the armature reaction fields [12]. In [14], a complex slotting function periodic along x with period equal to the tooth pitch size was defined as follows:

$$\begin{array}{cc}\hfill & \mathbf{\beta }\left(z\right)=\frac{{\displaystyle \sum _{n=1}^{N_h}j\frac{\alpha \left(n\right)}{sinh\frac{2\pi ng}{{\tau }_t}}\left[cos\frac{2\pi n\overline{z}}{{\tau }_t}+\frac{{\left(-1\right)}^n}{k_c-1}cos\frac{\pi n(z-\overline{z})}{{\tau }_t}\right]}}{{\displaystyle \sum _{n=1}^{N_h}{\left(-1\right)}^n\alpha \left(n\right)\left[\frac{{\tau }_t}{2\pi ng}+\frac{1}{k_c-1}\frac{cos\frac{\pi n(z-\overline{z})}{{\tau }_t}}{sinh\frac{2\pi ng}{{\tau }_t}}\right]}}\hfill \\ \hfill {\displaystyle }& \alpha \left(n\right)={\int }_0^{{\rho }_{so}/2}\left(\frac{1}{\sqrt[3]{{\rho }_{so}/2-\xi }}-\frac{1}{\sqrt[3]{{\rho }_{so}/2+\xi }}\right)sin\left(2\pi n\xi \right)d\xi .\hfill \end{array}$$

(7)

with $z=x+jy$ being a generic complex point inside the air-gap domain. After choosing a horizontal line at $y=y_e$, (7) was multiplied by the no load slottess flux density vector (retrieved along the same line) obtaining the slotted flux density no-load vector, which has been proven to work well [14].

Here, the same procedure will be applied to the armature reaction to see the outcomes. Starting from the slotless current sheet model stated in (4) it can be written [14]:

$${\mathbf{B}}_{{\mathbf{s}}_{\mathbf{cso}}}(x_2+j{y}_e)=-j\mathbf{\beta }(x_2+j{y}_e)·{\mathbf{B}}_{\mathbf{cso}}(x_2+j{y}_e)$$

(8)

that is the flux density generated by an horizontal current sheet centered in the origin, with the slotted effect included according to the classical theory. In Figure 11a,b, the normal and tangential flux density distributions in p.u. produced by (8) with $y_e=y_{e_2}$ in comparison with the FEM magneto-static simulation of case 1 are plotted.

It can be noticed that the application of the complex slotting function in this case does not perfectly fit the FEM pattern for both the magnetic field components and the effect of the slot opening seems to be overestimated. Hence, it can be reasonable to try to introduce a reduction coefficient $k_r$ applied to the slot opening complex function as follows:

$${\mathbf{\beta }}_{\mathbf{r}}\left(z\right)=k_r·{\beta }_x\left(z\right)+j\{k_r·[{\beta }_y\left(z\right)-1]+1\}$$

(9)

obtaining a complex slotting function reduced by a certain factor $k_r$ to be estimated. For what concern the p.u. normal component the reduction coefficient must not be applied to its average value which is first removed and added later, a procedure that is not applied for the p.u. tangential component which has null average value. Multiplying the reduced complex slotting function by the smooth current sheet flux density (4) gives:

$${\mathbf{B}}_{{\mathbf{s}}_{\mathbf{csr}}}(x_2+j{y}_e)=-j{\mathbf{\beta }}_{\mathbf{r}}(x_2+j{y}_e)·{\mathbf{B}}_{\mathbf{cso}}(x_2+j{y}_e)$$

(10)

which is the slotted flux density produced by the current sheet model but using the slotting function reduced by a certain coefficient $k_r$. Figure 12a,b shows the normal and tangential p.u. flux density components of (10) at $y_e=y_{e_2}=y_{e_1}$, with different values of $k_r$. A reduction coefficient $k_r=0.41$ fit perfectly for the considered case study, but it can be verified that it is the same for other slot opening values.

The reason for this at this stage is only empirically demonstrated by simulations but it can be stated that the slotting function, retrieved according to the classical theory, does not perfectly fit when applied to the armature reaction (in front of an energized slot) as was intuitively guessed looking at the different field maps at the beginning of this section. However, it seems there is a sort of correlation between the slot opening functions on segments ${\gamma }_{e_1}$ and ${\gamma }_{e_2}$, because using the slotted function obtained in front of the not energized slot (segment ${\gamma }_{e_1}$), multiplied to the slotless case with a reduction coefficient $k_r$, gives the flux density distribution in front of the energized slot (segment ${\gamma }_{e_2}$).

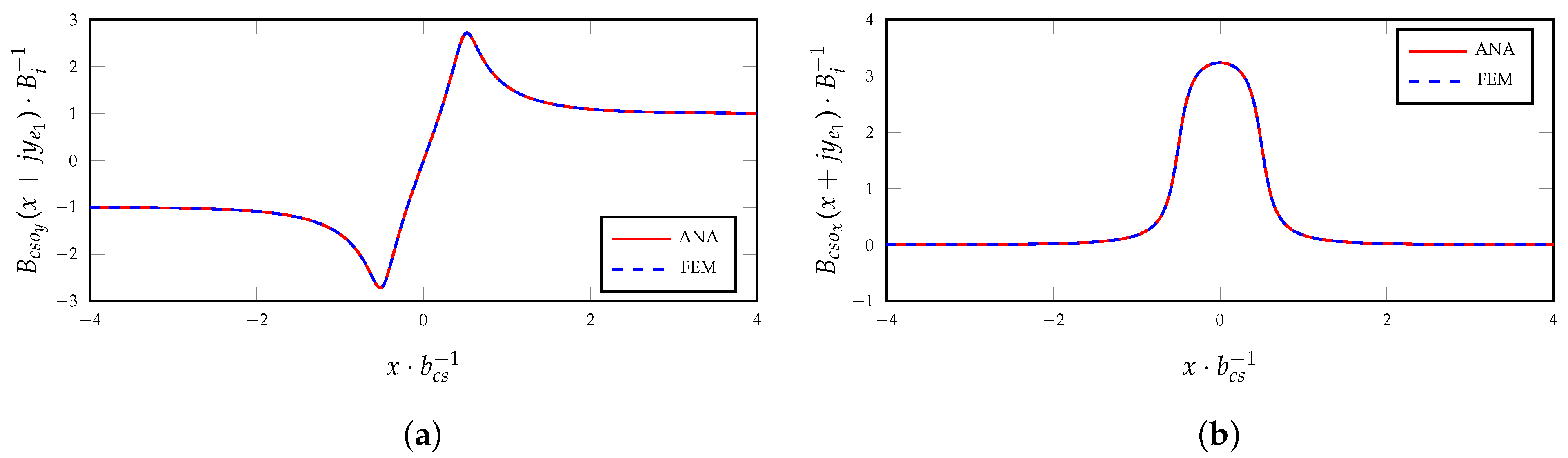
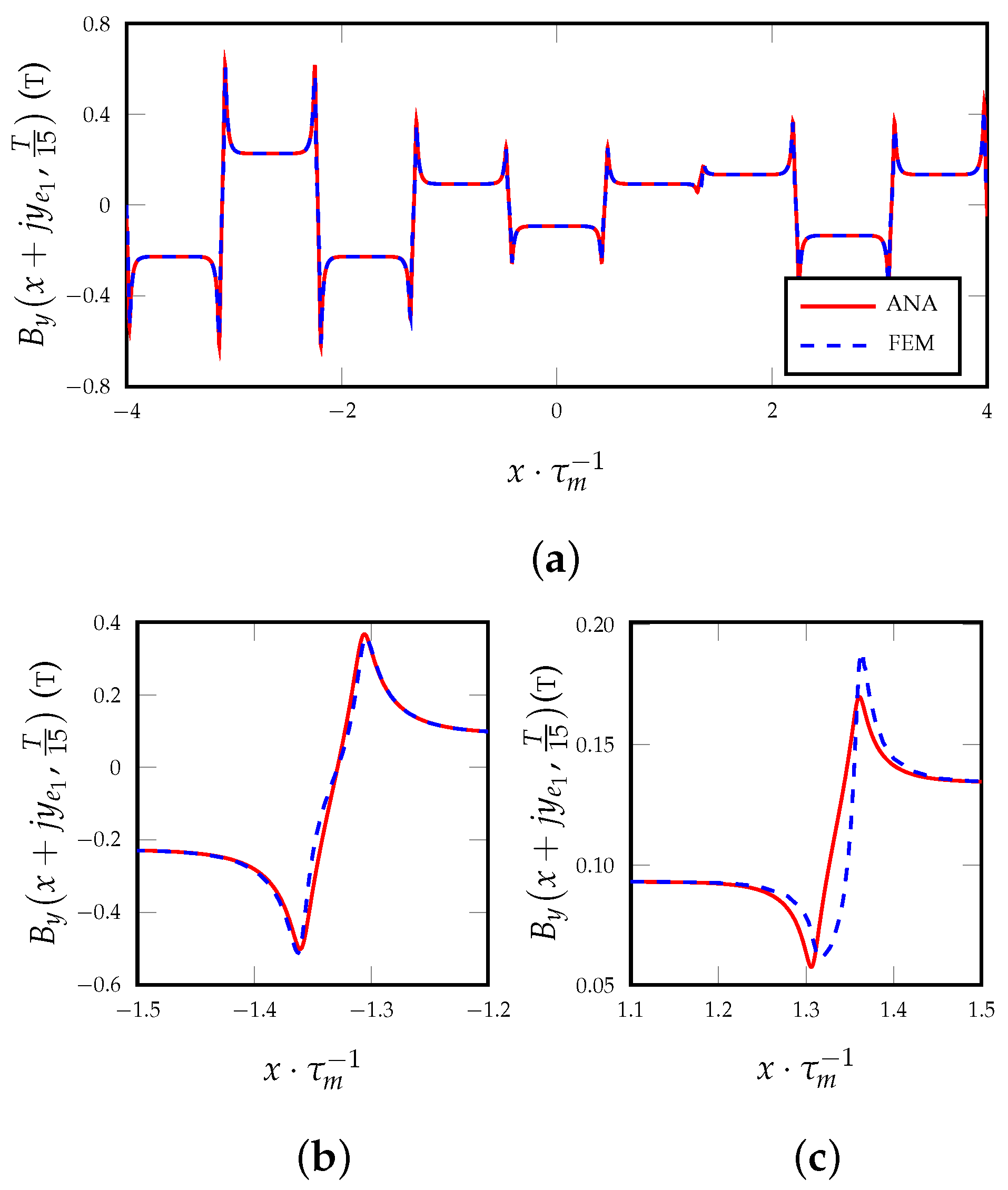
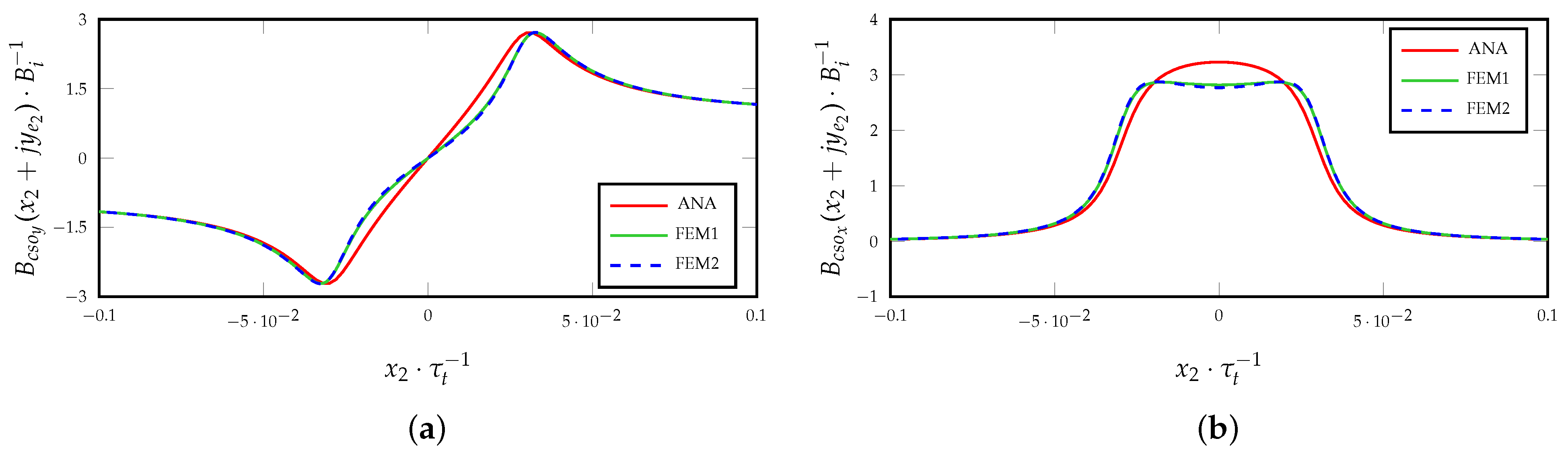
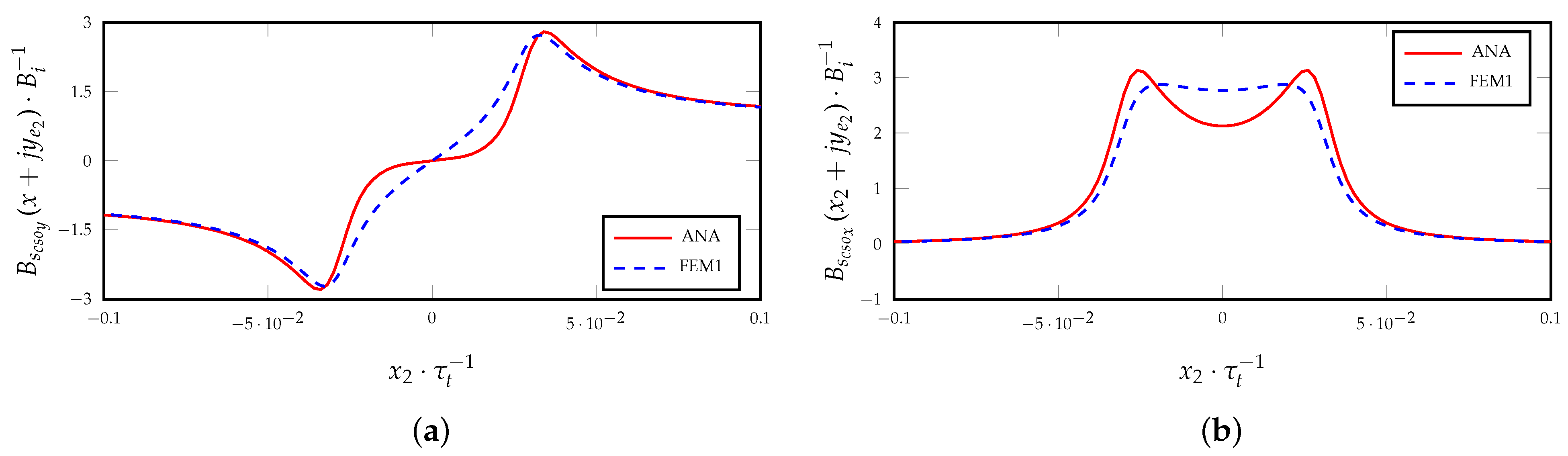
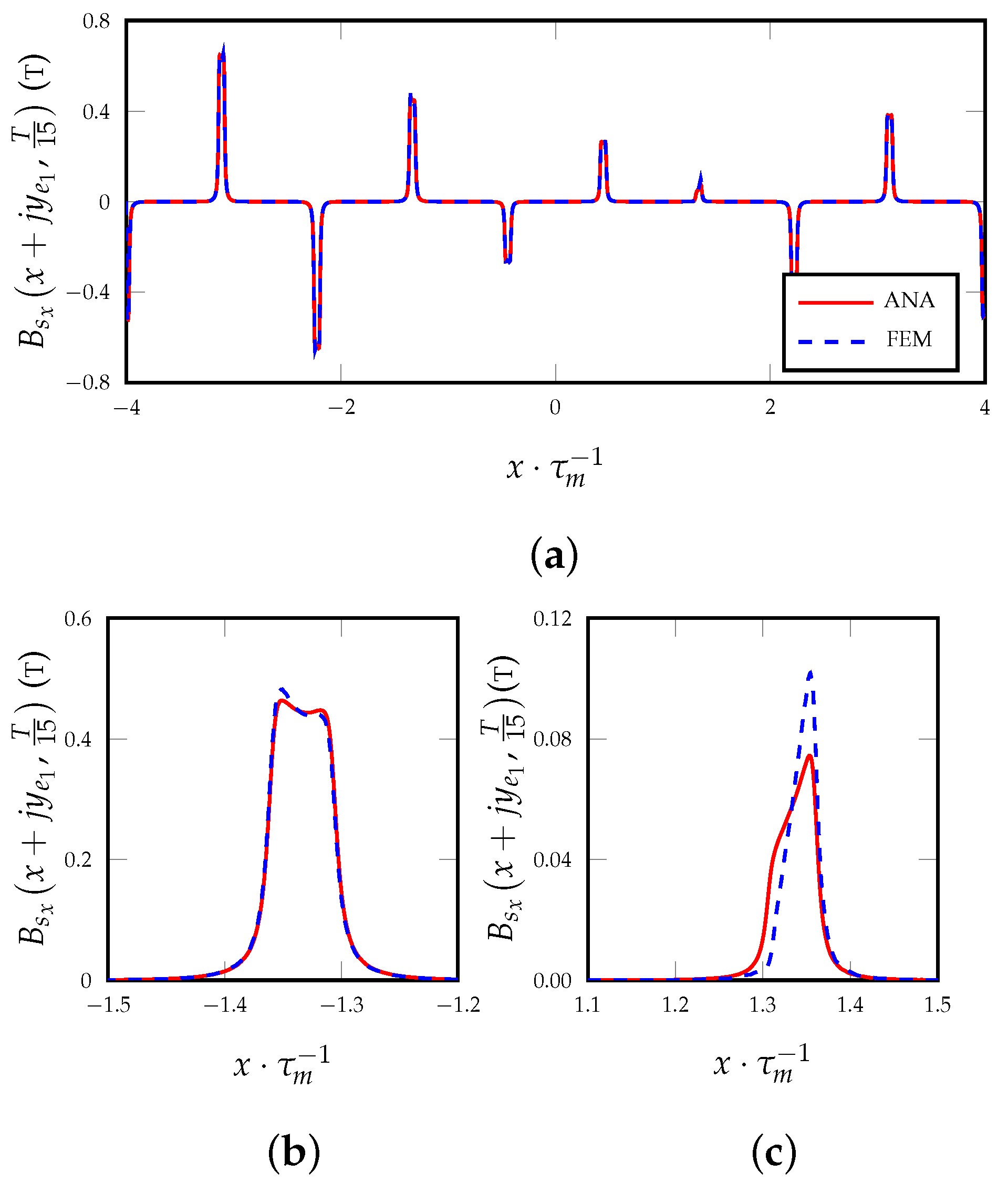
3.2. Magnetic Field Armature Reaction for Slotted Surfaces

Previously, it has been pointed out that applying the complex slotting function to the slotless flux density distribution in front of an energized slot overestimates its effect and the introduction of a reduction coefficient is needed. In the following subsection, ${\mathbf{\beta }}_{\mathbf{r}}$ will be used for the slotted machine pictured in Figure 4a, where Ⓐ is filled with iron and Ⓑ is filled with air. Indeed, in order to introduce the slotting effect, the expression of the slotless flux density distribution generated by the armature reaction and stated in (6) will be multiplied by the reduced slotting complex function:

$${\mathbf{B}}_{\mathbf{s}}(x+j{y}_e,t)=-j{\mathbf{\beta }}_{\mathbf{r}}(x+{\tau }_t/2+j{y}_e)·\mathbf{B}(x+j{y}_e,t)$$

(11)

obtaining the flux density distribution on a generic line at $y=y_e$ produced by the armature reaction inside the slotted geometry. Figure 13a and Figure 14a show the flux density normal and tangential distributions for $t=T/15$ on the exploration line at $y_{e_1}=g-\delta /2$ ($i_a\left(t\right)=I_{pk}·cos(2\pi t/T+\pi /2)$, $i_b\left(t\right)=i_a(t-T/3)$, $i_c\left(t\right)=i_a(t+T/3)$, $T=16.67$ ms).

The analytical pattern is well superimposed to the FEM one, except in some areas where there are slight differences, as it can be observed in Figure 13c and Figure 14c. This comes from the fact that, at a generic time instant t, in proximity of the slots wherein the total value of m.m.f. is almost null the pattern of slot opening complex functions is very much the same as the one in front of the not energized slot; thus, no reduction coefficient should be applied, for $t=T/15$ in fact the total m.m.f. inside slot $n_s=7$ (the one concerning patterns of Figure 13c and Figure 14c) is tiny and equal to $M_{s_7}(T/15)=382A$; just 9% of the peak m.m.f value $M_{pk}=4220A$.

4. Complex Integral Quantities

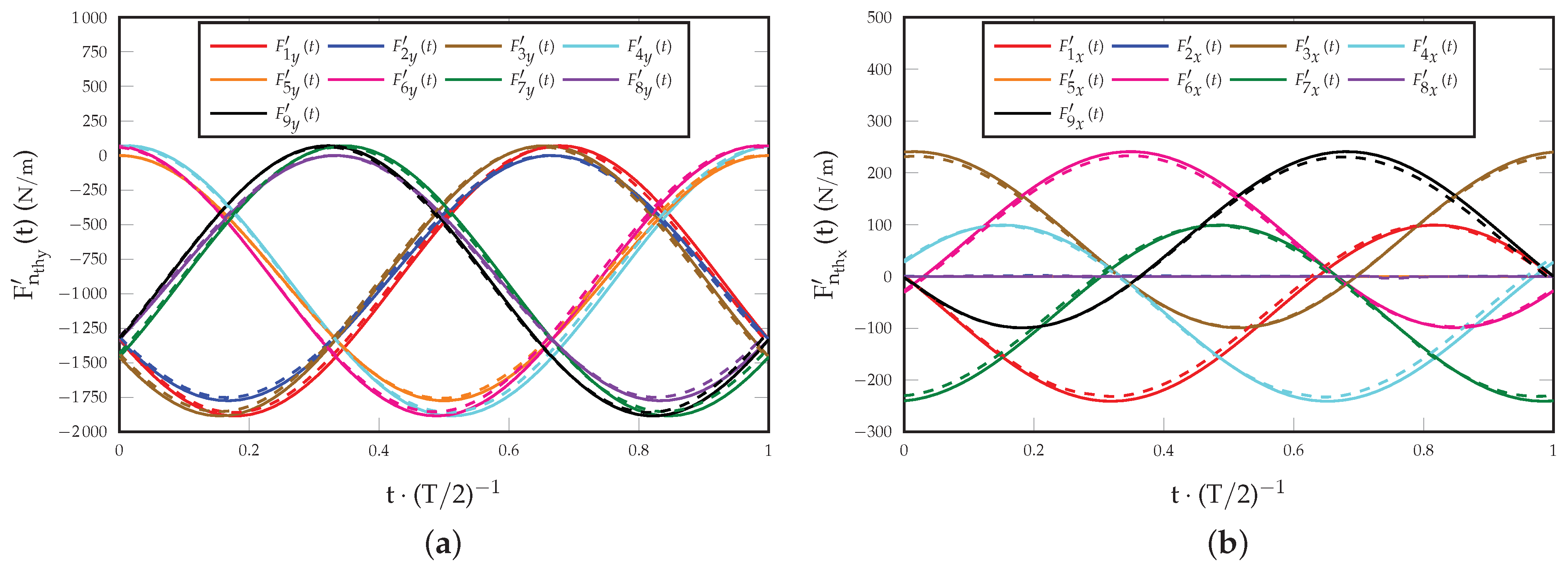
4.1. Calculation of Forces

In the following section, the previously introduced model will be used to calculate the forces acting on each tooth tip, making use of the Maxwell stress tensor. In [14], the Maxwell tensor was obtained in complex formulation as follows:

$${\mathbf{\sigma }}_{\mathbf{s}}(z,t)=j\frac{\overline{{\mathbf{B}}_{\mathbf{s}}{(z,t)}^2}}{2{\mu }_o}$$

(12)

and used for the calculation of forces under no load working conditions but, being a formulation of general validity, it can also be used for the field produced by the armature reaction. By plugging (11) into (12) the Maxwell complex tensor produced by the armature reaction of the slotted surface is obtained, Figure 15a,b show the normal and tangential components of the Maxwell tensor on the exploration line at $y_{e_1}=g-\delta /2$ over the entire machine periphery at a time instant $T/15$, in comparison to the FEM magneto-static simulation.

The pattern for the considered time instant is well superimposed with the simulation, validating the previously introduced model, although it is reasonable to validate it for more than one arbitrary time instant as it will be now performed for the calculation of forces. The objective is to calculate the forces produced by the armature reaction on each tooth tip of the machine. This calculation can be useful, for example, for Noise and Vibration Harshness (NVH) studies. Thus, to this purpose, the Maxwell stress tensor is integrated on the middle mechanical air-gap segment long ${\tau }_t$ in front of the considered $n_{th}$ tooth tip as follows:

$${\mathbf{F}}_{{\mathbf{n}}_{\mathbf{th}}}^{\prime }\left(t\right)={\int }_{x_{n_{{}_{th}}}-\frac{{\tau }_t}{2}}^{x_{n_{{}_{th}}}+\frac{{\tau }_t}{2}}{\mathbf{\sigma }}_{\mathbf{s}}(x+j{y}_{e_1},t)dx$$

(13)

wherein the real part $F_{n_{t{h}_x}}^{\prime }\left(t\right)=\mathfrak{Re}\left\{{\mathbf{F}}_{{\mathbf{n}}_{\mathbf{th}}}^{\prime }\left(t\right)\right\}$ and imaginary part $F_{n_{t{h}_y}}^{\prime }\left(t\right)=\mathfrak{Im}\left\{{\mathbf{F}}_{{\mathbf{n}}_{\mathbf{th}}}^{\prime }\left(t\right)\right\}$, represent the tangential and normal components of the total force per unit length acting on the $n_{th}$ tooth tip whose axis is at $x=x_{n_{th}}$ at a generic time instant t.

Figure 16a,b show, respectively, the normal and tangential component calculated with (13) in comparison with FEM transient simulations for each machine tooth tip ($1\le n_{th}\le N_{th}$), over a time interval equal to the forces period which is half the electrical period T.

The analytical and FEM pattern are fairly well superimposed for both the force components exhibiting a maximum relative percentage error around 2.5% and 3.9% for the normal and tangential component, respectively. The tangential components acting on the tooth tips 2, 5 and 8 are null because those teeth have adjacent slots on their left and right side which are filled by the same phase conductors, generating a flux line pattern that is symmetrical in respect to their own axis and so canceling out the resultant tangential component.

4.2. Computational Efficiency

The time required by the analytical and FEM for the calculation of forces is now compared.

Table 2. Computational time.

Method	Time
ANA (13) $N_h=150$,
$n_{\mathrm{th}}=1,\dots ,N_{\mathrm{th}}$
$x_{n_{{}_{\mathrm{th}}}}-{\tau }_t/2\le x\le x_{n_{{}_{th}}}+{\tau }_t/2$ $N_x=1111$,	6.7 s
$0\le t\le T/2$ $N_t=120$,
FEM MT(global system)
$0\le t\le T/2$ $N_t=120$,	$15.2$ min
N° of mesh triangles inside the global system:
stator: 3900, slider: 1870, coils = 648
equivalent air-gap: 17,150, slots: 300

shows the time necessary to compute (13) for the all the tooth tips of the considered machine in respect to a transient FEM simulation using the Maxwell tensor (MT).

The calculator is an i7-10850H @ 2.70GHz 32GB RAM; the analytical model has been implemented using MATLAB R2019b while the FEM simulations have been carried out with Ansys Electronics Desktop 2021 R2. Because the aim was to calculate the forces acting on the tooth tips of the machine, for the FEM, MT is mandatory to save the field maps for each time step of simulation; this significantly increases the computational time. The proposed method is proven to be fast and reasonably accurate, making it a useful tool to compute the forces generated by the armature reaction of the electrical machines.

5. Conclusions

The presented paper describes a fast, easy and accurate method to analyze the flux density generated in the air-gap by the armature reaction and calculates tooth tip forces. The flux density is modeled as a complex 2D function by the use of horizontal current sheets set between smooth ferromagnetic surfaces. Then, the flux density for the slotted configuration is obtained, multiplying the smooth flux density by the slotting complex function reduced by a certain coefficient. Magneto static FEM simulations show a very good agreement for both the smooth and the slotted model. Finally, the Maxwell tensor in complex formulation is integrated to obtain the forces acting on each tooth tip of the machine as a function of time. Moreover, these results show a very good agreement with FEM transient simulations, validating the model. The presented model has been applied to an SPM linear machine but it can be employed for any type of isotropic machine to study the armature reaction. Future research studies are aimed at dealing with the machine during load operation and to introduce the presence of saturation to overcome weaknesses of the model. Some further validation activities will be devoted to specific test procedures applied to prototypes, aimed to compare analytically calculated quantities with measured ones. Another aspect that will be studied is the analysis of end effects, by means of 3D FEM simulations, with the aim to identify suited correcting function to be applied to the developed 2D analytical expressions in order to fit at the best the 3D FEM numerical results.