A Review on Power Electronic Converters for Modular BMS with Active Balancing
Abstract
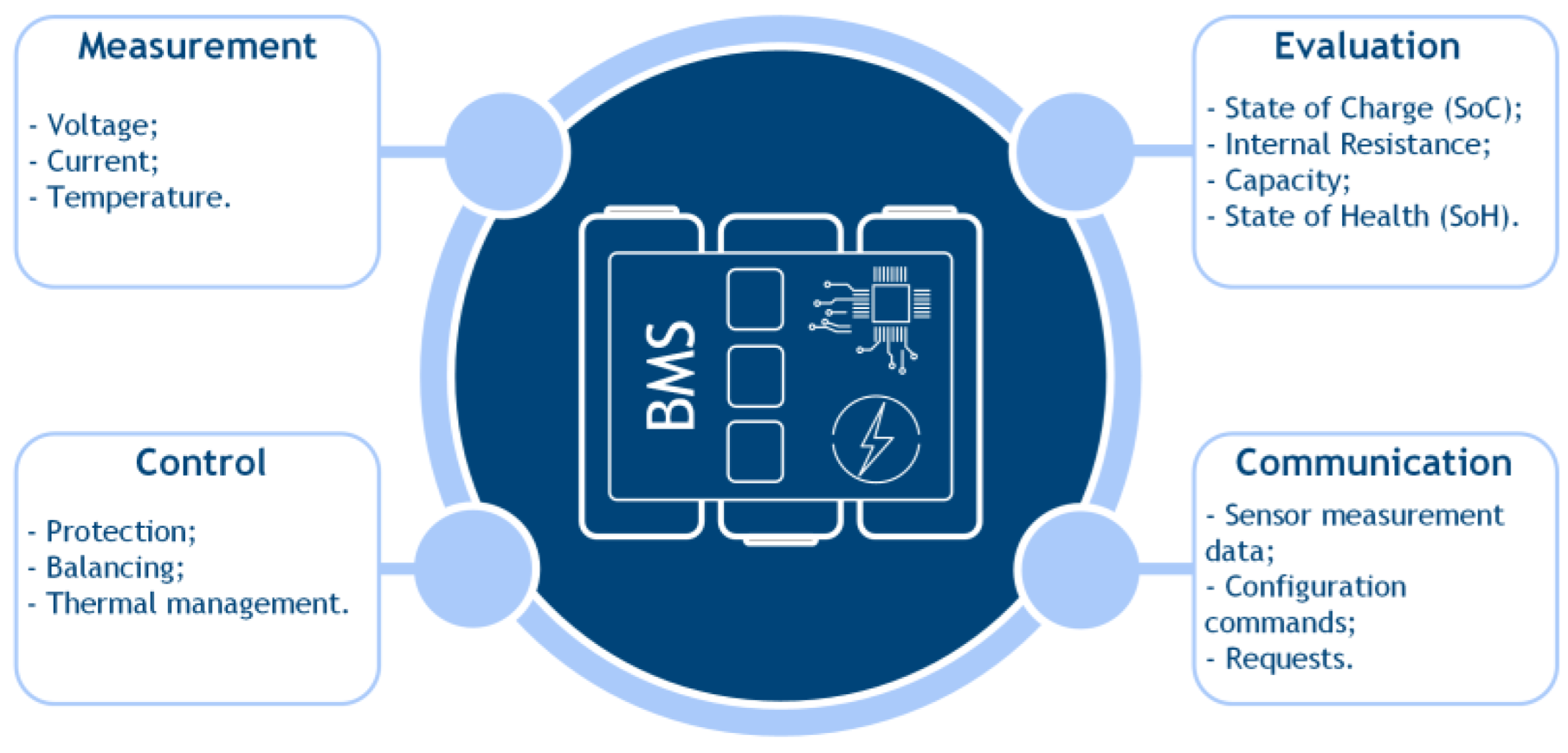
1. Introduction
2. Active Cell Equalizer Circuits Applied to EVs
2.1. Switched-Capacitor
2.2. Double-Tiered Switched-Capacitor
2.3. Switched Capacitor–Inductor
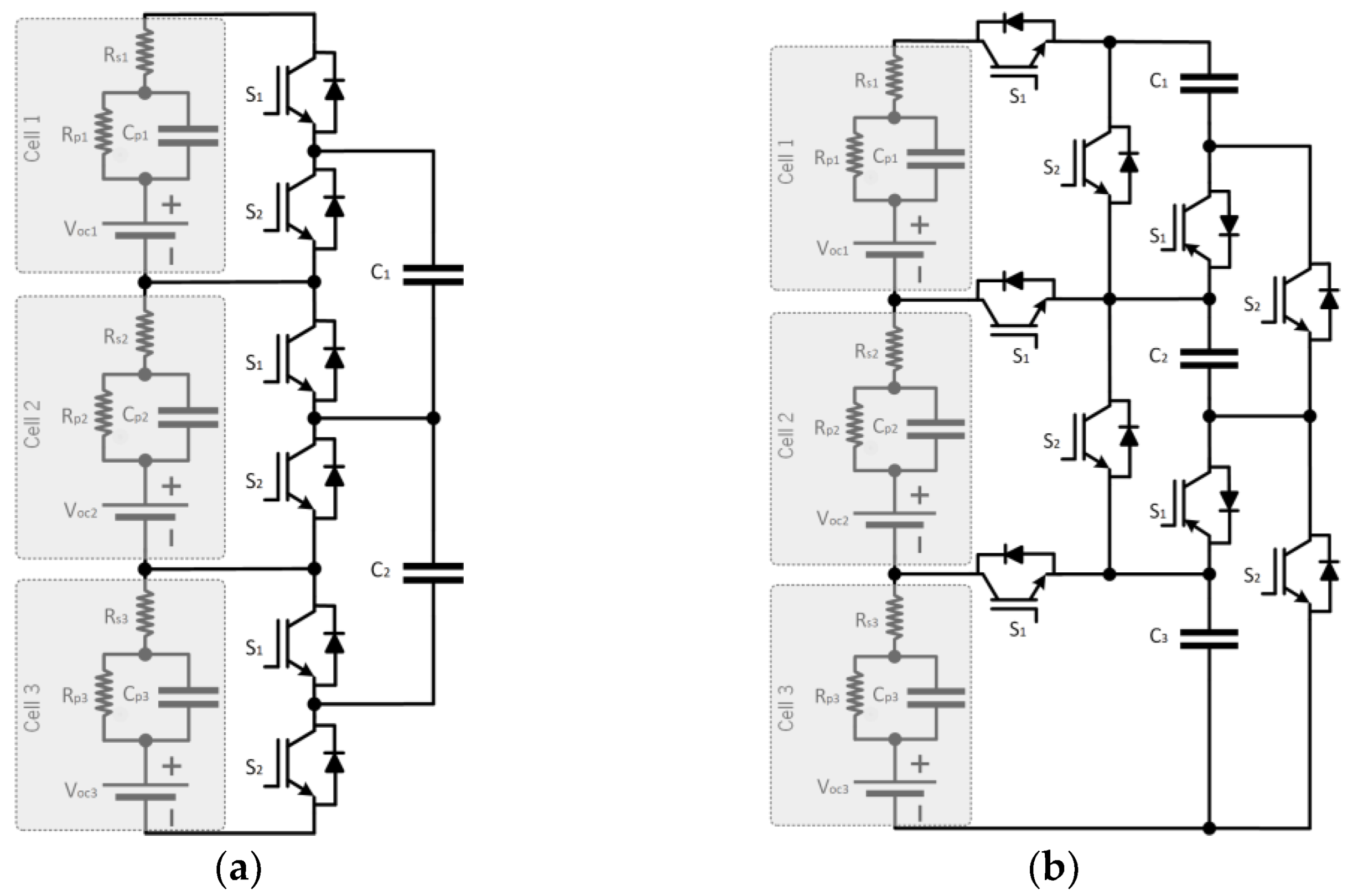
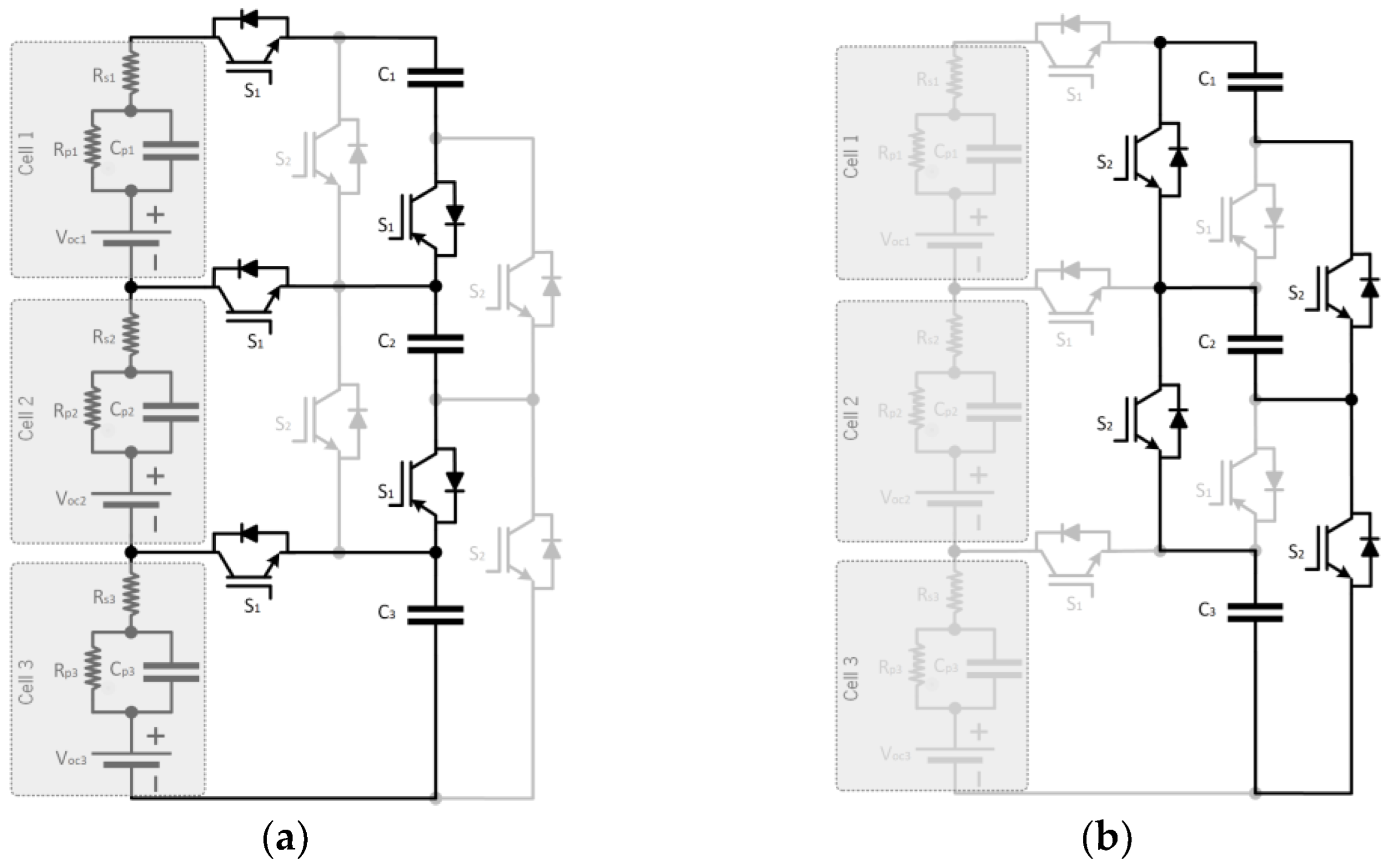
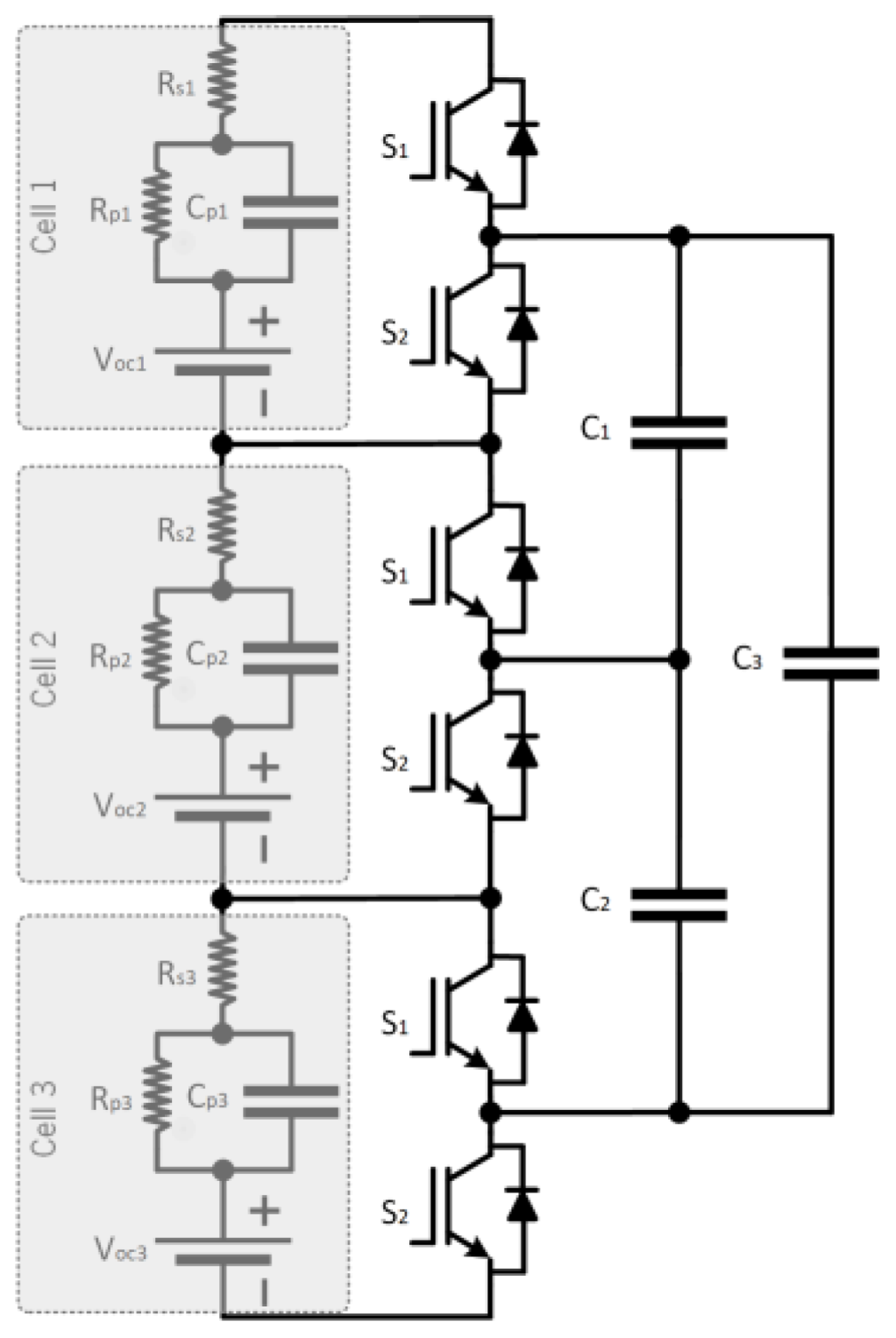
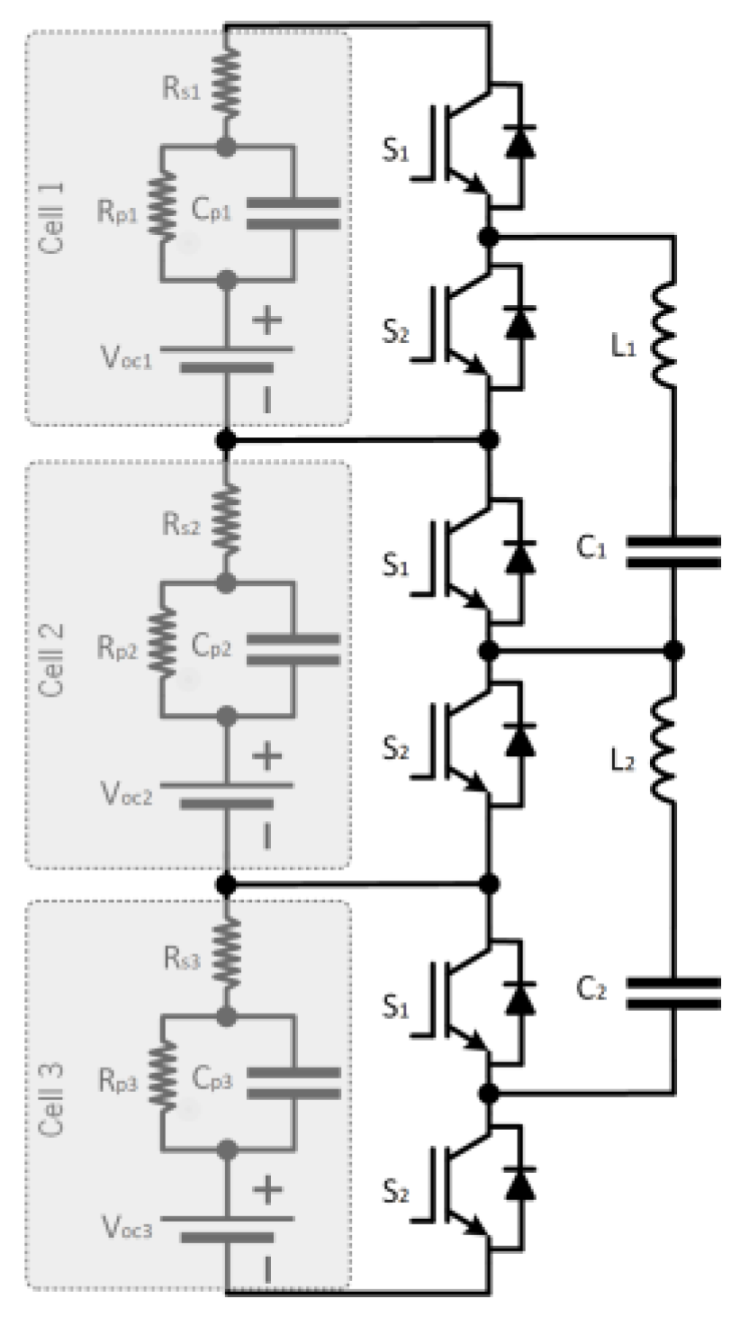
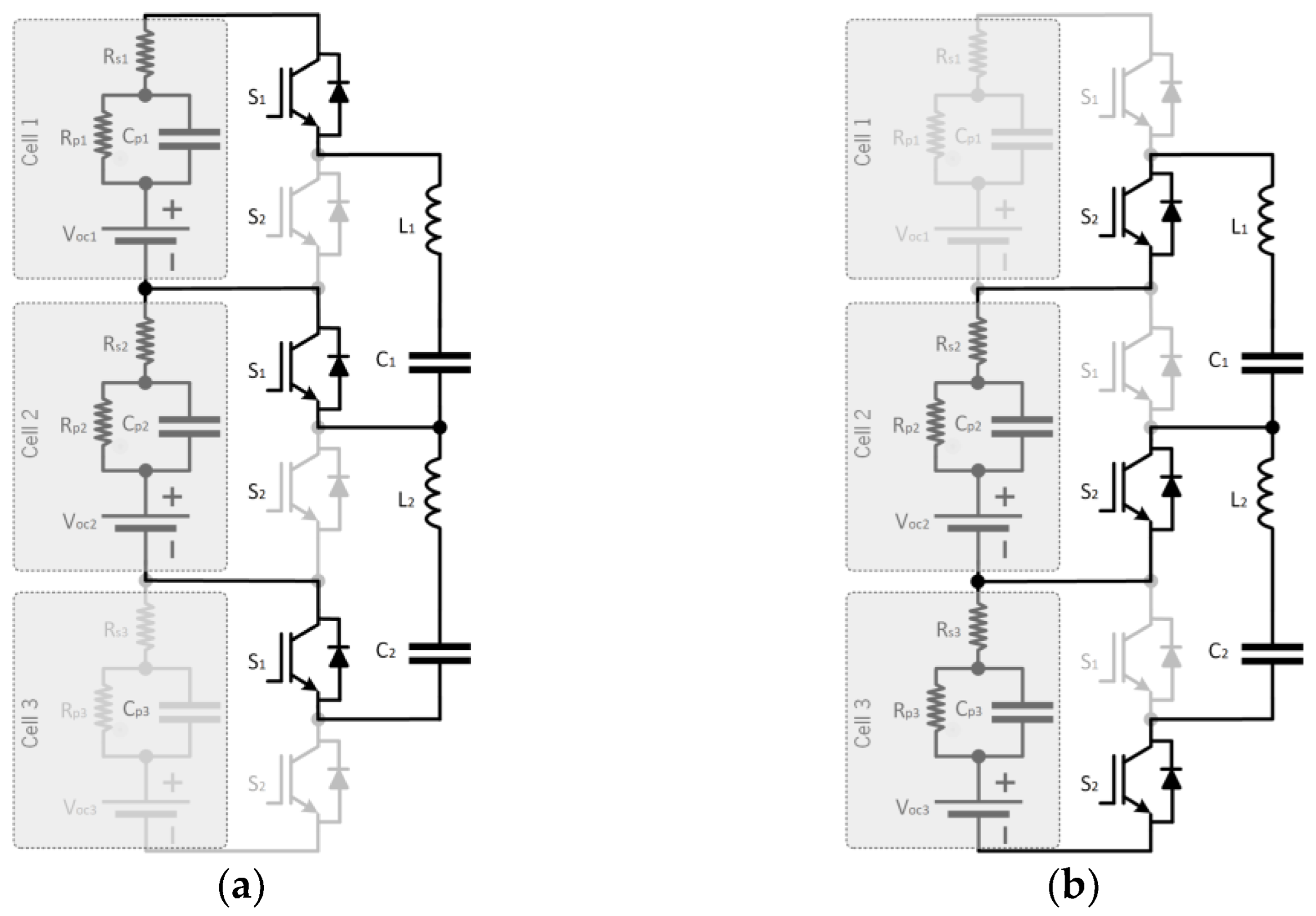
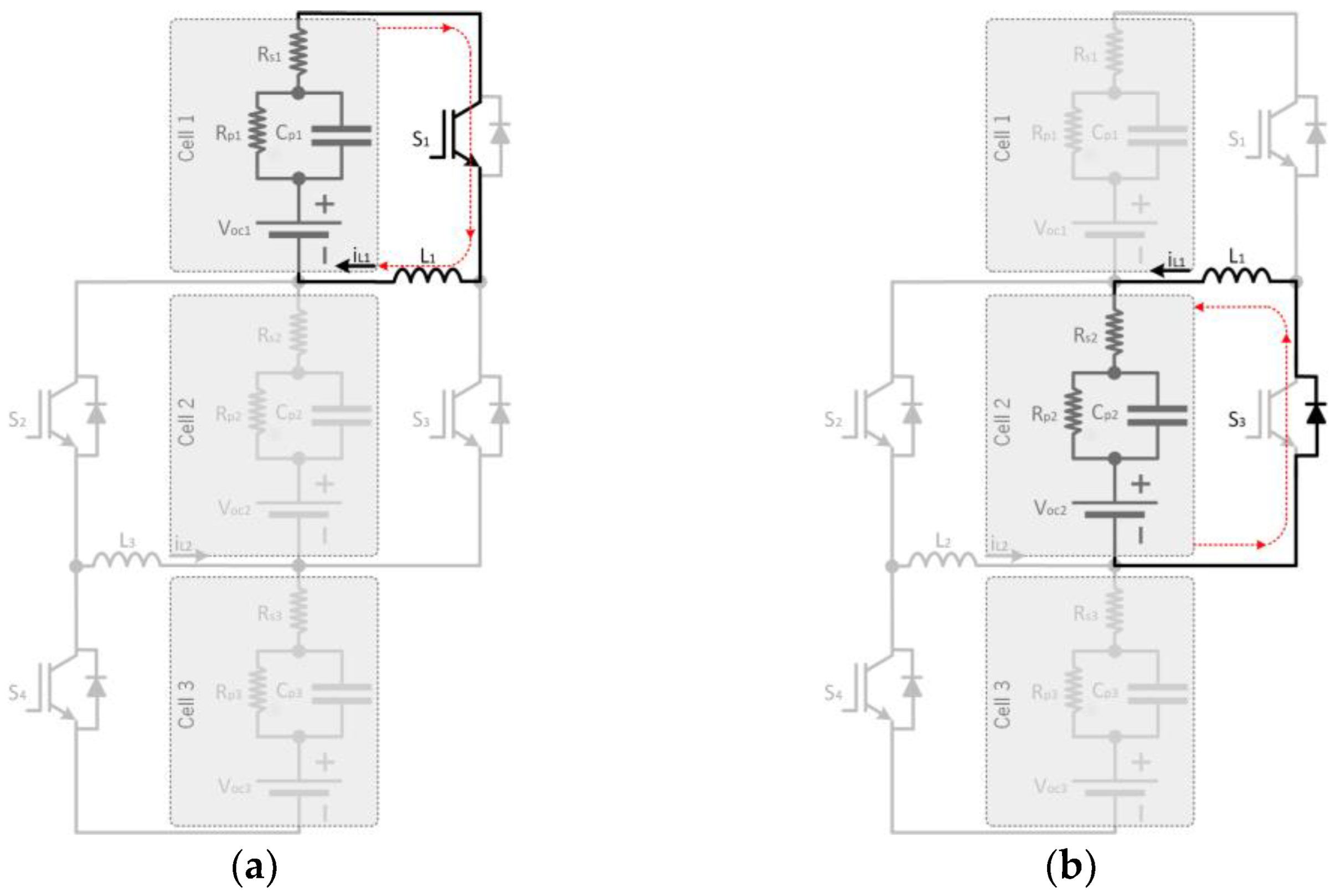
2.4. Single Inductor
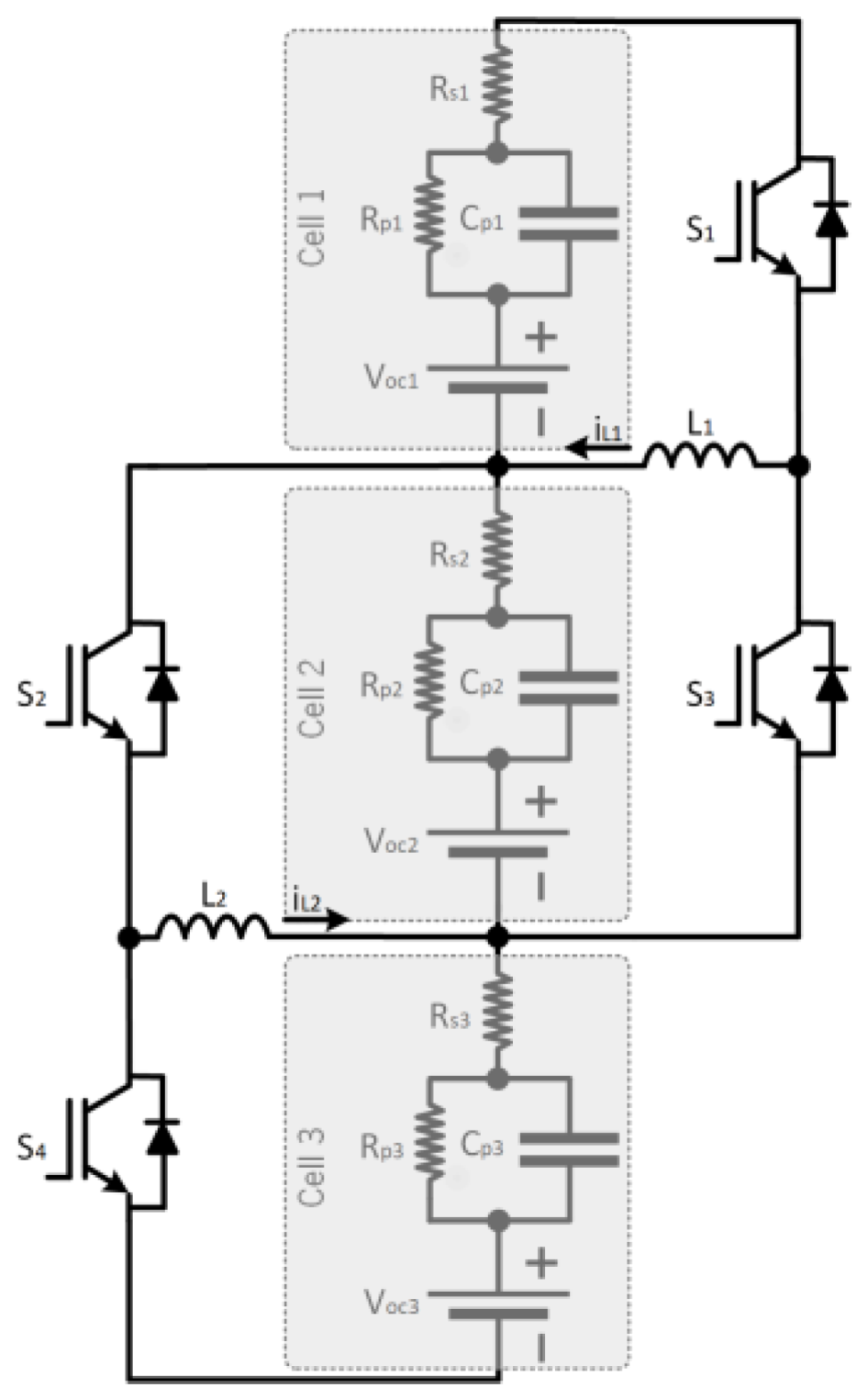
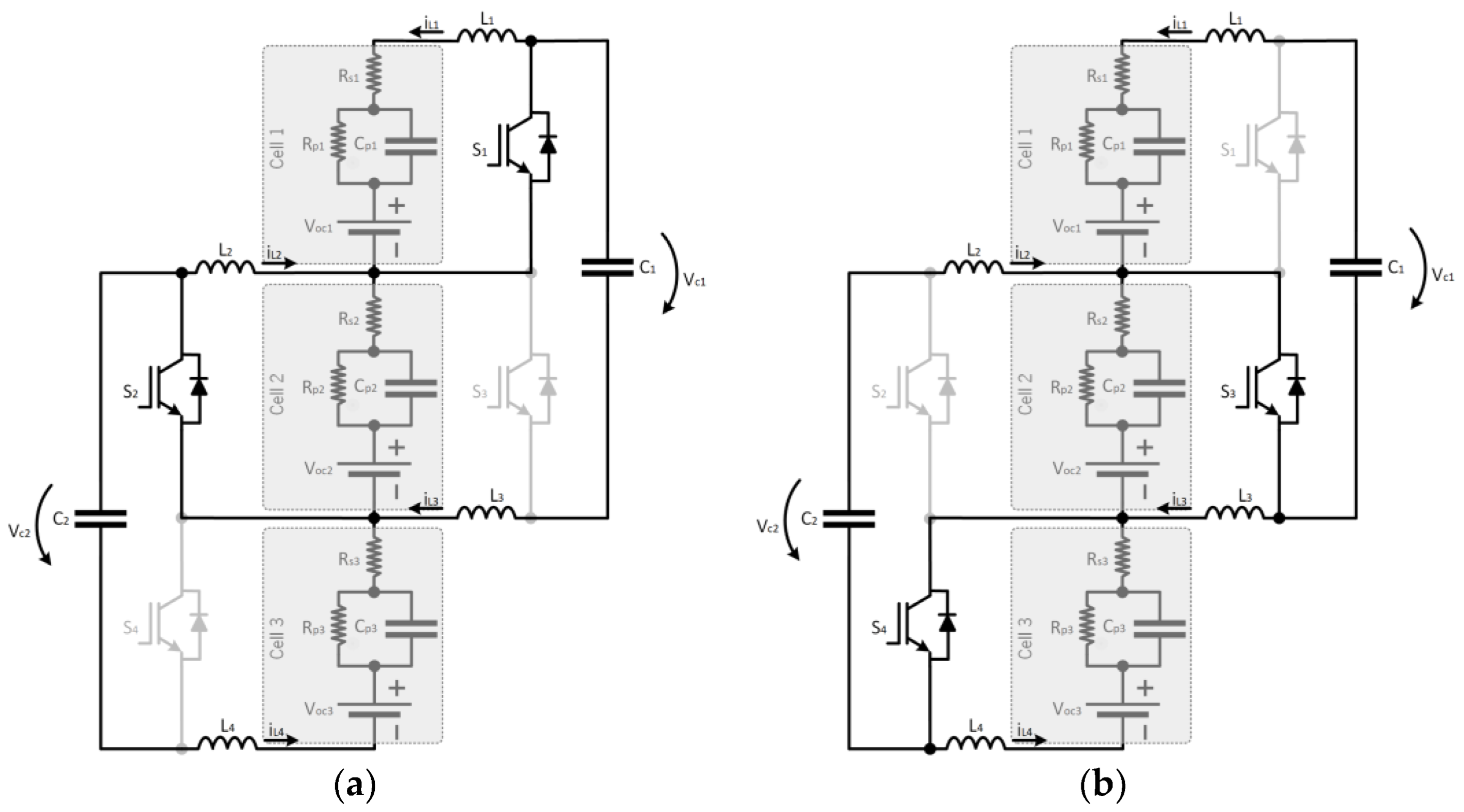
2.5. Switched Inductor
2.6. Cuk
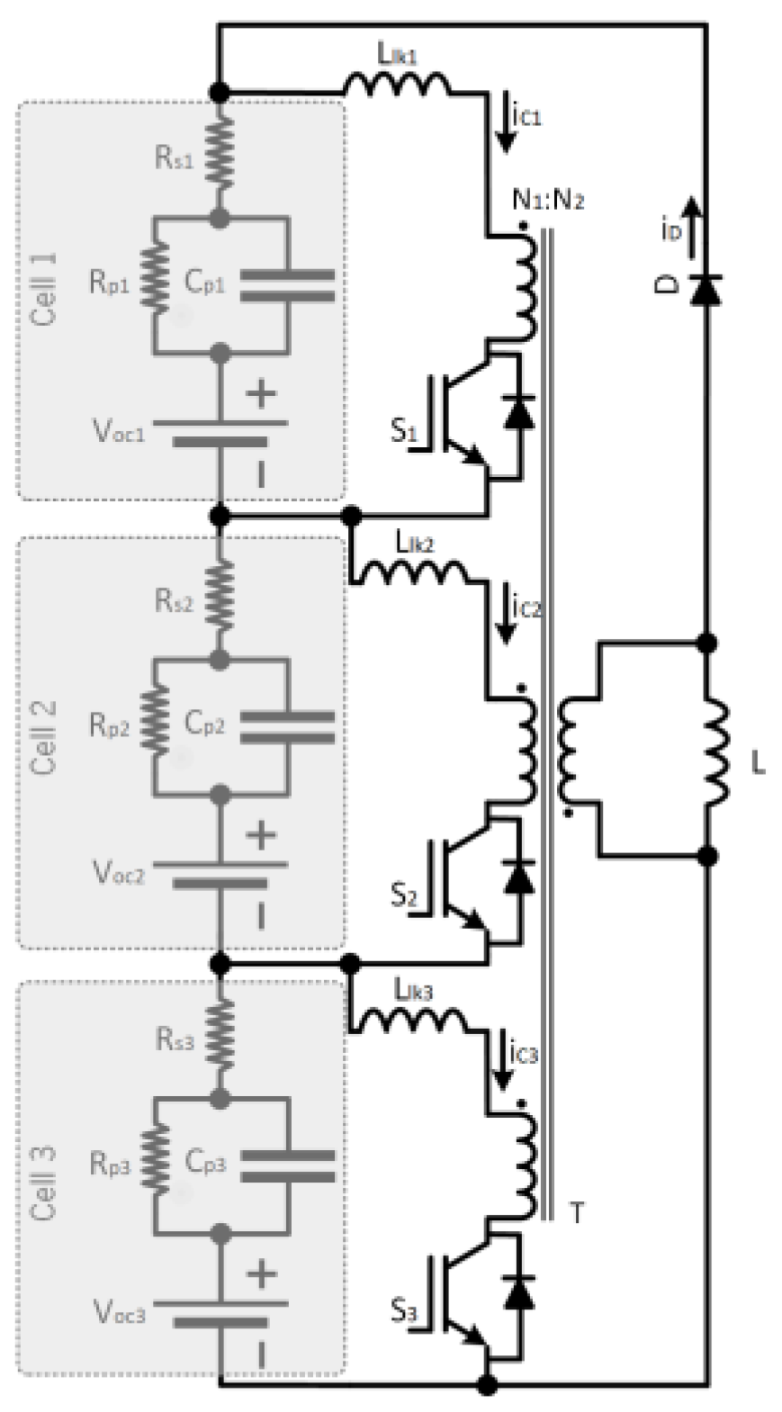
2.7. Single Flyback
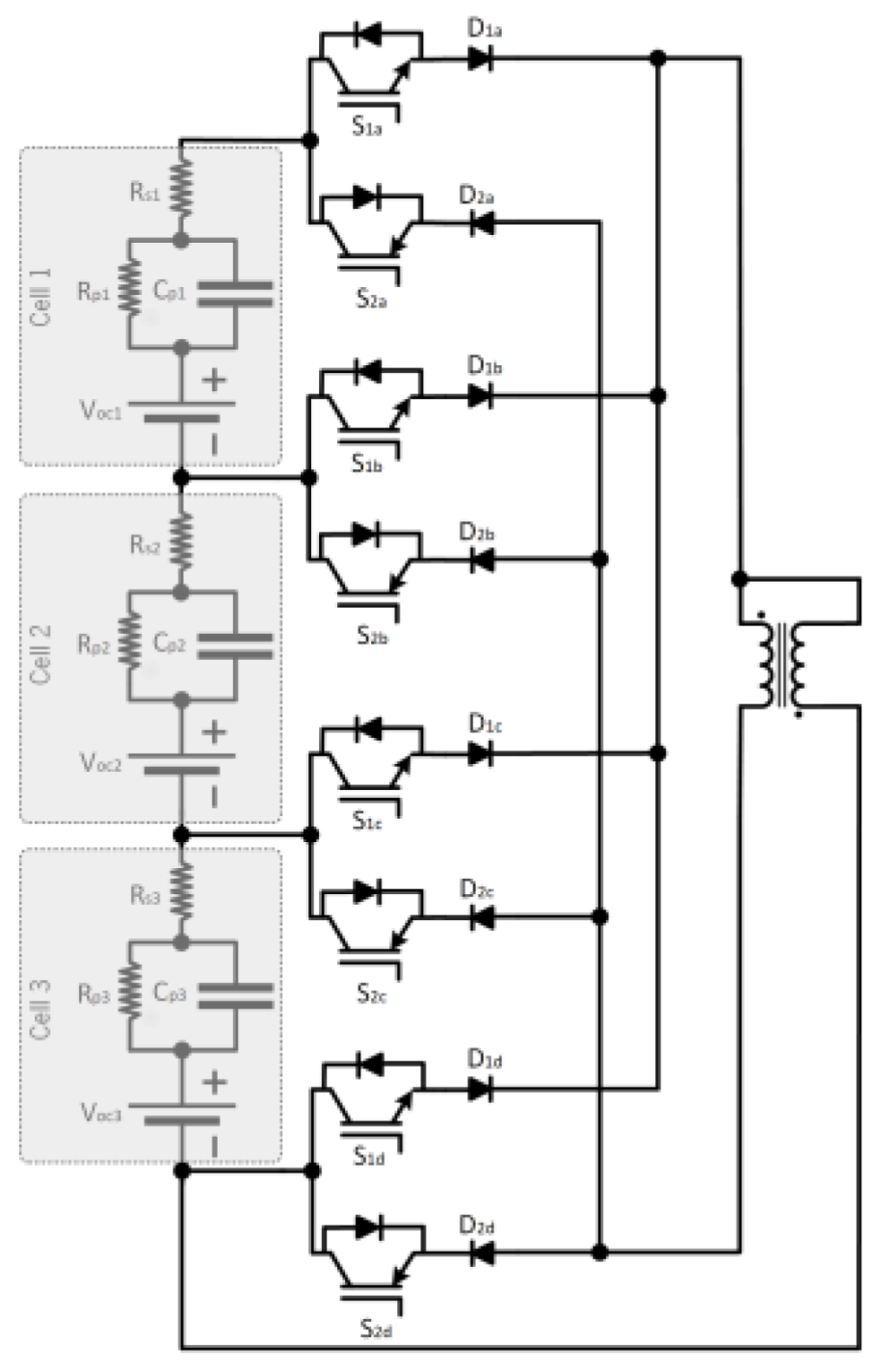
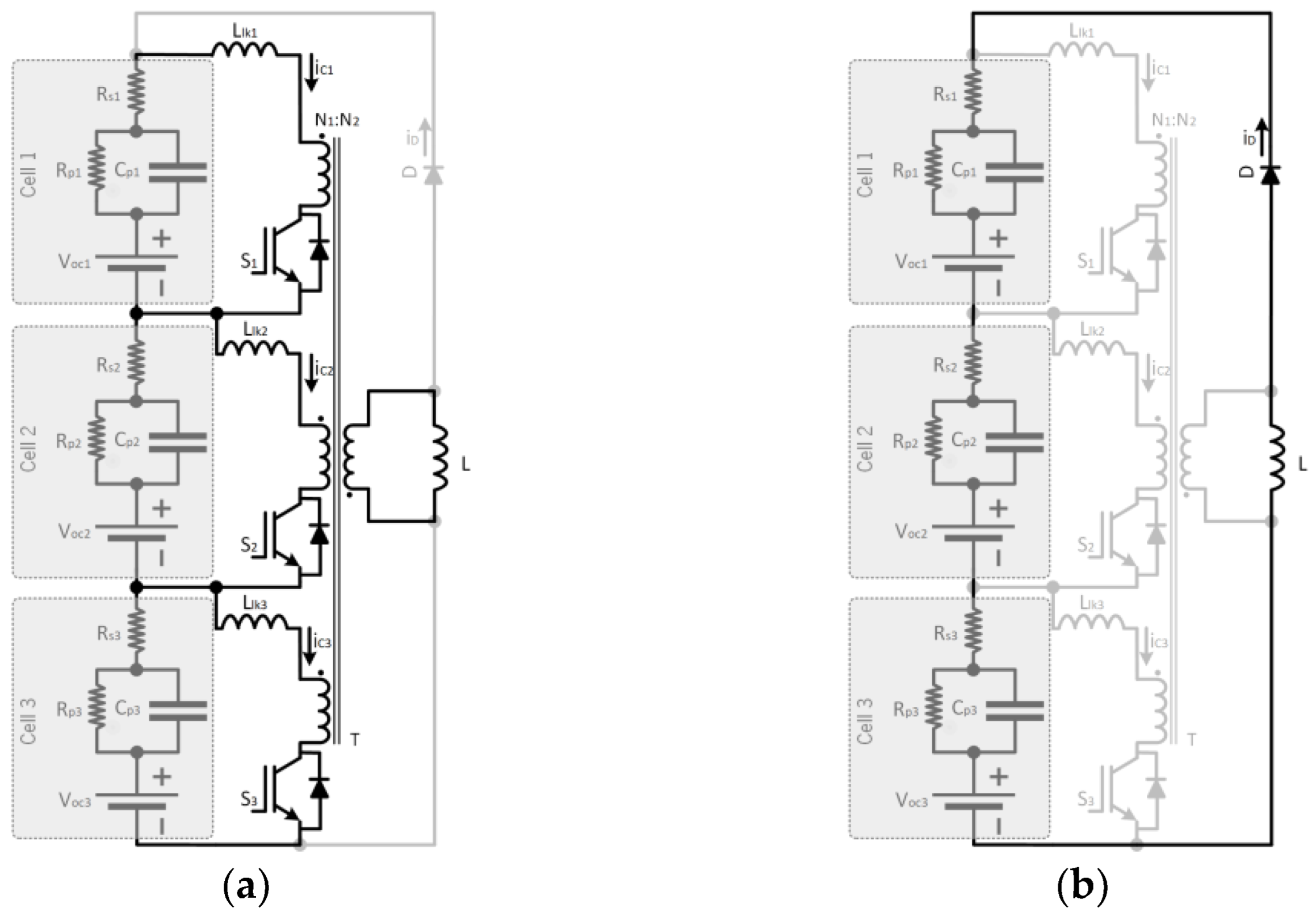
2.8. Multi-Winding Transformer
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Silva, C.M.; Santo, B.E.; Ferreira, L.T. The integration of E-Mobility in smart cities: The Portuguese scenario for EV charging in street light circuits. Inst. Eng. Technol. (IET) 2022, 2022, 472–475. [Google Scholar]
- Ahmed, A.A.; Nazzal, M.A.; Darras, B.M.; Deiab, I.M. Global warming potential, water footprint, and energy demand of shared autonomous electric vehicles incorporating circular economy practices. Sustain. Prod Consum. 2023, 36, 449–462. [Google Scholar] [CrossRef]
- Monteiro, V.; Gonçalves, H.; Afonso, J.L. Impact of Electric Vehicles on Power Quality in a Smart Grid Context. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 1–6. [Google Scholar]
- Greenhouse Gas Emissions from Energy Data Explorer–Data Tools-IEA. Available online: https://www.iea.org/data-and-statistics/data-tools/greenhouse-gas-emissions-from-energy-data-explorer (accessed on 9 February 2023).
- Silva, Ó.; Cordera, R.; González-González, E.; Nogués, S. Environmental impacts of autonomous vehicles: A review of the scientific literature. Sci. Total Environ. 2022, 830, 154615. [Google Scholar] [CrossRef] [PubMed]
- Barzkar, A.; Ghassemi, M. Electric power systems in more and all electric aircraft: A review. IEEE Access 2020, 8, 169314–169332. [Google Scholar] [CrossRef]
- Sumsurooah, S.; He, Y.; Torchio, M.; Kouramas, K.; Guida, B.; Cuomo, F.; Atkin, J.; Bozhko, S.; Renzetti, A.; Russo, A.; et al. ENIGMA—A Centralised Supervisory Controller for Enhanced Onboard Electrical Energy Management with Model in the Loop Demonstration. Energies 2021, 14, 5518. [Google Scholar] [CrossRef]
- Andrea, D. Battery Management Systems for Large Lithium-Ion Battery Packs; Artech House Publishers: London, UK, 2010. [Google Scholar]
- Rashid, M.H. Power Electronics Handbook; Elsevier: Amsterdam, The Netherlands, 2011; pp. 225–250. [Google Scholar]
- Suratgar, A.A.; Menhaj, M.B. Distributed Optimization and Its Application in Electricity Grids, Including Electrical Vehicles. In Electric Transportation Systems in Smart Power Grids; CRC Press: Boca Raton, FL, USA, 2022; pp. 493–520. [Google Scholar]
- Williamson, S.S.; Rathore, A.K.; Musavi, F. Industrial Electronics for Electric Transportation: Current State-of-the-Art and Future Challenges. IEEE Trans. Ind. Electron. 2015, 62, 3021–3032. [Google Scholar] [CrossRef]
- Tan, D. Transportation Electrification: Challenges and opportunities. IEEE Power Electron. Mag. 2016, 3, 50–52. [Google Scholar] [CrossRef]
- Nur Halimah, P.; Rahardian, S.; Budiman, B.A. Battery Cells for Electric Vehicles. Int. J. Sustain. Transp. Technol. 2019, 2, 54–57. [Google Scholar] [CrossRef]
- Iclodean, C.; Varga, B.; Burnete, N.; Cimerdean, D.; Jurchiş, B. Comparison of Different Battery Types for Electric Vehicles. IOP Conf. Ser. Mater. Sci. Eng. 2017, 252. [Google Scholar] [CrossRef]
- Rezvanizaniani, S.M.; Liu, Z.; Chen, Y.; Lee, J. Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility. J. Power Sources 2014, 256, 110–124. [Google Scholar] [CrossRef]
- Lim, K.C. Battery Management System for Electric Vehicles. Master Thesis, University of Wollongong, Hong Kong, 2017. [Google Scholar]
- dos Santos, B.M.B.; Manuel Rodrigues Rocha, R.; Simões Piedade, M. Battery Management System applied to Projecto FST’s EV prototype. Master’s Thesis, Instituto Superior Técnico, Lisboa, Portugal, 2014. [Google Scholar]
- Mauri Rodríguez, E. Disseny, fabricació y validació de la bateria d’alt voltatge del model de formula student CAT13. Bachelor’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2021. [Google Scholar]
- Jiang, B. Active Cell Balancing Algorithms in Lithium-ion Battery. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2020. [Google Scholar]
- Kassim, M.R.M.; Jamil, W.A.W.; Sabri, R.M. State-of-Charge (SOC) and State-of-Health (SOH) Estimation Methods in Battery Management Systems for Electric Vehicles. In Proceedings of the 2021 IEEE International Conference on Computing, ICOCO 2021, Kuala Lumpur, Malaysia, 17–19 November 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 91–96. [Google Scholar]
- Lee, C.Y.; Lee, S.J.; Tang, M.S.; Chen, P.C. In Situ Monitoring of Temperature inside Lithium-Ion Batteries by Flexible Micro Temperature Sensors. Sensors 2011, 11, 9942–9950. [Google Scholar] [CrossRef]
- Tessier, A.O.; Dubois, M.R.; Trovão, J.P. Real-Time Estimator Li-ion Cells Internal Resistance for Electric Vehicle Application. World Electr. Veh. J. 2016, 8, 410–421. [Google Scholar] [CrossRef]
- Alvarez-Diazcomas, A.; Estévez-Bén, A.A.; Rodríguez-Reséndiz, J.; Martínez-Prado, M.A.; Carrillo-Serrano, R.V.; Thenozhi, S. A review of battery equalizer circuits for electric vehicle applications. Energies 2020, 13, 5688. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Sun, D. Review of Battery Cell Balancing Methodologies for Optimizing Battery Pack Performance in Electric Vehicles. IEEE Access 2019, 7, 129335–129352. [Google Scholar] [CrossRef]
- Kıvrak, S.; Özer, T.; Oğuz, Y.; Kelek, M.M. Novel active and passive balancing method-based battery management system design and implementation. J. Power Electron. 2021, 21, 1855–1865. [Google Scholar] [CrossRef]
- Aminudin, I.R.; Aritonang, S. Comparison of Active and Passive Balancing Methods of Li-Ion Battery Management Systems in Vehicles and Communication Devices for Supporting Defense Systems in IKN. UIJRT United Int. J. Res. Technol. 2022, 3, 98–105. [Google Scholar]
- Gabbar, H.; Othman, A.; Abdussami, M. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E. Modeling and Analysis of Series-Parallel Switched-Capacitor Voltage Equalizer for Battery/Supercapacitor Strings. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 977–983. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E. An Automatic Switched-Capacitor Cell Balancing Circuit for Series-Connected Battery Strings. Energies 2016, 9, 138. [Google Scholar] [CrossRef]
- Yildirim, B.; Elgendy, M.; Smith, A.; Pickert, V. Evaluation and Comparison of Battery Cell Balancing Methods. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar]
- Sailaja, D.; Kiran, P.P.; Reddy, K. Modeling and Analysis of Series Parallel Switched-Capacitor Voltage Equalizer for Battery/Supercapacitor Strings; The Hong Kong Polytechnic University Department of Electrical Engineering: Hong Kong, 2016. [Google Scholar]
- Daowd, M.; Antoine, M.; Omar, N.; den Bossche, P.; van Mierlo, J. Single Switched Capacitor Battery Balancing System Enhancements. Energies 2013, 6, 2149–2174. [Google Scholar] [CrossRef]
- Baughman, A.C.; Ferdowsi, M. Double-tiered switched-capacitor battery charge equalization technique. IEEE Trans. Ind. Electron. 2008, 55, 2277–2285. [Google Scholar] [CrossRef]
- Yuanmao, Y.; Cheng, K.W.E.; Yeung, Y.P.B. Zero-current switching switched-capacitor zero-voltage-gap automatic equalization system for series battery string. IEEE Trans. Power Electron. 2012, 27, 3234–3242. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, Q.; Cui, N.; Zhang, C.; Editors, A.; Xiong, R.; Li, H.; Zhou, J. A Cell-to-Cell Equalizer Based on Three-Resonant-State Switched-Capacitor Converters for Series-Connected Battery Strings. Energies 2017, 10, 206. [Google Scholar] [CrossRef]
- Reynaud, J.F.; Carrejo, C.E.; Gantet, O.; Aloïsi, P.; Estibals, B.; Alonso, C. Active balancing circuit for advanced lithium-ion batteries used in photovoltaic application. Renew Energy Power Qual. J. 2010, 1423–1428. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, T.S.; Park, J.S.; Moon, G.W.; Yoon, M.J. A new battery equalizer based on buck-boost topology. In Proceedings of the 7th Internatonal Conference on Power Electronics, Daegu, Republic of Korea, 22–26 October 2007; pp. 962–965. [Google Scholar]
- Moghaddam, A.F.; van den Bossche, A. An Efficient Equalizing Method for Lithium-Ion Batteries Based on Coupled Inductor Balancing. Electronics 2019, 8, 136. [Google Scholar] [CrossRef]
- Sugumar S, H. Overview of cell balancing methods for Li-ion battery technology. Energy Storage 2021, 203, 3. [Google Scholar]
- Moghaddam, A.F.; van den Bossche, A. A Battery Equalization Technique Based on Ćuk Converter Balancing for Lithium Ion Batteries. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies, MOCAST 2019, Thessaloniki, Greece, 13–15 May 2019. [Google Scholar]
- Moghaddam, A.F.; van den Bossche, A. A ćuk converter cell balancing technique by using coupled inductors for lithium-based batteries. Energies 2019, 12, 2881. [Google Scholar] [CrossRef]
- Shin, J.W.; Seo, G.S.; Chun, C.Y.; Cho, B.H. Selective Flyback balancing circuit with improved balancing speed for series connected Lithium-ion batteries. In Proceedings of the 2010 International Power Electronics Conference-ECCE Asia-, IPEC 2010, Sapporo, Japan, 21–24 June 2010; pp. 1180–1184. [Google Scholar]
- Cui, X.; Shen, W.; Zhang, Y.; Hu, C. A novel active online state of charge based balancing approach for Lithium-ion battery packs during fast charging process in electric vehicles. Energies 2017, 10, 1766. [Google Scholar] [CrossRef]
- Minh Bui, T.; Kim, C.-H.; Kim, K.-H.; Bong Rhee, S. A Modular Cell Balancer Based on Multi-Winding Transformer and Switched-Capacitor Circuits for a Series-Connected Battery String in Electric Vehicles. Appl. Sci. 2018, 8, 1278. [Google Scholar]
- Lim, C.S.; Lee, K.J.; Ku, N.J.; Hyun, D.S.; Kim, R.Y. A modularized equalization method based on magnetizing energy for a series-connected lithium-ion battery string. IEEE Trans. Power Electron. 2014, 29, 1791–1799. [Google Scholar] [CrossRef]
- Kim, H.S.; Park, K.B.; Seong, H.W.; Moon, G.W.; Youn, M.J. Flyback battery equalizer with voltage doubler rectifier. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia: “Green World with Power Electronics”, ICPE 2011-ECCE Asia, Jeju, Republic of Korea, 30 May–3 June 2011; pp. 291–295. [Google Scholar]
- Kim, M.Y.; Kim, C.H.; Kim, J.H.; Moon, G.W. A chain structure of switched capacitor for improved cell balancing speed of lithium-ion batteries. IEEE Trans. Ind. Electron. 2014, 61, 3989–3999. [Google Scholar] [CrossRef]
- Thiruvonasundari, D.; Deepa, K. Evaluation and Comparative Study of Cell Balancing Methods for Lithium-Ion Batteries Used in Electric Vehicles. Int. J. Renew. Energy Dev. 2021, 10, 471–479. [Google Scholar]
- Imtiaz, A.M.; Khan, F.H. “Time shared flyback converter” based regenerative cell balancing technique for series connected li-ion battery strings. IEEE Trans. Power Electron. 2013, 28, 5960–5975. [Google Scholar] [CrossRef]



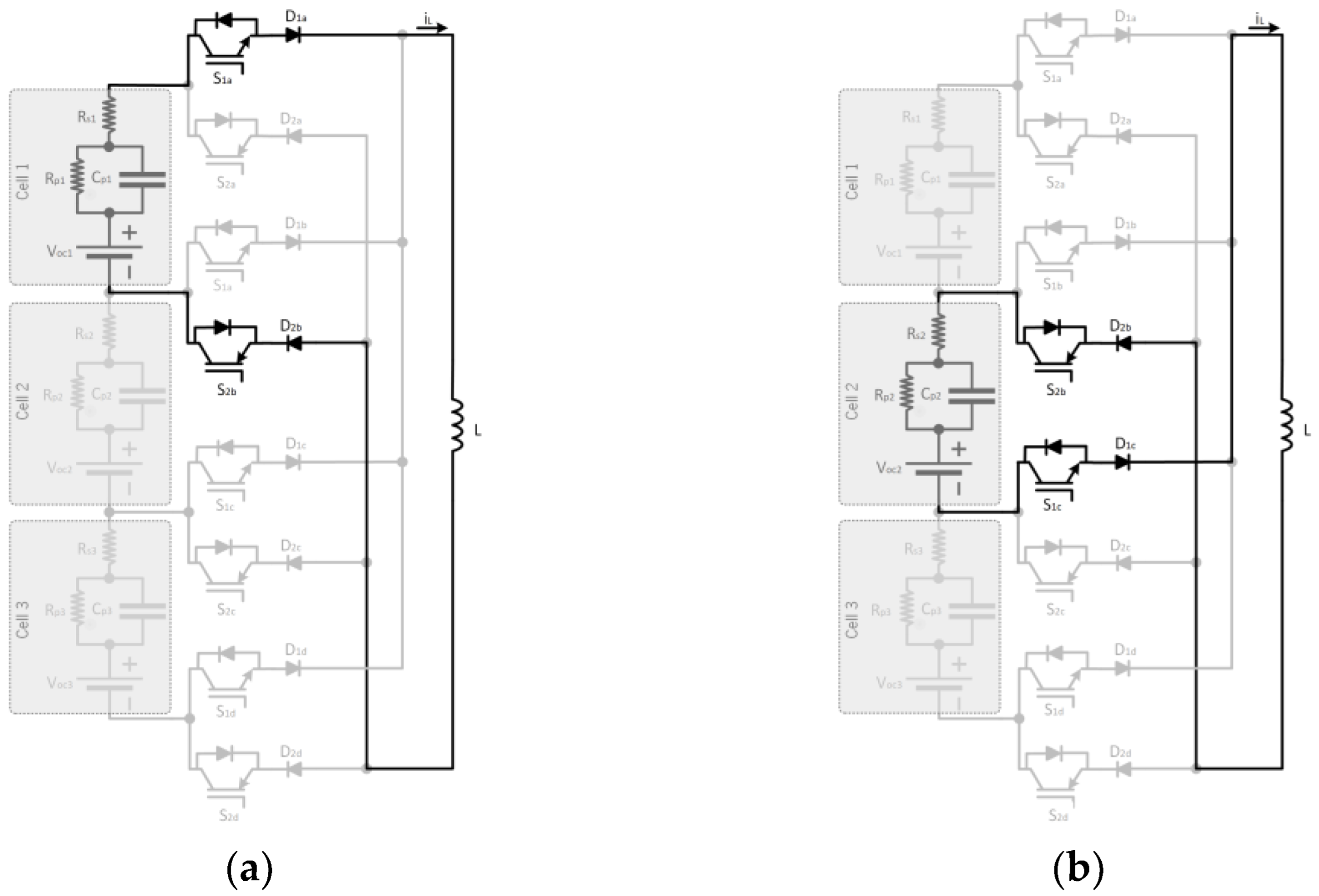





| Vcell1 > Vcell2 | Vcell1 > Vcell3 | Vcell2 > Vcell1 | Vcell2 > Vcell3 | Vcell3 > Vcell1 | Vcell3 > Vcell2 | |
|---|---|---|---|---|---|---|
| Ton | S1a − S2b | S1a − S2b | S1b − S2c | S1b − S2c | S1c − S2d | S1c − S2d |
| Toff = T − Ton | S2b − S1c | S2c − S1d | S2c − S1d | S2a − S1b | S2a − S1b | S2b − S1c |
| Balancer Type | Switch Amounts | Cell Amounts | Cell Type | Cell Capacity | Efficiency |
|---|---|---|---|---|---|
| Switched-capacitor [47] | 4n − 3 | 8 | Li-on | 15.5 Ah | 97.73% |
| Double-tiered capacitor [32] | 2n | 1 | Li-on | 12 Ah | 99% |
| Switched capacitor-inductor [35] | 2n | - | - | - | 89.1% |
| Single-inductor [36] | 2(n + 1) | 1 | Li-on | 10 Ah | 91.5% |
| Switched-inductor [48] | 2(n − 1) | 14 | LiFePO4 | 3.35Ah | 99.7% |
| Cuk [41] | 2(n − 1) | 1 | LiPo | 1 Ah | 94% |
| Single flyback [49] | 2(n + 1) | 1 | LiFePO4 | 2.65 Ah | 88% |
| Multi-winding flyback [46] | n | 4 | Li-on | 2.6 Ah | 73.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miranda, J.P.D.; Barros, L.A.M.; Pinto, J.G. A Review on Power Electronic Converters for Modular BMS with Active Balancing. Energies 2023, 16, 3255. https://doi.org/10.3390/en16073255
Miranda JPD, Barros LAM, Pinto JG. A Review on Power Electronic Converters for Modular BMS with Active Balancing. Energies. 2023; 16(7):3255. https://doi.org/10.3390/en16073255
Chicago/Turabian StyleMiranda, João P. D., Luis A. M. Barros, and José Gabriel Pinto. 2023. "A Review on Power Electronic Converters for Modular BMS with Active Balancing" Energies 16, no. 7: 3255. https://doi.org/10.3390/en16073255
APA StyleMiranda, J. P. D., Barros, L. A. M., & Pinto, J. G. (2023). A Review on Power Electronic Converters for Modular BMS with Active Balancing. Energies, 16(7), 3255. https://doi.org/10.3390/en16073255








