A Robust Participation in the Load Following Ancillary Service and Energy Markets for a Virtual Power Plant in Western Australia
Abstract
:1. Introduction
1.1. Ancillary Services in WEM
1.2. Contributions and Structure
- Developing an expert model for a fast and robust bidding strategy in the LFAS and energy markets, considering PV generation, energy storage scheduling and a gamified contribution of consumers to maximize the profit of the VPP and reduce consumers’ energy costs;
- Analysis of the economic viability of the realistic VPP when participating in the LFAS and energy markets, including the payback period, internal rate of return, cash flow, profit, etc., over the lifetime of the project;
- Comparison of the proposed fast bidding strategy with a traditional robust mathematical approach to show the effectiveness of the proposed strategy for deciding or changing the bidding values in a short period of time.
2. Problem Formulation
2.1. The Modelling of Gamification for Customer Engagement
2.2. The Constraints
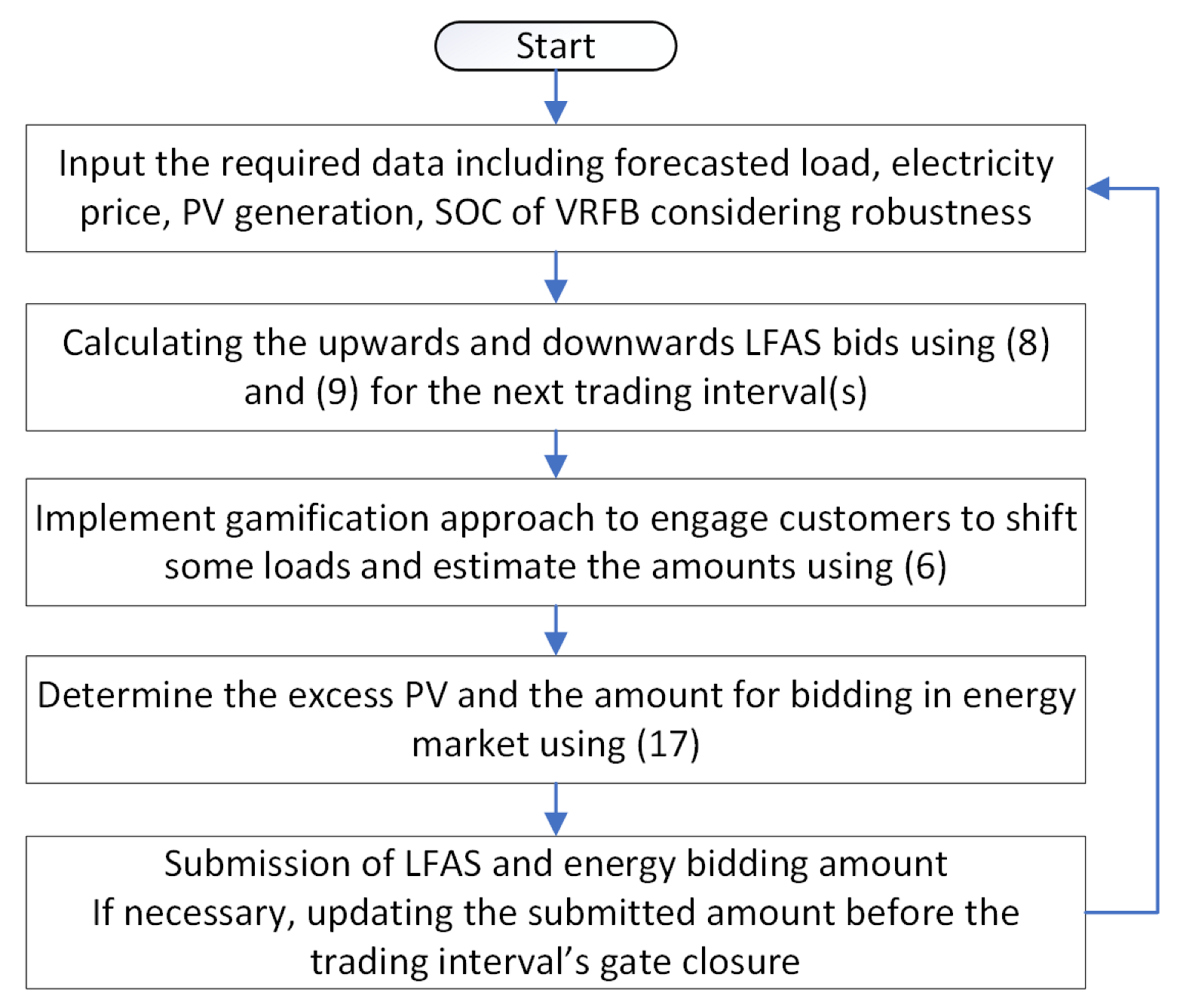
3. A Robust Bidding Strategy for the LFAS and Energy Markets
- The VRFB is dedicated to participating in the LFAS market;
- The excess PV generation is sold to the energy market after covering the customer’s load during PV generation.
3.1. Bidding Model in the LFAS Market
3.2. Bidding Model in Energy Market
3.3. Robustness Consideration
3.4. A Robust Bidding Strategy for the Energy Market Only
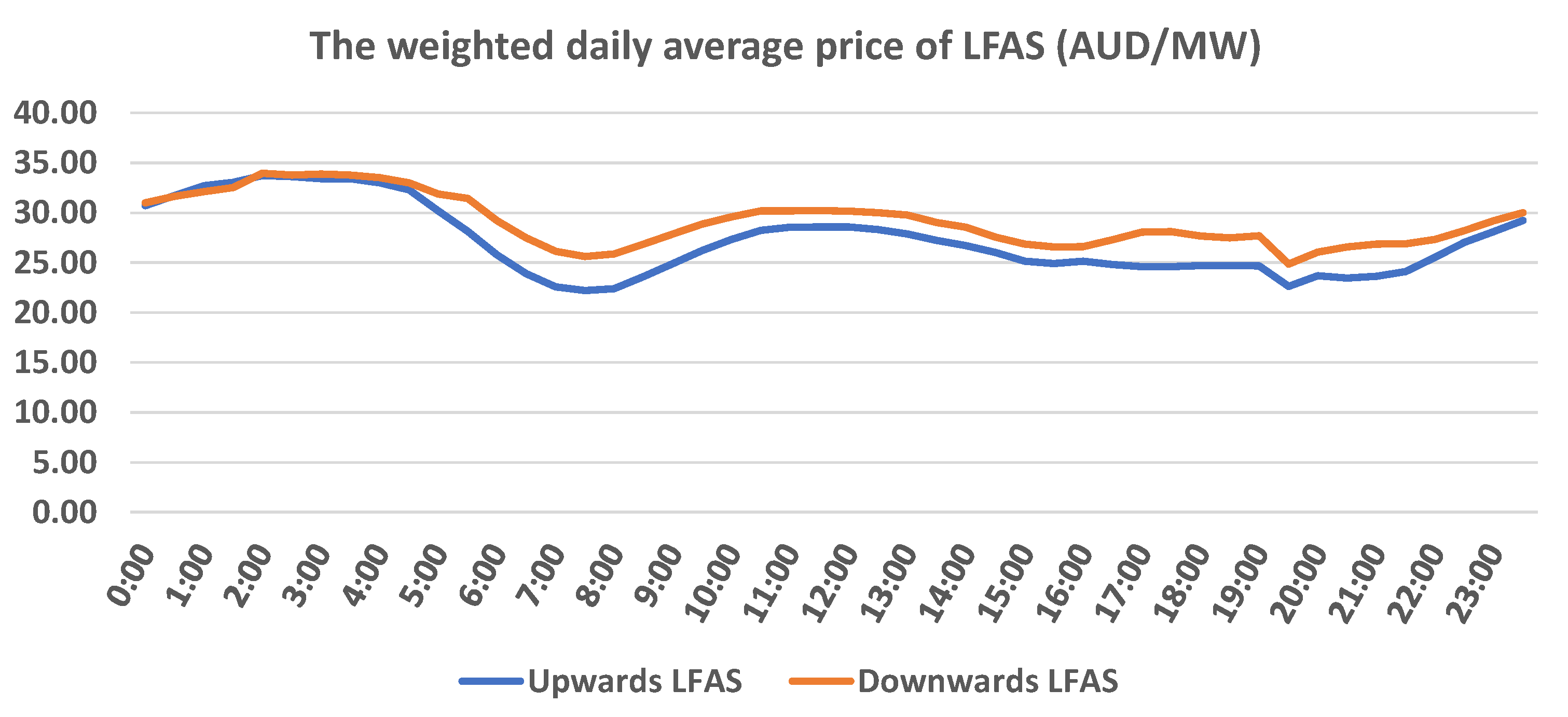
4. Simulation Results
4.1. Assumptions
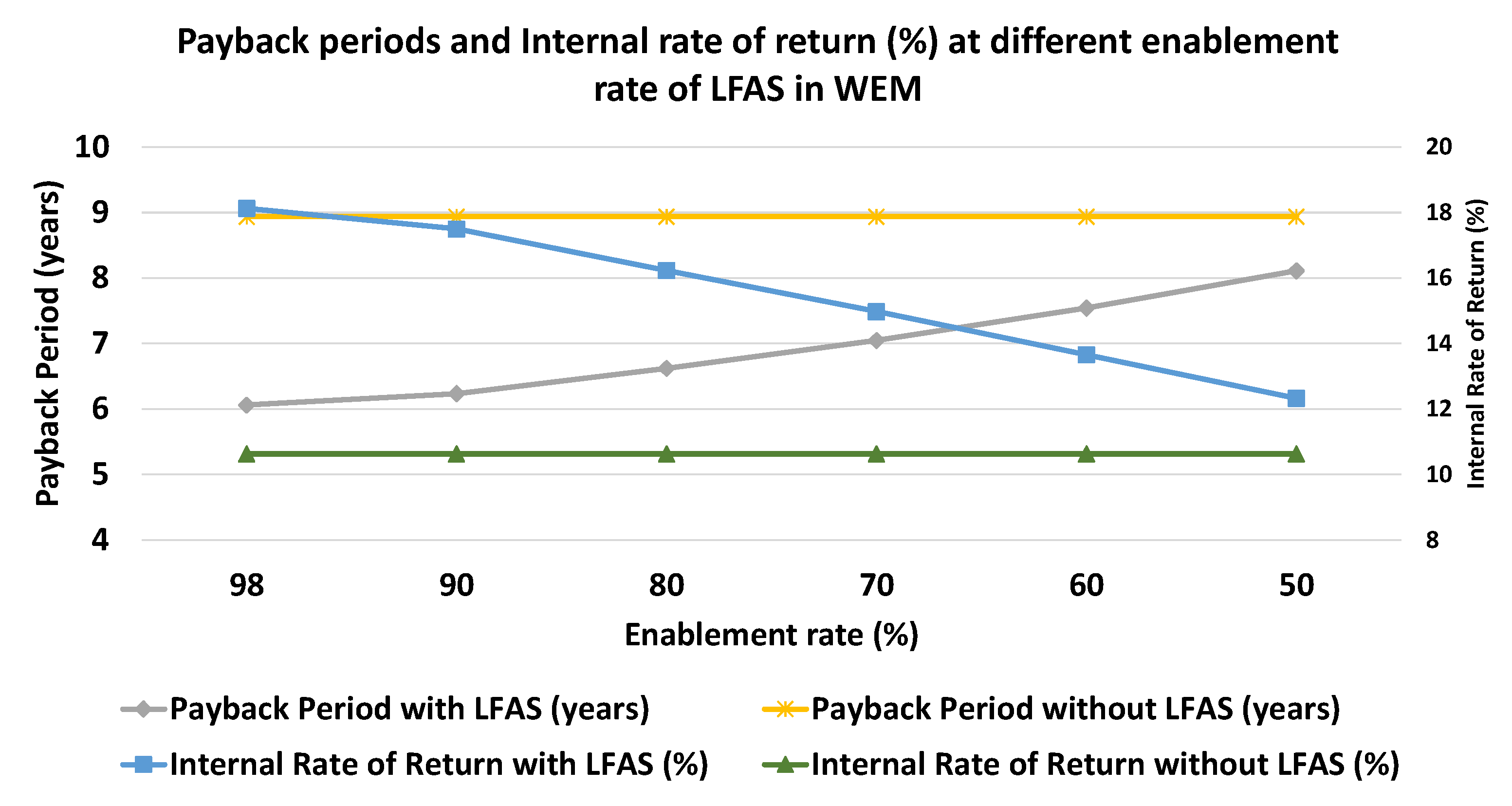
4.2. Economic Comparison
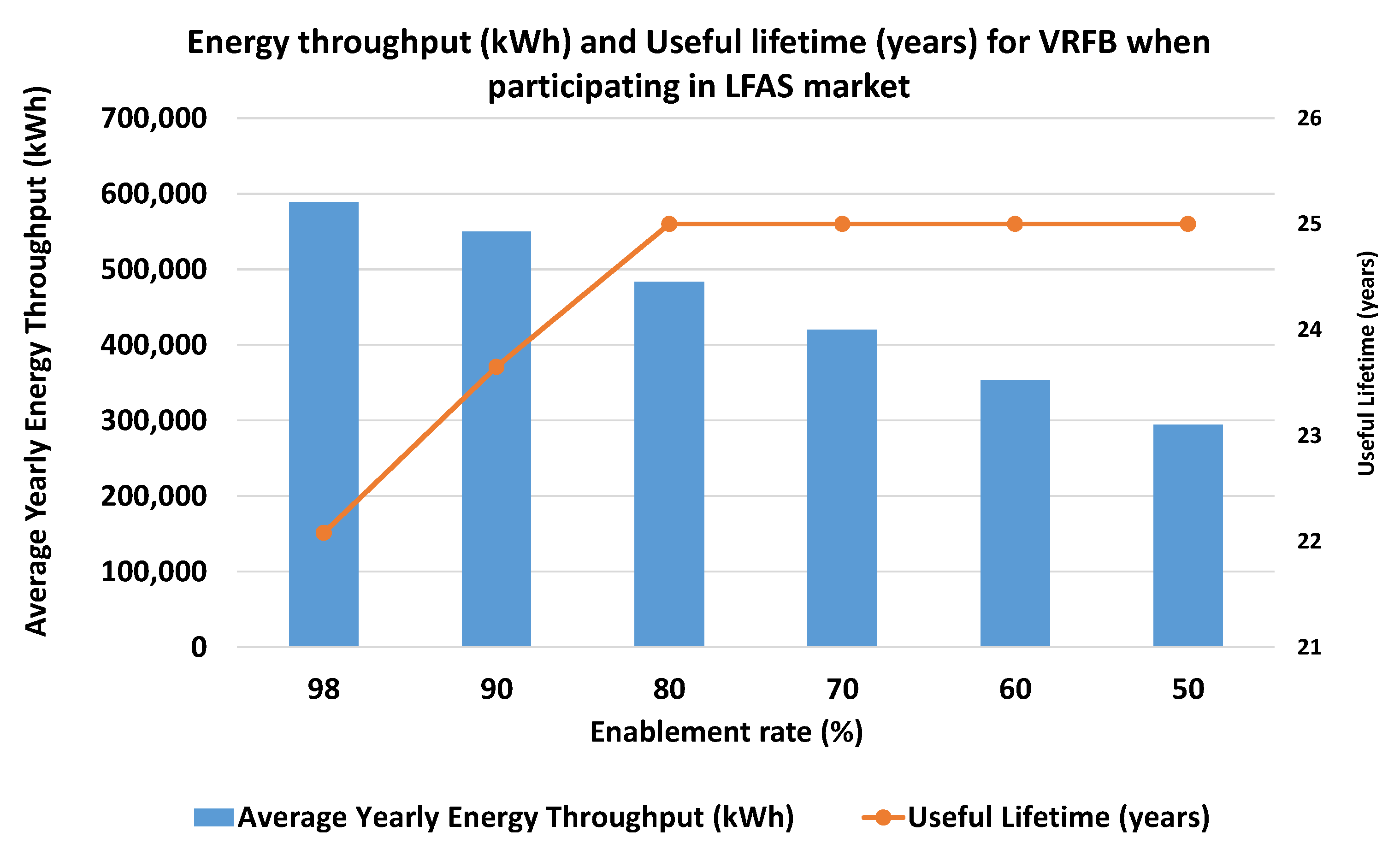
4.3. Energy Throughput and Lifetime of VRFB
4.4. Cash Flow Analysis
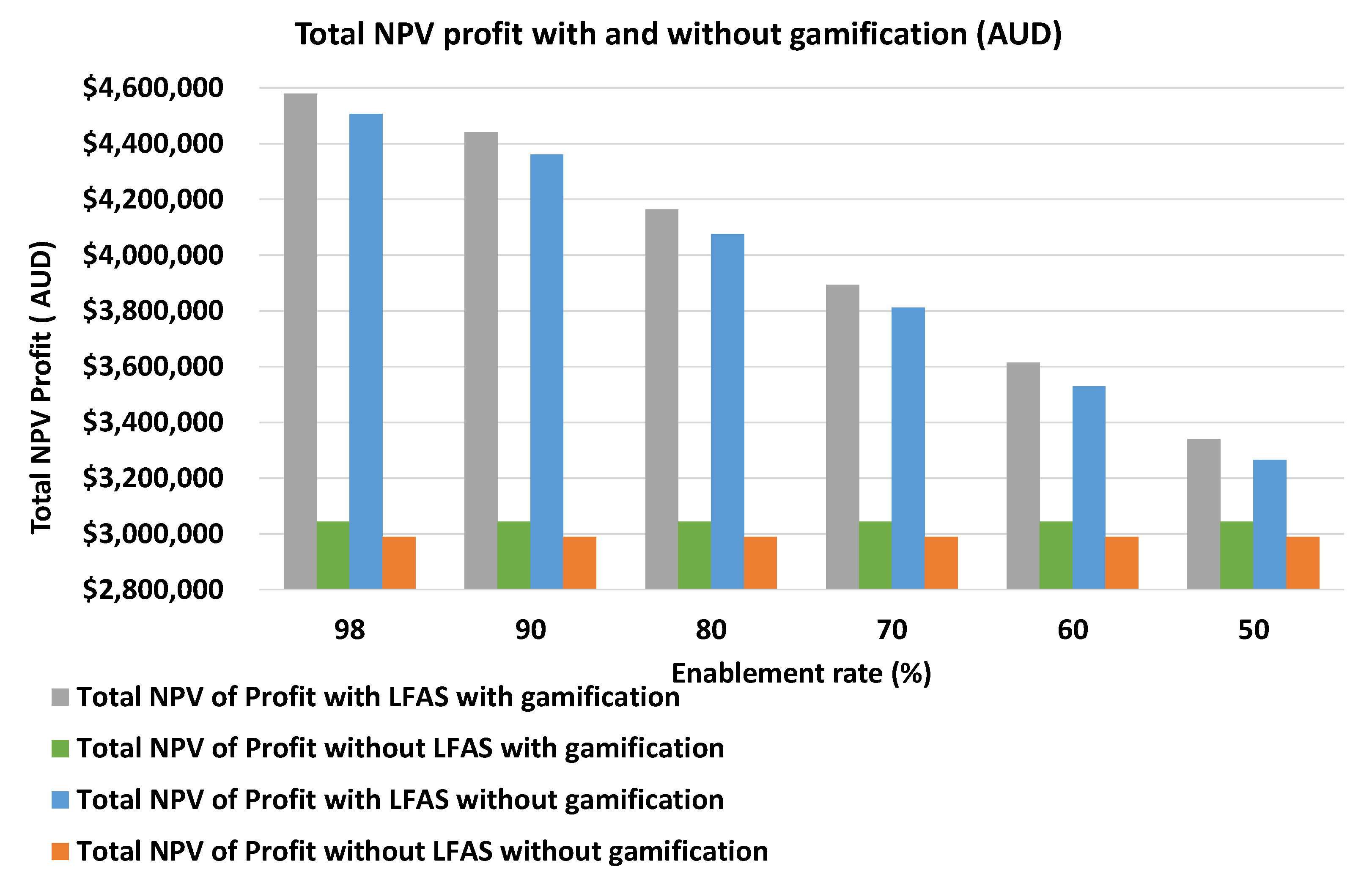
4.5. The Impact of Gamification
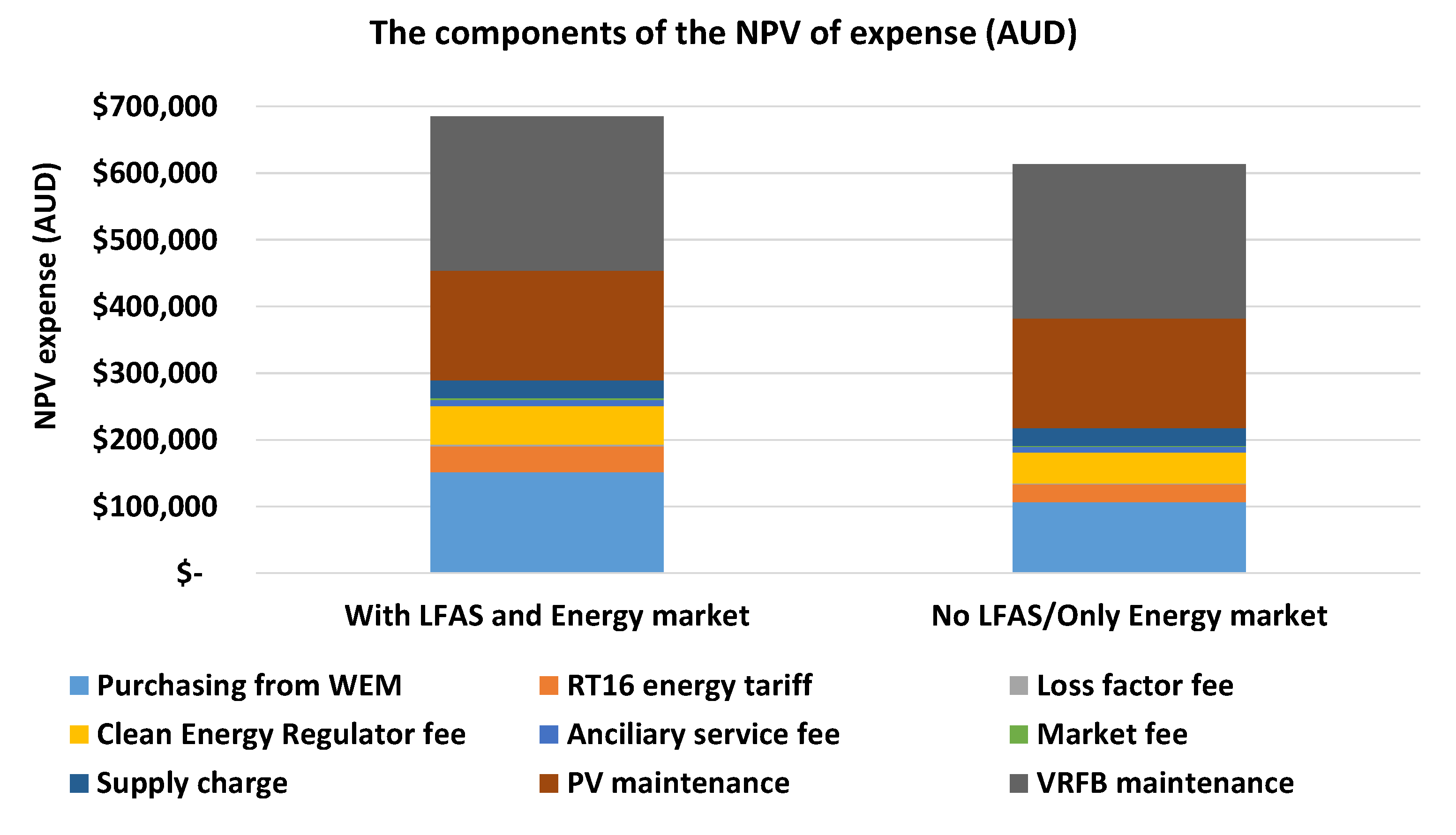
4.6. The Components of the NPV of Revenues and Expenses
4.7. Customer Benefit
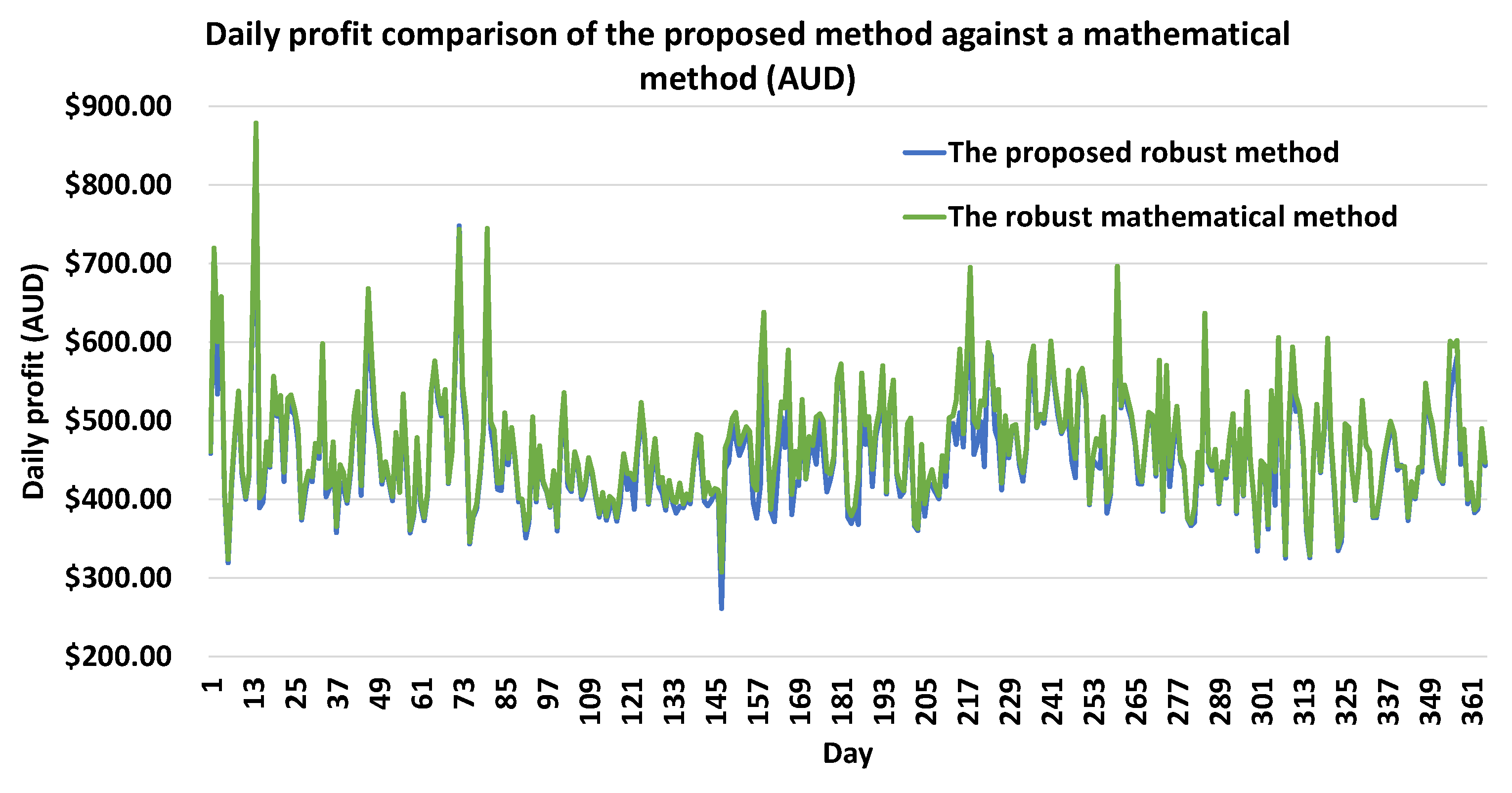
4.8. Comparison with a Robust Mathematical Algorithm
5. Discussion
- In the electricity market, there is a gate closure moment right before each trading interval [15]. The participants can provide an updated bid for the energy and LFAS markets based on the most recent and up-to-date data and information to maximise their profit. As this period for decision making is very short, many participants cannot effectively use this period due to the higher computational efforts of their bidding algorithm. Therefore, the speed of algorithm needs to be very high to accommodate the need for very quick decision making.Although the error of the proposed method is about 2.7%, the speed of the proposed algorithm (about 1435 times faster) enables the participants to maximise their profit by a better bidding value for each trading interval before the gate closure. If the proposed algorithm improves the bidding for each trading interval by as little as 5% (as an indication) on average, the total benefit of participants due to the use of the proposed algorithm would be higher when compared with the other strategies.
- Sometimes, participants want to analyse uncertainties and different input parameters before the closing gate of each trading interval to find an optimal bid. In such situations, the speed of the algorithm is much more critical. In these cases, the proposed algorithm can attain the opportunity for market participants.
- In long-term power system planning, we need thousands of iterations with thousands of variables. The inclusion of the electricity market in planning and analysis with a bidding strategy that is not fast enough, results in a huge computational effort in the scale of many days. Therefore, the proposed fast bidding strategy is crucial from the planning perspective. Another benefit of the fast algorithm is the much lower memory required for attaining an optimal bid, specifically in the context of planning.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Glossary
| Abbreviations | |
| AEMO | Australian Energy Market Operator |
| AGC | Automatic Generation Control |
| AUD | Australian Dollar |
| CAPEX | Capital expenditure |
| CRF | Capital recovery factor |
| DoD | Depth of discharge |
| DSS | Dispatch support service |
| HWS | Hot water system |
| IRR | Internal rate of return |
| LFAS | Load-following ancillary service |
| LRRAS | Load rejection reserve ancillary service |
| NPV | Net present value |
| PV | Photovoltaic |
| SD | Standard deviation |
| SOC | State of charge |
| SRAS | Spinning reserve ancillary service |
| SRS | System restart service |
| TOU | Time of use tariff |
| VPP | Virtual power plant |
| VRFB | Vanadium redox flow battery |
| WA | Western Australia |
| WEM | Wholesale electricity market |
| Variables | |
| Total revenue of the VPP | |
| Total expenses of the VPP | |
| The fixed revenue | |
| The variable revenue | |
| The amount of energy sold to the electricity energy market | |
| The amount of energy sold to customers | |
| The bidding power for the upwards LFAS market | |
| The bidding power for the downwards LFAS market | |
| The amount of energy generated by the PV system | |
| The maximum SOC of VRFB | |
| The bidding amount in the energy market | |
| The energy market price | |
| The agreed energy price for selling to customers | |
| Year, Day, Hour | |
References
- Prime Minister’s Office. Australia’s Plan to Reach Our Net Zero Target by 2050; Prime Minister’s Office: Barton, Australia, 2021. [Google Scholar]
- Nallainathan, S.; Arefi, A.; Lund, C.; Mehrizi-Sani, A.; Stephens, D. Reliability Evaluation of Renewable-Rich Microgrids Using Monte Carlo Simulation Considering Resource and Equipment Availability. In Proceedings of the 2020 IEEE International Conference on Power Systems Technology (POWERCON), Bangalore, India, 14–16 September 2020; pp. 1–6. [Google Scholar]
- Bhuiyan, E.A.; Hossain, M.Z.; Muyeen, S.M.; Fahim, S.R.; Sarker, S.K.; Das, S.K. Towards next generation virtual power plant: Technology review and frameworks. Renew. Sustain. Energy Rev. 2021, 150, 111358. [Google Scholar] [CrossRef]
- Behi, B.; Baniasadi, A.; Arefi, A.; Gorjy, A.; Jennings, P.; Pivrikas, A. Cost–Benefit Analysis of a Virtual Power Plant Including Solar PV, Flow Battery, Heat Pump, and Demand Management: A Western Australian Case Study. Energies 2020, 13, 2614. [Google Scholar] [CrossRef]
- Abdullah, W.S.W.; Osman, M.; Kadir, M.Z.A.A.; Verayiah, R.; Aziz, N.F.A.; Rasheed, M.A. Techno-economics analysis of battery energy storage system (BESS) design for virtual power plant (VPP)–A case study in Malaysia. J. Energy Storage 2021, 38, 102568. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, W.; Qian, F.; Li, Y. Evaluation of economic benefits of virtual power plant between demand and plant sides based on cooperative game theory. Energy Convers. Manag. 2021, 238, 114180. [Google Scholar] [CrossRef]
- Gong, H.; Jones, E.S.; Alden, R.E.; Frye, A.G.; Colliver, D.; Ionel, D.M. Virtual Power Plant Control for Large Residential Communities Using HVAC Systems for Energy Storage. IEEE Trans. Ind. Appl. 2022, 58, 622–633. [Google Scholar] [CrossRef]
- Rahimi, M.; Ardakani, F.J.; Olatujoye, O.; Ardakani, A.J. Two-stage interval scheduling of virtual power plant in day-ahead and real-time markets considering compressed air energy storage wind turbine. J. Energy Storage 2022, 45, 103599. [Google Scholar] [CrossRef]
- Liu, H.; Qiu, J.; Zhao, J. A data-driven scheduling model of virtual power plant using Wasserstein distributionally robust optimization. Int. J. Electr. Power Energy Syst. 2022, 137, 107801. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Latif, A.; Shaoo, S.C.; Das, D.C.; Hussain, S.M.S.; Ustun, T.S. Analysis of GOA optimized two-stage controller for frequency regulation of grid integrated virtual power plant. Energy Reports 2022, 8, 493–500. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, T.; Parisio, A. Frequency regulation and congestion management by Virtual Storage Plants. Sustain. Energy Grids Netw. 2022, 29, 100586. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, M.; Lin, H.; Li, W. Two-stage adjustable robust optimal dispatching model for multi-energy virtual power plant considering multiple uncertainties and carbon trading. J. Clean. Prod. 2022, 336, 130400. [Google Scholar] [CrossRef]
- Fang, F.; Yu, S.; Xin, X. Data-Driven-Based Stochastic Robust Optimization for a Virtual Power Plant With Multiple Uncertainties. IEEE Trans. Power Syst. 2022, 37, 456–466. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, J.; Zhao, J.; Chai, Q.; Dong, Z.Y. Bargaining Game-Based Profit Allocation of Virtual Power Plant in Frequency Regulation Market Considering Battery Cycle Life. IEEE Trans. Smart Grid 2021, 12, 2913–2928. [Google Scholar] [CrossRef]
- Wholesale Electricity Market Rules; Government of Western Australia: Perth, WA, Australia, 2021.
- Wang, H.; Riaz, S.; Mancarella, P. Integrated techno-economic modeling; flexibility analysis, and business case assessment of an urban virtual power plant with multi-market co-optimization. Appl. Energy 2020, 259, 114142. [Google Scholar] [CrossRef]
- Liang, H.; Ma, J. Data-Driven Resource Planning for Virtual Power Plant Integrating Demand Response Customer Selection and Storage. IEEE Trans. Ind. Inform. 2022, 18, 1833–1844. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive Dispatch Modes and Bidding Strategy of Multiple Virtual Power Plants Based on Demand Response and Game Theory. IEEE Trans. Smart Grid 2016, 7, 510–519. [Google Scholar] [CrossRef]
- Behi, B.; Arefi, A.; Jennings, P.; Pivrikas, A.; Gorjy, A.; Catalão, J.P.S. Consumer Engagement in Virtual Power Plants through Gamification. In Proceedings of the 2020 5th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 12–14 September 2020; pp. 131–137. [Google Scholar]
- System Management. Ancillary Service Report for the WEM 2021. AEMO, Western Australia 2021. Available online: https://www.aemo.com.au/-/media/files/electricity/wem/data/system-management-reports/2021-ancillary-services-report.pdf?la=en (accessed on 1 June 2021).
- Behi, B.; Arefi, A.; Jennings, P.; Pivrikas, A.; Gorjy, A.; Ghosh, A. A Robust Bidding Strategy for VPPs Including Gamified Customer Engagement. In Proceedings of the 2021 31st Australasian Universities Power Engineering Conference (AUPEC), Virtual Conference, 26–30 September 2021; pp. 1–6. [Google Scholar]
- Western Power. 2019/20 Price List. Available online: https://westernpower.com.au/media/3361/price-list-2019-2020.pdf (accessed on 28 February 2019).
- INVINITY Energy Systems. INVINITY VS3-022: Six Pack Vanadium Flow Battery; INVINITY: West Lothian, UK, 2021. [Google Scholar]
- Moghaddam, S.Z.; Akbari, T. Network-constrained optimal bidding strategy of a plug-in electric vehicle aggregator: A stochastic/robust game theoretic approach. Energy 2018, 151, 478–489. [Google Scholar] [CrossRef]
- Behi, B.; Arefi, A.; Jennings, P.; Gorjy, A.; Pivrikas, A. Advanced Monitoring and Control System for Virtual Power Plants for Enabling Customer Engagement and Market Participation. Energies 2021, 14, 1113. [Google Scholar] [CrossRef]
- Azizivahed, A.; Razavi, S.E.; Arefi, A.; Lund, C. A Linear-based Model for Multi-Microgrid Energy Sharing- A Western Australia Case Study. In Proceedings of the 2021 31st Australasian Universities Power Engineering Conference (AUPEC), Virtual Conference, 26–30 September 2021; pp. 1–6. [Google Scholar]
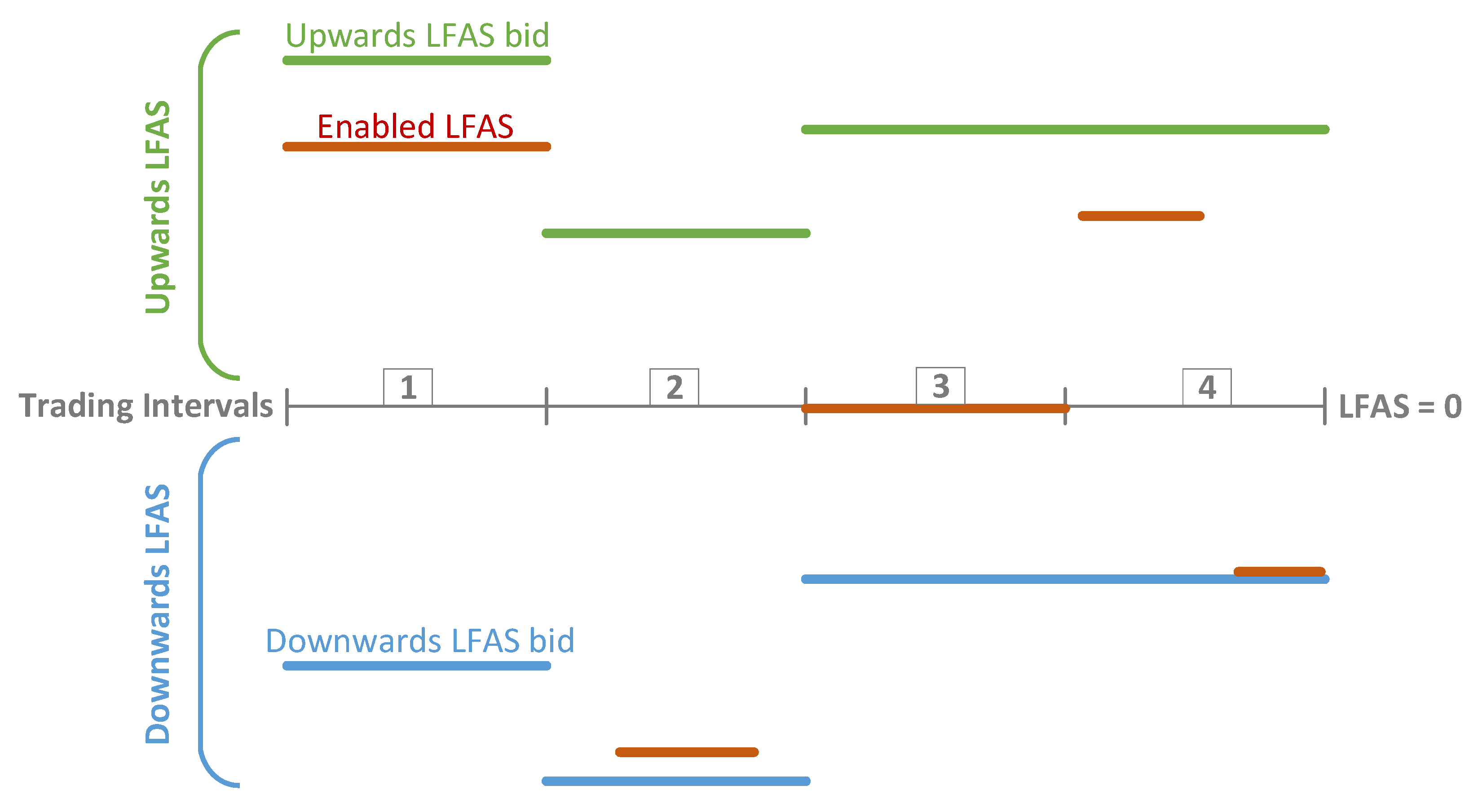





| PV Generation | Electricity Price | LFAS Price | |
|---|---|---|---|
| The VPP is selling energy to the energy market | low | low | ----- |
| The VPP is buying energy from the energy market | low | high | ----- |
| The VPP is participating in LFAS market | ----- | ----- | low |
| Parameters | Value | |
|---|---|---|
| Uncertainty levels (%) | PV generation | 10% |
| Electricity price | 10% | |
| LFAS price | 20% | |
| Gamification parameters | Electricity reduction factor | 50% |
| Customer participation | 80% | |
| VRFB | Efficiency (%) | 85% |
| Maximum energy throughput | 13,000,000 kWh | |
| Discount for customers | 10% | |
| Interest rate | 5% | |
| Horizon year (years) | 20 | |
| The Proposed Robust Method | The Robust Mathematical Method |
|---|---|
| 0.66 s | 947.10 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behi, B.; Jennings, P.; Arefi, A.; Azizivahed, A.; Pivrikas, A.; Muyeen, S.M.; Gorjy, A. A Robust Participation in the Load Following Ancillary Service and Energy Markets for a Virtual Power Plant in Western Australia. Energies 2023, 16, 3054. https://doi.org/10.3390/en16073054
Behi B, Jennings P, Arefi A, Azizivahed A, Pivrikas A, Muyeen SM, Gorjy A. A Robust Participation in the Load Following Ancillary Service and Energy Markets for a Virtual Power Plant in Western Australia. Energies. 2023; 16(7):3054. https://doi.org/10.3390/en16073054
Chicago/Turabian StyleBehi, Behnaz, Philip Jennings, Ali Arefi, Ali Azizivahed, Almantas Pivrikas, S. M. Muyeen, and Arian Gorjy. 2023. "A Robust Participation in the Load Following Ancillary Service and Energy Markets for a Virtual Power Plant in Western Australia" Energies 16, no. 7: 3054. https://doi.org/10.3390/en16073054
APA StyleBehi, B., Jennings, P., Arefi, A., Azizivahed, A., Pivrikas, A., Muyeen, S. M., & Gorjy, A. (2023). A Robust Participation in the Load Following Ancillary Service and Energy Markets for a Virtual Power Plant in Western Australia. Energies, 16(7), 3054. https://doi.org/10.3390/en16073054










