Soft Computing in Smart Grid with Decentralized Generation and Renewable Energy Storage System Planning
Abstract
1. Introduction
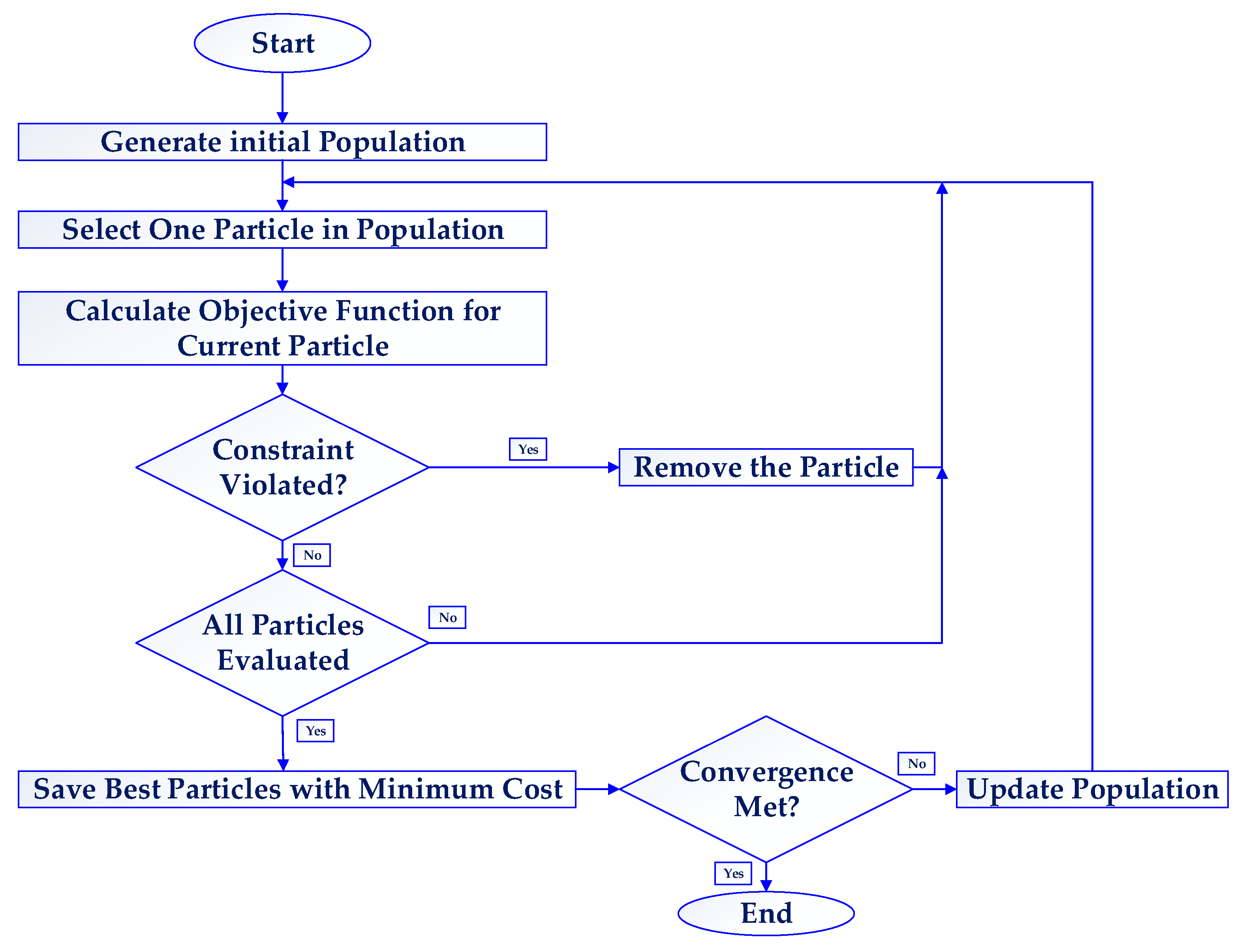
2. Distribution Network Planning with DPG and ESS
2.1. Distribution Network Expansion Planning with DPG Sources
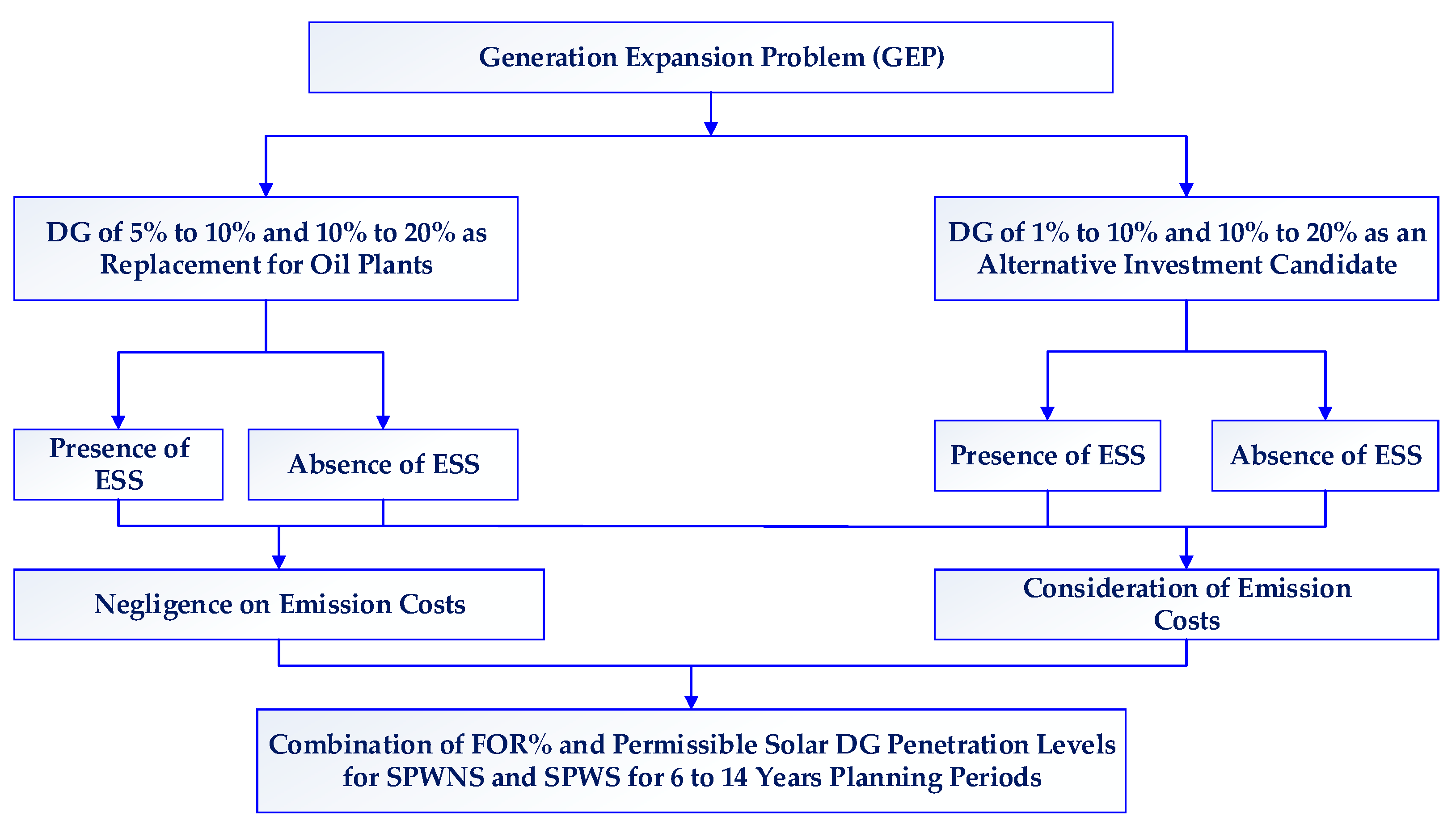
2.1.1. Generation Expansion Model
2.1.2. Demand Constraints
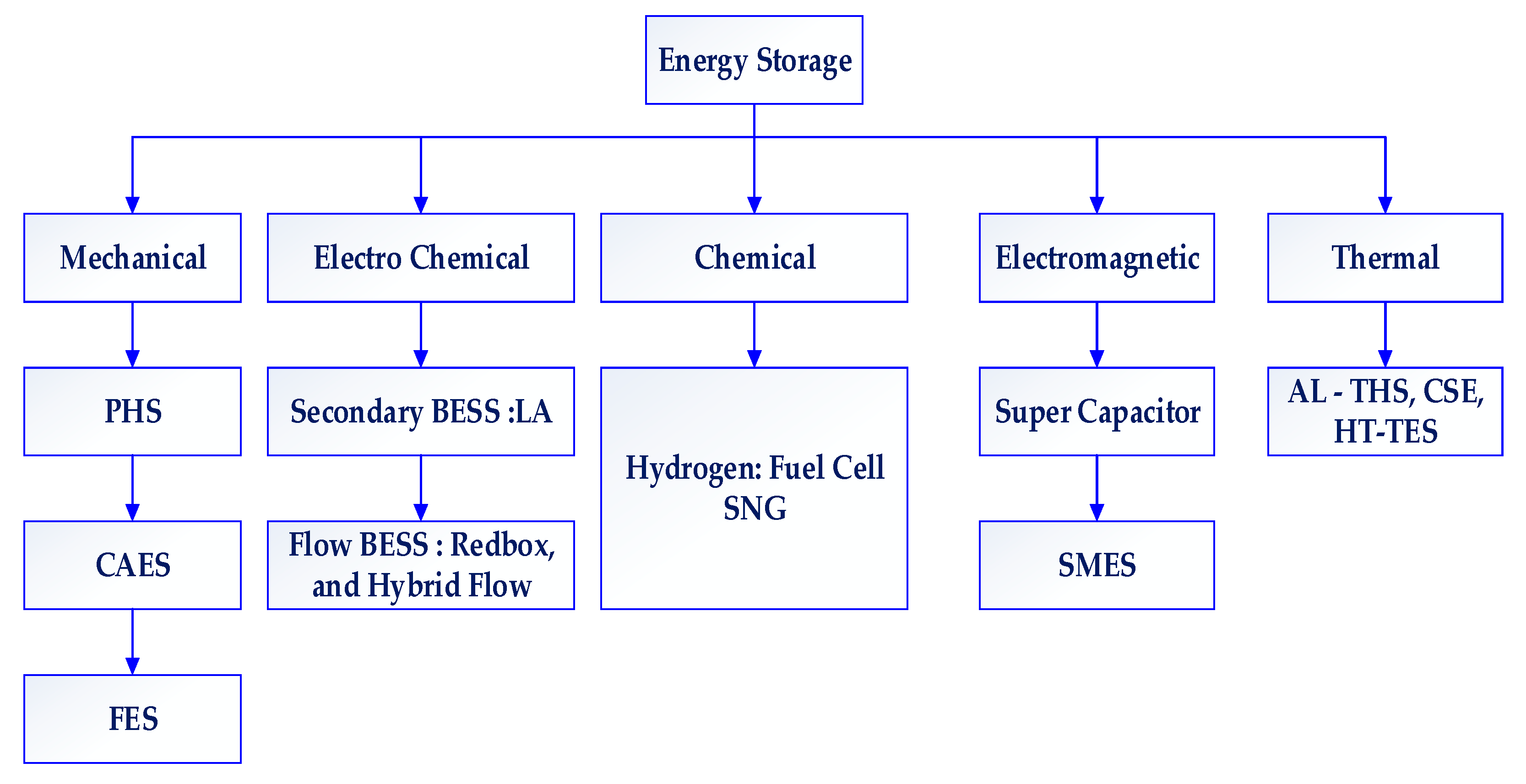
2.2. Distribution Network Expansion Planning with ESS
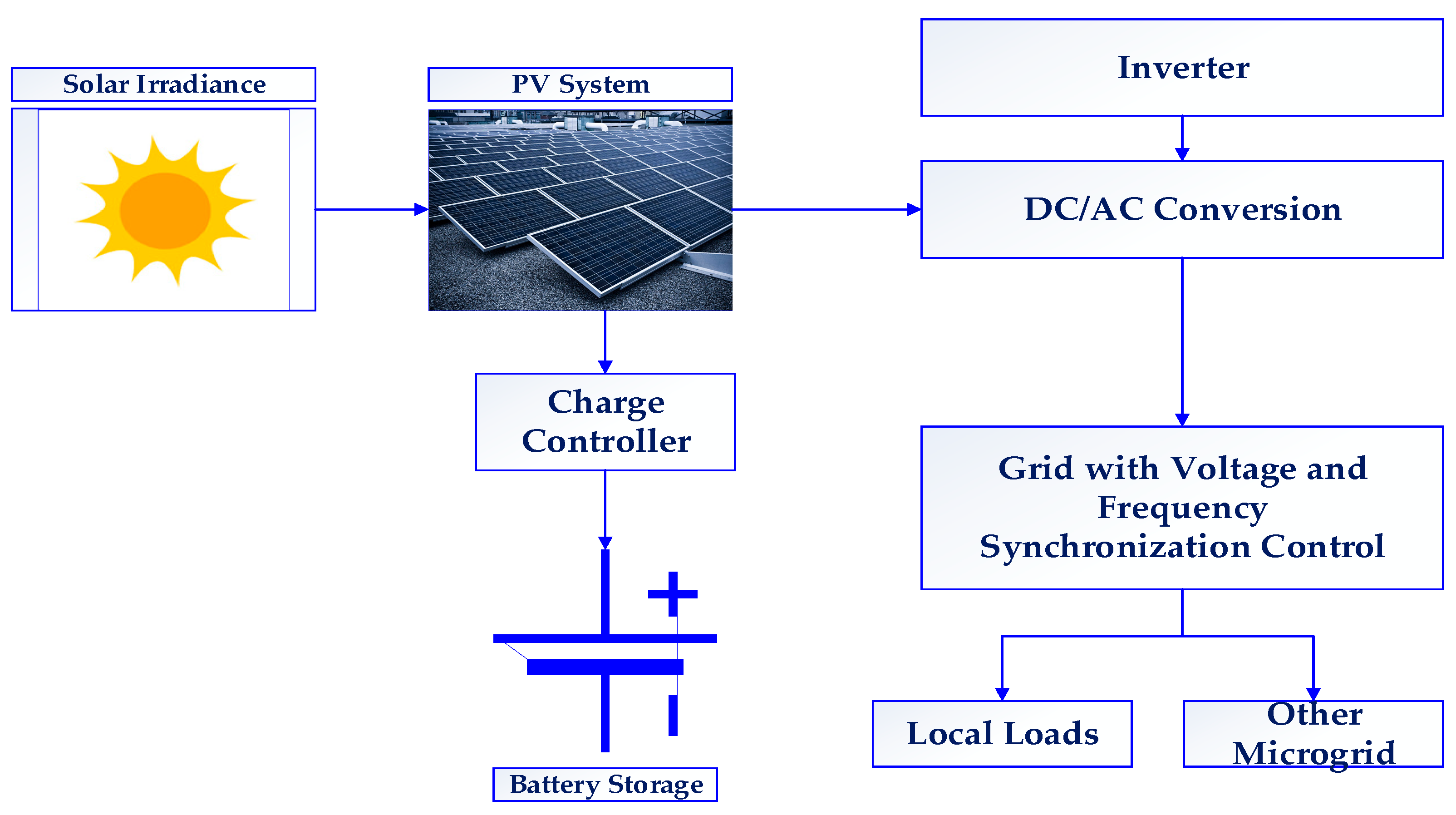
2.2.1. System Modeling
2.2.2. Storage Objective Functions
2.3. DN Planning under Deterministic and Probabilistic Loading Conditions
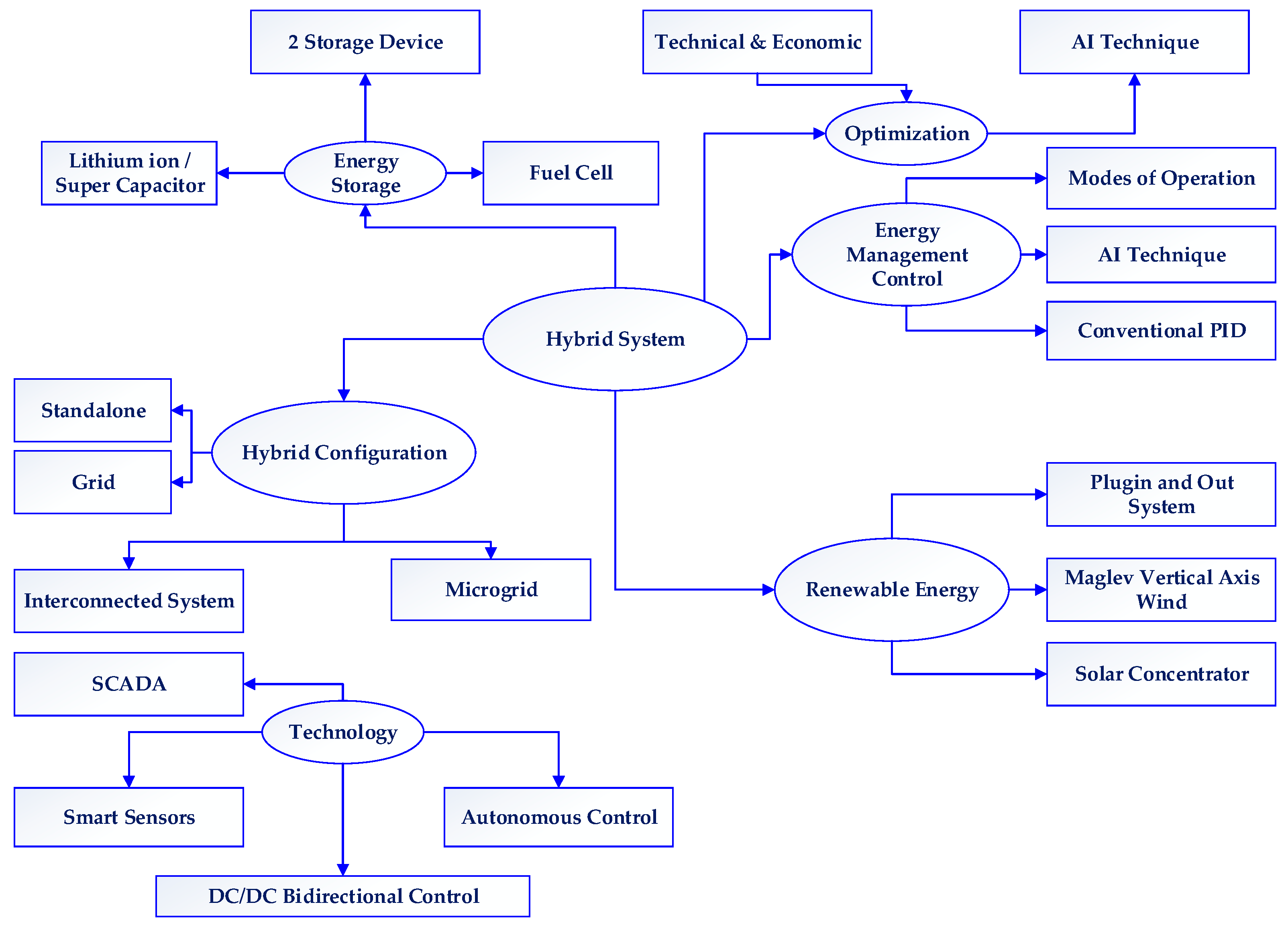
3. Modernized Considerations for DN Planning
3.1. Reliability Studies with DPG-ESS
3.2. Sensitivity Studies with DPG-ESS
3.3. Security Studies with DPG-ESS
- Defect Levels-The distribution networks in urban areas are made achievable with the highest short-circuit level. It helps keeping the consumer voltage as close as feasible to the nominal level while reducing one consumer’s impact on another. Due to economic considerations, distribution transformers, circuit breakers, and cables must be rated as close as feasible to their maximum load. The installation of embedded generation could increase the short circuit level above what the plant can tolerate because there is so little space between operation and rating.
- Variations in Voltage-Since radial circuit distribution involves supplying some dispersed clients. It is essential from an economic standpoint that they taper with time. A long rural connection with embedded generation at the end will likely raise the local voltage above the permitted limits.
- Network Security: The planning requirements for embedded generation network security connections maintain the pre-connection level of supply security. It adversely affects the size and type of the embedded generator. It is possible that the local system runs in island mode and is powered by the embedded generator in fault scenarios, where the SG’s supply is disrupted. Security is improved in this instance via embedded generation.
- Network Resilience: When a defect occurs, the system dynamics can obtain excited, and it is feasible that an embedded generator’s properties are such that the resulting oscillations could trip the local network. Before connecting, a stability investigation is performed using known generator dynamics, and if instabilities originate, stabilizing networks are created using control systems theory.
4. Result and Discussion
Utilization of Soft Computing Methodologies for Strategic Planning in DN
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AC | Alternating Current |
| ADN | Active Distribution Network |
| ALO | Ant-Lion Optimization |
| AI | Artificial Intelligence |
| APF | Active Power Filter |
| BESS | Battery Energy Storage System |
| CAESS | Compressed Air Energy Storage System |
| CHP | Combined Heat and Power |
| C-UC-CE | Consolidated-Unit-Commitment and Capacity Expansion |
| CSO | Crow Search Optimization |
| DC | Direct Current |
| DEP | Distribution Expansion Planning |
| DPG-ESS | Distributed Power Generation and Energy Storage Systems |
| DISCO | Distribution Company |
| DN | Distribution Network |
| EH | Energy Hub |
| ESS | Energy Storage Systems |
| EV | Electric Vehicle |
| FA | Fault Analysis |
| FESS | Flywheel Energy Storage System |
| FOR | Forged Outage Rate |
| FP | Flower Pollination |
| GA | Genetic Algorithm |
| GEP | Generation Expansion Planning |
| HEP | High emission Plants |
| HOA | Hybrid Optimization Algorithm |
| HV | High Voltage |
| LEP | Low emission Plants |
| LSF | Loss Sensitivity Factor |
| LV | Low Voltage |
| MILP | Mixed Integer Linear Programming |
| MO | Multi-Objective |
| MOA | Metaheuristic Optimization |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| OBJ | Objective |
| OPF | Optimal Power Flow |
| PG | Power Generation |
| PS | Power Supply |
| PSCI | Power Supply Capacity Index |
| PSO | Particle Swarm Optimization |
| PTHSS | Pumped Type Hydro Energy Storage System |
| PV | Photovoltaic unit |
| RE | Renewable Energy |
| SCESS | Super-Capacitor Energy Storage System |
| SD | Storage Devices |
| SG | Smart Grids |
| SMESS | Superconducting Magnetic Energy Storage System |
| SO | Single Objective |
| SOC | State-Of-Charge |
| SPWNS | Solar Plants with Non-Storage |
| SPWS | Solar Plants with Storage |
| VSI | Voltage Stability Indices |
| WO | Wolf Optimizer |
| Notations | |
| susceptance of power lines | |
| the start-up cost of generator type ‘g’ [USD] | |
| speculation cost annuity of generator type ‘g’ in year ‘x’ [USD/MW] | |
| unit span cost [USD/MWh] | |
| the variable expense of generator type ‘g’ in year ‘x’ | |
| operational expense | |
| D(X) | project interest in the specified number of hours (h) to prepare for (t) years/time and trimester tri (MWh) |
| conductance of power lines. | |
| extra unit installed in year ‘y’ of generator type | |
| load shedding at hour ‘t’ in year ‘x’ [MW] | |
| n | total number of the bus |
| quantity of generator | |
| Npump | the course of action of all power plants except for siphoning plants |
| OBJ | objective |
| price per energy from ESS | |
| the total amount of power injection at node ‘i’ | |
| power provided by generator type ‘g’ at hour ‘t’ in year ‘x’ [MW] | |
| Psrp (X) | output yield of all unique system |
| pump | arrangement of all pumping power plants. |
| charging power of SD | |
| discharging power of SD | |
| P | real power |
| Q | reactive power |
| unit electricity cost at the current time ‘t’ | |
| Str(t) | charge state rate of SD |
| srp | unique regime producer |
| the complex voltage at bus i, | |
| voltage level between bus ‘i’ and ‘k’ | |
| admittance between bus ‘i’ and ‘k’ | |
| phase difference profile between nodes, | |
| efficiency of SD | |
| corresponding discharge rate |
References
- Abbasi, F.; Hosseini, S.M. Optimal DG allocation and sizing in presence of storage systems considering network configuration effects in distribution systems. IET Gener. Transm. Distrib. 2016, 10, 617–624. [Google Scholar] [CrossRef]
- Huang, N.; Wang, S.; Wang, R.; Cai, G.; Liu, Y.; Dai, Q. Gated spatial-temporal graph neural network based short-term load forecasting for wide-area multiple buses. Int. J. Electr. Power Energy Syst. 2023, 145, 108651. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, X.; Gu, B.; Gao, F. Power Scheduling Optimization Method of Wind-Hydrogen Integrated Energy System Based on the Improved AUKF Algorithm. Mathematics 2022, 10, 4207. [Google Scholar] [CrossRef]
- Gómez-González, M.; Ruiz-Rodriguez, F.J.; Jurado, F. Metaheuristic and probabilistic techniques for optimal allocation and size of biomass distributed generation in unbalanced radial systems. IET Renew. Power Gener. 2015, 9, 653–659. [Google Scholar] [CrossRef]
- Yin, X.; Ye, C.; Ding, Y.; Song, Y. Exploiting Internet Data Centers as Energy Prosumers in Integrated Electricity-Heat System. IEEE Trans. Smart Grid 2023, 14, 167–182. [Google Scholar] [CrossRef]
- Sattarpour, T.; Farsadi, M. Parking lot allocation with maximum economic benefit in a distribution network. Int. Trans. Electr. Energy Syst. 2017, 27, e2234. [Google Scholar] [CrossRef]
- Ge, L.; Li, Y.; Li, Y.; Yan, J.; Sun, Y. Smart Distribution Network Situation Awareness for High-Quality Operation and Maintenance: A Brief Review. Energies 2022, 15, 828. [Google Scholar] [CrossRef]
- Sirat, A.P.; Mehdipourpicha, H.; Zendehdel, N.; Mozafari, H. Sizing and Allocation of Distributed Energy Resources for Loss Reduction using Heuristic Algorithms. In Proceedings of the 2020 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 20 February 2020. [Google Scholar]
- Guo, L.; Ye, C.; Ding, Y.; Wang, P. Allocation of Centrally Switched Fault Current Limiters Enabled by 5G in Transmission System. IEEE Trans. Power Deliv. 2021, 36, 3231–3241. [Google Scholar] [CrossRef]
- Ghiasi, M. Detailed study, multi-objective optimization, and design of an AC-DC smart microgrid with hybrid renewable energy resources. Energy 2019, 169, 496–507. [Google Scholar] [CrossRef]
- Guo, C.; Ye, C.; Ding, Y.; Wang, P. A Multi-State Model for Transmission System Resilience Enhancement Against Short-Circuit Faults Caused by Extreme Weather Events. IEEE Trans. Power Deliv. 2021, 36, 2374–2385. [Google Scholar] [CrossRef]
- Ghiasi, M.; Wang, Z.; Mehrandezh, M.; Jalilian, S.; Ghadimi, N. Evolution of smart grids towards the Internet of energy: Concept and essential components for deep decarbonisation. IET Smart Grid 2023, 6, 86–102. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Fouda, M.M.; Kato, N.; Takeuchi, A.; Iwasaki, N.; Nozaki, Y. Toward intelligent machine-to-machine communications in smart grid. IEEE Commun. Mag. 2011, 49, 60–65. [Google Scholar] [CrossRef]
- El-Hendawi, M.; Wang, Z.; Liu, X. Centralized and Distributed Optimization for Vehicle-to-Grid Applications in Frequency Regulation. Energies 2022, 15, 4446. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Fouda, M.M.; Kato, N.; Shen, X.; Nozaki, Y. An early warning system against malicious activities for smart grid communications. IEEE Netw. 2011, 25, 50–55. [Google Scholar] [CrossRef]
- Hegazy, H.I.; Eldien, A.S.T.; Tantawy, M.M.; Fouda, M.M.; TagElDien, H.A. Real-Time Locational Detection of Stealthy False Data Injection Attack in Smart Grid: Using Multivariate-Based Multi-Label Classification Approach. Energies 2022, 15, 5312. [Google Scholar] [CrossRef]
- Niazi, Y.; Golshan, M.E.H.; Alhelou, H.H. Combined Firm and Renewable Distributed Generation and Reactive Power Planning. IEEE Access 2021, 9, 133735–133745. [Google Scholar] [CrossRef]
- Badr, M.M.; Ibrahem, M.I.; Mahmoud, M.; Fouda, M.M.; Alsolami, F.; Alasmary, W. Detection of False-Reading Attacks in Smart Grid Net-Metering System. IEEE Internet Things J. 2022, 9, 1386–1401. [Google Scholar] [CrossRef]
- Pereira, S.; Ferreira, P.; Vaz, A. Generation expansion planning with high share of renewables of variable output. Appl. Energy 2017, 190, 1275–1288. [Google Scholar] [CrossRef]
- Tohidi, Y.; Hesamzadeh, M.R. A Mathematical Model for Strategic Generation Expansion Planning. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Fitiwi, D.Z.; Olmos, L.; Rivier, M.; de Cuadra, F.; Pérez-Arriaga, I. Finding a representative network losses model for large-scale transmission expansion planning with renewable energy sources. Energy 2016, 101, 343–358. [Google Scholar] [CrossRef]
- Ibrahem, M.I.; Nabil, M.; Fouda, M.M.; Mahmoud, M.M.E.A.; Alasmary, W.; Alsolami, F. Efficient Privacy-Preserving Electricity Theft Detection with Dynamic Billing and Load Monitoring for AMI Networks. IEEE Internet Things J. 2021, 8, 1243–1258. [Google Scholar] [CrossRef]
- Abdalzaher, M.S.; Fouda, M.M.; Ibrahem, M.I. Data Privacy Preservation and Security in Smart Metering Systems. Energies 2022, 15, 7419. [Google Scholar] [CrossRef]
- Swaminathan, D.; Rajagopalan, A. Multi-Objective Golden Flower Optimization Algorithm for Sustainable Reconfiguration of Power Distribution Network with Decentralized Generation. Axioms 2023, 12, 70. [Google Scholar] [CrossRef]
- Badr, M.M.; Ibrahem, M.I.; Mahmoud, M.; Alasmary, W.; Fouda, M.M.; Almotairi, K.H.; Fadlullah, Z.M. Privacy-Preserving Federated-Learning-Based Net-Energy Forecasting. In Proceedings of the SoutheastCon 2022, Mobile, AL, USA, 26 March–3 April 2022; pp. 133–139. [Google Scholar]
- Habbak, H.; Mahmoud, M.; Metwally, K.; Fouda, M.M.; Ibrahem, M.I. Load Forecasting Techniques and Their Applications in Smart Grids. Energies 2023, 16, 1480. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Najafi, H.R.; Anvari-Moghaddam, A.; Guerrero, J.M. Stochastic security and risk-constrained scheduling for an autonomous microgrid with demand response and renewable energy resources. IET Renew. Power Gener. 2017, 11, 1812–1821. [Google Scholar] [CrossRef]
- Sa’Ed, J.A.; Amer, M.; Bodair, A.; Baransi, A.; Favuzza, S.; Zizzo, G. A Simplified Analytical Approach for Optimal Planning of Distributed Generation in Electrical Distribution Networks. Appl. Sci. 2019, 9, 5446. [Google Scholar] [CrossRef]
- Chen, J.; Sun, B.; Li, Y.; Jing, R.; Zeng, Y.; Li, M. Credible capacity calculation method of distributed generation based on equal power supply reliability criterion. Renew. Energy 2022, 201, 534–547. [Google Scholar] [CrossRef]
- Zhong, C.; Zhou, Y.; Chen, J.; Liu, Z. DC-side synchronous active power control of two-stage photovoltaic generation for frequency support in Islanded microgrids. Energy Rep. 2022, 8, 8361–8371. [Google Scholar] [CrossRef]
- Li, J.; Shen, Z.; Chen, X.; Yang, S.; Zhou, W.; Wang, M.; Wang, L.; Kou, Q.; Liu, Y.; Li, Q.; et al. Grain-orientation-engineered multilayer ceramic capacitors for energy storage applications. Nat. Mater. 2020, 19, 999–1005. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Wen, Y.; Yu, R.; Yu, J.; Wen, H. Improved Weak Grids Synchronization Unit for Passivity Enhancement of Grid-Connected Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7084–7097. [Google Scholar] [CrossRef]
- Dhivya, S.; Arul, R.; Ramesh, S.; Kasinathan, P. An Efficient Energy Utilization Analysis Using Novel Chess Optimization Algorithm. Ann. Rom. Soc. Cell Biol. 2020, 24, 19–34. [Google Scholar]
- Li, S.; Wang, F.; Wang, Q.; Ouyang, L.; Chen, X.; Li, J. Numerical Modeling of Branching-Streamer Propagation in Ester-Based Insulating Oil Under Positive Lightning Impulse Voltage: Effects From Needle Curvature Radius. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 139–147. [Google Scholar] [CrossRef]
- Rajagopalan, A.; Swaminathan, D.; Alharbi, M.; Sengan, S.; Montoya, O.D.; El-Shafai, W.; Fouda, M.M.; Aly, M.H. Modernized Planning of Smart Grid Based on Distributed Power Generations and Energy Storage Systems Using Soft Computing Methods. Energies 2022, 15, 8889. [Google Scholar] [CrossRef]
- Giannitrapani, A.; Paoletti, S.; Vicino, A.; Zarrilli, D. Optimal Allocation of Energy Storage Systems for Voltage Control in LV Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 2859–2870. [Google Scholar] [CrossRef]
- Dhivya, S.; Arul, R.; Maheswari, S.; Kanimozhi, R.; Karthik, N. Optimal Scheduling and Sizing of Energy Storage System Using Hybrid Algorithm for Electric Vehicles. In Proceedings of the 2022 International Virtual Conference on Power Engineering Computing and Control: Developments in Electric Vehicles and Energy Sector for Sustainable Future (PECCON), Chennai, India, 5–6 May 2022; pp. 1–5. [Google Scholar]
- Ibrahem, M.I.; Mahmoud, M.; Fouda, M.M.; Alsolami, F.; Alasmary, W.; Shen, X. Privacy Preserving and Efficient Data Collection Scheme for AMI Networks Using Deep Learning. IEEE Internet Things J. 2021, 8, 17131–17146. [Google Scholar] [CrossRef]
- Nejad, H.C.; Tavakoli, S.; Ghadimi, N.; Korjani, S.; Nojavan, S.; Pashaei-Didani, H. Reliability based optimal allocation of distributed generations in transmission systems under demand response program. Electr. Power Syst. Res. 2019, 176, 105952. [Google Scholar] [CrossRef]
- Lata, P.; Vadhera, S. TLBO-based approach to optimally place and sizing of energy storage system for reliability enhancement of radial distribution system. Int. Trans. Electr. Energy Syst. 2020, 30, e12334. [Google Scholar] [CrossRef]
- Chedid, R.; Sawwas, A. Optimal placement and sizing of photovoltaics and battery storage in distribution networks. Energy Storage 2019, 1, e46. [Google Scholar] [CrossRef]
- Ibrahem, M.I.; Badr, M.M.; Fouda, M.M.; Mahmoud, M.; Alasmary, W.; Fadlullah, Z.M. PMBFE: Efficient and Privacy-Preserving Monitoring and Billing Using Functional Encryption for AMI Networks. In Proceedings of the 2020 International Symposium on Networks, Computers and Communications (ISNCC), Montreal, QC, Canada, 20–22 October 2020; pp. 1–7. [Google Scholar]
- Pandey, A.K.; Kirmani, S. Optimal location and sizing of hybrid system by analytical crow search optimization algorithm. Int. Trans. Electr. Energy Syst. 2020, 30, e12327. [Google Scholar] [CrossRef]
- Qiu, J.; Xu, Z.; Zheng, Y.; Wang, D.; Dong, Z.Y. Distributed generation and energy storage system planning for a distribution system operator. IET Renew. Power Gener. 2018, 12, 1345–1353. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Marjani, S.R.; Talavat, V. Optimal planning in active distribution networks considering nonlinear loads using the MOPSO algorithm in the TOPSIS framework. Int. Trans. Electr. Energy Syst. 2020, 30, e12244. [Google Scholar] [CrossRef]
- Fouda, M.M.; Fadlullah, Z.M.; Kato, N.; Takeuchi, A.; Nozaki, Y. A Novel Demand Control Policy for Improving Quality of Power Usage in Smart Grid. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 5154–5159. [Google Scholar]
- Das, C.K.; Bass, O.; Kothapalli, G.; Mahmoud, T.S.; Habibi, D. Optimal placement of distributed energy storage systems in distribution networks using artificial bee colony algorithm. Appl. Energy 2018, 232, 212–228. [Google Scholar] [CrossRef]
- Aladdin, S.; El-Tantawy, S.; Fouda, M.M.; Eldien, A.S.T. MARLA-SG: Multi-Agent Reinforcement Learning Algorithm for Efficient Demand Response in Smart Grid. IEEE Access 2020, 8, 210626–210639. [Google Scholar] [CrossRef]
- Bucciarelli, M.; Paoletti, S.; Vicino, A. Optimal sizing of energy storage systems under uncertain demand and generation. Appl. Energy 2018, 225, 611–621. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd-Elazim, S.; Abdelaziz, A. Optimal allocation and sizing of renewable distributed generation using ant lion optimization algorithm. Electr. Eng. 2018, 100, 99–109. [Google Scholar] [CrossRef]
- Peesapati, R.; Yadav, V.K.; Kumar, N. Flower pollination algorithm based multi-objective congestion management considering optimal capacities of distributed generations. Energy 2018, 147, 980–994. [Google Scholar] [CrossRef]
- Lakum, A.; Mahajan, V. Optimal placement and sizing of multiple active power filters in radial distribution system using grey wolf optimizer in presence of nonlinear distributed generation. Electr. Power Syst. Res. 2019, 173, 281–290. [Google Scholar] [CrossRef]
- Veeramsetty, V.; Venkaiah, C.; Kumar, D.M.V. Hybrid genetic dragonfly algorithm based optimal power flow for computing LMP at DG buses for reliability improvement. Energy Syst. 2018, 9, 709–757. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.; Montoya, O.D.; Gil-González, W. Integration of energy storage systems in AC distribution networks: Optimal location, selecting, and operation approach based on genetic algorithms. J. Energy Storage 2019, 25, 100891. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Li, G.; Qi, J.; Zhao, D.; Mu, Y. Optimal distributed generation planning in active distribution networks considering integration of energy storage. Appl. Energy 2018, 210, 1073–1081. [Google Scholar] [CrossRef]
- Swaminathan, D.; Rajagopalan, A. Optimized Network Reconfiguration with Integrated Generation Using Tangent Golden Flower Algorithm. Energies 2022, 15, 8158. [Google Scholar] [CrossRef]
- Nimalsiri, N.I.; Mediwaththe, C.P.; Ratnam, E.L.; Shaw, M.; Smith, D.B.; Halgamuge, S.K. A Survey of Algorithms for Distributed Charging Control of Electric Vehicles in Smart Grid. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4497–4515. [Google Scholar] [CrossRef]
- Zheng, Y.; Hill, D.J.; Dong, Z.Y. Multi-Agent Optimal Allocation of Energy Storage Systems in Distribution Systems. IEEE Trans. Sustain. Energy 2017, 8, 1715–1725. [Google Scholar] [CrossRef]
- Dai, J.; Feng, H.; Shi, K.; Ma, X.; Yan, Y.; Ye, L.; Xia, Y. Electrochemical degradation of antibiotic enoxacin using a novel PbO2 electrode with a graphene nanoplatelets inter-layer: Characteristics, efficiency and mechanism. Chemosphere 2022, 307, 135833. [Google Scholar] [CrossRef] [PubMed]
- Bala, R.; Ghosh, S. Optimal position and rating of DG in distribution networks by ABC–CS from load flow solutions illustrated by fuzzy-PSO. Neural Comput. Appl. 2019, 31, 489–507. [Google Scholar] [CrossRef]
- Li, S.; Ye, C.; Ding, Y.; Song, Y. Reliability Assessment of Renewable Power Systems Considering Thermally-Induced Incidents of Large-Scale Battery Energy Storage. IEEE Trans. Power Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Kumar, J.S.; Raja, S.C.; Srinivasan, D.; Venkatesh, P. Hybrid renewable energy-based distribution system for seasonal load variations. Int. J. Energy Res. 2018, 42, 1066–1087. [Google Scholar] [CrossRef]
- Imran, A.M.; Kowsalya, M.; Kothari, D. A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks. Int. J. Electr. Power Energy Syst. 2014, 63, 461–472. [Google Scholar] [CrossRef]
- Sedghi, M.; Ahmadian, A.; Aliakbar-Golkar, M. Assessment of optimization algorithms capability in distribution network planning: Review, comparison and modification techniques. Renew. Sustain. Energy Rev. 2016, 66, 415–434. [Google Scholar] [CrossRef]
- Roy, K.; Mandal, K.K.; Mandal, A.C. Application of ANFASO for optimal power flow management of MG-connected system with energy storage. Int. J. Energy Res. 2020, 44, 5272–5286. [Google Scholar] [CrossRef]
- Ibrahem, M.I.; Badr, M.M.; Mahmoud, M.; Fouda, M.M.; Alasmary, W. Countering Presence Privacy Attack in Efficient AMI Networks Using Interactive Deep-Learning. In Proceedings of the 2021 International Symposium on Networks, Computers and Communications (ISNCC), Dubai, United Arab Emirates, 31 October–2 November 2021; pp. 1–7. [Google Scholar]
- Han, Y.; Yan, X.; Piroozfar, P. An overall review of research on prefabricated construction supply chain management. Eng. Constr. Arch. Manag. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Babacan, O.; Torre, W.; Kleissl, J. Siting and sizing of distributed energy storage to mitigate voltage impact by solar PV in distribution systems. Sol. Energy 2017, 146, 199–208. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Z.Y.; Luo, F.J.; Meng, K.; Qiu, J.; Wong, K.P. Optimal Allocation of Energy Storage System for Risk Mitigation of DISCOs With High Renewable Penetrations. IEEE Trans. Power Syst. 2014, 29, 212–220. [Google Scholar] [CrossRef]
- Hussain, I.; Roy, A.K. Optimal Distributed Generation Allocation in Distribution Systems Employing Modified Artificial Bee Colony Algorithm to Reduce Losses and Improve Voltage Profile. In Proceedings of the IEEE-International Conference On Advances In Engineering, Science and Management (ICAESM-2012), Nagapattinam, India, 30–31 March 2012; pp. 565–570. [Google Scholar]
- Ibrahem, M.I.; Mahmoud, M.; Fouda, M.M.; ElHalawany, B.M.; Alasmary, W. Privacy-preserving and Efficient Decentralized Federated Learning-based Energy Theft Detector. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 287–292. [Google Scholar]
- Moravej, Z.; Akhlaghi, A. A novel approach based on cuckoo search for DG allocation in distribution network. Int. J. Electr. Power Energy Syst. 2013, 44, 672–679. [Google Scholar] [CrossRef]
- Han, Y.; Wang, L.; Kang, R. Influence of Consumer Preference and Government Subsidy on Prefabricated Building Developer’s Decision-Making: A Three-Stage Game Model. J. Civ. Eng. Manag. 2023, 29, 35–49. [Google Scholar] [CrossRef]
- Becerra, J.E.C.; Riaño, H.E.H. Distributed Generation Placement in Radial Distribution Networks using a Bat-inspired Algorithm. Dyna 2015, 82, 60–67. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Yang, J. Analysis of Stochastic Process to Model Safety Risk in Construction Industry. J. Civ. Eng. Manag. 2021, 27, 87–99. [Google Scholar] [CrossRef]
- Othman, M.M.; Hegazy, Y.G.; Abdelaziz, A. A Modified Firefly Algorithm for Optimal Sizing and Siting of Voltage Controlled Distributed Generators in Distribution Networks. Period. Polytech. Electr. Eng. Comput. Sci. 2015, 59, 104–109. [Google Scholar] [CrossRef]
- García, J.A.M.; Gil Mena, A.J. Optimal distributed generation location and size using a modified teaching–learning based optimization algorithm. Int. J. Electr. Power Energy Syst. 2013, 50, 65–75. [Google Scholar] [CrossRef]
- Awad, A.S.A.; El-Fouly, T.H.M.; Salama, M.M.A. Optimal ESS Allocation for Benefit Maximization in Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 1668–1678. [Google Scholar] [CrossRef]
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal Planning of Distributed Energy Storage Systems in Active Distribution Networks Embedding Grid Reconfiguration. IEEE Trans. Power Syst. 2018, 33, 1577–1590. [Google Scholar] [CrossRef]
- Xie, S.; Hu, Z.; Zhou, D.; Li, Y.; Kong, S.; Lin, W.; Zheng, Y. Multi-objective active distribution networks expansion planning by scenario-based stochastic programming considering uncertain and random weight of network. Appl. Energy 2018, 219, 207–225. [Google Scholar] [CrossRef]
- Han, Y.; Xu, X.; Zhao, Y.; Wang, X.; Chen, Z.; Liu, J. Impact of Consumer Preference on the Decision-Making of Prefabricated Building DeveloperS. J. Civ. Eng. Manag. 2022, 28, 166–176. [Google Scholar] [CrossRef]
- Kaveh, M.R.; Hooshmand, R.-A.; Madani, S.M. Simultaneous optimization of re-phasing, reconfiguration and DG placement in distribution networks using BF-SD algorithm. Appl. Soft Comput. 2018, 62, 1044–1055. [Google Scholar] [CrossRef]
- Amooi, R.; Moghaddas-Tafreshi, S.M. Operation of an active distribution network with PV and storage battery and vehicle charge station and modeling of uncertainty with copula model. In Proceedings of the 2019 10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 12–14 February 2019. [Google Scholar]
- Sok, V.; Tayjasanant, T. Determination of optimal siting and sizing of energy storage system in PV-connected distribution systems considering minimum energy losses. In Proceedings of the 2017 14th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 27–30 June 2017. [Google Scholar]
- Li, D.; Tan, J.; Yu, Q.; Li, Z. Deep-learning-assisted power loss management for active distribution networks. Electr. J. 2021, 34, 106888. [Google Scholar] [CrossRef]
- Sevilla, F.R.S.; Parra, D.; Wyrsch, N.; Patel, M.K.; Kienzle, F.; Korba, P. Techno-economic analysis of battery storage and curtailment in a distribution grid with high PV penetration. J. Energy Storage 2018, 17, 73–83. [Google Scholar] [CrossRef]
- Pires, V.F.; Lopes, R.; Costa, D. Integration of storage systems in distribution networks through multiobjective optimization. Electr. Eng. 2018, 100, 1939–1948. [Google Scholar] [CrossRef]
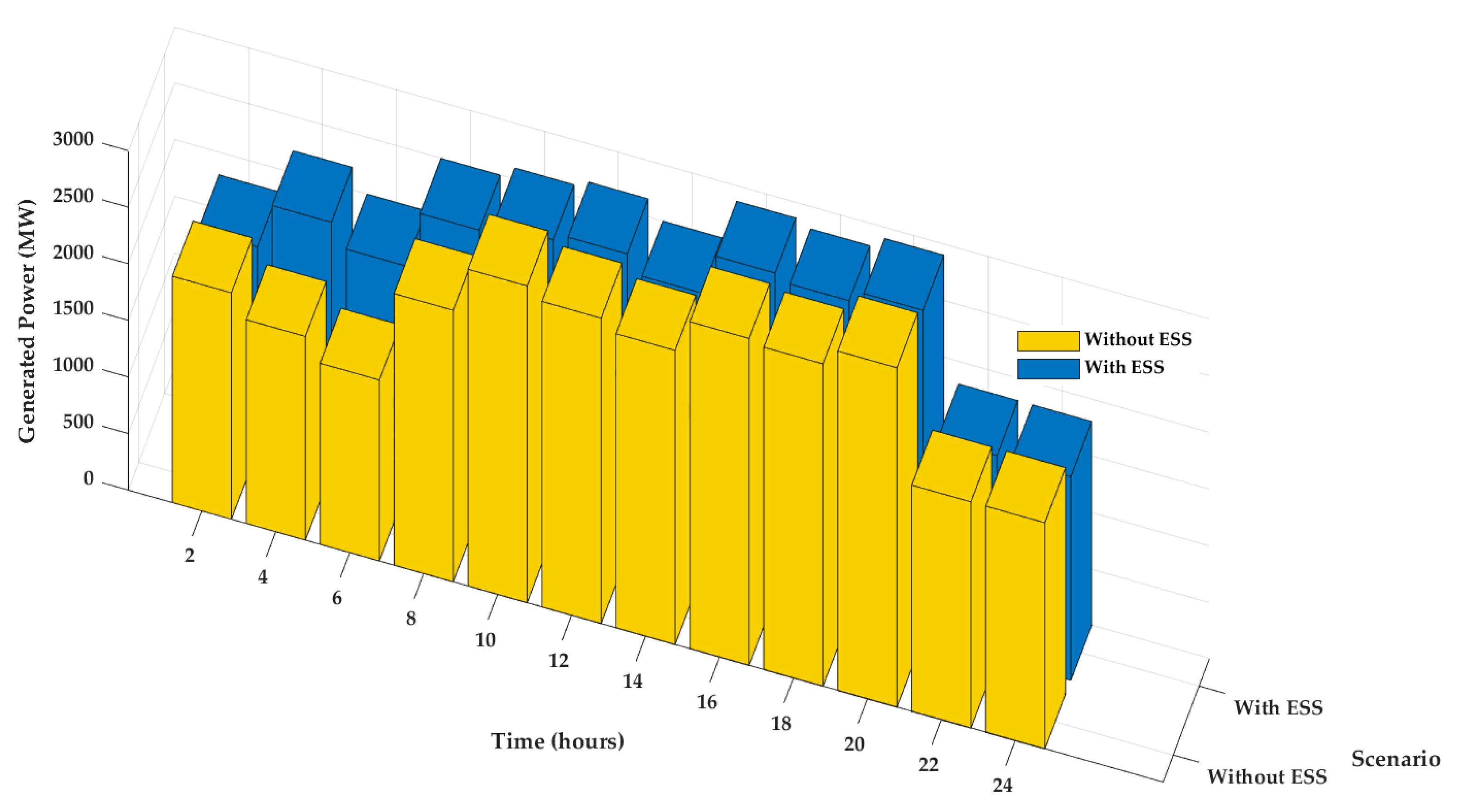
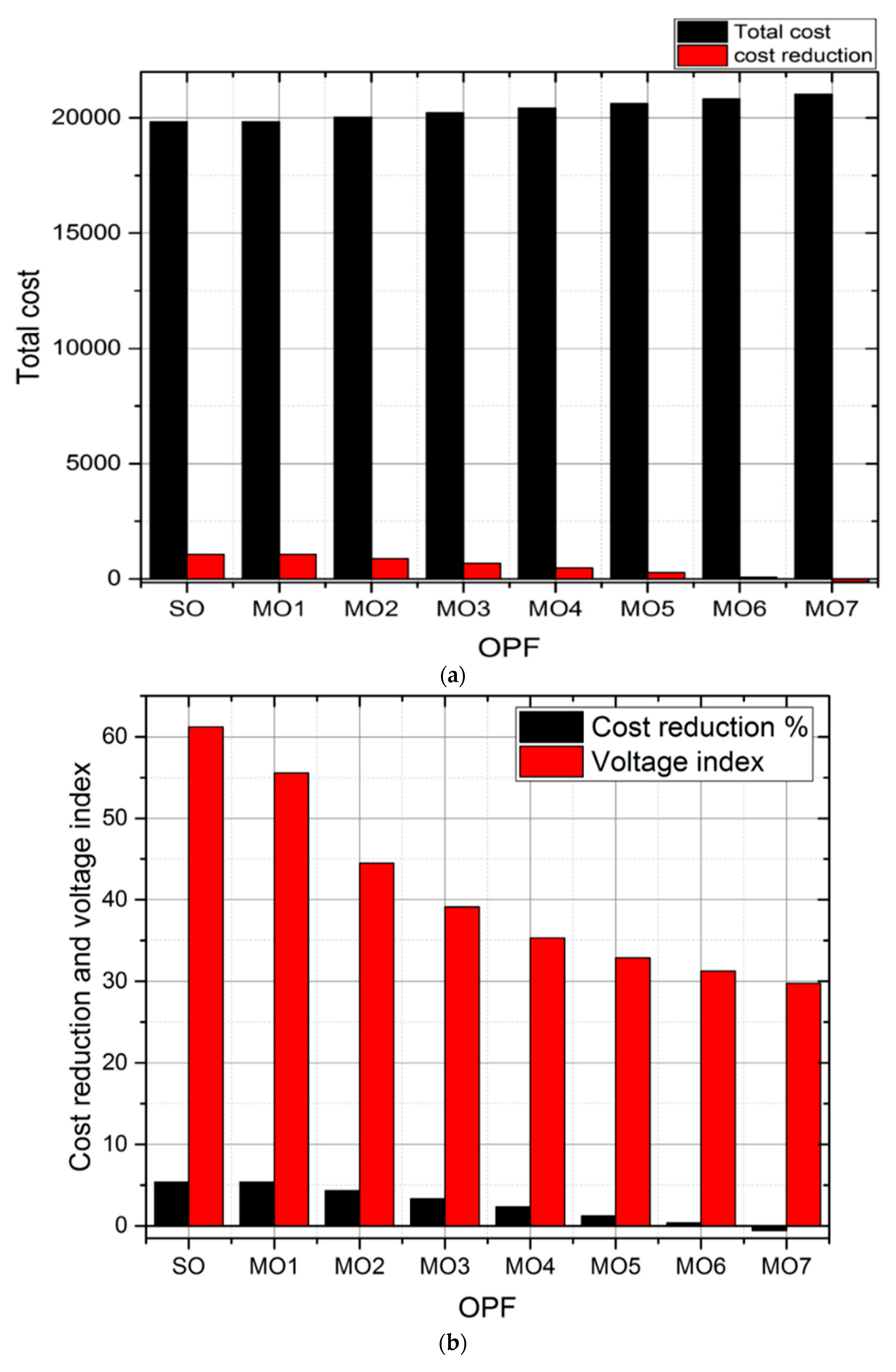
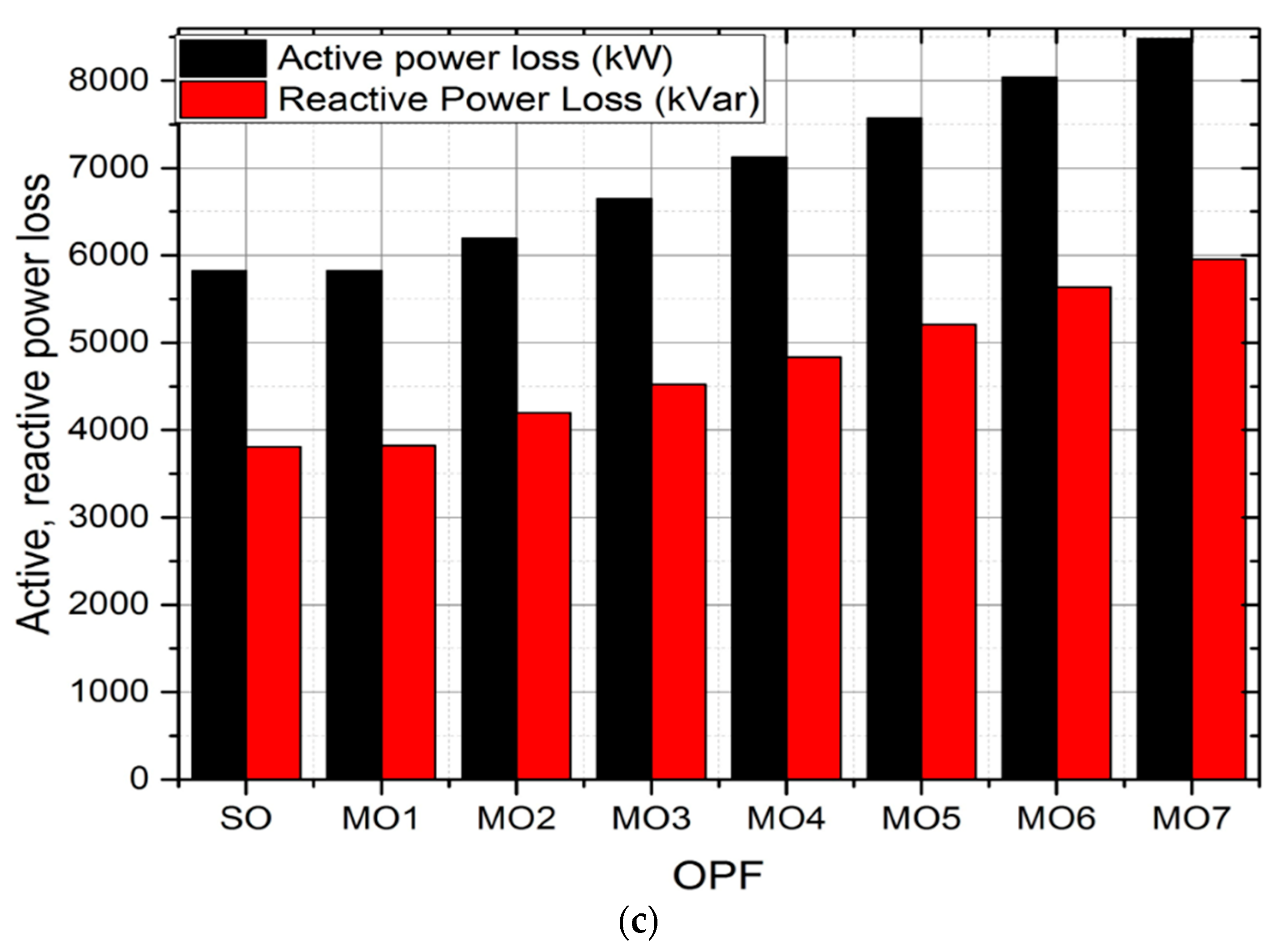

| Time (h) | Net Energy Exchange (MWh) | ESS Status | Generated SG Power (MW) | Load (MW) |
|---|---|---|---|---|
| 1 | 4 | Charging | 279 | 264 |
| 2 | 4 | Charging | 279 | 264 |
| 3 | 4 | Charging | 279 | 264 |
| 4 | 4 | Charging | 279 | 264 |
| 5 | 0 | No action | 330 | 360 |
| 6 | 0 | No action | 330 | 360 |
| 7 | 0 | No action | 330 | 360 |
| 8 | 0 | No action | 330 | 360 |
| 9 | 5 | Discharging | 362 | 361 |
| 10 | 5 | Discharging | 362 | 361 |
| 11 | 5 | Discharging | 362 | 361 |
| 12 | 5 | Discharging | 362 | 361 |
| 13 | 5 | Charging | 385 | 361 |
| 14 | 5 | Charging | 385 | 361 |
| 15 | 5 | Charging | 385 | 361 |
| 16 | 5 | Charging | 385 | 361 |
| 17 | 5 | Discharging | 350 | 348 |
| 18 | 5 | Discharging | 350 | 348 |
| 19 | 5 | Discharging | 350 | 348 |
| 20 | 5 | Discharging | 350 | 348 |
| 21 | 2 | Charging | 310 | 300 |
| 22 | 2 | Charging | 310 | 300 |
| 23 | 2 | Charging | 310 | 300 |
| Proposed Work | Algorithm | Objectives | OBJ Type |
|---|---|---|---|
| An Optimal Planning of Battery ESS [36] | clustering and sensitivity | annual net profit of BESS | MO |
| Optimal Placement and Sizing of ESS [40] | teacher-learner-based optimization | Low-operational cost | MO |
| BESS location [41] | GA | Low-cost | MO |
| Optimal Distributed ESS [42] | Column-and-Constraint Generation (C&CG) | Less investment and operation costs | MO |
| ADNs [45] | PSO | minimizing operational and investment costs | MO |
| Two-level Planning for Co-ordination of ESS [46] | PSO | minimize annual operation cost | MO |
| Optimal Placement of Distribution ESSs [47] | ABC Optimization | voltage deviations and PL are less | MO |
| DPG-based RE Sources [50] | ALO | minimal PL and consequently maximizing the net saving | MO |
| Optimal Capacities of DPG Units [51] | FP | less PL to obtain the optimal capacities of DPG units | MO |
| Optimal DPG Planning with Integration of ESS [55] | ALO | PL, investment benefit, voltage stability factor | MO |
| Article | DPG | ESS | Objectives | IEEE Bus Test System | Loading Conditions | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Placement | Sizing | Placement | Sizing | Minimization | Enhancement | |||||
| Cost | Loss | Voltage Profile | Stability | |||||||
| [57] | - | - | Yes | - | Yes | - | - | - | 15 | Probabilistic |
| [58] | - | - | Yes | Yes | - | Yes | - | - | 123 | Deterministic |
| [59] | - | - | Yes | Yes | Yes | - | - | Yes | 33 | Probabilistic |
| [60] | - | - | Yes | Yes | Yes | - | Yes | - | 8500 | Probabilistic |
| [61] | - | - | Yes | Yes | Yes | Yes | - | - | 15 | Probabilistic |
| [62] | Yes | - | - | - | - | Yes | Yes | Yes | 33 | Deterministic |
| [63] | Yes | - | - | - | - | Yes | Yes | - | 33, 69 | Deterministic |
| [64] | Yes | - | - | - | - | Yes | Yes | - | 38, 69 | Deterministic |
| [65] | Yes | - | - | - | - | Yes | Yes | Yes | 33 | Deterministic |
| [66] | Yes | Yes | - | - | - | Yes | - | - | 33, 69 | Deterministic |
| [67] | Yes | Yes | - | - | - | Yes | Yes | - | 12, 34, 69 | Deterministic |
| [68] | Yes | Yes | - | - | - | Yes | - | - | 69, 123 | Deterministic |
| [69] | Yes | Yes | - | - | - | Yes | - | - | 69, 119 | Deterministic |
| [70] | - | - | Yes | Yes | Yes | Yes | - | - | 33 | Probabilistic |
| [71] | - | - | Yes | Yes | Yes | Yes | Yes | - | 6, 70 | Probabilistic |
| [72] | - | - | Yes | Yes | Yes | Yes | Yes | Yes | 34 | Probabilistic |
| ( a) | ||||||||
| Article | Power Balance Equations | Voltage Limits | DPG Operating Limits | Radial Nature | Line Current indices | Location Indices | ESS Capacity Ranges | ESS Charge Rate Limit |
| [82] | Yes | Yes | Yes | - | - | - | - | - |
| [83] | Yes | Yes | Yes | Yes | Yes | - | - | - |
| [84] | Yes | - | - | - | - | Yes | - | - |
| [85] | Yes | Yes | - | - | Yes | - | Yes | - |
| [86] | Yes | Yes | Yes | - | - | - | - | Yes |
| (b) | ||||||||
| Methods | Merits | Demerits | Major Applicability | |||||
| Numerical [85] | Non-iterative in nature | Inaccurate | Deterministic Model | |||||
| No convergence problem | Hard to get a generalized solution | Single-Objective (SO) Problem | ||||||
| Easy to use | High-level simplification | Small DN | ||||||
| Derivative-free | Premature convergence | MO | ||||||
| Few iterations | A local trap of solution | Dynamic Models | ||||||
| Hybrid Soft Computing [86] | Accuracy in solutions | No commercial solver at ease | Medium DN | |||||
| Efficient computation | Slower convergence | Deterministic model | ||||||
| Effective for complex problems | Non-robust in Nature | Large DN | ||||||
| MO-Soft Computing [87] | Faster convergence | Massive training data | MO | |||||
| High accuracy in the solution | Finding global optima needs subsequent computation | Dynamic models | ||||||
| Greater robustness | No commercial solver at ease | Medium DN | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulkader, R.; Ghanimi, H.M.A.; Dadheech, P.; Alharbi, M.; El-Shafai, W.; Fouda, M.M.; Aly, M.H.; Swaminathan, D.; Sengan, S. Soft Computing in Smart Grid with Decentralized Generation and Renewable Energy Storage System Planning. Energies 2023, 16, 2655. https://doi.org/10.3390/en16062655
Abdulkader R, Ghanimi HMA, Dadheech P, Alharbi M, El-Shafai W, Fouda MM, Aly MH, Swaminathan D, Sengan S. Soft Computing in Smart Grid with Decentralized Generation and Renewable Energy Storage System Planning. Energies. 2023; 16(6):2655. https://doi.org/10.3390/en16062655
Chicago/Turabian StyleAbdulkader, Rasheed, Hayder M. A. Ghanimi, Pankaj Dadheech, Meshal Alharbi, Walid El-Shafai, Mostafa M. Fouda, Moustafa H. Aly, Dhivya Swaminathan, and Sudhakar Sengan. 2023. "Soft Computing in Smart Grid with Decentralized Generation and Renewable Energy Storage System Planning" Energies 16, no. 6: 2655. https://doi.org/10.3390/en16062655
APA StyleAbdulkader, R., Ghanimi, H. M. A., Dadheech, P., Alharbi, M., El-Shafai, W., Fouda, M. M., Aly, M. H., Swaminathan, D., & Sengan, S. (2023). Soft Computing in Smart Grid with Decentralized Generation and Renewable Energy Storage System Planning. Energies, 16(6), 2655. https://doi.org/10.3390/en16062655










