A Multiphysics Model Simulating the Electrochemical, Thermal, and Thermal Runaway Behaviors of Lithium Polymer Battery
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Methods
2.2. Numerical Methods
3. Results and Discussion
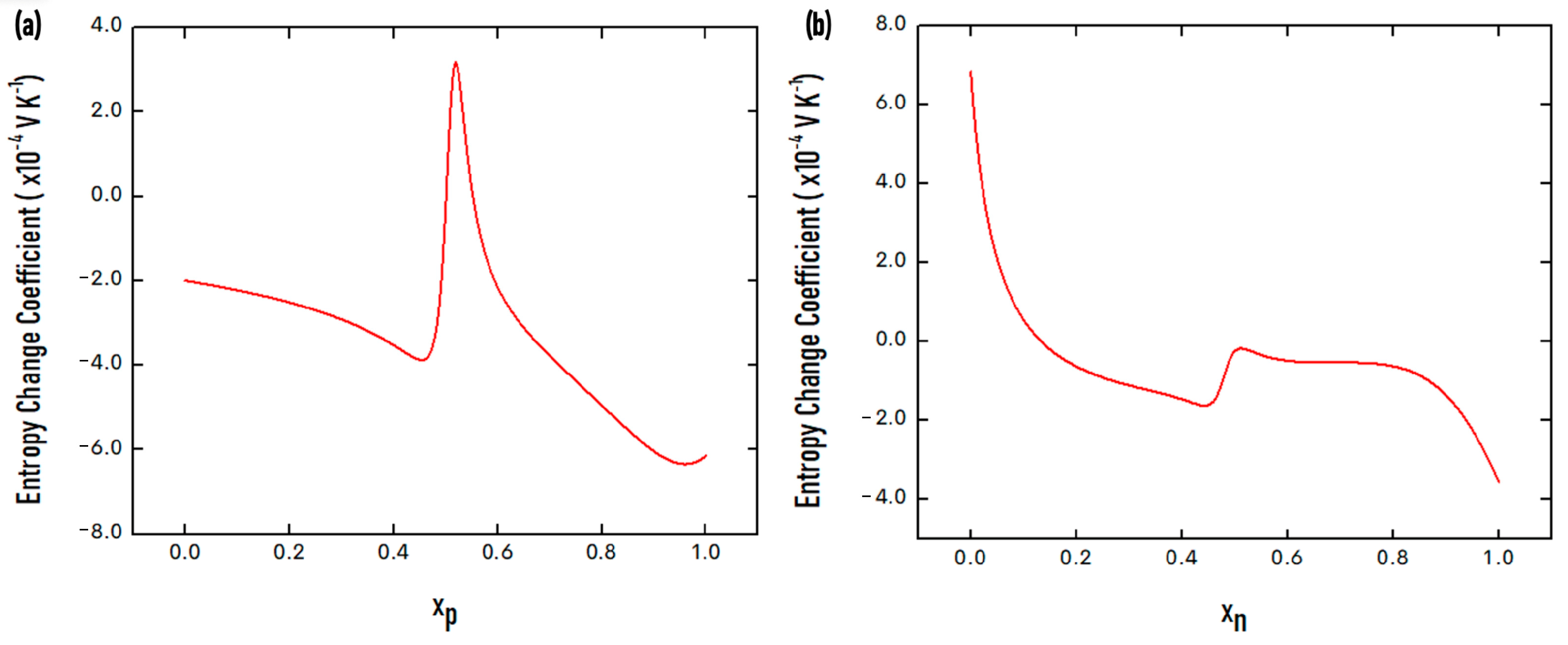
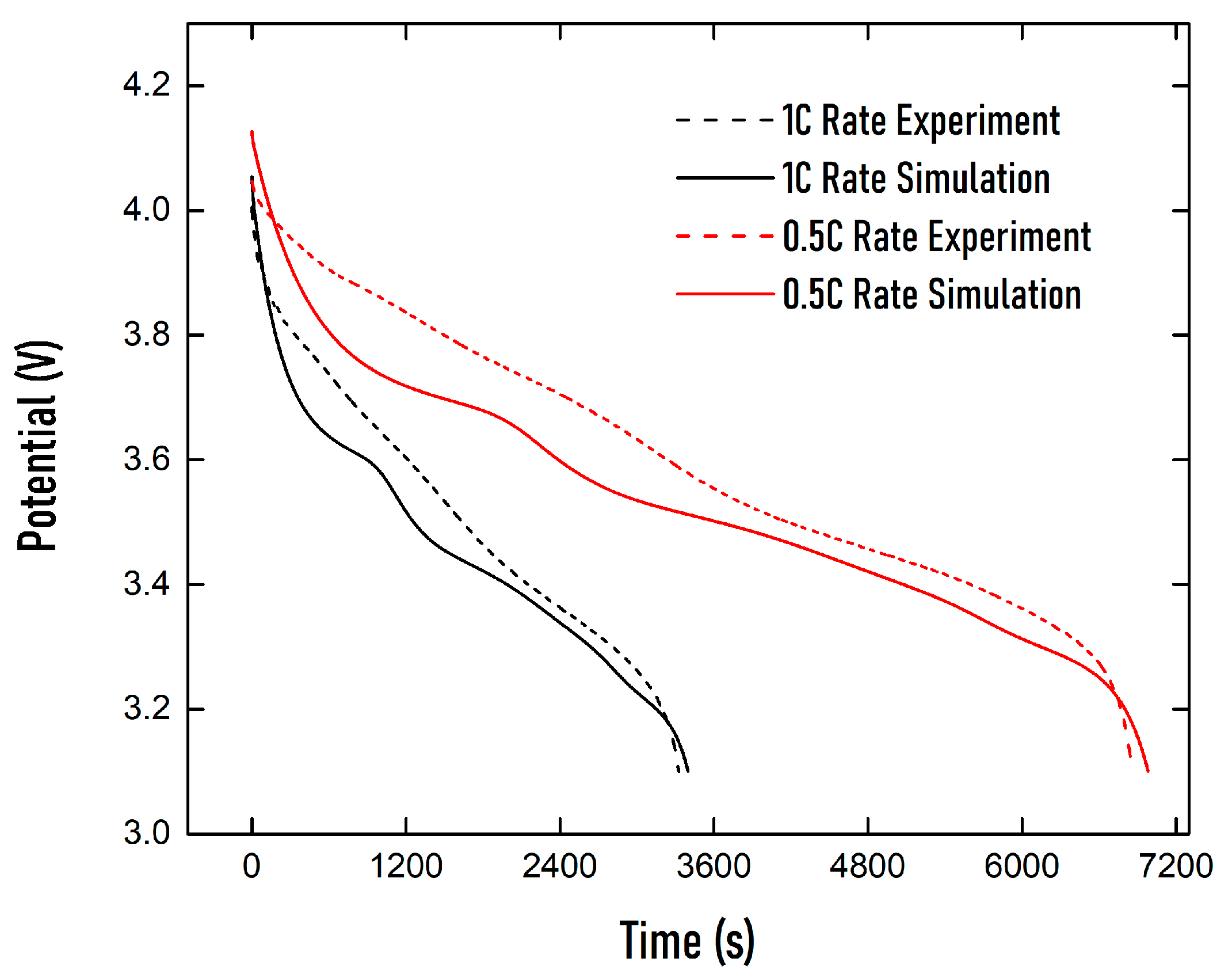
3.1. Electrochemical Behavior
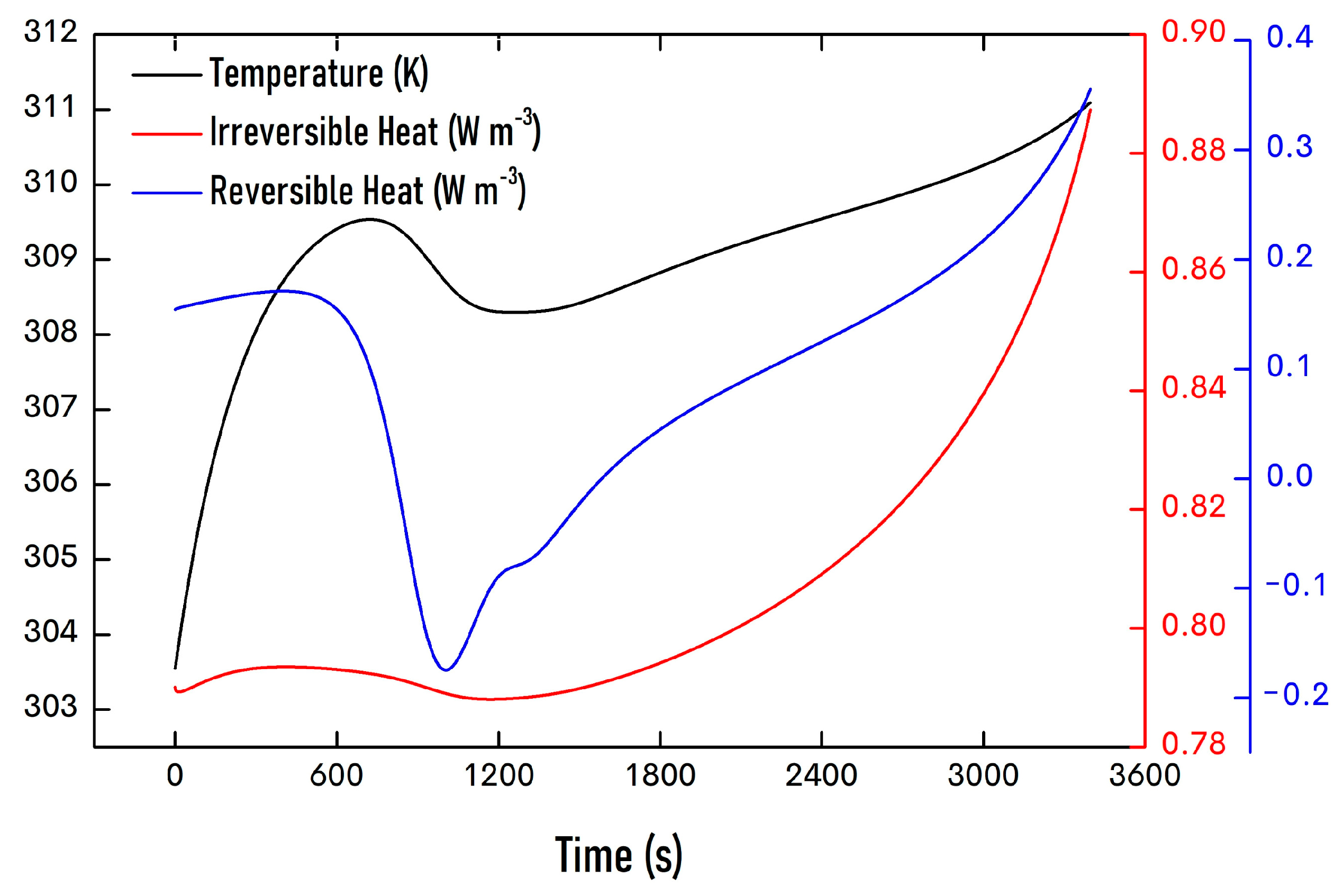
3.2. Thermal Behavior
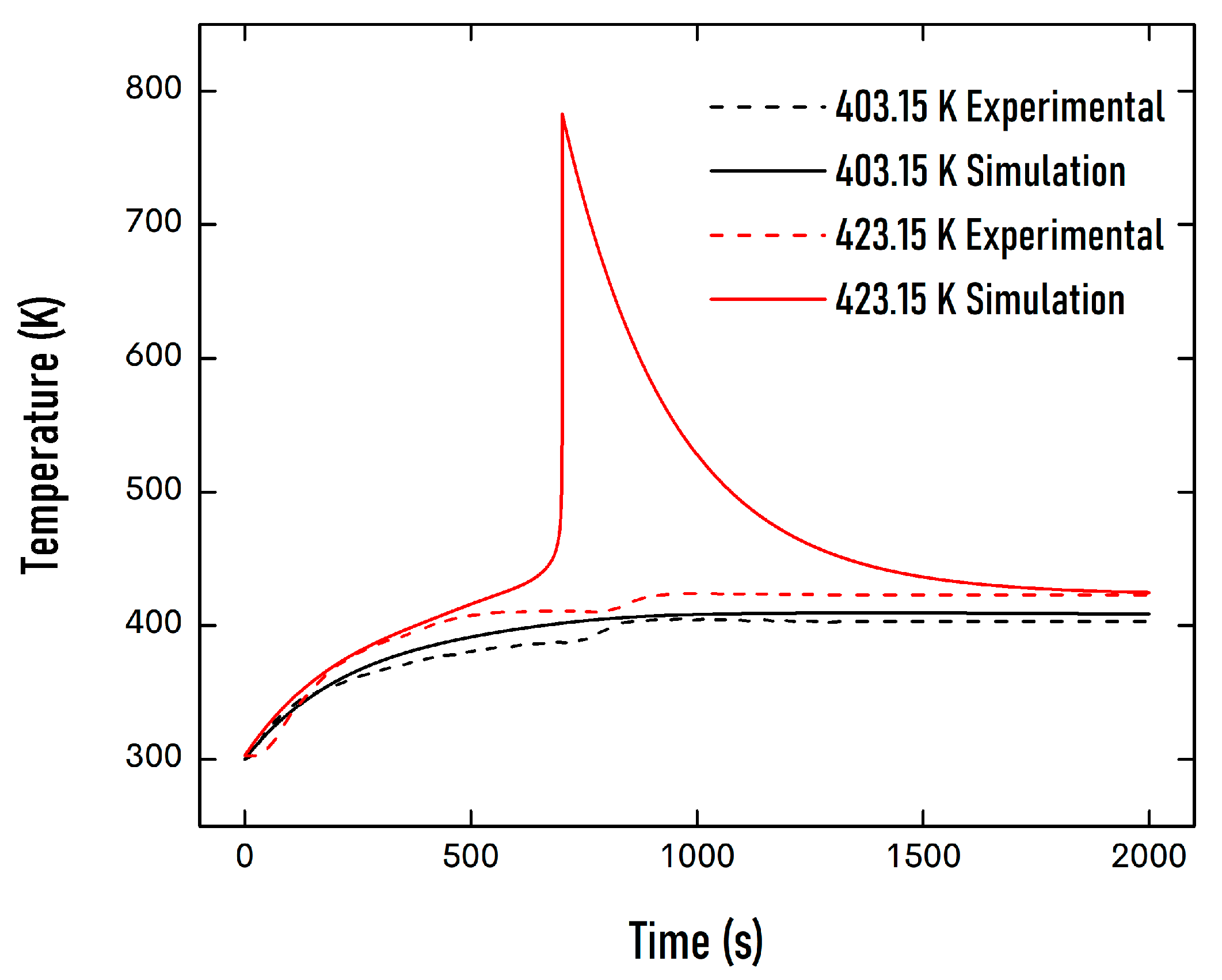
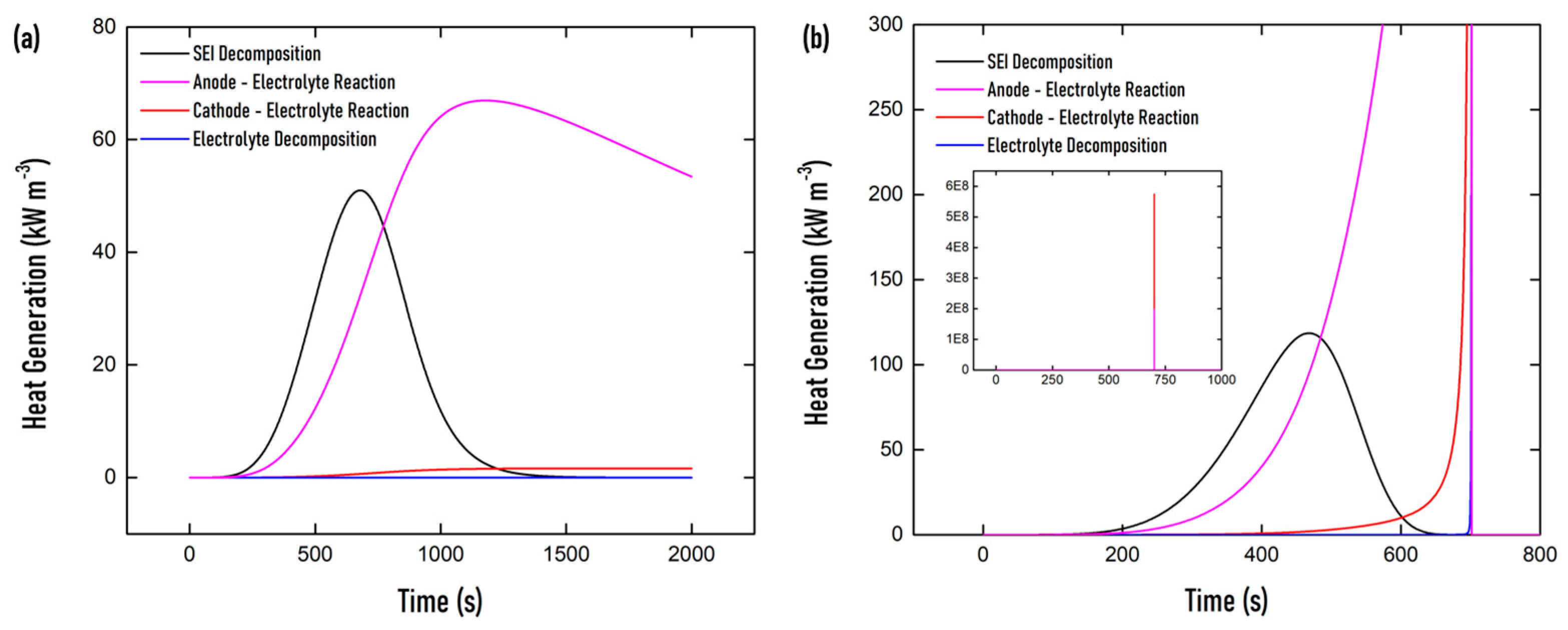
3.3. Thermal Runaway Behavior
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| CST | Concentrated solution theory |
| GPE | Gel polymer electrolyte |
| LCO | Lithium Cobalt Oxide |
| LIB | Lithium-ion battery |
| LiPo | Lithium-polymer |
| OCP | Open circuit potential |
| ODE | Ordinary differential equation |
| P2D | Pseudo-2-dimensional |
| PDE | Partial differential equation |
| PVdF-HFP | Poly(vinylidene fluoride-hexafluoropropylene) |
| RMSE | Root mean square error |
| SEI | Solid electrolyte interface |
| SOC | State of charge |
List of Symbols
| Symbol | SI Unit | Meaning |
| s−1 | Frequency factor | |
| m−1 | Specific surface area | |
| mol·m−3 | Concentration | |
| 1 | Dimensionless amount of lithium intercalated within the carbon | |
| 1 | The dimensionless concentration of electrolytes | |
| J·kg−1 K−1 | Specific heat at isobaric conditions | |
| 1 | Dimensionless amount of lithium-containing meta-stable species in the SEI | |
| m2·s−1 | Diffusion coefficient | |
| J·mol−1 | Activation energy | |
| C·mol−1 | Faraday constant | |
| 1 | The mean molar activity coefficient of an electrolyte | |
| J·kg−1 | Heat release | |
| W·m−3 K−1 | Heat transfer coefficient | |
| A·m−2 | Current density | |
| A·m−2 | Exchange current density | |
| k | m2.5·mol−0.5 s−1 | Reaction rate constant |
| L | m | Length |
| W·m−3 | Volumetric heat generation | |
| W·m−3 | Volumetric heat rejected | |
| J·mol−1 K−1 | Ideal gas constant | |
| M | Radial position across a spherical particle | |
| M | Radius of the particle | |
| K | Temperature | |
| S | Time | |
| 1 | Transference number of lithium-ion | |
| V | Equilibrium cell potential | |
| kg·m−3 | Specific material content | |
| m | Axial position along x-axis | |
| 1 | Dimensionless measure of the SEI layer thickness | |
| 1 | Reference dimensionless measure of the SEI layer thickness | |
| Greek symbols | ||
| 1 | Transfer coefficient | |
| 1 | Cathode–electrolyte conversion degree | |
| 1 | Volume fraction | |
| V | Overpotential | |
| S·m−1 | Ionic conductivity | |
| S·m−1 | Diffusional conductivity | |
| W·m−1 K−1 | Thermal conductivity | |
| kg·m−3 | Density | |
| S·m−1 | Electronic conductivity | |
| V | Electric potential |
List of Superscripts
| Superscript | Meaning |
| E | Electrolyte phase |
| S | Solid phase |
List of Subscripts
| Subscript | Meaning |
| Label | |
| … of the electrolyte decomposition | |
| amb | Ambient condition |
| Anode specific carbon content | |
| eff | Effective (accounts for tortuosity by Bruggeman correlation) |
| Cathode specific positive active content | |
| Length of the battery cell | |
| Species | |
| A | … of the anode |
| … of the anode–electrolyte interaction | |
| … of the anode–separator interface | |
| B | … of the battery model |
| C | … of the cathode |
| … of the cathode–electrolyte interaction | |
| … of the cathode–current collector interface | |
| Li | … of the lithium-ion |
| ohm | … from ohmic heat |
| pol | … from active polarization |
| rev | … from reversible reactions |
| SEI | … of the SEI decomposition |
| TR | … of the thermal runaway model |
References
- Treptow, R.S. Lithium Batteries: A Practical Application of Chemical Principles. J. Chem. Educ. 2003, 80, 1015. [Google Scholar] [CrossRef]
- Xu, P.; Chen, H.; Zhou, X.; Xiang, H. Gel Polymer Electrolyte Based on PVDF-HFP Matrix Composited with RGO-PEG-NH2 for High-Performance Lithium Ion Battery. J. Membr. Sci. 2020, 617, 118660. [Google Scholar] [CrossRef]
- Jia, Y.; Uddin, M.; Li, Y.; Xu, J. Thermal Runaway Propagation Behavior within 18650 Lithium-Ion Battery Packs: A Modeling Study. J. Energy Storage 2020, 31, 101668. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. A Pseudo Three-Dimensional Electrochemical–Thermal Model of a Prismatic LiFePO4 Battery during Discharge Process. Energy 2015, 80, 303–317. [Google Scholar] [CrossRef]
- Gandolfo, D.; Brandão, A.; Patiño, D.; Molina, M. Dynamic Model of Lithium Polymer Battery—Load Resistor Method for Electric Parameters Identification. J. Energy Inst. 2015, 88, 470–479. [Google Scholar] [CrossRef]
- Devillers, N.; Péra, M.-C.; Jemei, S.; Gustin, F.; Bienaimé, D. Complementary Characterization Methods for Lithium-Ion Polymer Secondary Battery Modeling. Int. J. Electr. Power Energy Syst. 2015, 67, 168–178. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, H.; Yu, H.; Li, J.; Xu, J. Multiphysics Computational Framework for Cylindrical Lithium-Ion Batteries under Mechanical Abusive Loading. Electrochim. Acta 2017, 256, 172–184. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. The Use of Mathematical Modeling in the Design of Lithium/Polymer Battery Systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1. [Google Scholar] [CrossRef]
- Thomas, K.E.; Newman, J.; Darling, R.M. Mathematical Modeling of Lithium Batteries. In Advances in Lithium-Ion Batteries; van Schalkwijk, W.A., Scrosati, B., Eds.; Springer US: Boston, MA, USA, 2002; pp. 345–392. ISBN 978-0-306-47508-5. [Google Scholar]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J.-M. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890–1903. [Google Scholar] [CrossRef]
- Ghalkhani, M.; Bahiraei, F.; Nazri, G.-A.; Saif, M. Electrochemical–Thermal Model of Pouch-Type Lithium-Ion Batteries. Electrochim. Acta 2017, 247, 569–587. [Google Scholar] [CrossRef]
- Yang, X.; Hu, X.; Chen, Z.; Chen, Y. Effect of Ambient Dissipation Condition on Thermal Behavior of a Lithium-Ion Battery Using a 3D Multi-Partition Model. Appl. Therm. Eng. 2020, 178, 115634. [Google Scholar] [CrossRef]
- Feng, X.; Ren, D.; He, X.; Ouyang, M. Mitigating Thermal Runaway of Lithium-Ion Batteries. Joule 2020, 4, 743–770. [Google Scholar] [CrossRef]
- Svoboda, V. BATTERIES|Fast Charging. In Encyclopedia of Electrochemical Power Sources; Garche, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 424–442. ISBN 978-0-444-52745-5. [Google Scholar]
- Warner, J.T. Lithium-Ion Battery Chemistries: A Primer; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 978-0-12-814779-5. [Google Scholar]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal Runaway Caused Fire and Explosion of Lithium Ion Battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Uchida, I.; Ishikawa, H.; Mohamedi, M.; Umeda, M. AC-Impedance Measurements during Thermal Runaway Process in Several Lithium/Polymer Batteries. J. Power Sources 2003, 119, 821–825. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, P.; Xu, M.; Wang, X. Computational Identification of the Safety Regime of Li-Ion Battery Thermal Runaway. Appl. Energy 2020, 261, 114440. [Google Scholar] [CrossRef]
- Domalanta, M.R.B.; Castro, M.T.; Ocon, J.D.; del Rosario, J.A.D. An Electrochemical-Thermal Multiphysics Model for Lithium Polymer Battery. Chem. Eng. Trans. 2022, 94, 145–150. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. Mathematical Modeling of a Lithium Ion Battery with Thermal Effects in COMSOL Inc. Multiphysics (MP) Software. J. Power Sources 2011, 196, 5985–5989. [Google Scholar] [CrossRef]
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety Focused Modeling of Lithium-Ion Batteries: A Review. J. Power Sources 2016, 306, 178–192. [Google Scholar] [CrossRef]
- Chen, J.; Ren, D.; Hsu, H.; Wang, L.; He, X.; Zhang, C.; Feng, X.; Ouyang, M. Investigating the Thermal Runaway Features of Lithium-Ion Batteries Using a Thermal Resistance Network Model. Appl. Energy 2021, 295, 117038. [Google Scholar] [CrossRef]
- Allen, J. Review of Polymers in the Prevention of Thermal Runaway in Lithium-Ion Batteries. Energy Rep. 2020, 6, 217–224. [Google Scholar] [CrossRef]
- Guo, M.; Sikha, G.; White, R.E. Single-Particle Model for a Lithium-Ion Cell: Thermal Behavior. J. Electrochem. Soc. 2011, 158, A122. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of Physics-Based Electrochemical Model for Lithium Ion Battery on Electric Vehicle. Part I: Diffusion Simplification and Single Particle Model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Lamorgese, A.; Mauri, R.; Tellini, B. Electrochemical-Thermal P2D Aging Model of a LiCoO2/Graphite Cell: Capacity Fade Simulations. J. Energy Storage 2018, 20, 289–297. [Google Scholar] [CrossRef]
- Thomas, K.E.; Bogatu, C.; Newman, J. Measurement of the Entropy of Reaction as a Function of State of Charge in Doped and Undoped Lithium Manganese Oxide. J. Electrochem. Soc. 2001, 148, A570. [Google Scholar] [CrossRef]
- Richter, F.; Gunnarshaug, A.; Burheim, O.S.; Vie, P.J.S.; Kjelstrup, S. Single Electrode Entropy Change for LiCoO2 Electrodes. ECS Trans. 2017, 80, 219. [Google Scholar] [CrossRef]
- Viswanathan, V.V.; Choi, D.; Wang, D.; Xu, W.; Towne, S.; Williford, R.E.; Zhang, J.G.; Liu, J.; Yang, Z. Effect of Entropy Change of Lithium Intercalation in Cathodes and Anodes on Li-Ion Battery Thermal Management. J. Power Sources 2010, 195, 3720–3729. [Google Scholar] [CrossRef]
- Rheinfeld, A.; Sturm, J.; Noel, A.; Wilhelm, J.; Kriston, A.; Pfrang, A.; Jossen, A. Quasi-Isothermal External Short Circuit Tests Applied to Lithium-Ion Cells: Part II. Modeling and Simulation. J. Electrochem. Soc. 2019, 166, A151–A177. [Google Scholar] [CrossRef]
- Yazami, R.; Reynier, Y. Thermodynamics and Crystal Structure Anomalies in Lithium-Intercalated Graphite. J. Power Sources 2006, 153, 312–318. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal Issues about Li-Ion Batteries and Recent Progress in Battery Thermal Management Systems: A Review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Jeon, D.H. Numerical Modeling of Lithium Ion Battery for Predicting Thermal Behavior in a Cylindrical Cell. Curr. Appl. Phys. 2014, 14, 196–205. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Z.; Guo, H.; Wang, J.; Li, X.; Yan, G. Simulating the Distribution of Electrochemical Characteristics: A Case Study of 4.35 V LiCoO2/Graphite Pouch Cell. Electrochim. Acta 2020, 354, 136634. [Google Scholar] [CrossRef]
- Jiang, F.; Peng, P. Elucidating the Performance Limitations of Lithium-Ion Batteries Due to Species and Charge Transport through Five Characteristic Parameters. Sci. Rep. 2016, 6, 32639. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Mathematical Modeling of the Capacity Fade of Li-Ion Cells. J. Power Sources 2003, 123, 230–240. [Google Scholar] [CrossRef]
- Peng, P.; Sun, Y.; Jiang, F. Thermal Analyses of LiCoO2 Lithium-Ion Battery during Oven Tests. Heat Mass Transf. 2014, 50, 1405–1416. [Google Scholar] [CrossRef]
- Kim, G.-H.; Pesaran, A.; Spotnitz, R. A Three-Dimensional Thermal Abuse Model for Lithium-Ion Cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Jiang, K.; Liao, G.; Jiaqiang, E.; Zhang, F.; Chen, J.; Leng, E. Thermal Management Technology of Power Lithium-Ion Batteries Based on the Phase Transition of Materials: A Review. J. Energy Storage 2020, 32, 101816. [Google Scholar] [CrossRef]
- Coman, P.T.; Rayman, S.; White, R.E. A Lumped Model of Venting during Thermal Runaway in a Cylindrical Lithium Cobalt Oxide Lithium-Ion Cell. J. Power Sources 2016, 307, 56–62. [Google Scholar] [CrossRef]
- Smekens, J.; Paulsen, J.; Yang, W.; Omar, N.; Deconinck, J.; Hubin, A.; van Mierlo, J. A Modified Multiphysics Model for Lithium-Ion Batteries with a LixNi1/3Mn1/3Co1/3O2 Electrode. Electrochim. Acta 2015, 174, 615–624. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Ni, R.; Xie, Z. Effects of Fast Charging Modes on Thermal Performance of Lithium-Ion Battery. Energy Technol. 2022, 10, 2200415. [Google Scholar] [CrossRef]
- Li, J.; He, K.; Meng, Q.; Li, X.; Zhu, Y.; Hwang, S.; Sun, K.; Gan, H.; Zhu, Y.; Mo, Y.; et al. Kinetic Phase Evolution of Spinel Cobalt Oxide during Lithiation. ACS Nano 2016, 10, 9577–9585. [Google Scholar] [CrossRef]
- Kim, D.S.; Sohn, J.S.; Lee, C.K.; Lee, J.H.; Han, K.S.; Lee, Y. il Simultaneous Separation and Renovation of Lithium Cobalt Oxide from the Cathode of Spent Lithium Ion Rechargeable Batteries. J. Power Sources 2004, 132, 145–149. [Google Scholar] [CrossRef]
- Shu, J.; Shui, M.; Huang, F.; Ren, Y.; Wang, Q.; Xu, D.; Hou, L. A New Look at Lithium Cobalt Oxide in a Broad Voltage Range for Lithium-Ion Batteries. J. Phys. Chem. C 2010, 114, 3323–3328. [Google Scholar] [CrossRef]
- Capron, O.; Samba, A.; Omar, N.; van den Bossche, P.; van Mierlo, J. Thermal Behaviour Investigation of a Large and High Power Lithium Iron Phosphate Cylindrical Cell. Energies 2015, 8, 10017–10042. [Google Scholar] [CrossRef]
- Celik, A.; Coban, H.; Göcmen, S.; Ezan, M.A.; Gören, A.; Erek, A. Passive Thermal Management of the Lithium-Ion Battery Unit for a Solar Racing Car. Int. J. Energy. Res. 2019, 43, 3681–3691. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Z.; Guo, H.; Wang, J.; Li, X.; Yan, G. Systematic Parameter Acquisition Method for Electrochemical Model of 4.35 V LiCoO2 Batteries. Solid State Ion 2019, 343, 115083. [Google Scholar] [CrossRef]
- Pan, S.; Ji, C.; Wang, S.; Wang, B. Study on the Performance of Parallel Air-Cooled Structure and Optimized Design for Lithium-Ion Battery Module. Fire Technol. 2020, 56, 2623–2647. [Google Scholar] [CrossRef]
- Yiding, L.; Wenwei, W.; Cheng, L.; Fenghao, Z. High-Efficiency Multiphysics Coupling Framework for Cylindrical Lithium-Ion Battery under Mechanical Abuse. J. Clean. Prod. 2021, 286, 125451. [Google Scholar] [CrossRef]
- Egorkina, O.Y.; Skundin, A.M. The Effect of Temperature on Lithium Intercalation into Carbon Materials. J. Solid State Electrochem. 1998, 2, 216–220. [Google Scholar] [CrossRef]
- Choudhari, V.G.; Dhoble, D.A.S.; Sathe, T.M. A Review on Effect of Heat Generation and Various Thermal Management Systems for Lithium Ion Battery Used for Electric Vehicle. J. Energy Storage 2020, 32, 101729. [Google Scholar] [CrossRef]
- Lai, Y.; Du, S.; Ai, L.; Ai, L.; Cheng, Y.; Tang, Y.; Jia, M. Insight into Heat Generation of Lithium Ion Batteries Based on the Electrochemical-Thermal Model at High Discharge Rates. Int. J. Hydrog. Energy 2015, 40, 13039–13049. [Google Scholar] [CrossRef]
- Takano, K.; Saito, Y.; Kanari, K.; Nozaki, K.; Kato, K.; Negishi, A.; Kato, T. Entropy Change in Lithium Ion Cells on Charge and Discharge. J. Appl. Electrochem. 2002, 32, 251–258. [Google Scholar] [CrossRef]
- Hatchard, T.D.; MacNeil, D.D.; Basu, A.; Dahn, J.R. Thermal Model of Cylindrical and Prismatic Lithium-Ion Cells. J. Electrochem. Soc. 2001, 148, A755. [Google Scholar] [CrossRef]
- Hosseinzadeh, E.; Genieser, R.; Worwood, D.; Barai, A.; Marco, J.; Jennings, P. A Systematic Approach for Electrochemical-Thermal Modelling of a Large Format Lithium-Ion Battery for Electric Vehicle Application. J. Power Sources 2018, 382, 77–94. [Google Scholar] [CrossRef]
- Macdonald, M.P.; Chandrasekaran, S.; Garimella, S.; Fuller, T.F. Thermal Runaway in a Prismatic Lithium Ion Cell Triggered by a Short Circuit. J. Energy Storage 2021, 40, 102737. [Google Scholar] [CrossRef]
- Joachin, H.; Kaun, T.D.; Zaghib, K.; Prakash, J. Electrochemical and Thermal Studies of Carbon-Coated LiFePO4 Cathode. J. Electrochem. Soc. 2009, 156, A401. [Google Scholar] [CrossRef]
- Xu, J.; Hendricks, C. A Multiphysics Simulation of the Thermal Runaway in Large-Format Lithium-Ion Batteries. In Proceedings of the 18th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 28–31 May 2019; pp. 815–821. [Google Scholar] [CrossRef]
- Yiding, L.; Wenwei, W.; Cheng, L.; Xiaoguang, Y.; Fenghao, Z. Multi-Physics Safety Model Based on Structure Damage for Lithium-Ion Battery under Mechanical Abuse. J. Clean. Prod. 2020, 277, 124094. [Google Scholar] [CrossRef]
- Shelke, A.V.; Buston, J.E.H.; Gill, J.; Howard, D.; Abbott, K.C.; Goddard, S.L.; Read, E.; Howard, G.E.; Abaza, A.; Cooper, B.; et al. Characterizing and Predicting 21700 NMC Lithium-Ion Battery Thermal Runaway Induced by Nail Penetration. Appl. Therm. Eng. 2022, 209, 118278. [Google Scholar] [CrossRef]



| Property | Value |
|---|---|
| Cathode | LCO |
| Anode | Graphite |
| Electrolyte | PVdF-HFP |
| Positive current collector | Aluminum |
| Negative current collector | Copper |
| Nominal capacity | 2000 mAh |
| Nominal voltage | 3.7 V |
| Maximum charge voltage | 4.2 V |
| Maximum charge current | 1 C |
| Maximum discharge current | 2 C |
| Discharge cut-off voltage | 2.75 V |
| Weight | 37.5 g |
| Dimensions (Length*Width*Thickness in mm) | 54.5*49.3*4.8 |
| Name | Equation | Reference | ||
|---|---|---|---|---|
| Charge transport | Solid phase | (1) (2) | [11,20] | |
| Electrolyte phase | (3) (4) | [11,20] | ||
| Mass transport | Solid phase | (5) | [11] | |
| Electrolyte phase | (6) (7) | [11,20] | ||
| Active surface area | (8) | [20] | ||
| Current density | (9) | [11] | ||
| Exchange current density | (10) | [20] | ||
| Overpotential | (11) | [11] | ||
| Name | Equation | Reference | |
|---|---|---|---|
| General energy balance | (16) | [22,28] | |
| Battery heat generation | (17) | [11] | |
| Heat generation in battery model | (18) | [20] | |
| Reversible heat | (19) | [11] | |
| Irreversible heat | (20) | [20] | |
| Polarization heat | (21) | [11] | |
| Ohmic heat | (22) (23) | [28] |
| Parameter (Symbol) | Positive Current Collector | Cathode | Separator | Anode | Negative Current Collector | Reference |
|---|---|---|---|---|---|---|
| Length (L) | 10 × 10−6 | 70 × 10−6 | 25 × 10−6 | 73.5 × 10−6 | 10 × 10−6 | [28] |
| Solid phase volume fraction ( | 0.59 | 0.49 | [35] | |||
| Electrolyte phase volume fraction ( | 0.45 | 0.45 | 0.45 | [36] | ||
| Radius of the particle ( | 8 × 10−6 | 1 × 10−5 | [37] | |||
| Solid phase Li + diffusivity | 10−14 | 3.9 × 10−14 | [38] | |||
| Reaction rate constant (k) | 1.0 × 10−11 | [36] | ||||
| Initial Li + concentration in solid () | 1 21,250 | 2 23,099.58 | 1—Fitted 2—[22] | |||
| Maximum Li + concentration in solid () | 51554 | 30555 | [20] | |||
| Initial electrolyte concentration () | 1000 | [38] | ||||
| Transference number of lithium-ion () | 0.435 | [28] | ||||
| Cathodic charge transfer coefficient () | 0.5 | 0.5 | [38] | |||
| Anodic charge transfer coefficient () | 0.5 | 0.5 | [38] | |||
| Electronic conductivity in the solid phase () | 1 3.8 × 107 | 2 10 | 2 100 | 1 6 × 107 | 1—[35] 2—[38] | |
| Ionic conductivity () | (Equation (12)) | [8] | ||||
| Electrolyte phase Li + diffusivity | (Equation (13)) | [4] | ||||
| LixCoO2 Equilibrium potential ( | (Equation (14)) | [26] | ||||
| LiyC6 Equilibrium potential ( | (Equation (15)) | [26] | ||||
| LixCoO2 Entropy coefficient | (Equation (26)) | [26] | ||||
| LiyC6 Entropy Coefficient | (Equation (27)) | [32] | ||||
| Thermal conductivity () | 238 | 1.48 | 0.45 | 1.04 | 398 | [39] |
| Isobaric heat capacity () | 903 | 700 | 133.9 | 1437.4 | 385 | [39] |
| Density () | 1500 | 2500 | 1290 | 2660 | 8900 | [39] |
| Name | Equation | Reference | |
|---|---|---|---|
| Heat generation in thermal runaway | (28) | [40] | |
| SEI decomposition heat | (29) | [40,42] | |
| Anode–electrolyte reaction heat | (30) | [34,42] | |
| Cathode–electrolyte reaction heat | (31) | [34,42] | |
| Electrolyte decomposition heat | (32) | [34,42] |
| Physics-Controlled Mesh Type | Number of Mesh Elements | Computational Time | RMSE [V] |
|---|---|---|---|
| Coarser | 19,152 | 45 s | 0.0599258 |
| Coarse | 35,805 | 57 s | 0.0599250 |
| Normal | 85,191 | 2 min 11 s | 0.0577542 |
| Fine | 300,673 | 9 min 42 s | 0.0599246 |
| Finer | 419,405 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domalanta, M.R.B.; Paraggua, J.A.D.R. A Multiphysics Model Simulating the Electrochemical, Thermal, and Thermal Runaway Behaviors of Lithium Polymer Battery. Energies 2023, 16, 2642. https://doi.org/10.3390/en16062642
Domalanta MRB, Paraggua JADR. A Multiphysics Model Simulating the Electrochemical, Thermal, and Thermal Runaway Behaviors of Lithium Polymer Battery. Energies. 2023; 16(6):2642. https://doi.org/10.3390/en16062642
Chicago/Turabian StyleDomalanta, Marcel Roy B., and Julie Anne D. R. Paraggua. 2023. "A Multiphysics Model Simulating the Electrochemical, Thermal, and Thermal Runaway Behaviors of Lithium Polymer Battery" Energies 16, no. 6: 2642. https://doi.org/10.3390/en16062642
APA StyleDomalanta, M. R. B., & Paraggua, J. A. D. R. (2023). A Multiphysics Model Simulating the Electrochemical, Thermal, and Thermal Runaway Behaviors of Lithium Polymer Battery. Energies, 16(6), 2642. https://doi.org/10.3390/en16062642





