Multi-Scroll Attractor and Multi-Stable Dynamics of a Three-Dimensional Jerk System
Abstract
1. Introduction
2. Model of Jerk System
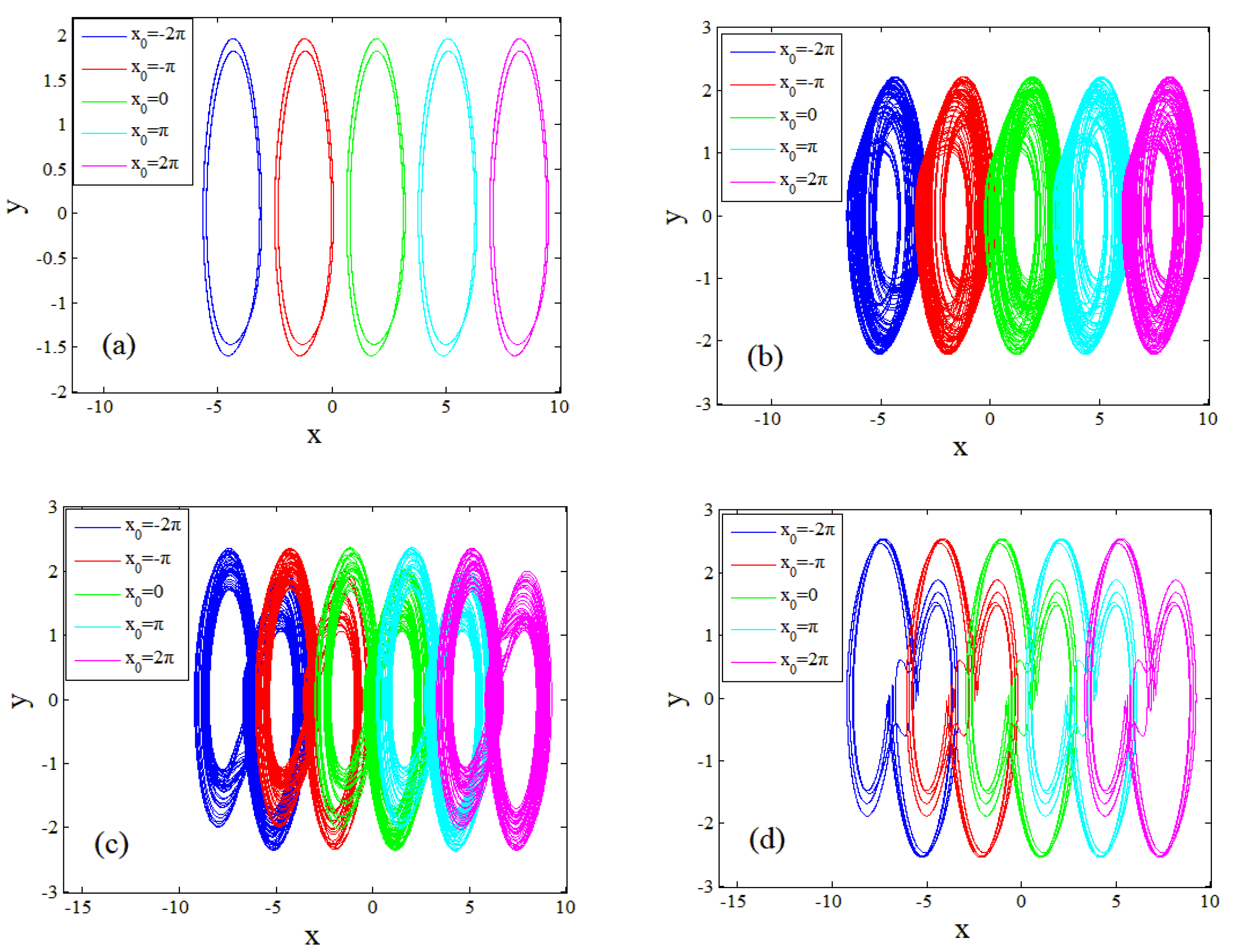
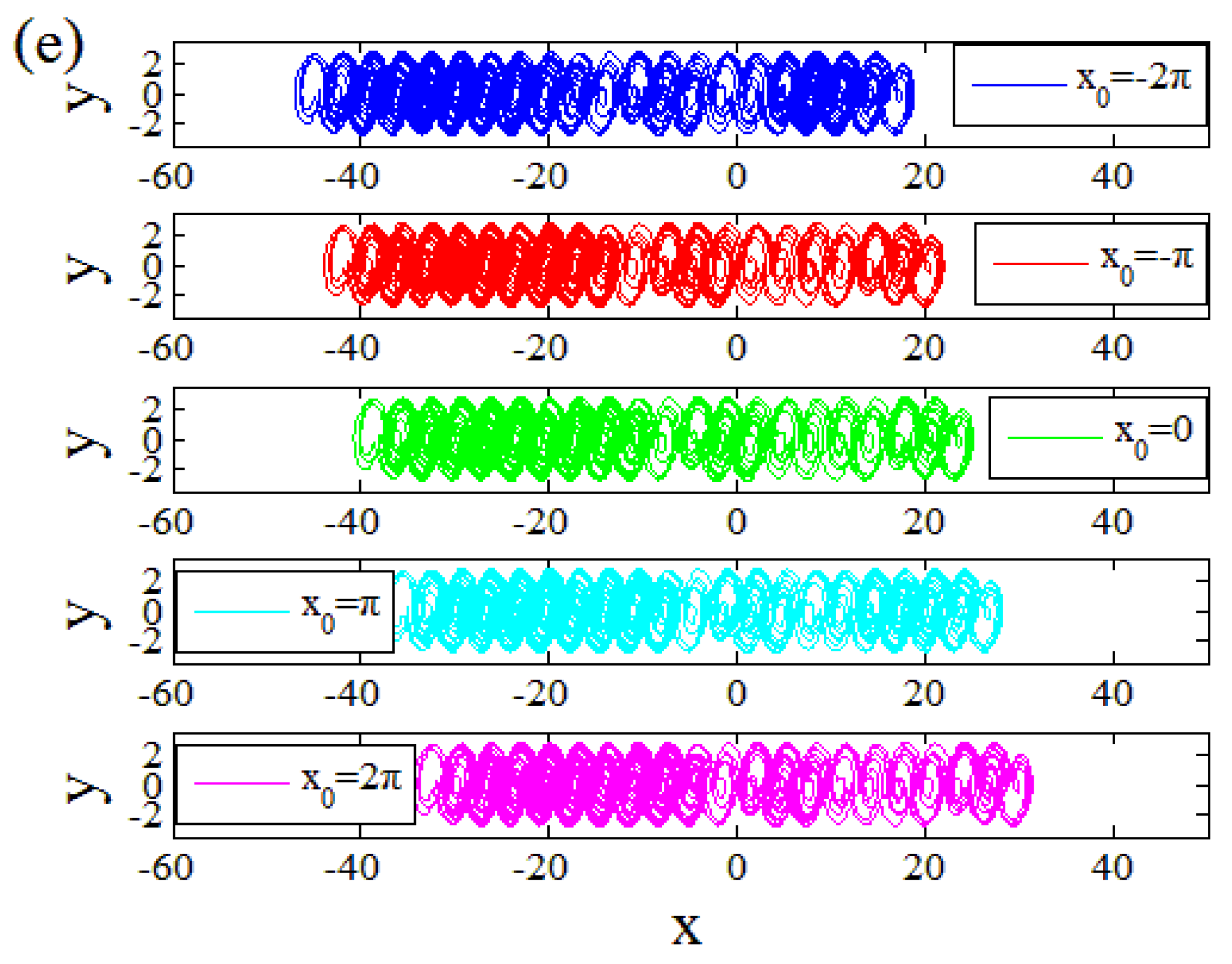
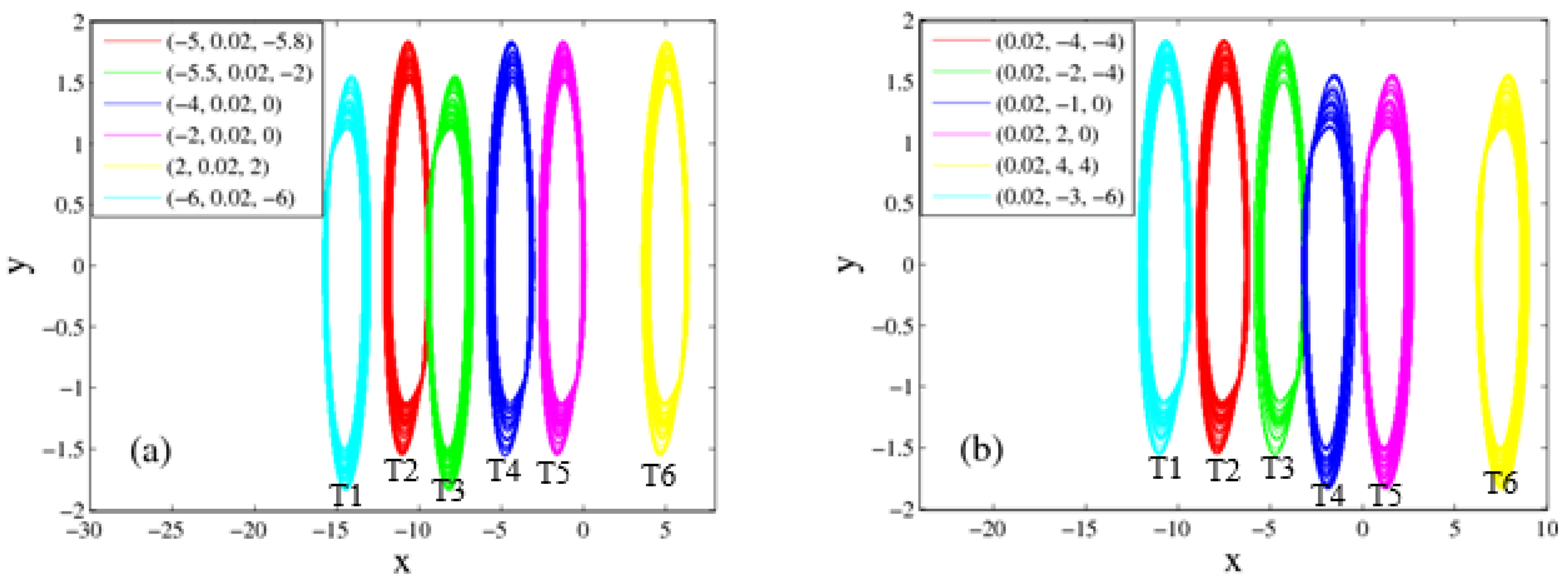
3. Multi-Scroll Attractor of Jerk System
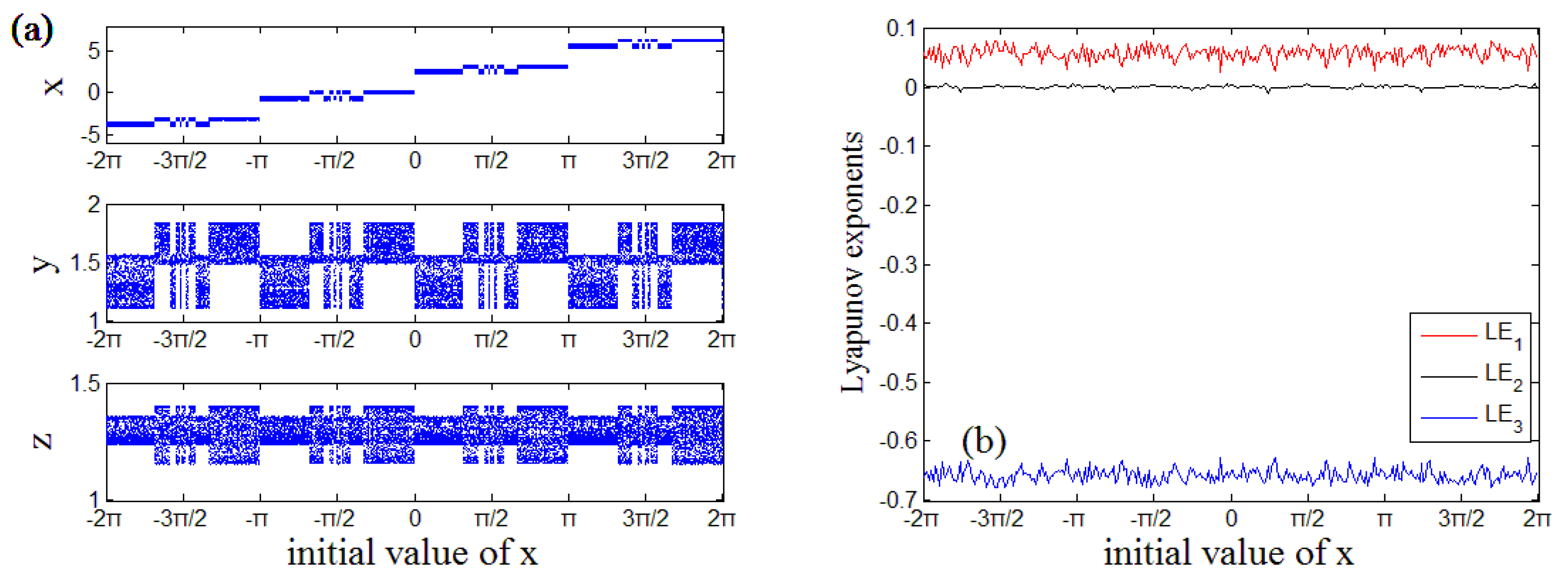
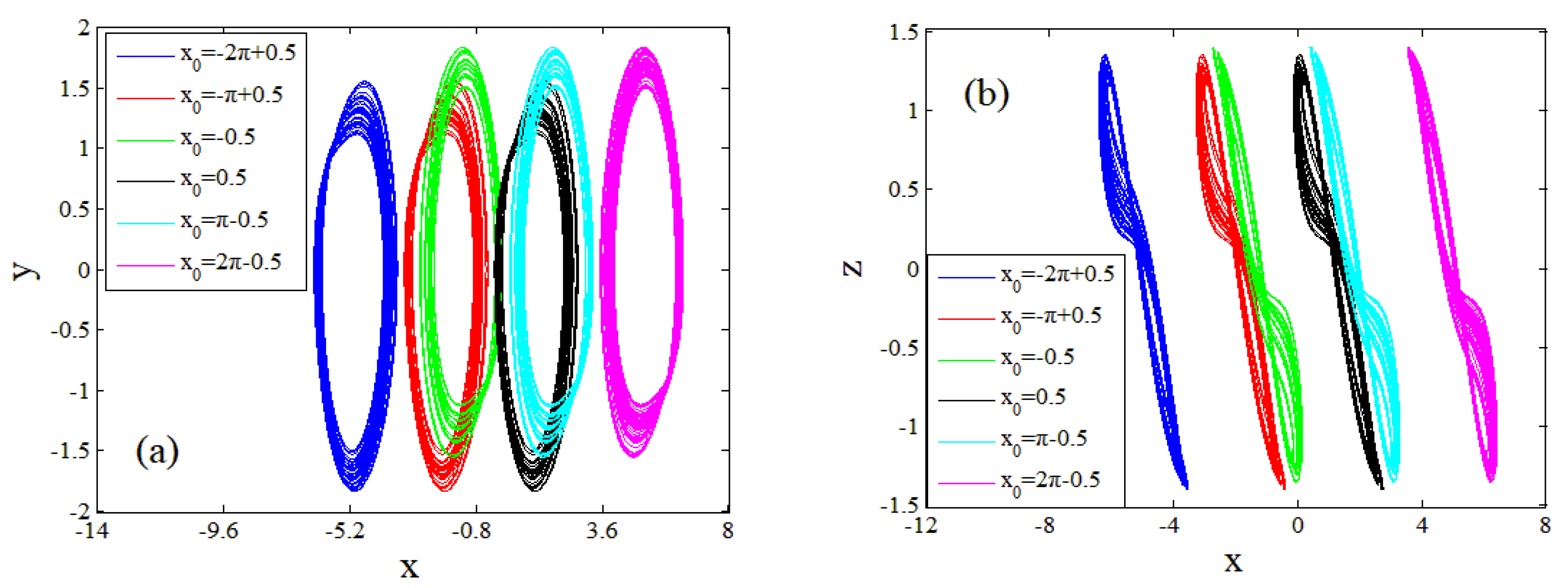
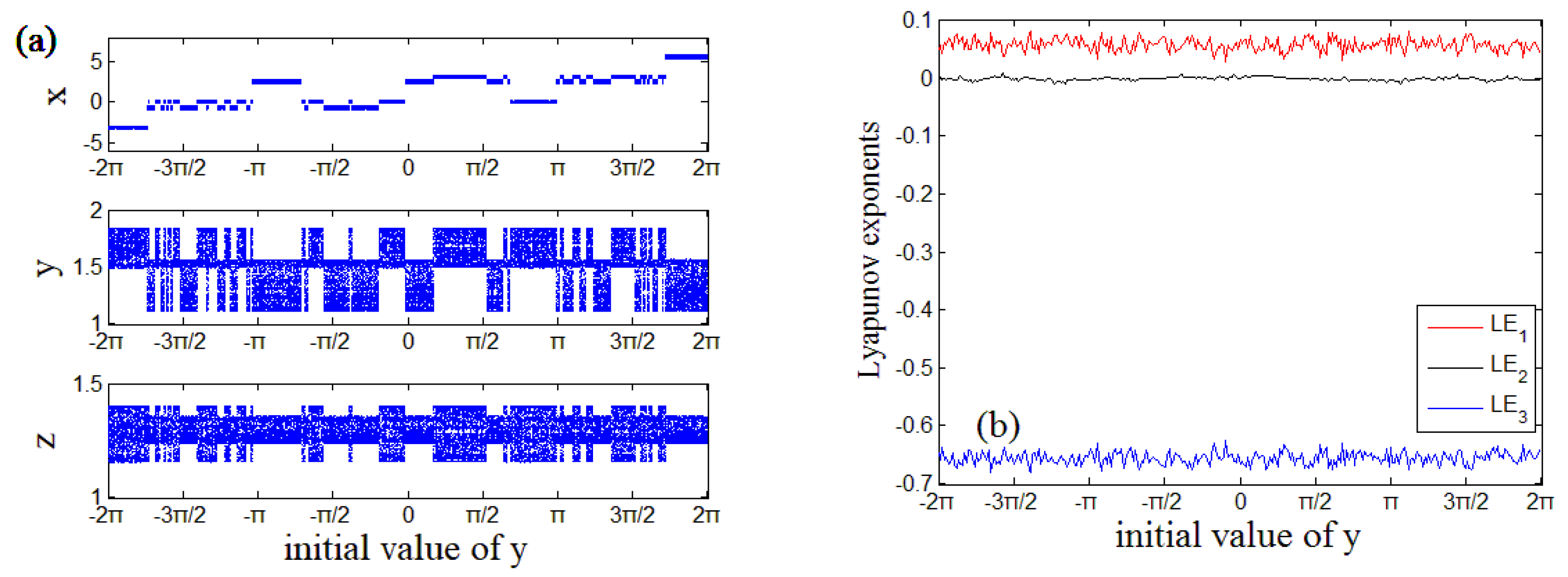
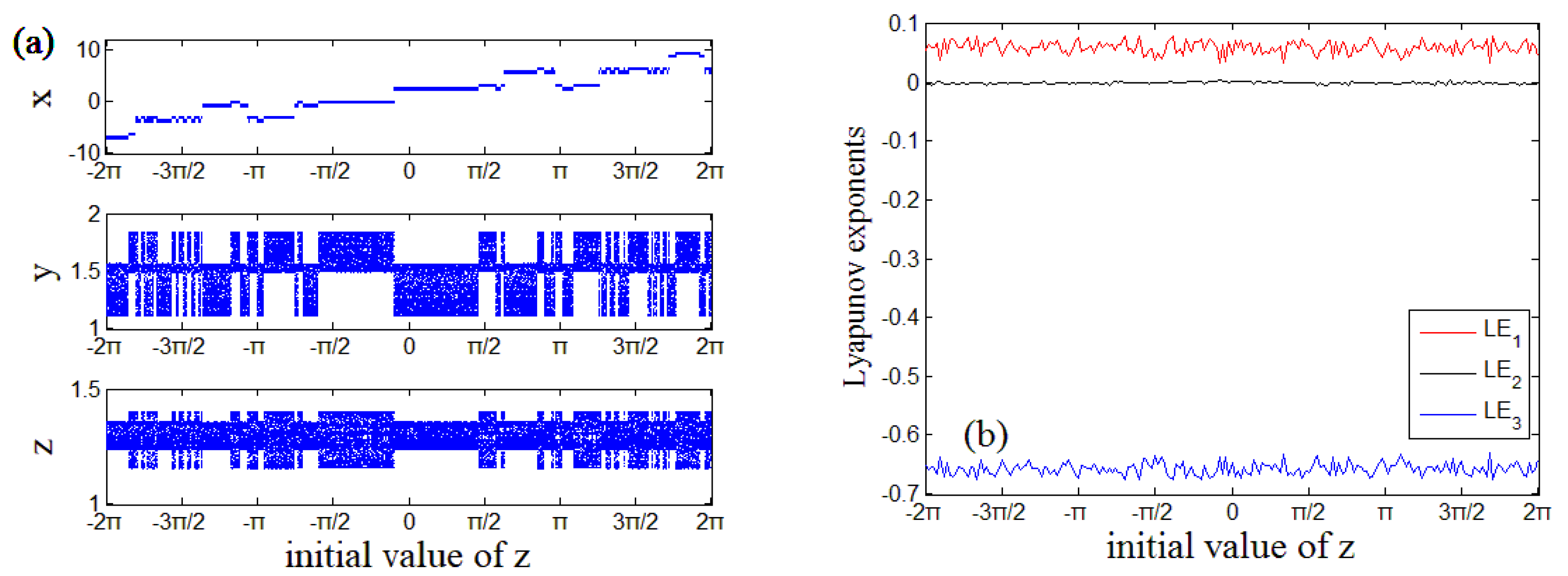
4. Multi-Stable Dynamics of Jerk System
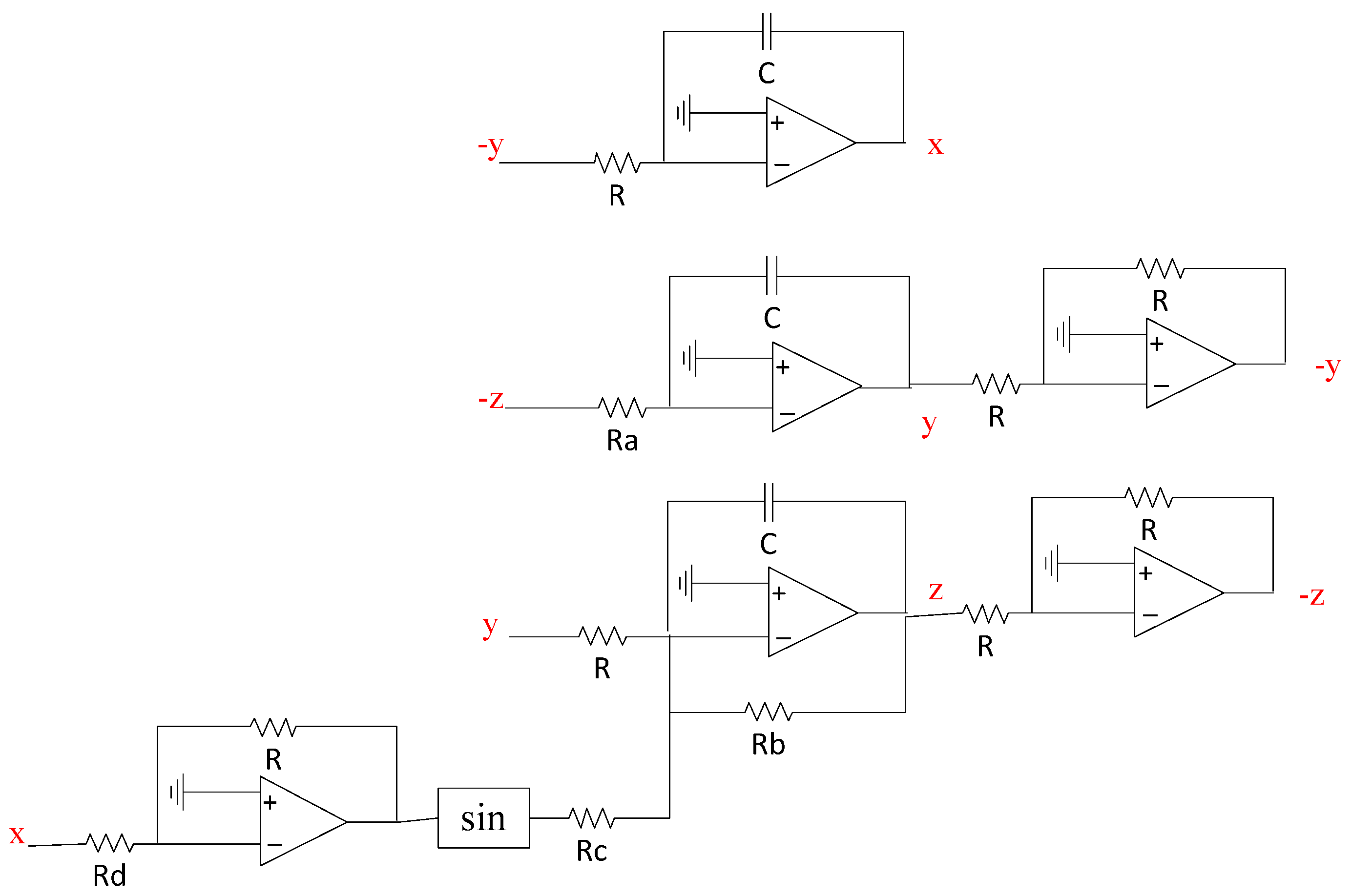
5. Circuit Verification of Jerk System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gámez-Guzmán, L.; Cruz-Hernandez, C.; Gutierrez, R.M.L.; Guerrero, E.E.G. Synchronization of Chua’s Circuits with Multi-Scroll Attractors: Application to Communication. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2765–2775. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Li, W.; Li, H.; Feng, W.; Qian, K. Image encryption algorithm with circle index table scrambling and partition diffusion. Nonlinear Dyn. 2021, 103, 2043–2061. [Google Scholar] [CrossRef]
- Yildirim, M. Optical color image encryption scheme with a novel DNA encoding algorithm based on a chaotic circuit. Chaos Solitons Fractals 2022, 155, 111631. [Google Scholar] [CrossRef]
- Li, C.L.; Zhou, Y.; Li, H.M.; Feng, W.; Du, J. Image encryption scheme with bit-level scrambling and multiplication diffusion. Multimed. Tools Appl. 2021, 80, 18479–18501. [Google Scholar] [CrossRef]
- Yang, H.; Xu, X.; Jiang, G.; Luo, R. A Novel Multi-User Carrier Index Differential Chaos Shift Keying Modulation Scheme. J. Circuits Syst. Comput. 2022, 31, 2350009. [Google Scholar] [CrossRef]
- Ding, P.; Feng, X. Generation of Multi-Scroll Chaotic Attractors from a Jerk Circuit with a Special Form of a Sine Function. Electronics 2020, 9, 842. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Rangel-Magdaleno, J.J.; Pano-Azucena, A.D.; Obeso-Rodelo, P.J.; Nuñez-Perez, J.C. FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 66–80. [Google Scholar] [CrossRef]
- Mathale, D.; Goufo, E.; Khumalo, M. Coexistence of multi-scroll chaotic attractors for a three-dimensional quadratic autonomous fractional system with non-local and non-singular kernel. Alex. Eng. J. 2021, 60, 3521–3538. [Google Scholar] [CrossRef]
- Li, C.L.; Yu, S.; Luo, X. A ring-scroll Chua system. Int. J. Bifurc. Chaos 2023, 23, 1350170. [Google Scholar] [CrossRef]
- Altun, K. Multi-Scroll Attractors with Hyperchaotic Behavior Using Fractional-Order Systems. J. Circuits Syst. Comput. 2022, 31, 2250085. [Google Scholar] [CrossRef]
- Li, C.L.; Li, Z.Y.; Feng, W.; Tong, Y.N.; Wei, D.Q. Dynamical behavior and image encryption application of a memristor-based circuit system. AEU-Int. J. Electron. Commun. 2019, 110, 152861. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Munoz-Pacheco, J.M.; Serrano, F.E.; Sánchez-Gaspariano, L.A.; Volos, C. Experimental verification of the multi-scroll chaotic attractors synchronization in PWL arbitrary-order systems using direct coupling and passivity-based control. Integr. VLSI J. 2021, 81, 56–70. [Google Scholar] [CrossRef]
- Peng, Y.; He, S.; Sun, K. Parameter identification for discrete memristive chaotic map using adaptive differential evolution algorithm. Nonlinear Dyn. 2022, 7, 1263–1275. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Yang, X.; Zi, X.; Xiao, F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn. 2022, 108, 1697–1717. [Google Scholar] [CrossRef]
- Ding, P.; Feng, X.; Lin, F. Generation of 3-D Grid Multi-Scroll Chaotic Attractors Based on Sign Function and Sine Function. Electronics 2020, 9, 2145. [Google Scholar] [CrossRef]
- Li, H.; Lu, Y.; Li, C. Dynamics in stimulation-based tabu learning neuron model. Int. J. Electron. Commun. 2021, 142, 153983. [Google Scholar] [CrossRef]
- Li, C.; Li, H.; Xie, W.; Du, J. A S-type bistable locally active memristor model and its analog implementation in an oscillator circuit. Nonlinear Dyn. 2021, 106, 1041–1058. [Google Scholar] [CrossRef]
- Suykens, J.; Vandewalle, J. Generation of n-double scrolls (n=1,2,3,4,...). IEEE Trans. Circuits Syst.-I 1993, 40, 861–867. [Google Scholar] [CrossRef]
- Yu, S.; Tang, W.K.S.; Lu, J. Generating 2n-wing attractors from Lorenz-like systems. Int. J. Circuit Theory Appl. 2010, 38, 243–258. [Google Scholar] [CrossRef]
- Yu, S.; Tang, W.K.S. Generation of n× m-scroll attractors in a two-port RCL network with hysteresis circuits. Chaos Soliton Fract. 2009, 39, 821–830. [Google Scholar] [CrossRef]
- Hu, X.; Liu, C.; Liu, L.; Ni, J.; Li, S. Multi-scroll hidden attractors in improved Sprott A system. Nonlinear Dyn. 2016, 86, 1725–1734. [Google Scholar] [CrossRef]
- Wang, F.; Liu, C. Generation of multi-scroll chaotic attractors via the saw-tooth function. Int. J. Mod. Phys. B 2008, 22, 2399–2405. [Google Scholar] [CrossRef]
- Lü, J.; Han, F.; Yu, X.; Chen, G. Generating 3-D multi-scroll chaotic attractors: A hysteresis series switching method. Automatica 2004, 40, 1677–1687. [Google Scholar] [CrossRef]
- Li, C.; Qian, K.; He, S.; Li, H.; Feng, W. Dynamics and optimization control of a robust chaotic map. IEEE Access 2019, 7, 160072–160081. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Cao, Y.; Liu, T.; Wang, J. Multistability analysis of a conformable fractional-order chaotic system. Phys. Scr. 2020, 7, 075204. [Google Scholar] [CrossRef]
- Chen, L.; Peng, H.; Wang, D. Studies on the construction method of a family of multi-scroll chaotic systems. Acta Phys. Sin. 2008, 57, 3337–3341. [Google Scholar] [CrossRef]
- Yu, S.; Lü, J.; Yu, X.; Chen, G. Design and implementation of grid multiwing hyperchaotic Lorenz system family via switching control and constructing super-heteroclinic loops. IEEE Trans Circuits Syst-I 2012, 59, 1015–1028. [Google Scholar] [CrossRef]
- Li, C.; Hai, W. Constructing multiwing attractors from a robust chaotic system with non-hyperbolic equilibrium points. Automatika 2018, 59, 184–193. [Google Scholar] [CrossRef]
- Ai, X.; Sun, K.; He, S.; Wang, H. Design of Grid Multiscroll Chaotic Attractors via Transformations. Int. J. Bifurc. Chaos 2015, 25, 1530027. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, J.; Cang, S.; Wang, Z.; Chen, Z. Simplified hyper-chaotic systems generating multi-wing non-equilibrium attractors. Optik 2016, 127, 2424–2431. [Google Scholar] [CrossRef]
- Ramadoss, J.; Kengne, J.; Koinfo, J.B.; Rajagopal, K. Multiple Hopf bifurcations, period-doubling reversals and coexisting attractors for a novel chaotic jerk system with Tchebytchev polynomials. Phys. A 2022, 587, 126501. [Google Scholar] [CrossRef]
- Ma, J.; Wu, X.; Chu, R.; Zhang, L. Selection of multi-scroll attractors in Jerk circuits and their verification using Pspice. Nonlinear Dyn. 2014, 76, 1951–1962. [Google Scholar] [CrossRef]
- Guo, M.; Zhu, Y.; Liu, R.; Zhao, K.; Dou, G. An associative memory circuit based on physical memristors. Neurocomputing 2022, 472, 12–23. [Google Scholar] [CrossRef]
- Li, C.; Chen, Z.; Yang, X.; He, S.; Du, J. Self-reproducing dynamics in a two-dimensional discrete map. Eur. Phys. J. Spec. Top. 2021, 230, 1959–1970. [Google Scholar] [CrossRef]
- Wang, X.Y.; Dong, C.T.; Zhou, P.F.; Nandi, S.K.; Nath, S.K.; Elliman, R.G.; Iu, H.H.; Kang, S.M.; Eshraghian, J.K. Low-Variance Memristor-Based Multi-Level Ternary Combinational Logic. IEEE Trans. Circuits Syst. I 2022, 69, 2423–2434. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Fotsin, H.B.; Negou, A.N.; Tchiotsop, D. Coexistence of Multiple Attractors and Crisis Route to Chaos in a Novel Chaotic Jerk Circuit. Int. J. Bifurc. Chaos 2016, 26, 1650081. [Google Scholar]
- Li, H.D.; Li, C.L.; Du, J.R. Discretized locally active memristor and application in logarithmic map. Nonlinear Dyn. 2022, 16, 736642. [Google Scholar] [CrossRef]
- Marszalek, W.; Sadecki, J. Complex two-parameter bifurcation diagrams of a simple oscillating circuit. IEEE Trans. Circuits Syst. II 2018, 66, 687–691. [Google Scholar] [CrossRef]
- Li, C.; Li, H.; Li, W.; Tong, Y.; Zhang, J.; Wei, D.; Li, F. Implementation and stability of a chaotic system with coexistence of hyperbolic and non-hyperbolic equilibria. Int. J. Electron. Commun. 2018, 84, 199–205. [Google Scholar] [CrossRef]
- Wang, M.; Li, J.; Zhang, X.; Iu, H.H.-C.; Fernando, T.; Li, Z.; Zeng, Y. A novel non-autonomous chaotic system with infinite 2-D lattice of attractors and bursting oscillations. IEEE Trans. Circuits Syst. II 2020, 68, 1023–1027. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zeng, J. Multi-Scroll Attractor and Multi-Stable Dynamics of a Three-Dimensional Jerk System. Energies 2023, 16, 2494. https://doi.org/10.3390/en16052494
Li F, Zeng J. Multi-Scroll Attractor and Multi-Stable Dynamics of a Three-Dimensional Jerk System. Energies. 2023; 16(5):2494. https://doi.org/10.3390/en16052494
Chicago/Turabian StyleLi, Fudong, and Jingru Zeng. 2023. "Multi-Scroll Attractor and Multi-Stable Dynamics of a Three-Dimensional Jerk System" Energies 16, no. 5: 2494. https://doi.org/10.3390/en16052494
APA StyleLi, F., & Zeng, J. (2023). Multi-Scroll Attractor and Multi-Stable Dynamics of a Three-Dimensional Jerk System. Energies, 16(5), 2494. https://doi.org/10.3390/en16052494





