Optimization of Setting Angle Distribution to Suppress Hump Characteristic in Pump Turbine
Abstract
1. Introduction
2. Numerical Model
2.1. Pump Turbine Model
2.2. Numerical Method and the Boundary Conditions
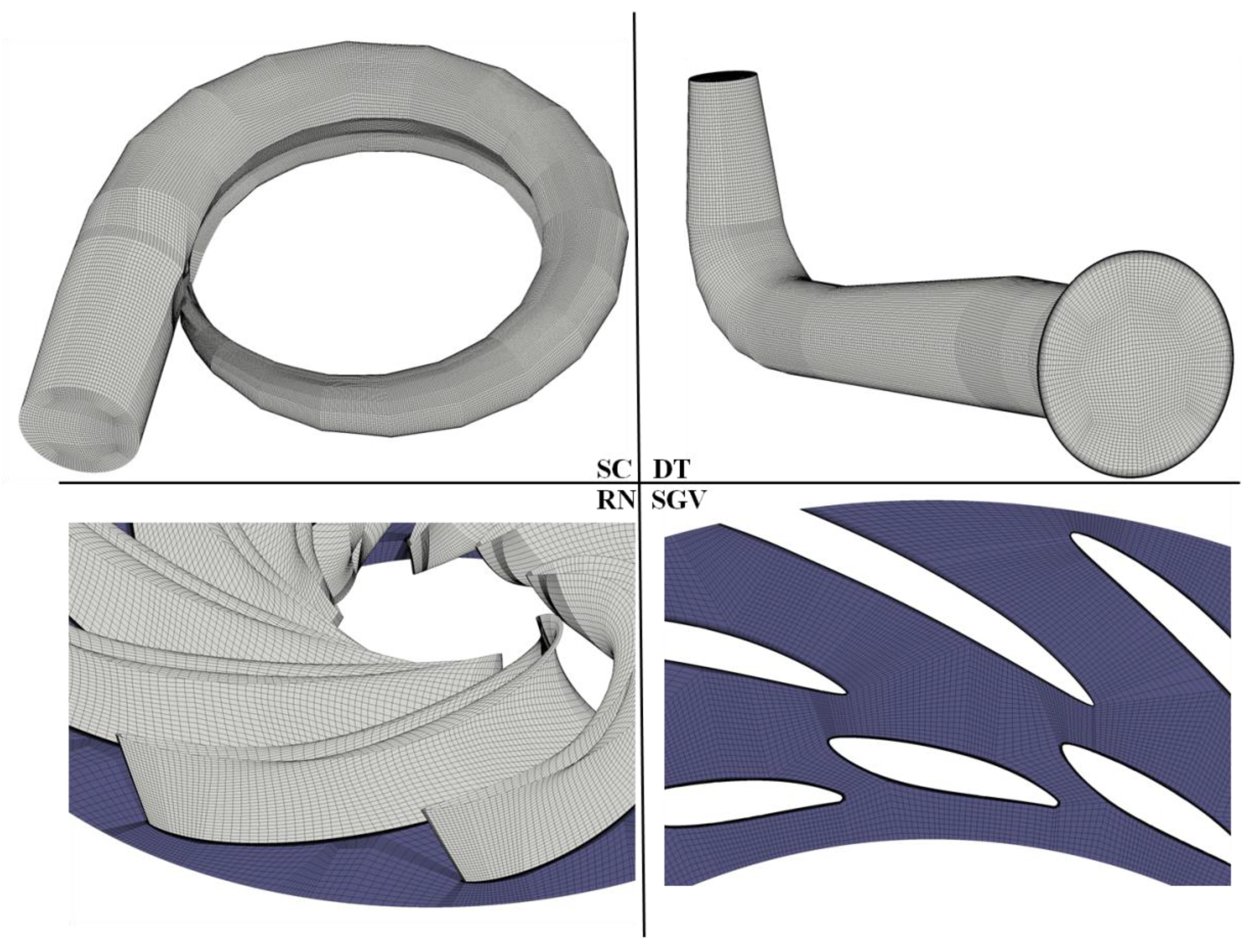
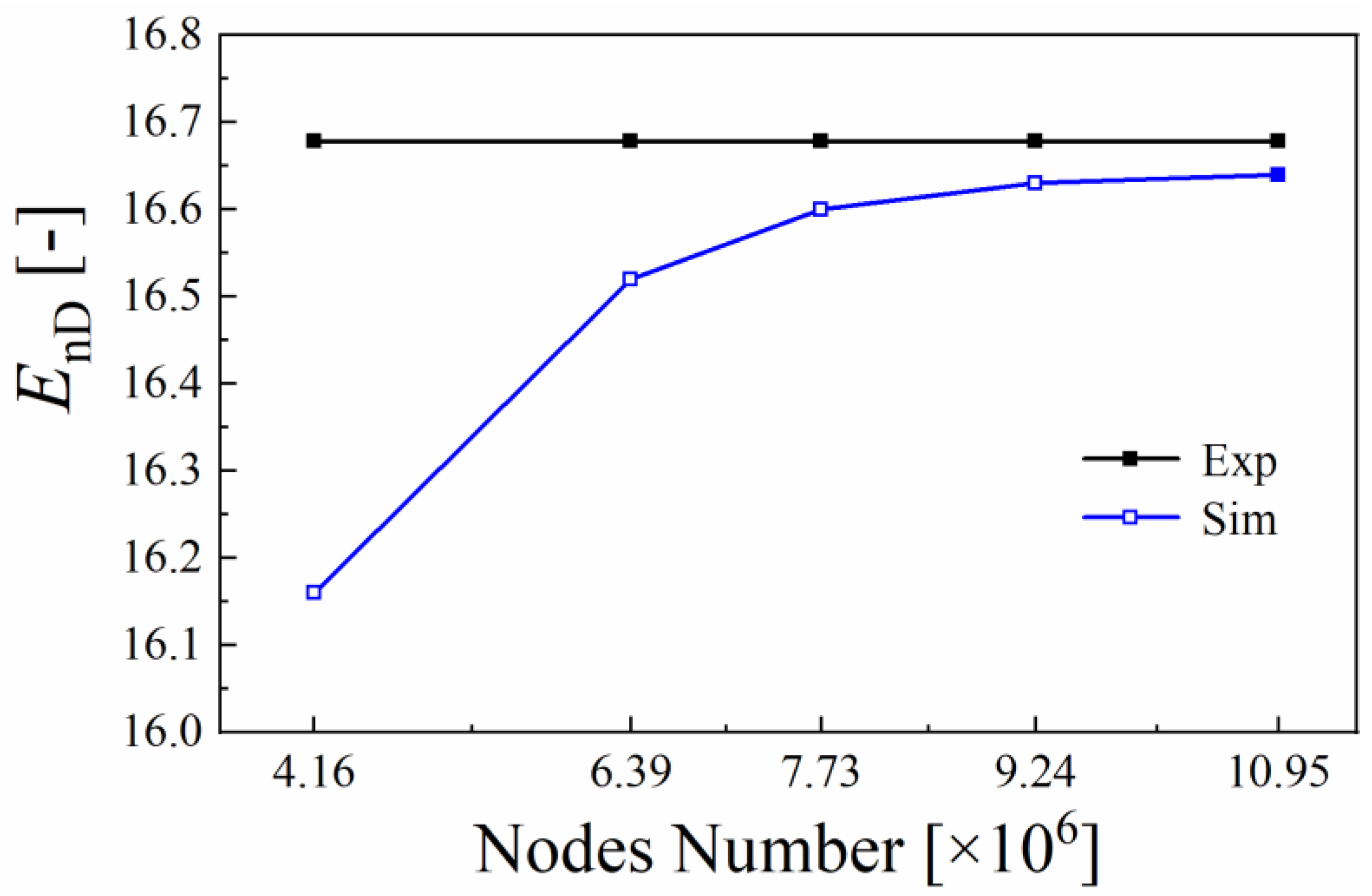
2.3. Grid Generation and Independence Validation
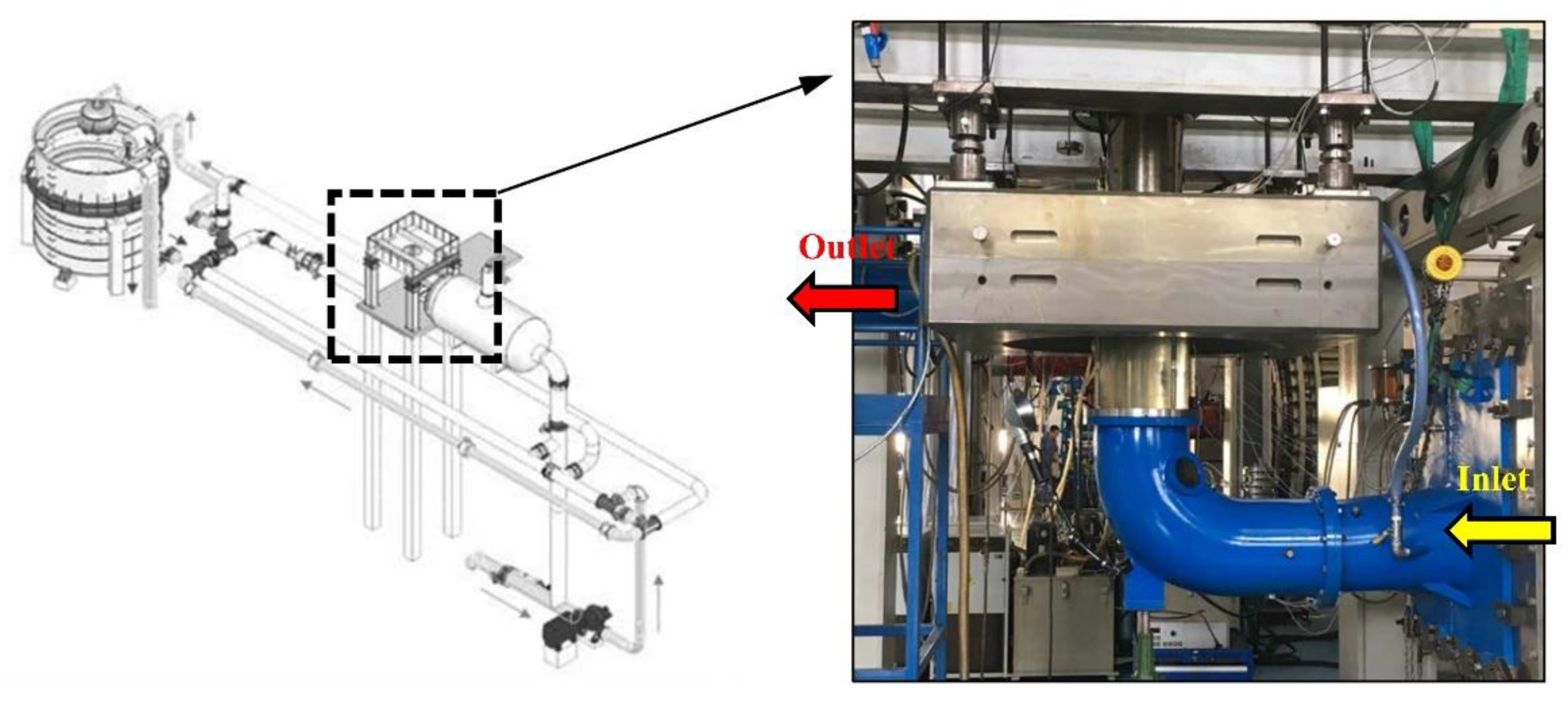
3. Experimental Setup and Validation
4. Setting Angle Distribution Plans
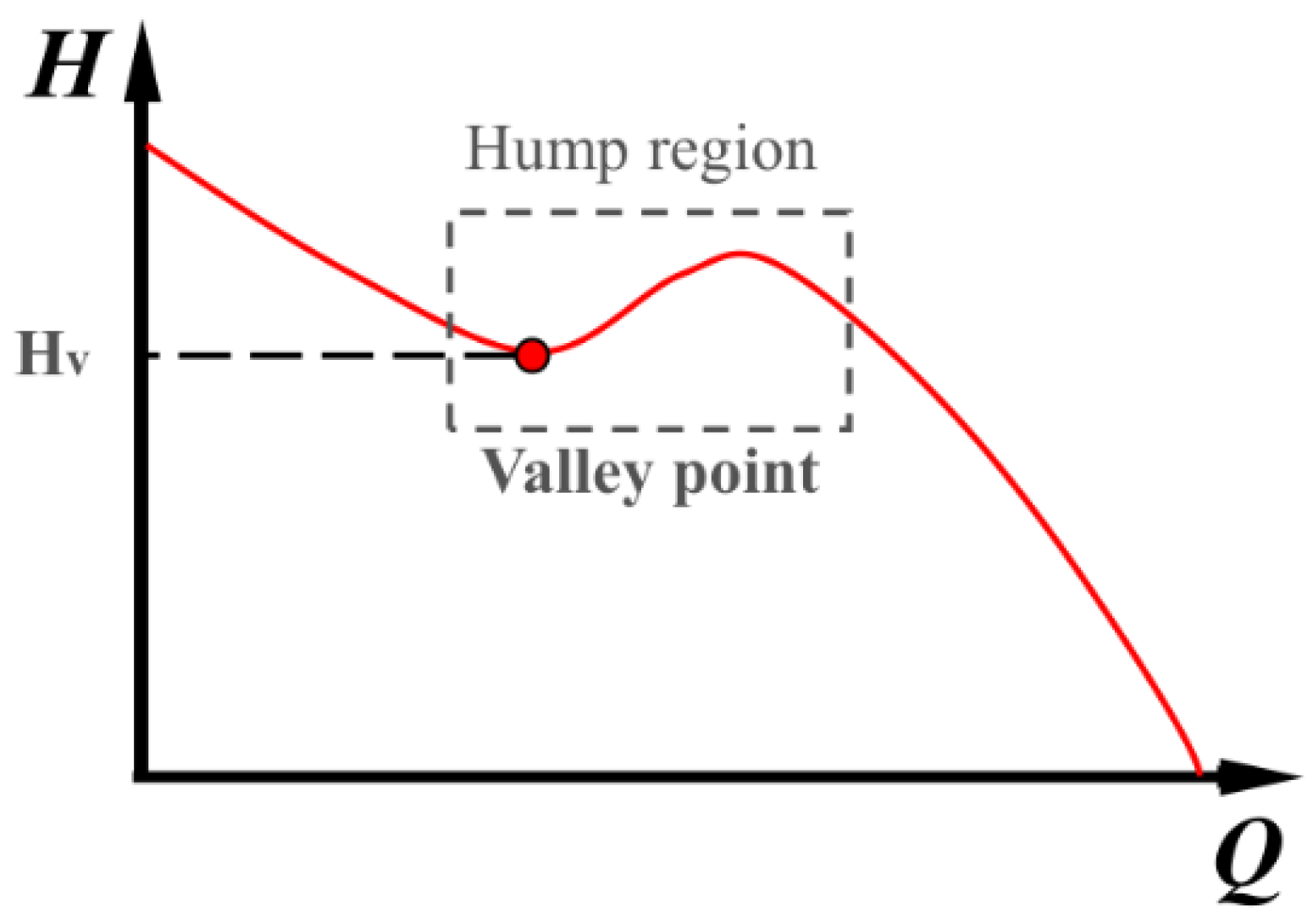
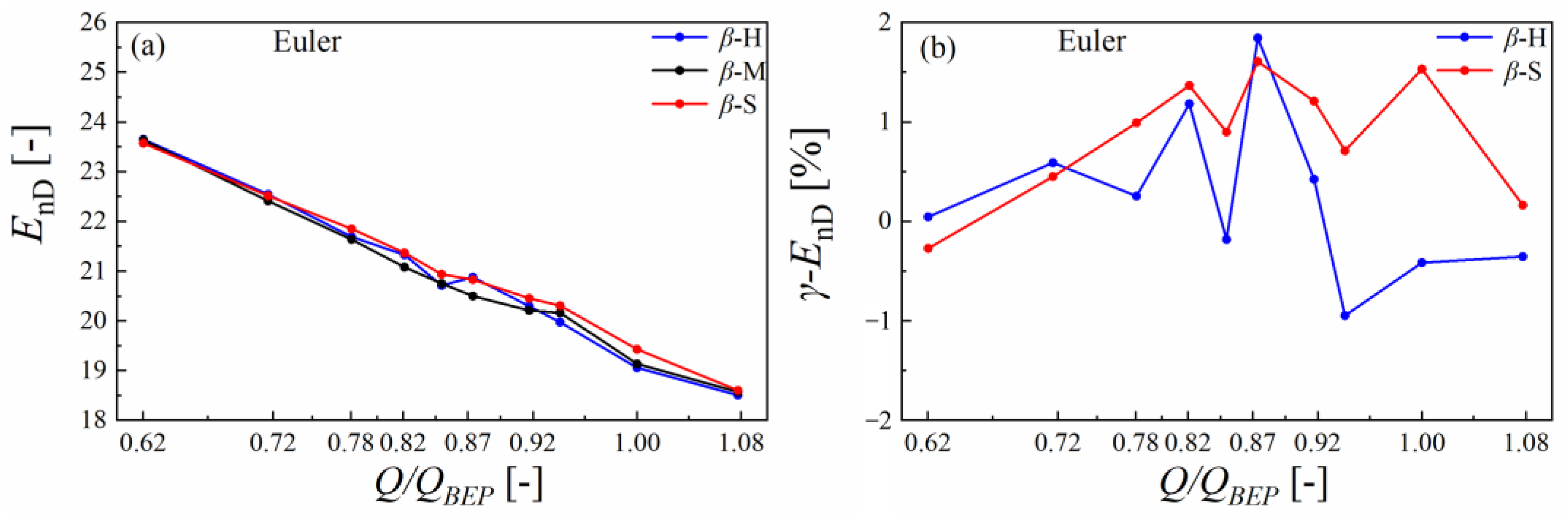
4.1. Euler Head Analysis
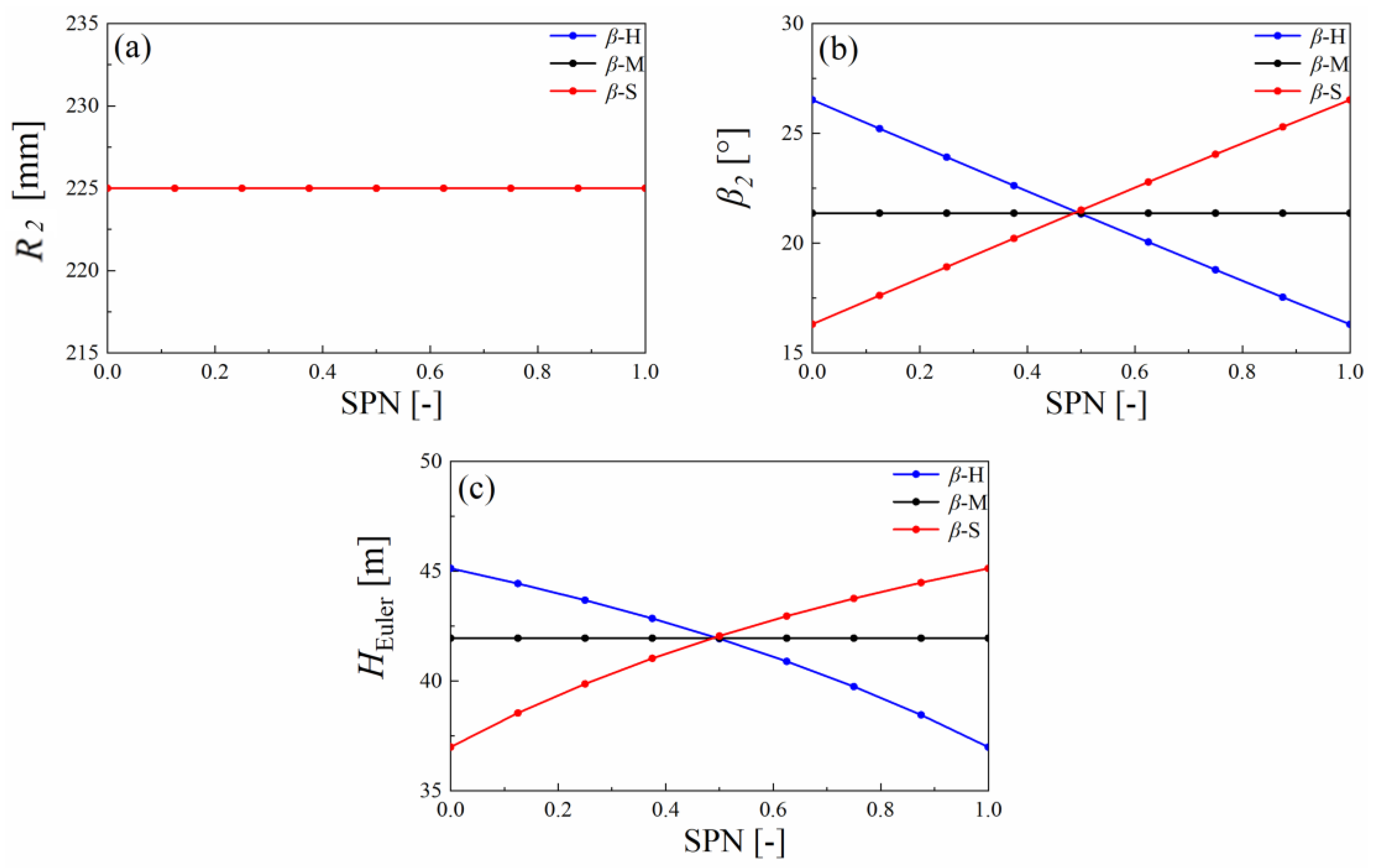
4.2. Setting Angle Distribution Plans at the Runner Outlet
5. Results and Discussions
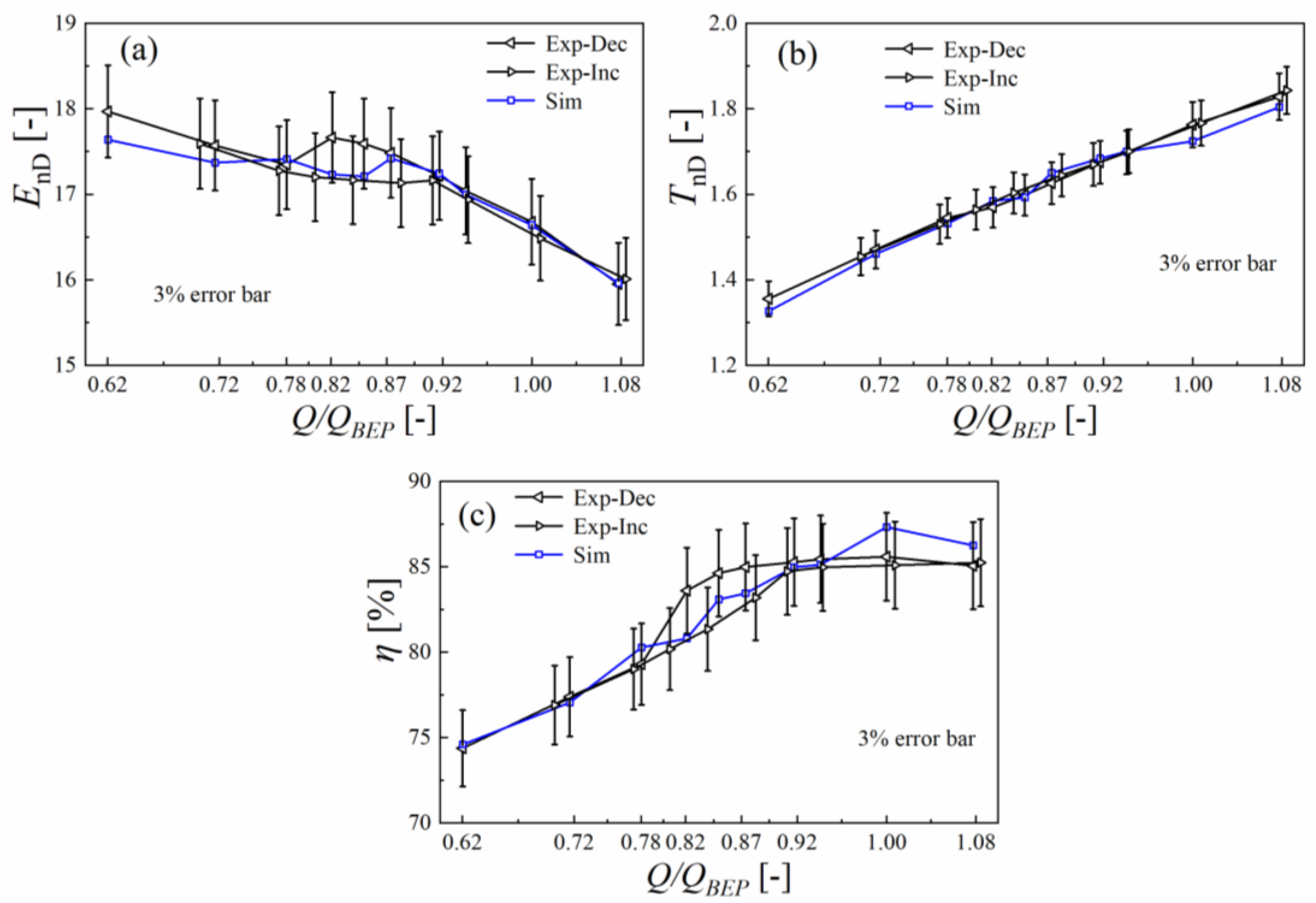
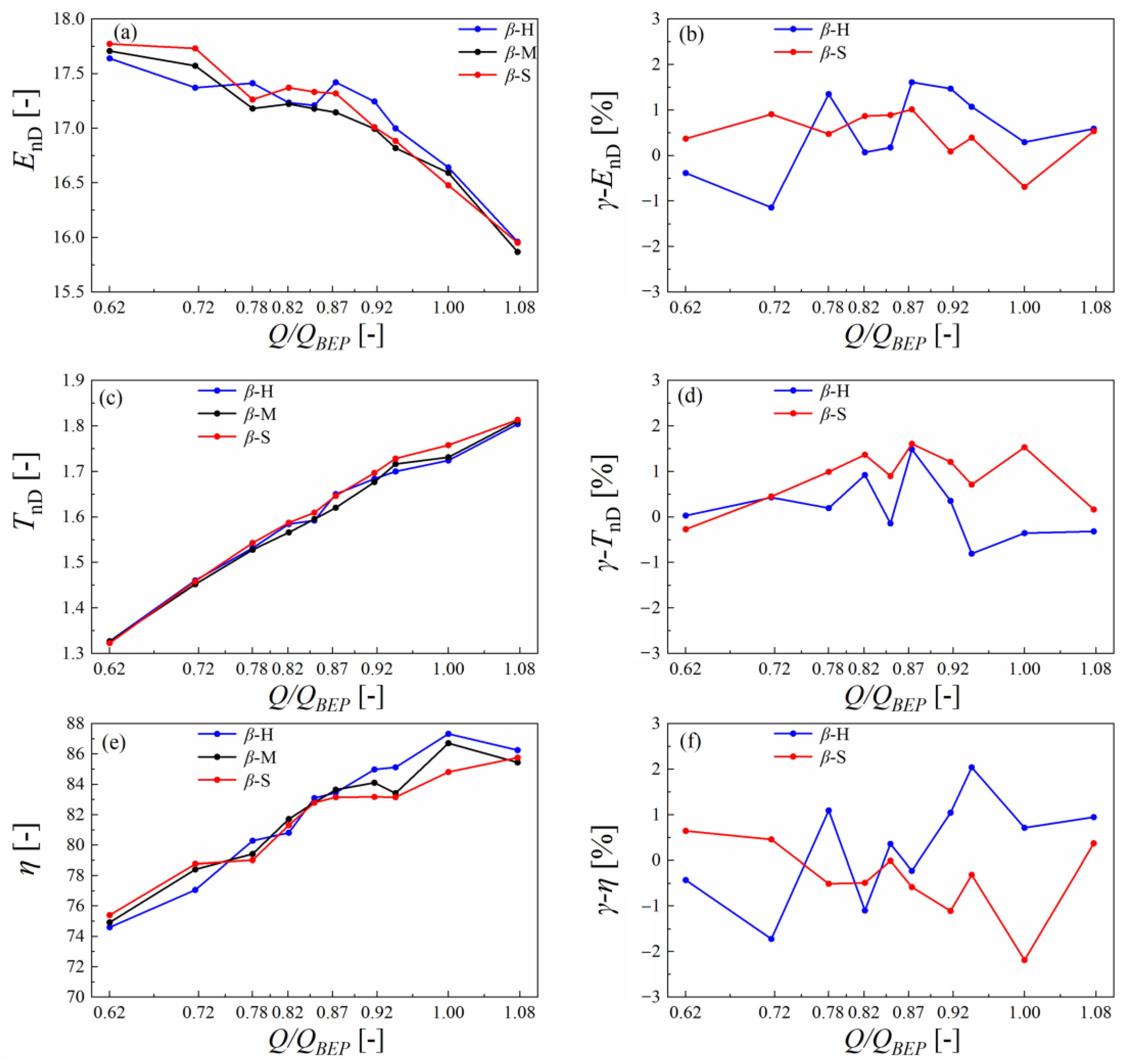
5.1. Analysis of the Performance Characteristics
5.2. Comparative Analysis on Euler Head
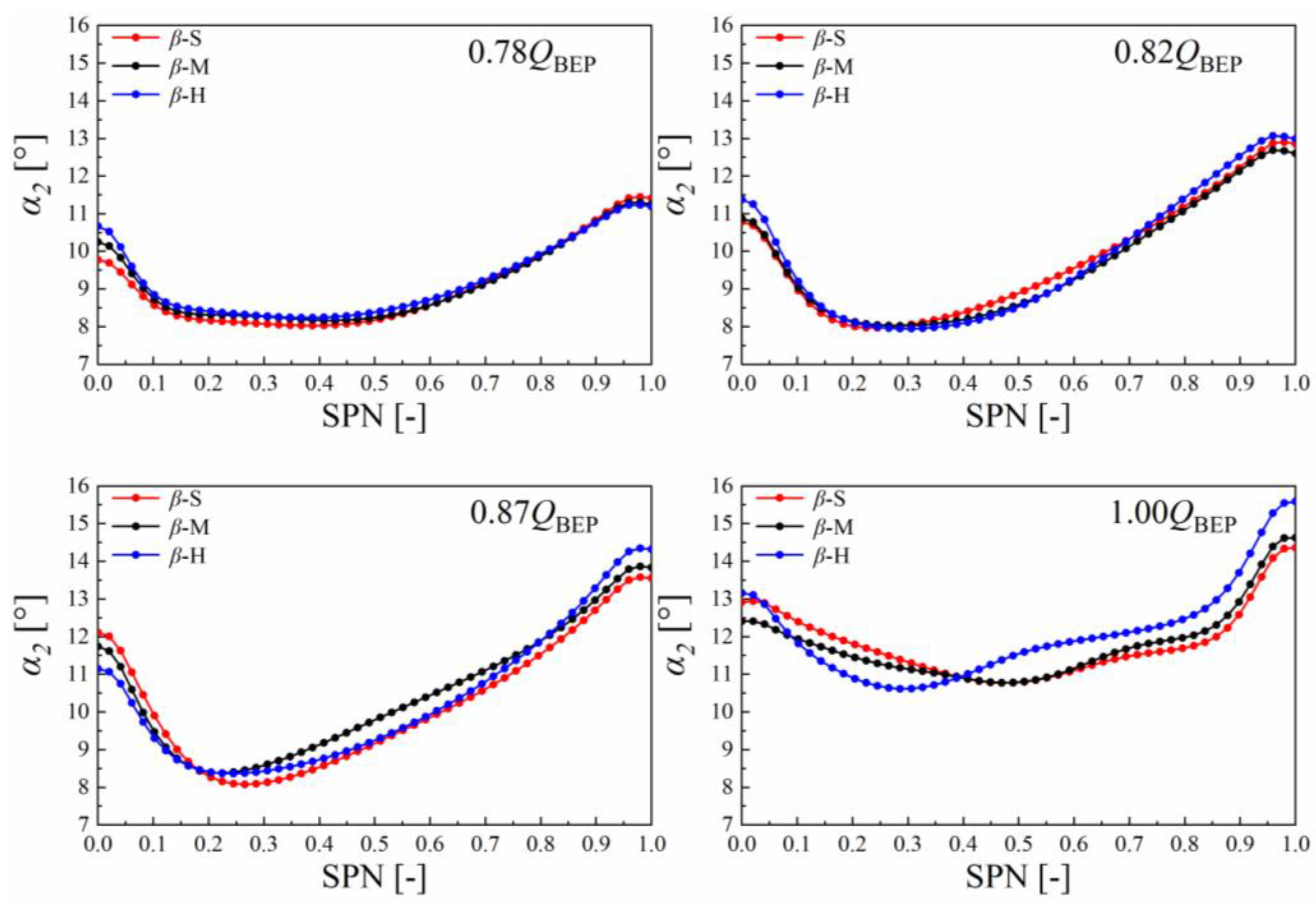
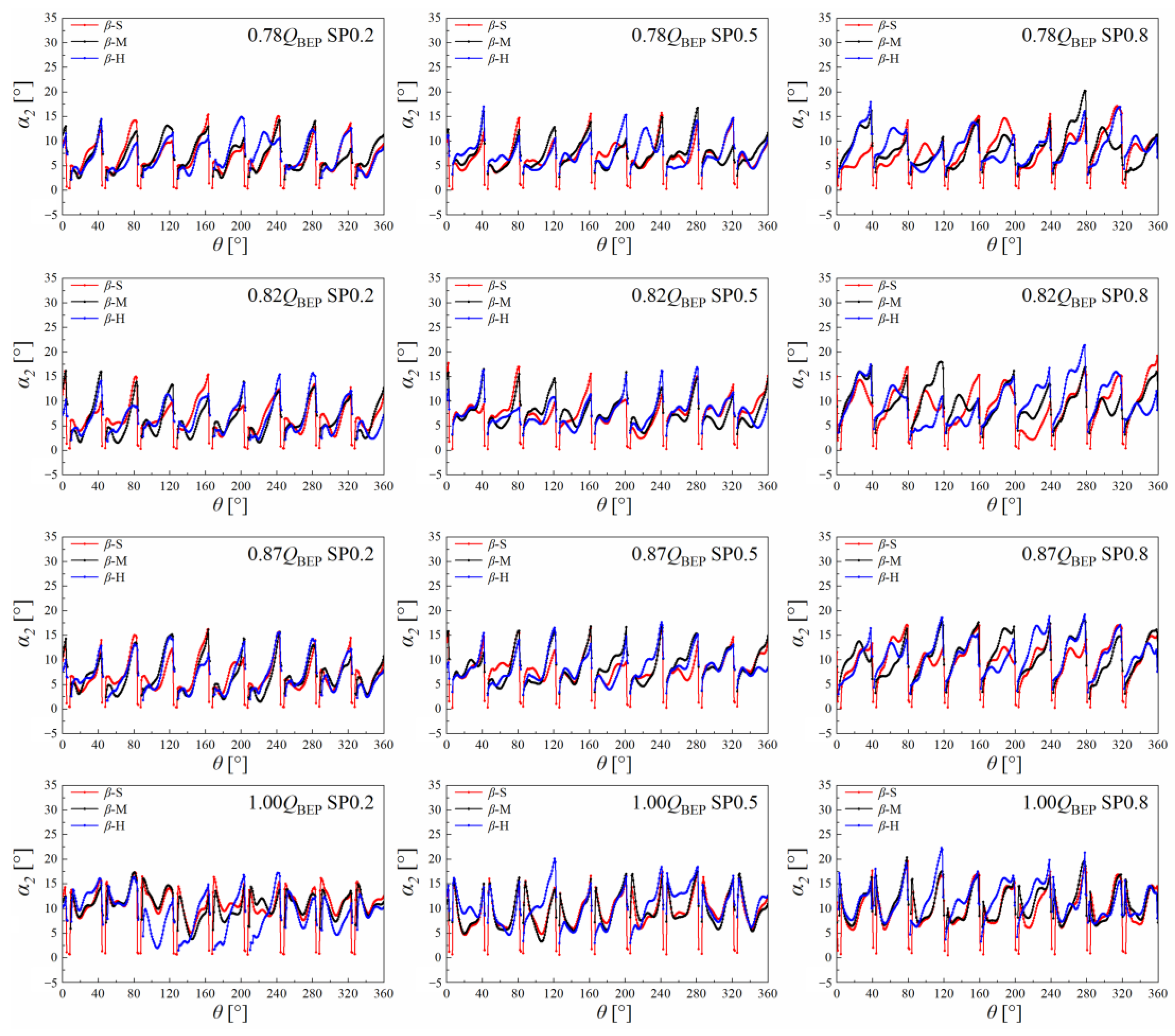
5.2.1. Absolute Flow Angle in Spanwise Direction
5.2.2. Absolute Flow Angle in Circumferential Direction
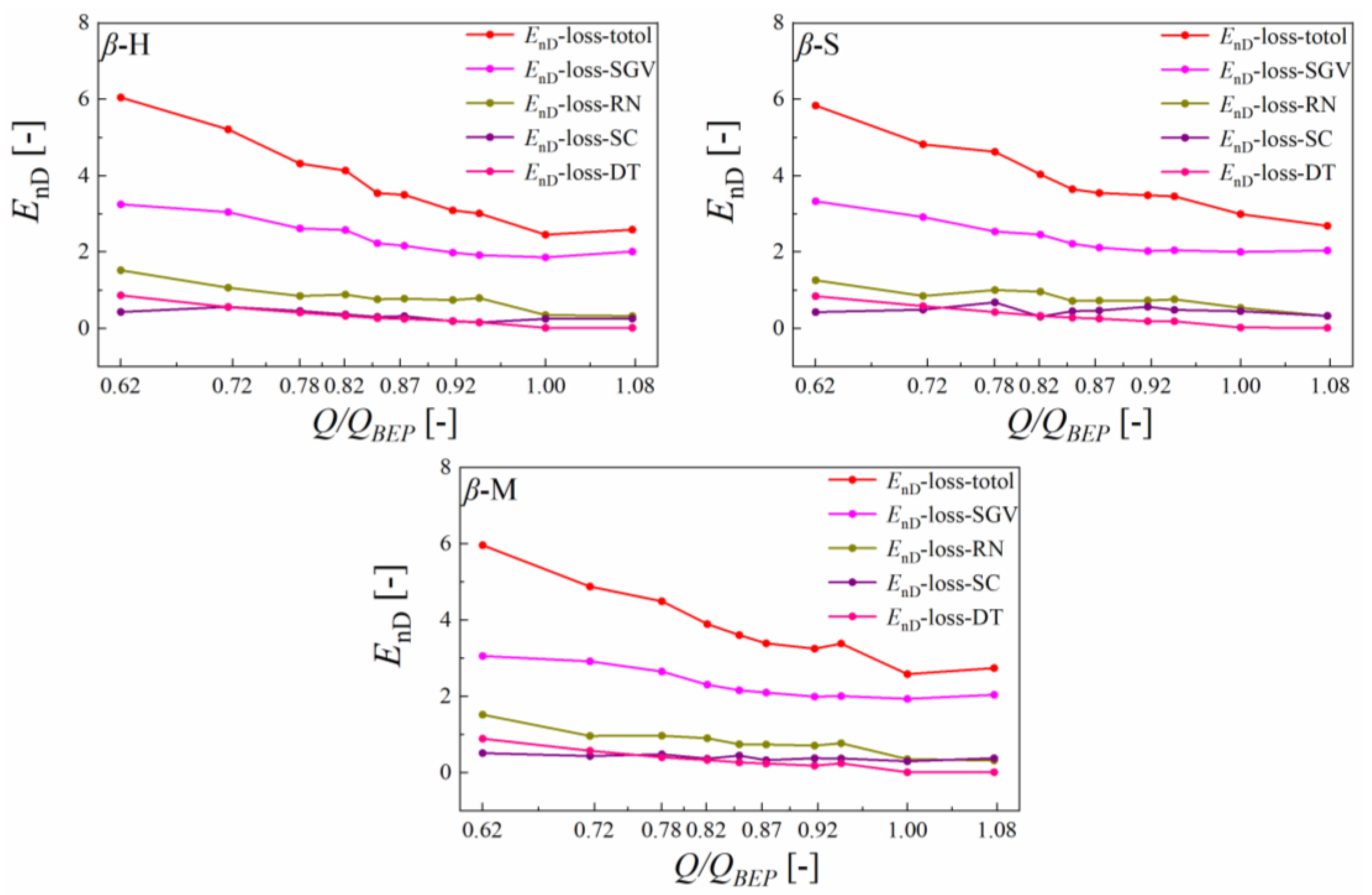
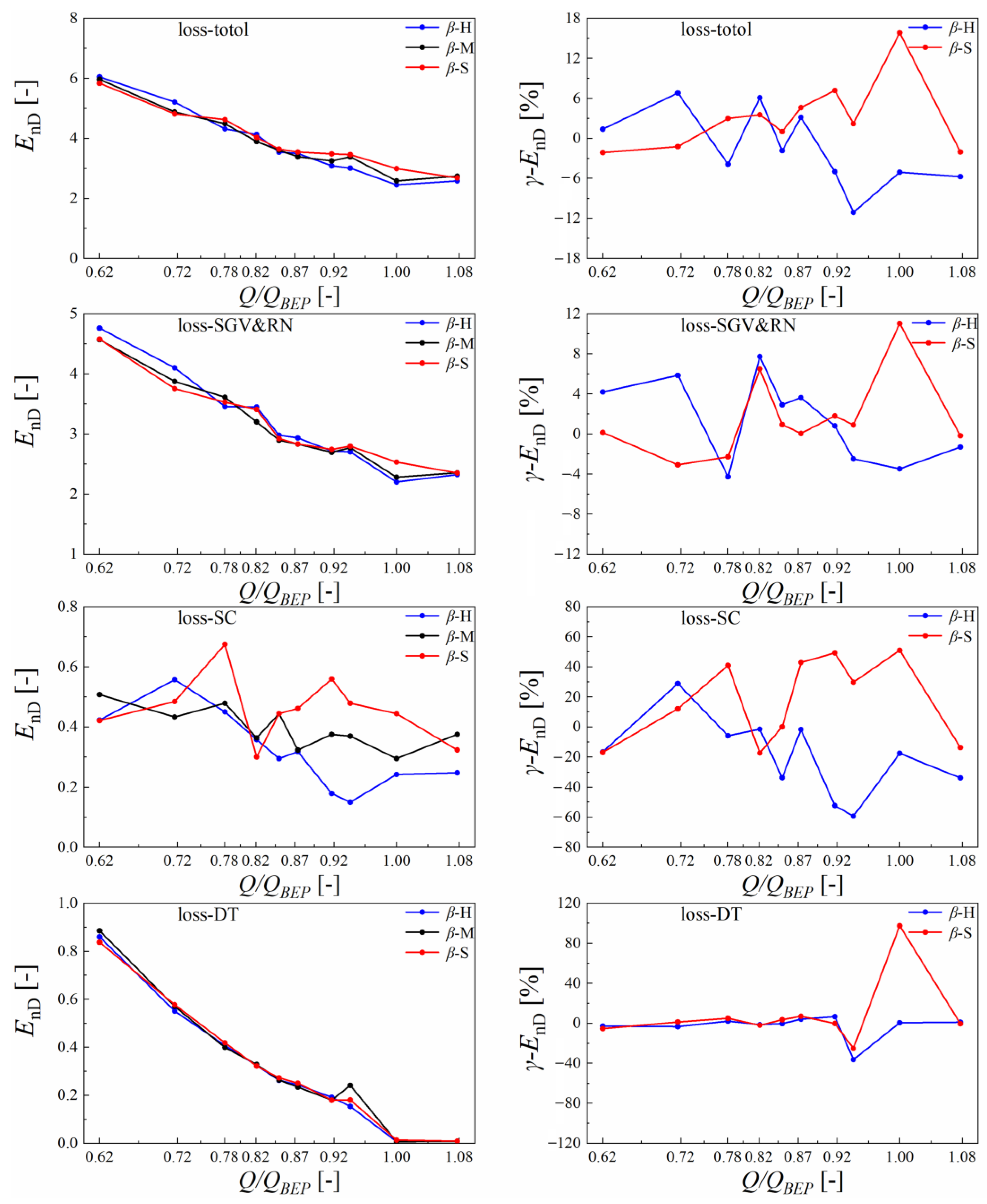
5.3. Hydraulic Loss Comparation
Hydraulic Loss Distribution Analysis
6. Conclusions
- (1)
- The hump characteristic is related to the setting angle distribution at the runner the outlet; however, the influence of setting angle distribution cannot be captured through conventional design methods and the Euler head theory. This can be attributed to the limitations of two-dimensional theory (conventional design methods and Euler head theory) when investigating the hump region.
- (2)
- In the different setting angle distribution plans, the runner whose setting angle at the shroud was 10° larger than that at the hub effectively increased the hump margin from 4% to 4.5% compared to the original runner β-M, which fully meets the engineering standard. Moreover, compared to other hump-region-elimination methods proposed by related papers, optimization of the runner outlet is more likely to be achieved in the design stage and applied in engineering applications.
- (3)
- Setting angle distribution at the runner outlet could affect the absolute flow angle α2 distribution in the spanwise direction as well as the hydraulic loss spatial distribution in the hump region, contributing to different hump performances under different plans.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A1 | Runner inlet area, m2 |
| A2 | Runner outlet area, m2 |
| BEP | Best efficiency point |
| B0 | Guide vane height, m |
| β1 | Relative flow angle at the runner inlet in pump mode |
| β2 | Relative flow angle at the runner outlet in pump mode |
| Δcu·U | Euler momentum (the change of velocity momentum), m2·s−2 |
| cu1 | Circumferential component of absolute velocity at the runner inlet in pump mode, m/s |
| cu2 | Circumferential component of absolute velocity at the runner outlet in pump mode, m/s |
| D1 | Runner inlet diameter in pump mode, m |
| D2 | Runner outlet diameter in pump mode, m |
| D0 | Guide vane distribution diameter, m |
| EnD | Dimensionless energy factor |
| GGI | General grid interface |
| GVO | Guide vane opening |
| Local gravity acceleration, 9.8 m/s2; | |
| HILEM | Harbin Institute of Large Electrical Machinery |
| LEPR | Local entropy production rate |
| η | Efficiency |
| n | Rotational speed of the runner, rpm |
| nq | Specific speed of the pump turbine in pump mode, , min−1 |
| ρ | Density of the water, 1000 kg·m−3 |
| QBEP | Best efficiency point under the 13 mm GVO in pump mode |
| RANS | Reynolds-averaged Navier–Stokes |
| RMS | Root mean square |
| SPN | Spanwise direction |
| SST | Shear stress transport |
| SPN | Spanwise direction |
| U1 | Circumferential velocity at the runner inlet in pump mode, m·s−1 |
| U2 | Circumferential velocity at the runner outlet in pump mode, m·s−1 |
| Relative change rate | |
| y+ | Dimensionless distance |
| Zr | Runner blade number |
| Zg | Guide vane number |
| Zs | Stay vane number |
References
- Zuo, Z.G.; Fan, H.G.; Liu, S.H.; Wu, Y. S-shaped characteristics on the performance curves of pump-turbines in turbine mode-a review. Renew. Sustain. Energy Rev. 2016, 60, 836–851. [Google Scholar] [CrossRef]
- Gentner, C.; Sallaberger, M.; Widmer, C.; Braun, O.; Staubli, T. Numerical and experimental analysis of instability phenomena in pump turbines. IOP conference series. Earth Environ. Sci. 2019, 15, 32042. [Google Scholar]
- Jia, J.; Zhang, J.F.; Qu, Y.F.; Cai, H.; Chen, S. Study on hump characteristics of pump turbine with different guide vane exit angles. IOP conference series. Earth Environ. Sci. 2019, 240, 72038. [Google Scholar]
- Ješe, U.; Fortes-Patella, R.; Dular, M. Numerical study of pump-turbine instabilities under pumping mode off-design conditions. In Proceedings of the ASME-JSME-KSME 2015 Joint Fluids Engineering Conference, Seoul, Reoublic of Korea, 26–31 July 2015. [Google Scholar]
- Yangyang, Y.; Yexiang, X.; Wei, Z.; Liming, Z.; Hwang, A.S.; Zhengwei, W. Numerical analysis of a model pump-turbine internal flow behavior in pump hump district. IOP conference series. Earth Environ. Sci. 2014, 22, 32040. [Google Scholar]
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Wei, X.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Qin, Y.; Li, D.; Wang, H.; Liu, Z.; Wei, X.; Wang, X. Investigation on hydraulic loss component and distribution in hydraulic machinery: A case study of pump-turbine in pump mode. J. Energy Storage 2022, 52, 104932. [Google Scholar] [CrossRef]
- Qin, Y.; Li, D.; Wang, H.; Liu, Z.; Wei, X.; Wang, X. Investigation on the relationship between hydraulic loss and vortex evolution in pump mode of a pump-turbine. J. Hydrodyn. 2022, 34, 555–569. [Google Scholar] [CrossRef]
- Li, D.; Chang, H.; Zuo, Z.; Wang, H.; Li, Z.; Wei, X. Experimental investigation of hysteresis on pump performance characteristics of a model pump-turbine with different guide vane openings. Renew. Energy 2020, 149, 652–663. [Google Scholar] [CrossRef]
- Ran, H.J.; Luo, X.W.; Chen, Y.L.; Xu, H.Y.; Farhat, M. Hysteresis phenomena in hydraulic measurement. IOP conference series. Earth Environ. Sci. 2012, 15, 62048. [Google Scholar]
- Li, D.; Song, Y.; Lin, S.; Wang, H.; Qin, Y.; Wei, X. Effect mechanism of cavitation on the hump characteristic of a pump-turbine. Renew. Energy 2021, 167, 369–383. [Google Scholar] [CrossRef]
- Anciger, D.; Jung, A.; Aschenbrenner, T. Prediction of rotating stall and cavitation inception in pump turbines. IOP conference series. Earth Environ. Sci. 2010, 12, 12013. [Google Scholar]
- Liu, J.; Liu, S.; Wu, Y.; Jiao, L.; Wang, L.; Sun, Y. Numerical investigation of the hump characteristic of a pump-turbine based on an improved cavitation model. Comput. Fluids 2012, 68, 105–111. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, R.F. Multiobjective optimization design of a Pump-Turbine impeller based on an inverse design using a combination optimization strategy. J. Fluids Eng. 2014, 136, 145011–145019. [Google Scholar] [CrossRef]
- Olimstad, G.; Nielsen, T.; Børresen, B. Dependency on runner geometry for Reversible-Pump turbine characteristics in turbine mode of operation. J. Fluids Eng. 2012, 134, 1211021–1211029. [Google Scholar] [CrossRef]
- Zhu, B.; Tan, L.; Wang, X.; Ma, Z. Investigation on flow characteristics of Pump-Turbine runners with large blade lean. J. Fluids Eng. 2018, 140, 031101. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, X.; Tan, L.; Zhou, D.; Zhao, Y.; Cao, S. Optimization design of a reversible pump-turbine runner with high efficiency and stability. Renew. Energy 2015, 81, 366–376. [Google Scholar] [CrossRef]
- Ran, H.; Luo, X.; Zhang, Y.; Zhuang, B.; Xu, H. Numerical simulation of the unsteady flow in a High-Head pump turbine and the runner improvement. In Proceedings of the ASME 2008 Fluids Engineering Division Summer Meeting collocated with the Heat Transfer, Energy Sustainability, and 3rd Energy Nanotechnology Conferences, Jacksonville, FL, USA, 10–14 August 2008. [Google Scholar]
- Liu, Y.; Ran, H.J.; Wang, D.Z. Research on groove method to suppress stall in pump turbine. Energies 2020, 13, 3822. [Google Scholar] [CrossRef]
- Xue, P.; Liu, Z.P.; Lu, L.; Tian, Y.J.; Wang, X.; Chen, R. Research and optimization of performances of a pump turbine in pump mode. IOP Conf. Ser. Earth Environ. Sci. 2012, 240, 72012. [Google Scholar] [CrossRef]
- Li, D.Y.; Gong, R.Z.; Wang, H.J.; Wei, X.Z.; Liu, Z.S.; Qin, D.Q. Unstable head-flow characteristics of pump-turbine under different guide vane openings in pump mode. J. Drain. Irrig. Mach. Eng. 2016, 34, 1–8. (In Chinese) [Google Scholar]
- Ren, Z.; Hao, H.; Li, D.; Wang, H.; Liu, J.; Li, Y. Dissolution and evolution effects on pressure fluctuations in a space micropump. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022. [Google Scholar] [CrossRef]
- Cavazzini, G.; Covi, A.; Pavesi, G.; Ardizzon, G. Analysis of the unstable behavior of a Pump-Turbine in turbine mode: Fluid-Dynamical and spectral characterization of the s-shape characteristic. J. Fluids Eng.-Trans. ASME 2015, 138, 21105. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS CFX-Solver Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Zhiwei, G.; Chihang, W.; Zhongdong, Q.; Xianwu, L.; Weipeng, X. Suppression of hump characteristic for a pump-turbine using leading-edge protuberance. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 187–194. [Google Scholar] [CrossRef]
- Pei, J.; Meng, F.; Li, Y.; Yuan, S.; Chen, J. Effects of distance between impeller and guide vane on losses in a low head pump by entropy production analysis. Adv. Mech. Eng. 2016, 8, 2071837044. [Google Scholar] [CrossRef]
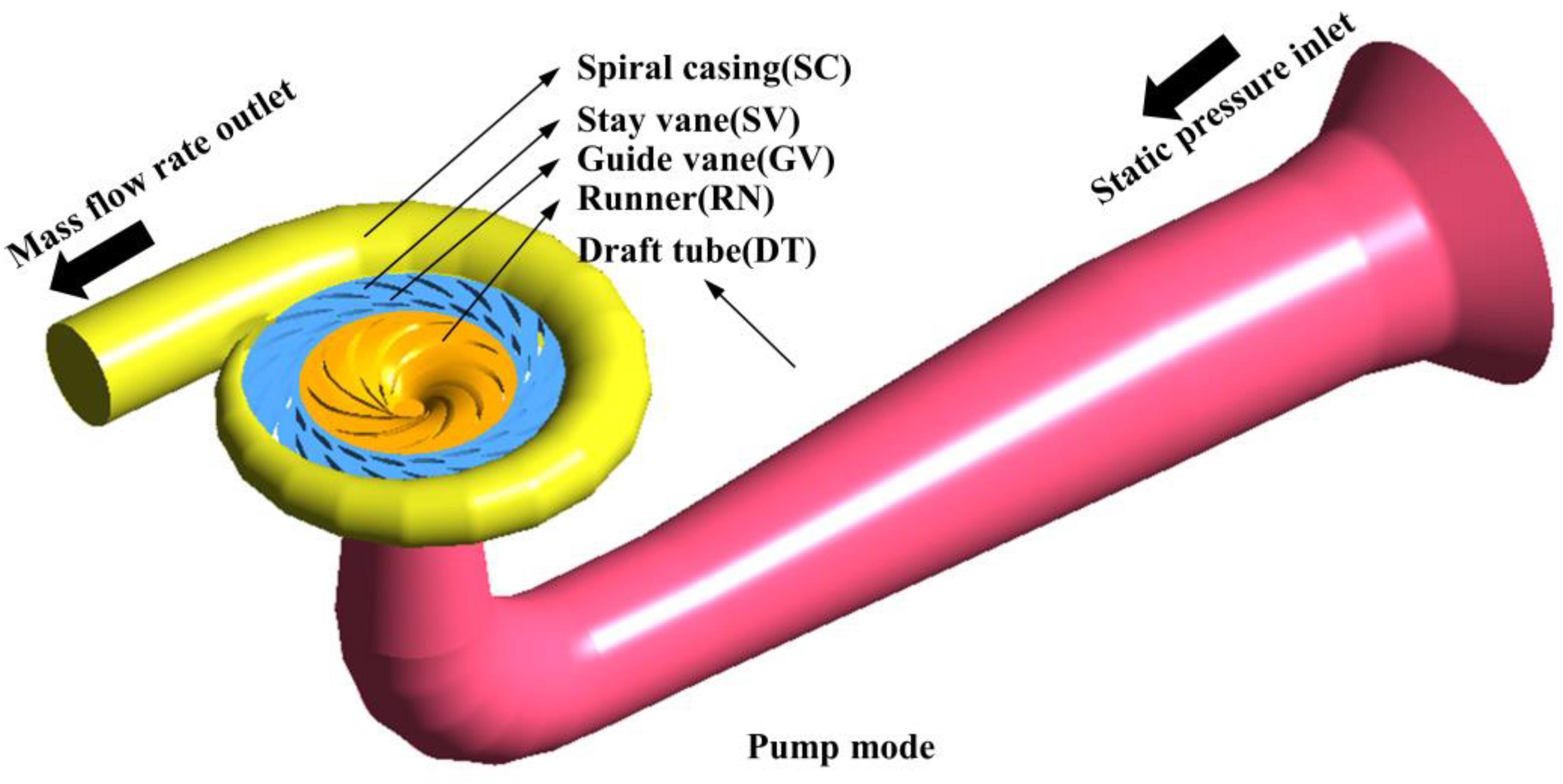
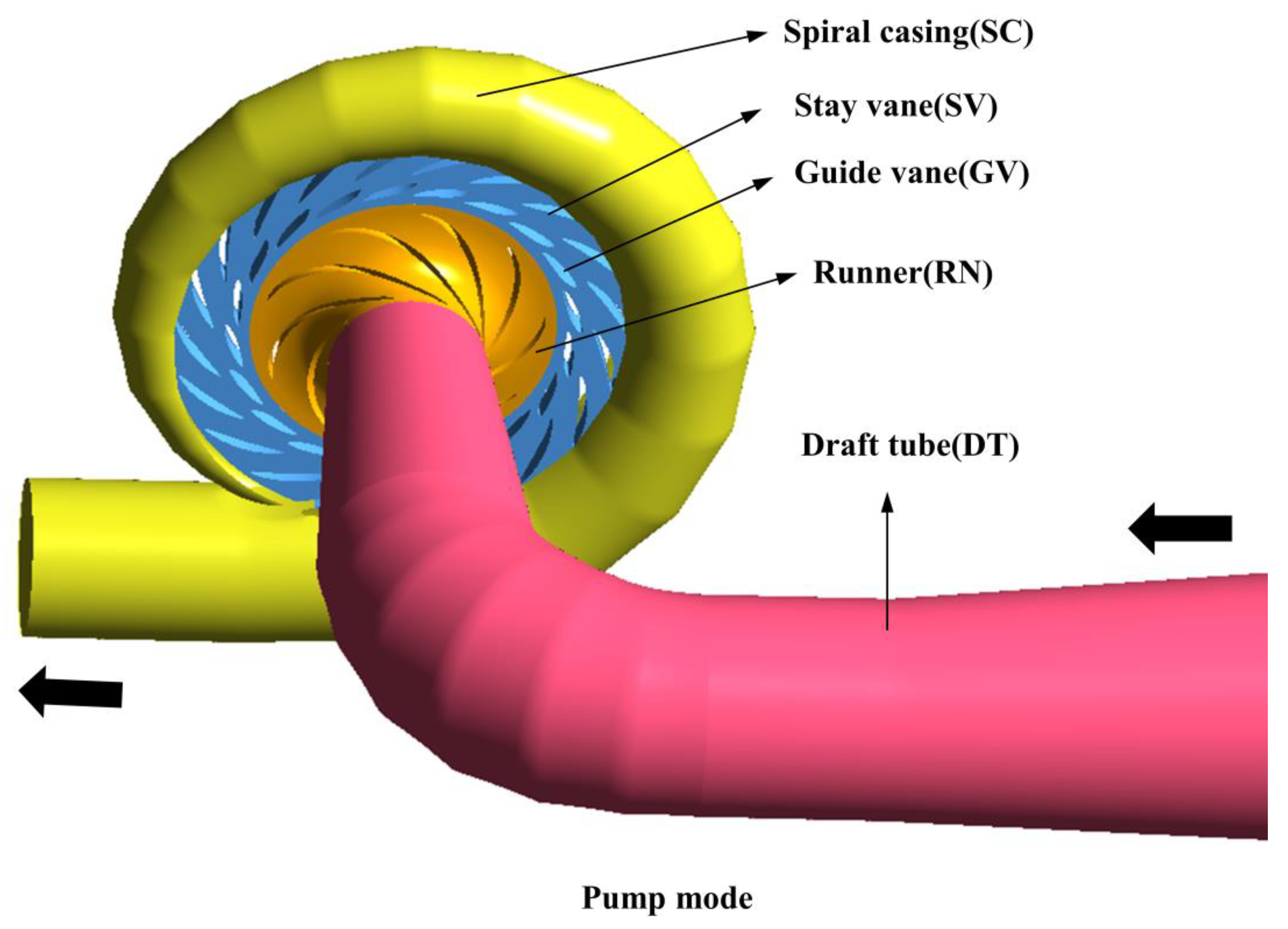
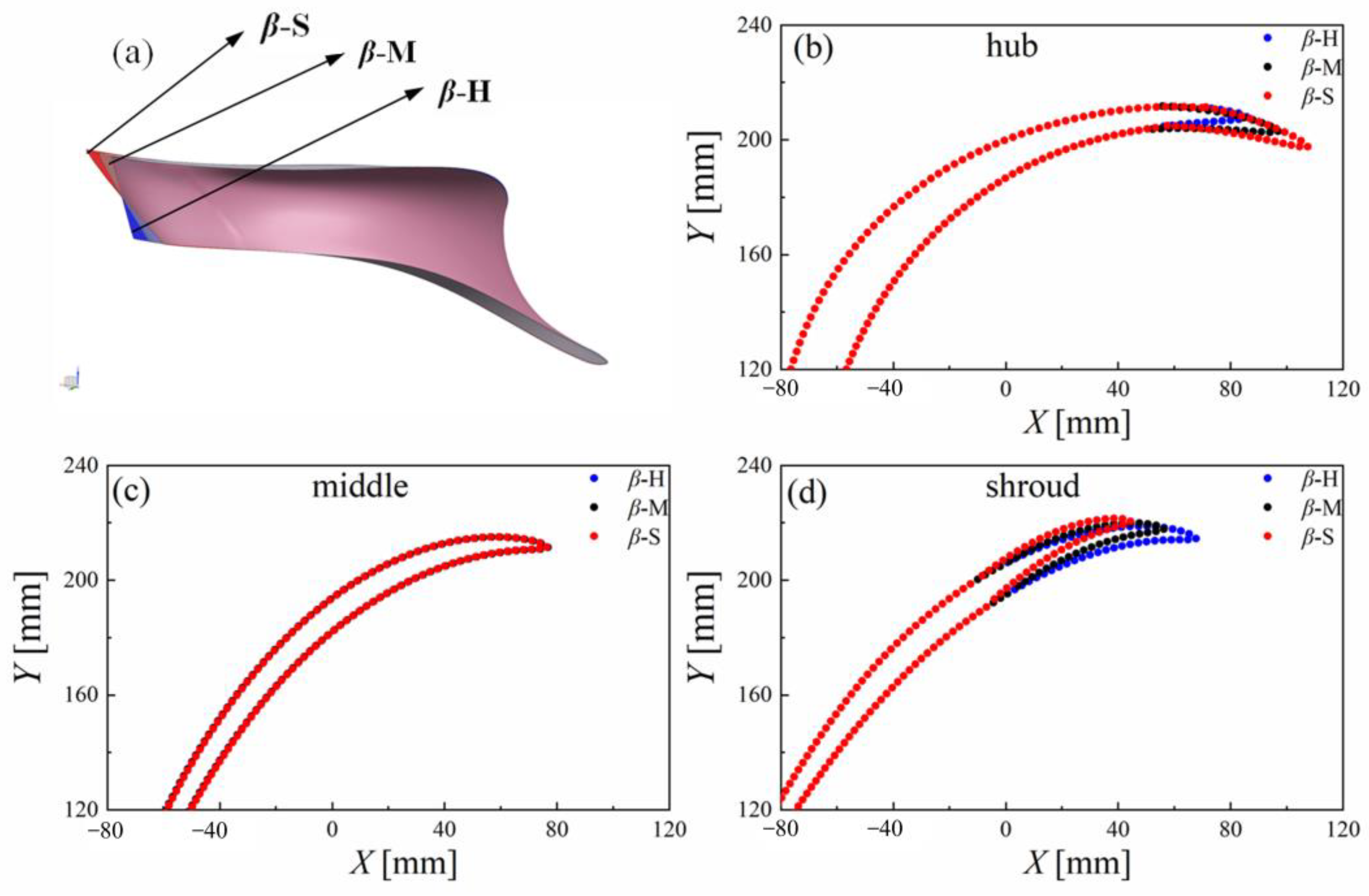
| Description | Symbol | Value |
|---|---|---|
| Distribution diameter of the guide vane | D0 | 540 mm |
| Runner inlet in pump mode | D1 | 450 mm |
| Runner outlet in pump mode | D2 | 250 mm |
| Runner blade number | Zr | 9 |
| Guide vane number | Zg | 20 |
| Stay vane number | Zs | 20 |
| Guide vane height | B0 | 43.73 mm |
| Domain | 1st | 2nd | 3rd | 4th | 5th |
|---|---|---|---|---|---|
| Draft tube | 0.57 | 1.03 | 1.32 | 1.69 | 2.09 |
| Runner | 1.83 | 2.29 | 2.75 | 3.20 | 3.56 |
| Guide/stay vane | 1.17 | 1.95 | 2.34 | 2.80 | 3.26 |
| Spiral casing | 0.59 | 1.12 | 1.32 | 1.55 | 2.04 |
| Total | 4.16 | 6.39 | 7.73 | 9.24 | 10.95 |
| Ref. | Method | Original Energy Factor at Hump Valley | Optimized Energy Factor at Hump Valley | Relative Improvement Rate/% |
|---|---|---|---|---|
| [25] | Bio-inspired leading-edge protuberances | 0.013625 | 0.014 | 2.75 |
| 0.013625 | 0.01417 | 4 | ||
| [19] | Groove method | 1.068 | 1.088 | 1.87 |
| Our case | Runner outlet | 17.18 | 17.262 (plan β-S) | 0.48 |
| 17.18 | 17.209 (plan β-H) | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Li, D.; Wang, H.; Wei, X. Optimization of Setting Angle Distribution to Suppress Hump Characteristic in Pump Turbine. Energies 2023, 16, 2471. https://doi.org/10.3390/en16052471
Qin Y, Li D, Wang H, Wei X. Optimization of Setting Angle Distribution to Suppress Hump Characteristic in Pump Turbine. Energies. 2023; 16(5):2471. https://doi.org/10.3390/en16052471
Chicago/Turabian StyleQin, Yonglin, Deyou Li, Hongjie Wang, and Xianzhu Wei. 2023. "Optimization of Setting Angle Distribution to Suppress Hump Characteristic in Pump Turbine" Energies 16, no. 5: 2471. https://doi.org/10.3390/en16052471
APA StyleQin, Y., Li, D., Wang, H., & Wei, X. (2023). Optimization of Setting Angle Distribution to Suppress Hump Characteristic in Pump Turbine. Energies, 16(5), 2471. https://doi.org/10.3390/en16052471








