Lightning Electromagnetic Fields Computation: A Review of the Available Approaches

Abstract

Lightning represents one of the most critical issues for electrical infrastructure. In dealing with overhead distribution line systems, indirect lightning strikes can lead to induced voltages overcoming the critical flashover value of the line, thus damaging the insulators. The computation of lightning-induced voltages requires the modeling of the lightning current, the evaluation of the lightning electromagnetic fields and the solution of the field-to-line coupling equations. The numerical calculation of the lightning electromagnetic fields is time-consuming and is strongly dependent on the lightning channel modeling and soil properties. This article presents a review of the most widely adopted methods to calculate the lightning electromagnetic fields, starting from the classical formulation, which requires numerical integration, and highlighting the most effective approaches that have been developed to reduce computational effort. This is done first for the case of a perfectly conducting ground, then the available formulations to account for the ground finite conductivity are presented together with their possible implementations in both the frequency and time domains.

1. Introduction

Power systems may experience a large number of outages and faults due to lightning strikes. Their strong current, fast rise time and, in some cases, high amount of transferred charge may lead to the flashover of the insulators. This phenomenon can be related to two different mechanisms related to lightning, i.e., direct and indirect strikes. Transmission and distribution systems can experience both mechanisms [1,2,3,4], but, while the effects of indirect strikes are usually negligible on transmission lines due to their high Critical FlashOver value (CFO), distribution lines can be seriously damaged by both striking mechanisms. Direct strikes on distribution lines lead to flashovers in the majority of cases, but fortunately, these events are rarer. Conversely, indirect strikes are much more frequent and, consequently, a deep analysis of this mechanism has been conducted in the past decades [1].

Lightning Electromagnetic (EM) field computation may be extremely useful for applications related to transmission and distribution lines, both for safety purposes and for economic aspects. In the last few decades, many studies addressed the issue, aiming at improving the correct initial design of the lines: the authors of [3] proposed a cost-related optimum design method to improve the Lightning Performance (LP) of overhead high voltage transmission lines. In [4] the optimum design parameters are calculated for the lines, considering the cost of lightning failures. In [5] the relationship between the cost associated with lightning protection systems and the Back-Flashover Rate (BFR) in high-voltage transmission lines is investigated. In [6] a methodology for the determination of the optimal value of protection design parameters to be considered in the planning stage of transmission lines is presented.

The evaluation of lightning-induced voltages can be done in several ways. In principle, the most reliable way consists of on-field experiments based on rocket-triggered lightning [7,8] or reduced-scale systems [9,10], but obviously, this requires a lot of effort from an economic point of view. Secondly, full-wave approaches (FEM, 3D-FDTD) can be adopted, by simulating the lightning and the power system with a high level of detail and solving Maxwell’s equations in a discretized mesh [11,12]. However, this approach may fail due to mesh discretization problems, which lead to huge computational effort. As a consequence, in the last few decades, several approaches have been developed, mainly based on the field-to-line coupling theory [13,14,15]; lightning electromagnetic fields are computed by neglecting the presence of the line and, then, lightning-induced voltages are evaluated by means of transmission-line theory, which is still applicable in lightning-induced voltages studies as shown in [16].

In this research line, several research groups have developed codes (e.g., LIOV, CiLIV, LIGHT-PESTO [17,18,19,20,21,22,23]) able to couple the solution of field-to-line equations with circuital models of classical power systems, thus guaranteeing a proper model of tower, insulators, surge arresters and grounding system.

As previously mentioned, these codes require the evaluation of the EM fields by neglecting the presence of the line. In principle, the exact evaluation in the case of finite soil conductivity is based on the solution of the Sommerfeld integrals [24]. This is the most time-consuming part since the radial and vertical electric fields should be evaluated at least in each discretization point of the illuminated line. For example, a 3 km long line with a space step of 10 m leads to 300 points in which the EM fields must be evaluated. Moreover, if different striking points are considered (i.e., if various distances between the line and the channel are taken into account, as necessary in LP studies [1,25]), the computational burden increases. Consequently, researchers have focused their effort on finding simplified approaches able to guarantee a speed-up in the computation of the electromagnetic fields.

In this context, one research line is related to the development of simplified methods to account for ground conductivity, which has been shown to mostly affect the radial component of the electric field. The most successful approach is the so-called Cooray–Rubinstein approximation (CR) [26,27], which basically corrects the radial component of the electric field over a Perfectly Conducting (PEC) Ground by considering a modified ground impedance expression involving the magnetic field at ground level. The CR approximation neglects the effect of soil conductivity on the vertical electric field and the magnetic field. The validity of the CR approximation has been deeply analyzed in [28], where it has been found that it provides reliable results for ground conductivities not lower than 1 mS/m and horizontal distances greater than 20 m.

The original formulation of the CR approximation was developed in the frequency domain; however, when it must be inserted in the majority of the field-to-line coupling codes (which are based on time domain methods), an Inverse Fourier Transform (IFT) procedure has to be applied, thus entailing a non-negligible computational burden. In order to overcome this issue, in 2006, the first time domain expression of the approximation was presented [29].

This certainly represents a step forward, but its expression in the time domain requires the solution of a convolution integral involving a modified Bessel function. Consequently, some researchers focused their efforts on providing a simplified but accurate kernel. Among these approaches, it is worth citing the solution utilizing the Prony expression [30] and the formulas proposed in [31,32] and references therein.

However, when dealing with the computational efficiency of lightning EM fields, it should be noted that the time required for the computation of EM fields in the case of PEC ground is not negligible. The expressions proposed in [33] show that the solution of three integrals with different kernels (vertical electric field, radial electric field and azimuthal magnetic field) is required. This feature may strongly affect the computation and, for this reason, several approaches have been developed to make those integrals as analytically solvable as possible. The first approach, introduced by [34], provides analytical expressions for the electric field by assuming a step current and no attenuation along the channel. Consequently, the author neglected the current front time, which is a key factor in lightning studies. A similar approach was proposed in [35]. An extension including a trapezoidal function is presented in [36], whereas [37] shows analytical expressions for the EM fields radiated by whatever channel-base current, by assuming that the propagation speed of the return stroke is equal to that of light and no attenuation exists along the channel. Unfortunately, this assumption is quite far from reality, since it is commonly known that the return stroke speed could be even one-third of that of light. Recently, a new approach has been proposed [38,39], where analytical expressions have been found starting from the work of [37], but including the case of a return stroke velocity different from light speed. Its computational efficiency is high but it still relies on the TL-model hypothesis (i.e., no attenuation along the channel [40]). A newer work [41], introduces semi-analytical expressions that are valid regardless of the channel-base current, the attenuation function and the return stroke speed. The proposed expressions have been found focusing on the Prony series expansion of different kernels, which leads to the analytical solution of the integrals. However, channel discretization is still required if attenuation functions that differ from the TL model are considered. This approach is characterized by computational times that are one order of magnitude lower than the traditional approach based on the solution of numerical integrals expressed in [33].

This paper is focused on semi-analytical methods to calculate lightning electromagnetic fields: we shall review both the classical formulation, which involves numerical integration procedures and more recent and effective techniques that have been conceived in order to diminish the computational burden. We point out that the methods presented in the next sections represent general tools applicable to coupling problems and are indispensable when good accuracy and high computational efficiency are mandatory (e.g., the LP assessment of overhead transmission and distribution lines). Clearly, although general and practical to use, the considered physical system is typically simplified, i.e., the lightning channel is modeled as a straight vertical conductor above a flat ground, and the electromagnetic properties of the ground and the air are assumed to be uniform. However, some research focuses on developing semi-analytical and computationally efficient approaches for more realistic scenarios, for example, computation of the EM fields generated by tortuous lightning channels [42] and evaluation of lightning EM fields along a mixed propagation path [43]. Further research in lightning EM field computation could concern these topics.

In this framework, in recent decades, the ever-increasing abilities of Machine Learning (ML) helped to improve the prediction skills of multi-data dependent phenomena in many research fields. ML algorithms were found to be effective in modeling highly nonlinear functions especially when the inputs are mapped to the output through an unknown function. Specifically, Pattern Recognition (PR) algorithms may be implemented for data-driven processes to statistically model, predict and classify the process itself. Recently, applications of ML for lightning protection applications have been developed. Lightning localization and nowcasting using ML-based techniques have been proposed in [44,45,46]. Moreover, the authors of [47] propose the use of Artificial Neural Networks (ANN) to assess the electric and magnetic fields radiated by electrostatic discharges (ESDs). The obtained results showed a good correlation between measured and predicted results for both peak values of electric and magnetic fields. Furthermore, ML also helped researchers to formulate prediction models for Lightning-Induced overvoltages. The authors of [48] propose a Gaussian Process Regression (GPR) model aimed at assessing lightning-induced overvoltages. The choice of GPR over other regression methods is due to its ability in modeling non-linear functions depending on large datasets of features. In [49] an ANN-based method has been presented to compute the peaks of lightning-induced overvoltages for the first and subsequent strokes. In [50], ML is used for the prediction of lightning flashovers on overhead distribution lines. Generally, the advantage of using ML-based techniques is the fact that simplification hypotheses and rigorous analytical manipulations are not required, as is the case for numeric techniques such as the finite difference time domain method. Nevertheless, the drawback of ML is the computational complexity in setting up a suitable dataset, and the consequential data pre-processing needed to perform the training phase of the algorithm. Consequently, the best compromise between simplification and computational effort has to be found to understand whether the retrieve and pre-process phase needed to train a ML-based algorithm is suitable for the research purposes of the work, which may vary depending on the application.

In this contribution, the state-of-the-art of lightning electromagnetic field computation, starting with the classic expression for perfect ground (Section 2) and continuing to all the approaches that reduce the computational effort are presented. Finally, brief discussions of the case of a lossy ground (Section 3) and field-to-line coupling (Section 4) are presented. In the Appendix A, some remarks on the frequency domain formulas for the lightning ideal fields conclude the work.

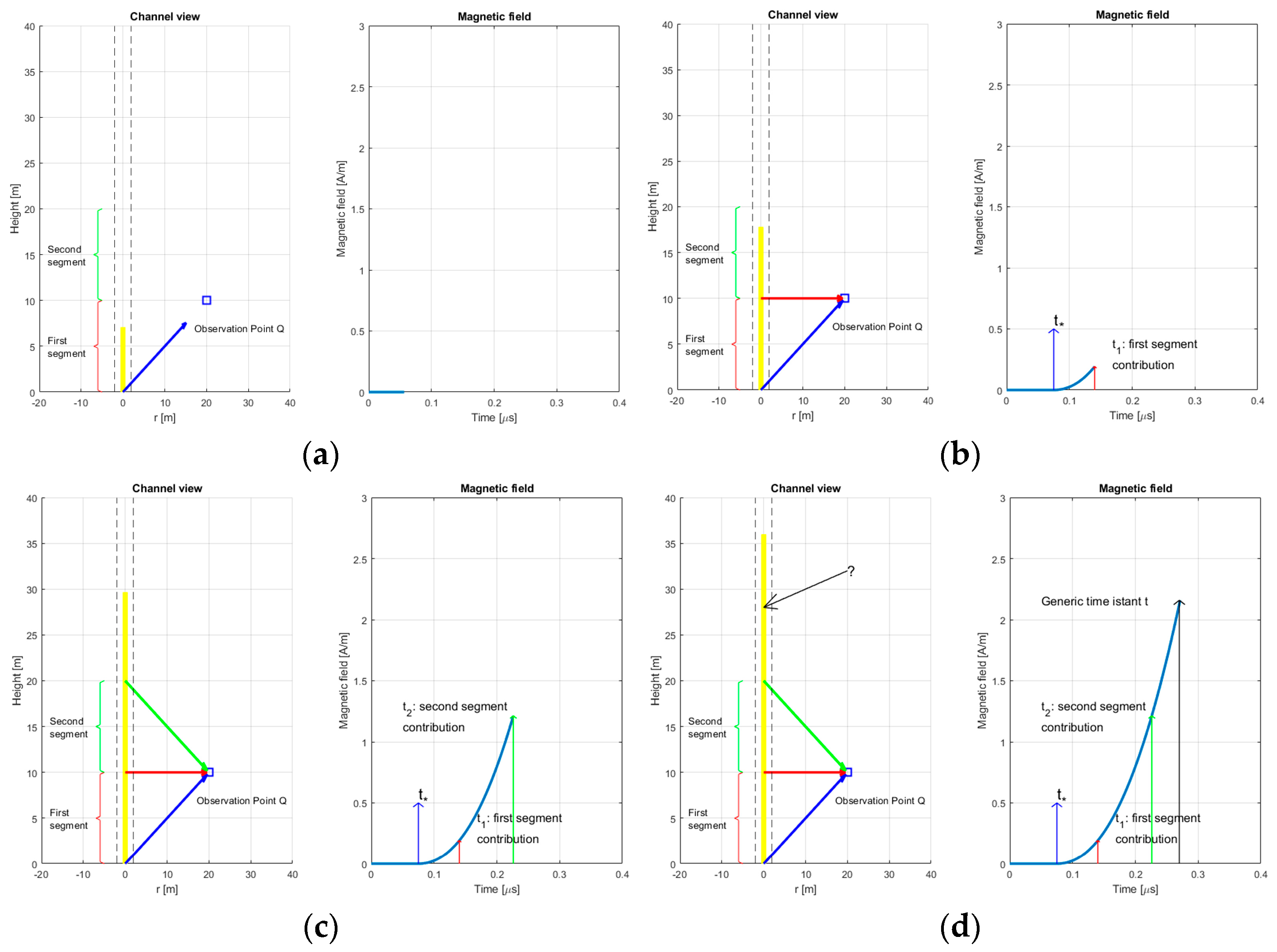
2. Time-Domain Expressions of EM Fields

Let us consider a vertical lightning channel of length H. According to TL models [51], the current flowing along the channel, observed at a height z′ and a time t can be expressed by

$$i\left(z^{\prime },t\right)=i\left(0,t-\frac{z^{\prime }}{v}\right)u\left(t-\frac{z^{\prime }}{v_f}\right)P\left(z^{\prime }\right)$$

(1)

where i₀(t) = i(0, t) is the channel-base current (CBC), v is the current wave propagation velocity, v_f is the return stroke speed, u is the unit step (or Heaviside) function and P is the attenuation function. In what follows, unless differently specified, we will assume v = v_f.

According to Figure 1 and [33], the system has a cylindrical symmetry and, consequently, an observer located at a distance r from the channel and at a height z above the ground experiences only the vertical and radial component of the electric field and the azimuthal component of the magnetic field. It is important to underline that, from the theoretical point of view, the EM fields above a PEC ground can be computed starting from the vector potential generated by a single dipole in the frequency domain by integrating it along the channel and coming back into the time domain by means on an IFT. However, for the sake of simplicity and due to the high number of applications in the time domain, the latter methods will be presented first, in subsection (a), while the frequency domain expressions considering an infinite time window are shown in subsection (b). Finally, in the Appendix A of the paper, some notes concerning frequency domain expressions in the case of infinite and finite time windows are proposed.

a.

Time domain expressions

The vertical component of the electric field is the sum of three terms, i.e., the static, induction and radiation components, respectively denoted by $e_{z,s}\left(t\right)$, $e_{z,\mathrm{i}}\left(t\right)$ and $e_{z,\mathrm{r}}\left(t\right)$:

$$e_z\left(t\right)=e_{z,s}\left(t\right)+e_{z,\mathrm{i}}\left(t\right)+e_{z,\mathrm{r}}\left(t\right)$$

(2)

$$e_{z,s}\left(t\right)=\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\left(\frac{2{\left(z-z^{\prime }\right)}^2-r^2}{R^5}{\displaystyle {\int }_0^{t}i\left(0,s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)ds}\right)}P\left(z^{\prime }\right)d{z}^{\prime }$$

(3)

$$e_{z,\mathrm{i}}\left(t\right)=\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\frac{2{\left(z-z^{\prime }\right)}^2-r^2}{c{R}^4}i\left(0,\mathrm{t}-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)P\left(z^{\prime }\right)d{z}^{\prime }$$

(4)

$$e_{z,\mathrm{r}}\left(t\right)=-\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\frac{r^2}{c^2{R}^3}\frac{\partial i\left(0,t-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}{\partial t}}P\left(z^{\prime }\right)d{z}^{\prime }$$

(5)

where c is the light speed in a vacuum, ${\epsilon }_0$ is the vacuum permittivity and $R=\sqrt{r^2+{\left(z-z^{\prime }\right)}^2}$.

Analogously, the radial component of the electric field is the sum of the static, induction and radiation terms, respectively denoted by $e_{\mathrm{r},s}\left(t\right)$, $e_{\mathrm{r},\mathrm{i}}\left(t\right)$ and $e_{\mathrm{r},\mathrm{r}}\left(t\right)$:

$$e_r\left(t\right)=e_{\mathrm{r},s}\left(t\right)+e_{\mathrm{r},\mathrm{i}}\left(t\right)+e_{\mathrm{r},\mathrm{r}}\left(t\right)$$

(6)

$$e_{r,s}\left(t\right)=\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\left(\frac{3r\left(z-z^{\prime }\right)}{R^5}{\displaystyle {\int }_0^{t}i\left(0,s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)ds}\right)1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}P\left(z^{\prime }\right)d{z}^{\prime }$$

(7)

$$e_{\mathrm{r},\mathrm{i}}\left(t\right)=\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\frac{3r\left(z-z^{\prime }\right)}{c{R}^4}i\left(0,\mathrm{t}-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)P\left(z^{\prime }\right)d{z}^{\prime }$$

(8)

$$e_{r,\mathrm{r}}\left(t\right)=\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\frac{r\left(z-z^{\prime }\right)}{c^2{R}^3}\frac{\partial i\left(0,t-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}{\partial t}1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}P\left(z^{\prime }\right)d{z}^{\prime }.$$

(9)

The azimuthal component of the magnetic field has only induction and radiation terms, denoted by $h_{\phi ,i}\left(t\right)$ and $h_{\phi ,\mathrm{r}}\left(t\right)$, that is

$$h_{\phi }\left(t\right)=h_{\phi ,i}\left(t\right)+h_{\phi ,\mathrm{r}}\left(t\right)$$

(10)

$$h_{\phi ,i}\left(t\right)=\frac{1}{4\pi }{\displaystyle {\int }_{-H}^H\frac{r}{R^3}i\left(0,\mathrm{t}-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)P\left(z^{\prime }\right)d{z}^{\prime }$$

(11)

$$h_{\phi ,\mathrm{r}}\left(t\right)=\frac{1}{4\pi }{\displaystyle {\int }_{-H}^H\frac{r}{c^2{R}^2}\frac{\partial i\left(0,t-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)}{\partial t}}1\left(s-\frac{R}{c}-\frac{\left|z^{\prime }\right|}{v}\right)P\left(z^{\prime }\right)d{z}^{\prime }.$$

(12)

b.

Frequency domain expressions

Similarly to time domain expressions, those in the frequency domain are the sum of static, induction and radiation terms as far as the vertical and radial components of the electric field are concerned, whereas the azimuthal component of the magnetic field is only formed by the induction and radiation terms. For the sake of brevity, in the following, the EM fields will be presented in their entirety without differentiating the three terms, which can be easily denoted as the term related to the time integral of the current ($\frac{1}{j\omega }$, static term), current (induction term) and time derivative of the current ($j\omega$, radiation term).

$$E_z\left(\omega \right)=\frac{I\left(0,\omega \right)}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\left[\frac{2{\left(z-z^{\prime }\right)}^2-r^2}{c{R}^4}+\frac{2{\left(z-z^{\prime }\right)}^2-r^2}{j\omega R^5}-j\omega \frac{r^2}{c^2{R}^3}\right]}{e}^{-j\omega \left(\frac{R}{c}+\frac{\left|z^{\prime }\right|}{v}\right)}P\left(z^{\prime }\right)d{z}^{\prime }$$

(13)

$$E_r\left(\omega \right)=\frac{I\left(0,\omega \right)}{4\pi {\epsilon }_0}{\displaystyle {\int }_{-H}^H\left[\frac{3r{\left(z-z^{\prime }\right)}^2-r^2}{c{R}^4}+\frac{3r{\left(z-z^{\prime }\right)}^2-r^2}{j\omega R^5}-\frac{j\omega r}{c^2{R}^3}\right]}{e}^{-j\omega \left(\frac{R}{c}+\frac{\left|z^{\prime }\right|}{v}\right)}P\left(z^{\prime }\right)d{z}^{\prime }$$

(14)

$$H_{\varphi }\left(\omega \right)=\frac{I\left(0,\omega \right)}{4\pi }{\displaystyle {\int }_{-H}^H\left[\frac{r}{R^3}+\frac{j\omega r}{c{R}^2}\right]}{e}^{-j\omega \left(\frac{R}{c}+\frac{\left|z^{\prime }\right|}{v}\right)}P\left(z^{\prime }\right)d{z}^{\prime },$$

(15)

where $I\left(0,\omega \right)$ is the FT of $i\left(0,t\right)$ Clearly, owing to the presence of $\omega$ at the denominator (involved by the static term), expressions (13) and (14) only hold for $\omega \ne 0$. A more precise treatment of the frequency-domain expressions of the electric fields will be presented in the Appendix A.

3. Simplified Approaches

This section describes the main approaches introduced throughout the years by several researchers. In the following, the main assumptions and simplifications characterizing each method, together with their final formulas and limits of applicability, are presented.

a.

Rusck’s formula [34]

Let us assume a vertical lightning channel above a PEC ground and a return stroke current modeled as follows:

$$i\left(z^{\prime },t\right)=I_{0}u\left(t-\frac{z^{\prime }}{v}\right).$$

(16)

Note that such a function is a special case of (1) in which the attenuation function is P(z′) = 1 and the CBC is constant with value I₀; in this case, the current wave propagation velocity is an unnecessary parameter. Moreover, according to the physics of lightning flash development, such current, flowing in the lightning channel, neutralizes the uniformly distributed per-unit-length charge q(z′,t) produced by the stepped leader prior to the return stroke itself. Such charge is given by:

$$q\left(z^{\prime },t\right)=-q_0+q_{0}u\left(t-\frac{z^{\prime }}{v}\right).$$

(17)

Finally, the continuity equation establishes the following relationship between q₀ and I₀:

$$\frac{I_0}{v}=q_0.$$

(18)

The PEC ground assumption allows applying the image method, which, as is well known, dictates that the charge in the image channel must be opposite to the charge of the source one, whereas the current is the same. Moreover, the parameterization of the image is simply obtained by changing z′ into −z′.

The source contribution ${\mathsf{\Phi }}_s$ to the scalar potential $\mathsf{\Phi }$ is given by:

$$\begin{array}{l}{\mathsf{\Phi }}_s\left(t\right)=\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_0^{+H}\frac{q\left(z^{\prime },t-\frac{R}{c}\right)}{R}}d{z}^{\prime }=\\ =\frac{1}{4\pi {\epsilon }_0}{\displaystyle {\int }_0^{+H}\frac{\left[-q_0+q_{0}u\left(t-\frac{z^{\prime }}{v}-\frac{R}{c}\right)\right]}{R}}d{z}^{\prime }=\\ =\frac{-q_0}{4\pi {\epsilon }_0}{\displaystyle {\int }_{s_1}^H\frac{d{z}^{\prime }}{R}}=\\ =-\frac{q_0}{4\pi {\epsilon }_0}\ln \frac{H-z+\sqrt{{\left(H-z\right)}^2+r^2}}{s_1-z+\sqrt{{\left(s_1-z\right)}^2+r^2}},\end{array}$$

(19)

where s₁ is the solution of the equation

$$t=\frac{s_1}{v}+\frac{\sqrt{\left(s_1-z\right)+r^2}}{c}.$$

(20)

An analogous derivation can be performed for the image. Then, by substituting the solution of (20) into (19) and summing both the source and image contributions, it is possible to obtain the gradient of the scalar potential as follows:

$$\begin{array}{l}{\left(\nabla \mathsf{\Phi }\right)}_z=\frac{q_0}{4\pi {\epsilon }_0}\left\{\frac{1}{\sqrt{{\left(H-z\right)}^2+r^2}}+\frac{1}{\sqrt{{\left(H+z\right)}^2+r^2}}-\right.\\ \left.-\frac{1}{\sqrt{{\left(vt-z\right)}^2+\left[1-{\left(\frac{v}{c}\right)}^2\right]r^2}}-\frac{1}{\sqrt{{\left(vt+z\right)}^2+\left[1-{\left(\frac{v}{c}\right)}^2\right]}{r}^2}\right\}.\end{array}$$

(21)

The current produces a vector potential that presents only a vertical component A; the contribution A_s of the source to A can be evaluated as:

$$\begin{array}{l}{A}_s\left(t\right)=\frac{{\mu }_0}{4\pi }{\displaystyle {\int }_0^H\frac{I\left(z^{\prime },t-\frac{R}{c}\right)}{R}}d{z}^{\prime }=\\ =\frac{{\mu }_0}{4\pi }{\displaystyle {\int }_0^H\frac{I_{0}u\left(t-\frac{z^{\prime }}{v}-\frac{R}{c}\right)}{R}}d{z}^{\prime }=\\ =\frac{{\mu }_0{I}_0}{4\pi }{\displaystyle {\int }_0^{s_1}\frac{1}{R}}d{z}^{\prime }=\\ =\frac{{\mu }_0{I}_0}{4\pi }\left\{\ln \left[vt-z+\sqrt{{\left(vt-z\right)}^2+\left[1-{\left(\frac{v}{c}\right)}^2\right]r^2}\right]-\right.\\ \left.-\ln \left(1+\frac{v}{c}\right)-\ln \left(-z+\sqrt{r^2+z^2}\right)\right\}.\end{array}$$

(22)

Repeating the same calculation for the image, summing the two terms thus computed, and taking the time derivative allows the writing of the relationship

$$\frac{\partial A}{\partial t}=\frac{{\mu }_0{I}_0}{4\pi }v\left\{\frac{1}{\sqrt{{\left(vt-z\right)}^2+\left[1-{\left(\frac{v}{c}\right)}^2\right]r^2}}\right.+\left.\frac{1}{\sqrt{{\left(vt+z\right)}^2+\left[1-{\left(\frac{v}{c}\right)}^2\right]r^2}}\right\}.$$

(23)

As a final remark, the vertical electric field strength can be easily computed as follows:

$$e_z\left(t\right)=-{\left(\nabla \mathsf{\Phi }\right)}_z-\frac{\partial A}{\partial t}.$$

(24)

By inserting (21) and (23) into (24), we obtain a fully analytical expression of the electric field strength in terms of the peak current, the return stroke velocity and the observation point.

The azimuthal component of the magnetic field can be computed recalling that $h_{\phi }\left(t\right)=\frac{1}{{\mu }_0}\nabla x \overrightarrow{A}$. Rusck in [34] provides its expression at ground level, which leads to a magnetic field strength equal to

$$h_{\phi }\left(t\right)=\frac{1}{2\pi }\frac{I_0}{c^{2}r}\frac{\frac{vt}{r}}{\sqrt{1+{\left(\frac{v}{c}\right)}^2\left[{\left(\frac{ct}{r}\right)}^2-1\right]}}.$$

(25)

b.

Rubinstein and Uman [28]

In 1989, Rubinstein and Uman provided a very interesting contribution in which they unified the so-called dipole approach with the monopole approach. The dipole approach assumes the knowledge of the current distribution in a source to determine the electromagnetic field it produces. The application of relationships like (22) expressing the link between the current flowing in the lightning channel and the vector potential allows finding the latter quantity. Then, by imposing the Lawrence Gauge condition, it is easy to calculate the scalar potential and finally obtain the expression of the electric and magnetic fields produced by the lightning current. If no other approximations are made, this leads to the exact formulas provided in Section 1.

Conversely, the monopole approach is largely the one proposed by Rusck and summarized in the previous subsection. As it can be read in [28], “the monopole technique requires a knowledge of both the current and the charge densities as a function of time and space. In most practical cases, the charge distribution is neither a variable of interest nor a known function. In any event, it is always constrained by the continuity equation once an initial charge distribution and the time and spatially varying current density are given. The monopole technique has been primarily used in the electric power literature, where it has been applied to simple lightning models”.

The main merit of the paper consists in showing that, when the current has the expression (16), it is possible to obtain analytical solutions in both methods and they provide the same results. Furthermore, the authors suggest that the application of the Duhamel theorem allows determining the electric field $\overrightarrow{e}$ generated by a lightning discharge when the CBC can be written as the sum of Heaviside functions with different amplitudes and eventually shifted in time. In formulas:

$$\overrightarrow{e}\left(t\right)={\overrightarrow{e}}_0\left(t\right)i\left(0,0\right)+{\displaystyle {\int }_0^t{\overrightarrow{e}}_0\left(s\right)\frac{di\left(0,t-s\right)}{dt}ds},$$

(26)

where ${\overrightarrow{e}}_0$ is the electric field from a unit step current (as shown in (22)–(24) for its vertical component).

c.

Thottappillil, Schoene and Uman [37]

In 2001, Thottappillil, Schoene and Uman showed that the time domain Expression (10)–(12) of the magnetic field, under the TL model assumption (i.e., P(z′) = 1), can be rewritten as:

$$\begin{array}{ll}{h}_{\phi }^{}(t)=\frac{c}{2\pi rv}i\left(0,t-\frac{R(0)}{c_{}}\right)+& \frac{c_{}}{4\pi r}\left(\frac{1}{c_{}^2}-\frac{1}{v^2}\right)\cdot \\ & \cdot {\displaystyle {\int }_{-H}^H\frac{\partial i\left(0,\xi (z^{\prime })\right)}{\partial t}}1\left(\xi (z^{\prime })\right)d{z}^{\prime },\end{array}$$

(27)

where

$$\xi (z^{\prime })=t-\frac{R(z^{\prime })}{c}-\frac{\left|z^{\prime }\right|}{v}$$

(28)

and, with a slight abuse of notations, the dependence of the distance R on the channel coordinate z′ has been highlighted.

Consequently, if the assumption v = c is made, we have

$$h_{\phi }^{}(t)=\frac{c}{2\pi rv}i\left(0,t-\frac{R(0)}{c_{}}\right),$$

(29)

which shows that the magnetic field has the same shape as the CBC, being scaled down by a factor depending on the horizontal distance, as well as time-shifted because of the delay time due to the propagation of the field produced by the “first dipole” located at the channel base. Moreover, for a geometry like the one depicted in Figure 1, Maxwell equations can be written as:

$$\begin{array}{l}{e}_r^i(t)=-{\mu }_0{c}_{}^2{\displaystyle {\int }_0^t\frac{\partial h_{\varphi }^{}}{\partial z}}d\tau \\ e_z^i(t)={\mu }_0{c}_{}^2{\displaystyle {\int }_0^t\frac{1}{r}}\frac{\partial (r{h}_{\varphi }^{})}{\partial r}d\tau ,\end{array}$$

(30)

which allow it to be proved that the electric field also has the same shape as the CBC.

The main strengths of this approach are that there is no restriction on the CBC formula and that there are no numerical integrations to be carried out. Unfortunately, if, on the one hand, the approximation of the unitary attenuation function is somehow acceptable especially for overvoltage calculations, on the other hand, the assumption of a return stroke speed equal to the speed of light in a vacuum sounds quite unrealistic. In [37], the authors state that “measurements on triggered-lightning return strokes indicate that the three waveforms (i.e., CBC, electric field and magnetic one) are similar for about 100 ns, potentially implying that the initial return stroke speed is actually near c for that time. Measurements further show that for both triggered and natural lightning the three waveforms are very different on a microsecond time scale, implying that the overall return stroke speed is less than c, consistent with typical optical speed measurements of c/3 to c/2 made on the same time scale.”

d.

Napolitano [36]

In 2011, Napolitano provided analytical formulas for lightning electromagnetic fields over PEC ground under the following assumptions:

• Attenuation function P(z′) = 1
• CBC is given by:

$$i_0\left(t\right)=\left\{\begin{array}{c}\frac{I_p}{t_f}t\hspace{1em}t\le t_f\\ I_p\hspace{1em}t>t_f\end{array}\right.$$

(31)

Starting from the expressions given in Section 2, it is not difficult to realize that, given: (i) the propagation of the current along the channel with speed v, (ii) the propagation of the electromagnetic fields in a vacuum with speed c, (iii) the Expression (31) of the CBC, the actual path of integration (in dz′) for the three fields can be divided into two segments. The first goes from zero to the height z₁ below which, at a specified time instant t, the current has a constant value, and the second from z₁ to the height z₀ above which the integrand is zero due to the Heaviside function. In formulas:

$$\begin{array}{l}{z}_1\mathrm{solves} t-t_f\ge \frac{z^{\prime }}{v}+\frac{R}{c}\\ z_0\mathrm{solves} t\ge \frac{z^{\prime }}{v}+\frac{R}{c}.\end{array}$$

(32)

This way, all the integrals can be solved analytically, thus yielding Formulas (9)–(17) of [36] (not reported here for the sake of brevity).

The main merit of the proposed approach is that the assumption of the step function in the CBC is removed, which allows accounting for the current front time. This is a noteworthy improvement, as the front time plays a crucial role in the field and overvoltage wave shape and peak. Moreover, in [36] it is shown that any sampled CBC can be linearly interpolated, thus originating a sum of many different currents of the kind (31). Unfortunately, a realistic waveform needs a huge number of terms in this sum, which impairs the computational advantage of those analytical formulas. For this reason, in many overvoltage applications, (31) is assumed in order to avoid cumbersome numerical calculations.

e.

Brignone et al. [38]

The general idea at the basis of the method proposed in [38] can be presented by using a graphical sketch. Assuming the geometry of Figure 1, when a PEC ground and the TL model are considered, the azimuthal component of the magnetic field produced at the observation point is given by (27). There, the Heaviside function identifies the portion of the channel that contributes to the field at the observation point Q and at time t; a such portion is determined by solving the inequality $\xi \left(z^{\prime }\right)\ge 0$ for the unknown z′.

If $t_{\mathrm{*}}$ denotes the time taken by the EM radiation produced by the dipole to propagate from the channel base to the observation point Q, it immediately turns out that the magnetic field $h_{\varphi }\left(t\right)$ is null for any time $t\le t_{\mathrm{*}}$, as shown in Figure 2a: in the left panel of the latter, the yellow line represents the portion of the lightning channel in which the current is propagating, whereas the right panel shows the time domain behavior of the magnetic field at the observation point Q.

If the lightning channel is subdivided into sufficiently small segments and $t_1$ is the time at which the fields produced by the last dipole in the first segment reach the point Q, then, for all the time instants t in the interval $t_{\mathrm{*}}\le t\le t_1$, a portion of the first segment (the complete segment is indicated by the red curly bracket) contributes to the field at Q. If we use a linear approximation of the function $\xi \left(z^{\prime }\right)$, then both the integral in (27) and the inequality $\xi \left(z^{\prime }\right)\ge 0$ can be analytically solved, allowing us to find the integral domain as a function of t (Figure 2b).

The same considerations can be repeated for the second segment, obtained, as before, by defining the time $t_2$ as the time at which the fields produced by the last dipole in the second segment reach the point Q. It is then possible to analytically compute the magnetic field at Q for any time t such that $t_1\le t\le t_2$, where the whole first segment and a portion of the second one are involved in the production of the field (Figure 2c).

Repeating the same procedure for other n segments of the lighting channel, a time sequence $t_1\le t_2\le \cdots \le t_n$ is uniquely defined. Once the linear approximation of the function $\xi \left(z^{\prime }\right)$ is available for each segment, the contribution of the field at Q can be analytically computed, as shown in Figure 2d.

The fundamental theorem of the integral calculus applied to (28) assures that the magnetic field is a linear combination of functions, where the CBC waveform is time-shifted by the time necessary for the current to reach the beginning of the corresponding interval. This approach allows the obtaining of a closed expression for the lightning magnetic field over a PEC ground, once the TL model is assumed. Let us note that the CBC can have an arbitrary waveshape and the return stroke speed v can assume any positive value lower than c (and typically greater than c/3).

Once the magnetic field is at our disposal, the vertical and radial components of the electric field can be obtained, once again analytically, by applying (30).

The method can be extended to the case of finite ground conductivity, provided that the CBC can be written as a linear combination of exponential functions [52].

A detailed validation of the method is proposed in [39]. An excellent agreement with the EM fields computed by means of the classical numerical approach is highlighted, both at close and far distances, and considering both an infinite and a finite ground conductivity, as well as different CBC waveforms. Assuming a PEC ground (resp. finite conductivity ground) and setting a 1% threshold for the approximation error of each field component, the computational time is reduced by a factor of more than 5000 (resp. 200). This represents an impactful advantage of such a method.

f.

Brignone et al. [41]

An extension of the method presented in [38] can be found in [41]. In this contribution, the authors propose an approach for the evaluation of lightning electromagnetic fields by considering a PEC ground and any CBC waveform but removing the assumption of the TL model for the current propagation along the channel. Thus, the novelty of this method is the possibility of including any attenuation function $P\left(z^{\prime }\right)$.

With reference to the geometry shown in Figure 1 again, the azimuthal component of the magnetic field at the observation point $Q\left(r,\varphi ,z\right)$ is given by Equations (10)–(12). In such equations, the Heaviside function identifies the portion of the channel that contributes to the field at the observation point Q and at time t.

The lightning channel is subdivided into n portions and in each, the attenuation function is approximated by a constant. Hence, if we introduce n + 1 points z_k along the channel, such that $0=z_0<z_1<...<z_k<z_n=H$, we can find $P_k\ge 0$ such that $P\left(z^{\prime }\right)\simeq P_k$ for any $z^{\prime }\in \left[z_{k-1},z_k\right].$ After some manipulations, it is possible to express the magnetic field observed in Q at time t as generated by a portion of length L of the channel (or the channel image) in the following form:

$$h_{\phi }^L\left(r,z,t\right)=\frac{r}{4\pi }{\displaystyle {\int }_0^L\left[\frac{1}{R^3(z^{\prime })}i\left(0,t-\frac{R(z^{\prime })}{c}-\frac{z^{\prime }}{v}\right)+\frac{1}{c{R}^2(z^{\prime })}\frac{\partial i\left(0,t-\frac{R(z^{\prime })}{c}-\frac{z^{\prime }}{v}\right)}{\partial t}\right]}d{z}^{\prime }.$$

(33)

Thus, the overall magnetic field in Q is a linear combination of the contributions from each channel portion, i.e.,

$$h_{\phi }^{}\left(r,z,t\right)={\displaystyle \sum _{k=1}^n{P}_k}\left[h_{\varphi }^{L_k}\left(r,z-z_{k-1},t-\frac{z_{k-1}}{v}\right)+h_{\varphi }^{L_k}\left(r,-z-z_{k-1},t-\frac{z_{k-1}}{v}\right)\right]$$

(34)

with $L_k=z_k-z_{k-1}$ being the length of the k-th portion of the lightning channel. By applying standard integration and derivation rules (and assuming the continuity of the CBC function), Equation (33) can be manipulated to obtain an expression containing an integral term where the integrand is the product of the CBC and a function in the form

$$y_1\left(x\right)={\left(1+x^2\right)}^{-\frac{3}{2}}.$$

(35)

Then, both the CBC function and y₁ are approximated by a linear combination of complex exponential functions (Prony series), so that the integral can be solved analytically. The number of terms of the series is given by the Prony algorithm, once the threshold on the error (with respect to the typical numerical method) is established. Following the approach of [52], the number of terms required to assess a reasonable fit is n₁ = 3 for y₁, whereas for the CBC such number, denoted by n_R, depends on the smoothness of the considered function. For the typical Heidler’s first (resp. subsequent) function [53], we have n_R = 3 (resp. n_R = 9), whereas for a measured CBC n_R = 81 is reported.

Therefore, the magnetic field is given by the sum of $n\cdot n_R\cdot n_1$ elements. The shape of the attenuation function affects the number n of channel portions. The trivial case n = 1 is valid when the TL model is assumed for the current propagation in the channel, i.e., $P\left(z^{\prime }\right)=1$. Conversely, n = 30 results from the assumption of the well-known MTLE model, i.e., $P\left(z^{\prime }\right)=e^{-\frac{z^{\prime }}{\mathrm{\lambda }}}$ with λ = 2000 [54]. Clearly, the approximation error can be reduced by increasing n, n_R and n₁, but this results in an increased computation time.

As regards the radial and vertical components of the electric field, equations similar to Equation (34) can be obtained, where the contribution from each channel portion can be calculated by using the Maxwell Equation (30) inputted with the magnetic field associated with the same channel portion. Then, the same procedure applied above for the magnetic field is followed, thus entailing the need to define another function, i.e.,

$$y_2\left(x\right)=x{\left(1+x^2\right)}^{-\frac{3}{2}},$$

(36)

which can be approximated by a truncated series of complex exponential functions formed by n₂ = 4 terms.

This method allows the computing of the lightning EM fields with a computational time that ranges from 10 to some hundred times lower than the time taken by the typical numerical method. It is worth highlighting that such an approach makes no assumption regarding the behavior of the attenuation function. Thus, it made it possible to calculate more realistic EM fields with a reduced computational effort.

4. Effect of Finite Soil Conductivity

In the last few decades, several studies have been dedicated to the propagation of lightning electromagnetic fields over and under a lossy homogeneous ground. The focus was mainly on the horizontal component of the electric field because:

• Such a component is mostly affected by finite ground conductivity. At the same time, the accuracy of the result is not compromised by the assumption of a PEC ground when the vertical component of the electric field and the azimuthal component of the magnetic one are to be evaluated [22].
• The horizontal component of the electric field is the source term of the field-to-line coupling differential equations when the effect of lightning on power and telecommunication lines is addressed. At the same time, the boundary conditions describing the line terminations are the only terms involving the vertical component of the electric field.

The first contribution was proposed by Cooray [21]. His formula leads to the evaluation of the horizontal electric field at the ground surface from the knowledge of the incident azimuthal magnetic field. In [20], Rubinstein proposes a review of the formula, suggesting the addition of a term allowing the computation of the horizontal electric field at all heights above the lossy ground. The resulting expression is known as the CR formula:

$${\mathrm{E}}_{\mathrm{r}}(\mathsf{\omega },\mathrm{z},\mathrm{r})=-{\mathrm{H}}_{\mathsf{\phi }\mathrm{i}}\left(\mathsf{\omega },0,\mathrm{r}\right)\mathrm{Z}\left(\mathsf{\omega }\right)+{\mathrm{E}}_{\mathrm{r}\mathrm{i}}\left(\mathsf{\omega },\mathrm{z},\mathrm{r}\right);$$

(37)

in (37), Z is the surface impedance computed as:

$$\mathrm{Z}\left(\mathsf{\omega }\right)=\frac{\sqrt{{\mathsf{\mu }}_0}}{\sqrt{\mathsf{\epsilon }+\frac{\mathsf{\sigma }}{\mathrm{j}\mathsf{\omega }}}},$$

(38)

where (1) ${\mathrm{E}}_{\mathrm{r}}(\mathsf{\omega },\mathrm{z},\mathrm{r})$ represents the horizontal component of the electric field at angular frequency ω, height z and horizontal distance r from the lighting channel; (2) ${\mathrm{H}}_{\mathsf{\phi }\mathrm{i}}\left(\mathsf{\omega },0,\mathrm{r}\right)$ indicates the azimuthal component of the magnetic field at the same frequency and horizontal distance and ground level; (3) ${\mathrm{E}}_{\mathrm{r}\mathrm{i}}(\mathsf{\omega },\mathrm{z},\mathrm{r})$ is the horizontal component of the electric field. Both the fields on the right-hand side of Equation (37) are computed by assuming a PEC ground. The parameters μ₀, ε, σ respectively represent the magnetic permittivity, the dielectric constant, and the conductivity of the soil. It should be noted that, for medium-high values of the soil conductivity (higher than 10⁻³ S/m), the propagation effects on the azimuthal magnetic field may reasonably be neglected. Such an assumption is considered to be valid for (i) distances lower than 200 m and conductivities of about 10³ S/m and (ii) distances lower than 100 m and conductivities of about 10⁻⁴ S/m [55].

In case of the need to switch to time domain methods, an Inverse Fast Fourier Transform (IFFT) procedure must be adopted to evaluate the lightning horizontal field by using the CR formula. As is well known, two main drawbacks must be faced when dealing with FFT and IFFT-based methods. The first deals with computational limitations, and the second is the error due to the truncation of the lightning current frequency spectrum. In this framework, the technological enhancement of the last decade enabled the direct evaluation of E_r in the time domain. The first expression of the CR formula in the time domain was proposed in [29] and the main steps are explained below. Since the involved quantities are identically zero before the instant in which the lightning return stroke current starts traveling up along the channel (i.e., for t < 0), the existence of the FT $\Im \left(\mathrm{f}\right)$ of a function $\mathrm{f}$ ensures the existence of its Laplace transform L(f) [21]. For the sake of simplicity, Equation (37) shall be expressed in the Laplace domain simply by setting $s=j\omega$. Thus, we can write

$$E_r(s,z,r)=-H_{\phi i}\left(s,0,r\right)Z\left(s\right)+E_{ri}(s,z,r),$$

(39)

where

$$Z\left(s\right)=\frac{\sqrt{{\mathsf{\mu }}_0}}{\sqrt{\mathsf{\epsilon }+\frac{\mathsf{\sigma }}{s}}}=\sqrt{\frac{{\mathsf{\mu }}_0}{\mathsf{\epsilon }}}\frac{1}{\sqrt{1+\frac{\mathsf{\sigma }}{s\mathsf{\epsilon }}}}=\mathsf{\eta }\frac{1}{\sqrt{1+\frac{\mathsf{\sigma }}{s\mathsf{\epsilon }}}}.$$

(40)

Considering that

$${\lim }_{\mathrm{s}\to \infty }\mathrm{Z}\left(\mathrm{s}\right)=\sqrt{{\mathsf{\mu }}_0/\mathsf{\epsilon }}=\mathsf{\eta }$$

(41)

it follows that

$$\mathrm{g}\left(\mathrm{s}\right)=\mathrm{Z}\left(\mathrm{s}\right)-\mathsf{\eta }=\frac{\sqrt{{\mathsf{\mu }}_0}}{\sqrt{\mathsf{\epsilon }+\mathsf{\sigma }/\mathrm{s}}}-\mathsf{\eta }.$$

(42)

The inverse Laplace transform of g can be analytically computed by introducing the modified Bessel function of the first type and order n, namely I_n:

$$\left\{{\mathrm{L}}^{-1}\left(\mathrm{g}\right)\right\}\left(\mathrm{t}\right)=\mathsf{\eta }\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}{\mathrm{e}}^{-\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}}\left[{\mathrm{I}}_1\left(\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}\right)-{\mathrm{I}}_0\left(\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}\right)\right].$$

(43)

Moreover, as the Laplace transform of the Dirac function δ is given by

$$\left\{\mathrm{L}\left(\mathsf{\delta }\right)\right\}\left(\mathrm{s}\right)=1,$$

(44)

the inverse Laplace transform of Z is

$$\left\{{\mathrm{L}}^{-1}\left(\mathrm{Z}\right)\right\}\left(\mathrm{t}\right)=\mathsf{\eta }\left\{\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}{\mathrm{e}}^{-\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}}\left[{\mathrm{I}}_1\left(\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}\right)-{\mathrm{I}}_0\left(\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}\right)\right]+\mathsf{\delta }\left(\mathrm{t}\right)\right\}.$$

(45)

The application of convolution integral properties allows obtaining the time domain expression of the CR formula for the horizontal electric field e_r, i.e.,

$${\mathrm{e}}_{\mathrm{r}}(\mathrm{t},\mathrm{z},\mathrm{r})=\mathsf{\eta }{\displaystyle \underset{0}{\overset{\mathrm{t}}{\mathsf{\int }}}{\mathrm{h}}_{\mathsf{\phi }\mathrm{i}}\left(\mathsf{\tau },0,\mathrm{r}\right)\left[\mathrm{K}\left(\mathrm{t}-\mathsf{\tau }\right)-\mathsf{\delta }\left(\mathrm{t}-\mathsf{\tau }\right)\right]}\mathrm{d}\mathsf{\tau }+{\mathrm{e}}_{\mathrm{r}\mathrm{i}}(\mathrm{t},\mathrm{z},\mathrm{r})$$

(46)

where

$$\begin{array}{l}\mathrm{K}\left(\mathrm{t}\right)=\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}{\mathrm{e}}^{-\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}}\left[{\mathrm{I}}_0\left(\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}\right)-{\mathrm{I}}_1\left(\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\mathrm{t}\right)\right]=\mathsf{\alpha }{\mathrm{e}}^{-\mathrm{t}}\left[{\mathrm{I}}_0\left(\mathsf{\alpha }\mathrm{t}\right)-{\mathrm{I}}_1\left(\mathsf{\alpha }\mathrm{t}\right)\right]\\ \mathsf{\alpha }=\frac{\mathsf{\sigma }}{2\mathsf{\epsilon }}\end{array}$$

(47)

and the terms e_ri and h_ϕi represent the inverse Laplace transform of the horizontal component of the electric field (E_ri) and the inverse Laplace transform of the azimuthal component of the magnetic (H_ϕi) field, respectively, both calculated as if the ground were a perfect conductor. Moreover, the properties of the Dirac function allow the writing of

$${\mathrm{e}}_{\mathrm{r}}(\mathrm{t},\mathrm{z},\mathrm{r})=\mathsf{\eta }{\displaystyle \underset{0}{\overset{\mathrm{t}}{\mathsf{\int }}}{\mathrm{h}}_{\mathsf{\phi }\mathrm{i}}(\mathsf{\tau },0,\mathrm{r})\mathrm{K}\left(\mathrm{t}-\mathsf{\tau }\right)}\mathrm{d}\mathsf{\tau }+{\mathrm{e}}_{\mathrm{r}\mathrm{i}}(\mathrm{t},\mathrm{z},\mathrm{r})-\mathsf{\eta }{\mathrm{h}}_{\mathsf{\phi }\mathrm{i}}(\mathrm{t},0,\mathrm{r})$$

(48)

The implementation of Equation (48) is detailed in [29] and is an example of linear convolution, which is computationally cumbersome. For this reason, the authors of [30] proposed an improvement, by expressing the surface impedance as

$$\mathrm{Z}(\mathrm{s})=\sqrt{\frac{\mathrm{s}{\mathsf{\mu }}_0}{\mathrm{s}\mathsf{\epsilon }+\mathsf{\sigma }}}=\sqrt{\frac{{\mathsf{\mu }}_0}{\mathsf{\epsilon }}}\sqrt{\frac{\mathrm{s}}{\mathrm{s}+\mathsf{\sigma }/\mathsf{\epsilon }}}=\mathsf{\eta }\sqrt{\frac{\mathrm{s}{\mathsf{\tau }}_{\mathrm{G}}}{\mathrm{s}{\mathsf{\tau }}_{\mathrm{G}}+1}},$$

(49)

being ${\mathsf{\tau }}_{\mathrm{G}}=\mathsf{\epsilon }/\mathsf{\sigma }$ A Rational Approximation (RA) for the function

$$\mathrm{z}({\mathrm{s}}^{\prime })=\sqrt{\frac{{\mathrm{s}}^{\prime }}{{\mathrm{s}}^{\prime }+1}}\approx 1+{\displaystyle \sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{R}\mathrm{A}}}\frac{{\mathrm{r}}_{\mathrm{k}}}{{\mathrm{s}}^{\prime }-{\mathrm{a}}_{\mathrm{k}}}}$$

(50)

would allow approximating Equation (39) as

$${\mathrm{E}}_{\mathrm{C}\mathrm{R}}(\mathrm{s},\mathrm{z},\mathrm{r})=-{\mathrm{H}}_{\mathsf{\phi }\mathrm{i}}\left(0,\mathrm{r},\mathrm{s}\right)\mathrm{Z}\left(\mathrm{s}\right)=-\mathsf{\eta }{\mathrm{H}}_{\mathsf{\phi }\mathrm{i}}\left(\mathrm{s},0,\mathrm{r}\right)-\mathsf{\eta }{\displaystyle \sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{R}\mathrm{A}}}\frac{{\mathrm{r}}_{\mathrm{k}}{\mathrm{H}}_{\mathsf{\phi }\mathrm{i}}\left(\mathrm{s},0,\mathrm{r}\right)}{\mathrm{s}{\mathsf{\tau }}_{\mathrm{G}}-{\mathrm{a}}_{\mathrm{k}}}},$$

(51)

where N_RA is the number of poles used in the expansion. The Vector Fitting (VF) technique [56] may help in effectively computing the RA. To shift in the time domain, the poles a_k and residues r_k from the VF are used, thus enabling a straightforward transformation from continuous to discrete time. To do so, the classical state space form is used, i.e.,

$$\left\{\begin{array}{l}\mathrm{s}{\mathrm{X}}_{\mathrm{k}}\left(\mathrm{s}\right)=\frac{{\mathrm{a}}_{\mathrm{k}}}{{\mathsf{\tau }}_{\mathrm{G}}}{\mathrm{X}}_{\mathrm{k}}\left(\mathrm{s}\right)+\frac{1}{{\mathsf{\tau }}_{\mathrm{G}}}{\mathrm{H}}_{\mathsf{\phi }\mathrm{i}}\left(\mathrm{s},0,\mathrm{r}\right),\hspace{1em}\mathrm{k}=1..{\mathrm{N}}_{\mathrm{R}\mathrm{A}}\hfill \\ {\mathrm{E}}_{\mathrm{C}\mathrm{R}}(\mathrm{s},\mathrm{z},\mathrm{r})=-\mathsf{\eta }{\mathrm{H}}_{\mathsf{\phi }\mathrm{i}}\left(\mathrm{s},0,\mathrm{r}\right)-\mathsf{\eta }{\displaystyle \sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{R}\mathrm{A}}}{\mathrm{r}}_{\mathrm{k}}{\mathrm{X}}_{\mathrm{k}}\left(\mathrm{s}\right)}\hfill \end{array}\right.,$$

(52)

with ${\mathrm{X}}_{\mathrm{k}}\left(\mathrm{s}\right)$ being the N_RA state variables of the system. Now, we can write Equation (52) in the time domain by assuming ${\mathrm{x}}_{\mathrm{k}}\left(0\right)=0,\hspace{1em}\mathrm{k}=1..{\mathrm{N}}_{\mathrm{R}\mathrm{A}}$ as initial conditions, thus finding

$$\left\{\begin{array}{l}{\dot{\mathrm{x}}}_{\mathrm{k}}\left(\mathrm{t}\right)=\frac{{\mathrm{a}}_{\mathrm{k}}}{{\mathsf{\tau }}_{\mathrm{G}}}{\mathrm{x}}_{\mathrm{k}}\left(\mathrm{t}\right)+\frac{1}{{\mathsf{\tau }}_{\mathrm{G}}}{\mathrm{h}}_{\mathsf{\phi }\mathrm{i}}\left(\mathrm{s},0,\mathrm{r}\right),\hspace{1em}\mathrm{k}=1..{\mathrm{N}}_{\mathrm{R}\mathrm{A}}\hfill \\ {\mathrm{e}}_{\mathrm{C}\mathrm{R}}(\mathrm{t},\mathrm{z},\mathrm{r})=-\mathsf{\eta }{\mathrm{e}}_{\mathsf{\phi }\mathrm{i}}\left(\mathrm{t},0,\mathrm{r}\right)-\mathsf{\eta }{\displaystyle \sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{R}\mathrm{A}}}{\mathrm{r}}_{\mathrm{k}}{\mathrm{x}}_{\mathrm{k}}\left(\mathrm{t}\right)}\hfill \end{array}\right..$$

(53)

To implement Equation (53) in computer code, some discretization is needed. In [30], a sequence t_n = Δt(n − 1) for n = 1. n_p is defined and the magnetic field is supposed to be constant in each time interval $[{\mathrm{t}}_{\mathrm{n}},{\mathrm{t}}_{\mathrm{n}+1})$:

$${\mathrm{h}}_{\mathsf{\phi }\mathrm{i}}\left(\mathrm{t},0,\mathrm{r}\right)\approx {\mathrm{h}}_{\mathrm{n}}\hspace{1em}\forall \mathrm{t}\in [{\mathrm{t}}_{\mathrm{n}},{\mathrm{t}}_{\mathrm{n}+1}).$$

(54)

In each interval, (54) reads:

$$\left\{\begin{array}{l}{\dot{\mathrm{x}}}_{\mathrm{k}}\left(\mathrm{t}\right)=\frac{{\mathrm{a}}_{\mathrm{k}}}{{\mathsf{\tau }}_{\mathrm{G}}}{\mathrm{x}}_{\mathrm{k}}\left(\mathrm{t}\right)+\frac{1}{{\mathsf{\tau }}_{\mathrm{G}}}{\mathrm{h}}_{\mathrm{n}}\hfill \\ {\mathrm{x}}_{\mathrm{k}}\left({\mathrm{t}}_{\mathrm{n}}\right)={\mathrm{x}}_{\mathrm{k},\mathrm{n}}\hfill \end{array}\right.,\hspace{1em}\mathrm{k}=1..{\mathrm{N}}_{\mathrm{R}\mathrm{A}},\mathrm{t}\in \left[{\mathrm{t}}_{\mathrm{n}},{\mathrm{t}}_{\mathrm{n}+\mathrm{1}}\right],$$

(55)

which admits the following analytical solution:

$${\mathrm{x}}_{\mathrm{k}}\left(\mathrm{t}\right)={\mathrm{x}}_{\mathrm{k},\mathrm{n}}{\mathrm{e}}^{({\mathrm{a}}_{\mathrm{k}}/{\mathsf{\tau }}_{\mathrm{G}})\left(\mathrm{t}-{\mathrm{t}}_{\mathrm{n}}\right)}+\frac{1}{{\mathrm{a}}_{\mathrm{k}}}\left({\mathrm{e}}^{({\mathrm{a}}_{\mathrm{k}}/{\mathsf{\tau }}_{\mathrm{G}})\left(\mathrm{t}-{\mathrm{t}}_{\mathrm{n}}\right)}-1\right){\mathrm{h}}_{\mathrm{n}}.$$

(56)

It should be noted that the coefficients ${\mathrm{e}}^{({\mathrm{a}}_{\mathrm{k}}/{\mathsf{\tau }}_{\mathrm{G}})\Delta \mathrm{t}}$ and $({\mathrm{e}}^{({\mathrm{a}}_{\mathrm{k}}/{\mathsf{\tau }}_{\mathrm{G}})\Delta \mathrm{t}}-1)/{\mathrm{a}}_{\mathrm{k}}$ do not change throughout the iterations. The algorithm to solve system (55) requires approximately 3N_RA products and 2N_RA sums, N_RA being of the order of ten. As the number of computations at each iteration is constant, the algorithm has a time complexity of order n. As observed in [57], the drawback of this approach is the fact that the accuracy of the horizontal electric field is dependent on the performance of the VF technique. In this framework, since 2011, researchers started focusing their attention on two main issues: (1) to improve the computational efficiency of the convolution integral Equation (48); and (2) to delve into the analysis of the properties of the integral kernel Equation (43) in order to find suitable approximations not involving special functions. The initial contribution related to the first research line was given by Zou et al. in 2012 [57] and summarized in [58]. In 2017 and 2018, Liu et al. proposed a review, presented in [59] and enhanced in [60]. The second research line, involving the properties of the integral kernel, has been investigated by the research group of the University of Naples since 2015 and the related results have been published in [31,61,62,63]. In particular, in [61,64,65], a new formulation for the CR expression in the time domain is proposed, in which the kernel of the convolution integral exhibits better properties in terms of smoothness. In 2019 the enhancement proposed by Barbosa and Paulino [32] turned out to be effective. Finally, in 2019 Liu et al. [58] further refined the approach.

5. Field-to-Line Coupling

The field-to-line coupling can be achieved by means of several approaches, mainly based on the Agrawal [13], Taylor [14], or Rachidi models [15]. They require as input the electromagnetic fields, which are computed according to one of the previously presented methods. In this framework, the well-known Agrawal method is presented.

Let us consider an overhead line with M conductors. The scattered voltage $V_i^s\left(x,t\right)$ and the current $I_i\left(x,t\right)$ flowing along the i-th conductor at the distance x from its left terminal can be expressed according to Equation (57), where L and C are the inductance and capacitance matrices respectively and the incident field $e_{inc,x,\mathrm{i}}$ is the tangential component of the radial electric field $e_r$.

$$\left\{\begin{array}{l}\frac{\partial V_i^s}{\partial x}\left(x,t\right)+{\displaystyle \sum _{j=1}^M{L}_{ij}}\frac{\partial I_j^{}}{\partial t}\left(x,t\right)+V_i^g\left(x,t\right)=e_{inc,x,i}\left(x,t\right)\\ \frac{\partial I_i^s}{\partial x}\left(x,t\right)+{\displaystyle \sum _{j=1}^M{C}_{ij}}\frac{\partial V_j^s}{\partial t}\left(x,t\right)=0\end{array}\right..$$

(57)

The expression of $V_i^g\left(x,t\right)$ can be obtained as follows:

$$V_i^g\left(x,t\right)={\displaystyle {\int }_0^t{\xi }_g^i\left(t-s\right)\frac{\partial I_i\left(x,s\right)}{\partial s}}\left(x,s\right)ds,$$

(58)

with ${\xi }_g^i$ being the time-domain expression of the ground impedance [66].

The solution of Equation (57) can be obtained by discretizing the line in N segments and solving the system by means of a second-order FDTD solution, where the time step and the space step have to satisfy the well-known Courant stability condition, as proposed in [67].

From Equation (57) it is clear that the radial component of the electric field should be computed at every point of the overhead line, thus leading to a huge computational effort, which can be drastically reduced if one of the previously mentioned methods is used.

6. Discussion

The reduction in the computational effort for the evaluation of lightning EM fields can be achieved by means of several approaches. The great advantage of the methods proposed by Rusck [34] and by Rubinstein and Uman [35] is the possibility of obtaining analytical formulas, which are extremely fast from a computational point of view. However, their expressions are evaluated by assuming a step channel-base current, which is quite far from reality, as the current front duration is an important factor. The possibility of including the front duration, while keeping the computational time as low as possible, has been achieved with the approaches proposed by Thottapillil [37] and Napolitano [36]. However, while the first relies on the assumption of lightning return stroke velocity equal to the speed of light, the second assumes a trapezoidal channel base current. Moreover, both approaches assume that the attenuation along the channel is neglected, i.e., they based their theory on the TL model. The latter hypothesis is also maintained in the approach proposed by Brignone in 2020 [38], which, however, can be generalized to allow for any CBC and any return stroke velocity. The most general approach has been proposed by Brignone in 2022 [41], where semi-analytical formulas for the EM fields have been provided without relying on any of the previous assumptions and by expanding the integral kernels by means of the Prony series.

7. Conclusions

The paper proposed a survey on the main methods for lightning electromagnetic field evaluation. First, the classical expressions of such fields were presented both in the time and frequency domains, by assuming a vertical lightning channel and a PEC ground. The proposed expressions are valid insofar as the current propagation along the channel can be described by the TL models, which basically express the current on a certain position along the channel as the current at the base, attenuated according to a proper function and delayed according to the traveling time necessary for reaching the desired position along the channel. Then, we thoroughly analyzed the most common formulations developed to reduce the computational effort entailed by the exact formulas: the main assumptions necessary for providing approximate formulations are based on neglecting the channel-base current waveform, the current propagation, the return stroke velocity, or the current attenuation along the channel. The effect of ground conductivity was investigated by highlighting that it mostly affects the radial component of the electric field and providing a sketch of the most important formulas that “correct” the PEC expression. Among them, the CR approximation is the most commonly used due to its easy implementation in the frequency domain. In the time domain, several approaches for reducing the computational effort exist; among them, this work presented the one based on the Prony series of the Cooray–Rubinstein kernel. Finally, the well-known Agrawal method for computing the lightning-induced voltages was presented and discussed. In the Appendix A, some mathematical notes on the frequency domain expressions of the lightning electric field (in the case of a PEC ground) were presented; in particular, both infinite and finite time windows were considered as durations of the measurements.