Abstract
The development of a machine-learning method with high accuracy, high generalization, and strong robustness for evaluating battery health states is essential in the field of battery health management. In this work, the data-driven stacking regressor (SR) method with a two-layer diagnostic framework was proposed to estimate the state of health (SOH) and predict the remaining useful life (RUL). Five individual estimators were merged in the first layer, including bagging, gradient boosting regression (GBR), support vector regression (SVR), Hist-GBR, and AdaBoost, and linear regression (LR) was used in the second layer to construct the SR model. The SR model produces highly accurate results without the requirement of excessive parameter adjustment. Fifteen batteries from the NASA dataset were used for our experiments, resulting in rather low values of average root mean square error (ARMSE) and relative error (RE) for the SOH estimation and RUL predictions of the different batteries, demonstrating the superiority of the SR model.
1. Introduction
Lithium-ion batteries (LIBs) have been widely applied as energy storage devices in many areas, such as portable consumer electronics, electric vehicles, energy storage power-station, etc., because of their high energy and power density, low self-discharge rate, and long life cycle [1,2,3]. However, it is well-known that the lifespan (especially the efficient service time) of LIBs is limited, and the performance of LIBs gradually degrades during usage, which is mainly because of inner complicated electrochemical reactions, including an increase in impedance, loss of active materials, growth of dendrites, inner short-circuits, etc. [4,5]. Battery aging is usually determined by an increase in internal resistance (IR) [6] or a decrease in capacity, where the IR increasing to twice of the initial resistance or a decrease in capacity to 80% of the initial capacity is usually defined as the end-of-life (EOL) of the battery. The degraded traction batteries usually have to be taken out of service when the capacity drops to the threshold [7,8]; otherwise, the aging of LIBs would inevitably cause an increase in the usage cost and the probability of serious safety accidents. Furthermore, plenty of LIBs retired from electric vehicles need to be recycled for cascade utilization or element extraction. The safety and utilization of the surplus value of the retired LIBs are both highly dependent on the key technology of state of health (SOH) [9,10] estimation and remaining useful life (RUL) [11] prediction.
As important indicators for predicting battery states, SOH and RUL have been extensively studied [12]. The estimation accuracy of SOH also directly affects the RUL prediction. In principle, the SOH represents the battery aging degree using the relevant parameters measured during cycling, such as capacity or resistance; the RUL is defined as the number of cycles where the battery capacity first deteriorates to the failure threshold [13].
There are many technologies for the prognostics and health management (PHM) of batteries, and they can be classified into two categories: experimental analysis methods and model-based approaches. The experimental analysis methods calibrate the SOH by measuring the characteristic parameters during battery cycling: current, voltage, IR, temperature, etc. Nevertheless, the limited accuracy and harsh application conditions of these methods make it difficult to achieve an online prediction of the battery states. The model-based approaches can be further divided into adaptive algorithms and data-driven based methods. Adaptive algorithms identify parameters to estimate the SOH based on the electrochemical model or equivalent circuit model (ECM) [14]; however, there is currently no adaptive algorithm available to accurately describe the aging mechanism and estimate the SOH of the battery due to the complex electrochemical reactions and non-linear degradation within the battery.
Different from other technologies, the data-driven methods do not rely on the complex mathematical or electrochemical models but alternatively focus on the historical aging data of batteries, estimating the battery states by employing specific learning algorithms. Machine learning and deep learning techniques have been extensively employed for estimating battery SOHs and RULs. Hu et al. [15] have achieved high accuracy and strong robustness using the jointed sample entropy (SE) [16] and sparse Bayesian predictive modeling (SBPM) method for the first time to prognosticate the battery health state, which was based on the aging data at different temperatures. Meru et al. [17] employed the support vector machine (SVM) [18,19] method to predict the battery RUL and achieved an accurate estimation for multiple batteries simultaneously. Other available methods, such as the probabilistic neural network (PNN) [20], recurrent neural network (RNN) [21], particle filtering (PF) [22,23,24], extended Kalman filter (EKF) [25,26], adaptive EKF (AEKF) [27,28], support vector regression (SVR) [11], relevance vector machine (RVM) [29], principal component analysis (FCA), etc., have been widely used recently to prognosticate battery health state and investigate battery degradation behavior. Long short-term memory (LSTM) [30] has recently become a hot data-driven research method, as battery SOHs and RULs are truly time-series research problems. Yang et al. [31] employed the LSTM and unscented Kalman filter (UKF) methods for filtering out the noise to estimate the state-of-charge (SOC) of batteries, confirming that the proposed method could learn the influence of ambient temperature well and achieve low estimation errors at different temperatures. Furthermore, a variant of the long short-term memory neural network (namely AST-LSTM NN) proposed by Li et al. [32] reached high accuracy in SOH estimation with an average root mean square error (ARMSE) of 0.0216 and in RUL prediction with a conjunct error (CE) of 0.0831, respectively.
It is notable that many data-driven methods have to adjust many parameters to achieve the accuracy and stability for short-term prediction; however, the generalization of these methods is rather limited, possibly because they adopt a single estimator in each of their models. In this work, we attempted to integrate multiple deep-learning learners into a two-layer estimation framework. Specifically, various meta-learners were combined within the first layer to perform multiple deep learning processes of the input data simultaneously, effectively filtering the invalid information; sequentially, the generated data flow into the trainer in the secondary layer as inputs to be fitted again for the estimation of the battery states. Therefore, the accuracy of the battery SOH and RUL prediction and generalization ability of the model can be significantly improved.
2. Methodology
The stacking regressor (SR) [33] method was employed in this work to train a two-layer model, where five individual estimators selected from twenty candidates were merged in the first layer and the LR method was used in the second layer, as shown in Figure 1. The six meta-learners (bagging, GBR, SVR, Hist-GBR, AdaBoost, and LR) are described in the Supplementary Materials. The training set was divided into Z copies, in which Z-1 copies were used for training and the remaining copies were used for testing. The training process was carried out continuously until all samples were predicted by each basic model. After that, the results predicted in the first layer were used as the input of the second layer to obtain the final results of the SR model.
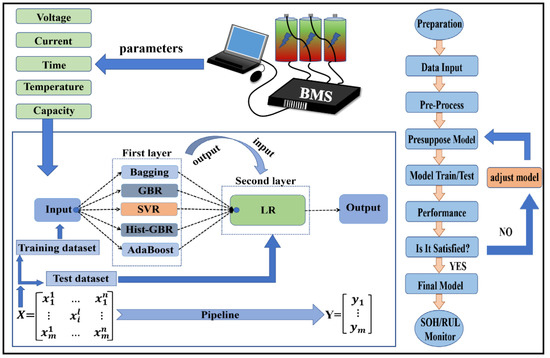
Figure 1.
The frame and workflow of the SR model. The estimators, including bagging, gradient boosting regression (GBR), support vector regression (SVR), Hist-GBR, and AdaBoost, were integrated into the first layer. The linear regression (LR) method was used in the second layer.
Moreover, K-folds can be added to meta-learners to ensure prediction accuracy with vast amounts of data. In the first layer of the SR, the training dataset was subdivided into K equal parts for each estimator to individually train. The five sets of average values predicted by the five learners were then added to the training set of the second layer. Simultaneously, each estimator in the learning layer also trains the test set. The average values of the generated five sets were transferred to the test set in the second layer. In the second layer, the LR algorithm fitted the obtained new datasets to generate the final prediction results. K-folds are friendly to various scale datasets by adjusting the value of K, and it adopts non-repetitive sampling to ensure adequate training, enabling the model to find the optimal parameters to achieve the generalization.
The stacking algorithm does not require many parameter adjustments and has currently become one of the most effective machine learning methods. It utilizes the benefits of multiple models to achieve the accurate prediction of the dataset, and it is also very flexible in meta-model selection. In this work, we applied the SR algorithm to deal with the NASA Prognostics Center of Excellence (PCoE) [34] battery datasets to validate our proposed methods. Upon the accurate estimation of the four lithium-ion batteries, the results demonstrate the superiority of the SR models in both SOH and RUL predictions.
3. Data Preprocess
This work mainly focuses on the efficiency, generalization, and robustness of the SR model prediction with respect to the SOH and RUL of fifteen batteries (four battery sample sets) from the NASA dataset, which were measured at different discharge policies and temperatures. The critical parameters of current, voltage, capacity, cycle numbers, and temperatures were collected to build and train our model.
As shown in Table S1, four sample sets were collected at three different temperatures (4 °C, 24 °C, and 43 °C), the charging process for all batteries was carried out at a constant current (CC) mode at 1.5A until the battery voltage reached 4.2 V, and then a constant voltage (CV) mode was performed until the charge current dropped to 20 mA. The discharge process was carried out at different policies until the voltage dropped to the cut-off value. When the capacity of the battery degraded to the threshold, the experiments were ended.
Figure S3 shows the degradation curves of the capacity with respect to the cycle numbers of the four sample sets of batteries. Obviously, the battery capacity degradation curves are different at various discharge policies and ambient temperatures; the capacity decreases overall with the increase in cycle numbers, but not in a monotone decline mode. The regeneration phenomenon occurring during the charging–discharging process manifests the non-linear degradation characteristics of the batteries, which is also the critical factor influencing the accuracy of the battery state estimation [35]. Therefore, developing a highly accurate and reliable data-driven method for battery state estimation based on the battery non-linear degradation characteristic is extremely necessary.
The SOH is the ratio of the immediate performances of battery to its initially standard values, which can be defined by a variety of indicators including IR, cycle number, capacity, etc. Here, we adopt the ratio of capacity to measure the battery’s SOH [36]:
where and denote the measured capacity at the moment and battery’s initial capacity, respectively. Here, EOL is defined as the point at which the capacity drops to 70% of its initial value (e.g., dropping from 2.0 Ahr to 1.4 Ahr):
Thus, the RUL is defined as the time or the cycle number at which the device’s performance first drops to the failure threshold. It can be written as:
where and denote the cycle number at EOL and moment , respectively.
Three indices were used to assess the performance of the proposed model in SOH and RUL estimation, i.e., the coefficient of determination (R2), the mean absolute error (MAE), and the root mean square error (RMSE), are given as follow:
where and denote the predicted and real values of SOH, respectively. represents the mean of test data.
A series of characteristic parameters from the raw dataset was extracted using MATLAB software. Taking battery #B0005 as an example, the curves in Figure S4 and S5 depict the parameters during the charge or discharge process, respectively. Figure S6 shows the variation in the average temperatures of the batteries with respect to the cycle numbers during the battery discharge. The battery temperatures measured at the room temperature condition fluctuate more dramatically with the increase in cycles than those measured at harsh environmental temperatures. It is worth noting that the temperature curves of batteries #B0041, #B0043, and #B0044 show a multiple ladder descent, which is likely related to their special discharge pattern, i.e., multiple fixed-load current levels. Furthermore, Pearson correlation coefficients (PCCs) were employed to eliminate a large amount of irrelevant or redundant information from the selected performance parameters. Note that the NASA dataset provides more than twenty parameters for batteries, but some parameters, including sense current, current ratio, time, current measured at charger, current in battery branch, voltage measured at load, etc., are not important and were directly removed. Furthermore, some parameters with incomplete data were also removed. Eventually, voltage, current, cycle number, and temperature were chosen as health indicators (HIs) to feed the SR model. The PCCs of the HIs were divided into five classes: no (0~0.2), weak (0.2~0.4), moderate (0.4~0.6), strong (0.6~0.8), and extremely strong (0.8~1) correlations, as shown in Table 1.

Table 1.
The PCCs of the different health indicators.
Obviously, the SOH and RUL are strongly correlated with voltage, current, and cycle time, but weakly with temperature. However, it is well-known that temperature is an important parameter of the battery. As shown in Figure S6, the battery temperature changes remarkably during the charging–discharging cycles. However, because we used the average temperatures in each cycle to calculate the PCC, it makes the correlation of the temperature with the RUL and SOH appear to be not as strong. We tried to use every single temperature during the cycles to calculate the PCC, resulting in the much higher values. Furthermore, it should be mentioned that the battery SOH has an extremely high correlation with RUL with PCCs of 0.9117. Thus, it is reliable to use the same methods and parameters to estimate both the SOH and RUL. In some cases, the SOH was even used as an input indicator of the model to measure the RUL due to their projecting relationships [37].
4. Results and Discussion
4.1. SOH Estimation
The degradation data of fifteen batteries from the NASA dataset repository were used to estimate the SOH and RUL. At the beginning, the order of the dataset of each battery was disrupted to avoid overfitting. After that, the dataset was divided into training and test subsets in different proportions, as listed in Table 2 and 3. The vectors of the nth battery, including the voltage (), current (, cycle number , and temperature (, were used as the initial inputs of the model to estimate the SOH.

Table 2.
The values of the MAE, RMSE, and ARMSE of the SOH estimation using the SR model on batteries discharged at 2A and 4A, respectively. The temperature was 24 °C.
Different proportions of historical discharge data from sample sets 1 and 3 were used to train the SR model to estimate the SOH. Table 2 presents the performance of the SR model on the estimation of the battery SOH under various discharge policies at room temperature (24 °C). For batteries discharging at 2A and 4A, the errors of the ARMSE are in the range of 0.0077–0.0156 and 0.0355–0.0784, respectively. Consistently, the values of the MAE are in the range of 0.0040–0.0115 and 0.0171–0.0316, respectively. In general, the SR model performs worse for the estimation of batteries discharged at 4 A than for those discharged at 2 A at the same temperature; nevertheless, the average MAE and RMSE are less than 0.04 and 0.08, respectively. To further explore the estimation performance of the SR model on batteries at extreme environmental temperatures, historical data from samples 2 (43 °C) and 4 (4 °C) were divided into the same scale as in Table 2 and used to train the SR model; the estimation results are shown in Table 3. The error of the ARMSE is in the range of 0.0042–0.0688 and 0.0065–0.1843 for samples 2 and 4, respectively, suggesting that the SR model has a relatively high MAE value for the estimation of the batteries’ SOH at lower temperatures. In addition, when comparing the estimation result of batteries under the same discharge policy but at different temperatures (i.e., batteries #29, #30, #31, and #32 vs. #33 and #34), the estimation error of ARMSE at 43 °C is slightly smaller than that at 24 °C. Furthermore, the prediction accuracy of the SOH generally increases with the increase in the ratio of the training set to the test set.

Table 3.
The values of the MAE, RMSE, and ARMSE of the SOH estimation using the SR model on batteries discharged at different currents and temperatures (43 °C and 4 °C).
The high accuracy of the estimation of the four sample sets demonstrates the robustness of the SR model. The PCCs between the true and predicted values with the different proportion of training sets were further calculated to be higher than 99% for all batteries, indicating an extremely strong correlation relationship between the predicted results and the real values. The results also confirm the great validity, high accuracy, and strong robustness of the SR model.
To intuitively illustrate the fitting efficiency, we took sample set 1 as an example to discuss the degradation of batteries with respect to the temperature and cycles. The prediction performances of the SOH using 20% historical data as the training set for four batteries were visualized in Figure 2. Obviously, the overall degradation trends are consistent, although the predicted degradation curve deviates around the real SOH values with negligible fluctuation. For battery #18, because less data (26 cycle number) can be fed into SR model to estimate the SOH, the accuracy at the early stage of the prediction is a slightly larger error.
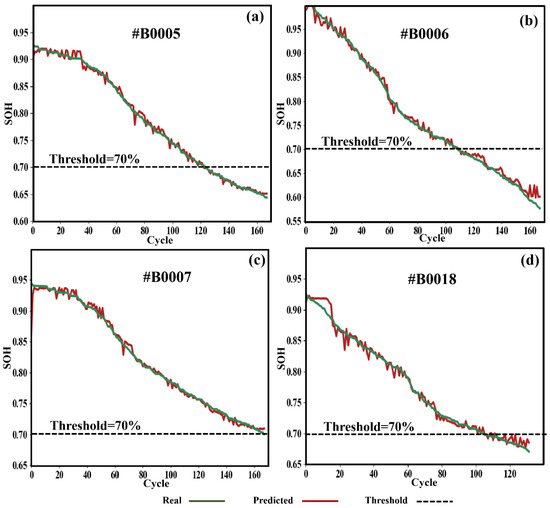
Figure 2.
The real and estimated SOH of batteries #5 (a), #6 (b), #7 (c), and #18 (d), discharged at 2A and 24 °C, respectively.
Furthermore, the performances of the SR model and individual estimators on the SOH prediction of the four batteries were compared in Table 4 with 20% of the historical data being used as training sets. The experimental results show that the R2 of the SR model for batteries #5, #6, #7, and #18 are 0.99, 0.98, 0.99, and 0.97, respectively, which demonstrates its good fitting performance. Although taking a little bit more time than other single predictors for predicting the SOH of different batteries, the SR model exhibits higher estimation accuracy and more excellent generalization. Sequentially, we also performed the SOH prediction with a higher proportion of the training set, where the results further evidence that the SR model has greater precision than other predictors; all predictors show an increasing accuracy of SOH estimation with the increase in the size of the training set.

Table 4.
The prediction performance of the single predictor and SR models for batteries #5, #6, #7, and #18, respectively.
In order to further demonstrate the superiority of our SR model, 30% of the datasets were used for training, and the same was performed with the other data-driven methods, including the RNN, LSTM, SVR, RVM, GPR, and AST-LSTM models. The values of the RMSEs are listed in Table 5 to compare the performances of the models. The AST-LSTM model yields the smallest value of RMSE for battery #5 at 0.0038, whereas our SR model yields the lowest errors of 0.0068, 0.0080, and 0.0070 for batteries #6, #7, and #18, respectively. Furthermore, our RMSEs of the four batteries are quite close to each other (0.0063–0.0080). However, the values generated by the other algorithm varies a lot. As listed in Table 5, the RMSE of B0005 is remarkably lower than the values of the other three batteries as predicted by the AST-LSTM model. The RMSEs of the four batteries as generated by other algorithms are in a wide range, and some of values are quite large. The smallest ARMSE value of 0.0070 generated by our model suggests that SR has the best robustness and generalization ability for SOH estimation.

Table 5.
The RMSEs and ARMSEs of the SOH estimation using different methods with 30% historical data.
4.2. RUL Prediction
The stacking method was then employed for the RUL prediction, which is strongly correlated with SOH estimation; we still used sample set 1 for interpretation. At different predicting points, we predicted the RUL values of four batteries (#5, #6, #7, and #18) and compared the SR performance with the results from other data-driven methods. As mentioned above, the battery RUL reaches zero when the capacity drops to EOL. The error (E), relative error (RE), and average absolute error (AAE) were used to evaluate the performance of the different methods. The parameters were defined as:
where and denote the actual and predicted values, respectively. represents the absolute error (AE) of the th prediction.
A comparison of the prediction efficiency of the SR model with that of the other methods for battery #5 is presented in Table 6. In general, the PA-LSTM, RVM, AST-LSTM-II, and SR models exhibit excellent prediction capability using the variable predicting points. It is worth noting that our SR model generates the lowest errors of −1 and 0 with the predicting points at the 50th and 70th cycles, respectively, whereas the model presents a slightly larger error of −5 when predicting using the 90th cycle as the predicting point. The small ARMSE and AAE values evidence the high accuracy of the SR model for the RUL prediction.

Table 6.
The errors generated by several methods for the RUL prediction of battery #B0005 with different predicting (Pred.) points.
The errors of the RUL prediction using the SR model for batteries #5, #6, #7, and #18 are presented in their entirety in Table 7. Because the available cycle numbers of the batteries are different, we tried to predict the RUL at different predicting points in the range of the 30–150th cycles. Interestingly, the prediction errors are rather low at the predicting points of the 30–70th cycles. Obviously, the RSME errors of the RUL prediction generally decrease with the increase in the number of prediction points. Specifically, when using the 70th, 70th, and 50th cycles (both around 40% historical data) as the predicting points for batteries # 5, #6 and #18, respectively, the SR model generates no error. The results are interesting. As we all know, the outcomes generated by machine learning are relatively weak in terms of interpretability. We assume that it might be because the training volumes at these points are at about exactly 40% of the historical data, which might be the best training volume for the SR model. Inadequate or excessive training data will cause the underfitting or overfitting of the model and reduce the accuracy. As for battery #7, slightly higher E values of 3 and 5 were generated at the 90th and 150th prediction points, respectively, while E values of 1 were obtained at other points. The small ARMSE, AAE, and RE values suggest the strong robustness and excellent generalization ability of the SR model for the RUL prediction.

Table 7.
The errors of the RUL prediction of batteries #5, #6, #7, and #18 at different predicting (Pred.) points with the SR model.
The general trends of the RUL estimation with the SR model were visualized and compared with the real degradation of batteries #5, #6, #7, and #18 in Figure 3. We utilized 20%, 30%, 30%, and 30% of the historical data (corresponding to the cycle numbers of 33, 50, 50, and 40) as the training sets for batteries #5, #6, #7, and #18, respectively, which was used for the RUL prediction. In general, the predicted RUL results match well with the real values. The accuracy of the RUL prediction at almost all of the predicting points of battery #5 is higher than 95%, as marked with the yellow dash lines in Figure 3a, and very few points are beyond the boundary, leading the AEE value to be lower than 0.05. The accuracy of the RUL prediction in batteries #6, #7, and #18 is slightly worse. As shown in Figure 3b–d, the majority of the results appears within the boundary of yellow lines, and several abnormal fluctuations of the predicted RUL reach the blue dash lines (with the accuracy of 90%), but the curve quickly returns to the high accurate prediction range.
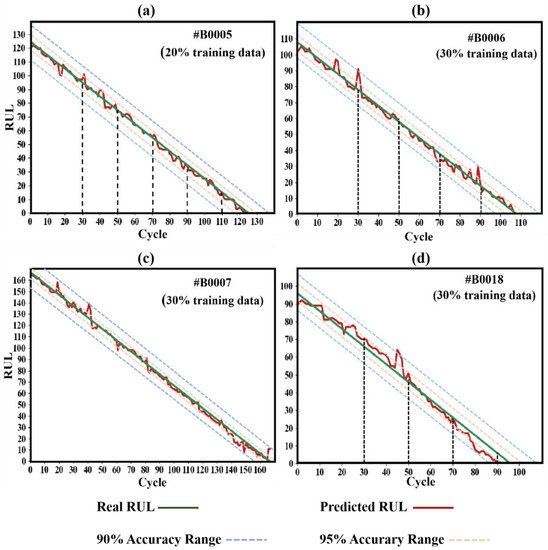
Figure 3.
The SR model of the predicted and real RUL of batteries #5 (a), #6 (b), #7 (c), and #18 (d), discharged at 2A and 24 °C, respectively.
In order to explore the potential application of our model in the online estimation of the battery states, the dynamic stacking regressor (DSR) method was employed to predict the SOH. A starting point and a moving step with fixed size is the requirement of the DSR model. The cycles before the starting point were disordered and used as the training set. With the continuous addition of new cycles to the training set, the DSR model carried out the multi-step-ahead prediction until the batteries reached the EOL. The starting point of 30 cycles, failure threshold of 1.4 Ahr, and sliding size of 5 steps were set for the RUL prediction performed with DSR model on the batteries #5, #6, #7, and #18. A comparison of the predicted results with the real capacity trajectories is shown in Figure 4. In general, the predicted degradation trends fit well with the real decay of the capacities, and the estimated RUL for batteries #5, #6, and #18 are 131, 112, and 99 (the real RULs are 125, 108, and 96), respectively. The generated RE values are 0.048, 0.037, and 0.031, respectively, and the AAE is 0.038, suggesting the high accuracy of the DSR method. Additionally, neither the predicted RUL nor the real RUL of battery #7 drops to 0 after 168 cycles, as the capacity has not degraded to 1.40 Ahr yet. Note that the outstanding peaks on the predicted curves and real trajectories match well in Figure 4, indicating the excellent prediction capability of the DSR model in the locations of abnormal capacity changes. Therefore, it is reasonable to assume that the DSR model can be potentially applied to early safety warning before battery accidents.
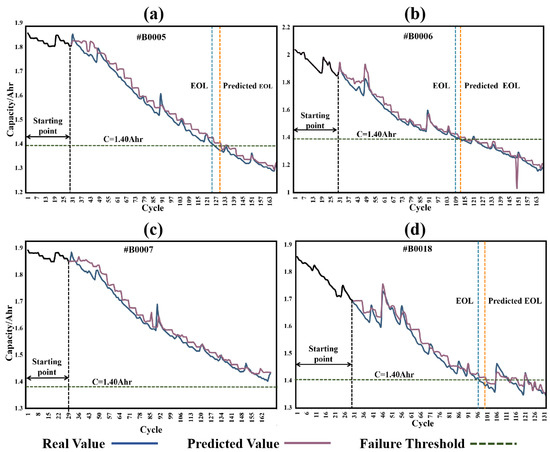
Figure 4.
The DSR model’s predicted results and real decay trajectories with the increase in cycles for batteries #5 (a), #6 (b), #7 (c), and #18 (d), discharged at 2A and 24 °C, respectively.
5. Conclusions
To improve the data-driven method for the evaluation of the battery states, this work proposed the SR model with a two-layer prognostic framework to predict the SOH and RUL. The SR model consists of six individual estimators, of which bagging, GBR, SVR, Hist-GBR, and AdaBoost were merged in the first layer and LR was used in the second layer. With the integration of the advantages of the different regressors, the SR model guarantees the high performance of the SOH and RUL estimation without too many parameter adjustments.
The low errors for the estimation of fifteen batteries at different discharge policies demonstrate the excellent robustness and generalization ability of the SR model. The high values compared with those of the five meta-predictors confirm the high reliability of the SR model in battery state estimation. Furthermore, the low errors occurring in the states estimation with the NASA dataset demonstrate that the SR model hits excellent SOH estimation (ARMSE of 0.0070) while using only 30% of the historical data, as well as better RUL prediction (AAE of 2 and ARMSE of 0.0173). We believe that the accuracy, robustness, and generalization of the algorithm can be improved if we continue to train this model, which could be further applied to evaluate the health states of other ion batteries.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/en16052313/s1, The algorithms used in this work. Figure S1: The prognostic framework of meta-learner: Bagging; Figure S2: The prognostic framework of meta-learners: GBR(a), SVR(b), AdaBoost(c) and LR(d); Figure S3: Discharge capacity deterioration curves of sample sets 1(a), 2(b), 3(c) and 4(d), respectively; Figure S4: The variation of charge voltage (a) and current (b) of battery #5, respectively. Figure S5: The variation of discharge voltage (a) and current (b) of battery #5, respectively; Figure S6: The variation of temperatures during discharge process of sample sets 1(a), 2(b), 3(c) and 4(d), respectively. Ambient temperatures are 24 °C, 43 °C, 24 °C and 4 °C, respectively. Table S1: The experimental strategy of the four sample sets (15 batteries). References [42,43,44,45,46,47,48,49,50,51,52,53] are cited in supplementary materials.
Author Contributions
Methodology, Z.Q. and B.L.; Validation, S.L.; Investigation, J.Y., H.H., X.G. and S.L.; Resources, B.L.; Data curation, H.H. and S.L.; Writing—original draft, J.Y., Z.Q., H.H., X.G., S.L. and B.L.; Supervision, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (11874005), the Key R&D Projects of the Science and Technology Department of Sichuan Province (2021YFG0070), and the Startup Funds of Yangtze Delta Region Institute (Huzhou), UESTC (U03210019).
Data Availability Statement
NASA Data Sources: https://www.nasa.gov/content/prognostics-center-of-excellence accessed on 16 July 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Song, L.; Liang, T.; Lu, L.; Ouyang, M. Lithium-ion battery pack equalization based on charging voltage curves. Int. J. Electr. Power 2020, 115, 105516. [Google Scholar] [CrossRef]
- Cao, W.; Wang, S.; Fernandez, C.; Zou, C.; Yu, C.; Li, X. A novel adaptive state of charge estimation method of full life cycling lithium-ion batteries based on the multiple parameter optimization. Energy Sci. Eng. 2019, 7, 1544–1556. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, K.; Che, Y.; Lin, X.; Jin, G.; Liu, B. A Practical and Comprehensive Evaluation Method for Series-Connected Battery Pack Models. IEEE Trans. Transp. Electrif. 2020, 6, 391–416. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energ. Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Liu, H.; Chen, F.; Tong, Y.; Wang, Z.; Yu, X.; Huang, R. Impacts of Driving Conditions on EV Battery Pack Life Cycle. World Electr. Veh. J. 2020, 11, 17. [Google Scholar] [CrossRef]
- White, C.; Thompson, B.; Swan, L.G. Comparative performance study of electric vehicle batteries repurposed for electricity grid energy arbitrage. Appl. Energy 2021, 288, 116637. [Google Scholar] [CrossRef]
- Shahriari, M.; Farrokhi, M. Online State-of-Health Estimation of VRLA Batteries Using State of Charge. IEEE Trans. Ind. Electron. 2013, 60, 191–202. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K.; Chen, G.; Liu, B.; He, Z.; Gao, F. A fast estimation algorithm for lithium-ion battery state of health. J. Power Sources 2018, 396, 453–458. [Google Scholar] [CrossRef]
- Dong, H.; Jin, X.; Lou, Y.; Wang, C. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter. J. Power Sources 2014, 271, 114–123. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining Useful Life Prediction and State of Health Diagnosis for Lithium-Ion Batteries Using Particle Filter and Support Vector Regression. IEEE Trans. Ind. Electron. 2018, 65, 5634–5643. [Google Scholar] [CrossRef]
- Ng, S.; Xing, Y.; Tsui, K. A naive Bayes model for robust remaining useful life prediction of lithium-ion battery. Appl. Energy 2014, 118, 114–123. [Google Scholar] [CrossRef]
- Ng, M.-F.; Zhao, J.; Yan, Q.; Conduit, G.; Seh, Z. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery Health Prognosis for Electric Vehicles Using Sample Entropy and Sparse Bayesian Predictive Modeling. IEEE Trans. Ind. Electron. 2016, 63, 2645–2656. [Google Scholar] [CrossRef]
- Widodo, A.; Shim, M.-C.; Caesarendra, W.; Yang, B.-S. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Patil, M.; Tagade, P.; Hariharan, K.; Kolake, S.; Song, T.; Yeo, T.; Doo, S. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Fei, Z.; Yang, F.; Tsui, K.-L.; Li, L.; Zhang, Z. Early prediction of battery lifetime via a machine learning based framework. Energy 2021, 225, 120205. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, G.; Lin, M.; Wu, J.; Zheng, G. A Novel Estimation Method for the State of Health of Lithium-Ion Battery Using Prior Knowledge-Based Neural Network and Markov Chain. IEEE Trans. Ind. Electron. 2019, 66, 7706–7716. [Google Scholar] [CrossRef]
- Liu, J.; Saxena, A.; Goebel, K.; Saha, B.; Wang, W. An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries. In Proceedings of the Annual Conference of the Prognostics and Health Management Society 2010, NASA Moffett Field CA ARC, Oregon, Portland, 10–16 October 2010; Available online: https://apps.dtic.mil/sti/citations/ADA562707 (accessed on 10 October 2010).
- Dong, G.; Chen, Z.; Wei, J.; Ling, Q. Battery Health Prognosis Using Brownian Motion Modeling and Particle Filtering. IEEE Trans. Ind. Electron. 2018, 65, 8646–8655. [Google Scholar] [CrossRef]
- Dalal, M.; Ma, J.; He, D. Lithium-ion battery life prognostic health management system using particle filtering framework. J. Risk Reliab. 2011, 225, 81–90. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Modeling Li-ion battery capacity depletion in a particle filtering framework. Annu. Conf. PHM Soc. Mar. 2021, 1, 1–10. [Google Scholar]
- Charkhgard, M.; Farrokhi, M. State-of-Charge Estimation for Lithium-Ion Batteries Using Neural Networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Kim, J.; Cho, B.-H. State-of-charge estimation and state-of-health prediction of a Li-ion degraded battery based on an EKF combined with a per-unit system. IEEE Trans. Veh. Technol. 2011, 60, 4249–4260. [Google Scholar] [CrossRef]
- Hongwen, H.; Rui, X.; Xiaowei, Z.; Fengchun, S.; JinXin, F. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, G.; Liu, Y.; Zhang, B.; Hu, C. Lithium-ion battery remaining useful life prediction with deep belief network and relevance vector machine. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 7–13. [Google Scholar]
- He, Z.; Shen, X.; Sun, Y.; Zhao, S.; Fan, B.; Pan, C. State-of-health estimation based on real data of electric vehicles concerning user behavior. J. Energy Storage 2021, 41, 102867. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-charge estimation of lithium-ion batteries using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Xiong, Q.; Ding, B.; Hou, J.; Luo, D.; Rong, Y.; Li, S. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network. J. Power Sources 2020, 459, 228069. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Saha, K.G.B. Battery Data Set, NASA Ames Prognostics Data Repository 2007. Available online: http://ti.arc.nasa.gov/project/prognostic-datarepository (accessed on 10 October 2007).
- Olivares, B.; Munoz, M.; Orchard, M.; Silva, J.F. Particle-filtering-based prognosis framework for energy storage devices with a statistical characterization of state-of-health regeneration phenomena. IEEE Trans. Instrum. Meas. 2012, 62, 364–376. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Qu, J.; Liu, F.; Ma, Y.; Fan, J. A Neural-Network-Based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 2019, 7, 87178–87191. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, J.; Pan, D.; Peng, Y.; Peng, X. Lithium-ion battery remaining useful life estimation with an optimized Relevance Vector Machine algorithm with incremental learning. Measurement 2015, 63, 143–151. [Google Scholar] [CrossRef]
- Bühlmann, P.; Yu, B. Analyzing bagging. Ann. Stat. 2002, 30, 927–961. [Google Scholar] [CrossRef]
- Chandran, V.; Patil, C.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of charge estimation of lithium-ion battery for electric vehicles using machine learning algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Xu, F.; Huang, Z.; Tsui, K.-L. Lifespan prediction of lithium-ion batteries based on various extracted features and gradient boosting regression tree model. J. Power Sources 2020, 476, 228654. [Google Scholar] [CrossRef]
- Prettenhofer, P.; Louppe, G. Gradient boosted regression trees in scikit-learn. In Proceedings of the PyData 2014, London, UK, 21–23 February 2014. [Google Scholar]
- Guryanov, A. Histogram-based algorithm for building gradient boosting ensembles of piecewise linear decision trees. In AIST 2019: Analysis of Images, Social Networks and Texts; Springer International Publishing: New York, NY, USA, 2019; pp. 39–50. [Google Scholar]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springer: Cham, Switzerland, 2015; pp. 67–80. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Shi, Q.; Zhang, C.; Cui, N. Estimation of battery state-of-charge using ν-support vector regression algorithm. Int. J. Auto Technol. 2008, 9, 759–764. [Google Scholar] [CrossRef]
- Solomatine, D.; Shrestha, D. AdaBoost. RT: A boosting algorithm for regression problems. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 1163–1168. [Google Scholar]
- Zhu, X.; Zhang, P.; Xie, M. A Joint Long Short-Term Memory and AdaBoost regression approach with application to remaining useful life estimation. Measurement 2021, 170, 108707. [Google Scholar] [CrossRef]
- Vilsen, S.; Stroe, D.-I. Battery state-of-health modelling by multiple linear regression. J. Clean. Prod. 2021, 290, 125700. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.-Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
