1. Introduction
The rising demand for electrical energy and the crises of conventional energy sources such as coal, oil, and so on [
1] requires a solution. Thus, in the global energy competition, renewable energy sources (RESs) (wind, solar, geothermal, and so on) garner a lot of attention. Solar energy is seen as a possible source of energy among these RESs. Despite the unavailability of sunshine throughout the year, solar energy has various advantages, such as ease of installation, low maintenance requirements, lack of pollution, and so on. The photovoltaic (PV) system has two significant disadvantages: high deployment costs and low efficiency.
Increased demand for PV generation for home and industrial power demands necessitates the optimization of solar power generation to improve system efficiency [
1].
This reduces the need for a PV panel for a given load, lowering the overall cost. At the moment, PV technology is being developed specifically in two directions: (i) PV cell material and (ii) power converters, with the goal of improving total conversion efficiency. Despite advancements in PV cell materials, PV conversion efficiency is still poor, resulting in expensive system costs. As a result, power converters play an important role in improving overall performance and lowering expenses. PV arrays have nonlinear current voltage (I-V) and power voltage (P-V) characteristics, and their power production varies depending on the climatic circumstances. P-V characteristics have a maximum power point (MPP) [
2]. MPP evolves when the climate changes. As a result, it is required to monitor the MPP under various environmental circumstances, a procedure known as maximum power point tracking (MPPT). The superiority of MPPT approaches is often determined by their complexity, speed, precision, and other factors. Currently, virtually all MPPT approaches function efficiently when the PV array is exposed to uniform sunshine. However, their efficiency suffers when the PV array is subjected to partial shade situations (PSCs). Under these conditions, the PV curve contains several local picks (LP), whereas to discover a global maximum power point under PSC, an effective and efficient MPPT method is required (GMPP).
Solar water pumping reduces reliance on coal-, gas-, or diesel-based electricity. Water pumping systems that run on diesel or propane not only consume expensive fuels, but also produce noise and air pollution. Solar pumping systems do not use fuel, need little maintenance, and are environmentally benign. In the literature, a number of solar pumping structures have been suggested [
3,
4,
5]. The photovoltaic pumping system in standalone mode is examined in induction machine entraining centrifugal pumps. Additionally, the chop-cut to extract the most output power from the photovoltaic generator and battery for storage are employed.
One of the main alternative energy sources that can be used for satellites, motor drives, and metropolitan areas is solar energy. The most crucial component in the process of converting solar energy into electric energy is a photovoltaic module (PVM). In this conversion, it is required to run the photovoltaic (PV) energy conversion systems installed close to the maximum power point in order to improve the performance of the PV system. The PV array’s power and current in this system depend on the array’s terminal operating voltage. The tracking control of the maximum power point is a challenging problem since the maximum power operating point (MPPT) fluctuates with temperature and insolation levels.
By using approaches like constant voltage control, perturb and observe (P&O), incremental conductance, fuzzy logic, and neural networks, numerous studies have been conducted to improve PV. Because it is typically used for traffic light applications, the first technique is straightforward to apply [
6]. Fuzzy control and neural networks are further MPPT approaches [
7,
8,
9]. The best performance and lowest tracking time are, in fact, attributes of incremental conductance, which does not oscillate [
10,
11,
12,
13,
14,
15]. To implement MPPT, a DC-to-DC converter is required, which ensures the maximum power is sent from the PV module to the load by controlling the duty cycle and permits the distribution of the highest power if the load is altered [
6]. Additionally, the P&O technique was used in several works due to its straightforward feedback structure, a small number of observed parameters, and straightforward implementation. Peak power tracker operation is closely correlated with the regular increnation or decrenation of solar array voltage [
16,
17]. The aforementioned procedures have some limitations, such as high cost, difficulty, complexity, and instability [
18], despite their significance.
The motor pumping system is operated at the highest possible efficiency in this manuscript by tracking the maximum power point and using a nonlinear controller. When a DC motor pump is fed by a solar array through a DC–DC buck converter, the MPPT can be operated by adjusting the rotational speed of the motor. The tracking of the maximum power has the effect of boosting the DC motor speed and the associated centrifugal pump’s water discharge rate.
The hydraulic power is at its peak when the PV generator’s output power is determined by a certain circumstance.
In order to adjust the duty ratio so that the DC motor rotational speed stays constant at a reference maximum rotational speed, our method integrates the input–output linearizing control technique and the Lyapunov stability theory. Computer simulations were used to demonstrate the effectiveness of the PV generator, pumping system, and newly introduced nonlinear Lyapunov controller. The proposed controller is also contrasted with the system that is connected directly. Based on the outcomes of the simulation, our controller has the best overall performance.
There are five sections in the manuscript. We describe the system component modeling in
Section 2. The nonlinear approach to the control is then presented in
Section 3.
Section 4 provides examples of the simulation results. Finally,
Section 5 makes a few closing observations.
2. System Component Modelling
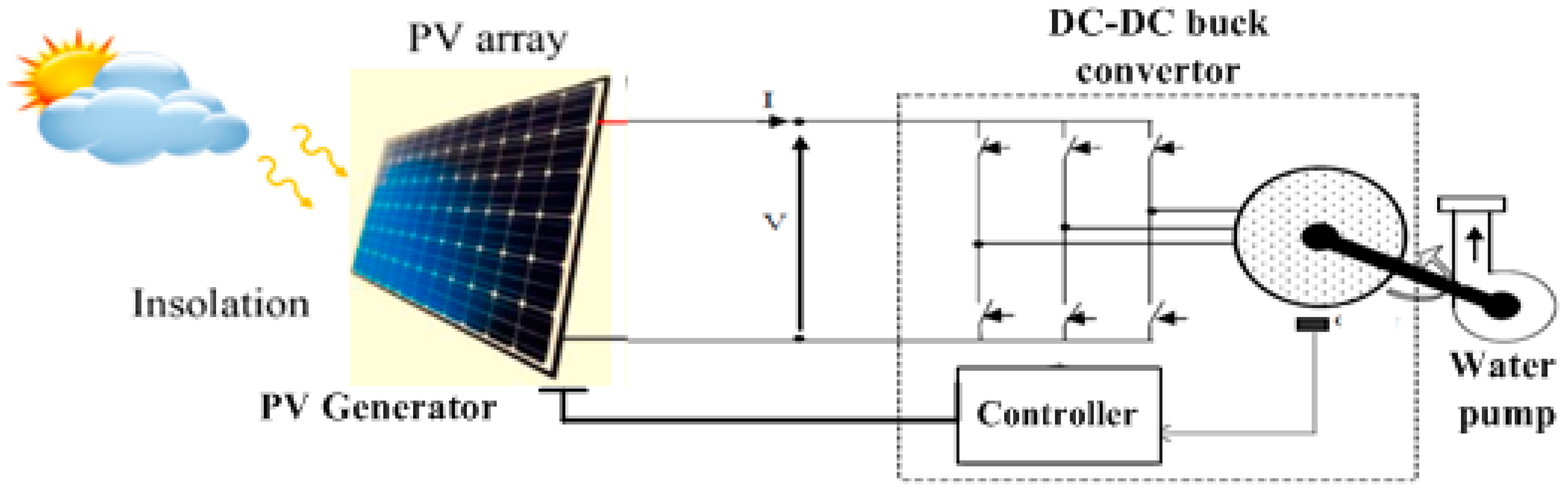
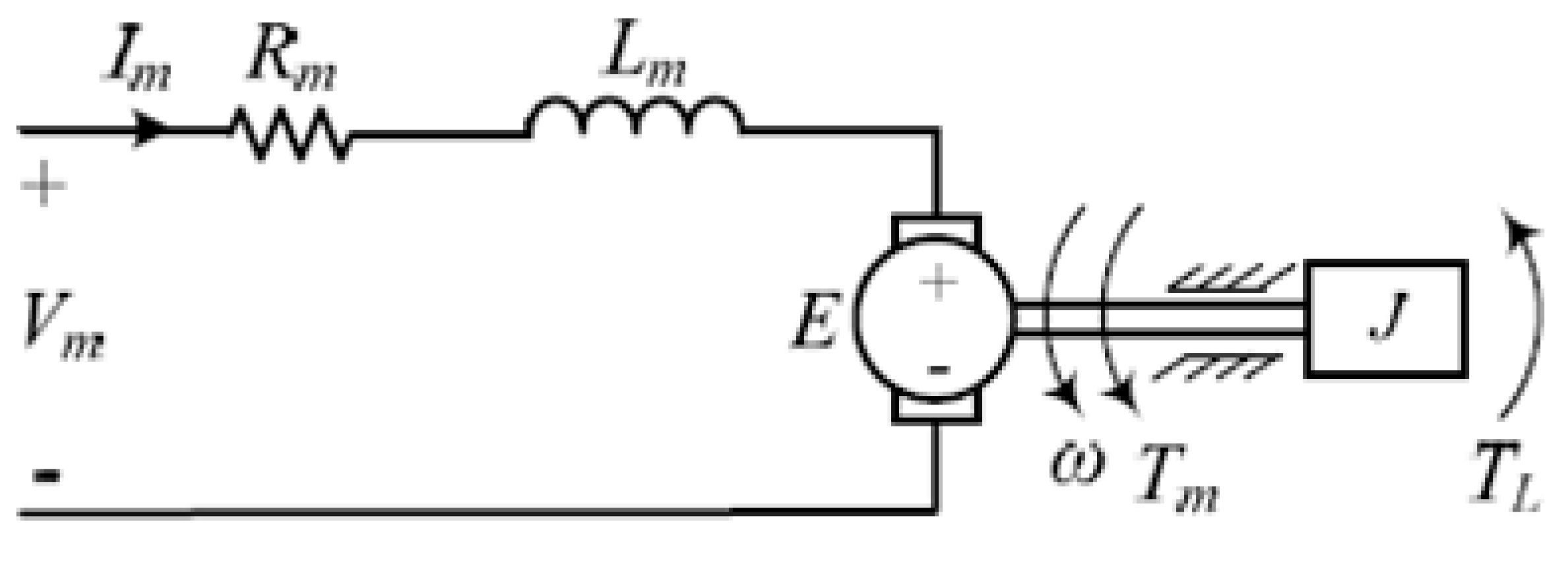
As shown in
Figure 1, the designed isolated generation system consists primarily of a centrifugal pump, a DC motor, and a PV generator connected to a buck converter. In the subsections that follow, we demonstrate how to create a comprehensive mathematical model for each device. Later, this model is used in simulation and controller design investigations.
2.1. PV Module
A PV array is a device that turns sunlight into electricity using two or more solar panels. Solar cells are connected together to form a PV array. A new form of sustainable green energy conversion has arisen using modern, efficient photovoltaic solar cells. In the suggested DVR, a DC supply for the DVR is provided by a PV array. Due to the variable nature of the solar power produced as a result of abrupt changes in weather that alter the solar irradiation level and cell operating temperature, the electrical system powered by a solar array requires a DC/DC converter. Solar arrays are constructed using solar cell combinations in parallel and series. A low step-up boost converter is incorporated into the PV array’s design and modeling to charge the batteries. The basic equations of photovoltaic cells, which take into account the effects of temperature variations and sun irradiation, are used to build the PV model. The photo current, which is primarily governed by load current dependent on the level of solar irradiation present during operation, determines the PV cell output voltage.
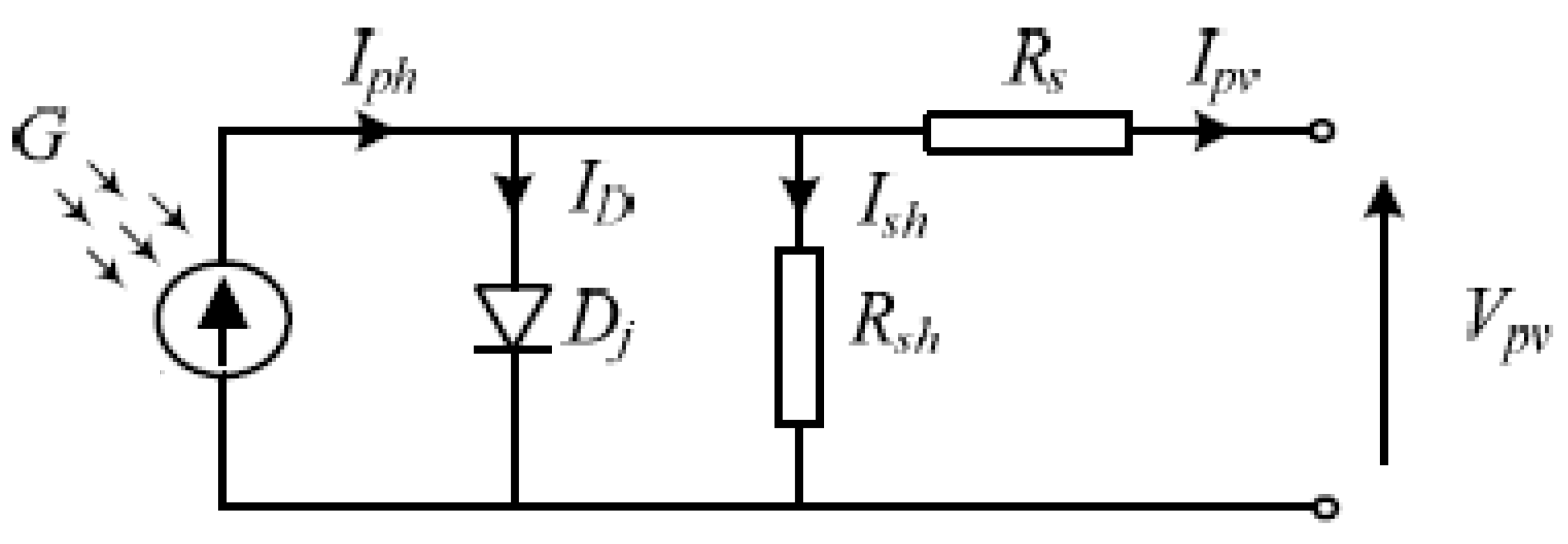
The equivalent circuit of a PV cell is shown in
Figure 2. The cell photocurrent is displayed by the current source and stand for the cell’s inherent shunt and series resistances, respectively. In general, its importance is minor compared to the value. Therefore, to make the analysis simpler, these two values may be disregarded.
PV modules, which are made up of several smaller units called PV cells, are connected to one another in a parallel-series arrangement to create PV arrays.
PV cells are grouped to create PV modules, which are bigger units. PV arrays are then created by connecting them in a parallel-series manner. Equations (1)–(4) are applied to produce the mathematical modeling of a solar panel [
19,
20].
The module photocurrent (
Iph) is given by
where
T indicates for the module operating temperature in Kelvin,
G stands for the solar insulation per unit (1.0 per unit), and
ISC stands for the short-circuit current at reference temperature
Tref and denotes the temperature coefficient of short-circuit current [
21,
22].
The module reverse saturation current
is given by
In Equation (2), stands for the output voltage of the PV module, is the electron charge, is the circuit ideality factor, K is the Boltzmann constant , and is the number of cells connected in series.
The module saturation current
changes as a function of the cell temperature provided by
where
stands for the band-
gap energy of the semiconductor utilized in the cell (1.1 eV) and
denotes an ideality factor.
The PV module current output is obtained as follows,
where
is the number of cells connected in parallel.
We use a 36 W PV module from Solar as the simulation reference, and information regarding the name-plate is shown in
Table 1 [
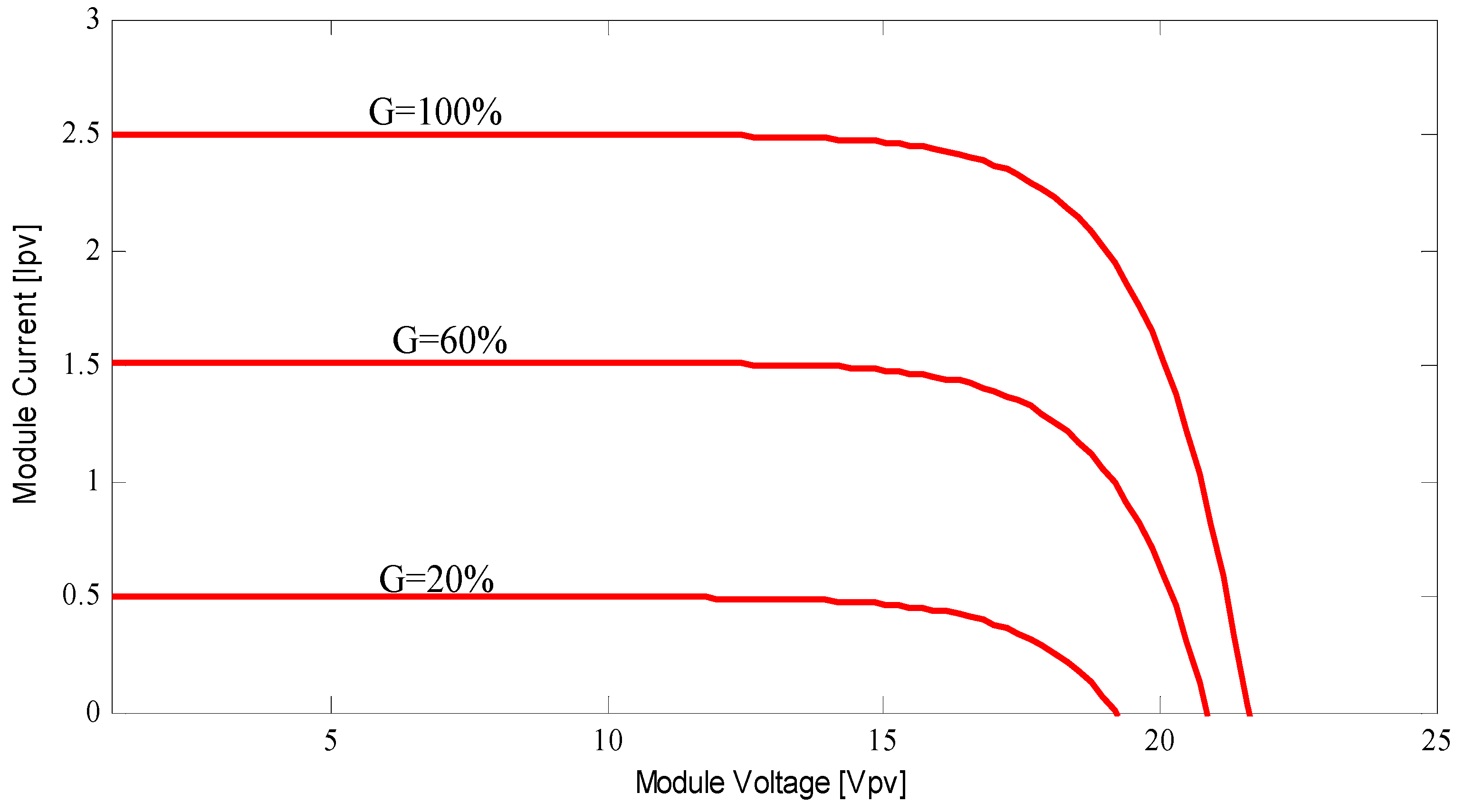
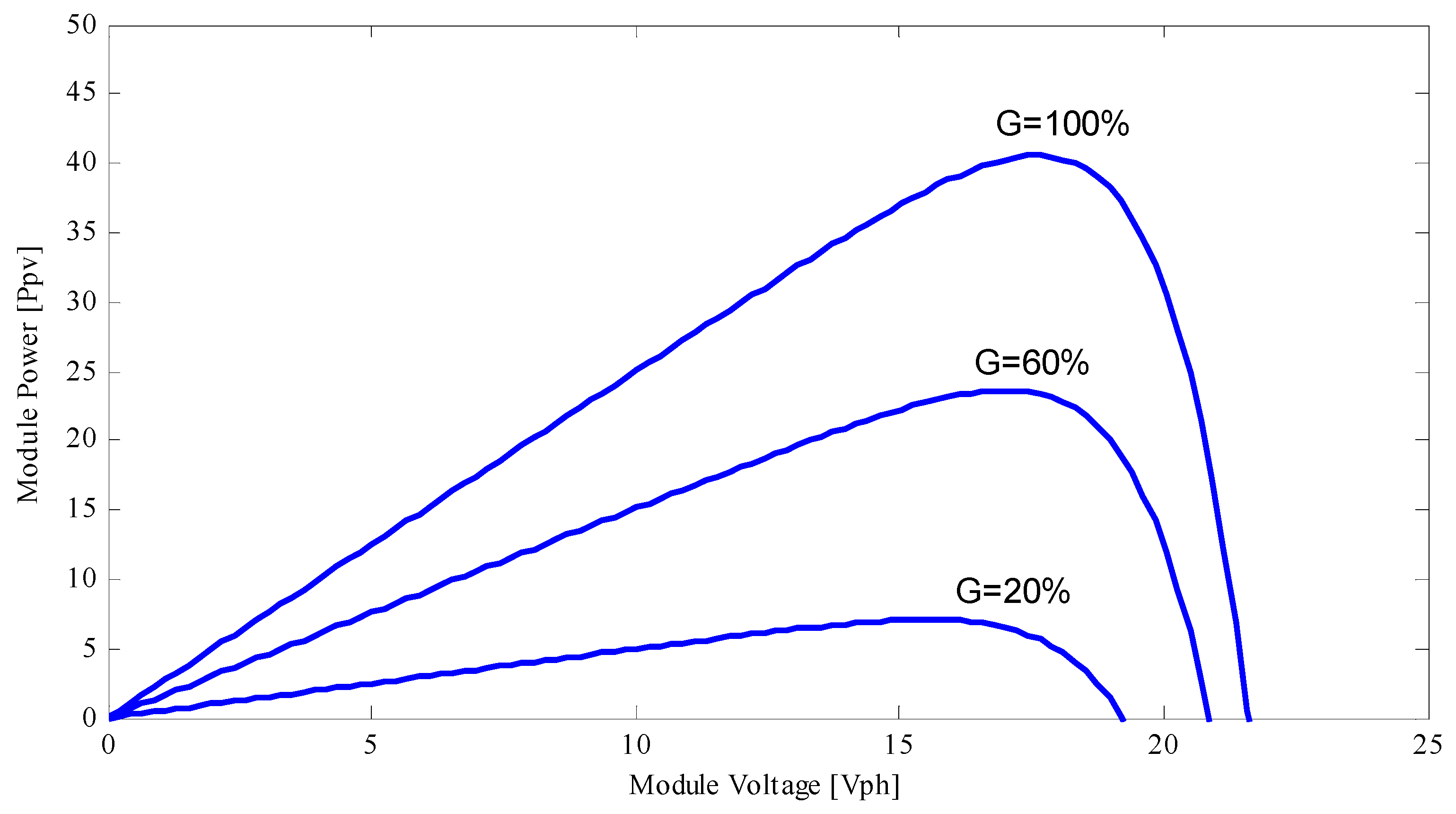
21]. The voltage-current and voltage-power characteristics of PV generators at five different
G values are shown, respectively, in
Figure 3 and
Figure 4. There is, of course, only one location at any given
G value where the PV generator power is at its maximum. We must first establish the corresponding maximum voltage
and the maximum current
in order to discover this maximum power point (MPP).
2.2. Buck Converter
A DC-DC converter is an electrical circuit used to change the level of a DC voltage source. Also, as the battery’s reserve of power is used up, its voltage drops. Instead of employing numerous batteries to achieve the same goal, switched DC-DC converters provide a way to raise voltage from a partially decreased battery voltage while also regulating the DC voltage.
Buck converter is installed in between the PV generator and the load. To push the PV generator to give the maximum amount of power to the load, the buck DC-DC converter controlled by MPPT tracking algorithm (duty cycle D) enables getting the voltage appropriate to the load. A microcontroller, a signal conditioning board, and a trigger circuit for the converter’s IGBTs make up the power converter’s control stage. The microcontroller software incorporates an algorithm that makes use of maximum power point tracking methods and adequate voltage modulation techniques for motor operation.
Two microcontroller timers and a lookup table with values for a half-cycle of the sine function stored in the memory are required to produce trigger pulses of various widths. The duty cycle of the IGBT is determined by each value in the table. The switching frequency is determined by the Timer 0’s base frequency, which was set to 7.8 kHz. Timer 1 reads the sinewave table to finish the count sequence before loading the value of the sine table (the transistor turn-on time). Timer 1 establishes the sinewave frequency, i.e., it chooses the frequency at which the sine table will be read.
The transistor driver circuit receives the microcontroller’s trigger pulses. The trigger circuit enables the semiconductor and microcontroller connection and supplies the 15 V power required to turn on the IGBT. The electrical separation between the control stage and the power stage is another benefit.
The buck converter is installed in between the PV generator and the load. To push the PV generator to give the maximum amount of power to the load, the buck DC–DC converter controlled by MPPT tracking algorithm (duty cycle D) enables one to get the voltage appropriate to the load.
Two components make up the buck converter: a free-wheeling diode and a power transistor. Through a PWM external driver circuit, the former is used as a switch that is regularly turned on or off. The calculation shown below calculates the average output voltage,
where
and
represent the output voltage (DC motor voltage) and input voltage (PV generator voltage) of the DC–DC converter, whereas
D designates the duty cycle
. It is clear from Equation (5) that the control of the output voltage can be performed by changing the chopper duty cycle
D through applying pulse width modulation (PWM) technique [
22,
23].
Suppose that power is loss less, the supply power (PV power) will be the same as the load power:
and
which shows that the converter can be considered as a DC transformer having modifiable turn ration
D.
2.3. DC Motor Model
The use of DC motors instead of AC motors in PV pumping systems has been the topic of past research, which has typically found that DC motors may be usefully operated when directly linked to PV generators where the total system cost and complexity are modest. However, the goal here is to increase PV system usage and give additional control flexibility by including a DC–DC power converter.
Previous studies on using DC motors in PV pumping systems instead of AC motors came to the general conclusion that DC motors can be operated effectively when connected directly to the PV generators when there is a need for a system with a low overall cost and complexity. For this application, a permanent magnet DC motor is suggested since it offers relatively efficient and low-maintenance operation and does not call for a separate field power source. Also, compared to other PV electro-mechanical systems, the PMDCM coupled with centrifugal pump has a low starting torque and can be reasonably readily matched with the output characteristics of the PV array. But, the purpose of this is to increase control flexibility and improve PV system utilization by adding a DC/DC power converter.
We choose permanent magnet DC motors for this application as they don’t require a separate field power source and offer rather efficient and low-maintenance operation. Additionally, the PMDCM connected to the centrifugal pump differs from conventional PV electromechanical systems in that it has a low beginning torque. In actuality, PMDCM may be rather easily matched to the PV array’s output characteristics [
24].
The corresponding circuit of the permanent magnet DC motor is shown in
Figure 5. The following set of differential equations gives the dynamics equation of the motor at constant flux:
In Equation (8),
denotes the applied voltage,
represents the armature winding resistance,
refers to the armature self-inductance,
stands for the motor armature current,
designates the back e.m.f. constant, and
shows the angular speed of the rotor. We have
where
represents the torque constant,
J refers to the moment of inertia,
denotes the viscous torque constant for rotational losses, and
C stands for the torque constant for rotational losses.
2.4. Pump
Although both the volumetric pump and the centrifugal pump are widely used in PV pumping systems, ref. [
25] discovered that the centrifugal pump uses much more PV generator energy than the volumetric pump because the centrifugal pump works for longer periods even at low insolation levels and its load characteristic is well matched to the PV generator’s maximum power locus. Furthermore, centrifugal pumps are economical, simple, need little maintenance, and come in a variety of flow rates and heads. As a result, a centrifugal pump is taken into account in this job.
In this study, we take into account centrifugal pump whose driving torque is relative to the square of the rotational speed as stated in [
25]. Therefore, we have
where
denotes the torque necessary to ensure the pump driving, and
represents the constant for a specific centrifugal pump.
3. System Controller
The PV voltage current (I-V) and voltage power (V-P) characteristic curves each have a unique point, as seen in (
Figure 3 and
Figure 4). The array’s maximum output power for each
G is produced at this location, known as the maximum power point (MPP).
The aim of the control is to track the maximum power, which slows down the DC motor speed and lowers the associated centrifugal pump’s water discharge rate. When a particular circumstance’s PV generator’s output power is at its maximum, the hydraulic power will be maximum. We have
As a result, at the maximum power point , the maximum rotational speed is reached. A controller is utilized to control the buck converter duty ratio, which adapts the PVG output power online in order to increase the rotational speed, taking into account the relationship between the PVG output power and the rotational speed.
The following stages provide the basis for applying the MPPT algorithm’s simple method.
Step 1: The insulation level is measured online by using a photo sensor.
Step 2: The computing of the reference maximum rotational speed for each insulation level value is done on line. Applying Equation (12), the relation between the solar radiation
G and the reference speed
is obtained:
Step 3: This step consists in measuring the real rotational speed from the PV generator and comparing it to the reference rotational speed .
Step 4: In this step, the control variable (duty cycle of the DC-DC converter) is determined so that the actual generated rotational speed from the PV generator will be able to track the reference rotational speed
employing the input–output feedback linearization [
26] and the Lyapunov stability theory [
27].
In this work, assuming that all PV energy is delivered to the DC motor (power converter is ideal). The motor is driven by the maximum power , for tracking maximum power points of PV (MPPT).
The idea of accurate input–output feedback linearization and the Lyapunov stability theory are applied to the control variable (duty cycle of the DC-DC converter) (u = D) with the ultimate goal of producing a control structure that realizes asymptotic output tracking in the rotational speed.
Our primary goal is to create a Lyapunov controller that, because of its success in output tracking, mimics a preset input–output linearizing controller. The PV system’s state space equations are shown below:
The goal of this study is to construct a nonlinear Lyapunov controller by using the notion of accurate input–output linearization. The input–output feedback linearization, which uses differential geometric control theory, is well-known in the domain of affine system control [
27]. The core principle of this strategy is to use a coordinate transformation and nonlinear feedback to convert a nonlinear system to a (fully or partially) linear one. In reality, for single-input, single-output affine nonlinear systems, input–output feedback linearization is an excellent technique for attaining complete control of a set point tracking.
Significant advances in nonlinear control over the last decade have enabled the creation of nonlinear tracking control schemes that make full use of current nonlinear models over a greater working region. Input-output feedback linearization, which uses differential geometric control theory, and input-state feedback linearization techniques based on an approximate linearization of the process model are two key approaches to the construction of control structures for nonlinear systems. Some researchers have investigated their usage in the control of nonlinear systems such as aircraft and power electrical systems.
To begin, the input-output feedback linearization theory is well-known in the domain of affine system control. The core principle of this strategy is to use a coordinate transformation and nonlinear feedback to convert a nonlinear system to a (fully or partially) linear one.
In reality, for single-input single-output affine nonlinear systems, input-output feedback linearization is an efficient DC-DC converter for obtaining flawless control of a fixed point tracking. Second, for nonlinear controller design, the linearization-based input-state has been used in a variety of engineering applications or following preset reference trajectories.
The model depicting the dynamics of a PV system (13) is written under the dynamical form below:
with
the state vector,
,
and
.
First of all, we derive the output
to the relative degree
The relative degree
r = 2, is equal to the order of the system (13). Employing
z as state variable, system (13), we have
Because our objective consists in obtaining
, a tracking error is defined as follows:
We select an input–output linearizing controller so that
The resulting closed loop system becomes linear and one has
We take into account the Lyapunov controller analytic expression written below,
where
is adjusted such that in the limit we have
The asterisk in
designates the optimal gain vector. By replacing
in (16), the following equation is obtained:
This equation can be reformulated as follows:
If we define
we get the closed loop system shown below:
Because is Hurwitz stable, it should be noted that for any positive definite matrix, there exists a positive definite matrix that satisfies the following Lyapunov equation:
Considering system (24), we apply a Lyapunov candidate function
The Lyapunov controller
is so well defined by choosing
that
Therefore, the Lyapunov controller output can be written under the following form:
where
and
4. Simulation Results
The proposed PV water-pumping system was simulated by using MATLAB/Simulink by utilizing the component models, shown in
Section 2, along with the control system described in
Section 3. The values of the taken numerical parameter are shown in
Table 2 [
24].
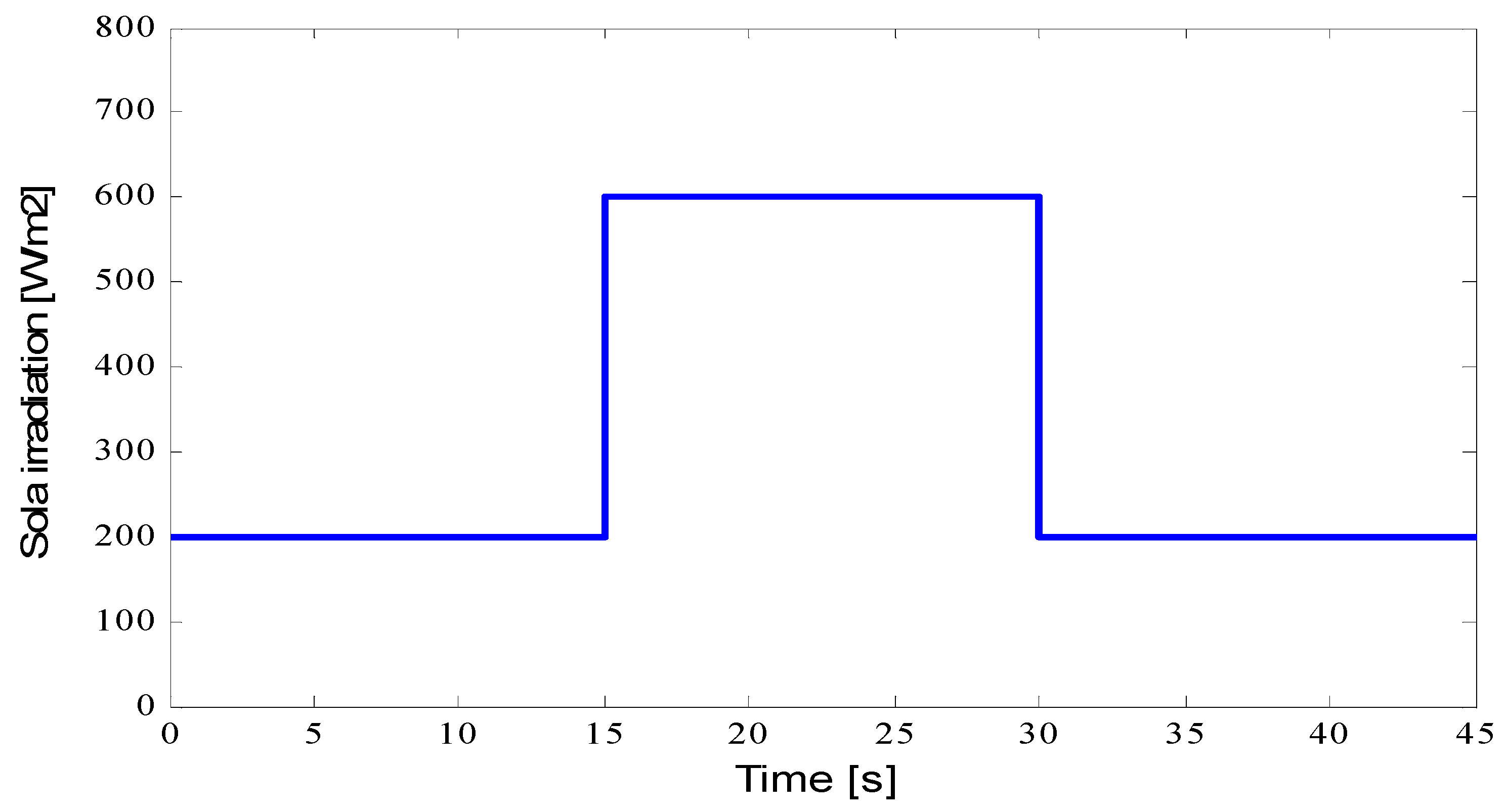
For that reason, a comparison between a directly linked system and the suggested technique under various solar insolation levels has been done in order to verify the effectiveness of the proposed control law. As depicted in
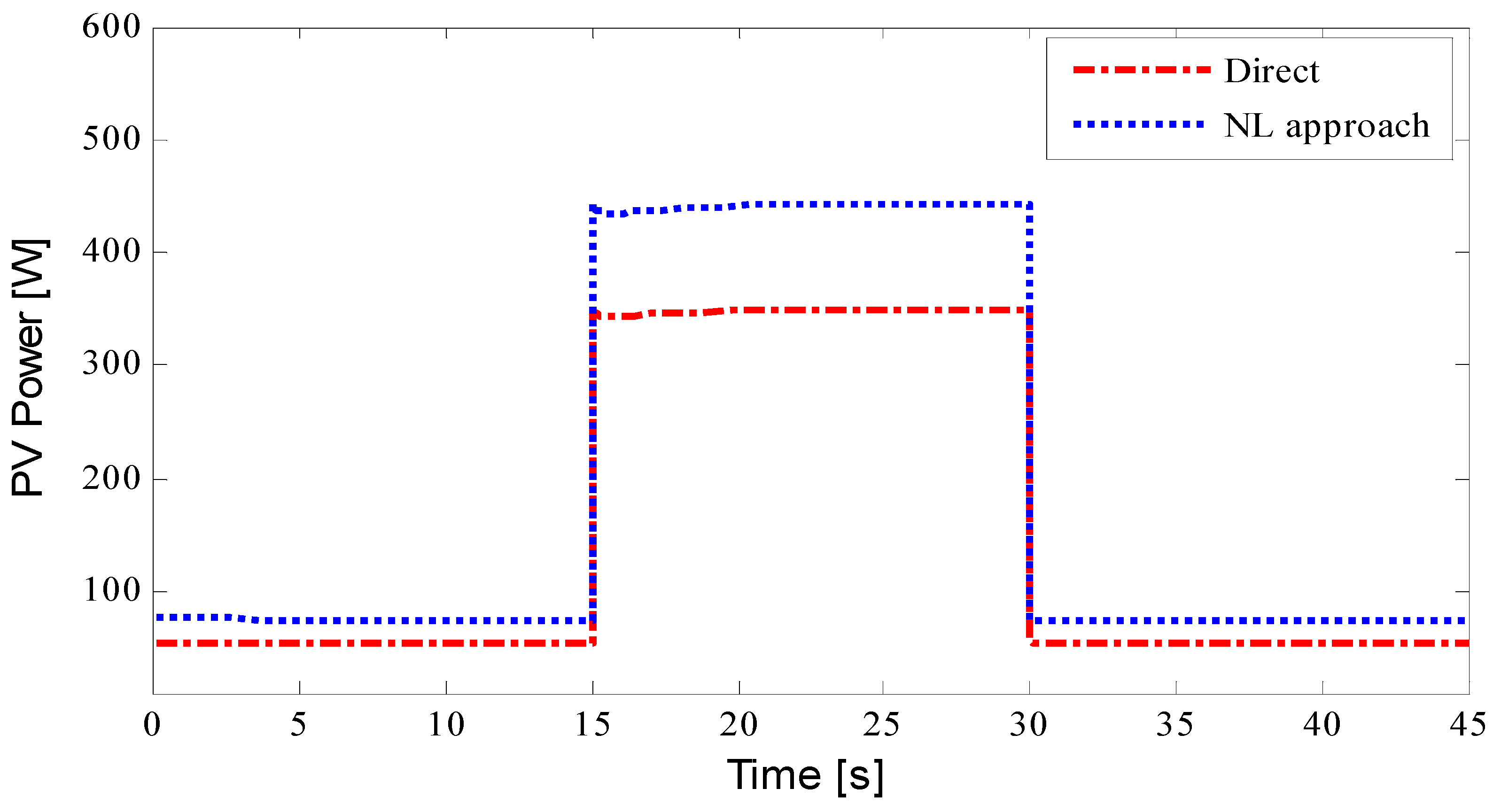
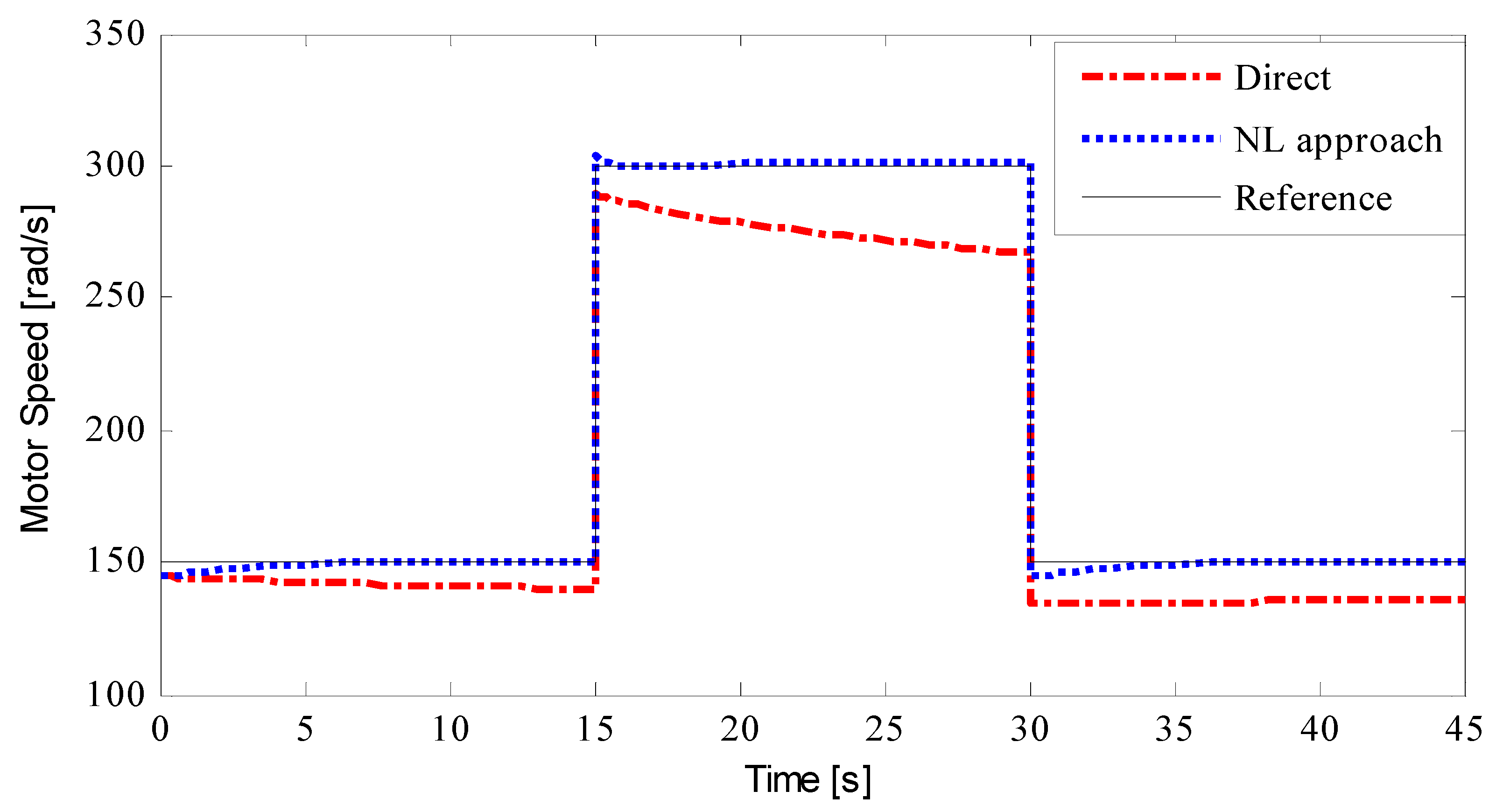
Figure 6, it is assumed that the solar insolation level would vary abruptly to and from. The proposed approach and the directly linked system’s corresponding PV power and motor speed responses to changes in solar insolation are depicted in
Figure 7 and
Figure 8. These figures show how the new technique and the directly connected system’s motor speed alter in response to changes in solar insolation, respectively.
Simulation results demonstrate that our method outperforms the directly connected system in the event of a sudden variation in insolation.
Figure 8 demonstrates how our controller’s use was responsible for the case’s flawless concordance between the reference rotational speed trajectory and the tracking trajectory.
As a result, the amount of water that is daily pumped by using the suggested method is more significant than the amount of water that is pumped by a directly connected system.