A Comprehensive Review of Maximum Power Point Tracking (MPPT) Techniques Used in Solar PV Systems

Abstract

Renewable Energy technologies are becoming suitable options for fast and reliable universal electricity access for all. Solar photovoltaic, being one of the RE technologies, produces variable output power (due to variations in solar radiation, cell, and ambient temperatures), and the modules used have low conversion efficiency. Therefore, maximum power point trackers are needed to harvest more power from the sun and to improve the efficiency of photovoltaic systems. This paper reviews the methods used for maximum power point tracking in photovoltaic systems. These methods have been classified into conventional, intelligent, optimization, and hybrid techniques. A comparison has also been made of the different methods based on criteria such as tracking speed, efficiency, cost, stability, and complexity of implementation. From the literature, it is clear that hybrid techniques are highly efficient compared to conventional methods but are more complex in design and more expensive than the conventional methods. This review makes available useful information that can be exploited when choosing or designing MPPT controllers.

1. Introduction

The need for universal electricity access is a global issue pushing many researchers towards looking for new and cleaner ways of power generation, as well as optimization of existing generation methods for efficiency in generation and cost [1,2,3,4]. The shift towards cleaner power generation has also been motivated by the finite nature of fossil fuels used in conventional power plants for electricity generation [5]. Due to the negative environmental impacts posed by conventional coal and thermal power plants, renewable energy (RE) technologies are seen to be safer pathways for sustainable energy transition in the power sector [6,7]. Moreover, hybridization of these energy-generating sources to supply the same load makes the electricity supply even more reliable [8,9,10,11,12,13,14]. However, despite their viability, RE resources are variable in nature. Solar and wind, for example, are not stable because of the constant variation of solar radiation and wind speed, respectively [12]. Additionally, photovoltaic (PV) systems use solar modules for harvesting the sun’s energy, but the conversion efficiency of these modules is still very low, limiting optimum solar energy harvesting [15,16,17,18,19,20,21,22,23]. For these reasons, different control techniques are currently being employed to track maximum power from these energy systems.

Power output in PV systems reaches its peak at a point called the Maximum Power Point (MPP), whose position changes continuously with respect to the level of solar radiation and temperature. This affects the sized PV output power for a given system since the systems are designed to produce a predetermined power before installation [24,25,26,27,28]. Tracking the peak power of the PV generator requires the operating point to be at MPP, which is a point on the PV curve showing the peak power a given PV module can produce at a specific time. Therefore, MPP must be continuously tracked by MPPT (Maximum Power Point Tracking) algorithms [29]. Tracking MPP is a technique for maximizing energy extraction from PV modules. All MPPT controllers operate with the same aim of ensuring that the change in power with respect to voltage on the P-V characteristic curve is always zero. This is completed by measuring the output current and voltage of the PV module and matching the source impedance to the load by appropriately adjusting the duty cycle of the converter used. When the impedance is properly matched, the MPP is tracked [30]. Utilizing solar tracking techniques is advantageous because it leads to an increase in efficiency and output power of PV systems [31]. A major challenge in MPPT systems comes during the voltage tracking and the appropriate variation of duty ratio to harness the maximum output power from the PV system [32,33,34,35,36,37,38,39]. Figure 1 and Figure 2 shows the variation of voltage, current, and power for a typical solar panel during solar radiation and temperature variations.

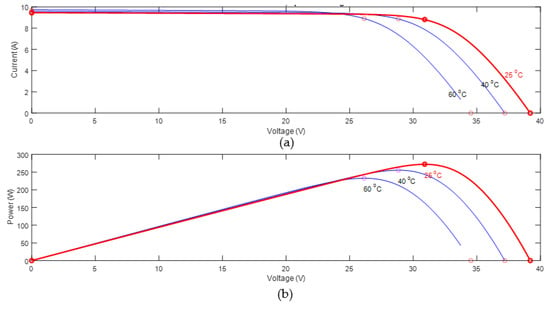
Figure 1. (a) I-V and (b) P-V characteristics of a solar module under varying temperature [21,22].

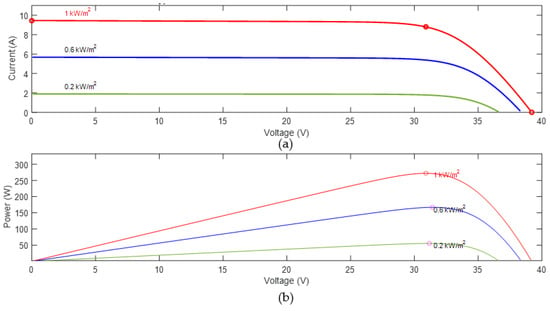
Figure 2. (a) I-V and (b) P-V characteristics of a solar module under varying solar radiation [21,22].

From the above figures, it can be seen that temperature variation greatly affects the voltage at the output of a solar module compared to the output current. Additionally, the variation in solar radiation greatly affects the current of the module compared to its output voltage. In both cases, the output power of the solar panel also varies [40]. Furthermore, the module’s I-V and P-V characteristics are never the same when it is subject to full sunshine conditions and when partial shading occurs because the output voltage and power of PV modules vary with the solar radiation falling on the module and temperature variation [41,42]. Under full sunshine, the P-V and I-V curves are uniform, having a single peak power point, whereas local maxima are observed under partial shading conditions, making it difficult to track the global maximum [43].

MPPT techniques can be classified based on their tracking methods into four, namely the classical methods, the intelligent methods, the optimization methods, and the hybrid methods [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Additionally, the efficiency of each tracking technique varies based on its capacity to monitor peak power in changing environmental weather conditions [44,56,57]. Table 1 below gives a summary of the different classes of MPPT techniques.

Table 1. Classification of MPPT techniques (redrawn with data from [44]).

Class	Sub-Class	Acronym
Classical MPPT control techniques	Perturb and observe	P&O
	Constant Voltage	CV
	Ripple Correlation Control	RCC
	Hill Climbing	HC
	Improved Perturb and Observe	IP&O
	Short Circuit Current	SCC
	Open Circuit Voltage	OCV
	Adaptive Reference Voltage	ARV
	Incremental Conductance	InC
	Look-Up Table-Based MPPT	LTB MPPT
Intelligent MPPT control techniques	Artificial Neural Network	ANN
	Fuzzy Logic Controller	FLC
	Sliding Mode Control	SMC
	Fibonacci Series-Based MPPT	FSB MPPT
	Gauss Newton Technique	GNT
Optimization techniques	Particle Swarm Optimization	PSO
	Cuckoo Search	CS
	Artificial Bee Colony	ABC
	Ant Colony Optimization	ACO
	Grey Wolf Optimization	GWO
	Genetic Algorithms	GA
Hybrid techniques	Adaptive Neuro Fuzzy Inference System	ANFIS
	Fuzzy Particle Swarm Optimization	FPSO
	Grey Wolf Optimization Perturb and Observe	GWO-P&O
	Particle Swarm Optimization Perturb and Observe	PSO-P&O
	Hill Climbing Adaptive Neuro Fuzzy Inference System	HC-ANFIS

The rest of the manuscript is organized as follows: Section 2 presents the classical MPPT techniques, Section 3 discusses the intelligent MPPT techniques used in PV systems, Section 4 presents optimization techniques, and Section 5 focuses on the hybrid techniques, which are a combination of conventional, intelligent, and optimization techniques. Furthermore, Section 6 provides a summary of related works conducted on the topic of MPPT, Section 7 outlines the criteria used for ranking MPPT techniques, Section 8 presents a comparative analysis of different MPPT techniques, Section 9 is the conclusion, and Section 10 finalizes the manuscript with recommendations.

2. Classical MPPT Control Techniques

The classical methods are easily implemented due to their simplicity. They perform best under constant irradiance. However, with these methods, oscillations are higher near the MPP during tracking, which leads to poor performance. In addition, the neglect of the effect of partial shading by these classical strategies means that the real MPP cannot be tracked [49,57].

2.1. Perturb and Observe (P&O) MPPT Techniques

The Perturb and Observe (P&O) method is one of the most used control methods in commercial MPPT controllers [44,58]. Basically, in this method, the change in power (dP) of the PV module is monitored. When this is executed, the sign of the PV module voltage (dV) is also verified to adjust the duty cycle (D) for eventual update and correction. Generally, the module’s power and voltage (P-V) characteristic is used to track the course of the operating point of the module’s output power [59]. A positive gradient (dP/dV) means the actual point is located on the left of the MPP. A negative gradient means the point is on the right side of the power curve. This tracking is repeated several times until the point where dP/dV is zero, which is the tracked MPP for the PV module. The number of perturbations made in one second is called the frequency of perturbation, which can also be called the frequency of the MPPT [60,61].

Equations (1)–(3) below are the general equations used by the P&O method for voltage perturbation. The difference comes when the step size for duty cycle control is either fixed or variable (adaptive control). After measuring the PV power P(t), it is compared with the previous maximum power P(t − 1), and that difference (Delta) is used to generate a duty ratio that controls the converter to either increase the voltage V(t) by $\mathsf{\Delta }V$ or decrease the voltage by $\mathsf{\Delta }V.$

$$\mathrm{P}\left(\mathrm{t}\right)=\mathrm{V}\left(\mathrm{t}\right)\times \mathrm{I}\left(\mathrm{t}\right)$$

(1)

$$\mathrm{Delta}=\mathrm{P}\left(\mathrm{t}\right)-\mathrm{P}\left(\mathrm{t}-1\right)$$

(2)

$$\mathrm{V}\left(\mathrm{t}\right)=\mathrm{V}\left(\mathrm{t}-1\right)\pm \mathsf{\Delta }\mathrm{V}$$

(3)

P&O MPPT methods are conventionally implemented and modified with fixed and adaptive step sizes [58]. Figure 3 shows a flowchart followed by this method.

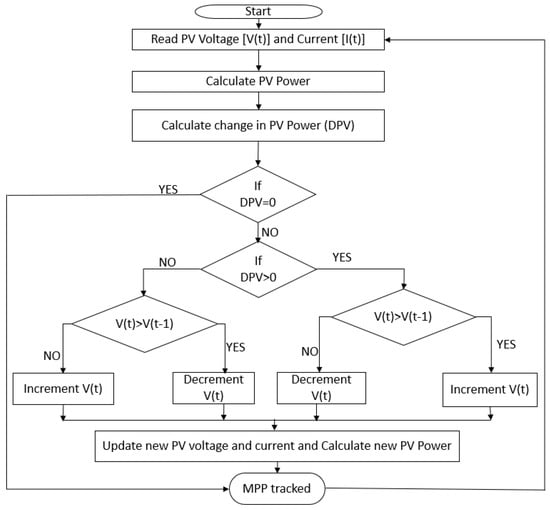
Figure 3. P&O method’s flow diagram [44].

2.1.1. Conventional P&O Algorithms

For the conventional P&O method with fixed perturbation approach, the system designer chooses a predetermined step size for the monitoring method to track the peak power. The tracking algorithm is based on two primary criteria: speed of tracking and perturbation step. The oscillations at steady-state are proportional to the value of the step size for fixed perturbation levels. Higher oscillations are caused by larger step values. Unfortunately, a slower response is the effect of smaller step values. As a result, it is unavoidable to experience the well-known trade-off between faster responsiveness and steady-state oscillations. Furthermore, MPPT with a fixed step is system-dependent because the perturbation step value is not constant.

With the conventional P&O method with adaptive perturbation, the process of hill-climbing involves adjusting the perturbation value, which, in this case, is the voltage. The step size for the voltage perturbation is initially set to 10% of the voltage at open-circuit (V_oc). Despite the satisfactory outcomes, this strategy is not entirely adaptive due to the planned steps. It also relies on the V_oc, which fluctuates depending on the environment [50].

Table 2 shows a comparison of the different conventional P&O MPPT algorithms. These methods are less complex, making them cost-effective. Moreover, the time of response for the adaptive step size is better than that of the fixed step size.

Table 2. Comparison of conventional P&O algorithms.

SN	Comparative Parameter	Fixed Step Size	Adaptive
1	Response Time	Slow	Fast
2	Complexity	Simple	Simple
3	Performance under varying solar radiation and temperature	Moderate	Good
4	Oscillations at maximum power point	Yes	Yes, but minimal
5	Cost	Moderate	Moderate
6	Efficiency	Low	High
7	Memory requirement	No	Depends

2.1.2. Improved (Modified) P&O (IP&O) Method

This method is an upgrade of the conventional P&O technique. In this method, to avoid unnecessary power while tracking the global MPP, the reference voltage used for tracking is scaled by a factor of 0.8 of the V_oc of the PV modules. This method can be subdivided into modified P&O with fixed perturbation step (WFPS) and modified P&O with adaptive perturbation step (WAPS).

In the modified P&O WFPS, instead of the module voltage, the converter duty cycle is employed as the perturbed signal.

The modified P&O WAPS is more advanced as it uses a variable duty ratio. Despite its excellent performance, this technique has some flaws, including a high computational burden versus accuracy trade-off and a reliance on specified constants [50].

Table 3 shows a comparison of the modified P&O methods, which demonstrates an improvement in terms of response time for the fixed step size method. From these comparisons, it can be seen that the P&O methods are generally less complex, making them less costly and therefore widely used in the industry.

Table 3. Comparison of modified P&O algorithms.

SN	Comparative Parameter	Fixed Step Size	Adaptive Step Size
1	Response Time	Fast	Fast
2	Complexity	Moderate	Moderate
3	Performance under varying solar radiation and temperature	Good	Very good
4	Oscillations at maximum power point	Minimal	Minimal
5	Cost	Moderate	High
6	Efficiency	High	High
7	Memory requirement	Yes	Yes

Kolluru et al. [62] designed a novel P&O MPPT controller with a settling time of 0.05 s, which was capable of tracking 10% extra power from the PV source. Their model was simulated in MATLAB Simulink. From their findings, using their controller enabled more power to be harvested from the PV system compared to when the tracker was not used. Sera et al. [63] compared the InC and P&O methods and found that the two methods are the same. This was experimentally confirmed according to the European standard EN 50530. They achieved efficiency deviations of 0.02% under static and 0.13% under dynamic conditions. Pandey et al. [64] presented a P&O technique for peak power harvesting from PV modules. They incorporated this technique with the MPPT controller, and their system could match the output generated PV power to the variable load power demanded. Their work was simulated using SIMULINK in MATLAB. Elgendy et al. [60] presented an analysis and practical assessment of the reference voltage perturbation and direct duty ratio perturbation methods, examining the effects of perturbation rate and step size. They concluded that direct duty ratio perturbation makes it possible to employ large perturbation rates up to the Pulse Width Modulation (PWM) rate without overall loss of system stability. Similar work on this topic has been presented in [65,66].

2.2. Hill Climbing (HC) Method

Hill Climbing (HC) method involves perturbing the converter’s duty cycle [67]. Although it shares a similar premise with P&O, it is not precisely equivalent. To execute MPPT, P&O requires perturbation in the terminal voltage, while the hill climbing approach requires duty cycle perturbation [52,68]. This means that the duty cycle used for the converter’s control keeps changing as the PV power deviates from the maximum value at any given moment. The change in duty cycle direction is determined by the perturbation on the duty ratio, which determines the tracking direction on the P-V characteristics of the module. Equation (4) governs the duty cycle.

$$\mathrm{D}\left(\mathrm{i}\right)=\mathrm{D}\left(\mathrm{i}-1\right)\pm \mathrm{S}$$

(4)

$\mathrm{D}\left(\mathrm{i}\right)$ is the duty ratio at ith iteration that controls the converter, $\mathrm{D}\left(\mathrm{i}-1\right)$ is the duty at $\left(\mathrm{i}-1\right)$th iteration, and S is the step size. The step size S can be fixed, depending on the algorithm used. The variable step calculation is found in Jately et al. [68].

The step size can either be negative or positive depending on the direction of the power point on the curve. A positive or negative change in power and voltage means that S will be negative. A difference in sign for the change in power means that S will be positive.

2.3. Constant Voltage (CV)

In the Constant Voltage (CV) method, a fixed voltage value for the MPP is assumed, which is identical to the value observed at the manufacturer’s Standard Test Conditions (STCs). This fixed voltage value is usually between 72% and 80% of the V_oc [22,69,70]. This reference voltage is then used to adjust the duty cycle of the MPPT converter via a feedback control loop. Constant voltage MPPT control is simple to construct and requires only the measurement of the array voltage. It can be implemented using both analogue and digital circuitry [71]. Equation (5) describes the relationship between the voltage at MPP (V_mpp) and V_oc, where k is a constant that falls within the range 0.72 to 0.8.

$${\mathrm{V}}_{\mathrm{mpp}}=\mathrm{k}\times {\mathrm{V}}_{\mathrm{oc}}$$

(5)

The CV method is depicted in Figure 4.

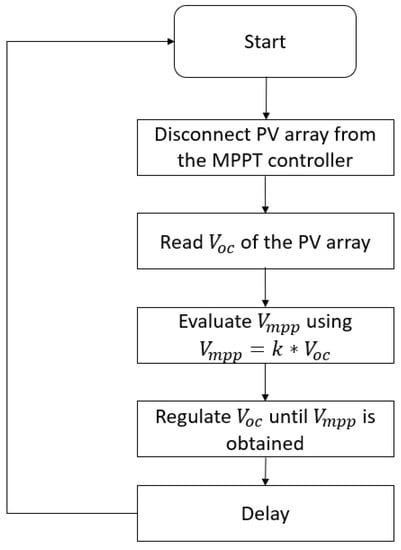
Figure 4. Flowchart of the CV method [22].

During the voltage comparison process, the solar module is temporarily isolated from the MPPT, and V_oc is measured. The MPPT then calculates the correct operating point using Equation (5) and the preset value of k and adjusts the module’s voltage until the calculated V_mpp is reached. Leedy et al. [70] presented a CV MPP algorithm that automatically fixes the reference voltage to take into account the various environmental conditions.

2.4. Ripple Correlation Control (RCC)

When a PV array is connected to a power converter, it causes voltage and current ripples. These ripples are imposed on the PV array by the converter’s switching action. As a result, the power of the PV array is likewise affected by ripples. RCC is a tracking technique that uses current and voltage ripples to track the MPP. To achieve the MPP and drive the power gradient to zero, the derivatives of the varying PV power are correlated to those of the variable PV voltage or current. The operating point is below the MPP when either current or voltage increases while the power increases. In contrast, if the power falls and the current or voltage rises, the operating point rises above the MPP [50]. The advantage of RCC is that it does not introduce any interference from outside into the system but rather makes use of the system’s existing current or voltage ripple [70,72,73]. This method makes use of Equation (6) below [52].

$$\frac{\mathrm{dP}}{\mathrm{dt}}\times \frac{\mathrm{dV}}{\mathrm{dt}}=0\mathrm{or}\frac{\mathrm{dP}}{\mathrm{dt}}\times \frac{\mathrm{dI}}{\mathrm{dt}}=0$$

(6)

2.5. Open Circuit Voltage (OCV)

The Open Circuit Voltage (OCV) method assumes that the voltage at MPP is the product of V_oc of the solar module and a constant coefficient ranging from 0.7 to 0.8 [74]. Although this method is easy to implement due to its simplified procedure, each time V_oc is being measured, the load has to be disconnected, leading to power supply interruptions and hence reduced system efficiency [75]. Therefore, it is not a recommended technique to be used in areas where continuity of supply to the load is of utmost importance.

2.6. Short Circuit Current (SCC)

This tracking method, similar to the OCV tracking method, is based on the observed linear relationship between the PV current at MPP and the short-circuit current. It makes use of a proportional constant K₁ as shown in Equation (7), which is primarily determined by PV cell technology, meteorological circumstances, and the fill factor. For polycrystalline PV modules, the constant can be estimated to be approximately 0.85. In many cases, the constant is established by running a PV scan every few minutes. After obtaining it, the system uses the updated estimate until the next calculation is performed. The control flowchart is then comparable to that of the OCV approach. As a result, this strategy has the same benefits and drawbacks as the OCV control method [50].

$${\mathrm{I}}_{\mathrm{MPP}}={\mathrm{K}}_1\times {\mathrm{I}}_{\mathrm{sc}}$$

(7)

K₁ varies between 0.78 and 0.92 [76].

2.7. Adaptive Reference Voltage (ARV)

Adaptive Reference Control (ARC) is a similar method to the CV approach but takes into consideration the climatic conditions of the environment. The temperature and solar radiation are sensed in addition to the voltage, increasing the number of sensors used. For a particular temperature, the solar radiation is separately partitioned into numerous divisions, and the equivalent reference voltage is recorded in an offline table. The corresponding proportional integral controller generates a duty cycle to control the converters by using the error obtained after comparing the PV voltage and the reference voltage [44]. ARC is capable of maintaining its efficiency even under varying solar radiation, as shown in [77].

2.8. Incremental Conductance (InC)

Incremental Conductance (InC) is another conventional method used for tracking the maximum power from PV systems. The technique uses the current and voltage of the PV modules to find the MPP and can track the MPP with varying weather conditions. The equations governing this technique are detailed in Subudhi et al. [56]. Although more complicated compared to P&O, the implementation of InC is easier thanks to the advancement of DSPs (Digital Signal Processors) [68,78].

2.9. Look-Up Table Based (LTB) Method

With the LTB approach, the observed current and voltage values of the array are compared to stored values in the system that harmonize the array’s operating point with respect to the MPP. Different system conditions for every temperature and insolation, as well as related MPPs for individual solar PV arrays, are maintained in the database [79]. The method’s biggest drawback is the demand for bulk storage memory. The number of operational situations increases as tracking accuracy improves, necessitating additional data storage. The tracking scheme is array-specific, so it’s difficult to implement, and keeping track of all conceivable system states is inconvenient to save and archive [52].

3. Intelligent MPPT Control Techniques

These are methods which use soft computing techniques to perform MPPT. These techniques are more advanced in that they employ machine learning in their approaches.

3.1. Artificial Neural Network (ANN)

ANN is a soft computing approach inspired by our central nervous system (brain). To create a network similar to a biological neural network, these computer models, which are capable of machine learning, are represented as interconnected neurons (artificial nodes). Connection weights are modified during the training process until the best fit, or the reference voltage corresponding to MPP, is attained [52,80]. The model has three levels: input, hidden, and output layers, as shown in Figure 5. Atmospheric data such as temperature and irradiance, PV module parameters such as V_oc and I_sc, or a mix of the two, can be used as input variables. The output represents the duty cycle signal that causes the converter to follow the MPP, according to the hidden layer. The link between nodes I and j is given the weight W_ij. In the neural network technique, node-to-node links are weighted based on a training process where PV parameters are assessed and recorded over months or years to obtain the proper weight for each node. The drawback of this approach is that the neural network cannot be generalized to operate on multiple types simultaneously because it must be trained specifically for the PV module being used. Additionally, because the PV panel’s characteristics change over time, the neural network needs to be trained frequently in order to precisely follow the MPP [50]. To make this technology broadly applicable, more research is required to confirm that an algorithm trained on one PV system can be utilized on another system to track MPP.

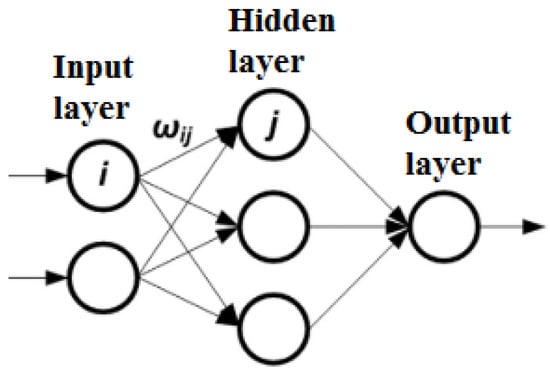
Figure 5. Layers of ANN.

3.2. Fuzzy Logic Controller (FLC)

In contrast to binary logic, which has just two states (true or false), fuzzy logic uses multiple values. The range of fuzzy logic variables is 0 to 1, introducing the notion of partial truth, where the variable value can be either completely true or completely untrue [52]. Fuzzy computation trackers are deemed smart because they monitor the MPP even if the inputs are erroneous. A mathematical model is not required for fuzzy controllers. Fuzzification, rule base lookup table, and defuzzification are the three stages of fuzzy control in general. The numerical input variables are translated into linguistic variables in the first modeling stage using a membership function with five fuzzy levels: NB (negative big), NS (negative small), ZE (zero), PS (positive small), and PB (positive big). An error E and a change in error ΔE are typically the inputs of a MPPT fuzzy logic controller, and these input parameters can be calculated using the Equations (8) and (9), respectively, as described by Ngan and Tan [22].

$$E\left(\mathrm{i}\right)=\frac{{\mathrm{P}}_{\mathrm{pv}}\left(\mathrm{i}\right)-{\mathrm{P}}_{\mathrm{pv}}\left(\mathrm{i}-1\right)}{{\mathrm{V}}_{\mathrm{pv}}\left(\mathrm{i}\right)-{\mathrm{V}}_{\mathrm{pv}}\left(\mathrm{i}-1\right)}$$

(8)

$$\mathsf{\Delta }\mathrm{E}\left(\mathrm{i}\right)=\mathrm{E}\left(\mathrm{i}\right)-\mathrm{E}\left(\mathrm{i}-1\right)$$

(9)

The fuzzy controller’s output, given by ΔD (change in duty-cycle) of the power converter, may be found in Table 4 once E and ΔE have been calculated and transformed into linguistic variables. The fuzzy logic controller’s linguistic output variable is transformed into a numerical variable at the defuzzification stage, resulting in an analog signal that drives the power converter to the MPP. Under varying climatic circumstances, the MPPT fuzzy logic controller performs admirably [81]. However, its success is contingent on selecting the appropriate error computation and formulating the rule base table [32,50,82]. When using this method for MPPT, there is no need for mathematical modeling. Additionally, the system’s stability around the MPP is enhanced as fewer oscillations are observed. This method, however, presents difficulties in tuning the membership function, scaling factor, and the control rules. These are areas where more research should be conducted to optimize the use of this technique in MPPT development.

Table 4. Fuzzy Logic Rule Table.

	Change in Error (ΔE)	NB	NS	ZE	PS	PB
Error (E)
NB		ZE	ZE	NB	NB	NB
NS		ZE	ZE	NS	NS	NS
ZE		NS	ZE	ZE	ZE	PS
PS		PS	PS	PS	ZE	ZE
PB		PB	PB	PB	ZE	ZE

3.3. Sliding Mode Control (SMC)

The Sliding Mode Control (SMC) method is used for nonlinear systems. When used for MPPT, it operates using the sliding mode and the approaching mode. At MPP, the condition in Equation (11) must be fulfilled [52,83].

$$P=\mathrm{VI}={\mathrm{I}}^2\mathrm{R}$$

(10)

$\frac{\mathrm{dP}}{\mathrm{dI}}=0$ which implies:

$$2\mathrm{R}+\mathrm{I}\frac{\mathrm{dR}}{\mathrm{dI}}=\mathsf{\sigma }=0$$

(11)

where $\mathsf{\sigma }$ is the sliding surface [84], P is the power, I is the current, V is the voltage, and R is the resistance. The duty ratio δ, which is then used to control the converter in the system to track the MPP, is updated based on the value of σ as in Equation (4). $\mathsf{\Delta }\mathsf{\delta }$ is the change in duty ratio, ${\mathsf{\delta }}_{\mathrm{i}}$ is the duty ratio after the ith iteration, while $\mathsf{\delta }\left(\mathrm{i}+1\right)$ is the updated duty cycle after the $\left(\mathrm{i}+1\right)$th iteration given by Equation (12).

$$\mathsf{\delta }\left(\mathrm{i}+1\right)=\{\begin{array}{c}{\mathsf{\delta }}_{\mathrm{i}}+\mathsf{\Delta }\mathsf{\delta } \mathrm{for} \mathsf{\sigma }>0\\ {\mathsf{\delta }}_{\mathrm{i}}-\mathsf{\Delta }\mathsf{\delta } \mathrm{for} \mathsf{\sigma }<0\end{array}$$

(12)

Due to its highly efficient mathematical model, MPPTs designed with this technique can precisely track the maximum power. However, it has a limitation that the quality of tracking is highly dependent on the choice of sliding surface that has been chosen.

3.4. Fibonacci Series Based (FSB) Method

Tracking the MPP across the entire search region increases processing time and creates a big concern for storing data. The issue is considerably addressed by the FSB technique of tracking, which significantly cuts the search time by constricting the range of operation. This sophisticated iterative algorithm narrows its search and then moves on to scan the range for the best working location. It makes use of two roughly equivalent range points, V_min and V_max, to determine the direction in which it must change. This method is similar to a divide-and-conquer strategy, in that it changes its operational range by using the preceding iterative values [85,86,87]. The iterative sequence used to fast-track the MPP is given in Equation (13) below [44]:

$${\mathrm{R}}_{\left(\mathrm{n}+2\right)}={\mathrm{R}}_{\left(\mathrm{n}+1\right)}+{\mathrm{R}}_{\mathrm{n}},\left(\mathrm{n}=1,2,3,\dots \mathrm{and}{\mathrm{R}}_1={\mathrm{R}}_2=1\right)$$

(13)

where R represents the points used on the PV curve to track the MPP. However, this technique requires complex calculations to locate the MPP, which is a setback.

3.5. Gauss Newton Technique (GNT)

The GNT [88], which employs a root-finding algorithm, has the fastest tracking speed when compared to other mathematical computation algorithms. The first and second derivatives of the change in power are utilized in this algorithm to establish the direction and number of iterations required to solve the governing equation [44,56]. Its disadvantage is that it has a complex architecture due to the high level of mathematical modeling. This complexity can be made simple through further research in this direction.

4. Optimization Techniques

These techniques are grouped under the family of metaheuristic optimization algorithms. Due to their particular benefits over conventional algorithms, metaheuristic optimization methods are becoming highly desirable. They are used to find excellent answers to an increasing variety of complicated real-world problems because they can address multiple-objective, multiple-solution, and nonlinear formulations. Table 5 is a summary of these algorithms.

Table 5. Metaheuristic optimization techniques.

Methods	Description	Advantages	Disadvantages
Particle Swarm Optimization (PSO)	The core concept of PSO is inspired by the behavior of crowded birds or schooling fish [89]. To find the best solution, PSO entails certain particles forming a swarm of wandering wasps across the search space [90,91,92]. PSO is used to extract the Global MPP from a PV array by taking into account the converter duty cycle and the output power as the objective function [93,94,95,96,97].	High tracking speed under varying weather and partial shading conditions.	It has a complex objective function which depends on the velocity of the particles.
Cuckoo Search (CS)	The cuckoo search (CS) method is a cuckoo bird’s bio-inspired parasitic reproduction scheme [93,98].	High convergence speed and efficiency, lesser number of tuning variables as compared to PSO, which gives it a more robust performance.	It has a composite mathematical function, which is being used in the algorithm
Artificial Bee Colony (ABC)	Artificial bee colony (ABC) algorithm is a bio-inspired method that is basic, requires a small number of controllable parameters, and the algorithm convergence criteria are independent of the system’s initial conditions. The food source of the ABC algorithm is maximum power, and the duty cycle is the food position [98].	It uses very few parameters	Complexity, slow tracking speed, and at times it is limited to track the local MPP instead of tracking the GMPP.
Ant Colony Optimization (ACO)	This is a probabilistic algorithm that aids in the discovery of the optimal output based on the ants’ food-seeking behavior. ACO is used in both centralized and distributed type MPPT controllers to limit the number of local maximum power points on the I-V curve [98].	Faster convergence speed, simple control strategy, low cost, capable of tracking under partial shading conditions.	It uses a complex estimation approach.
Genetic Algorithm (GA)	GA is based on Darwin’s theory of theoretical determination and the action of the natural-part. GA is used to train an artificial neural network (ANN) to forecast the maximum voltage and current at the PV array’s MPP. Furthermore, GA has been used to stratify the economic design of PV arrays using different inverters [95].	It is good at optimizing and training other MPP algorithms to track quickly and accurately.	It has a slow tracking speed.
Grey Wolf Optimization (GWO)	The wolf strategy for hunting prey is used in this optimization method [95]. Grey wolves typically hunt in three stages, first searching for prey, then encircling prey, and lastly attacking prey [95,99,100,101,102,103].	It is more efficient at tracking, has no transient or steady-state oscillations, is more robust, and is faster.	High computational complexity, a huge search space, and a high cost.

5. Hybrid Techniques

5.1. Adaptive Neuro Fuzzy Inference System (ANFIS)

This method is a combination of ANN and fuzzy logic control techniques. In approximating the GMPP, this method is highly efficient because of its proper membership function design. Based on the input supplied at a given instant, the membership functions are capable of adaptively adjusting themselves making it possible for the ANFIS technique to be used in PV systems with partial shading conditions. The ANN is used to reduce the tracking error and parameter optimization, while the FLC is used to control nonlinear inputs without necessarily needing any prior knowledge of the system [104,105,106,107,108,109,110,111,112]. However, because of the complexity of the algorithm used, this method it is not cost-effective for MPPT.

5.2. Fuzzy Particle Swarm Optimization (FPSO)

This method is a combination of FLC and PSO. Using these two highly optimized techniques improves the efficiency of the controller. This hybrid technique is highly recommended because of its parameter adjustment and reduced mathematical computation, which leads to the best distribution of membership functions. This method has been described in [6,113,114]. It has several advantages, such as reduced switching losses and the ability to self-tune the membership function, eliminating the need for proportional integral controllers and reducing complexity. However, a major setback of this method is that fuzzy rules have to be designed using trial-and-error methods that rely on human intelligence.

5.3. Grey Wolf Optimization Perturb and Observe (GWO-P&O)

In order to enable faster convergence to GMPP, P&O is utilized after GWO in the early phases of MPPT. As a result, GWO’s search space is reduced, and the computational cost is dropped. The positions of the wolves indicate the converter’s duty cycle. The need of a PI controller is fully eliminated in the MPPT implementation. This method is more efficient and has a higher tracking capability than conventional GWO and P&O methods. It also has a faster convergence speed [98]. The drawback with this method is the high level of mathematical computation.

5.4. Particle Swarm Optimization Perturb and Observe (PSO-P&O)

PSO is utilized for global search at the start of the algorithm, and P&O is employed for the final stage. The PSO approach is used to find the GMPP. This combined approach detects GMPP in less time than the traditional PSO method [98]. It also reduces the oscillations in output power during tracking. On the other hand, it has a complex control structure, poor convergence if the GMPP is located outside of the search area, and it is costly in hardware implementation. Addressing the poor convergence issue whenever the GMPP falls outside the search space should be a point of concern.

5.5. Hill Climbing Adaptive Neuro Fuzzy Inference System (HC-ANFIS)

The combination of this HC and ANFIS MPPT approach is coined to the limitations individually encountered by these different methods. This tracking technique has been proven to be faster than other conventional techniques, as can be seen in the work presented in Kamran [115]. The flow diagram followed by this algorithm is shown in Figure 6. Solar radiation (G) and temperature (T) for the PV system are first used as input to the ANFIS, and the duty ratio (D) is obtained. This duty ratio is then passed to the HC system, which uses the PV voltage (V_pv) and the PV current (I_pv) as inputs to calculate the optimal duty ratio that is then used to drive the converter to track the MPP.

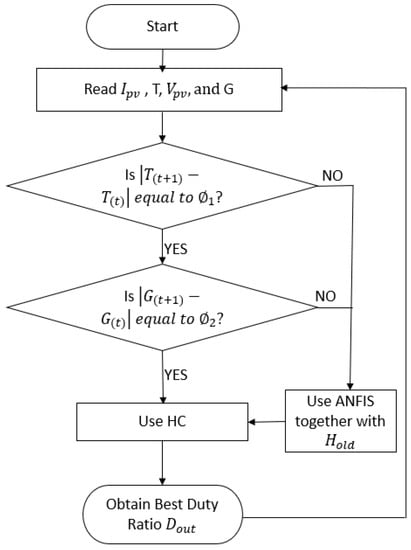
Figure 6. Flow diagram of the HC-ANFIS MPPT technique [44].

This method is advantageous because it has a higher tracking speed and does not need mathematical modelling. However, the complex nature of membership function design and the tedious process of training the ANN are disadvantages of the system. Introducing new approaches to train the ANNs and simplify the membership function design would increase adoption of this MPPT technique.

6. Summary of Related Works Done on the Different MPPT Techniques

Various researchers have conducted research works on different MPPT techniques, as presented in Table 6.

Table 6. Summary of related works for different MPPT methods.

MPPT Method	Reference	Year	Observations
ANFIS	[106]	2019	In this research, an ANFIS-based approach was developed using a significant amount of data, experimentally trained so that high error due to training is prevented in the system. These figures were gathered through tests conducted experimentally on a PV array in 2018. The performance of the suggested ANFIS approach was evaluated through simulation in MATLAB/Simulink. The average efficiency of the suggested approach under varying climatic conditions was calculated using an actual measurement test on a semi-cloudy day. The results showed that the suggested method accurately tracked the optimal maximum power, with an efficiency of over 99.3%.
ANFIS	[116]	2020	They performed simulations using the ANFIS MPPT technique. Their results showed that the MPP could be tracked during partial shading conditions.
ANN	[117]	2014	They proposed a novel method for tracking the MPP using the ANN and concluded that the MPP could easily be tracked using their approach.
ARV	[77]	2017	They showed that although ARV is similar to CV, it is capable of maintaining its efficiency even under varying solar radiation.
CS	[93]	2017	In this work, the PSO, INC, and CS are compared, and results showed that the CS performs better than the PSO under partial shading conditions.
CV	[70]	2012	They designed a CV MPP algorithm that automatically modifies the reference voltage to take into consideration changing environmental factors. They used MATLAB/Simulink to simulate their work, and the simulation results were consistent with the experimental results.
FLC	[118]	2014	They compared the FLC method with the P&O method and concluded that the FLC method outperforms the P&O method under varying weather conditions.
FPSO	[119]	2015	They designed a hybrid FPSO system for frequency stabilization under various loading conditions and concluded that the frequency stability was improved compared to using only the FLC method.
GWO-P&O	[120]	2016	They proposed a new hybrid maximum power point tracking (MPPT) method that combines P&O and GWO techniques. The proposed MPPT approach was initially built in MATLAB/Simulink, and then an experimental setup was created in order to test it out in practice. The gathered data demonstrated that, in all weather conditions, the proposed MPPT outperformed both the GWO and PSO-P&O MPPT algorithms.
HC	[68]	2021	The performance of eight hill-climbing algorithms for two different step sizes was examined on a small-scale experimental prototype under both uniform and rapid fluctuations in low irradiance. According to their statistical research, the adaptive HC drift-free MPPT algorithm outperformed conventional HC algorithms when used with the ideal perturbation step-size in low irradiance conditions.
HC-ANFIS	[115]	2018	Their results showed that irradiance and temperature could be taken in real time and the maximum voltage predicted.
InC	[121]	2008	A modified variable step InC MPPT algorithm for MPP tracking was proposed. The proposed system could automatically adjust the step size to track peak power from the PV array. Their method could improve effectively the accuracy and speed of the MPPT at the same time. Moreover, its implementation in DSPs is simple. Their approach was verified using simulation results from MATLAB-Simulink and experimentally using a DSP. They used a sampling period of 0.025 s. Their experimental results showed a tracking efficiency of 99.2% and a response time of 1.5 s.
IP&O	[122]	2020	Their suggested method confines the search space for the power curve to a 10% region that encompasses the MPP before starting perturbation and observation. The proposed P&O algorithm was evaluated in MATLAB/Simulink, and a solar tracker ensured that, as the sun moved across the sky throughout the day, the solar module received constant and maximum illumination. Due to the algorithm’s limited search space, the steady-state oscillations at the MPP and the response time to changing weather conditions were both slowed down. The proposed system was experimentally tested, and the results proved that the proposed P&O algorithm was effective.
IP&O	[123]	2022	They simulated an improved P&O MPPT algorithm for solar PV system using MATLAB/SIMULINK software. Their results showed a tracking efficiency of 99.7%.
LTB MPPT	[124]	2021	In their article, a unique 2-D lookup table-based MPPT system was developed. A 2-D optimal-duty-cycle table was used. They concluded that the method deserved further development because it outperformed the fixed-step P&O MPPT in terms of power tracking.
OCV	[125]	2021	They used OCV method to harvest peak power. Their results showed that the system’s response time was fast with fewer oscillations and 99% efficiency.
P&O	[126]	2018	They presented a P&O algorithm based on voltage sensors. Their simulation and experiment results demonstrated that the suggested method was successfully enhancing the PV system’s dynamic and steady-state tracking performance at a lower cost.
PSO-P&O	[127]	2017	In their work, they used a hybrid PSO-P&O technique to track peak power from a 1.2 MW PV system subjected to partial shading condition. Their results showed proper dynamic and steady-state responses.
RCC	[73]	2007	Their study looked at a digital formulation that uses less power and is more reliable. An MPP tracker for a solar panel with a tracking efficiency of more than 99% and a quick convergence rate was designed using the RCC technique.
SCC	[128]	2021	They implemented an improved MPPT using the SCC method and obtained minimal energy losses, better accuracy, and low oscillations compared to the classic fractional SCC algorithm.

7. Criteria for Ranking Different MPPT Techniques

Due to the variation in the technological approaches used in designing MPPT controllers, their comparison is based on different criteria. In Ahmad et al. [43], some criteria for ranking MPPTs have been presented, as shown in Table 7.

Table 7. Criteria for determining MPPT rankings redrawn with data from [43].

Criterion	Considerations	Ranking
Algorithm’s complexity	Similar to P&O	Best
	Requires small adjustment of the P&O algorithm
	Combines P&O and other methods
	Uses some artificial intelligence or bio-inspired algorithm
	Modified or advanced level of artificial intelligence or bio-inspired	Very complex
Hardware implementation	DC-DC converter with I and V sensor	Best
	Needs modification of DC-DC converter
	Use of PI/PID controller for duty cycle modulation of converter
	Use of high-tech embedded system	Very complex
Tracking Speed	0 ms to 100 ms	Best
	100 ms to a few hundred milliseconds
	From a few hundred milliseconds to seconds	Very slow
Uniform condition Efficiency	97% to ≈100%	Best
	93% to 96.9%
	<92.9%	Less efficient
Ability to track accurately under partial shading	Tracks global maximum Better performance than an MPPT of the same complexity	Best
	Not being able to track GMPP under partial shading
	Performs better than P&O
	Often caught in the local maximum, similar to P&O	Less accurate

8. Comparative Analysis of Different MPPT Techniques

When using MPPT controllers to harvest peak power from PV systems, it is also necessary to choose the most appropriate tracker based on its application. These design approaches for MPPT controllers differ from one another in several aspects. Among the parameters of interest used for comparison, cost, response time, and efficiency are particularly important considerations when making a choice. This study compares various MPTT controllers using criteria such as cost, circuitry, complexity, response time, periodic tuning, sensed parameters, stability, accuracy, and partial shading (PS) conditions. Table 8 below shows a summary of this comparison. In addition, the efficiency of the different techniques has also been used for comparison based on reported values in the literature, as presented in Figure 7.

Table 8. Comparison of different MPPT techniques (reconstructed by authors with data from [44,50,129,130]).

MPPT Method	Cost	Circuitry (A/D)	Complexity	Response Time	Periodic Tuning	Sensed Parameters	Stability	Accuracy	PS
ABC	E	D	Medium	Fast	No	V, I	VS	Medium	Yes
ACO	AF	D	Low	Fast	Yes	V, I	VS	Medium	Yes
ANFIS	E	D	High	Fast	Yes	V, I	Stable	Medium	Yes
ANN	E	D	High	Medium	Yes	V, I or G, T	VS	High	Yes
ARV	IE	A/D	Low	Medium	Yes	V, I	NS	Medium	No
CS	VE	D	Low	Fast	No	V, I	VS	High	Yes
CV	IE	A	Low	Slow	Yes	V	NS	Low	No
FLC	AF	D	High	Medium	Yes	V, I	VS	High	Yes
FPSO	VE	D	Low	Fast	No	V, I	VS	High	Yes
FSB MPPT	AF	D	Low	Very Fast	Yes	V, I	VS	High	Yes
GA	AF	D	High	Fast	No	V, I	VS	Medium	Yes
GNT	AF	D	Very High	Fast	No	V, I	Stable	Medium	No
GWO	AF	D	Low	Medium	Yes	V	VS	High	Yes
GWO-P&O	AF	D	High	Medium	Yes	V	Stable	High	Yes
HC	IE	D	Low	Medium	No	V, I	Stable	Medium	No
HC-ANFIS	AF	D	High	Fast	No	V, I	VS	High	Yes
InC	E	D	Medium	Varies	No	V, I	Stable	Medium	No
IP&O	E	D	Medium	Medium	No	V, I	Stable	High	No
LTB MPPT	IE	D	Low	Fast	Yes	G, T or I, T	Memory-based	High	No
OCV	IE	A	Low	Slow	Yes	V	NS	Low	No
P&O	IE	A/D	Low	Slow	No	V, I	NS	Medium	No
PSO	AF	D	Medium	Fast	Yes	V, I	VS	Medium	Yes
PSO-P&O	AF	D	High	Fast	Yes	V, I	Stable	Medium	Yes
RCC	E	A	Low	Fast	Yes	V, I	VS	High	Yes
SCC	IE	A/D	Low	Slow	Yes	I	NS	Medium	No
SMC	E	D	Very High	Very fast	No	V, I	VS	Medium	Yes

VS: Very Stable, NS: Not Stable, V: Voltage, I: Current, VE: Very Expensive, E: Expensive, IE: Inexpensive, AF: Affordable, T: Temperature, G: Irradiance, PS: Partial Shading Condition, A: Analog, D: Digital.

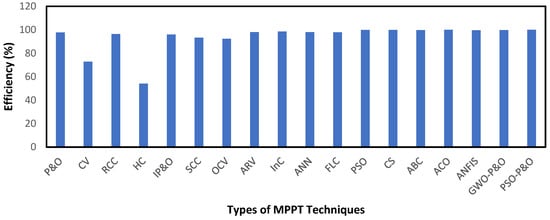
Figure 7. Reported efficiencies obtained from different MPPT techniques.

Based on the above comparison, it can be noted that conventional techniques are generally not suitable for MPPT in areas with partial shading (PS) conditions, as they face challenges in tracking the global MPP. Intelligent, hybrid, and optimization methods are more suitable to track the global MPP when partial shading occurs. In terms of cost and complexity, conventional methods are less expensive and less complex compared to the other three approaches. Some efficiency values obtained by different MPPT techniques have been reported in [44]. From the data presented, the PSO-P&O method has the highest efficiency, going up to 100%, while with the HC method has the least efficiency at 54.12%. These data are presented in Figure 7.

9. Conclusions

In this review paper, four MPPT approaches, and their classification based on nine factors have been presented. The four approaches presented in this review are: conventional, intelligent, optimization, and hybrid. The conventional approaches for tracking MPP are generally good under full sunshine conditions but have limitations in tracking the MPP when partial shading occurs. Intelligent, hybrid and optimization methods are complex in their designs, but are able to track the global MPP under partial shading conditions. These advanced methods, however, are more expensive compared to the conventional methods, making the choice of conventional approaches such as the P&O to be the most widely used in the industry for MPPT controller design. On the other hand, in terms of tracking speed and stability, conventional methods have a higher response time compared to the intelligent, optimization, and hybrid techniques. This work provides guidance in choosing among the different MPPT techniques.

10. Recommendations

To minimize the cost of MPPTs, further research should be conducted on improving the efficiency and tracking stability of the already existing conventional P&O algorithm, which is cost-effective. This can be achieved by exploring ways of selecting and adjusting step sizes used in the P&O method. In addition to that, further research on reducing the complexity of advanced MPPT algorithms will lower production cost, resulting in lower consumers prices.