Effect of Microchannel Diameter on Electroosmotic Flow Hysteresis
Abstract
:1. Introduction
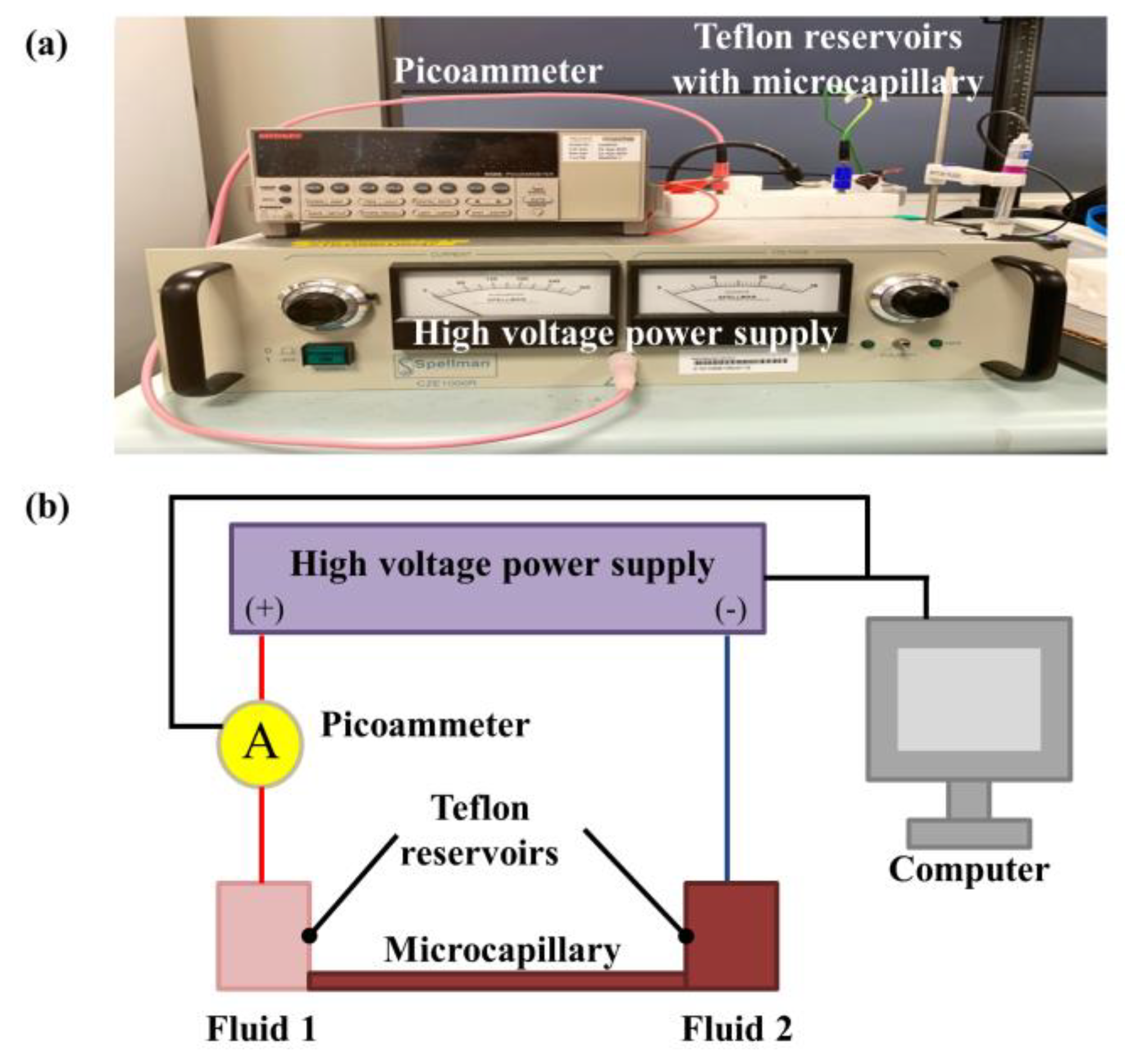
2. Experimental Setup, Materials and Procedures
3. Numerical Simulation
3.1. Governing Equations
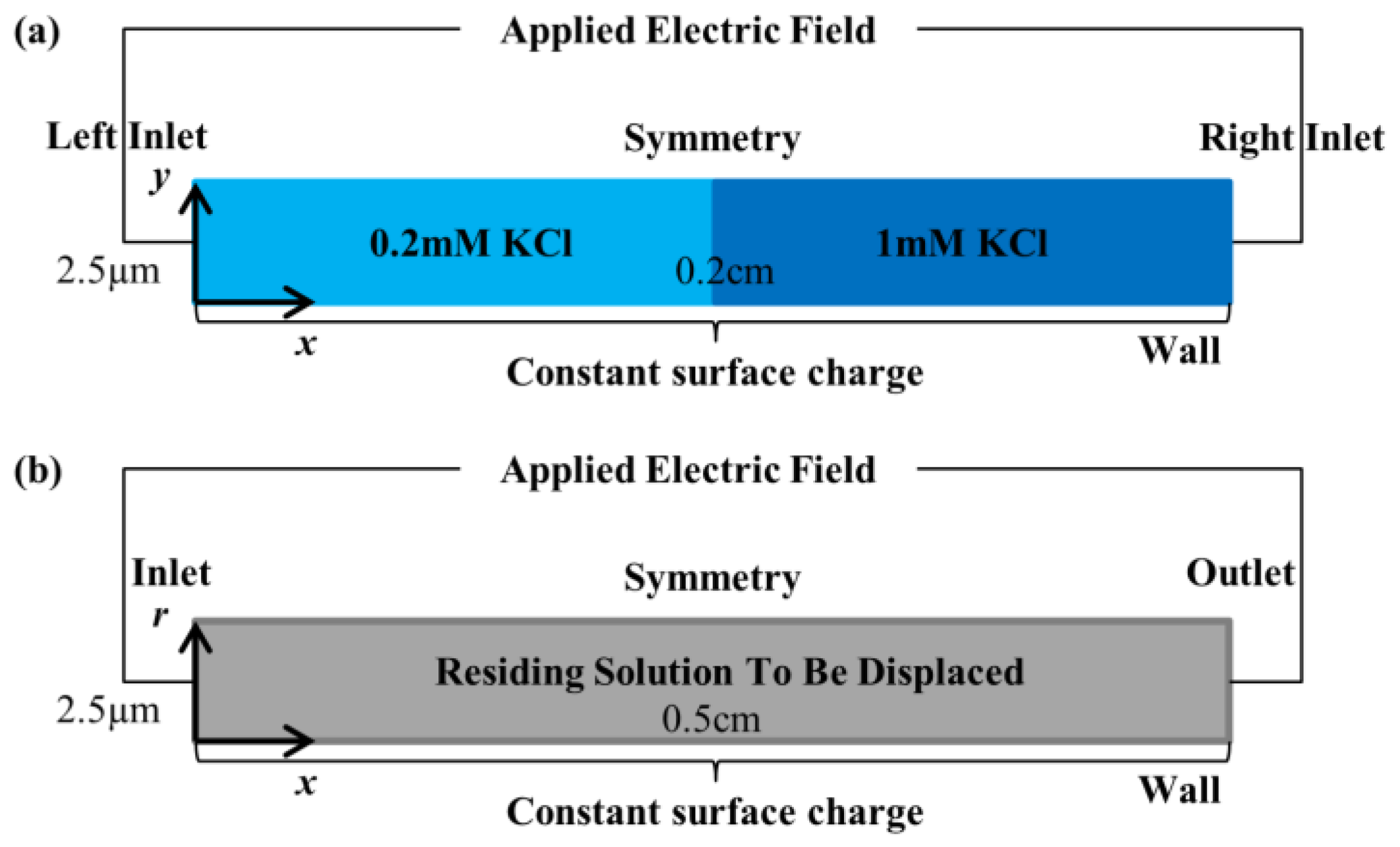
3.2. Simulation Domain
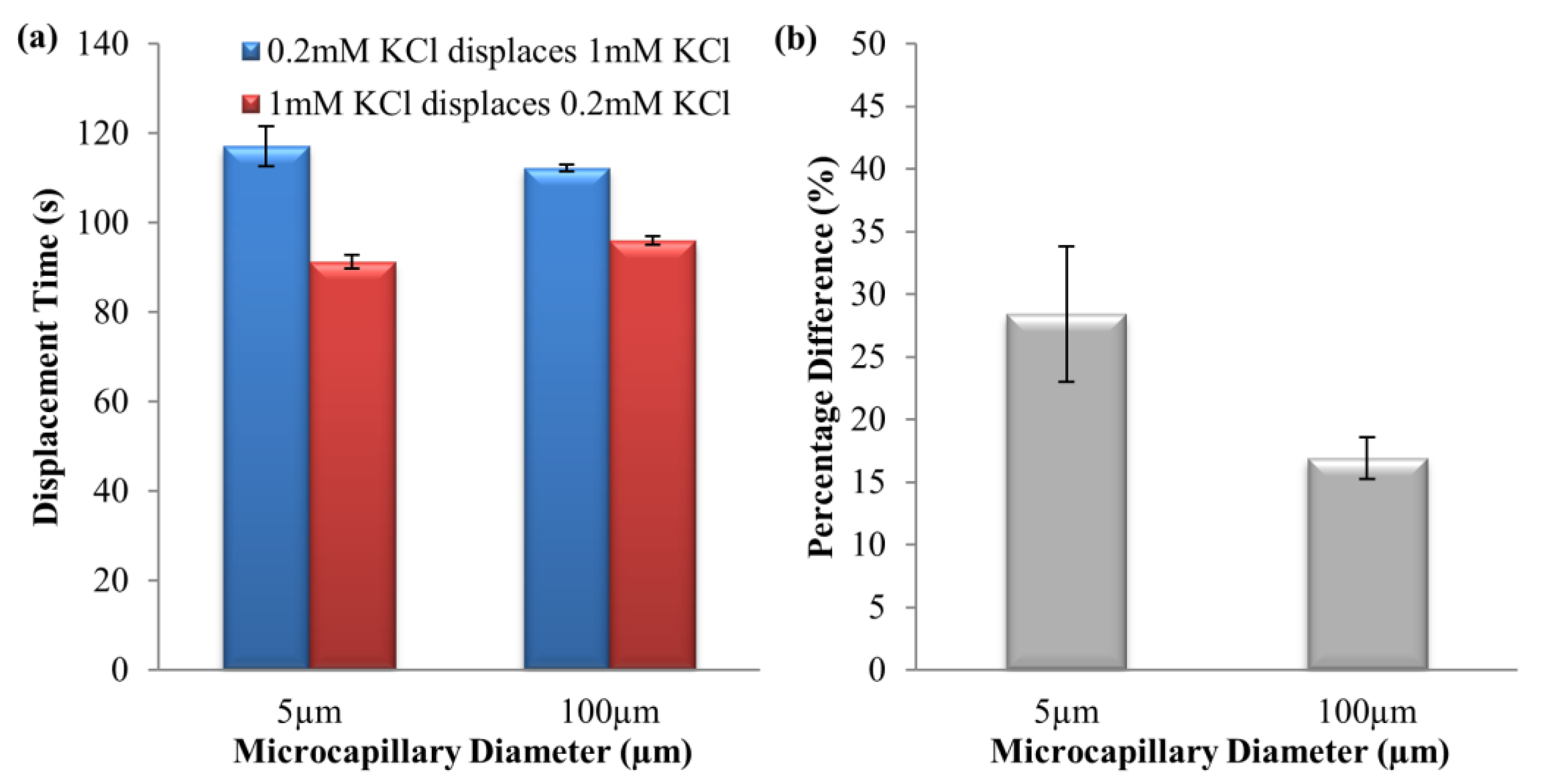
4. Results and Discussion
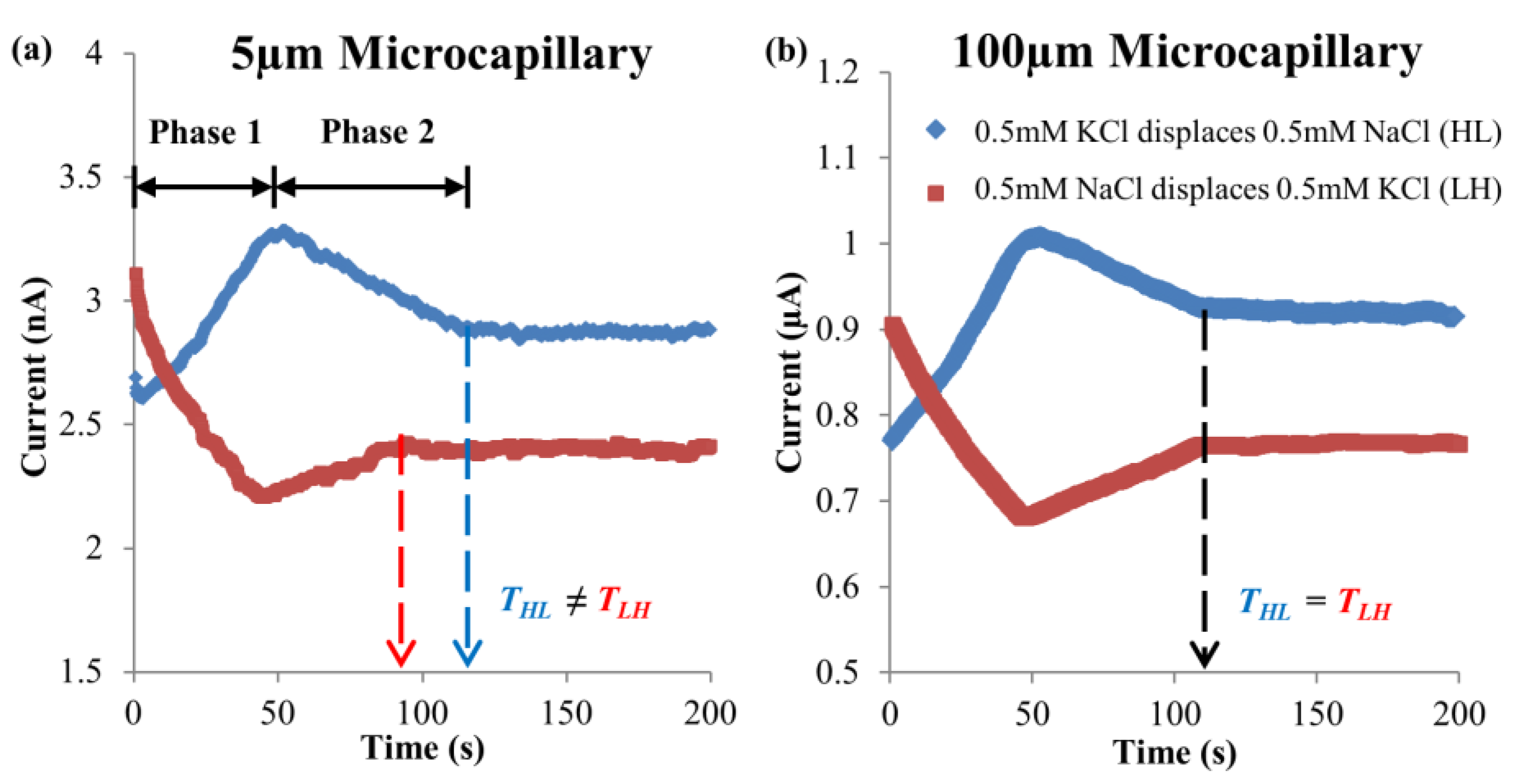
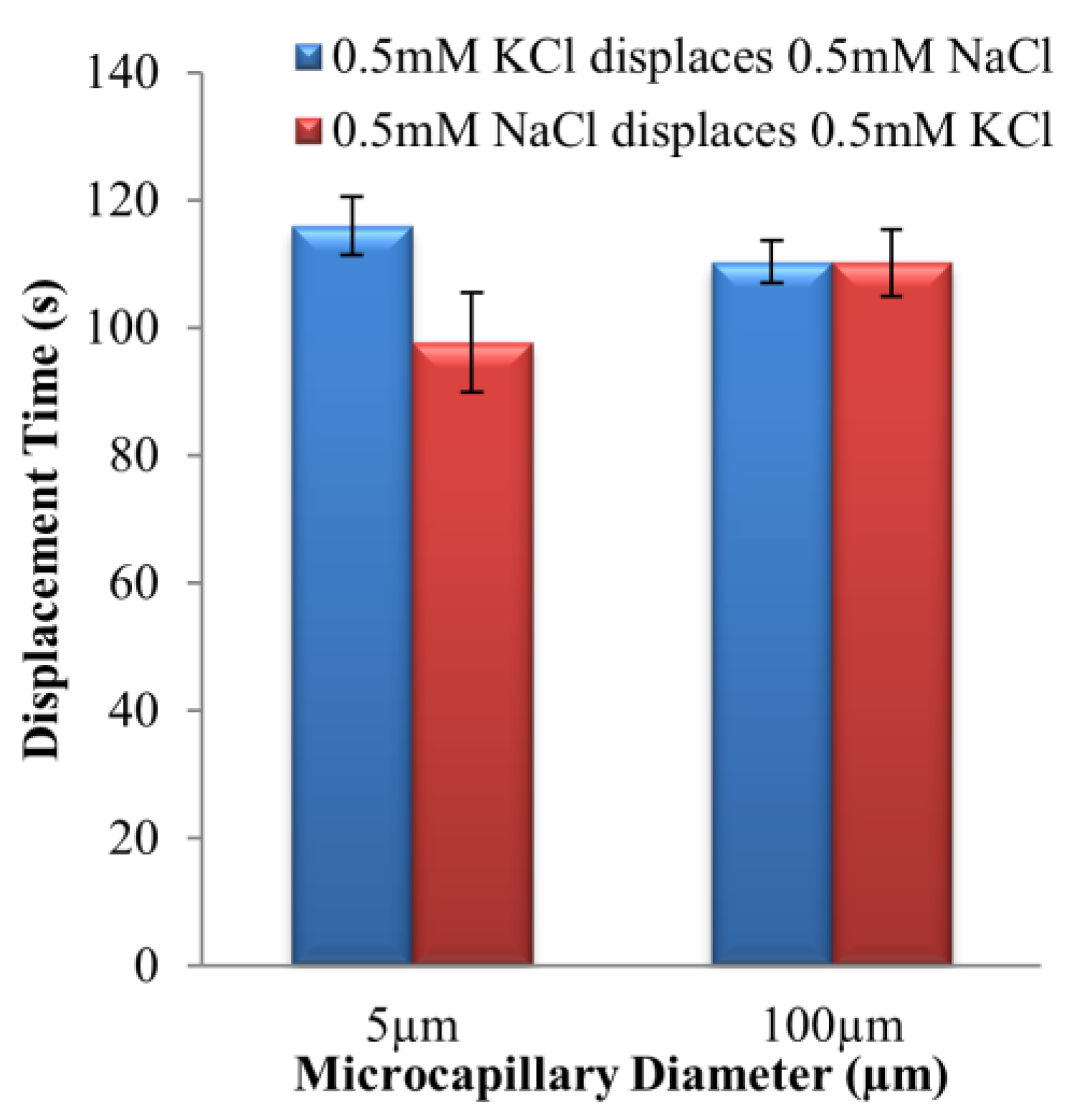
4.1. Dissimilar Ionic Species System: KCl–NaCl Solution Pair
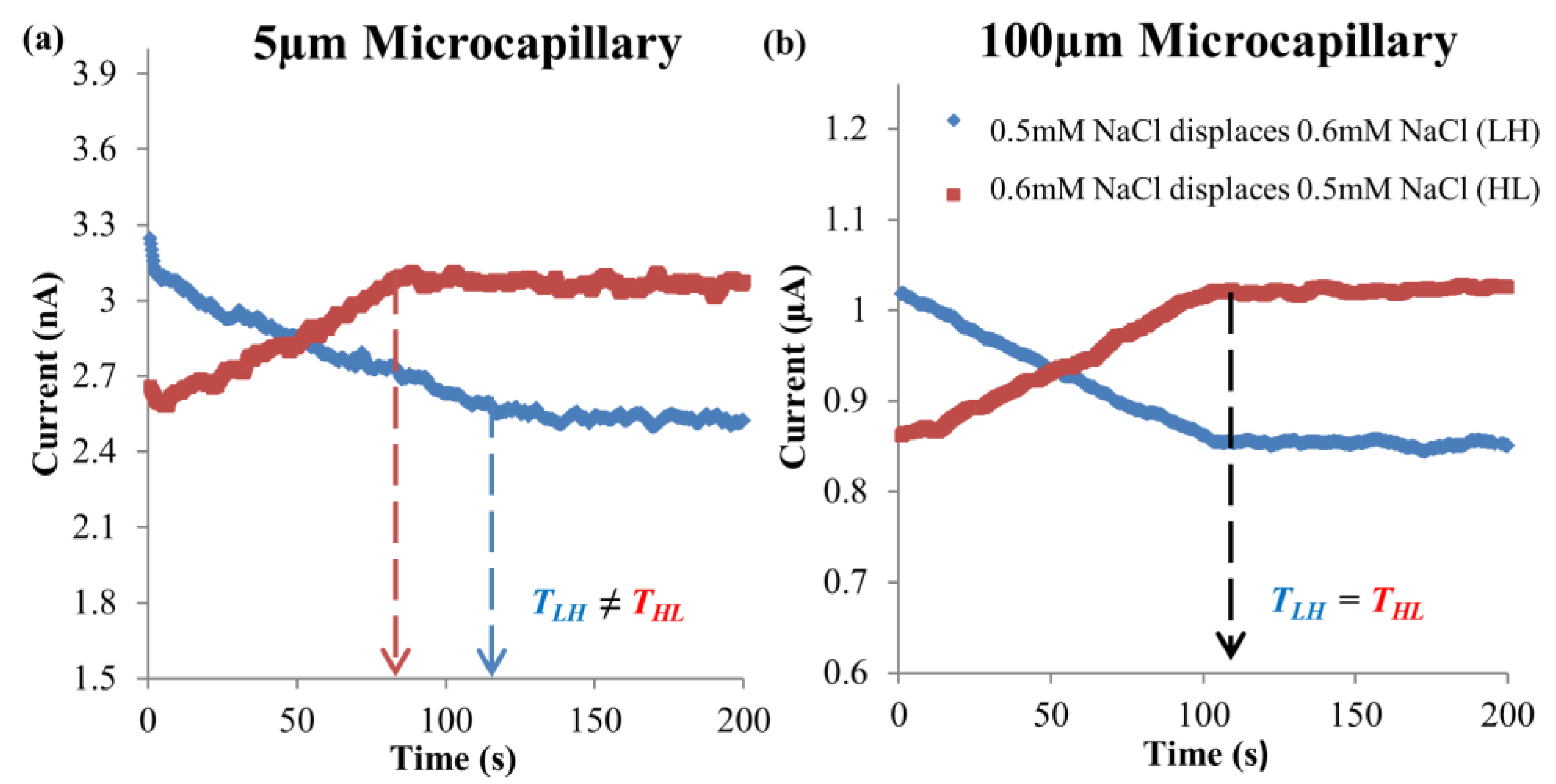
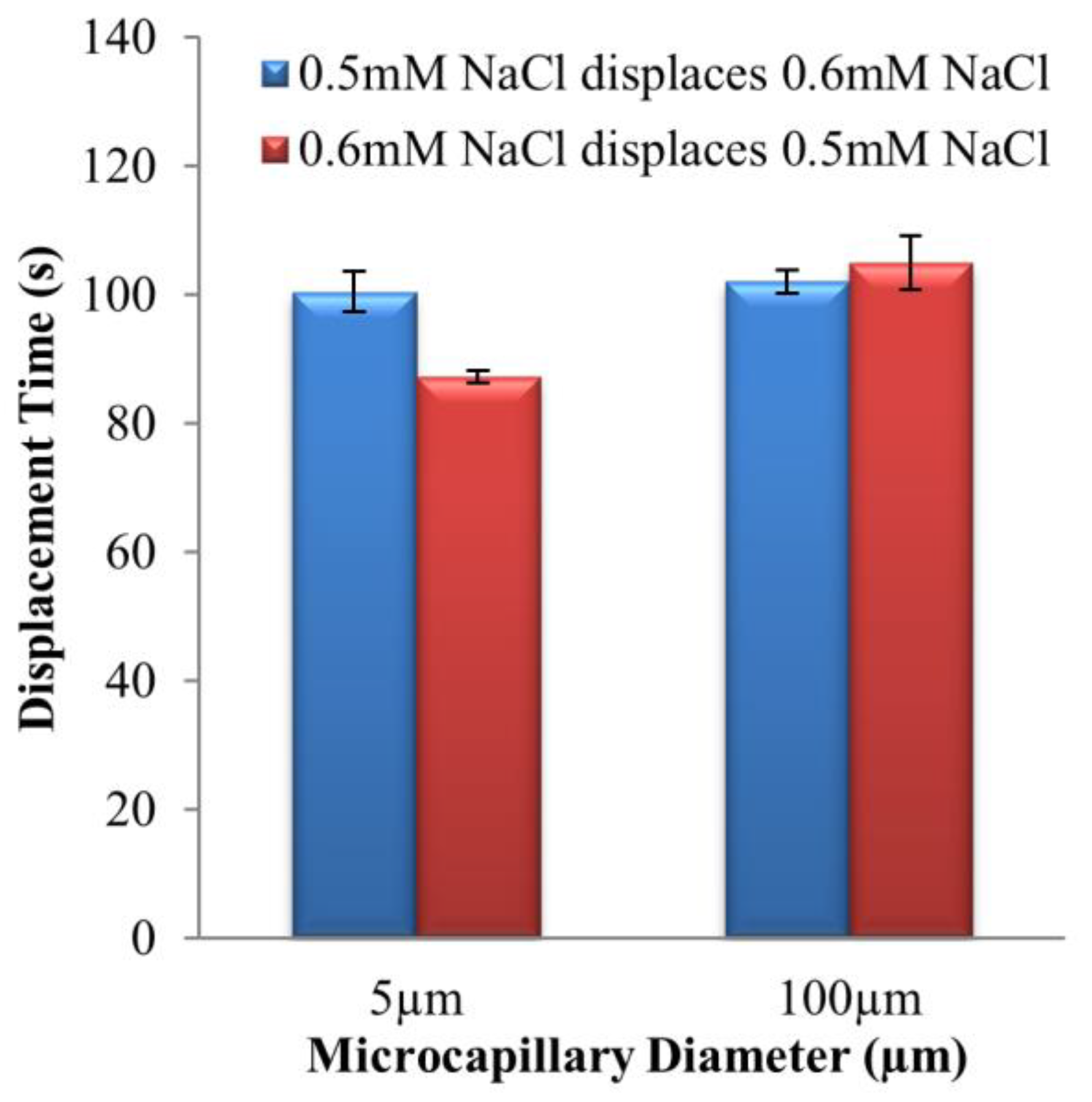
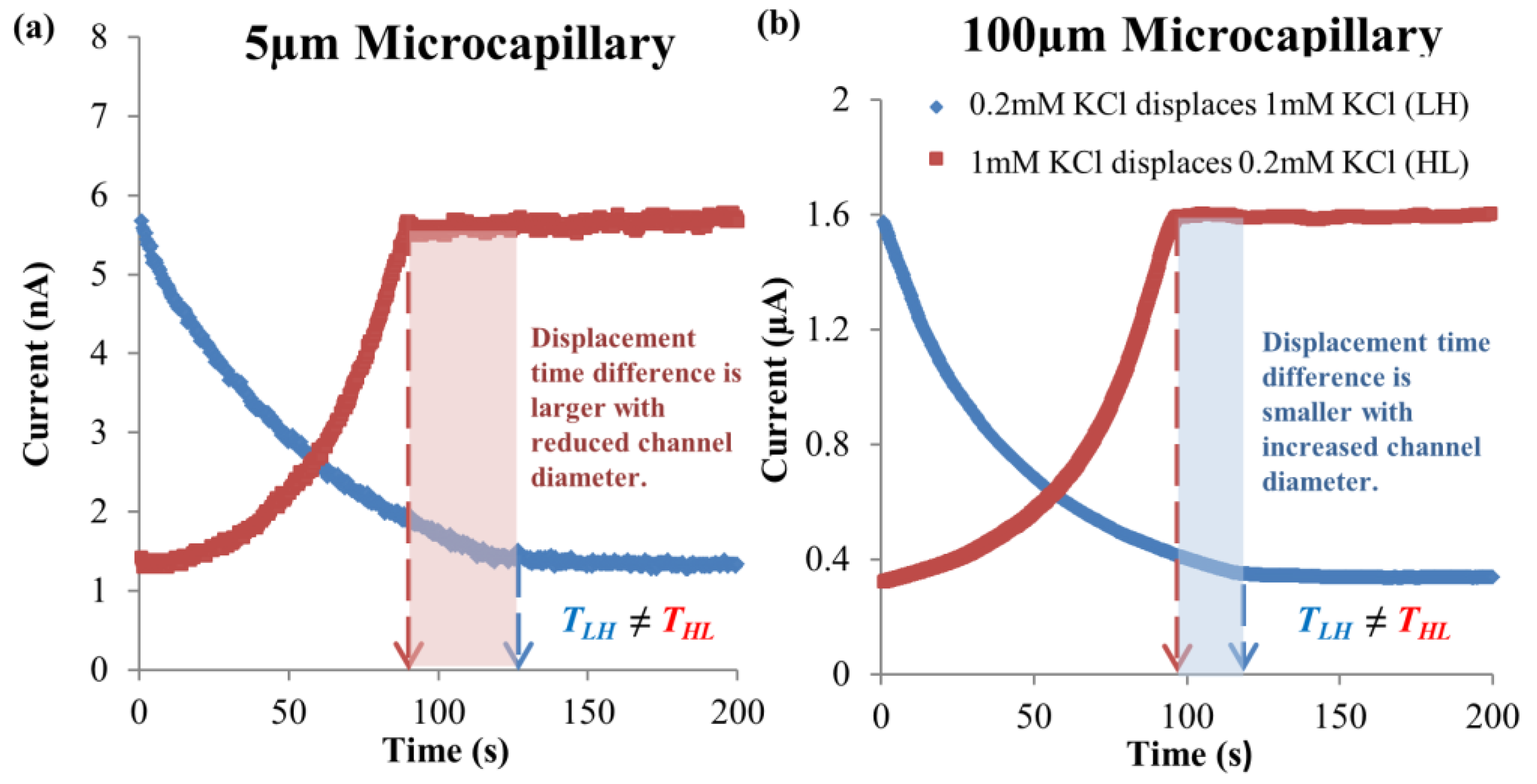
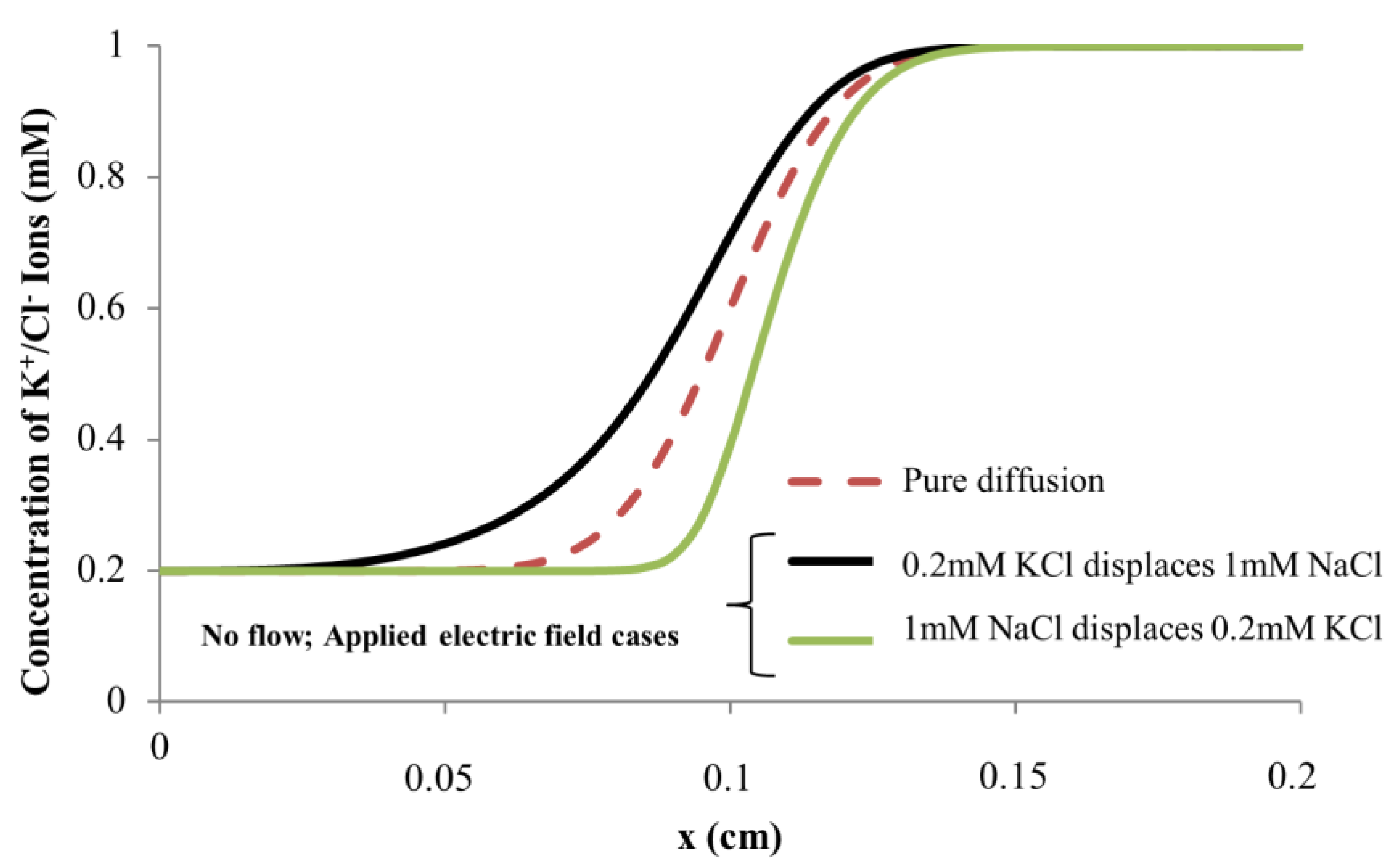
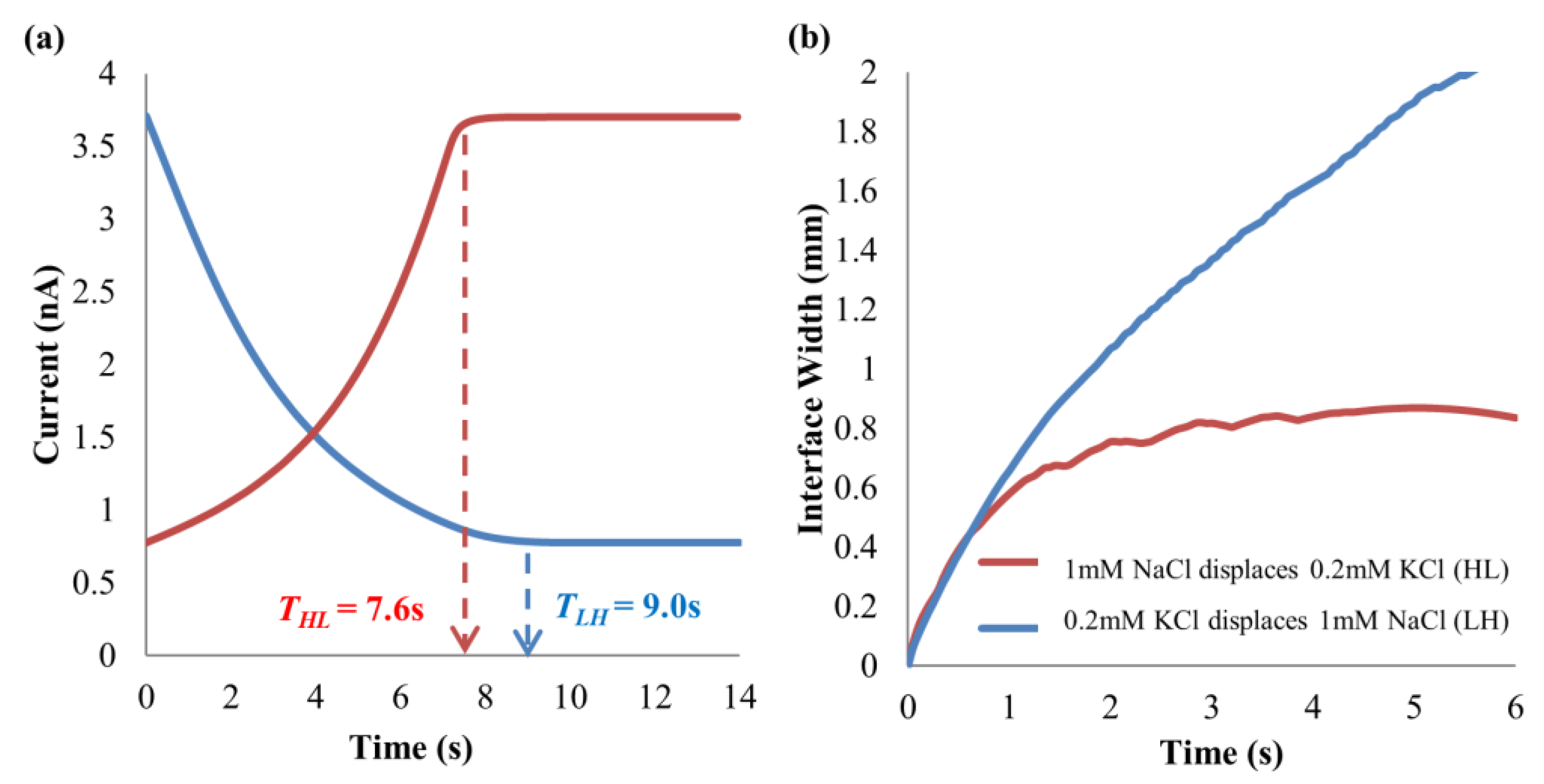
4.2. Dissimilar Concentration System—NaCl and KCl Solution Pairs
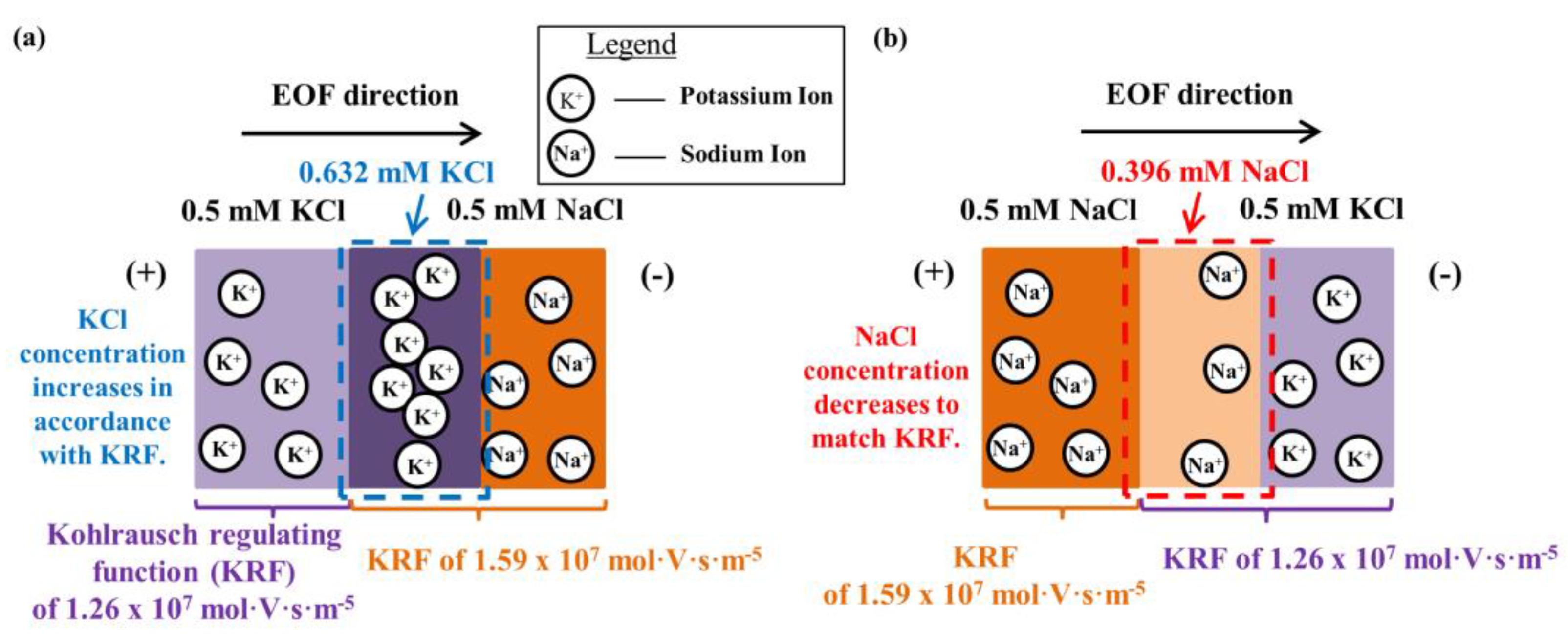
4.3. Simulation Results on Mechanics Contributing to Augmentation of EOF hysteresis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kusama, S.; Sato, K.; Matsui, Y.; Kimura, N.; Abe, H.; Yoshida, S.; Nishizawa, M. Transdermal electroosmotic flow generated by a porous microneedle array patch. Nat. Commun. 2021, 12, 658. [Google Scholar] [CrossRef] [PubMed]
- Buie, C.R.; Posner, J.D.; Fabian, T.; Cha, S.W.; Kim, D.; Prinz, F.B.; Eaton, J.K.; Santiago, J.G. Water management in proton exchange membrane fuel cells using integrated electroosmotic pumping. J. Power Sources 2006, 161, 191–202. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Y.; Guo, Q.; Yang, J. Modeling of electroosmotic pumping of nonconducting liquids and biofluids by a two-phase flow method. J. Electroanal. Chem. 2009, 636, 86–92. [Google Scholar] [CrossRef]
- Balasuriya, S. Dynamical systems techniques for enhancing microfluidic mixing. J. Micromech. Microeng. 2015, 25, 094005. [Google Scholar] [CrossRef]
- Modarres, P.; Tabrizian, M. Electrohydrodynamic-driven micromixing for the synthesis of highly monodisperse nanoscale liposomes. ACS Appl. Nano Mater. 2020, 3, 4000–4013. [Google Scholar] [CrossRef]
- Trabzon, L.; Karimian, G.R.; Khosroshahi, A.; Gül, B.G.; Bakhshayesh, A.; Koçak, A.F.; Akyıldız, D.; Aldi, Y.E. High-throughput nanoscale liposome formation via electrohydrodynamic-based micromixer. Phys. Fluids 2022, 34, 102011. [Google Scholar] [CrossRef]
- Mohammad Jafarpour, A.; Rostamzadeh Khosroshahi, A.; Hanifi, M.; Sadegh Moghanlou, F. Experimental study on the performance of a mini-scale Y-type mixer with two liquid metal-enabled pumps. Phys. Fluids 2022, 34, 112110. [Google Scholar] [CrossRef]
- Huang, M.F.; Hsu, C.E.; Tseng, W.L.; Lin, Y.C.; Chang, H.T. Separation of dsDNA in the presence of electroosmotic flow under discontinuous conditions. Electrophoresis 2001, 22, 2281–2290. [Google Scholar] [CrossRef]
- Giordano, B.C.; Burgi, D.S.; Hart, S.J.; Terray, A. On-line sample pre-concentration in microfluidic devices: A review. Anal. Chim. Acta 2012, 718, 11–24. [Google Scholar] [CrossRef]
- Nguyen, N.V.T.; Smadja, C.; Taverna, M.; El Mousli, S.; Secret, E.; Siaugue, J.M.; Nguyen, L.T.H.; Mai, T.D. Electroosmotic flow modulation for improved electrokinetic preconcentration: Application to channel electrophoresis of fluorescent magnetic nanoparticles. Anal. Chim. Acta 2021, 1161, 338466. [Google Scholar] [CrossRef]
- Horvath, J.; Dolník, V. Polymer wall coatings for channel electrophoresis. Electrophoresis 2001, 22, 644–655. [Google Scholar] [CrossRef]
- Preisler, J.; Yeung, E.S. Characterization of nonbonded poly (ethylene oxide) coating for channel electrophoresis via continuous monitoring of electroosmotic flow. Anal. Chem. 1996, 68, 2885–2889. [Google Scholar] [CrossRef]
- Lim, A.E.; Lim, C.Y.; Lam, Y.C.; Taboryski, R.; Wang, S.R. Effect of nanostructures orientation on electroosmotic flow in a microfluidic channel. Nanotechnology 2017, 28, 255303. [Google Scholar] [CrossRef] [Green Version]
- Lim, A.E.; Lam, Y.C. Numerical investigation of nanostructure orientation on electroosmotic flow. Micromachines 2020, 11, 971. [Google Scholar] [CrossRef]
- Ren, L.; Masliyah, J.; Li, D. Experimental and theoretical study of the displacement process between two electrolyte solutions in a microchannel. J. Colloid Interface Sci. 2003, 257, 85–92. [Google Scholar] [CrossRef]
- Ren, L.; Escobedo, C.; Li, D. Electroosmotic flow in a microchannel with one solution displacing another solution. J. Colloid Interface Sci. 2001, 242, 264–271. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.W.; Chang, C.H.; Wei, H.H. Roles of solution conductivity mismatch in transient current and fluid transport in electrolyte displacement by electro-osmotic flow. Microfluid. Nanofluid. 2011, 10, 337–353. [Google Scholar] [CrossRef]
- Mampallil, D.; van den Ende, D.; Mugele, F. A simple method to determine the surface charge in microfluidic channels. Electrophoresis 2010, 31, 563–569. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical models of electro-magnetohydrodynamic multiphase flows synthesis with nano-sized hafnium particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef] [Green Version]
- Mekheimer, K.S.; Zaher, A.Z.; Hasona, W.M. Entropy of AC electro-kinetics for blood mediated gold or copper nanoparticles as a drug agent for thermotherapy of oncology. Chin. J. Phys. 2020, 65, 123–138. [Google Scholar] [CrossRef]
- Lim, A.E.; Lim, C.Y.; Lam, Y.C. Electroosmotic flow hysteresis for dissimilar ionic solutions. Biomicrofluidics 2015, 9, 024113. [Google Scholar] [CrossRef] [Green Version]
- Lim, A.E.; Lim, C.Y.; Lam, Y.C. Electroosmotic flow hysteresis for dissimilar anionic solutions. Anal. Chem. 2016, 88, 8064–8073. [Google Scholar] [CrossRef]
- Lim, A.E.; Lam, Y.C. Electroosmotic Flow Hysteresis for Fluids with Dissimilar pH and Ionic Species. Micromachines 2021, 12, 1031. [Google Scholar] [CrossRef]
- Lim, C.Y.; Lam, Y.C. Direction dependence of displacement time for two-fluid electroosmotic flow. Biomicrofluidics 2021, 6, 012816. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.Y.; Lim, A.E.; Lam, Y.C. Ionic origin of electro-osmotic flow hysteresis. Sci. Rep. 2016, 6, 22329. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.Y.; Lim, A.E.; Lam, Y.C. pH change in electroosmotic flow hysteresis. Anal. Chem. 2017, 89, 9394–9399. [Google Scholar] [CrossRef]
- Zhang, L.; McNeece, C.J.; Hesse, M.A.; Wang, M. Reactive transport of protons in electro-osmotic displacements with electrolyte concentration difference in a microchannel. Anal. Chem. 2018, 90, 11802–11811. [Google Scholar] [CrossRef]
- Jing, D.; Zhan, X. Cross-sectional dimension dependence of electroosmotic flow in fractal treelike rectangular microchannel network. Micromachines 2020, 11, 266. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.H.; Moon, Y.R.; Chung, B.Y.; Kim, J.S.; Lee, K.S.; Cho, J.Y.; Kim, J.H. Practical use of chemical probes for reactive oxygen species produced in biological systems by γ-irradiation. Radiat. Phys. Chem. 2009, 78, 323–327. [Google Scholar] [CrossRef]
- Britton, G. Carotenoid research: History and new perspectives for chemistry in biological systems. Biochim. Biophys. Acta Mol. Cell Biol. Lipids 2020, 1865, 158699. [Google Scholar] [CrossRef]
- Allec, S.I.; Sun, Y.; Sun, J.; Chang, C.E.A.; Wong, B.M. Heterogeneous CPU+ GPU-enabled simulations for DFTB molecular dynamics of large chemical and biological systems. J. Chem. Theory Comput. 2019, 15, 2807–2815. [Google Scholar] [CrossRef]
- Yan, D.G.; Yang, C.; Huang, X.Y. Effect of finite reservoir size on electroosmotic flow in microchannels. Microfluid. Nanofluid. 2007, 3, 333–340. [Google Scholar] [CrossRef]
- Rodríguez, I.; Chandrasekhar, N. Experimental study and numerical estimation of current changes in electroosmotically pumped microfluidic devices. Electrophoresis 2005, 26, 1114–1121. [Google Scholar] [CrossRef] [PubMed]
- Almutairi, Z.A.; Glawdel, T.; Ren, C.L.; Johnson, D.A. A Y-channel design for improving zeta potential and surface conductivity measurements using the current monitoring method. Microfluid. Nanofluid. 2009, 6, 241–251. [Google Scholar] [CrossRef]
- Tang, G.; Yan, D.; Yang, C.; Gong, H.; Chai, J.C.; Lam, Y.C. Assessment of Joule heating and its effects on electroosmotic flow and electrophoretic transport of solutes in microfluidic channels. Electrophoresis 2006, 27, 628–639. [Google Scholar] [CrossRef] [PubMed]
- Arulanandam, S.; Li, D. Determining ζ potential and surface conductance by monitoring the current in electro-osmotic flow. J. Colloid Interface Sci. 2002, 225, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems; John Wiley & Sons: Haboken, NJ, USA, 2012. [Google Scholar]
- Hruška, V.; Gaš, B. Kohlrausch regulating function and other conservation laws in electrophoresis. Electrophoresis 2007, 28, 3–14. [Google Scholar] [CrossRef] [PubMed]

| Solutions | Conductivities (µS·cm−1) | pH |
|---|---|---|
| 0.5 mM NaCl | 63.5 ± 0.1 | 5.68 ± 0.03 |
| 0.6 mM NaCl | 76.2 ± 0.2 | 5.49 ± 0.05 |
| 0.2 mM KCl | 30.8 ± 0.1 | 5.62 ± 0.02 |
| 0.5 mM KCl | 75.5 ± 0.2 | 5.57 ± 0.02 |
| 1 mM KCl | 147.9 ± 0.1 | 5.73 ± 0.01 |
| Constants | Value | Symbol (Unit) |
|---|---|---|
| Free space permittivity | 8.85 × 10−12 | ɛo (C·V−1·m−1) |
| Fluid relative permittivity | 80 | ɛr |
| Fluid viscosity | 8.90 × 10−4 | µ (kg·m−1·s−1) |
| Fluid density | 1000 | ρ (kg·m−3) |
| Boltzmann constant | 1.381 × 10−23 | kb (m2·kg·s−2·K−1) |
| Faraday constant | 96,485 | F (C·mol−1) |
| Avogadro constant | 6.022 × 1023 | Na (mol−1) |
| Gas constant | 8.314 | R (J·mol−1·K−1) |
| Boltzmann constant | 1.381 × 10−23 | kb (m2·kg·s−2·K−1) |
| Temperature | 298 | T (K) |
| Electron charge | 1.602 × 10−19 | e (C) |
| K+ diffusion coefficient | 1.957 × 10−9 [37] | DK+ (m2·s−1) |
| Na+ diffusion coefficient | 1.334 × 10−9 [37] | DNa+ (m2·s−1) |
| Cl− diffusion coefficient | 2.032 × 10−9 [37] | DCl− (m2·s−1) |
| K+ mobility | 7.930 × 10−8 | um(K+) (m2·V−1·s−1) |
| Na+ mobility | 5.194 × 10−8 | um(Na+) (m2·V−1·s−1) |
| Cl− mobility | −7.919 × 10−8 | um(Cl−) (m2·V−1·s−1) |
| K+ charge number | +1 | zK+ |
| Na+ charge number | +1 | zNa+ |
| Cl− charge number | −1 | zCl− |
| Variable | Condition a | Boundary |
|---|---|---|
| Applied potential φ | φ = 25 V or 62.5 V | Inlet |
| φ = 0 V | Outlet | |
| −n·σ∇φ = 0 | Wall and symmetry | |
| Electrostatic wall potential ψ | n·∇ψ = 0 | Inlet, outlet and symmetry |
| n·∇ψ = S/(ɛoɛr) = −4.16 × 10−3/(ɛoɛr) | Wall | |
| Concentrations of ions ci | ci = co(i)exp[−zieψ/(kbT)] | Inlet and outlet |
| −n·[−Di∇ci − um(i)ci∇φ + vci] = 0 Note: The term vci will be removed for cases without flow. | Wall and symmetry | |
| Flow velocity v and Pressure p Note: This will be removed for cases without flow. | v = 0 | Wall |
| n·u = 0 | Symmetry | |
| p = 0 | Inlet and outlet |
| Microchannel Diameter | t-Score |
|---|---|
| 5 µm | −4.49 |
| 100 µm | 0.07 |
| Microchannel Diameter | t-Score |
|---|---|
| 5 µm | 9.09 |
| 100 µm | −1.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, A.E.; Goh, S. Effect of Microchannel Diameter on Electroosmotic Flow Hysteresis. Energies 2023, 16, 2154. https://doi.org/10.3390/en16052154
Lim AE, Goh S. Effect of Microchannel Diameter on Electroosmotic Flow Hysteresis. Energies. 2023; 16(5):2154. https://doi.org/10.3390/en16052154
Chicago/Turabian StyleLim, An Eng, and Shireen Goh. 2023. "Effect of Microchannel Diameter on Electroosmotic Flow Hysteresis" Energies 16, no. 5: 2154. https://doi.org/10.3390/en16052154
APA StyleLim, A. E., & Goh, S. (2023). Effect of Microchannel Diameter on Electroosmotic Flow Hysteresis. Energies, 16(5), 2154. https://doi.org/10.3390/en16052154






