Data-Driven Prediction of Unsteady Vortex Phenomena in a Conical Diffuser
Abstract
1. Introduction
2. Research Methods
2.1. Physical Flow Parameters
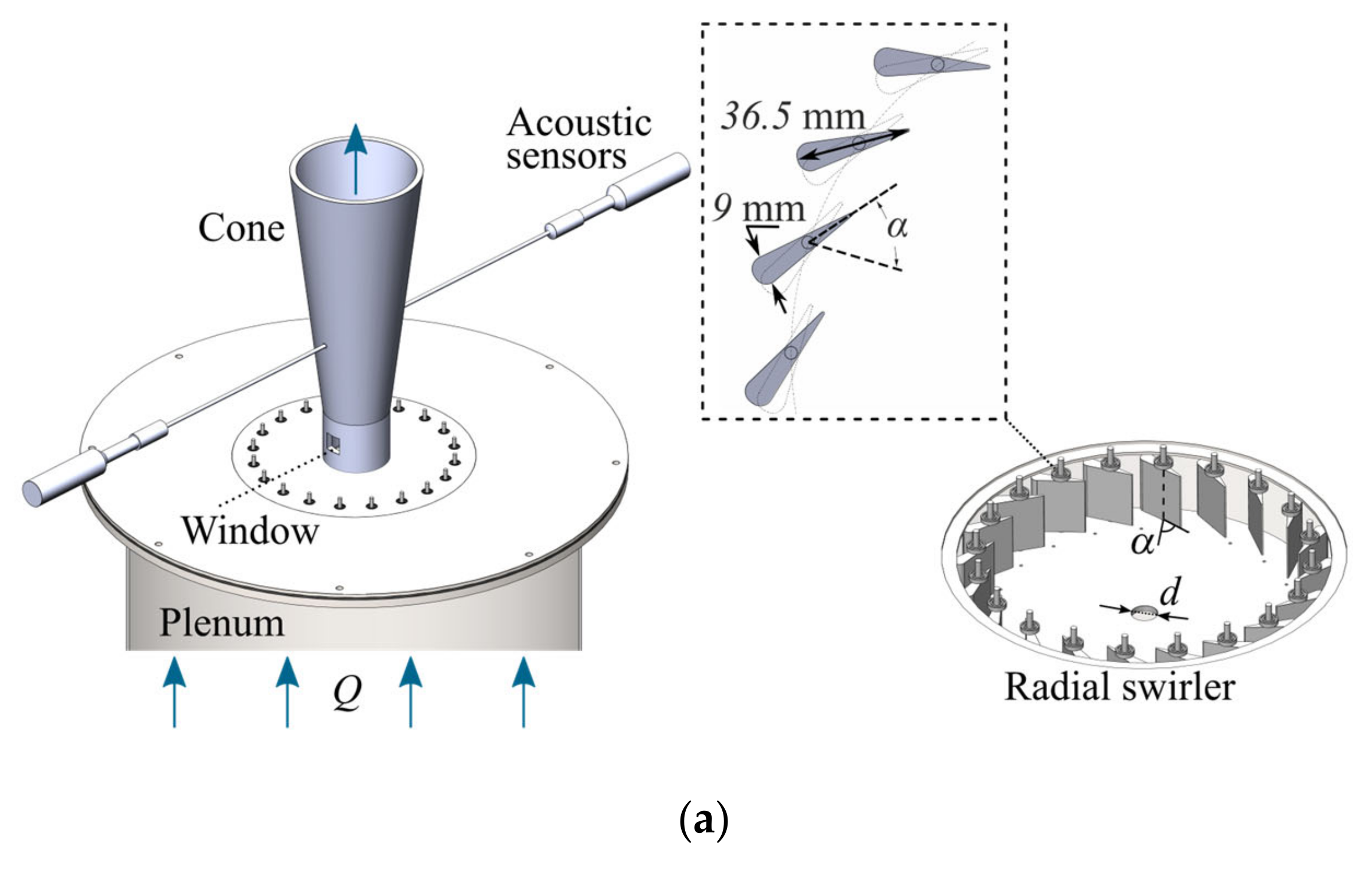
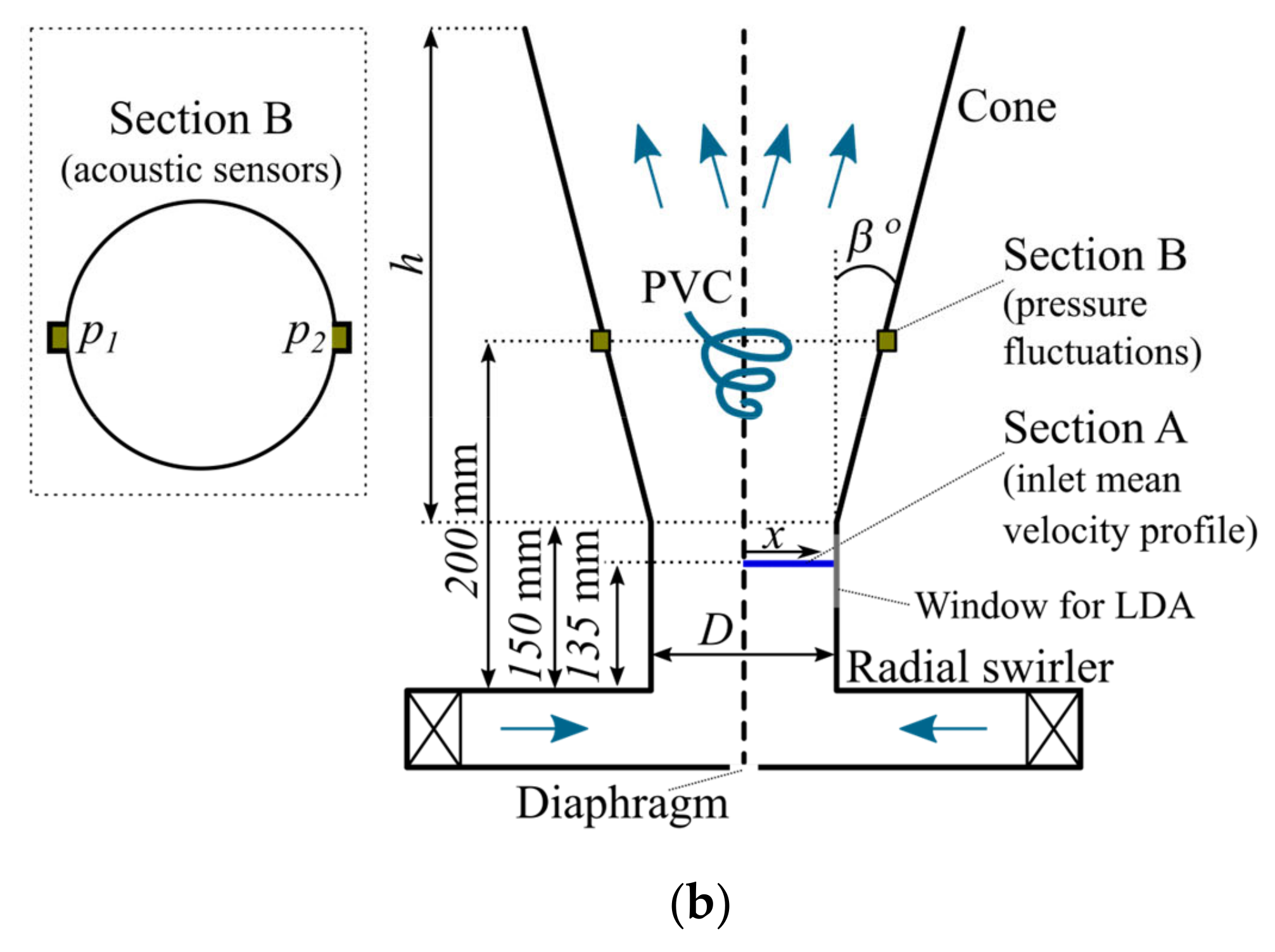
2.2. Experimental Setup
2.3. Adapting the LDA System of the Velocity Meter
2.4. Measuring Pressure Pulsations Caused by PVC
2.5. Empirical Database
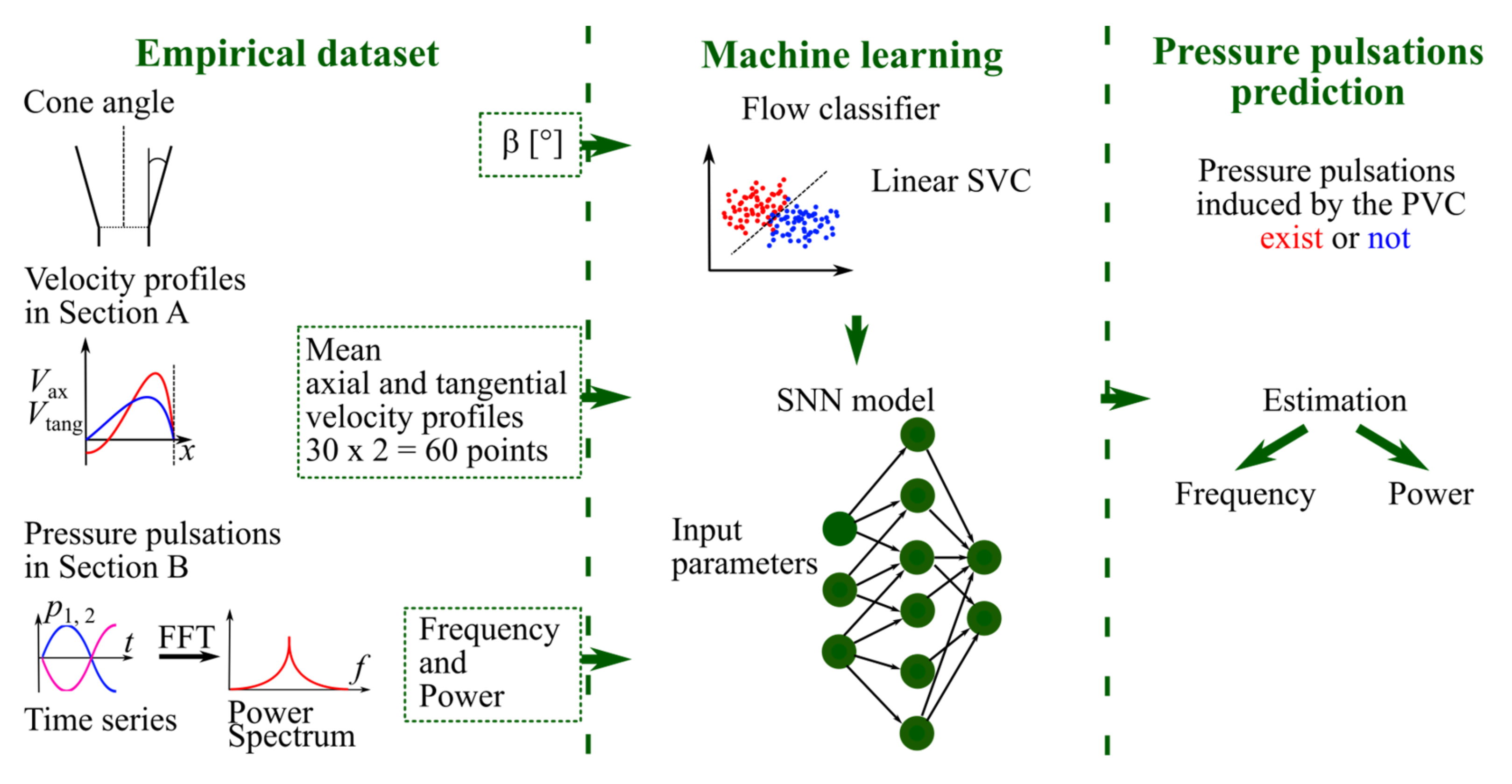
2.6. Machine Learning
3. Results and Discussion
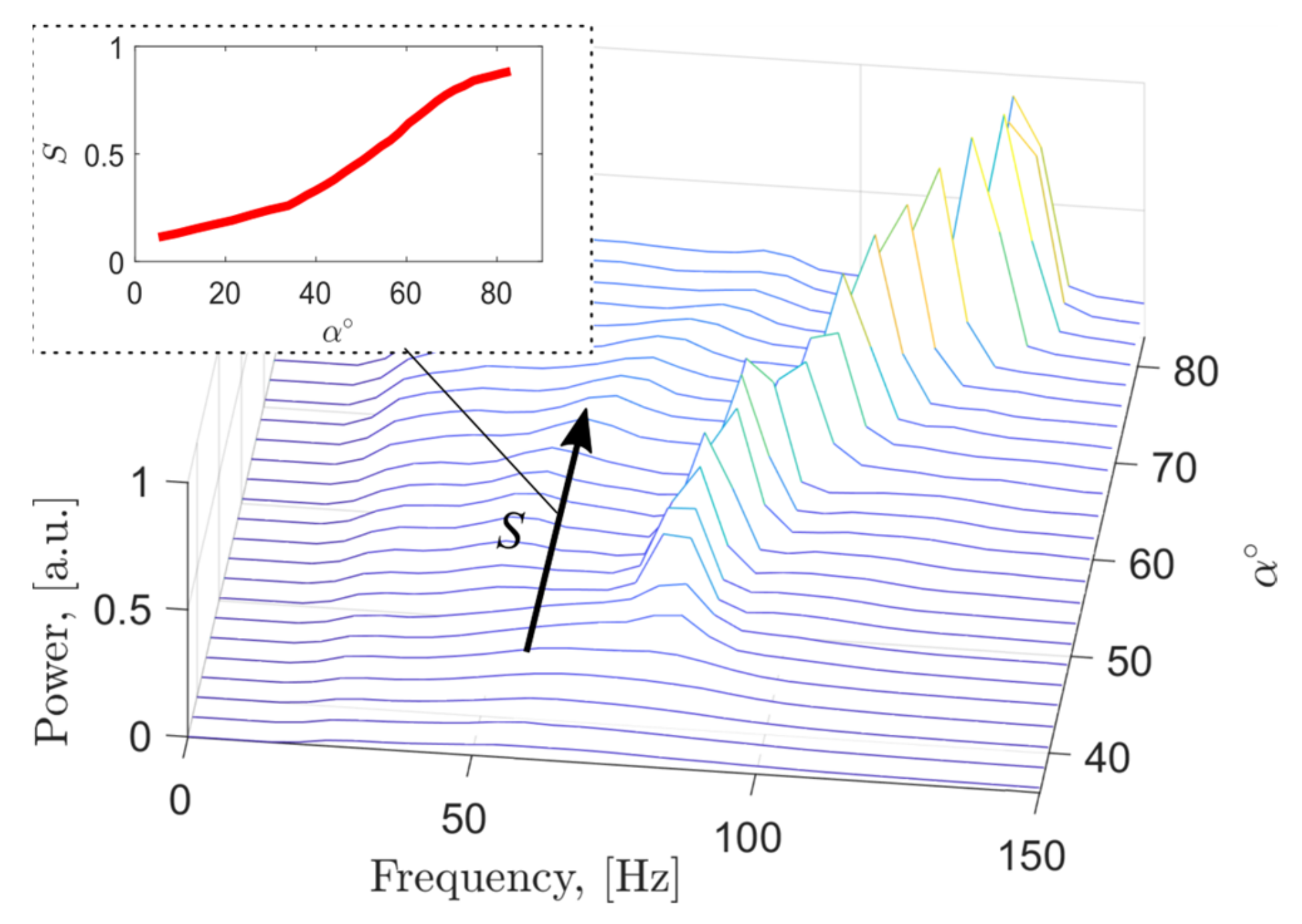
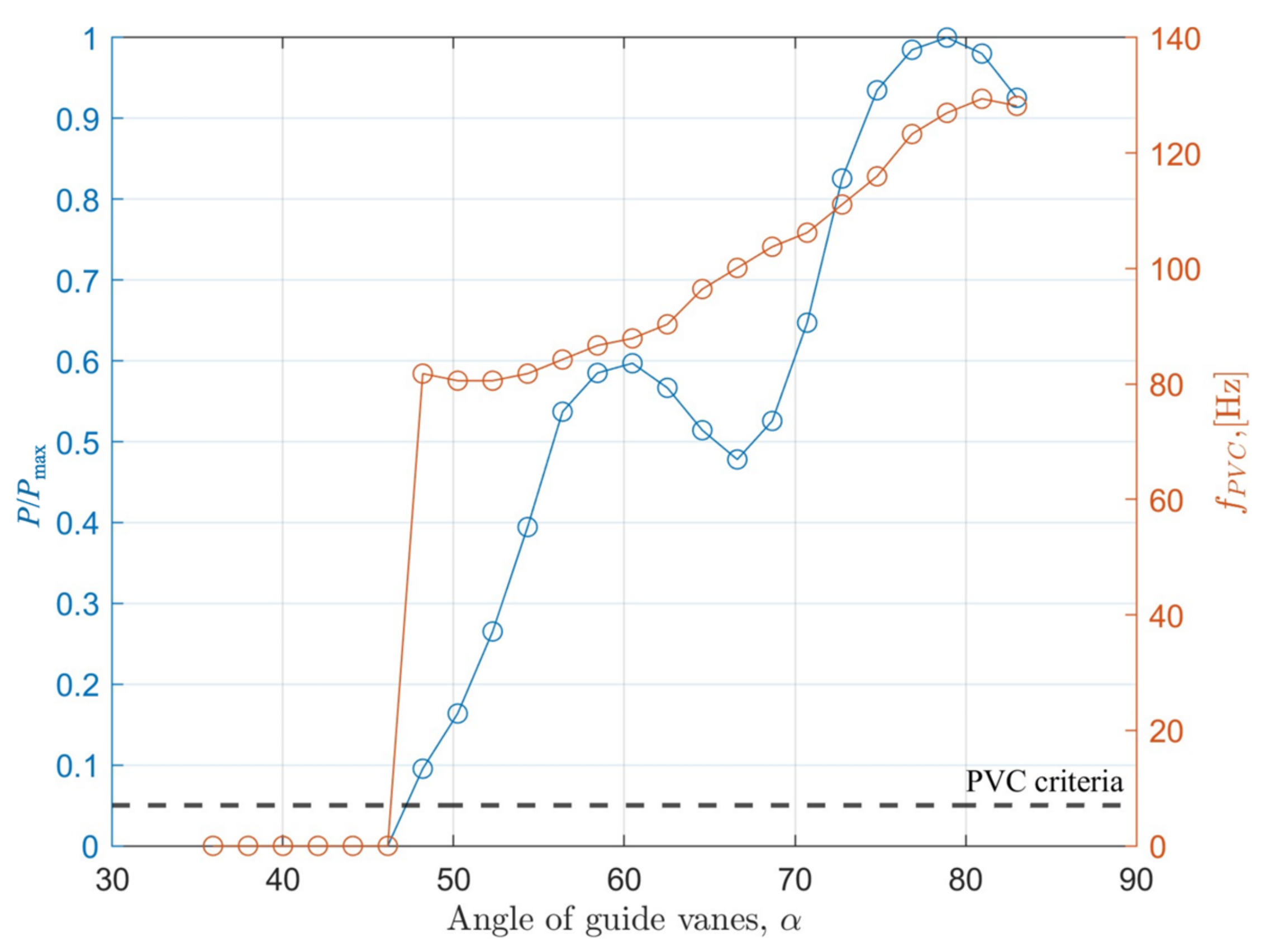
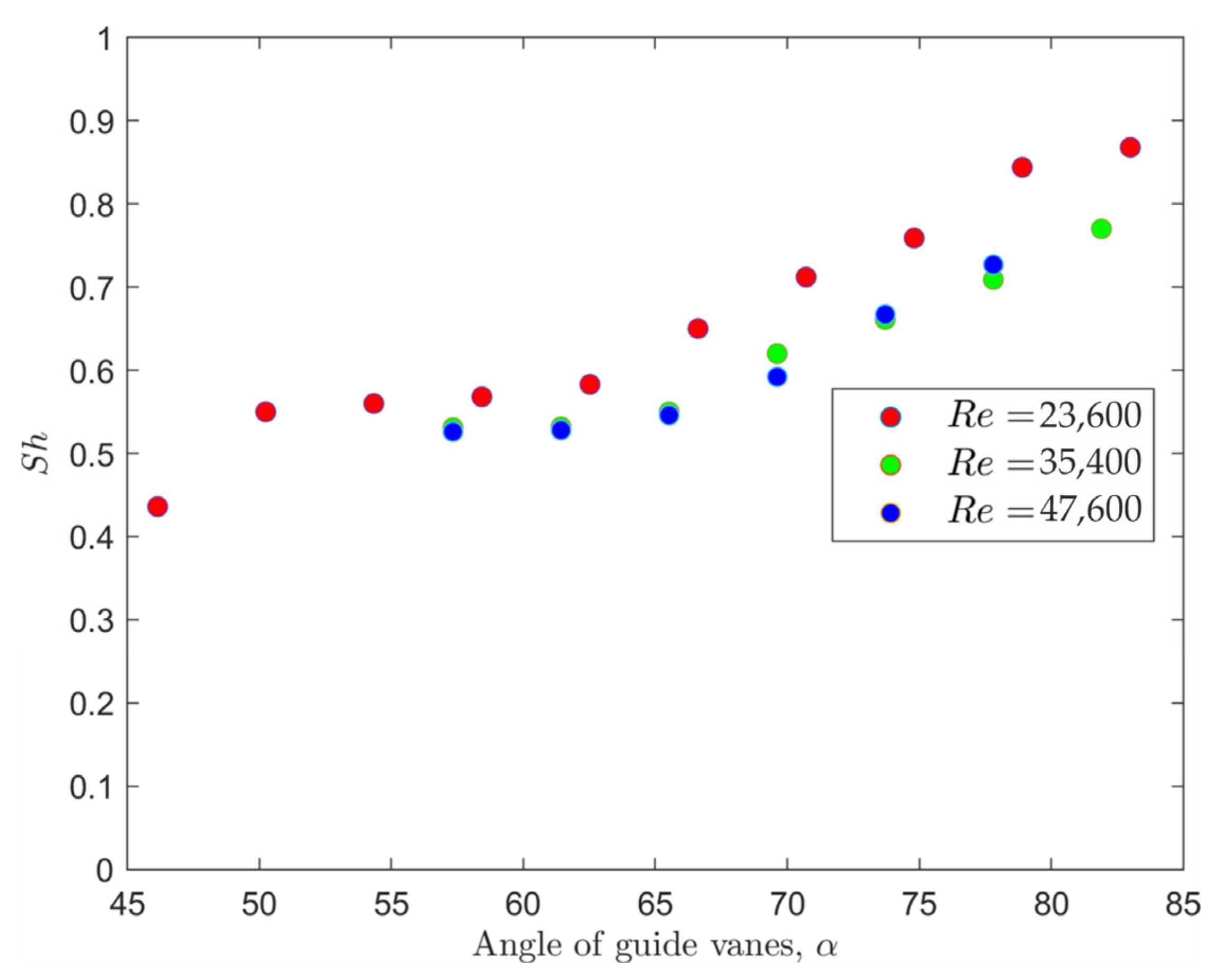
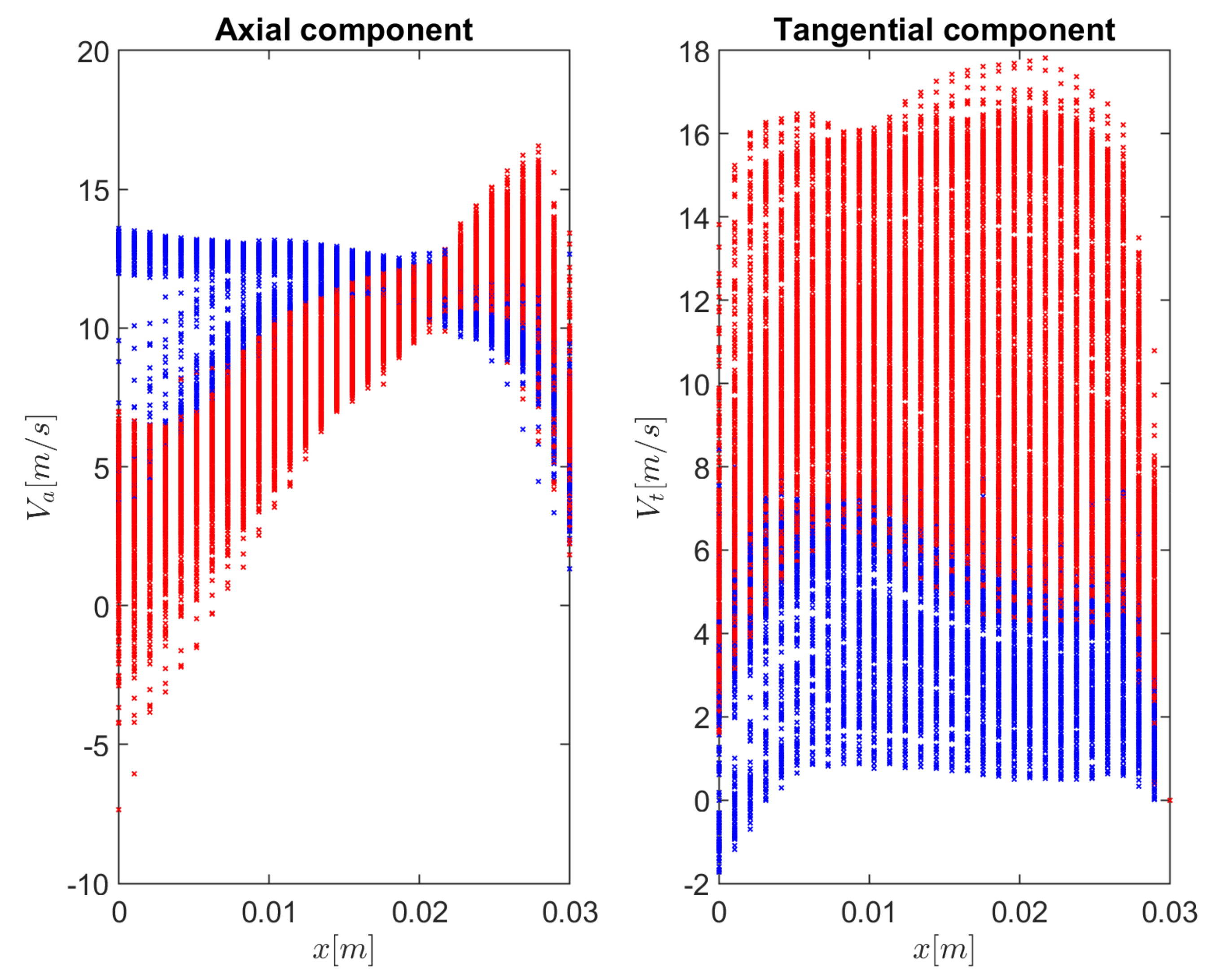
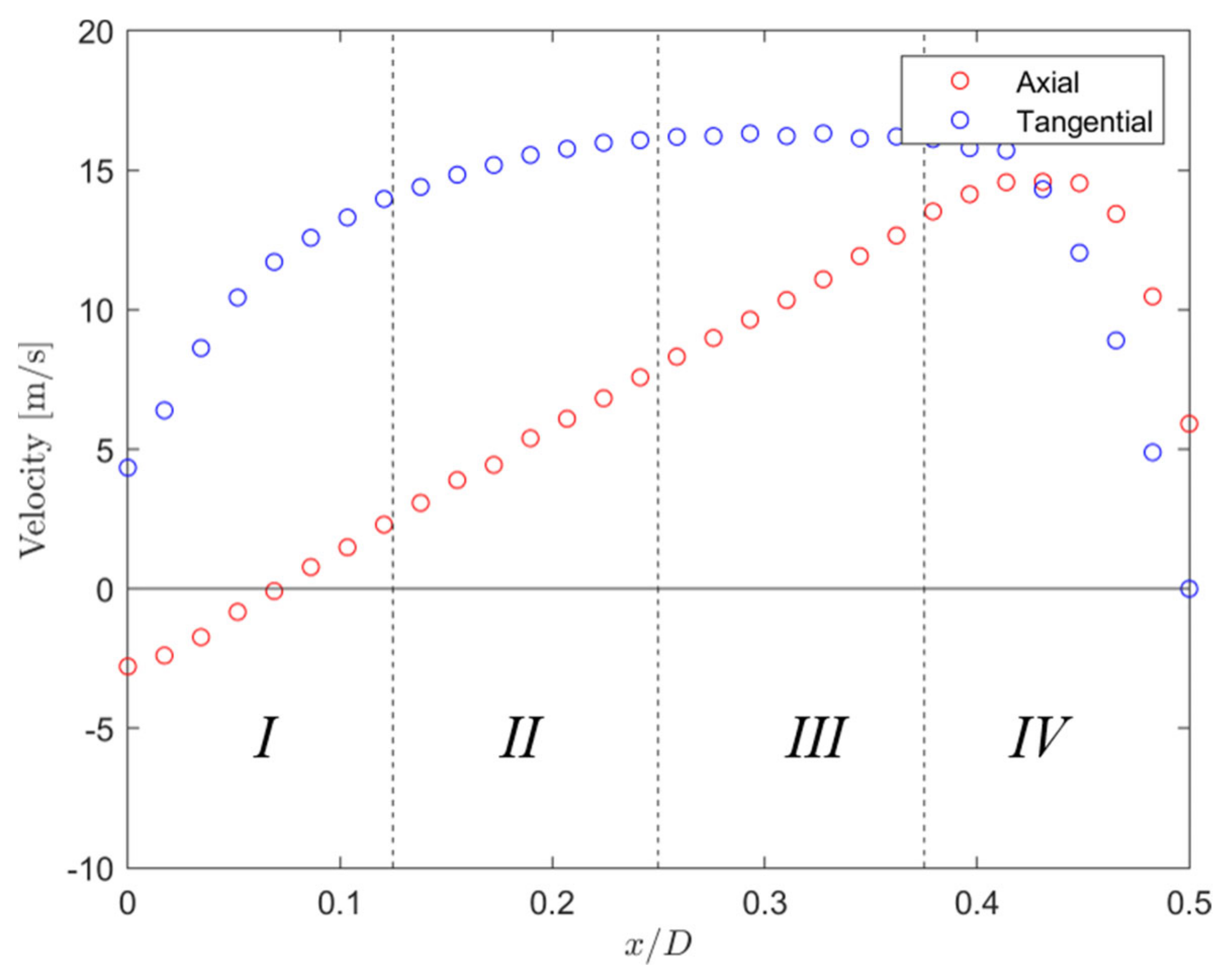
3.1. Flow Characteristics
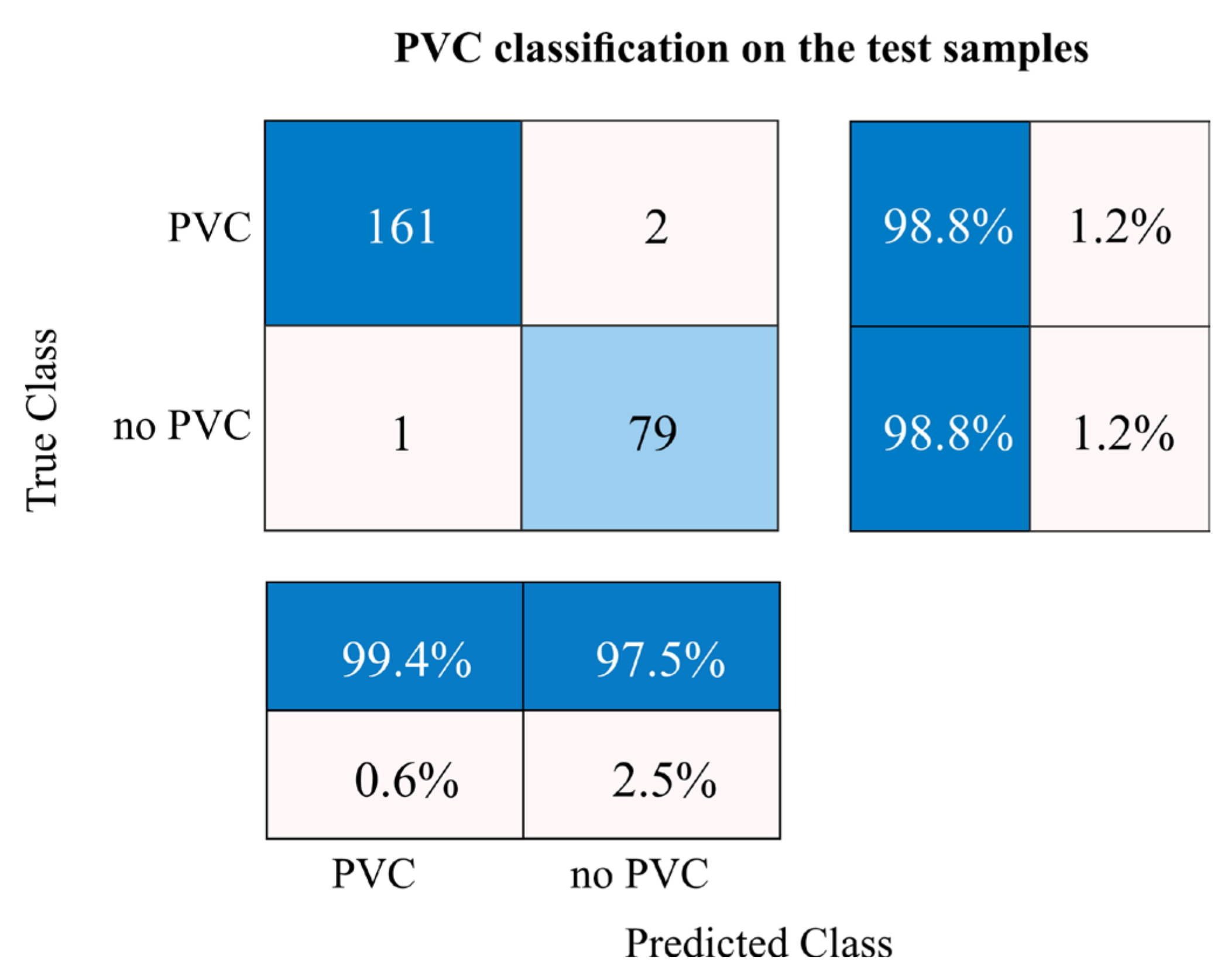
3.2. The Classifier
3.3. Self-Normalizing Neural Network (SNN)
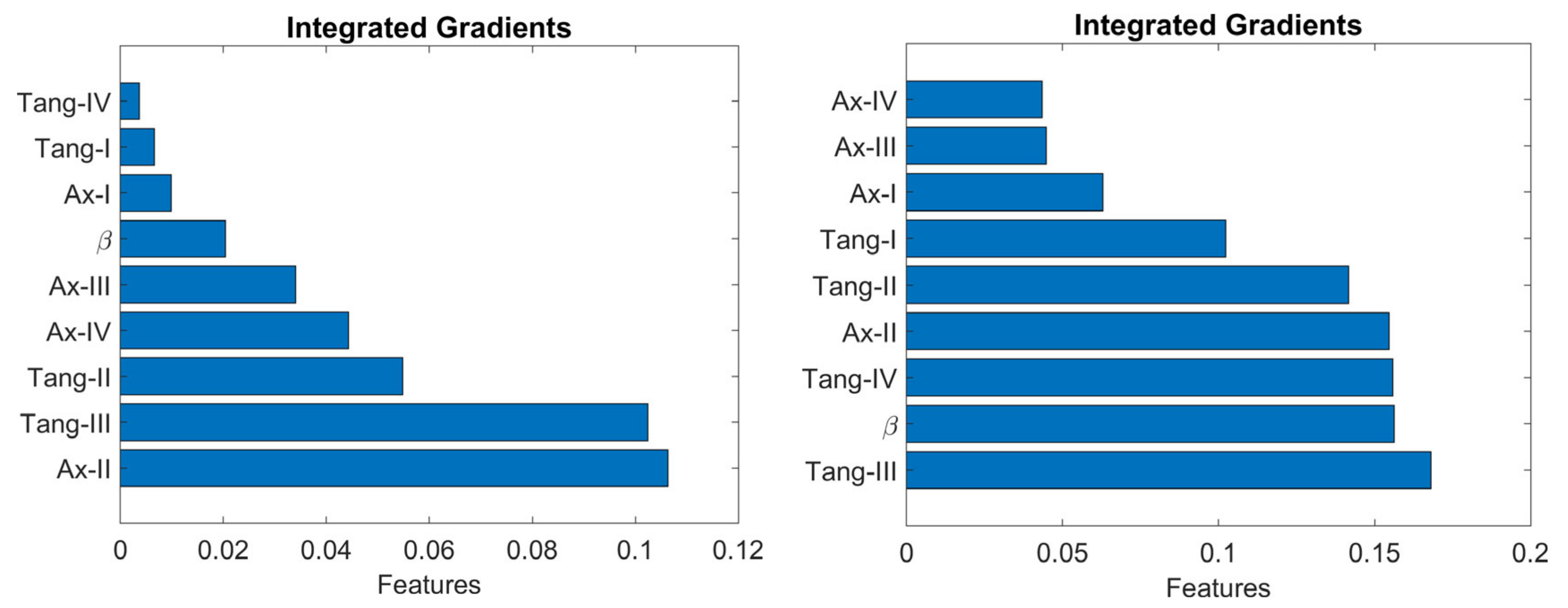
3.4. Feature Importance
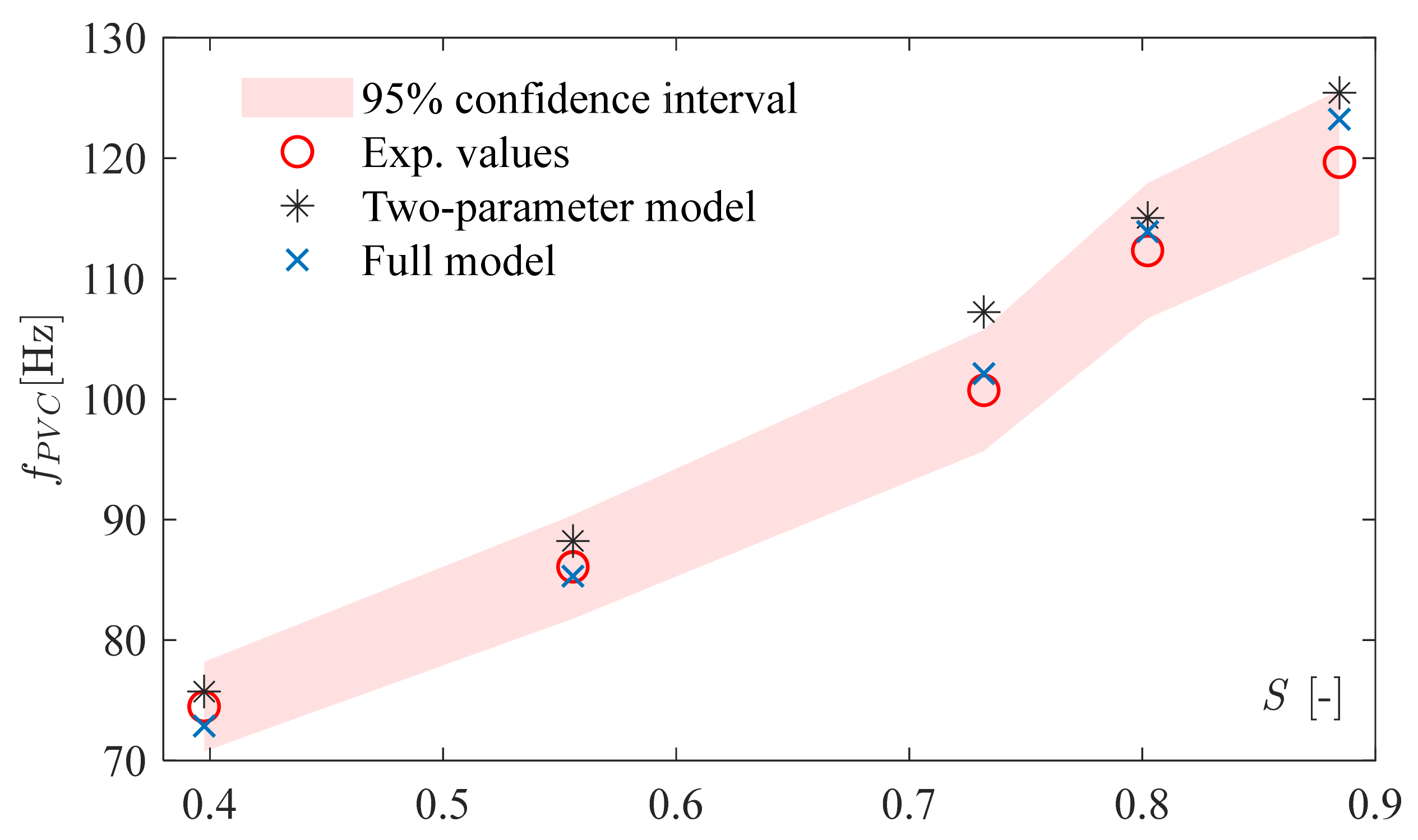
3.5. The Two-Parameter Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rheingans, W.J. Power Swings in Hydroelectric Power Plants. Trans. ASME 1940, 62, 171–184. [Google Scholar] [CrossRef]
- Dörfler, P.; Sick, M.; Coutu, A. Flow-Induced Pulsation and Vibration in Hydroelectric Machinery: Engineer’s Guidebook for Planning, Design and Troubleshooting; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Goyal, R.; Gandhi, B.K. Review of Hydrodynamics Instabilities in Francis Turbine during Off-Design and Transient Operations. Renew. Energy 2018, 116, 697–709. [Google Scholar] [CrossRef]
- Kumar, S.; Cervantes, M.J.; Gandhi, B.K. Rotating Vortex Rope Formation and Mitigation in Draft Tube of Hydro Turbines—A Review from Experimental Perspective. Renew. Sustain. Energy Rev. 2021, 136, 110354. [Google Scholar] [CrossRef]
- Fanelli, M. The Vortex Rope in the Draft Tube of Francis Turbines Operating at Partial Load: A Proposal for a Mathematical Model. J. Hydraul. Res. 1989, 27, 769–807. [Google Scholar] [CrossRef]
- Nicolet, C.; Zobeiri, A.; Maruzewski, P.; Avellan, F. Experimental Investigations on Upper Part Load Vortex Rope Pressure Fluctuations in Francis Turbine Draft Tube. Int. J. Fluid Mach. Syst. 2011, 4, 179–190. [Google Scholar] [CrossRef]
- Yamamoto, K.; Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Pressure Measurements and High Speed Visualizations of the Cavitation Phenomena at Deep Part Load Condition in a Francis Turbine. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 022011. [Google Scholar] [CrossRef]
- Skripkin, S.; Tsoy, M.; Shtork, S.; Hanjalić, K. Comparative Analysis of Twin Vortex Ropes in Laboratory Models of Two Hydro-Turbine Draft-Tubes. J. Hydraul. Res. 2016, 54, 450–460. [Google Scholar] [CrossRef]
- Wahl, T.L. Draft Tube Surging Times Two: The Twin Vortex Phenomenon. Hydro Rev. States 1994, 8, 60–69. [Google Scholar]
- Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Fluid–Structure Interaction Mechanisms Leading to Dangerous Power Swings in Francis Turbines at Full Load. J. Fluids Struct. 2017, 69, 56–71. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Kuibin, P.A.; Shtork, S.I.; Skripkin, S.G.; Tsoy, M.A. Vortex Reconnection in a Swirling Flow. JETP Lett. 2016, 103, 455–459. [Google Scholar] [CrossRef]
- Minakov, A.; Sentyabov, A.; Platonov, D.; Dekterev, A.; Gavrilov, A. Numerical Modeling of Flow in the Francis-99 Turbine with Reynolds Stress Model and Detached Eddy Simulation Method. J. Phys. Conf. Ser. 2015, 579, 12004. [Google Scholar] [CrossRef]
- Platonov, D.V.; Minakov, A.V.; Dekterev, D.A.; Maslennikova, A.V.; Kuibin, P.A. Experimental Observation of the Precessing-Vortex-Core Reconnection Phenomenon in a Combined-Flow Turbine. Tech. Phys. Lett. 2017, 43, 969–971. [Google Scholar] [CrossRef]
- Susan-Resiga, R.; Muntean, S.; Tanasa, C.; Bosioc, A. Hydrodynamic Design and Analysis of a Swirling Flow Generator. In Proceedings of the 4th GRoWTH, Stuttgart, Germany, 12 June 2008. [Google Scholar]
- Chigier, N.A.; Chervinsky, A. Experimental Investigation of Swirling Vortex Motion in Jets. J. Appl. Mech. 1967, 34, 443–451. [Google Scholar] [CrossRef]
- Gupta, K.; Lilley, D.G.; Syred, N. Swirl Flows; Abacus Press: Kent, DC, USA, 1984. [Google Scholar]
- Alligne, S.; Nicolet, C.; Tsujimoto, Y.; Avellan, F. Cavitation Surge Modelling in Francis Turbine Draft Tube. J. Hydraul. Res. 2014, 52, 399–411. [Google Scholar] [CrossRef]
- Kuibin, P.A.; Okulov, V.L.; Susan-Resiga, R.F.; Muntean, S. Validation of Mathematical Models for Predicting the Swirling Flow and the Vortex Rope in a Francis Turbine Operated at Partial Discharge. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012051. [Google Scholar] [CrossRef]
- Susan-Resiga, R.; Dan Ciocan, G.; Anton, I.; Avellan, F. Analysis of the Swirling Flow Downstream a Francis Turbine Runner. J. Fluids Eng. 2006, 128, 177. [Google Scholar] [CrossRef]
- Skripkin, S.; Zuo, Z.; Tsoy, M.; Kuibin, P.; Liu, S. Oscillation of Cavitating Vortices in Draft Tubes of a Simplified Model Turbine and a Model Pump–Turbine. Energies 2022, 15, 2965. [Google Scholar] [CrossRef]
- Müller, J.; Sieber, M.; Litvinov, I.; Shtork, S.; Alekseenko, S.; Oberleithner, K. Prediction of Vortex Precession in the Draft Tube of a Model Hydro Turbine Using Mean Field Stability Theory and Stochastic Modelling. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 774, p. 012003. [Google Scholar]
- Pasche, S.; Avellan, F.; Gallaire, F. Part Load Vortex Rope as a Global Unstable Mode. J. Fluids Eng. 2017, 139, 051102. [Google Scholar] [CrossRef]
- Muller, J.; Luckoff, F.; Kaiser, T.; Oberleithner, K. On the Relevance of the Runner Crown for Flow Instabilities in a Francis Turbine. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2022; in press. [Google Scholar]
- Minakov, A.; Platonov, D.; Litvinov, I.; Shtork, S.; Hanjalić, K. Vortex ropes in draft tube of a laboratory Kaplan hydroturbine at low load: An experimental and LES scrutiny of RANS and DES computational models. J. Hydraul. Res. 2017, 55, 668–685. [Google Scholar] [CrossRef]
- Minakov, A.V.; Platonov, D.V.; Dekterev, A.A.; Sentyabov, A.V.; Zakharov, A.V. The Analysis of Unsteady Flow Structure and Low Frequency Pressure Pulsations in the High-Head Francis Turbines. Int. J. Heat Fluid Flow 2015, 53, 183–194. [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, S.; Liu, D.; Qin, D.; Wu, Y. Numerical Analyses of Pressure Fluctuations Induced by Interblade Vortices in a Model Francis Turbine. J. Hydrodyn. Ser B 2015, 27, 513–521. [Google Scholar] [CrossRef]
- Galván, S.; Reggio, M.; Guibault, F. Numerical Optimization of the Inlet Velocity Profile Ingested by the Conical Draft Tube of a Hydraulic Turbine. J. Fluids Eng. 2015, 137, 071102. [Google Scholar] [CrossRef]
- Faller, W.E.; Schreck, S.J. Neural Networks: Applications and Opportunities in Aeronautics. Prog. Aerosp. Sci. 1996, 32, 433–456. [Google Scholar] [CrossRef]
- Grant, I.; Pan, X. An Investigation of the Performance of Multi Layer, Neural Networks Applied to the Analysis of PIV Images. Exp. Fluids 1995, 19, 159–166. [Google Scholar] [CrossRef]
- Teo, C.; Lim, K.; Hong, G.; Yeo, M. A Neural Net Approach in Analyzing Photograph in PIV. In Proceedings of the 1991 IEEE International Conference on Systems, Man, and Cybernetics, Charlottesville, VA, USA, 13–16 October 1991; pp. 1535–1538. [Google Scholar]
- Bishop, C.M.; James, G.D. Analysis of Multiphase Flows Using Dual-Energy Gamma Densitometry and Neural Networks. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 1993, 327, 580–593. [Google Scholar] [CrossRef]
- Baldi, P.; Hornik, K. Neural Networks and Principal Component Analysis: Learning from Examples without Local Minima. Neural Netw. 1989, 2, 53–58. [Google Scholar] [CrossRef]
- Milano, M.; Koumoutsakos, P. Neural Network Modeling for near Wall Turbulent Flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, Y. Predictive Control Strategy of Hydraulic Turbine Turning System Based on Bgnn Neural Network. In Proceedings of the International Symposium on Intelligence Computation and Applications, Wuhan, China, 19–21 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 331–341. [Google Scholar]
- Jambunathan, K.; Hartle, S.; Ashforth-Frost, S.; Fontama, V. Evaluating Convective Heat Transfer Coefficients Using Neural Networks. Int. J. Heat Mass Transf. 1996, 39, 2329–2332. [Google Scholar] [CrossRef]
- Pierret, S.; Van den Braembussche, R. Turbomachinery Blade Design Using a Navier-Stokes Solver and Artificial Neural Network. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 1998; Volume 78620, p. V001T01A002. [Google Scholar]
- Abdurakipov, S.; Tokarev, M.; Pervunin, K.; Dulin, V. Modeling of the Tonal Noise Characteristics in a Foil Flow by Using Machine Learning. Optoelectron. Instrum. Data Process. 2019, 55, 205–211. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. Modeling, Analysis and Optimization of Aircyclones Using Artificial Neural Network, Response Surface Methodology and CFD Simulation Approaches. Powder Technol. 2011, 212, 115–133. [Google Scholar] [CrossRef]
- Zhao, B.; Su, Y. Artificial Neural Network-Based Modeling of Pressure Drop Coefficient for Cyclone Separators. Chem. Eng. Res. Des. 2010, 88, 606–613. [Google Scholar] [CrossRef]
- Gruber, P.; Farhat, M.; Odermatt, P.; Etterlin, M.; Lerch, T.; Frei, M. The Detection of Cavitation in Hydraulic Machines by Use of Ultrasonic Signal Analysis. Int. J. Fluid Mach. Syst. 2015, 8, 264–273. [Google Scholar] [CrossRef]
- Hocevar, M.; Sirok, B.; Blagojevic, B.; Grabec, I. Experimental Modeling of a Cavitation Vortex in the Draft Tube of a Francis Turbine Using Artificial Neural Networks. J. Hydraul. Res. 2007, 45, 538–546. [Google Scholar] [CrossRef]
- Hočevar, M.; Širok, B.; Blagojevič, B. Prediction of Cavitation Vortex Dynamics in the Draft Tube of a Francis Turbine Using Radial Basis Neural Networks. Neural Comput. Appl. 2005, 14, 229–234. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Raghavan, B.V. Free Vortex Turbulent Swirling Flow Reconstruction Using a Neural Network. In Proceedings of the Fluids Engineering Division Summer Meeting, American Society of Mechanical Engineers, Rio Grande, PR, USA, 8–12 July 2012; Volume 44755, pp. 783–788. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep Learning of Vortex-Induced Vibrations. J. Fluid Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Véras, P.; Balarac, G.; Métais, O.; Georges, D.; Bombenger, A.; Ségoufin, C. Reconstruction of Numerical Inlet Boundary Conditions Using Machine Learning: Application to the Swirling Flow inside a Conical Diffuser. Phys. Fluids 2021, 33, 085132. [Google Scholar] [CrossRef]
- Véras, P.; Métais, O.; Balarac, G.; Georges, D.; Bombenger, A.; Ségoufin, C. Reconstruction of Proper Numerical Inlet Boundary Conditions for Draft Tube Flow Simulations Using Machine Learning. Comput. Fluids 2023, 254, 105792. [Google Scholar] [CrossRef]
- Brunton, S.L. Applying Machine Learning to Study Fluid Mechanics. Acta Mech. Sin. 2021, 37, 1718–1726. [Google Scholar] [CrossRef]
- Liu, Z.; Favrel, A.; Miyagawa, K. Effect of the Conical Diffuser Angle on the Confined Swirling Flow Induced Precessing Vortex Core. Int. J. Heat Fluid Flow 2022, 95, 108968. [Google Scholar] [CrossRef]
- Litvinov, I.V.; Sharaborin, D.K.; Shtork, S.I. Reconstructing the Structural Parameters of a Precessing Vortex by SPIV and Acoustic Sensors. Exp. Fluids 2019, 60, 139. [Google Scholar] [CrossRef]
- Valera-Medina, A.; Syred, N.; Griffiths, A. Visualisation of Isothermal Large Coherent Structures in a Swirl Burner. Combust. Flame 2009, 156, 1723–1734. [Google Scholar] [CrossRef]
- Litvinov, I.V.; Shtork, S.I.; Kuibin, P.A.; Alekseenko, S.V.; Hanjalic, K. Experimental Study and Analytical Reconstruction of Precessing Vortex in a Tangential Swirler. Int. J. Heat Fluid Flow 2013, 42, 251–264. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Kuibin, P.A.; Okulov, V.L. Theory of Concentrated Vortices: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 1, ISBN 978-3-540-73376-8. [Google Scholar]
- Cassidy, J.J.; Falvey, H.T. Observations of Unsteady Flow Arising after Vortex Breakdown. J. Fluid Mech. 1969, 41, 727–736. [Google Scholar] [CrossRef]
- Chanaud, R.C. Observations of Oscillatory Motion in Certain Swirling Flows. J. Fluid Mech. 1965, 21, 111–127. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Kuibin, P.A.; Okulov, V.L.; Shtork, S.I. Helical Vortices in Swirl Flow. J. Fluid Mech. 1999, 382, 195–243. [Google Scholar] [CrossRef]
- Skripkin, S.; Suslov, D.; Litvinov, I.; Gorelikov, E.; Tsoy, M.; Shtork, S. Comparative Analysis of Air and Water Flows in Simplified Hydraulic Turbine Models. J. Phys. Conf. Ser. 2022, 2150, 012001. [Google Scholar] [CrossRef]
- Litvinov, I.; Gorelikov, E.; Shtork, S. Frequency Response of the Flow in a Radial Swirler. J. Mech. Sci. Technol. 2022, 36, 2397–2402. [Google Scholar] [CrossRef]
- Tropea, C.; Yarin, A.L.; Foss, J.F. Springer Handbook of Experimental Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 46, ISBN 978-3-540-25141-5. [Google Scholar]
- Yanta, W.J.; Smith, R.A. Measurements of Turbulence-Transport Properties with a Laser Doppler Velocimeter. In Proceedings of the 11th Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics, Washington, DC, USA, 10–12 January 1973. AIAA Paper 73–169. [Google Scholar]
- Cala, C.E.; Fernandes, E.C.; Heitor, M.V.; Shtork, S.I. Coherent Structures in Unsteady Swirling Jet Flow. Exp. Fluids 2006, 40, 267–276. [Google Scholar] [CrossRef]
- Goyal, R.; Cervantes, M.J.; Gandhi, B.K. Characteristics of Synchronous and Asynchronous Modes of Fluctuations in Francis Turbine Draft Tube during Load Variation. Int. J. Fluid Mach. Syst. 2017, 10, 164–175. [Google Scholar] [CrossRef]
- Yazdabadi, P.A.; Griffiths, A.J.; Syred, N. Characterization of the PVC Phenomena in the Exhaust of a Cyclone Dust Separator. Exp. Fluids 1994, 17, 84–95. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic Attribution for Deep Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Favrel, A.; Pereira, J.G., Jr.; Landry, C.; Müller, A.; Nicolet, C.; Avellan, F. New Insight in Francis Turbine Cavitation Vortex Rope: Role of the Runner Outlet Flow Swirl Number. J. Hydraul. Res. 2017, 56, 367–379. [Google Scholar] [CrossRef]
- Skripkin, S.; Tsoy, M.; Kuibin, P.; Shtork, S. Swirling Flow in a Hydraulic Turbine Discharge Cone at Different Speeds and Discharge Conditions. Exp. Therm. Fluid Sci. 2019, 100, 349–359. [Google Scholar] [CrossRef]


| Parameter | Parameter Range | Number of Regimes |
|---|---|---|
| Flow rate, Q [m3/h] | constant, 100 | 1 |
| Angle of the guide vanes, α° | 0–76.6 | 34 |
| Cone angle, β° | 4–15 | 12 |
| Diaphragm, d [mm] | 0 and 6 | 2 |
| Total regimes involved in machine learning: | 816 | |
| Hyperparameter Name | Range of Variation (Model Parameters with the Best Accuracy Are Underlined) |
|---|---|
| Penalty (the standard for determining the penalty) | l1, l2 |
| Loss (loss function): | hinge, squared_hinge |
| Tol (tolerance parameter to stop training) | 10−6, 10−5, 10−4, 10−3, 10−2 |
| C (regularization parameter) | 0.1, 0.25, 0.5, 0.75, 1.0 |
| Max_iter (maximum number of learning iterations) | 1000, 10,000 |
| Frequency of Pressure Pulsations | Power of Pressure Pulsations | |
|---|---|---|
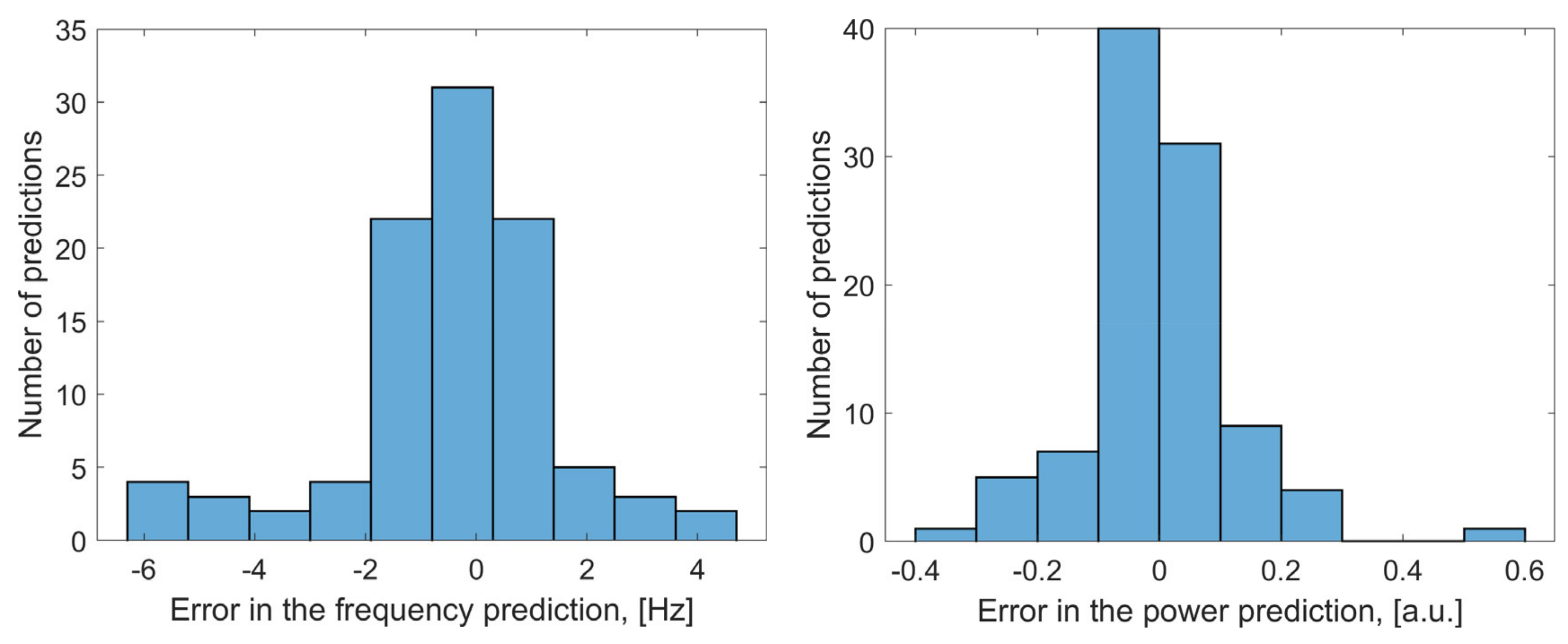
| Mean absolute percentage error (MAPE), % | 1.01 | 5.40 |
| Mean absolute error (MAE) | 1.38 | 0.08 |
| Frequency | Power | |
|---|---|---|
| Mean absolute percentage error (MAPE), % | 2.68 | 6.38 |
| Mean absolute error (MAE) | 3.66 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skripkin, S.; Suslov, D.; Plokhikh, I.; Tsoy, M.; Gorelikov, E.; Litvinov, I. Data-Driven Prediction of Unsteady Vortex Phenomena in a Conical Diffuser. Energies 2023, 16, 2108. https://doi.org/10.3390/en16052108
Skripkin S, Suslov D, Plokhikh I, Tsoy M, Gorelikov E, Litvinov I. Data-Driven Prediction of Unsteady Vortex Phenomena in a Conical Diffuser. Energies. 2023; 16(5):2108. https://doi.org/10.3390/en16052108
Chicago/Turabian StyleSkripkin, Sergey, Daniil Suslov, Ivan Plokhikh, Mikhail Tsoy, Evgeny Gorelikov, and Ivan Litvinov. 2023. "Data-Driven Prediction of Unsteady Vortex Phenomena in a Conical Diffuser" Energies 16, no. 5: 2108. https://doi.org/10.3390/en16052108
APA StyleSkripkin, S., Suslov, D., Plokhikh, I., Tsoy, M., Gorelikov, E., & Litvinov, I. (2023). Data-Driven Prediction of Unsteady Vortex Phenomena in a Conical Diffuser. Energies, 16(5), 2108. https://doi.org/10.3390/en16052108





