Computational Modelling of Airflow and Heat Transfer during Cooling of Stacked Tomatoes: Optimal Crate Design
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Study
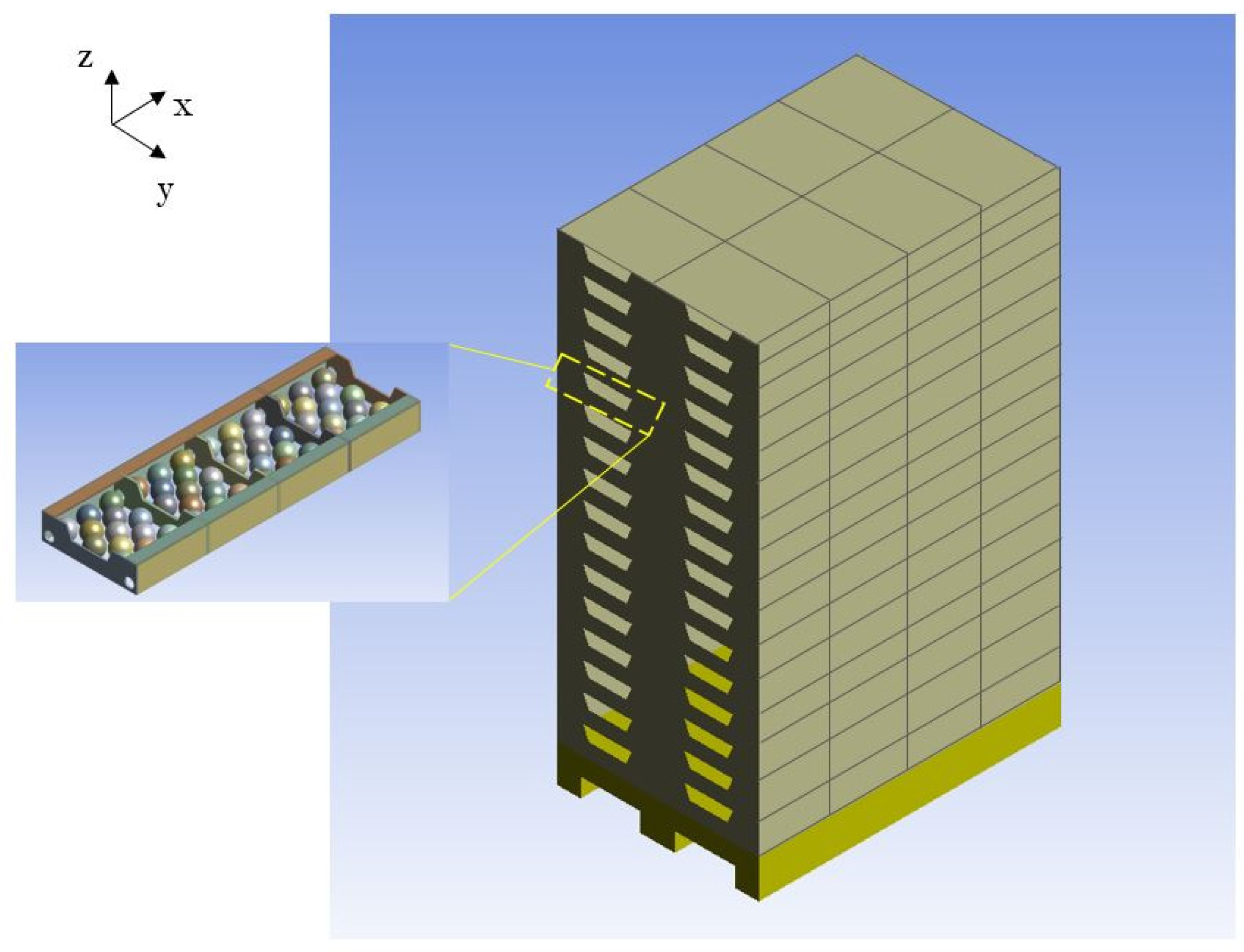
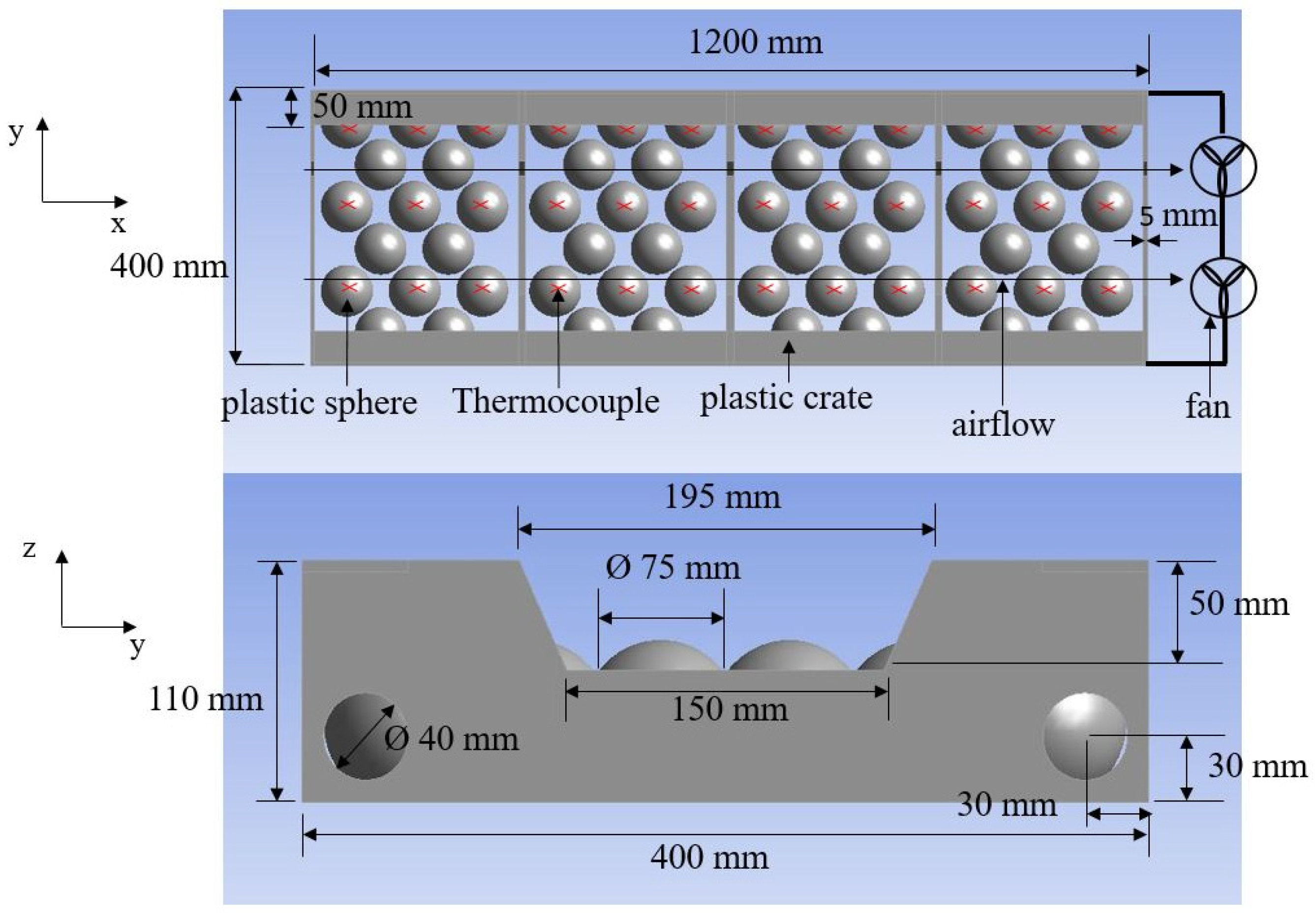
2.1.1. Experimental Bench
2.1.2. Cooling Experiments
2.1.3. Analysis of Cooling Rate and Temperature Uniformity
2.1.4. Air Velocity Measurement
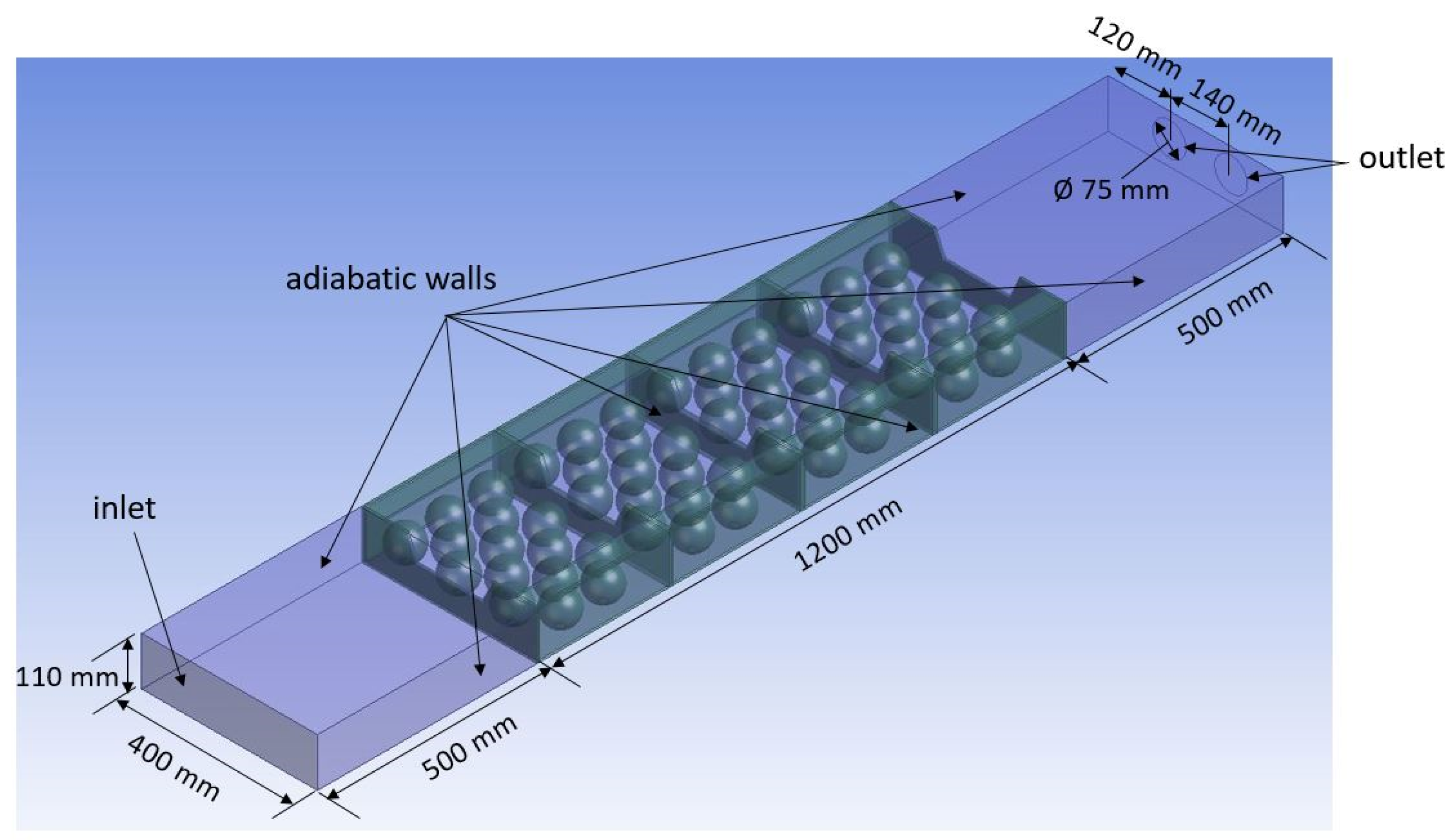
2.2. CFD Modelling
2.2.1. Governing Equations
- Air is an incompressible fluid with constant properties.
- Radiation between the carrageenan spheres and the PMMA crates was considered to be negligible.
- Due to the similarity in the thermal diffusivity of the carrageenan gel with that of polyethylene, the thermal properties of the carrageenan gel were used on the entire volume of the 75 mm diameter sphere.
- The effect of the experimental instruments on the airflow is negligible.
2.2.2. Initial and Boundary Conditions
2.2.3. Mesh Discretisation and Sensitivity Analysis
2.2.4. Simulation Procedure
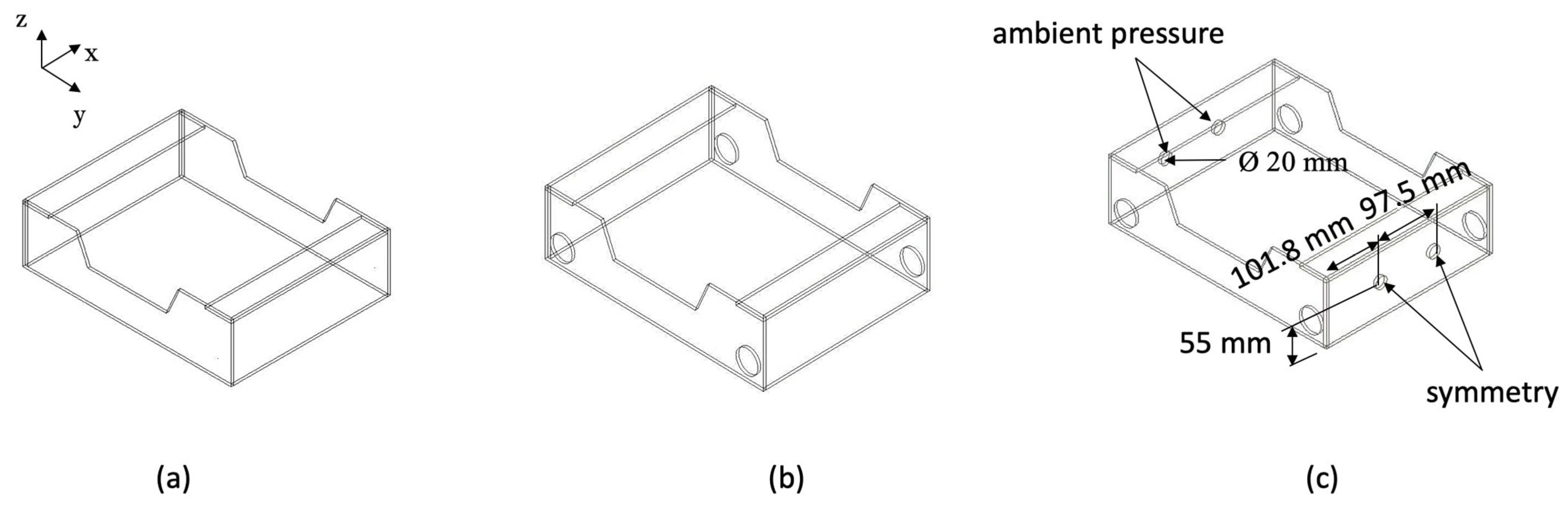
2.2.5. Crate Designs
2.2.6. Prediction Error and Temperature Uniformity
3. Results and Discussion
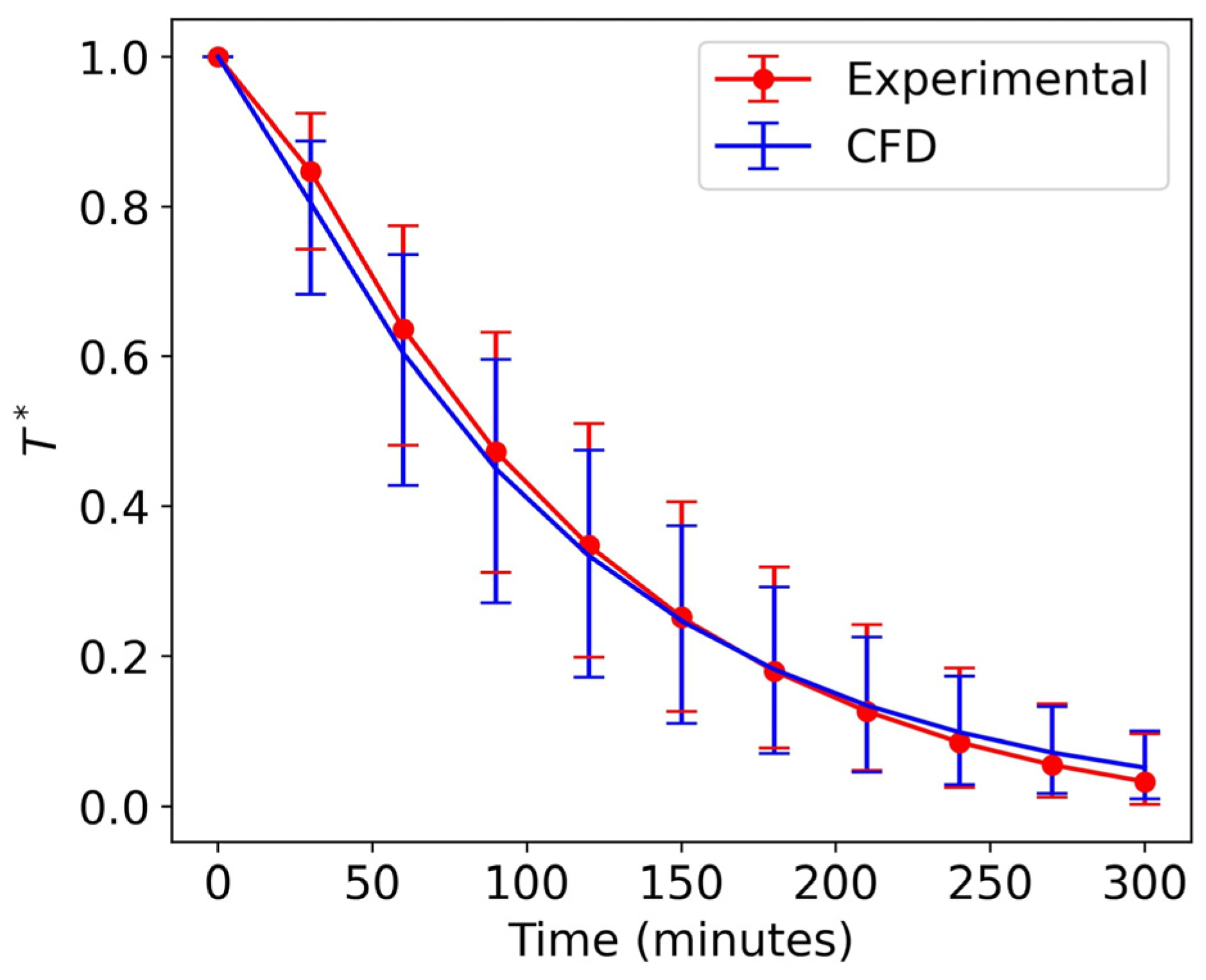
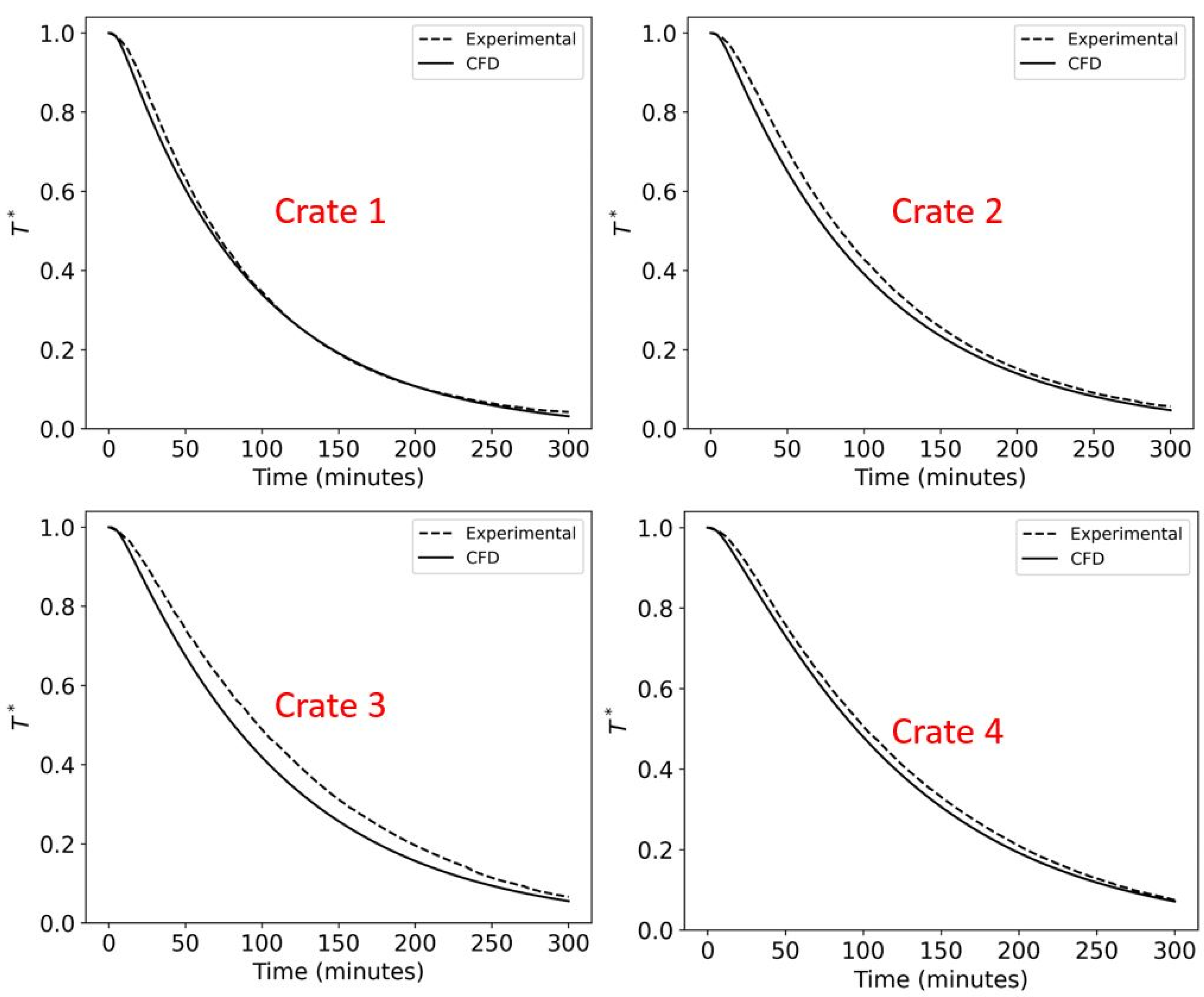
3.1. Model Validation
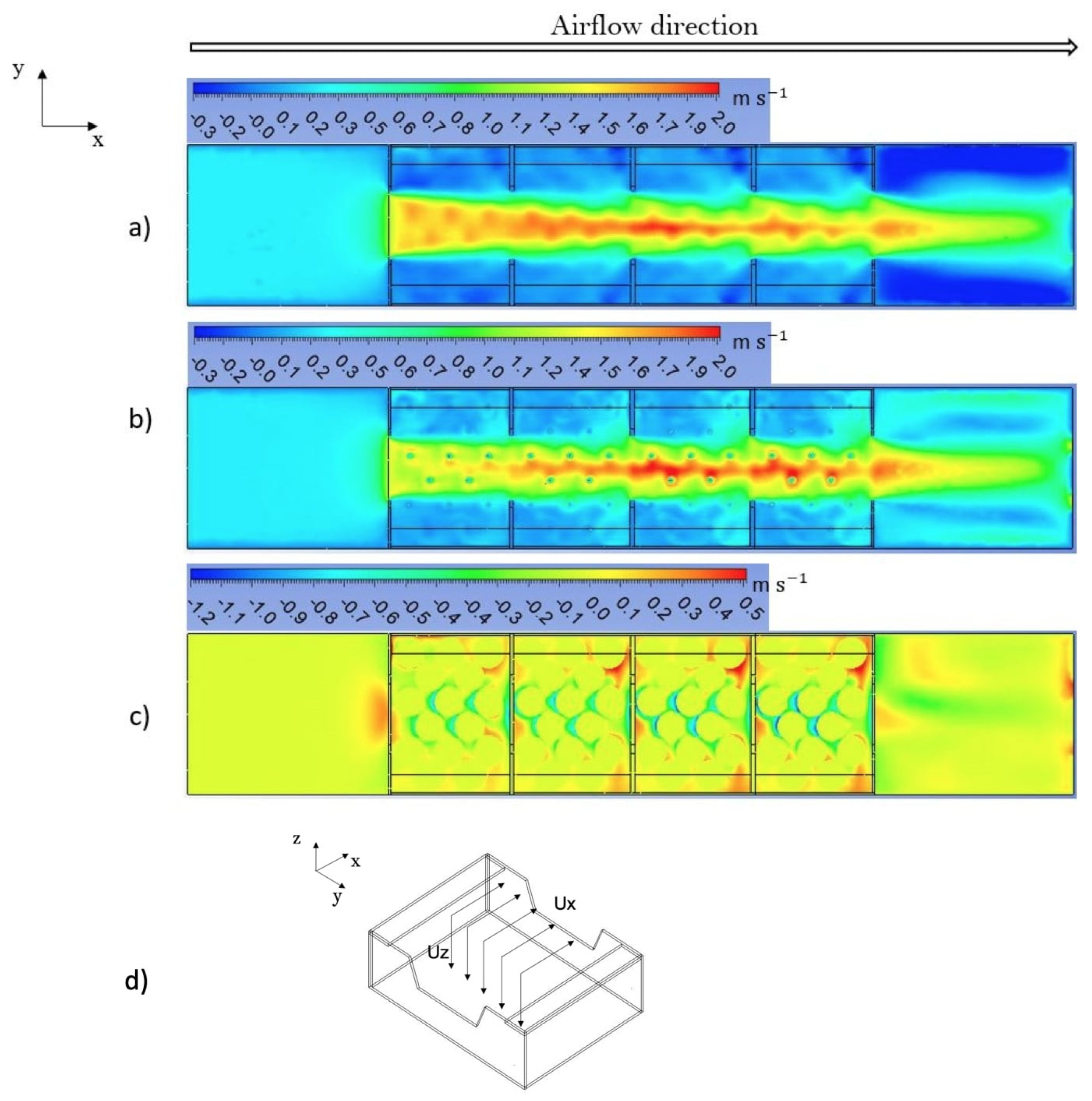
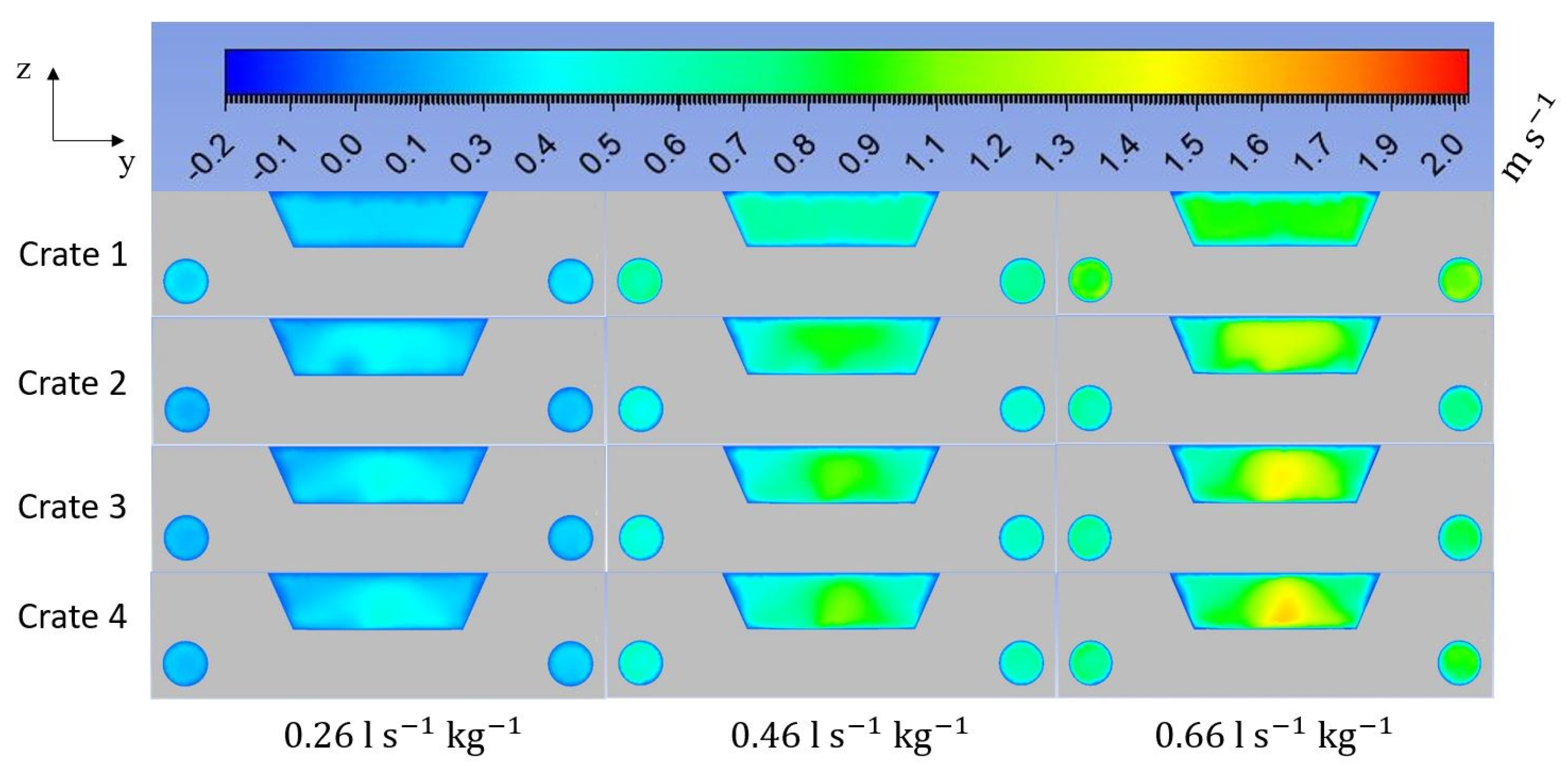
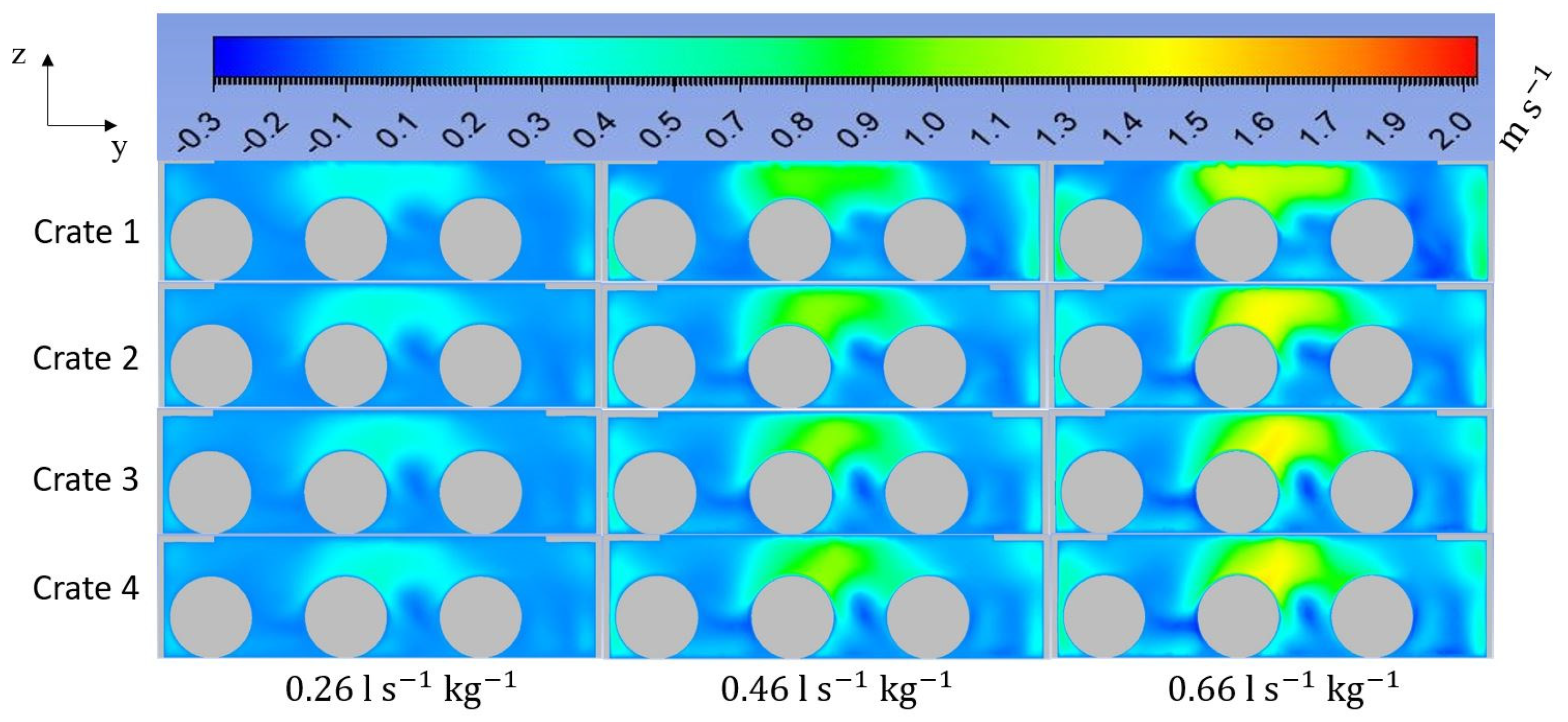
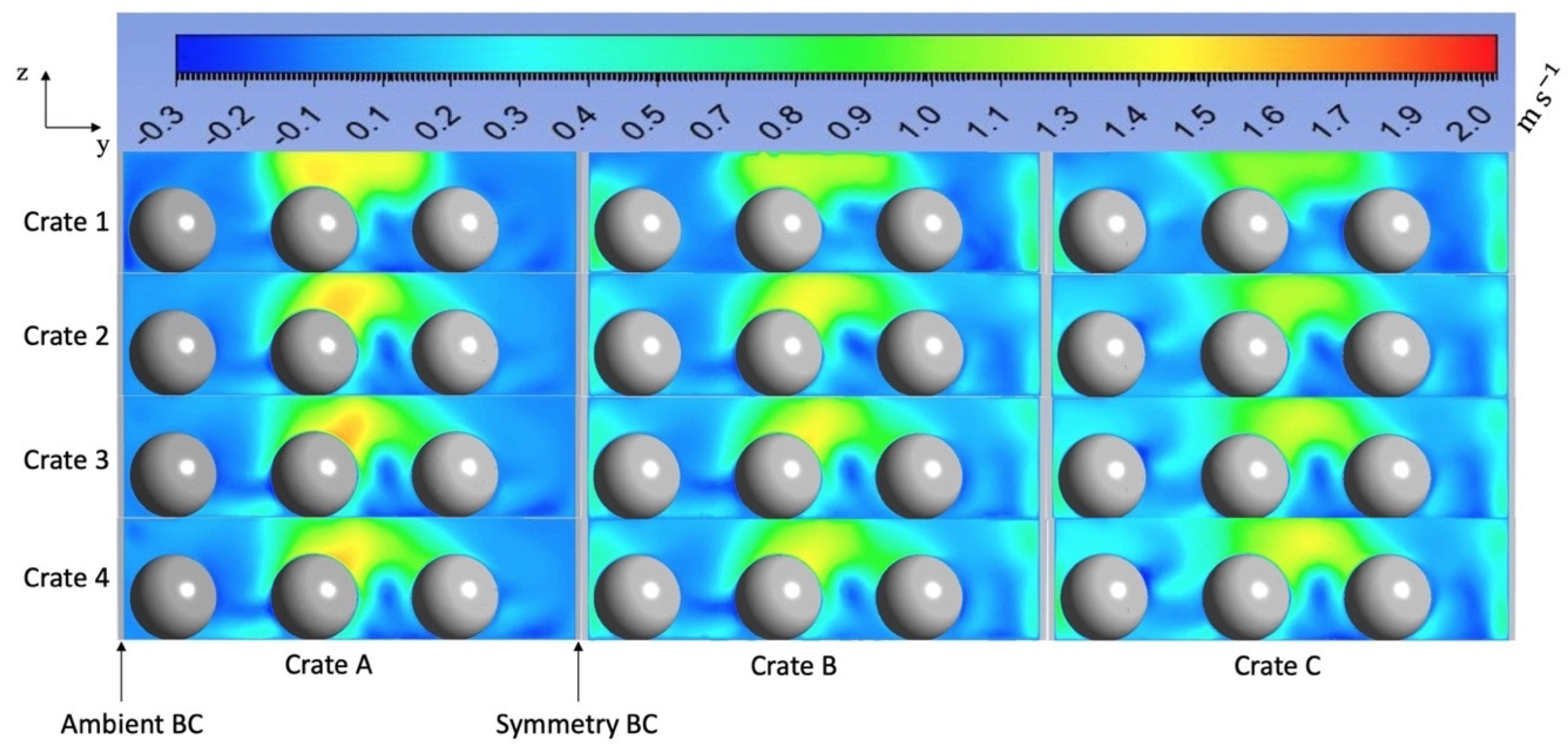
3.2. Airflow Analysis of the Confined Wall Jet (Crate A Design)
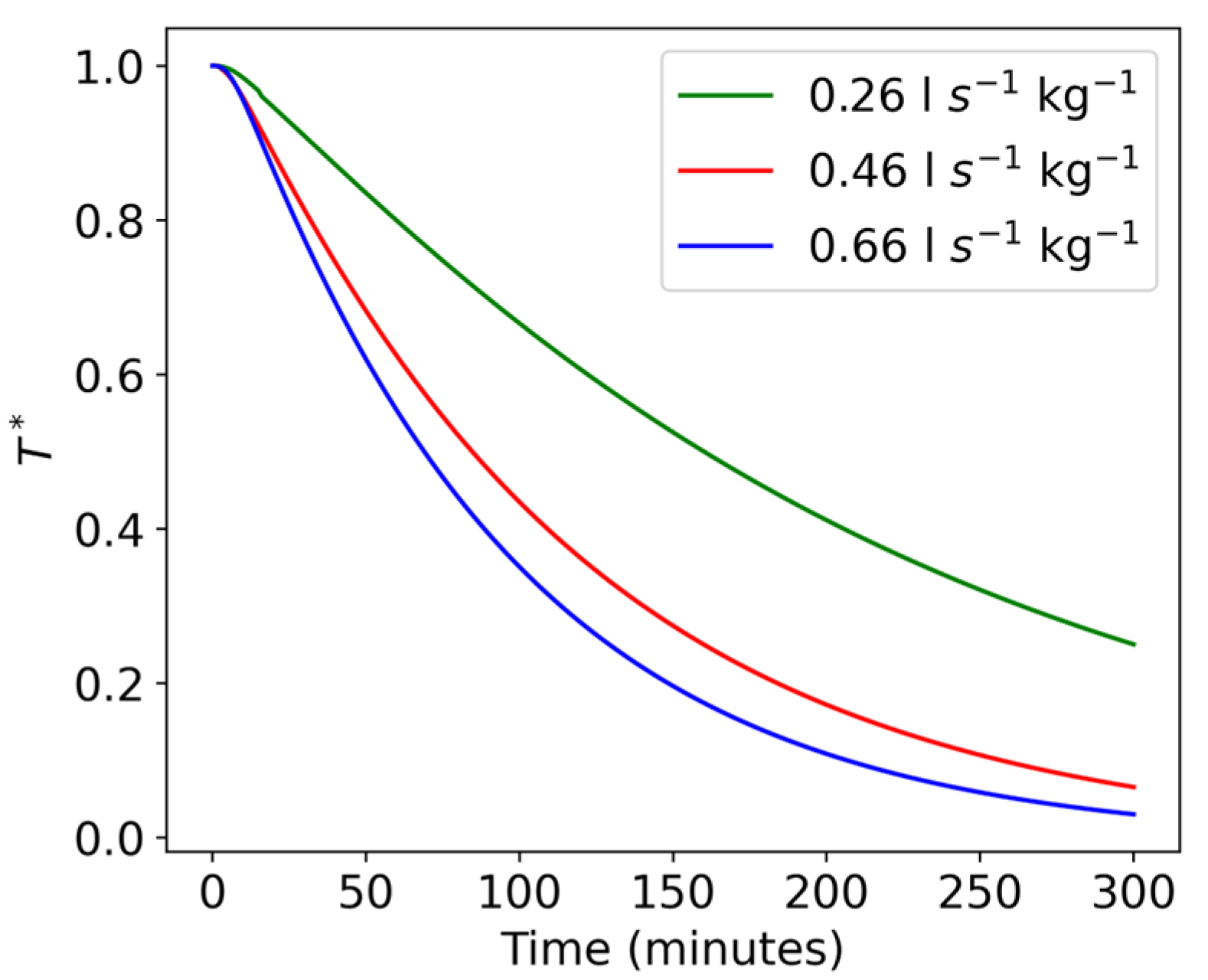
3.3. Influence of Inlet Velocity on Product Cooling Rate and Temperature Uniformity
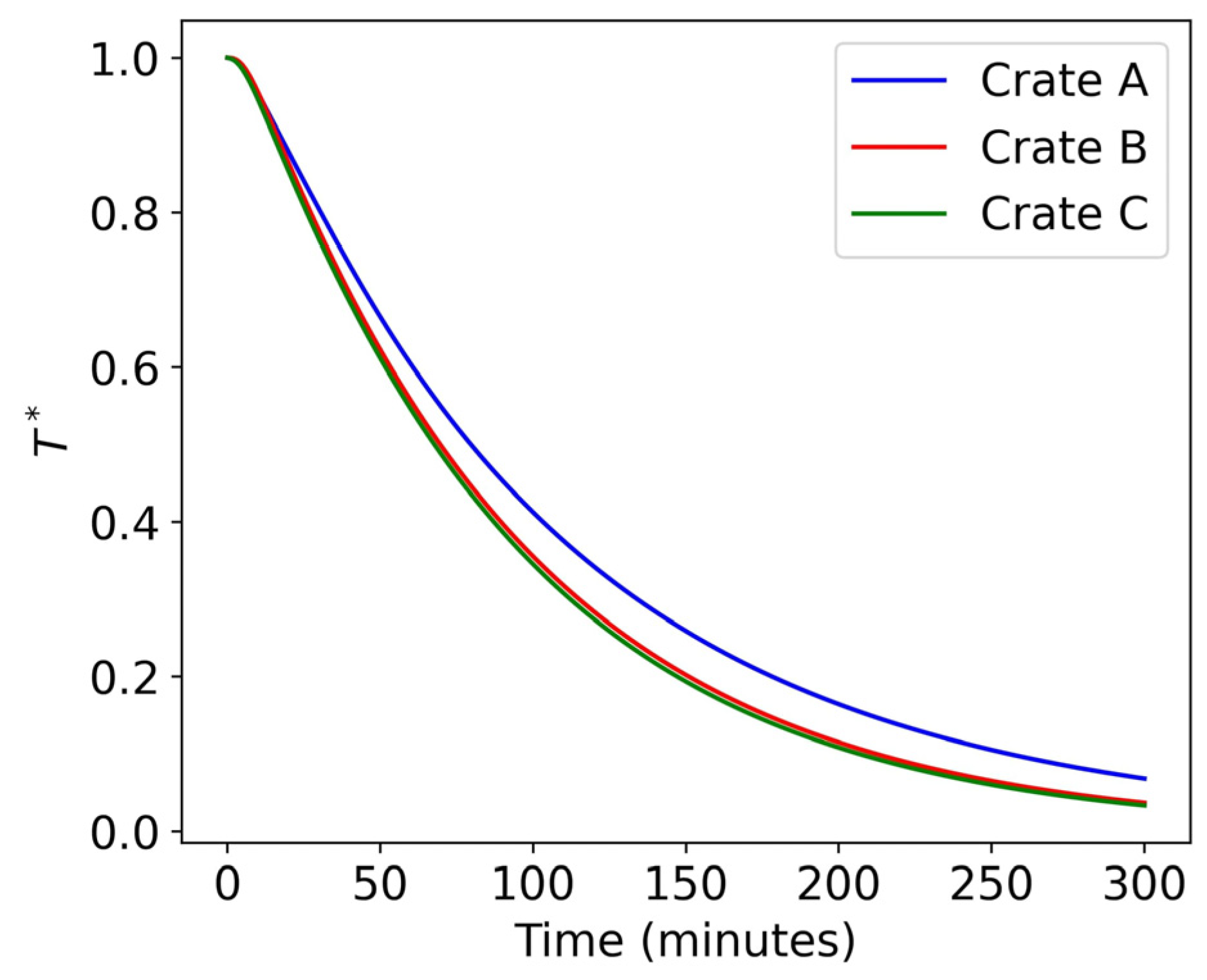
3.3.1. Influence of Airflow Rate on Product Cooling Rate
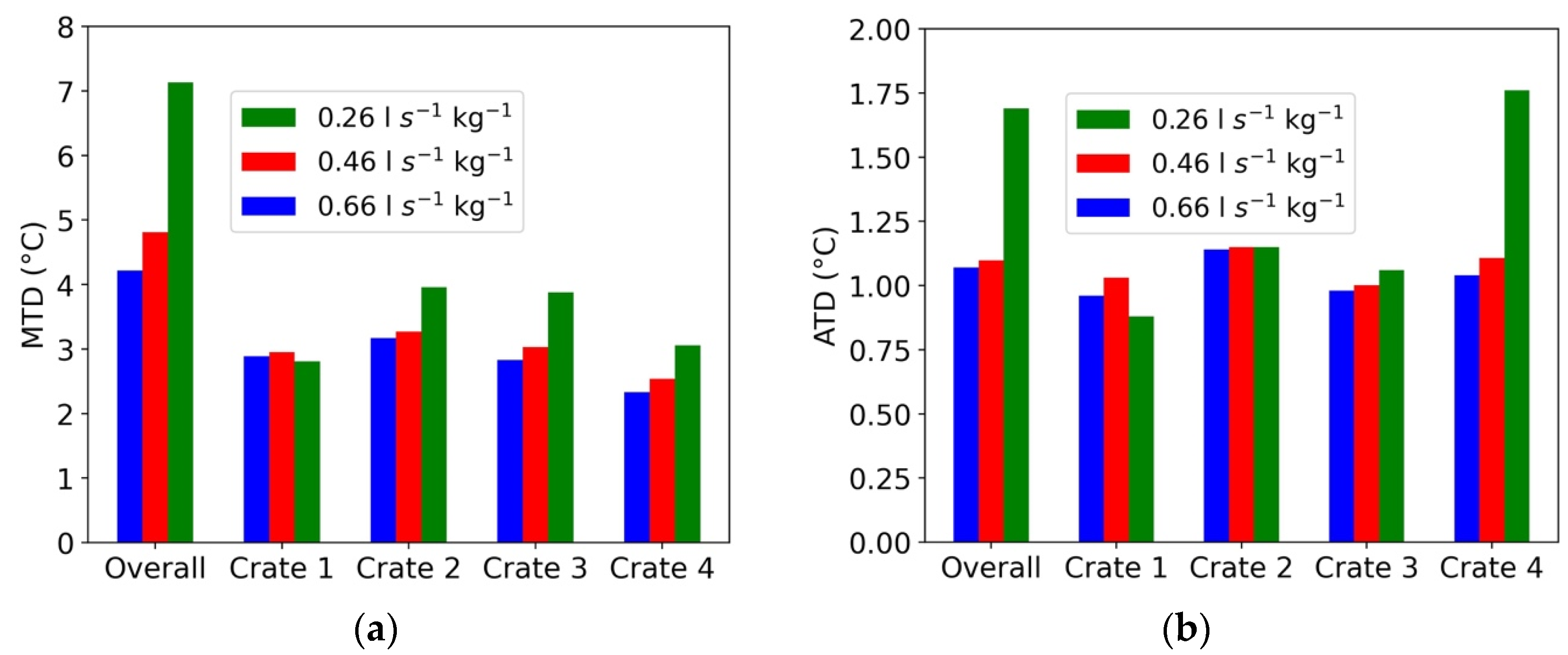
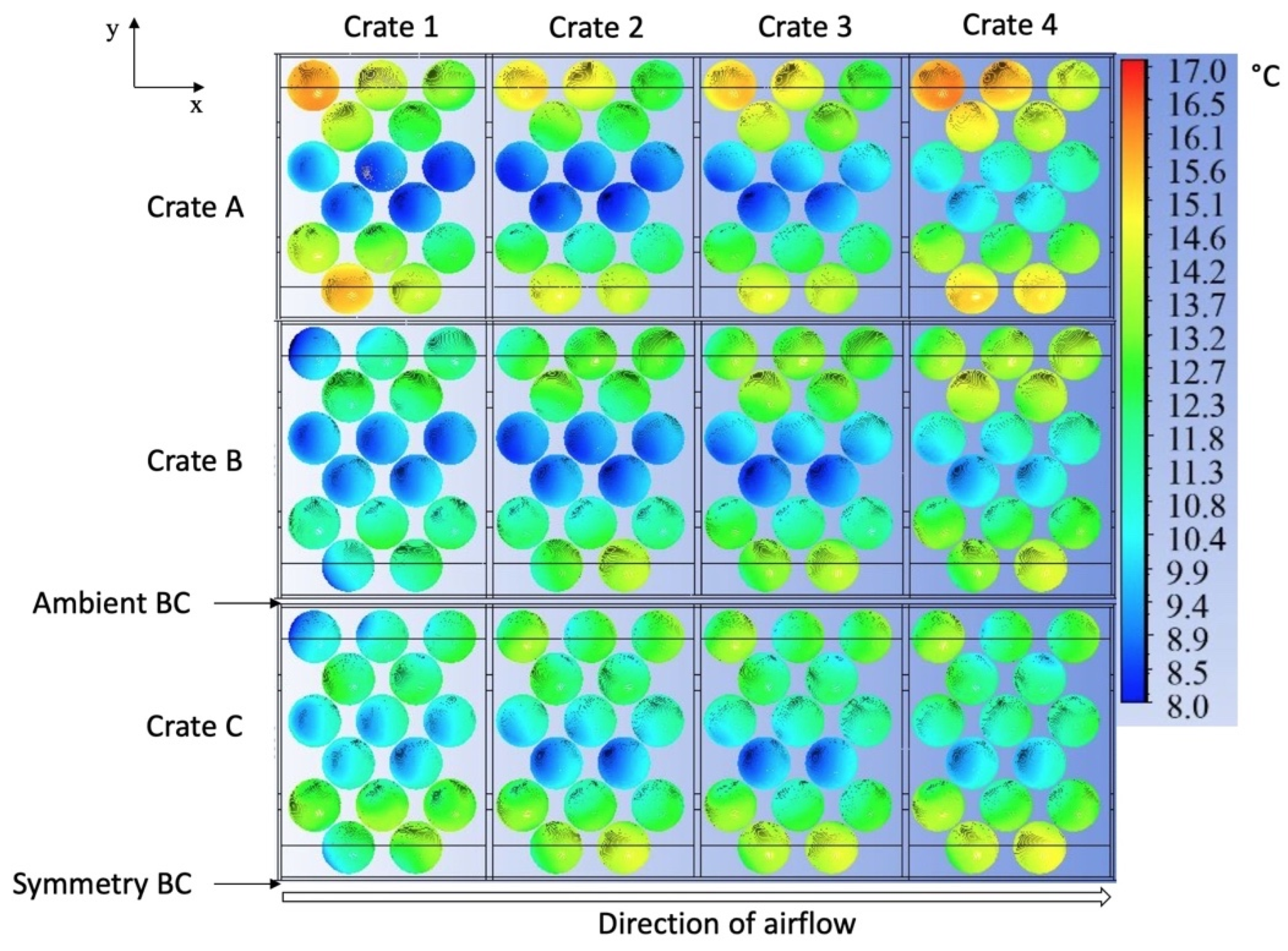
3.3.2. Influence of Airflow Rate on Product Temperature Uniformity
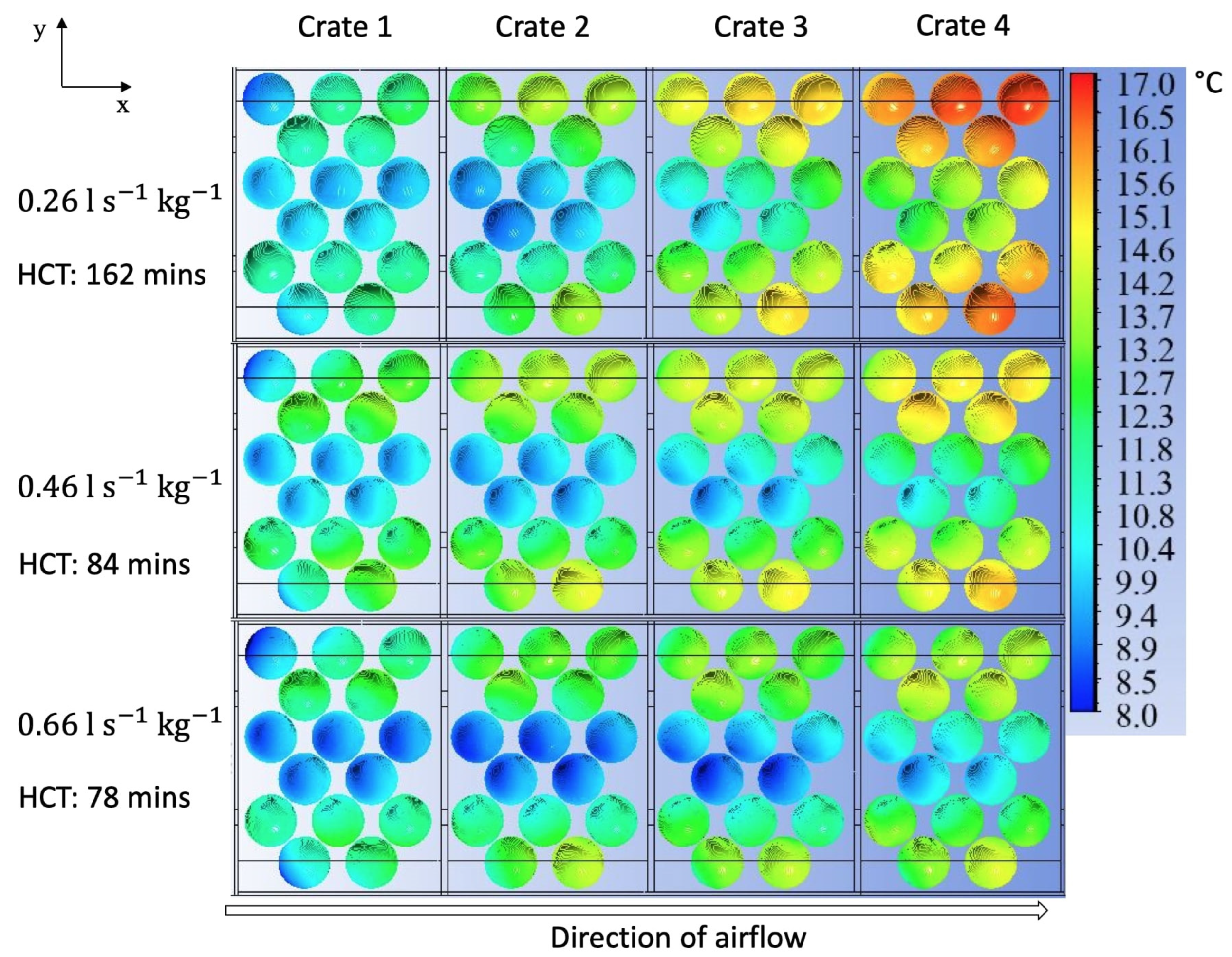
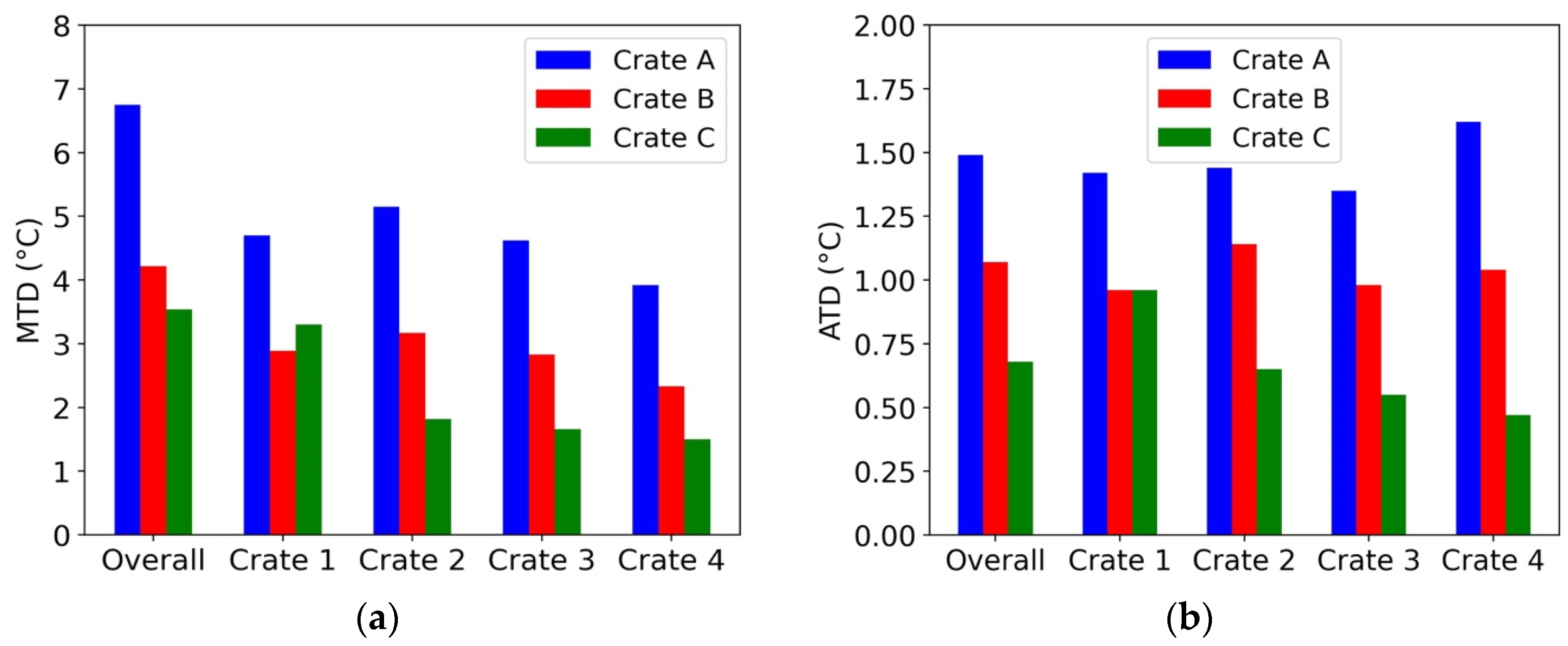
3.4. Influence of Crate Design on Product Cooling Rate and Uniformity
3.4.1. Influence of Crate Design on Product Cooling Rate
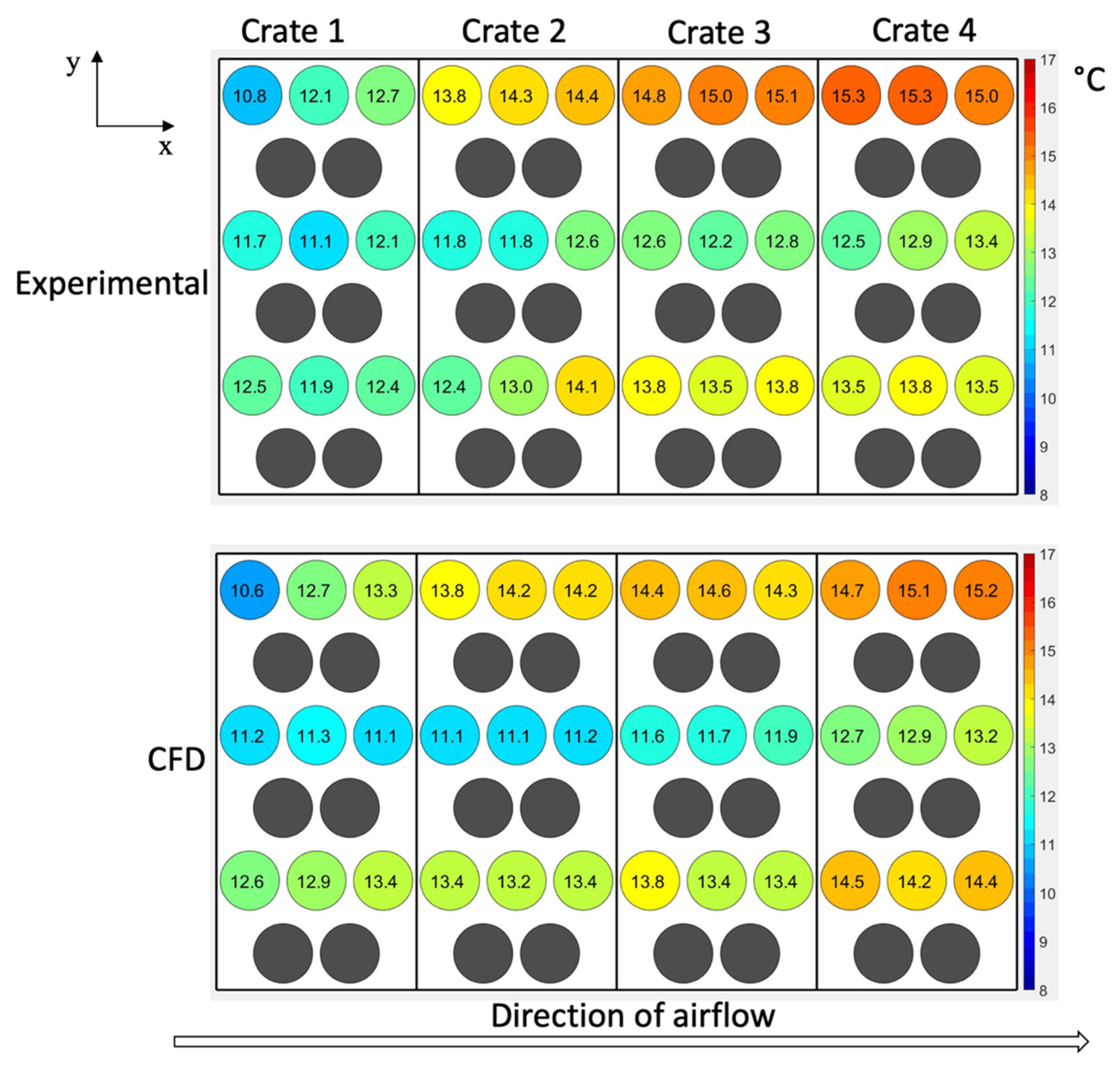
3.4.2. Influence of Crate Design on Product Cooling Uniformity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ARD | Absolute relative deviation | % |
| ATD | Average temperature difference | °C |
| CWJ | Confined wall jet | |
| HCT | Half-cooling time | s |
| MTD | Maximum temperature difference | °C |
| P | Pressure | Pa |
| Q | Flow rate | L s−1 kg−1 |
| RMSE | Root-mean-square error | °C |
| S | Surface area | m2 |
| T | Temperature | °C |
| TVA | Total ventilated area | % |
| u | Velocity | m s−1 |
| Greek symbols | ||
| ρ | Density | [kg m−3] |
| θ | Dimensionless temperature | |
| µ | Dynamic viscosity | kg m−1 s−1 |
| δij | Kronecker delta | |
| Cp | Specific heat | J kg−1 K−1 |
| λ | Thermal conductivity | W m−1 K−1 |
| α | Thermal expansion coefficient | K−1 |
| t | Time | s |
| ε | Turbulent dissipation rate | m2 s−3 |
| k | Turbulent kinetic energy | m2 s−2 |
| µt | Turbulent viscosity | kg m−1 s−1 |
| Dimensionless numbers | ||
| Prt | Turbulent Prandtl number | |
| Cµ | Empirical constant | |
| Indices | ||
| a | Air | |
| amb | Ambient | |
| * | Average dimensionless temperature | |
| avg | Average | |
| i | Initial | |
| max | Maximum | |
| min | Minimum | |
| m | Measured | |
| o | Operating | |
| p | Product | |
| s | Simulation | |
References
- Defraeye, T.; Cronjé, P.; Berry, T.; Opara, U.L.; East, A.; Hertog, M.; Verboven, P.; Nicolai, B. Towards integrated performance evaluation of future packaging for fresh produce in the cold chain. Trends Food Sci. Technol. 2015, 44, 201–225. [Google Scholar] [CrossRef]
- Han, J.; BadÍa-melis, R.; Yang, X.; Ruiz-garcia, L.; Qian, J.; Zhao, C. CFD Simulation of Airflow and Heat Transfer During Forced-Air Precooling of Apples. J. Food Process Eng. 2017, 40, e12390. [Google Scholar] [CrossRef]
- Han, J.-W.; Zhao, C.-J.; Qian, J.-P.; Ruiz-Garcia, L.; Zhang, X. Numerical modeling of forced-air cooling of palletized apple: Integral evaluation of cooling efficiency. Int. J. Refrig. 2018, 89, 131–141. [Google Scholar] [CrossRef]
- Wu, W.; Defraeye, T. Identifying heterogeneities in cooling and quality evolution for a pallet of packed fresh fruit by using virtual cold chains. Appl. Therm. Eng. 2018, 133, 407–417. [Google Scholar] [CrossRef]
- Laguerre, O.; Denis, A.; Bouledjeraf, N.; Duret, S.; Bertheau, E.D.; Moureh, J.; Aubert, C.; Flick, D. Heat transfer and aroma modeling of fresh fruit and vegetable in cold chain: Case study on tomatoes. Int. J. Refrig. 2022, 133, 133–144. [Google Scholar] [CrossRef]
- FLeitão, F.; Silva, P.D.; Gaspar, P.D.; Pires, L.C.; Duarte, D. Experimental Study of Thermal Performance of Different Fruit Packaging Box Designs. Energies 2021, 14, 3588. [Google Scholar] [CrossRef]
- Delele, M.A.; Ngcobo, M.E.K.; Getahun, S.T.; Chen, L.; Mellmann, J.; Opara, U.L. Studying airflow and heat transfer characteristics of a horticultural produce packaging system using a 3-D CFD model. Part II: Effect of package design. Postharvest Biol. Technol. 2013, 86, 546–555. [Google Scholar] [CrossRef]
- Berry, T.M.; Fadiji, T.S.; Defraeye, T.; Opara, U.L. The role of horticultural carton vent hole design on cooling efficiency and compression strength: A multi-parameter approach. Postharvest Biol. Technol. 2017, 124, 62–74. [Google Scholar] [CrossRef]
- Berry, T.M.; Defraeye, T.; Nicola, B.M.; Opara, U.L. Multiparameter Analysis of Cooling Efficiency of Ventilated Fruit Cartons using CFD: Impact of Vent Hole Design and Internal Packaging. Food Bioprocess Technol. 2016, 9, 1481–1493. [Google Scholar] [CrossRef]
- Defraeye, T.; Lambrecht, R.; Tsige, A.A.; Delele, M.A.; Opara, U.L.; Cronjé, P.; Verboven, P.; Nicolai, B. Forced-convective cooling of citrus fruit: Package design. J. Food Eng. 2013, 118, 8–18. [Google Scholar] [CrossRef]
- Dehghannya, J.; Ngadi, M.; Vigneault, C. Mathematical modeling of airflow and heat transfer during forced convection cooling of produce considering various package vent areas. Food Control 2011, 22, 1393–1399. [Google Scholar] [CrossRef]
- Ferrua, M.J.; Singh, R.P. Improved airflow method and packaging system for forced-air cooling of strawberries. Int. J. Refrig. 2011, 34, 1162–1173. [Google Scholar] [CrossRef]
- Han, J.-W.; Zhao, C.-J.; Yang, X.-T.; Qian, J.-P.; Fan, B.-L. Computational modeling of airflow and heat transfer in a vented box during cooling: Optimal package design. Appl. Therm. Eng. 2015, 91, 883–893. [Google Scholar] [CrossRef]
- Ilangovan, A.; Curto, J.; Gaspar, P.D.; Silva, P.D.; Alves, N. CFD Modelling of the Thermal Performance of Fruit Packaging Boxes: Influence of Vent-Holes Design. Energies 2021, 14, 7990. [Google Scholar] [CrossRef]
- Ambaw, A.; Mukama, M.; Opara, U.L. Analysis of the effects of package design on the rate and uniformity of cooling of stacked pomegranates: Numerical and experimental studies. Comput. Electron. Agric. 2017, 136, 13–24. [Google Scholar] [CrossRef]
- O’Sullivan, J.L.; Ferrua, M.J.; Love, R.; Verboven, P.; Nicolaï, B.; East, A. Forced-air cooling of polylined horticultural produce: Optimal cooling conditions and package design. Postharvest Biol. Technol. 2017, 126, 67–75. [Google Scholar] [CrossRef]
- Wu, W.; Cronjé, P.; Verboven, P.; Defraeye, T. Unveiling how ventilated packaging design and cold chain scenarios affect the cooling kinetics and fruit quality for each single citrus fruit in an entire pallet. Food Packag. Shelf Life 2019, 21, 100369. [Google Scholar] [CrossRef]
- Pham, A.T.; Moureh, J.; Belaidi, M.; Flick, D. CFD modelling of a pallet of heat-generating product applied to a cheese product. Int. J. Refrig. 2021, 128, 163–176. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Cãnada, CA, USA, 1998. [Google Scholar]
- Kader, B.A. Temperature and concentration profiles in fully turbulent boundary layers. Int. J. Heat Mass Transf. 1981, 24, 1541–1544. [Google Scholar] [CrossRef]
- Ali, R.K.; Refaey, H.A.; Salem, M.R. Effect of package spacing on convective heat transfer from thermal sources mounted on a horizontal surface. Appl. Therm. Eng. 2018, 132, 676–685. [Google Scholar] [CrossRef]
- Asako, Y.; Faghri, M. Parametric study of turbulent three-dimensional heat transfer of arrays of heated blocks encountered in electronic equipment. Int. J. Heat Mass Transf. 1994, 37, 469–478. [Google Scholar] [CrossRef]
- O’Sullivan, J.; Ferrua, M.J.; Love, R.; Verboven, P.; Nicolaï, B.; East, A. Modelling the forced-air cooling mechanisms and performance of polylined horticultural produce. Postharvest Biol. Technol. 2016, 120, 23–35. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, Y.H.; Kim, Y.S.; Park, Y.G.; Ha, M.Y. Numerical study on the effect of different hole locations in the fan case on the thermal performance inside a gas oven range. Appl. Therm. Eng. 2018, 137, 123–133. [Google Scholar] [CrossRef]
- Alvarez, G. Etude de Transferts de Chaleur et de Matière au Sein d’un échangeur Complexe de Type ‘Palette’. Ph.D. Thesis, ENGREF, Paris, France, 1992. [Google Scholar]
- Material Properties. Available online: https://www.engineeringtoolbox.com/material-properties-t_24.html (accessed on 15 May 2022).
- Diop, M.; Flick, D.; Alvarez, G.; Moureh, J. Experimental Study of the Diffusion of a Confined Wall Jet through a Perforated Plate: Influence of the Porosity and the Geometry. Open J. Fluid Dyn. 2022, 12, 96–126. [Google Scholar] [CrossRef]
- Kaffel, A.; Moureh, J.; Harion, A.; Russeil, S. Experimental investigation of a plane wall jet subjected to an external lateral flow. Exp. Fluids 2015, 56, 95. [Google Scholar] [CrossRef]
- Karimipanah, M.T. Deflection of wall-jets in ventilated enclosures described by pressure distribution. Build. Environ. 1998, 34, 329–333. [Google Scholar] [CrossRef]
- Moureh, J.; Flick, D. Airflow characteristics within a slot-ventilated enclosure. Int. J. Heat Fluid Flow 2005, 26, 12–24. [Google Scholar] [CrossRef]
- Yu, H.; Jou, L.-J.; Ouyang, H.-T.; Liang, H.-M.; Liao, C.-M. Similitude Criteria for a Two-dimensional Wall Jet in an Isothermal Mechanically Ventilated Enclosure. Biosyst. Eng. 2006, 93, 415–425. [Google Scholar] [CrossRef]
- Craft, T.J.; Launder, B.E. On the spreading mechanism of the three-dimensional turbulent wall jet. J. Fluid Mech. 2001, 435, 305–326. [Google Scholar] [CrossRef]
- Forthmann, E. Turbulent Jet Expansion; National Advisory Commitee for Aeronautics: Washington, DC, USA, 1936.
- Choi, J.U.; Kim, G.M.; Lee, H.C.; Kwak, J.S. Optimization of the Coanda bump to improve the film cooling effectiveness of an inclined slot. Int. J. Therm. Sci. 2019, 139, 376–386. [Google Scholar] [CrossRef]

| Property | Carrageenan Gel [26] | PMMA [27] | Air [27] |
|---|---|---|---|
| λ (W m−1 K−1) | 0.519 | 0.2 | 0.0242 |
| ρ (kg m−3] | 1013 | 1450 | 1.264 @ 6 °C |
| Cp (J kg−1 K−1) | 4100 | 1170 | 1006.43 |
| µ (kg m−1 s−1) | - | - | 1.7894 × 10−5 |
| ΔP (Pa) | u (m s−1) | Q (L s−1 kg−1) |
|---|---|---|
| 0.4 | 0.08 | 0.26 |
| 2.4 | 0.14 | 0.46 |
| 4.5 | 0.22 | 0.66 |
| RMSE (°C) | ARD (%) | |
|---|---|---|
| Crate 1 | 0.44 | 2.35 |
| Crate 2 | 0.62 | 4.20 |
| Crate 3 | 0.71 | 5.50 |
| Crate 4 | 0.26 | 2.05 |
| Overall | 0.48 | 3.56 |
| 0.26 L s−1 kg−1 | 0.46 L s−1 kg−1 | 0.66 L s−1 kg−1 | |
|---|---|---|---|
| Inlet crate 1 | 6.0 | 6.0 | 6.0 |
| Inlet crate 2 | 9.1 | 8.6 | 8.0 |
| Inlet crate 3 | 10.4 | 9.6 | 8.8 |
| Inlet crate 4 | 12.1 | 10.4 | 9.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agyeman, E.K.K.; Duret, S.; Flick, D.; Laguerre, O.; Moureh, J. Computational Modelling of Airflow and Heat Transfer during Cooling of Stacked Tomatoes: Optimal Crate Design. Energies 2023, 16, 2048. https://doi.org/10.3390/en16042048
Agyeman EKK, Duret S, Flick D, Laguerre O, Moureh J. Computational Modelling of Airflow and Heat Transfer during Cooling of Stacked Tomatoes: Optimal Crate Design. Energies. 2023; 16(4):2048. https://doi.org/10.3390/en16042048
Chicago/Turabian StyleAgyeman, Emmanuel Kwadwo Kale, Steven Duret, Denis Flick, Onrawee Laguerre, and Jean Moureh. 2023. "Computational Modelling of Airflow and Heat Transfer during Cooling of Stacked Tomatoes: Optimal Crate Design" Energies 16, no. 4: 2048. https://doi.org/10.3390/en16042048
APA StyleAgyeman, E. K. K., Duret, S., Flick, D., Laguerre, O., & Moureh, J. (2023). Computational Modelling of Airflow and Heat Transfer during Cooling of Stacked Tomatoes: Optimal Crate Design. Energies, 16(4), 2048. https://doi.org/10.3390/en16042048







