Energy Trading Strategy of Distributed Energy Resources Aggregator in Day-Ahead Market Considering Risk Preference Behaviors
Abstract
1. Introduction
- (1)
- At present, most of the methods to deal with uncertain problems are based on probability and statistical analysis methods, which require a large amount of data. However, China’s electricity market construction is in the primary stage and there are few market transaction data. Therefore, this paper uses the GMM and IGDT to effectively deal with the uncertainty of new energy output and price fluctuations in the spot market. Meanwhile, to address the issue of the GMM easily convergent to the local optimal solution, this paper employs Spearman as the distance calculation formula based on the traditional algorithm, which effectively reduces the probability of the local optimal solution.
- (2)
- The majority of recent papers only run robust models to develop decision schemes; this paper adds opportunity decision models on this basis, which can provide a basis for trading decisions for DERAs with different risk preferences given that DERAs with different risk preferences will exhibit risk-averse or risk-chasing behavioral characteristics in the face of market risks.
- (3)
- Based on the characteristics of China’s dual-track market, this paper employs prospect theory to examine the probability and utility value of aggregators’ perceptions of “gain” and “loss” under various settlement methods, and then, solves them using the MPA optimizer to determine the optimal utility strategy. The difficulty of the algorithm’s local optimal solution is decreased, and the model solving effect is enhanced, allowing the best utility strategy to be identified.
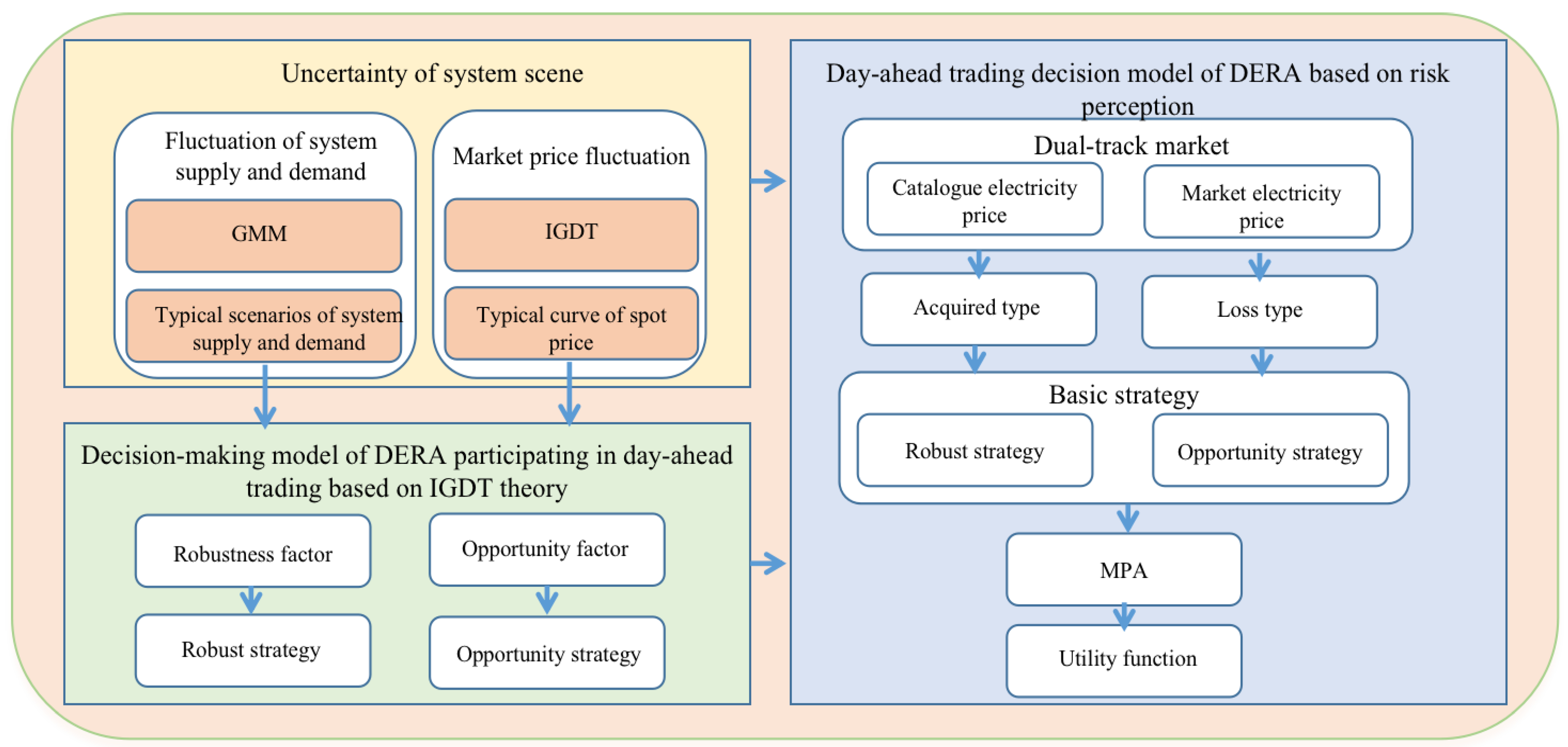
2. Uncertainty Treatment of System Supply and Demand and Market Price Fluctuation
2.1. Uncertainty Treatment of System Supply and Demand Fluctuation
- Step 1: initialize the parameters and of multivariate Gaussian distributions, assuming that each mixture element has a diagonal matrix.
- Step 2: iterate over all sample points and calculate the probability of the Gaussian distribution of the sample points , as shown in Formula (1).where is the probability function, denotes the class to which belongs, and is the dimension of .
- Step 3: the updated values and of the Gaussian distribution parameters and are obtained according to Formulas (2) and (3).
- Step 4: repeat steps 2 and 3 until all Gaussian parameters converge.
- Step 5: using the calculated Gaussian parameters, all samples are traversed, and the samples are classified into the class with the maximum probability .
2.2. Uncertainty Treatment of Market Price Fluctuation
3. Day-Ahead Trading Decision Model of DERAs Based on IGDT and Prospect Theory
3.1. The Optimal Model of Day-Ahead Trading Decisions of DERAs
3.1.1. Objective Function
3.1.2. Constraints
- (1)
- PV
- (2)
- Wind powerwhere is the actual output of wind power.
- (3)
- Micro gas turbines (MT)
- (1)
- Equipment output constraintwhere and are the maximum and minimum output of equipment g, respectively, and is a binary variable indicating the operating state of MT g. The operating state is taken as 1, otherwise, it is taken as 0.
- (2)
- Equipment start-stop constraintswhere and , respectively, represent the startup and shutdown state variables of MT g at time t. In the startup state, takes 1 and takes 0. In the shutdown state, takes 0 and takes 1.
- (3)
- Climbing power constraintwhere and are the up-climbing rate and down-climbing rate of equipment g, respectively.
- (4)
- Rotate alternate constraint
- (5)
- Gas fired boilerwhere and are the thermal power and a maximum power of the gas boiler, respectively.
- (6)
- Electrochemical energy storagewhere and are the minimum and maximum energy storage capacity of energy storage equipment i, respectively. and are the binary state variables indicating the charging and discharging of energy storage equipment i. In the charging state, takes 1 and takes 0, which is the opposite when discharging.
- (7)
- Suction chillerwhere is the cooling power of the suction chiller, is the input thermal power, and is the efficiency of the electric refrigerator.
- (8)
- Electric chillerwhere and are the electric chiller output and input power, respectively. is the electric chiller performance coefficient. is the maximum input power of the electric chiller.
- (9)
- Transaction constraints with the main networkwhere and are the purchasing power and selling of the DERA to the main network at time t. Considering the capacity limitation of the transmission network, and are the maximum values of the power interacting with the system with the external grid. and indicate the binary variables of the DERA power purchase and sale states, which ensures that the aggregator does not purchase and sells power at time t. When purchasing electricity, takes 1 and takes 0, and the opposite is true when selling electricity.
- (10)
- Power balance constraints of system operationwhere are the load of electricity, heat, and cold at time t, respectively. and are energy storage discharge power and charging power, respectively. is the electric chiller input power. is the heat exchange coefficient. is the cooling efficiency of the electric chiller. is the maximum cold demand of the RDES.
3.2. Decision-Making Model of a DERA Participating in the Day-Ahead Trading Based on IGDT
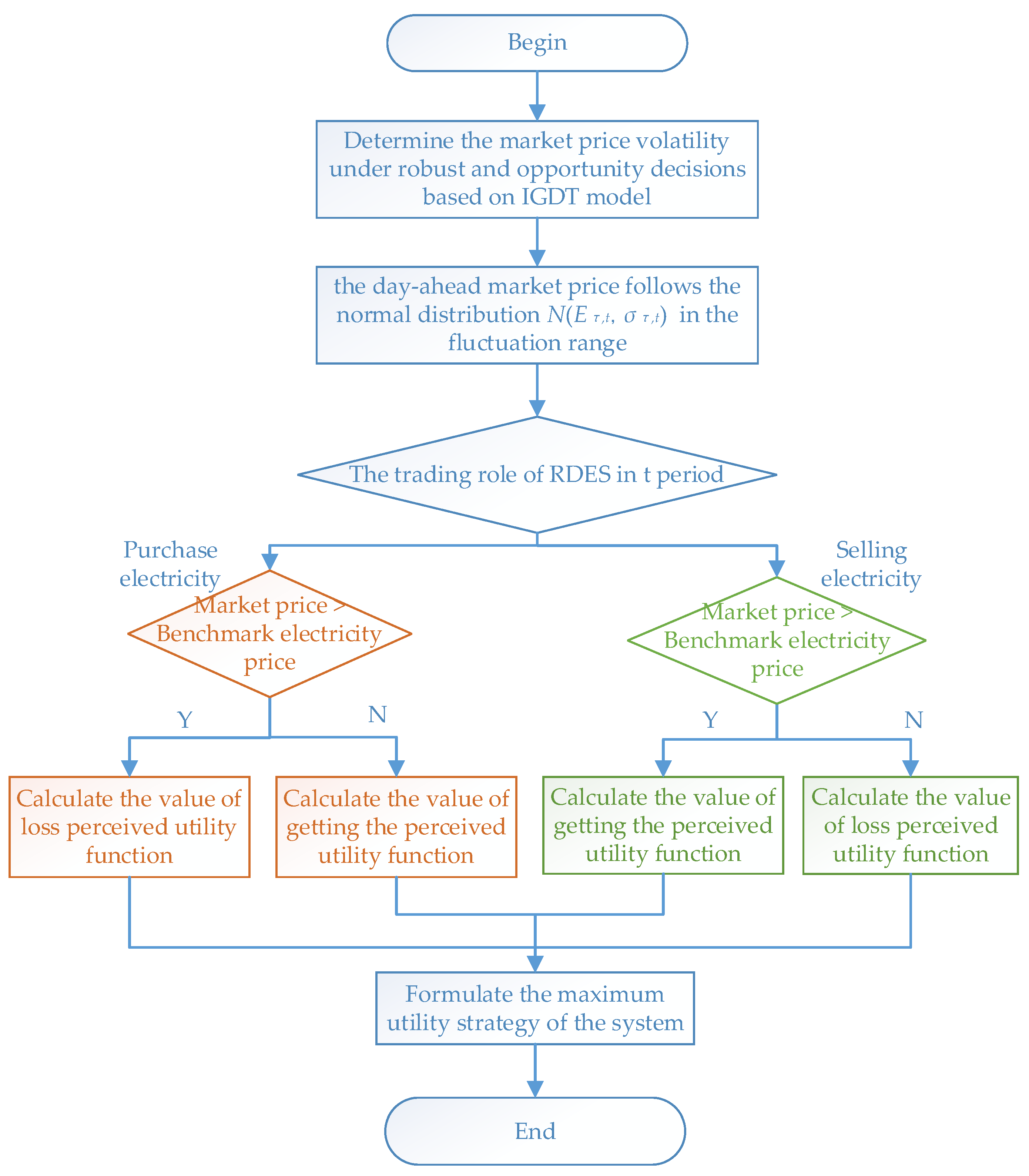
3.3. Day-Ahead Trading Decision Model of the DERA Based on Risk Perception
- (1)
- Power purchase decision model based on prospect theory
- (1)
- The market price is lower than the benchmark price
- (2)
- Market price is higher than the benchmark electricity price
- (2)
- Power sale decision model based on prospect theory
- (1)
- Market price is higher than the benchmark electricity price
- (2)
- The market price is lower than the benchmark price
3.4. Solution to the Day-Ahead Transaction Decision-Making Model of a DERA Based on MPA
- (1)
- Initialization phase. Set the algorithm parameters and initialize the prey position within the search range, as shown in Formulas (56)–(65):where and denote the range of prey search space, and is a random number within [0, 1].
- (2)
- Optimization stage. The optimization phase is divided into the early iteration, middle iteration, and late iteration [41]. In the early iteration, the number of iterations is less than 1/3 of the maximum number of iterations, the predator is faster than the prey, a global search is performed, and the prey is updated by Brown’s random wandering.where is the step size, is a normally distributed Brownian wandering random vector, is the elite matrix constructed by the top predator, is a prey matrix with the same dimension as the , is the item-by-item multiplication operation, takes 0.5, and is a uniform random vector on [0, 1]. N is the population size, and and denote the current and maximum number of iterations, respectively.
- (3)
- Fish aggregation devices (FADs) or eddy current effect. This strategy typically alters the disorientation behavior of ocean predators, allowing the MPA to overcome the premature convergence problem and avoid falling into local extremes during the optimization search [43].where is the influence probability, which is set to 0.2, is the binary vector, is the random number within [0, 1], and and are the random indexes of the prey matrix, respectively. The solution process is shown in Figure A1.
4. Case Analysis
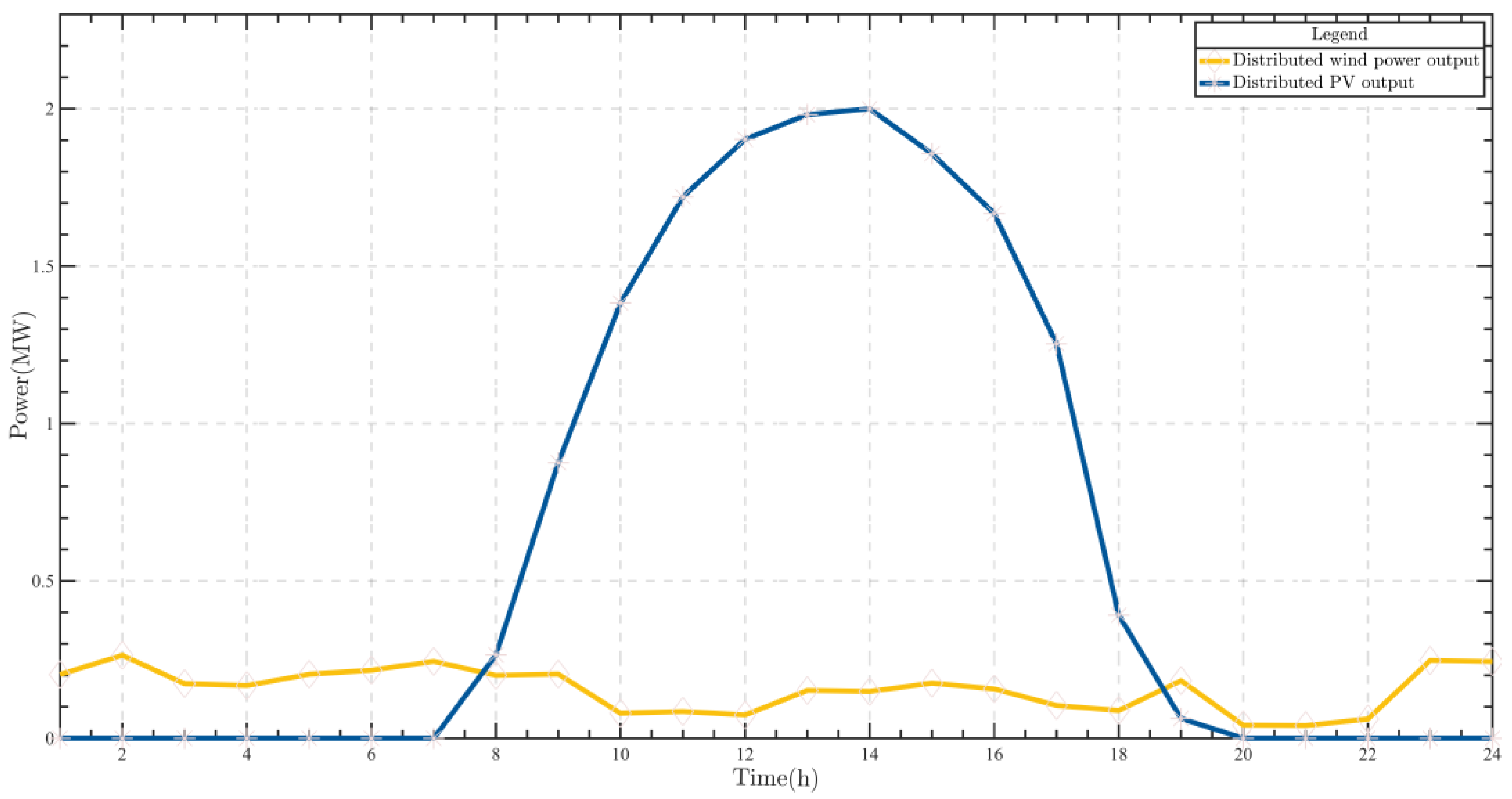
4.1. Basic Data and Scenario Settings
- (1)
- Basic Data
- (2)
- Scene Settings
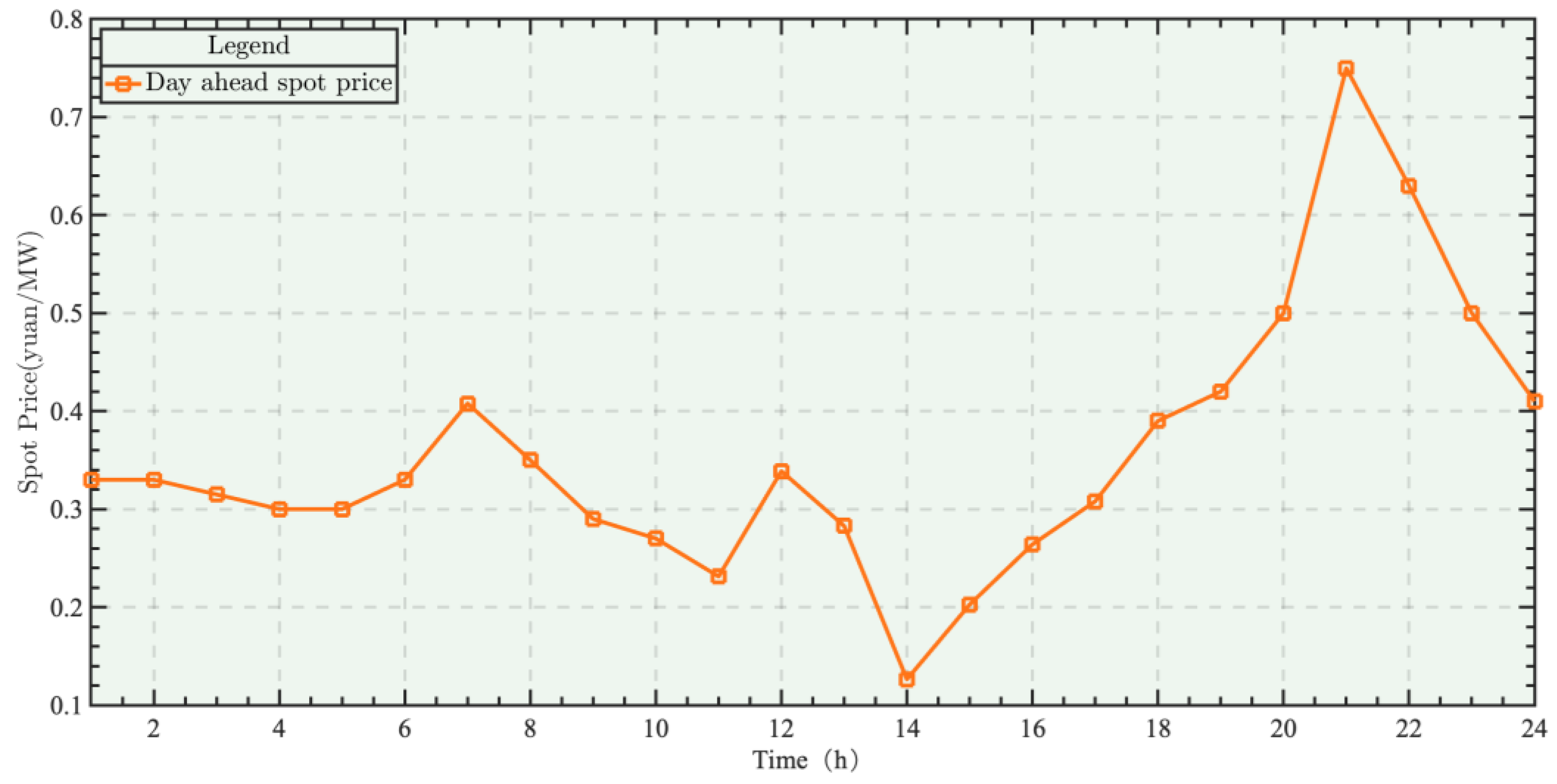
4.2. Analysis of Day-Ahead Trading Strategy of Aggregators Based on the IGDT
- (1)
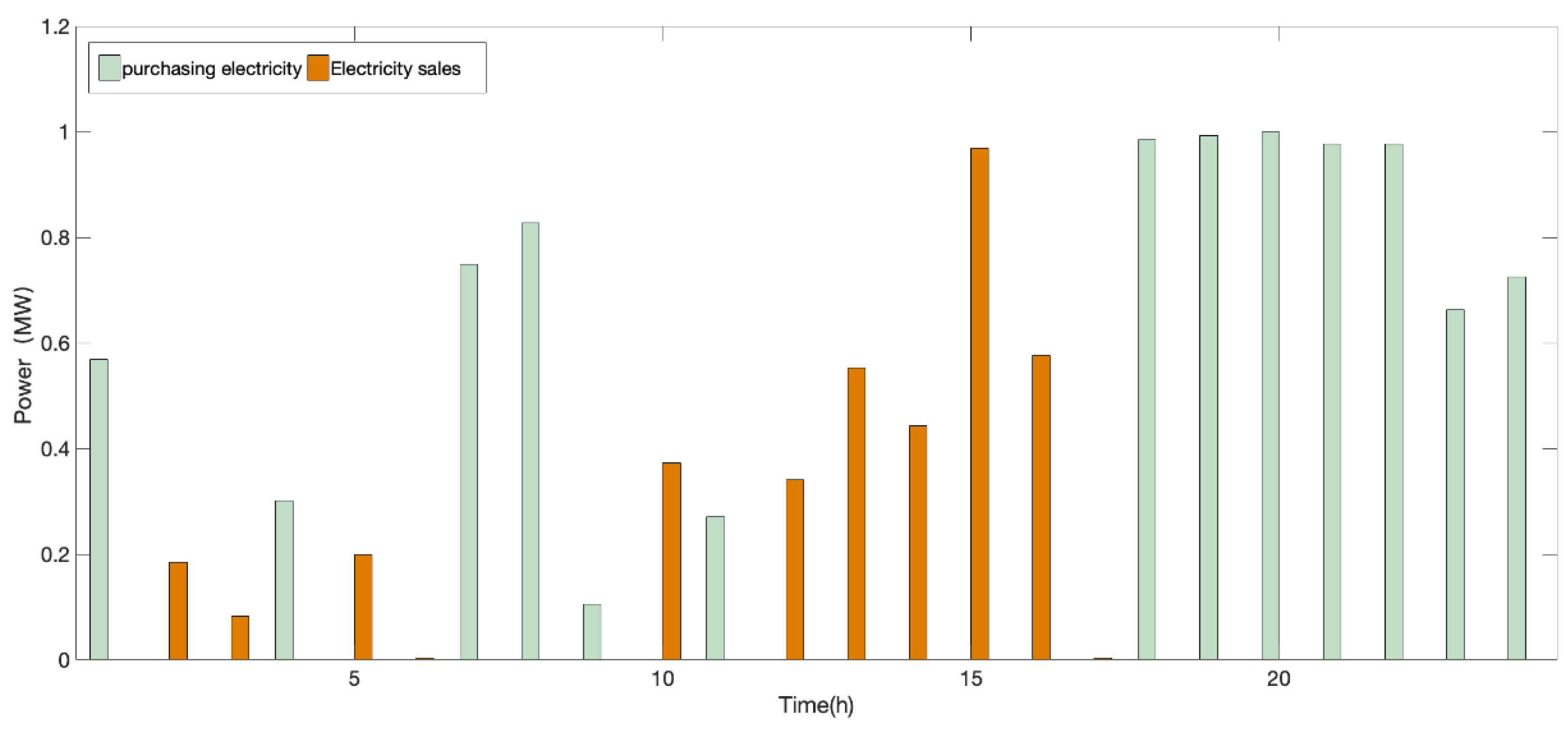
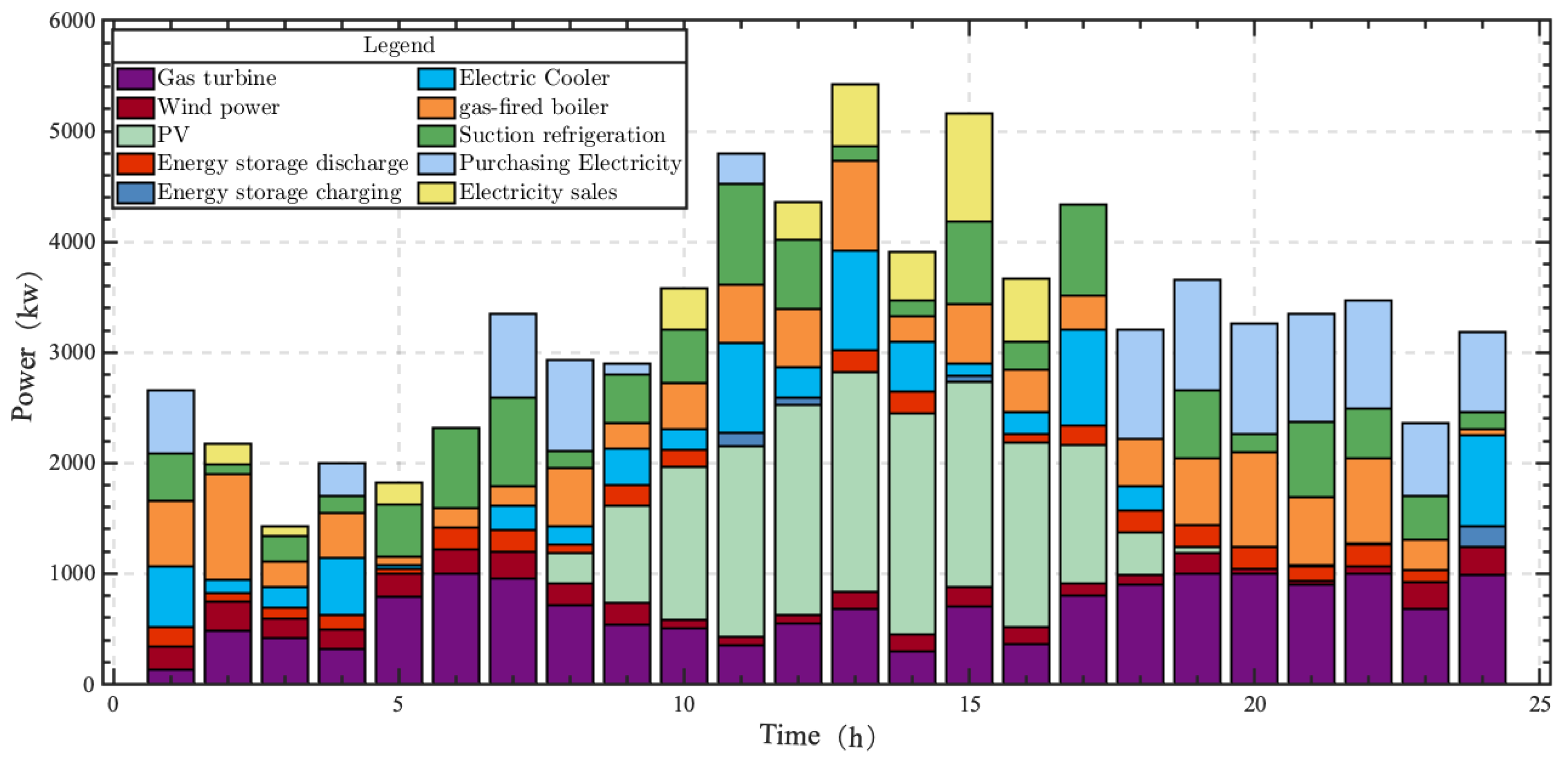
- Analysis of day-ahead trading strategies for DERAs under a deterministic scenario
- (2)
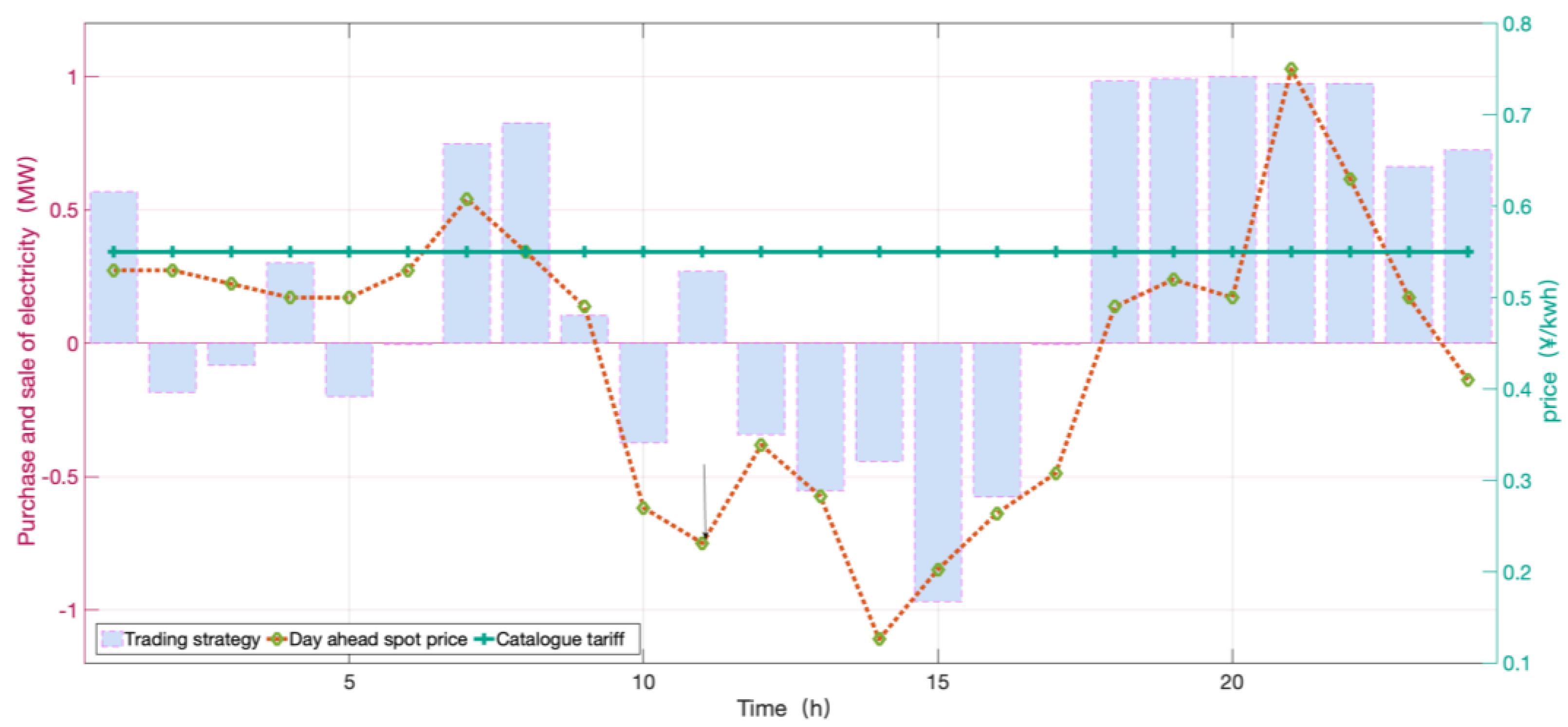
- Analysis of IGDT decision of the DERA considering risk preference of day-ahead market price fluctuation
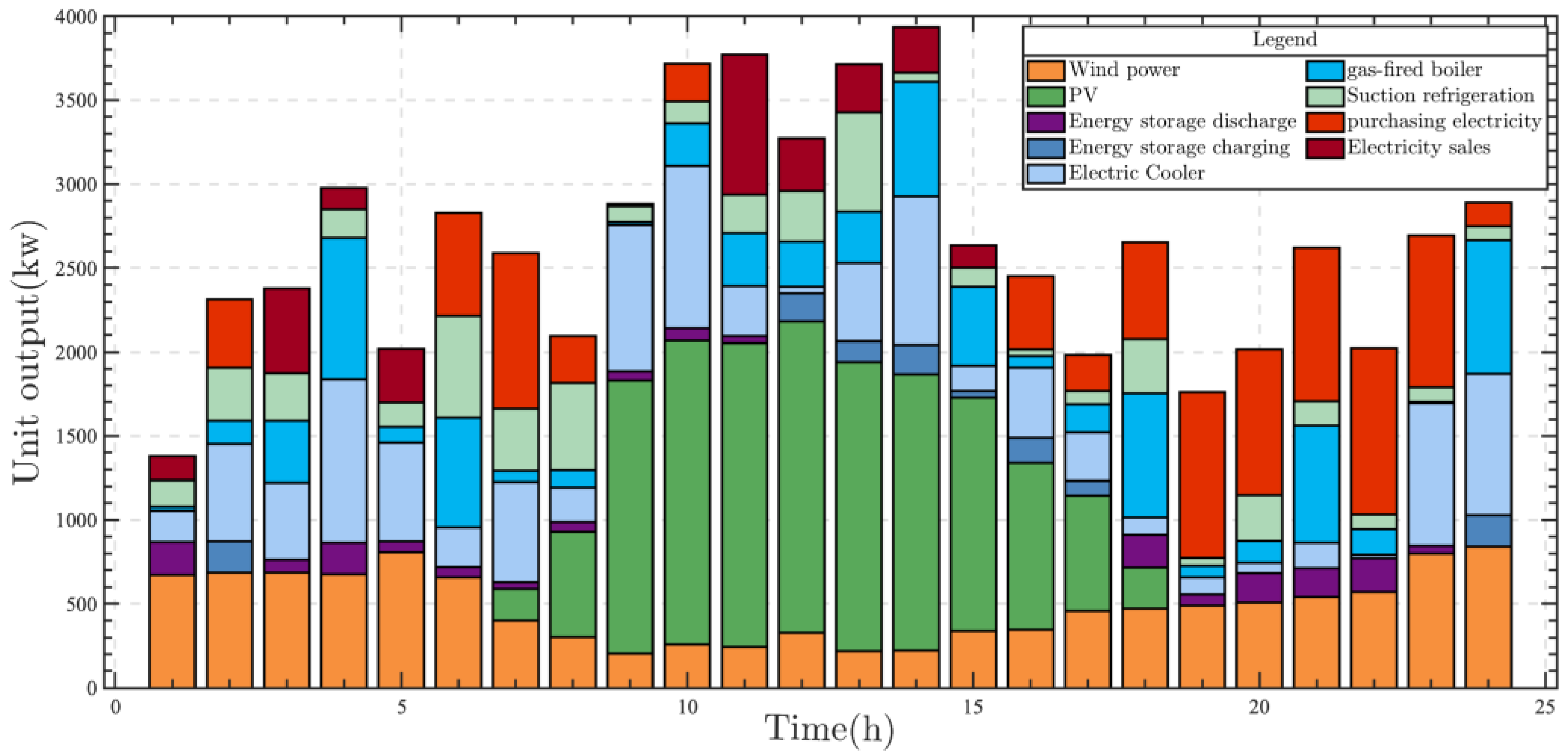
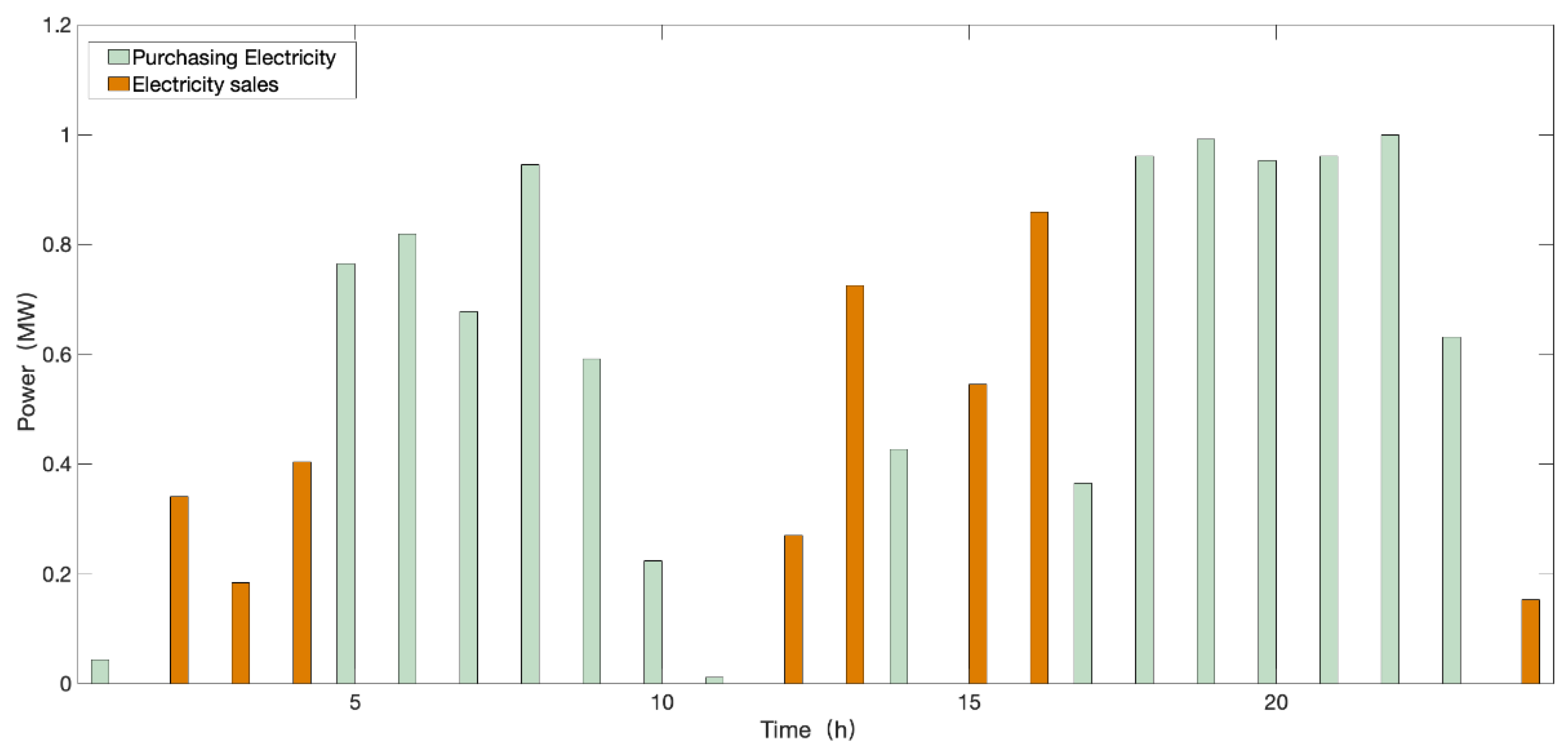
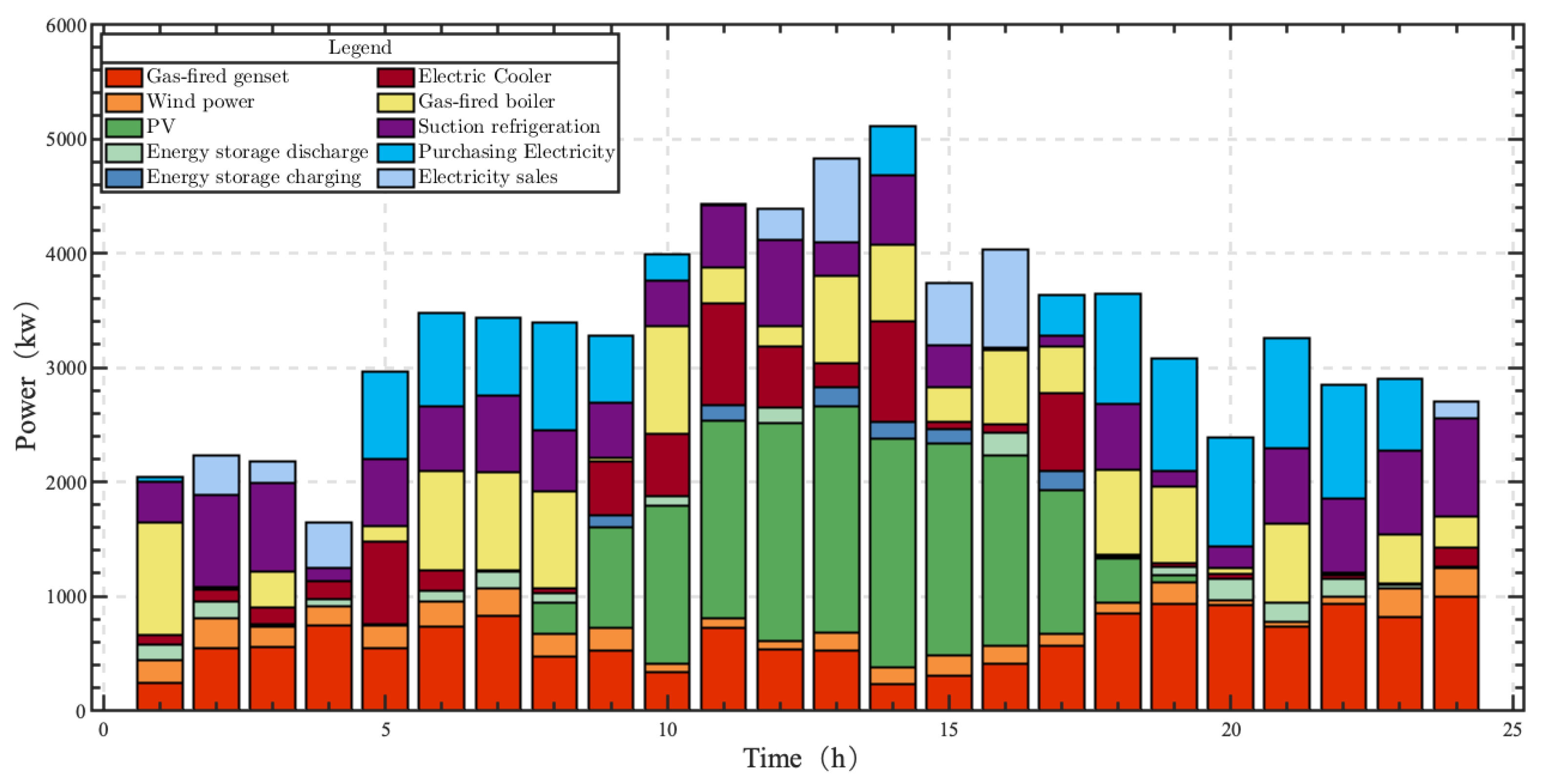
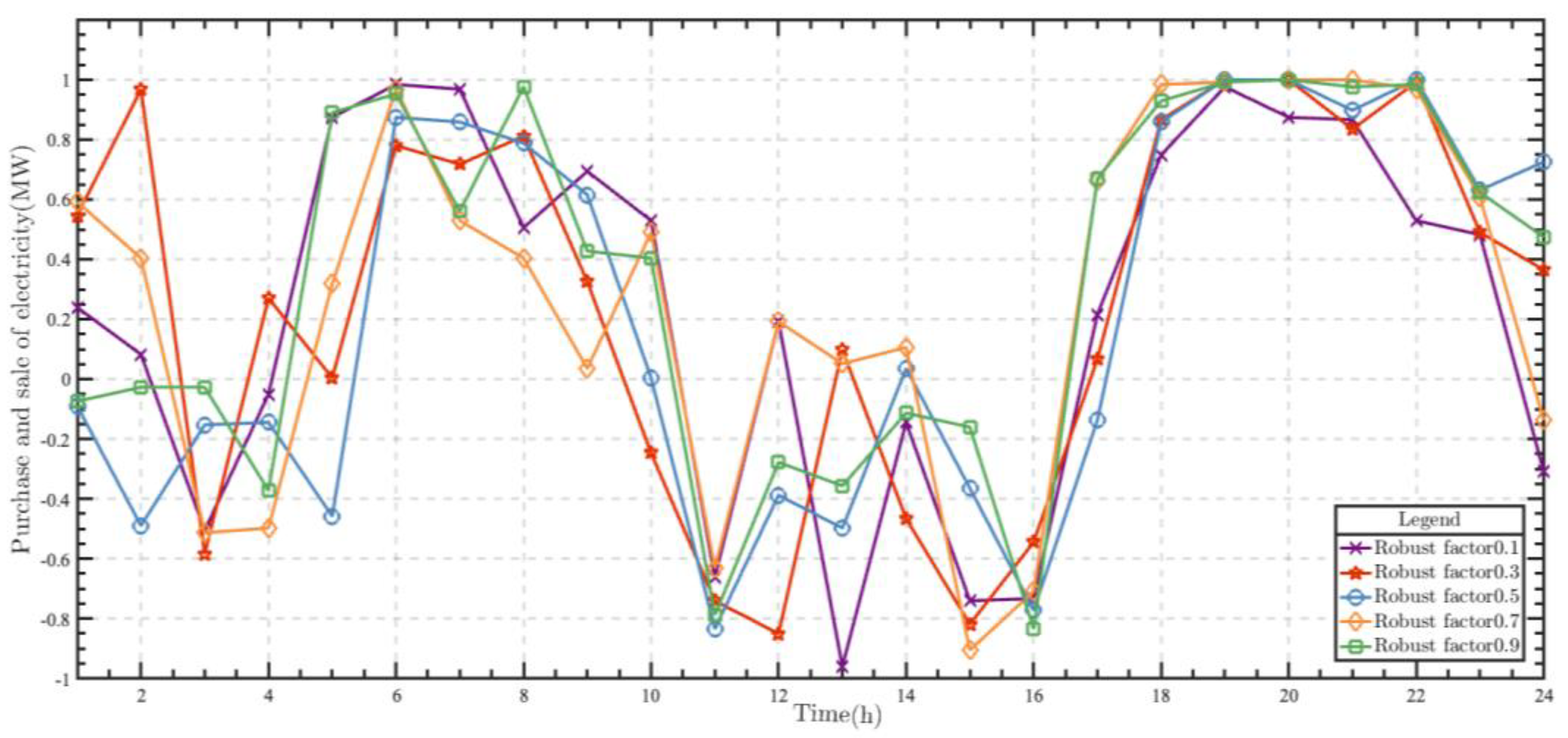
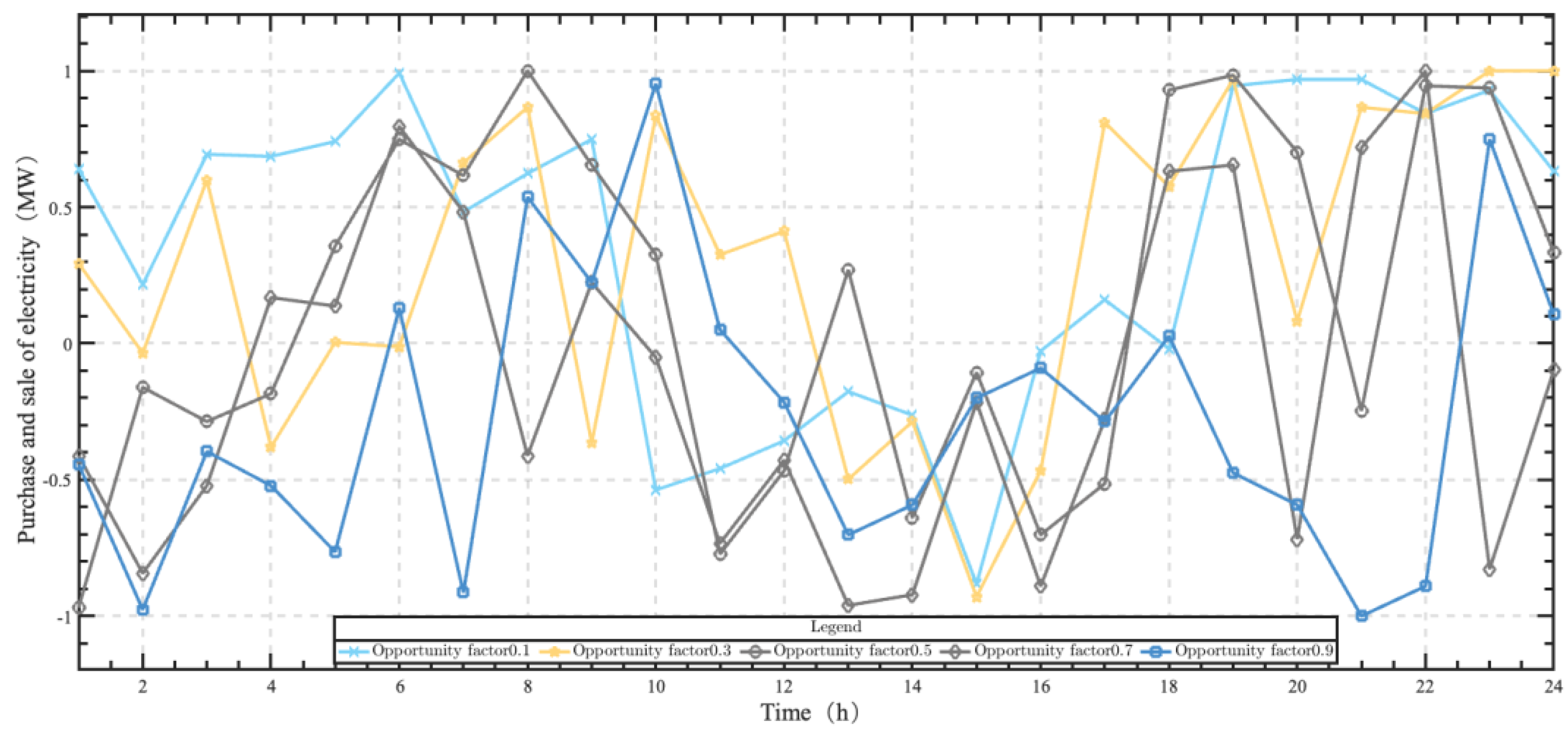
4.3. Analysis of Day-Ahead Trading Strategy of Aggregators under Different Factor Scenarios
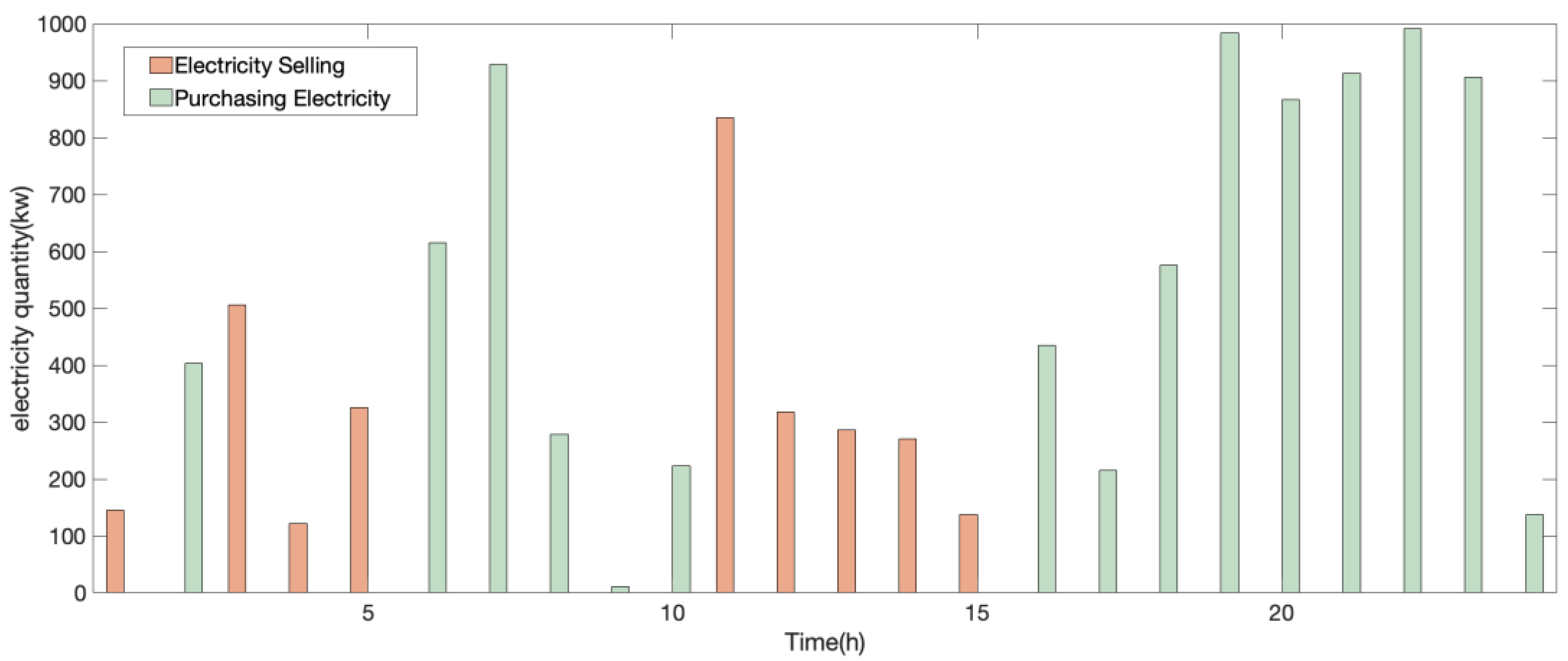
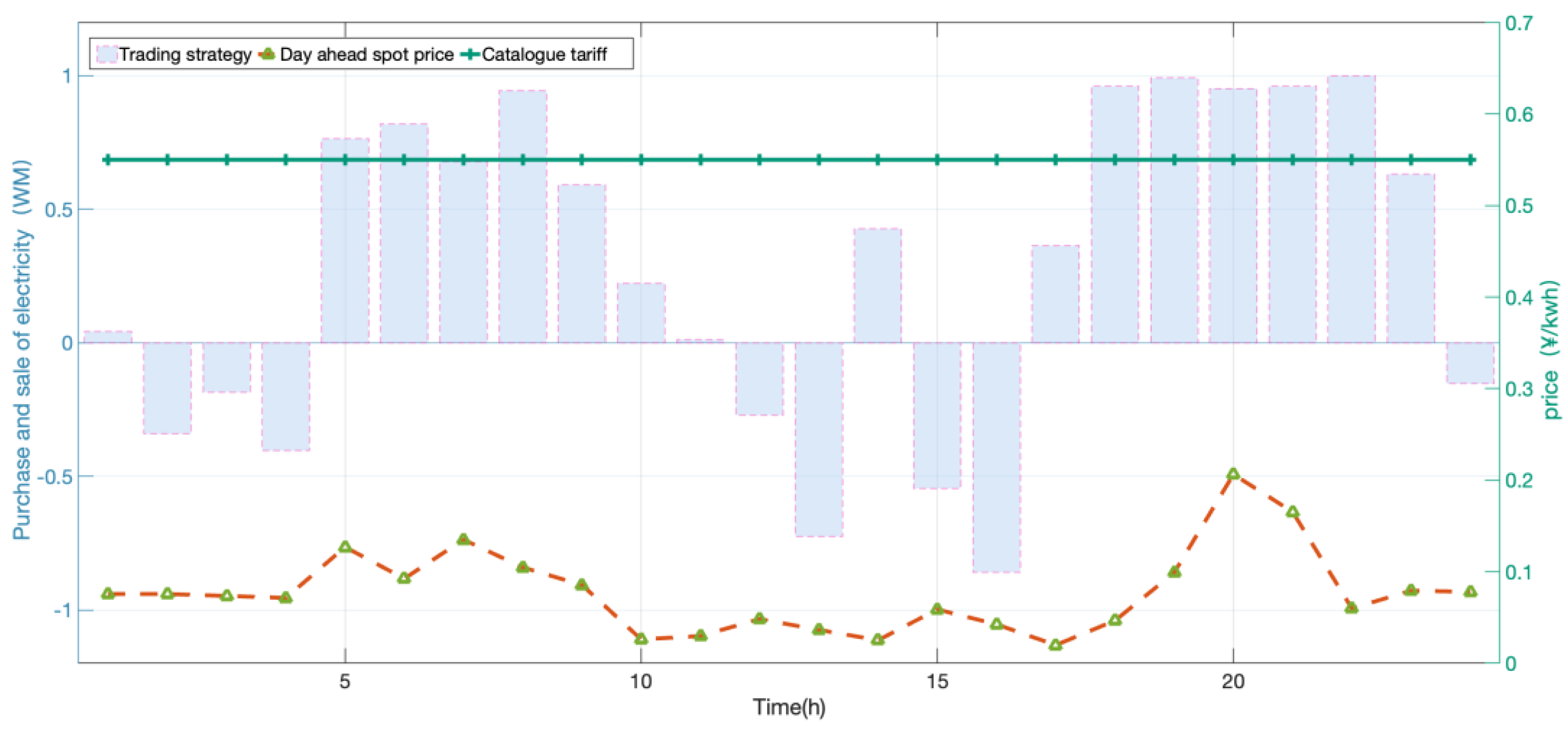
4.4. DERA Decision Analysis Based on Prospect Theory
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Zheng, B.; Wei, W.; Chen, Y.; Wu, Q.; Mei, S. A peer-to-peer energy trading market embedded with residential shared energy storage units. Appl. Energy 2022, 308, 118400. [Google Scholar] [CrossRef]
- Rodrigues, D.L.; Ye, X.; Xia, X.; Zhu, B. Battery energy storage sizing optimisation for different ownership structures in a peer-to-peer energy sharing community. Appl. Energy 2020, 262, 114498. [Google Scholar] [CrossRef]
- Di Silvestre, M.L.; Gallo, P.; Sanseverino, E.R.; Sciume, G.; Zizzo, G. Aggregation and remuneration in demand response with a blockchain-based framework. IEEE Trans. Ind. Appl. 2020, 56, 4248–4257. [Google Scholar] [CrossRef]
- Kang, J.; Yu, R.; Huang, X.; Maharjan, S.; Zhang, Y.; Hossain, E. Enabling localized peer-to-peer electricity trading among plug-in hybrid electric vehicles using consortium blockchains. IEEE Trans. Ind. Inform. 2017, 13, 3154–3164. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Optimal bidding strategy for microgrids considering renewable energy and building thermal dynamics. IEEE Trans. Smart Grid 2014, 5, 1608–1620. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Hemmati, M.; Zare, K.; Abapour, M.; Mohammadi-Ivatloo, B.; Marzband, M.; Anvari-Moghaddam, A. A novel hybrid two-stage framework for flexible bidding strategy of reconfigurable micro-grid in day-ahead and real-time markets. Int. J. Electr. Power 2020, 123, 106293. [Google Scholar] [CrossRef]
- Mashhour, E.; Moghaddas-Tafreshi, S.M. Bidding strategy of virtual power plant for participating in energy and spinning reserve markets—Part I: Problem formulation. IEEE Trans. Power Syst. 2010, 26, 949–956. [Google Scholar] [CrossRef]
- Sadeghi, S.; Jahangir, H.; Vatandoust, B.; Golkar, M.A.; Ahmadian, A.; Elkamel, A. Optimal bidding strategy of a virtual power plant in day-ahead energy and frequency regulation markets: A deep learning-based approach. Int. J. Electr. Power 2021, 127, 106646. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, X.; Wang, X.; Bie, C.H. Review and prospect of research on multi energy market coupling transaction. Glob. Energy Internet 2020, 3, 487–496. [Google Scholar] [CrossRef]
- Conejo, A.J.; Nogales, F.J.; Arroyo, J.M. Price-taker bidding strategy under price uncertainty. IEEE Trans. Power Syst. 2002, 17, 1081–1088. [Google Scholar] [CrossRef]
- Wen, F.; David, A.K. Optimal bidding strategies and modeling of imperfect information among competitive generators. IEEE Trans. Power Syst. 2001, 16, 15–21. [Google Scholar]
- Kang, D.; Kim, B.H.; Hur, D. Supplier bidding strategy based on non-cooperative game theory concepts in single auction power pools. Electr. Pow Syst. Res. 2007, 77, 630–636. [Google Scholar] [CrossRef]
- Jing, C.; Yang, Y. Application of the EWA Algorithm in Electricity Market Simulation. Autom. Electr. Power Syst. 2010, 34, 46–50. [Google Scholar]
- Zhu, J.Y. Study on Bidding Strategy of Generation Company with Evolutionary Game Theory based on Repast Platform. Diploma Thesis, North China Electric Power University, Beijing, China, 2010. [Google Scholar]
- Zhu, J.L. Agent-Based Bidding Strategy of Generators. Diploma Thesis, Beijing Jiaotong University, Beijing, China, 2010. [Google Scholar]
- Ren, X.G. A Study of Generator Bidding Behavior Based-on Multi-Agent Simulation. Diploma Thesis, North China Electric Power University, Beijing, China, 2010. [Google Scholar]
- Liang, Z.H. Simulation Research on Bidding Transaction System of Generation Market Based on MAS. Diploma Thesis, North China Electric Power University, Beijing, China, 2012. [Google Scholar]
- Akbari, E.; Hooshmand, R.; Gholipour, M.; Parastegari, M. Stochastic programming-based optimal bidding of compressed air energy storage with wind and thermal generation units in energy and reserve markets. Energy 2019, 171, 535–546. [Google Scholar] [CrossRef]
- Ansari, M.M.; Guo, C.; Shaikh, M.; Chopra, N.; Yang, B.; Pan, J.; Zhu, Y.; Huang, X. Considering the uncertainty of hydrothermal wind and solar-based DG. Alex. Eng. J. 2020, 59, 4211–4236. [Google Scholar] [CrossRef]
- Yi, M.Y.; Tong, X.Y. Dynamic Economic Dispatch Considering Uncertainties of Wind Power and Load Forecast Error. Power Syst. Technol. 2019, 43, 4050–4057. [Google Scholar] [CrossRef]
- Dong, J.; Dou, X.; Bao, A.; Zhang, Y.; Liu, D. Day-Ahead Spot Market Price Forecast Based on a Hybrid Extreme Learning Machine Technique: A Case Study in China. Sustainability 2022, 14, 7767. [Google Scholar] [CrossRef]
- Ben-Haim, Y. Info-Gap Decision Theory: Decisions under Severe Uncertainty; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Soroudi, A.; Ehsan, M. IGDT based robust decision making tool for DNOs in load procurement under severe uncertainty. IEEE Trans. Smart Grid 2012, 4, 886–895. [Google Scholar] [CrossRef]
- Mavalizadeh, H.; Ahmadi, A.; Gandoman, F.H.; Siano, P.; Shayanfar, H.A. Multi objective robust power system expansion planning considering generation units retirement. IEEE Syst. J. 2017, 12, 2664–2675. [Google Scholar] [CrossRef]
- Sun, G.Q.; Zhou, Y.Z.; Wei, Z.N.; Geng, T.X.; Wang, Y.; Li, Y.C. Dispatch optimization model of virtual power plant based on hybrid stochastic programming and Information gap decision theory. Electr. Power Autom. Equip. 2017, 37, 112–118. [Google Scholar] [CrossRef]
- Song, K.L.; Xie, Y.Y.; Chen, X.; Zhang, L.D.; Wang, C.G.; Yin, M.H. Robust Restoration Method for Power System Load Based on Information Gap Decision Theory. Autom. Electr. Power Syst. 2017, 41, 113–120+175. [Google Scholar]
- Wang, C.Q.; Wei, H.; Wu, S.Y. Multi-power Combined Unit Commitment Based on Information Gap Decision Theory. Proc. CSEE 2018, 38, 3431–3440+3442. [Google Scholar] [CrossRef]
- Pan, Z.X.; Liu, S.M.; Wang, Z.J.; Wang, S.; Ding, C.R. Dispatch Based on Information Gap Decision Theory for Power System with Wind Power. Electr. Power Constr. 2018, 39, 87–94. [Google Scholar]
- Mazzi, N.; Kazempour, J.; Pinson, P. Price-taker offering strategy in electricity pay-as-bid markets. IEEE Trans. Power Syst. 2017, 33, 2175–2183. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, Z.Y.; Kang, Z.Q.; Xia, Q.; Dai, G.H. Strategic bidding with application of game theory. Power Syst. Autom. 2002, 26, 7–11. [Google Scholar]
- Li, T.; Shahidehpour, M. Strategic bidding of transmission-constrained GENCOs with incomplete information. IEEE Trans. Power Syst. 2005, 20, 437–447. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, S.H. Generation asset allocation strategies based on. Control Decis. 2017, 32, 751–754. [Google Scholar] [CrossRef]
- Tang, L.; Liu, J.C.; Yang, Y.F.; Zhou, L. Study on Strategies of Electricity Procurement and Sale of Power Retailer with Multiple Retail Contract Modes Based on Information Gap Decision Theory. Power Syst. Technol. 2019, 43, 1978–1988. [Google Scholar]
- El Rahi, G.; Etesami, S.R.; Saad, W.; Mandayam, N.B.; Poor, H.V. Managing price uncertainty in prosumer-centric energy trading: A prospect-theoretic Stackelberg game approach. IEEE Trans. Smart Grid 2017, 10, 702–713. [Google Scholar] [CrossRef]
- Etesami, S.R.; Saad, W.; Mandayam, N.B.; Poor, H.V. Stochastic games for the smart grid energy management with prospect prosumers. IEEE Trans. Automat. Contr. 2018, 63, 2327–2342. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, Y.; Xia, Q.; Sun, X.; Yang, M.H.; Zhang, J. A Full-scenario SCED With Coordinative Optimization of Hydro-thermal-wind Power. Proc. CSEE 2013, 33, 2–9. [Google Scholar]
- Ben-Haim, Y. Uncertainty, probability and information-gaps. Reliab. Eng. Syst. Saf. 2004, 85, 249–266. [Google Scholar] [CrossRef]
- Zhao, Y.X. The Scheduling Strategies of Concentrating Solar Power Plants Considering Multi-Uncertainties and Multi-Resources Coordination. Diploma Thesis, Zhejiang University, Hangzhou, China, 2020. [Google Scholar]
- Zhang, R.F.; Zhong, H.; Li, S.C.; Yao, S.K. Medium and Long Term Electric Power Decomposition Model of Wind-storage Combined System Based on Prospect Theory. Smart Power 2021, 49, 56–62. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. In Handbook of the Fundamentals of Financial Decision Making: Part I; World Scientific: Singapore, 2013; pp. 99–127. [Google Scholar]
- Yousri, D.; Abd Elaziz, M.; Oliva, D.; Abraham, A.; Alotaibi, M.A.; Hossain, M.A. Fractional-order comprehensive learning marine predators algorithm for global optimization and feature selection. Knowl. Based Syst. 2022, 235, 107603. [Google Scholar] [CrossRef]
- Yousri, D.; Ousama, A.; Fathy, A.; Babu, T.S.; Allam, D. Managing the exchange of energy between microgrid elements based on multi-objective enhanced marine predators algorithm. Alex. Eng. J. 2022, 61, 8487–8505. [Google Scholar] [CrossRef]
- Rashad, A.; Hassan, M.H.; Kamel, S.; Shahinzadeh, H. In Reconfiguration of Zafarana Stage-l Wind Farm Layout Based on Marine Predators Algorithm Considering Wake Effect. In Proceedings of the 2022 9th Iranian Conference on Renewable Energy & Distributed Generation (ICREDG), Mashhad, Iran, 23–24 February 2022; IEEE: Piscataway, NJ, USA; pp. 1–4. [Google Scholar]

| Maximum Output Power (MW) | Minimum Output Power (MW) | Efficiency (%) | Energy Loss Rate (%) | Climbing Speed (MW/h) | Gas Price (CNY/m3) |
|---|---|---|---|---|---|
| 1 | 0.2 | 80 | 10 | 0.5 | 3.24 |
| Equipment | Maximum Output Power (MW) | Minimum Output Power (MW) | Efficiency (%) | Climbing Speed (MW/h) | Operation and Maintenance Cost (CNY/MWh) |
|---|---|---|---|---|---|
| Wind power | 1 | 0 | - | 0.6 | 110 |
| PV | 2 | 0 | - | 1.5 | 80 |
| Energy storage | 0.2 | 0.04 | 95 | 0.2 | 20 |
| Electric chillers | 1 | 0 | 95 | - | 30 |
| Suction chiller | 1 | 0 | 70 | - | 30 |
| Gas fired boiler | 1 | 0 | 73 | - | 20 |
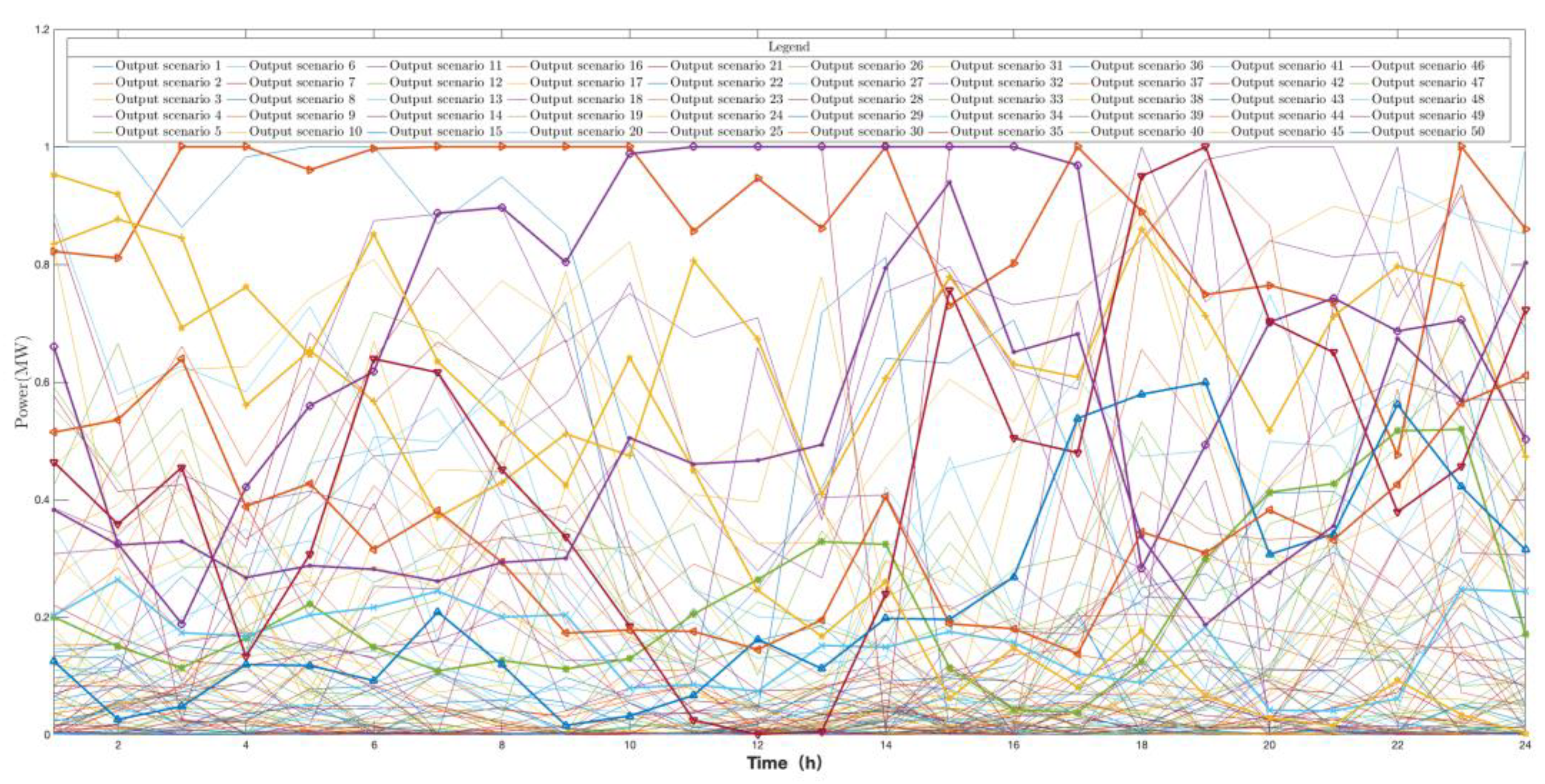
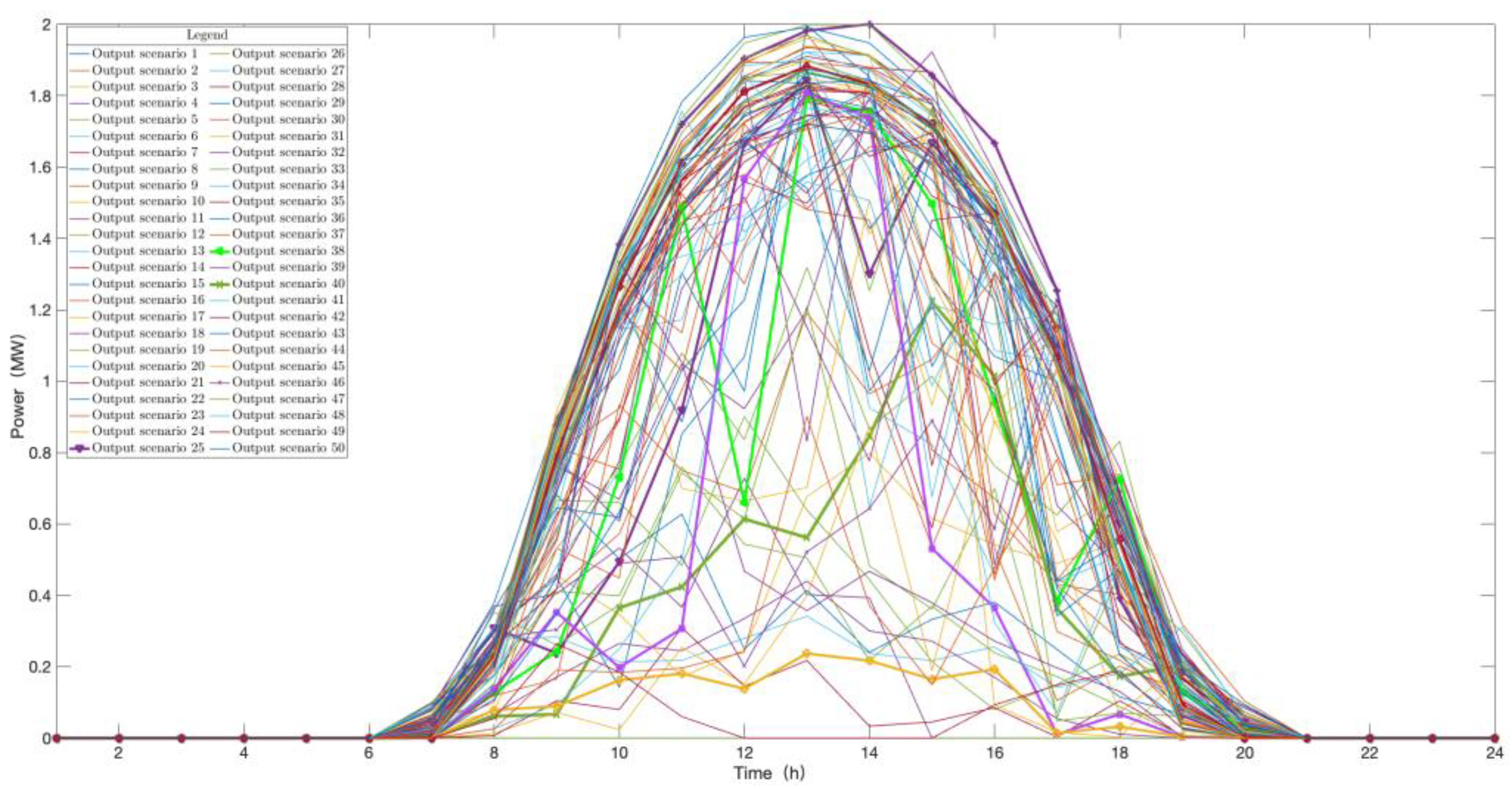
| Wind Power Scenarios | Probability | PV Power Scenarios | Probability |
|---|---|---|---|
| 1 | 0.0109 | 1 | 0.0543 |
| 2 | 0.0217 | 2 | 0.0326 |
| 3 | 0.0109 | 3 | 0.0217 |
| 4 | 0.1304 | 4 | 0.4239 |
| 5 | 0.4891 | 5 | 0.0761 |
| 6 | 0.0326 | 6 | 0.0761 |
| 7 | 0.0543 | 7 | 0.0870 |
| 8 | 0.1957 | 8 | 0.0543 |
| 9 | 0.0217 | 9 | 0.0978 |
| 10 | 0.0326 | 10 | 0.0761 |
| Number | Scenario Description |
|---|---|
| Scenario 1 | It is assumed that the actual clearing price of the day-ahead market and the actual output of wind power and PV in RDES are both predicted values: that is, the decision scenario without considering the effect of uncertainty factors. |
| Scenario 2 | Consider RDES’s robust risk appetite and opportunistic risk appetite for market price fluctuations. |
| Scenario 3 | Based on Scenario 2, consider the subjective behavioral impact of DERA’s perceived “gain” and “loss” decisions in the dual-track market environment. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Dou, X.; Liu, D.; Bao, A.; Wang, D.; Zhang, Y. Energy Trading Strategy of Distributed Energy Resources Aggregator in Day-Ahead Market Considering Risk Preference Behaviors. Energies 2023, 16, 1629. https://doi.org/10.3390/en16041629
Dong J, Dou X, Liu D, Bao A, Wang D, Zhang Y. Energy Trading Strategy of Distributed Energy Resources Aggregator in Day-Ahead Market Considering Risk Preference Behaviors. Energies. 2023; 16(4):1629. https://doi.org/10.3390/en16041629
Chicago/Turabian StyleDong, Jun, Xihao Dou, Dongran Liu, Aruhan Bao, Dongxue Wang, and Yunzhou Zhang. 2023. "Energy Trading Strategy of Distributed Energy Resources Aggregator in Day-Ahead Market Considering Risk Preference Behaviors" Energies 16, no. 4: 1629. https://doi.org/10.3390/en16041629
APA StyleDong, J., Dou, X., Liu, D., Bao, A., Wang, D., & Zhang, Y. (2023). Energy Trading Strategy of Distributed Energy Resources Aggregator in Day-Ahead Market Considering Risk Preference Behaviors. Energies, 16(4), 1629. https://doi.org/10.3390/en16041629







